
Non-optimal Semi-autonomous Agent Behavior Policy Recognition
Mathieu Lelerre and Abdel-Illah Mouaddib
Greyc, Universit
´
e de Caen Normandie, Esplanade de la Paix, 14032 Caen, France
Keywords:
Behavior, Recognition, MDP, Reinforcement Learning.
Abstract:
The coordination between cooperative autonomous agents is mainly based on knowing or estimating the be-
havior policy of each others. Most approaches assume that agents estimate the policies of the others by
considering the optimal ones. Unfortunately, this assumption is not valid when an external entity changes
the behavior of a semi-autonomous agent in a non-optimal way. We face such problems when an operator
is guiding or tele-operating a system where many factors can affect his behavior such as stress, hesitations,
preferences, etc. In such situations the recognition of the other agent policies becomes harder than usual since
considering all situations of hesitations or stress is not feasible.
In this paper, we propose an approach able to recognize and predict future actions and behavior of such agents
when they can follow any policy including non-optimal ones and different hesitations and preferences cases
by using online learning techniques. The main idea of our approach is based on estimating, initially, the policy
by the optimal one, then we update it according to the observed behavior to derive a new estimated policy.
In this paper, we present three learning methods of updating policies, show their stability and efficiency and
compare them with existing approaches.
1 INTRODUCTION
Recent developments on autonomous systems lead to
a more consideration on limited capacities of sens-
ing and acting in difficult environments to accom-
plish complex missions such as patrolling (Vorobey-
chik et al., 2012), security (Paruchuri et al., 2008) and
search and rescue (H
¨
uttenrauch and Severinson Ek-
lundh, 2006) applications. Introducing the human
in the control loop is a challenging and promising
research direction that attracts more and more re-
searchers because it can help autonomous systems to
perceive more information, to act more efficiently or
to guide is behavior (Shiomi et al., 2008). Adjustable
autonomous is the concept of considering different
levels of autonomy from full autonomy to full tele-
operation. A semi-autonomous agent is an agent fol-
lowing a policy where some human advice are con-
sidered. For example, an operator can send advice to
a robot to avoid an area, or not to use an action on a
specific state. When considering a system composed
of semi-autonomous agents, the coordination of semi-
autonomous agents becomes a challenging issue.
We are studying a multi-agent system, in which
the agents can have different levels of autonomy:
fully autonomous, semi-autonomous or tele-operated.
The autonomous agents should compute a coordi-
nated policy considering the tele-operated and semi-
autonomous agents. To this end, we consider the
Leader-Follower (Panagou and Kumar, 2014) model.
We focus, in this paper, on the situation where an au-
tonomous agent (follower) should coordinate its be-
havior to a semi-autonomous or tele-operated agent
(leader) where its policy is not known, but only ac-
tions and feedbacks from the environment are ob-
served. We propose to use these observations to ap-
proximate the policy of the leader to compute the
best-response policy of the follower using some exist-
ing algorithms such as Best-Response (Monderer and
Shapley, 1996) or JESP (Nair et al., 2003). However,
a semi-autonomous agent or a tele-operated agent do
not, always, follow an optimal policy. Indeed, the
operator may have preferences or hesitations which
might influence the agent’s policy, leading to a satis-
fying behavior rather than an optimal one. Trying to
model each hesitation, or each preference is impossi-
ble, due to the high number of cases. That is why we
consider an online model to learn the human behavior,
based on the action selected by the operator.
The aim of this paper is to propose a new ap-
proach, based on a combination of Markov Decision
Processes (Sigaud and Buffet, 2010) and Reinforce-
ment learning (Sutton and Barto, 1998), to predict an-
other agent’s action when assuming that the optimal
Lelerre, M. and Mouaddib, A-I.
Non-optimal Semi-autonomous Agent Behavior Policy Recognition.
DOI: 10.5220/0006054401930200
In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 1: ECTA, pages 193-200
ISBN: 978-989-758-201-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
193

one is not realistic. Indeed, we consider an approach
where the optimal policy is initially assumed and by
learning from previous actions, the initial policy is up-
dated. We present three update methods: (i) the first
method consists in learning from a complete history
of the couples state and the last executed action, for
all states; (ii) the second method consists in learning
from the last executed actions the preferences of the
human on the agent behavior considering a reward
function update in all the state space; (iii) the third
method is similar to the second method but focused
only on a local update where only the states in the
neighborhood of the current state, from which a devi-
ation is observed, are considered.
The paper is organized as follow, in the second
section we present the target applications, the third
one is dedicated to the background necessary for the
paper, the fourth section describes our approach, the
fifth one presents the experiments and the obtained
results and we finish the paper by a conclusion.
2 THE TARGET APPLICATIONS:
SECURITY MISSIONS
Surveillance of Sensitive Sites with Robots. We
consider a heterogeneous system composed of robots
and operators for a surveillance mission of a sensitive
site. The operators and robots can move from one
checkpoint to another as a team, but an operator can
send some advice to a robot to change its behavior and
considers some constraints such as watching or not a
specific area or it’s desirable that the robot secure a
hidden area (Abdel-Illah Mouaddib and Zilberstein,
2015), etc. The operator can also tele-operate a robot
to head a specific point to get more accurate informa-
tion with the onboard camera. The other robots fully
autonomous have to adapt their behaviors to the tele-
operated and the semi-autonomous ones while they
don’t know their policies if they didn’t get informa-
tion sent by the operators.
Maritime Coast Surveillance. In this example, we
consider with our partners to deploy a fleet of UAV
for watching the coasts where some UAV will re-
ceive from the control unit some advice about spe-
cific checkpoints while the other UAV should com-
pute a coordinated policy to sweep all the coast for
surveillance. Semi-autonomous UAVs compute their
policies by considering the advice of the control unit
while the autonomous UAV should adapt their behav-
ior according to the semi-autonomous ones.
3 BACKGROUND
Markov Decision Processes: is a decision model
for autonomous agent allowing us to derive an opti-
mal policy dedicating to the agent the optimal action
to perform at each state. More formally, an MDP is a
tuple hS,A, p,ri where S is the state space and A is the
action space. p is the transition function and r is the
reward function. The expected value V
∗
maximiza-
tion allows us to derive the optimal policy π
∗
using
the Bellman equation (Pashenkova et al., 1996):
V
∗
(s) = max
a∈A
∑
s
0
∈S
p(s
0
|s,a)(r(s
0
|s,a) +V
∗
(s
0
)) (1)
π
∗
(s) = argmax
a∈A
∑
s
0
∈S
p(s
0
|s,a)(r(s
0
|s,a) +V
∗
(s
0
)) (2)
There exists many algorithms to solve this equa-
tion where the most popular are value iteration and
policy iteration (Puterman, 1994). In our approach,
we consider an MDP-based model.
Reinforcement Learning: is a method allowing an
autonomous agent to adapt his behavior during the ex-
ecution by updating his model.
Agent Environnement
Action
Feedback
State
Figure 1: Representation of reinforcement learning.
The agent starts with an initial model to compute
the policy to be followed during the execution. The
execution of this initial policy leads to feed-backs
from the environment, particularly the reward ob-
tained after the execution. The obtained feed-backs
allow us to update the model and to compute a new
policy.
Many algorithms have been developed such as Q-
learning (Watkins and Dayan, 1992), temporal dif-
ference TD(λ) or SARSA (Sutton and Barto, 1998).
Our approach uses a reinforcement learning similar to
techniques with a reward function update procedure.
TAMER (Knox and Stone, 2008): is an algorithm
used to train an agent with deterministic actions. It
uses an MDP model without a reward function. An
operator will train the robot by sending a positive or a
negative signal H to the agent. This algorithm differs
with what we want to do, because the agent needs to
be trained before executing the algorithm. Moreover,
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
194

we are not trying to train an agent, but to learn his pol-
icy to adapt the observer behavior. We can, however,
adapt the model by sending a positive reward for each
state reached by the agent.
TAMER&RL(Knox and Stone, 2010)(Knox and
Stone, 2012) is the computation between TAMER and
a Reinforcement Learning method. It allows us to re-
duce the time of training.
Imitation Learning. Is a training method. The
agent first observes an operator to complete the mis-
sion, and learns the policy with this observation.
Many algorithms exist for imitation learning and pre-
sented in (He et al., 2012).
The idea of this algorithm is similar to our idea.
However, the agent tries to learn the Master (leader in
our case) policy to imitate him. In our approach we
learn the Leader policy not to imitate him but to com-
pute a best-response to better coordinate with him.
4 OUR APPROACH
The policy prediction is mainly based on series of pol-
icy estimation followed by a policy update. The ob-
served agents are semi-autonomous or tele-operated.
Consequently, the MDP model of the observed agent
is already defined, even in the tele-operation case.
First, we compute an optimal policy from their MDP
model as an approximate initial policy and then we
update it during the execution of this policy using the
reinforcement learning techniques. Indeed, we, ini-
tially, assume that the Leader (the semi-autonomous
agent) follows an optimal policy and when observ-
ing its behavior, we get information on the executed
action, the rewarded value and the state o = (a,r,s).
When the observation o shows that the executed ac-
tion a is different from the expected action π(s)), the
autonomous agent (follower) updates the predicted
policy π considering this deviation. The policy update
to predict a new policy is based on three methods.
During the execution of the mission, the agent
may choose different action from the estimated pol-
icy, due to the operators hesitations, preferences or
perception. These changes are stored in a history H.
Let H
s
(t) and H
a
(t) be respectively the history of the
state and the action of the last operations up to time
t. These histories represent the feed-backs of the en-
vironment during the last t operations which will be
considered for updating the initial policy π
init
. To this
end, we will present three update methods to generate
a new estimated policy π from π
init
and (H
s
(t), H
a
(t)).
The ”Force” Method. The idea behind this
method is to update the current estimated policy by
modifying some actions at some states using the his-
tory. Indeed, this method is a ”forcing” approach
where actions performed at some states in the last op-
erations are introduced in the current estimated pol-
icy when a deviation from the estimated policy is ob-
served. We assign, then, states in H
s
(t) with actions
in H
a
(t), and then we compute the optimal actions
for the other states not concerned with the changes to
generate a new estimated policy. More formally :
π
new
=
∀0 ≤ k ≤ t,s
k
∈ H
s
(t) and a
k
∈ H
a
(t) :
π
new
(s
k
) = a
k
∀s /∈ H
s
(t) : π
new
(s) =
argmax
a∈A
∑
s
0
∈S
p(s
0
|s,a)(r(s
0
|s,a) +V
∗
(s
0
))
The ”Learn” Method. Instead of the previous
method where we change actions at some states of
the current policy, this method is based on adapting
the reward function to consider the preferences of the
operator observed from the last previous operations.
To this end, we assume that the operator acts to reach
the desired and preferred states. More formally, we
will define X as the set of n variables composing the
states of the agent. Each of these variables x
i
∈ X are
defined in a domain D
i
. The idea is to assign a reward
to each variable which may interest the operator, and
apply a cost for each variable which could be unpleas-
ant to him. Then, by changing the reward function,
the policy might evolve consequently. Let x
i
(s) be the
value of the variable x
i
from the state s, and let Q
i
be
the preference function for the operator for the vari-
able x
i
. Q
i
(v) is the reward function to the variable x
i
when it takes the value v. Consequently, Q
i
(x
i
(s)) is
the reward attributed to the variable x
i
from the state
s. Initially, every variables Q
i
are set to 0, and c is
the constant value to add to the reward function. The
constant c might be chosen by considering the values
on the reward function. With a high value, each action
executed different from the estimated action will have
a high impact on the policy update.
Algorithm 1 allows us to assign, to each successor
state reachable from the deviation of the original pol-
icy, a reward according to the probability to reach it
from the deviation. In the same way, we assign a cost
for each state which should be reached by the current
policy. To generate the new policy, we then compute a
new reward function r
0
, with the equation 3. We then
generate a new policy with the MDP hS,A, p,r
0
i.
r
0
(s
0
|s,a) = r(s
0
|s,a) +
∑
x
i
∈X
Q
i
(x
i
(s
0
)) (3)
Non-optimal Semi-autonomous Agent Behavior Policy Recognition
195

Algorithm 1: Reward update.
1 for t ∈ [0..k] do
2 if H
a
(t) 6= π(H
s
(t)) then
3 for s
0
successor of (H
s
(t),H
a
(t)) do
4 for i ∈ [0..n] do
5 Q
i
(x
i
(s
0
)) = Q
i
(x
i
(s
0
)) +
p(s
0
|H
s
(t),H
a
(t)) × c;
6 for s
0
successor of (H
s
(t),π(H
s
(t)) do
7 for i ∈ [0..n] do
8 Q
i
(x
i
(s
0
)) = Q
i
(x
i
(s
0
)) −
p(s
0
|H
s
(t),π(H
s
(t)) × c;
Generalization: Consider a factored representation of
states with n variables such that s = (v
1
,...,v
n
), as
depicted in Fig.2. The expected action at s is π(s)
leading to s
0
= (v
0
1
,v
0
2
,...,v
0
n−1
,v
0
n
) while the semi-
autonomous agent executes action a(s) leading to
s
00
= (v
00
1
,v
0
2
,...,v
0
n−1
,v
00
n
). Let’s consider that s
00
dif-
fers from s
0
at the first and the last variables. v
0
1
6= v
00
1
and v
0
n
6= v
00
n
while the other variables are identical.
s = hv
1
, v
2
, . . . , v
n
i
s
′
= hv
′
1
, v
′
2
, . . . , v
′
n
i s
′′
= hv
′′
1
, v
′
2
, . . . , v
′′
n
i
π(s) a(s)
Figure 2: Representation of a derivation.
Learn method will increase the reward of all states
s = (v
00
1
,∗, . . . , ∗, ∗) and s = (∗,∗,...,∗,v
00
n
) represent-
ing the preferred states of the operator and will re-
duce the reward of states s = (v
0
1
,∗,...,∗,∗) and s =
(∗,∗,...,∗,v
0
n
) representing unpleasant states by as-
suming that the operator prefers a(s) to π(s) to reach
preferred states with features v
00
1
and v
00
n
rather than the
ones with features v
0
1
and v
0
n
.
Reward increase
r
0
(s = hv
00
1
,∗,...,∗i) = r
0
(s) + Q
1
(v
00
1
)
...
r
0
(s = h∗, ∗, . . . , v
00
n
i) = r
0
(s) + Q
n
(v
00
n
)
Reward decrease
r
0
(s = hv
0
1
,∗,...,∗i) = r
0
(s) + Q
1
(v
0
1
)
...
r
0
(s = h∗, ∗, . . . , v
0
n
i) = r
0
(s) + Q
n
(v
0
n
)
This algorithm estimates the operator preferences
according to the concerned states. Meanwhile, when
a deviation occurs, the reward update is propagated
into the all state space and will affect the behavior
policy of the semi-autonomous agent. This latter may
overreact to derivations leading to the generation of
more prediction errors than corrections, and then may
create an unstable prediction process.
The ”Dist” Method. This method is similar to the
”Learn” Method by reducing the impact of the local
updates. To this end, we should restrict the propa-
gation to some states which are close to the updated
state. To assess the closeness, we define the distance
between two states in an MDP as the number of vari-
ables different from each other. Each state reach-
able by the predicted action will receive a cost and
reversely. however, each state reachable by the pre-
dicted action will get a reward corresponding to the
value of the parameters with reward for the observed
action, in the condition that the distance between this
state and another reachable by the observed action is
less or equals to a threshold δ.
Generalization: We consider, at time t, that the oper-
ator derives from the predicted policy.
s
1
= hv
1
, v
2
, . . . , v
n
i
s
2
= hv
′
1
, v
′
2
, . . . , v
n
i s
3
= hv
′
1
, v
′
2
, . . . , v
′
n
i
h1, 0, . . . , 1i
π(s) a(s)
Figure 3: Calculation of a distance.
The distance between s
0
and s
00
is 2 because
(v
0
1
,v
0
2
,...,v
0
n
) differs from (v
00
1
,v
0
2
,...,v
00
n
) on vari-
ables v
1
and v
n
. For example, if δ = 1, considering s
o
as a state reachable by the observed action and s
p
as a
state reachable by the predicted action, we will obtain
the following modifications on the reward function:
r
0
(s
00
) = r(s
00
) +
∑
n
i=1
Q
i
(v
00
i
)
r
0
(s
0
) = r(s
0
) +
∑
n
i=1
Q
i
(v
0
i
)
r
0
(s
o
= hv
0
1
,v
0
2
,...,v
00
n
i) = r(s
o
) + Q
n
(v
00
n
)
...
r
0
(s
o
= hv
00
1
,v
0
2
,...,v
0
n
i) = r(s
o
) + Q
1
(v
00
1
)
r
0
(s
p
= hv
00
1
,v
00
2
,...,v
0
n
i) = r(s
p
) + Q
n
(v
0
n
)
...
r
0
(s
p
= hv
0
1
,v
0
2
,...,v
00
n
i) = r(s
p
) + Q
1
(v
0
1
)
The first two equations are about decreasing the
reward for the states reachable by the estimated action
and increasing the reward for the ones reachable by
the executed action. The next two equations represent
the increase of states closed to the ones reachable by
the executed actions, oppositely to the last two ones.
5 EXPERIMENTS
We develop experiments to show the efficiency and
the impact of the operator hesitation on the prediction
to show the robustness of the methods to the operator
mistakes. We also develop experiments on the im-
pact of delta in the Dist method to assess their perfor-
mances. We consider two kinds of environments of
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
196

the site surveillance, an indoor environments where
the robots evolve in a restricted space and an outdoor
environment where the space is open and there is a
limited impact of locality. We consider that in these
environments the areas have three levels of lighting
from very bright to dark leading the agent to select
the right actions (using the right sensor) to better be-
have. An optimal policy allows the agent to use the
best action at a state according to the lighting level
and when the agent uses an action different from the
optimal one, it gets a cost. The mission of the agent is
to start at a location and targets a new one for surveil-
lance. We formalize the tele-operation process of the
agent by an MDP. To simulate the operator prefer-
ences, we will force the MDP policy to choose one
action on specific states (to force the agent to follow
or to avoid a path) before generating the optimal pol-
icy. To formalize the hesitation, we define probabilis-
tic policies, in which the operator selects probabilisti-
cally some actions at some states. During the execu-
tion, we used the learning methods described above
to predict the behavior of the semi-autonomous agent,
and compare the prediction results. To evaluate their
efficiency, we consider the number of prediction er-
rors made by each prediction method.
We also compare these methods with an adapted
TAMER&RL (TAMER combined with SARSA(λ)),
on which the learning algorithm will receive a re-
ward for each action dictated by the operator to the
semi-autonomous agent. TAMER&RL was config-
ured with the Table 1. ”Learn” and ”Dist” methods
are configured with the following parameters c = 3
and k = 10.
Table 1: Configuration of TAMER&RL.
Parameter value
TAMER
α 0.2
SARSA-LAMBDA:
α 0.8
ε 0
γ 1
λ 1
β 0.98
5.1 Results in Indoor Environments
During the experiments, we recorded the number of
prediction errors during the 50 executions of the mis-
sions. In this experiment, we compare the algorithms
in different situations: deterministic and stochastic
actions, operator doesn’t hesitate representing an ex-
pert and self-control operator, operator hesitates fre-
quently representing a non-expert operator and oper-
ator hesitates sometimes representing an expert oper-
0 5 10 15 20 25 30 35 40 45 49
0
1
2
3
4
5
6
7
8
9
Autonomous
FORCE
LEARN
Dist-0
Dist-1
Dist-2
TAMER&RL
Execution Number
Number of prediction errors
Figure 4: Results with no hesitation.
ator, but can make some mistakes in some stressed
situations.
Without Hesitation: Expert and Self-control Op-
erator. Fig.4 represents the number of prediction
errors according to the number of the mission execu-
tion. The autonomous curve corresponds to the opti-
mal policy of an autonomous agent, without learning
during the execution. This algorithm is used here to
show the impact of learning. Note that ”Dist-i” corre-
sponds to the ”Dist” method, with δ=i.
We can see that almost all curves converge to 0,
which means that almost all algorithms learn correctly
the agent policy. The only exception is TAMER&RL,
which keeps one prediction error over the time. How-
ever, it’s under the autonomous curve. TAMER&RL
starts with a high number of prediction error because
the algorithm starts the learning from scratch without
considering the past mission executions. ”Force” and
”Learn” curves are similar in this case, and they con-
verge quickly. However, we can see that ”Dist” meth-
ods are not stable, in the beginning, but they converge
and find the agent policy after some periods of time.
To conclude, our methods outperform TAMER&RL
and converge more quickly.
0 5 10 15 20 25 30 35 40 45 49
0
2
4
6
8
10
12
14
Autonomous
FORCE
LEARN
Dist-0
Dist-1
Dist-2
TAMER&RL
Execution Number
Number of prediction errors
Figure 5: Results with 30% hesitation on some states.
Non-optimal Semi-autonomous Agent Behavior Policy Recognition
197
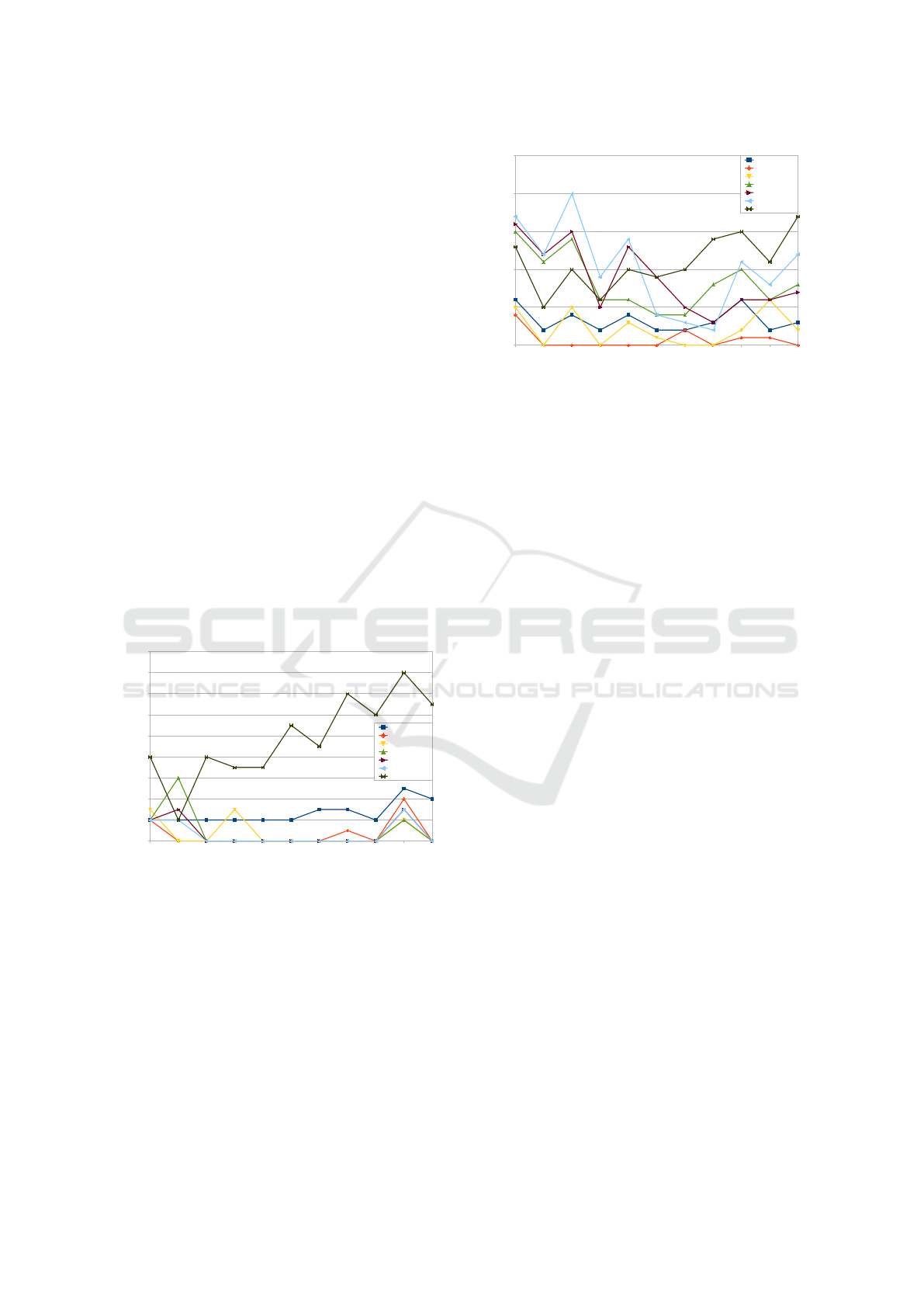
With 30% Hesitation: Non-expert Operator. We
can see in Fig.5 that the prediction methods are
more unstable during the whole execution, except
for the ”Learn”, ”Force” and TAMER&RL methods.
”Learn” and ”Force” curves are similar and converge,
but they still get few errors in some cases. How-
ever, these algorithms learn globally the agent policy.
”Dist” methods are more unstable than before, and get
a lot of prediction errors at the beginning. The only
one who seems to be stable is for δ = 0. The others
seem to be close to the agent policy, but each variation
on the agent policy generates many perturbations on
the prediction. The ”Learn” method does not present
a high number of mistakes, but he is much perturbed
by hesitations than the ”Force” or the TAMER&RL
methods. The ”Force” method gets an error every
time the agent changes the action of the policy at a
state. Otherwise he is the most efficient.
Impact of Stochastic Transitions. For the experi-
ments, we first used deterministic actions to compare
the results with TAMER&RL, because this method
needs deterministic transitions. We repeated the ex-
periments to see the impact of stochastic transitions,
to analyze the robustness of the different algorithms.
To do so, we adapted the TAMER&RL policy by con-
sidering the stochastic transition function.
0 5 10 15 20 25 30 35 40 45 49
0
2
4
6
8
10
12
14
16
18
Autonomous
FORCE
LEARN
Dist-0
Dist-1
Dist-2
TAMER&RL
Execution Number
Number of prediction errors
Figure 6: Results without hesitation, but with stochastic ac-
tions.
We can see in Fig.6 that TAMER&RL does not
present the same results with stochastic transitions.
Indeed, TAMER&RL seems inappropriate for learn-
ing if transitions are not deterministic. All our
approaches outperform TAMER&RL. On the other
hand, without hesitation, ”Dist” methods seems to be
more efficient with stochastic transitions than deter-
ministic ones. The reason may be that each transition
leads to several states, so the Dist methods learn on
more states, but still locally.
0 5 10 15 20 25 30 35 40 45 49
0
5
10
15
20
25
Autonomous
FORCE
LEARN
Dist-0
Dist-1
Dist-2
TAMER&RL
Execution Number
Number of prediction errors
Figure 7: Results with 30% hesitation, but with stochastic
actions.
On Fig.7, we can see that with a high rate of hes-
itations, every method get unstable. This is not sur-
prising because it implies a lot of execution changes.
For each time a new state is reached, each time the
pilot policy can derive from the autonomous policy.
It implies a lot of policy modifications to learn. The
”Force” and the ”Learn” methods seem predict well.
However, ”Dist” methods and TAMER&RL are to-
tally unstable and does not predict well. ”Dist” meth-
ods seem to learn after the 20th execution. This is
due to the fact that a lot of new states were reached
between the 35th and the 40th, since every method
started to get prediction errors at this moment.
Nevertheless the hesitation is implemented by
choosing between two actions randomly. Moreover,
the agent policy is generated with transition functions
adapted with hesitation, but an operator would not
know when he will have doubts, and doesn’t know his
probability to choose an action at this moment. Fur-
thermore, the hesitations rate may decease over the
time since the operator learns also from his previous
experiments of the mission.
5.2 Results in Outdoor Environment
We developed a new serie of experiments in outdoor
environment where the branching factor in the state
space is high.
With 0% Hesitation: Expert and Self-control Op-
erator. We can see in Fig.8 that the ”Force” method
is still better than the others including TAMER&RL.
”Learn” method is not as efficient as in restricted
space, and is less efficient than the autonomous pol-
icy. The reason is that in such environments the
branching factor is high and the number of states
reachable from the current one is high. Then, updat-
ing the operator preferences in all the state space may
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
198

0 5 10 15 20 25 30 35 40 45 49
0
2
4
6
8
10
12
14
16
18
Autonomous
FORCE
LEARN
Dist-0
Dist-1
Dist-2
TAMER&RL
Execution Number
Number of prediction errors
Figure 8: Results with 0% hesitation on an open space, with
deterministic actions.
0 5 10 15 20 25 30 35 40 45 49
0
2
4
6
8
10
12
14
16
18
20
Autonomous
FORCE
LEARN
Dist-0
Dist-1
Dist-2
TAMER&RL
Execution Number
Number of prediction errors
Figure 9: Results with 30% hesitation in an open determin-
istic space.
impact all the policy, while in indoor environments
the state space is restricted. By limiting the learning
field, ”Dist” method avoids this effect and learns the
agent policy, except with a δ=0.
With 30% Hesitation: Non-expert Operator.
With hesitation, on Fig.9, almost no method, excepted
TAMER&RL and ”Force” method, can predict cor-
rectly the agent policy. ”Dist” methods show best re-
sults than ”Learn”, but they are still less efficient than
the autonomous policy. Indeed, when the operator is
not stable is difficult to learn from this behavior the
operator preferences while maintaining a policy with
local update is better because it’s still not far from the
optimal policy which in such cases are suitable.
Impact of Stochastic Transitions. With stochastic
transitions on Fig.10, as expected, TAMER&RL can-
not predict anything, and Force method remain effi-
cient. The other policy predictions are unstable, and
less efficient than the optimal policy, excepted Dist-0.
0 5 10 15 20 25 30 35 40 45 49
0
5
10
15
20
25
30
Autonomous
FORCE
LEARN
Dist-0
Dist-1
Dist-2
TAMER&RL
Execution Number
Number of prediction errors
Figure 10: Results without hesitation in an open space with
stochastic transitions.
5.3 Synthesis
The table 2 shows the efficiency of each method in
different cases. ++ means that the method learns
quickly the policy. + Means that the algorithm learns
the policy, but the convergence is slow, and − means
that the algorithm is not efficient. However, ”Force”
is efficient in any situation. ”Learn” is efficient only
with restricted environments, such as indoor ones.
TAMER&RL is efficient on deterministic transitions,
but there exist a more efficient alternative in any sit-
uation. ”Dist” method is much efficient without hes-
itations. Also, in indoor environments, it works bet-
ter with stochastic transitions. However, in outdoor
environments, the algorithm is efficient only when in
deterministic transition cases.
6 CONCLUSION
We addressed in this paper the problem of estimating
the policy of a semi-autonomous agent where this lat-
ter could follow a policy other than the optimal one.
To this end, we develop an approach based on ini-
tializing the policy to the optimal one and then up-
date this policy according to the observed behavior
and the operator actions. We propose three update
methods to predict the next behavior of the system by
estimating the new policy. These methods are based
on the history of the last operations to change the cur-
rent policy or to update the reward function. We dis-
tinguished between a method propagating the reward
update in the whole state space and a method restrict-
ing the propagation to subspace by defining a notion
of distance among states.
The experiments show satisfying and promising
results and showing a robustness to the operator mis-
takes in indoor environments, except for the ”Dist”
Non-optimal Semi-autonomous Agent Behavior Policy Recognition
199
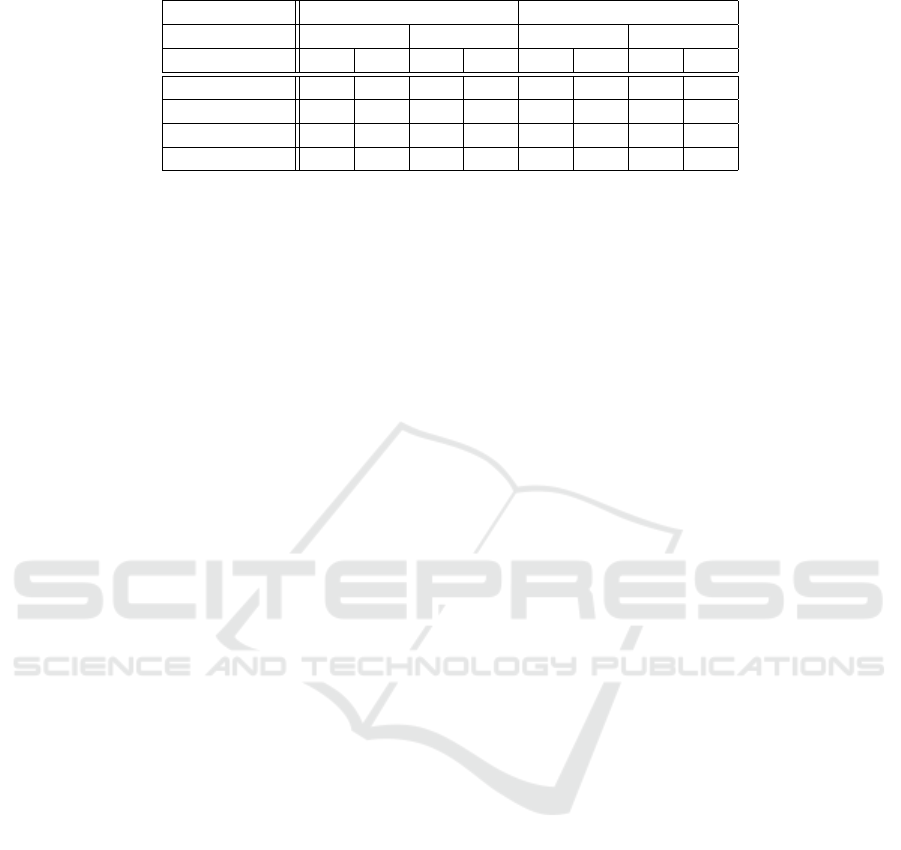
Table 2: Efficiency of prediction methods, considering the situation.
environment Indoor Outdoor
transitions Det. Stoc. Det. Stoc.
hesitation no yes no yes no yes no yes
Force ++ ++ ++ ++ ++ ++ ++ ++
Learn ++ ++ ++ + − − − −
Dist + + ++ − ++ − − −
TAMER&RL + + − − + + − −
method who learns mistakes and take a lot of time
before learning. TAMER&RL is much stable with
deterministic actions than ”Force” and ”Learn” meth-
ods, but less efficient. In stochastic transition cases,
TAMER&RL is outperformed by every other method.
In outdoor environment, ”Dist” method seems to be
much adapted, contrary to ”Learn” method.
In short-term, we will integrate our methods in a
multi-robot system, developed in a national project,
on the sensitive site surveillance example where a
robot is tele-operated by a professional operator and
the other should predict its policy and compute a co-
ordinated policy to head the same destination.
ACKNOWLEDGEMENT
We would like to thank the DGA (General Direction
of Arming), Dassault-Aviation and Nexter Robotics
for their financial participation for these results.
REFERENCES
Abdel-Illah Mouaddib, L. J. and Zilberstein, S. (2015).
Handling advice in mdps for semi-autonomous sys-
tems. In ICAPS Woskhop on Planning and Robotics
(PlanRob), pages 153–160.
He, H., Eisner, J., and Daume, H. (2012). Imitation learning
by coaching. In Pereira, F., Burges, C., Bottou, L., and
Weinberger, K., editors, Advances in Neural Informa-
tion Processing Systems 25, pages 3149–3157. Curran
Associates, Inc.
H
¨
uttenrauch, H. and Severinson Eklundh, K. (2006). Be-
yond usability evaluation: Analysis of human-robot
interaction at a major robotics competition. Interac-
tion Studies, 7(3):455–477.
Knox, W. and Stone, P. (2008). Tamer: Training an agent
manually via evaluative reinforcement. In Develop-
ment and Learning, 2008. ICDL 2008. 7th IEEE In-
ternational Conference on, pages 292–297.
Knox, W. B. and Stone, P. (2010). Combining manual
feedback with subsequent MDP reward signals for re-
inforcement learning. In Proc. of 9th Int. Conf. on
Autonomous Agents and Multiagent Systems (AAMAS
2010).
Knox, W. B. and Stone, P. (2012). Reinforcement learning
with human and mdp reward. In Proceedings of the
11th International Conference on Autonomous Agents
and Multiagent Systems (AAMAS 2012).
Monderer, D. and Shapley, L. S. (1996). Potential games.
Games and economic behavior, 14(1):124–143.
Nair, R., Tambe, M., Yokoo, M., Pynadath, D. V., and
Marsella, S. (2003). Taming decentralized pomdps:
Towards efficient policy computation for multiagent
settings. In IJCAI-03, Proceedings of the Eighteenth
International Joint Conference on Artificial Intelli-
gence, Acapulco, Mexico, August 9-15, 2003, pages
705–711.
Panagou, D. and Kumar, V. (2014). Cooperative Visibility
Maintenance for Leader-Follower Formations in Ob-
stacle Environments. Robotics, IEEE Transactions on,
30(4):831–844.
Paruchuri, P., Pearce, J. P., Marecki, J., Tambe, M., Or-
donez, F., and Kraus, S. (2008). Playing games
for security: An efficient exact algorithm for solving
bayesian stackelberg games. In Proceedings of the 7th
International Joint Conference on Autonomous Agents
and Multiagent Systems - Volume 2, AAMAS ’08,
pages 895–902, Richland, SC. International Founda-
tion for Autonomous Agents and Multiagent Systems.
Pashenkova, E., Rish, I., and Dechter, R. (1996). Value it-
eration and policy iteration algorithms for markov de-
cision problem. In AAAI’96: Workshop on Structural
Issues in Planning and Temporal Reasoning. Citeseer.
Puterman, M. L. (1994). Markov Decision Processes: Dis-
crete Stochastic Dynamic Programming. John Wiley
& Sons, Inc., New York, NY, USA, 1st edition.
Shiomi, M., Sakamoto, D., Kanda, T., Ishi, C. T., Ishiguro,
H., and Hagita, N. (2008). A semi-autonomous com-
munication robot: a field trial at a train station. In
Proceedings of the 3rd ACM/IEEE International Con-
ference on Human Robot Interaction, pages 303–310,
New York, NY, USA. ACM.
Sigaud, O. and Buffet, O. (2010). Markov Decision Pro-
cesses in Artificial Intelligence. Wiley-ISTE.
Sutton, R. S. and Barto, A. G. (1998). Introduction to Re-
inforcement Learning. MIT Press, Cambridge, MA,
USA.
Vorobeychik, Y., An, B., and Tambe, M. (2012). Adver-
sarial patrolling games. In Proceedings of the 11th
International Conference on Autonomous Agents and
Multiagent Systems - Volume 3, AAMAS ’12, pages
1307–1308, Richland, SC. International Foundation
for Autonomous Agents and Multiagent Systems.
Watkins, C. and Dayan, P. (1992). Q-learning. Machine
Learning, 8(3-4):279–292.
ECTA 2016 - 8th International Conference on Evolutionary Computation Theory and Applications
200
