Differential GNSS for Outdoor Sports -

Testing of Applicability for Alpine Sports

Johan Samuelsson

, Magnus Karlsteen

and Christian Finnsgård

1,2

Centre for Sports and Technology, Dept. of Physics, Chalmers University of Technology, Gothenburg, Sweden

SSPA Sweden AB, Research, Gothenburg, Sweden

Keywords: GNSS, Positioning, Tracking, Alpine Sports, GPS, Wearable Technology.

Abstract: The purpose of this paper is to evaluate a differential GNSS (global navigation satellite system) tracking

technology and whether it can be applied in alpine sports. Wearable technology is a technology undergoing

extensive development. Wearable technology is an umbrella term for technology that can be worn,

providing the user with different kinds of information. In sports, this is often related to performance of

athletes. This paper is evaluating a tracking technology and whether it can be applied in an alpine

environment, tracking both cross country skiers as well as down hill skiers. The technology applied in the

product is a DGNSS, a differential Global Navigation Satellite System, a high accuracy positioning

technology. The GNSS is using several satellite systems, providing coverage at all times. The differential

part comes from the use of an accurately surveyed reference station, providing the rover with correction

signals and thereby give a higher accuracy on tracking data. The technology shows promising results in

accuracy in the measurement method used, but needs further evaluation using continuous measurements.

1 INTRODUCTION

GNSS stands for global navigation satellite system

that allows the user to measure position, velocity and

local time in a highly accurate way. The global

navigation satellite system’s signal consists of a

variety of satellite systems in space that broad- cast

navigation signals. The navigation signals can in its

turn be picked up by a GNSS receiver on the earth to

determine that receiver’s position and velocity.

GNSS is useful in navigational applications and

provides fairly accurate position (2.5 metres) and

velocity (0.03 metres/second). A GNSS receiver

must have a clear signal from at least 4 satellites to

function. GNSS satellite signals are weak and

struggle to penetrate through buildings and other

objects obstructing view of the sky. GNSS can also

occasionally drop out due to disturbances in the

upper atmosphere. The GNSS used in this test is a

differential GNSS (or DGNSS). The differential

GNSS is using a reference station with an accurately

calibrated position. The reference station is installed

temporarily on a known position, and calculates

correction parameters and sending them to the

mobile GNSS rover. This technology results in a

reduction of the deviation of the measured position

to the actual position of the GNSS user receivers

(Granby, 2016).

The technology can be applied to several areas

outside of sports. The areas of applications include

for instance such as surveying, flying unmanned

aerial vehicles, robotics, marine applications, and

motor sports.

1.1 Problem

A television production company has expressed a

wish for more information and data on the athlete’s

performance, to complement their sports event

productions. This is to provide the end user with

additional value information and providing the

television companies with services that are giving

the production company an advantage over other

production companies. The linking of positioning

data and live video-feed is considered as extra

difficult to achieve. An increase in the precision in

the positioning will provide additional features

possible to combine with the viewer experience, and

is thus desirable.

GNSS positioning technology can be applied to

gather information on the athlete’s position, velocity

188

Samuelsson, J., Karlsteen, M. and Finnsgård, C.

Differential GNSS for Outdoor Sports - Testing of Applicability for Alpine Sports.

DOI: 10.5220/0006055701880196

In Proceedings of the 4th International Congress on Sport Sciences Research and Technology Support (icSPORTS 2016), pages 188-196

ISBN: 978-989-758-205-9

and acceleration in both team sports and individual

sports. In an application in an alpine skiing

environment, demands are put on the positioning

technology’s performance in accuracy. It should also

allow large capturing volumes of data in order to be

able to analyse the run. The positioning device

should not restrict in motion or cause discomfort for

the tracked athlete in motion, putting demands on

the size of the device.

The problem to be solved is to track and position

athletes in different contexts, providing athletes,

coaches, and spectators with data. The data can be

used by athletes and coaches to understand what

improvements that can be made or as an escort for

visually impaired athletes. The data can also be used

to create a surplus value in sporting events for the

spectators. The extra information that can be elicited

can be used both for live spectators and for

television broadcasting of sports. Extra data that can

be provided to the audience is the trajectory of the

slope, exact positions during the race, choice of line,

velocity and acceleration (

Spörri et al., 2014).

An evaluating and testing of the product is

desirable (for different sports and accuracy) to what

needs to be improved and if the technology will be

meeting the requirements put on it.

1.2 Present DGNSS Research

In alpine skiing, testing and research carried out are

using the differential GNSS for time measurements

and force measurements. The differential GNSS that

often are used in these contexts are often expensive

and well calibrated and not built for applications

where athletes are carrying it with them. In the

research where differential GNSS are used, it is for

proving the technology and accuracy of other

positioning devices.

In research where athletes actually have carried

the differential GNSS, the research performed have

shown promising results in using the differential

GNSS for time measurements in both alpine skiing

as well as 100 m sprints. In the 100 m sprint a

regular GNSS was tested and the results in the time

measurements were compared to the data from a

photocell. The study proves that regular GNSS can

be used for time measurements of smaller segments

of a slope. The technology could also be used for

deciding on location comparisons between the

athletes. The researchers also finds data that can be

used for professional athletes and their coaches to

analyse training and competition performance.

(Advanced Navigation, 2015).

Similar tests have been made using a differential

GNSS to measure the trajectories of slopes and

make time measurements with a regular GNSS to

compare to the time measurements of photocells.

Also in this study, tests proved that the data

provided by the GNSS gives an applicable time

measurement method and will provide better

opportunities for analysing the ride than from just

the use of photocells for measurements (Murray,

2014).

Low cost GNSS using lower sampling

frequencies have shown not to be appropriate for

tracking and time measuring. This goes for devices

using a sampling rate of 1 Hz or lower. The reason

for this is the distance travelled changes too much

during the sampling time (Mercator, 2016).

The differential GNSS is also often used as a

reference value when testing other positioning

devices in surveying. The differential GNSS used in

these cases are using real time kinematics (RTK)

that provides high accuracies close to a base station.

Real time kinematics uses a reference station and an

open channel for broadcasts information in real time.

With this information, the rover equipment is able to

fix the phase ambiguities and determine its location

relative to the base with high precision (Advanced

Navigation, 2016).

What can be said overall by the current research

is that not many providers on the market are testing

and using differential GNSS for measurements. The

technology is still under development and is

considered expensive and ungainly to wear in sports

and is not yet considered wearable technology.

1.3 Purpose of the Paper

From the above background and described problems,

the purpose of this paper is to evaluate a differential

GNSS tracking technology and whether it can be

applied in alpine sports.

1.4 Outline of the Paper

The paper describes an evaluation a differential

GNSS tracking technology and whether it can be

applied in alpine sports. The paper is divided as

follows: Section 1 introduces the problem

background, current research and the purpose of the

paper. Section 2 provides the theoretical framework.

Section 3 describes the method used in the study,

followed by Section 4, addressing the results.

Section 5 progresses into the discussion of the

results. Finally, Section 6 will summarise the

contributions made in the paper.

Differential GNSS for Outdoor Sports - Testing of Applicability for Alpine Sports

189

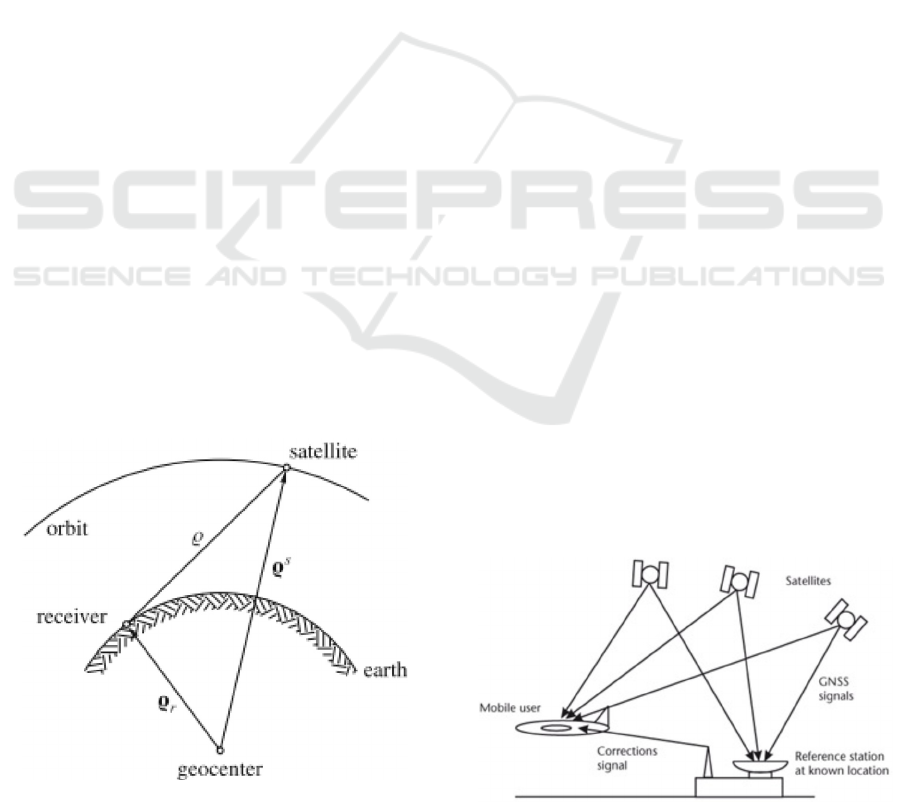
2 THEORETICAL FRAMEWORK

Satellite based positioning is the determination of

positions of observing sites. Satellites provide the

user with the capability of determining a position

expressed by for instance latitude, longitude and

height.

Latitude and longitude can be described as the angle

between where the object is positioned and the

reference axis. For latitude, the reference axis is the

equator. For longitude, the reference meridian is the

international prime meridian. This way, every

location on earth can be specified by a set of

numbers. Latitude is specified as the lateral positions

on a spherical shape, and the longitude as the

vertical positions on a spherical shape. The latitude

and longitude is measured in degrees or radians. The

altitude that needs to be used when specifying

positions is measured in meters over the reference

ellipsoid WGS84, a model used for approximating

sea level across the Earth (Hofmann-Wellenhof et

al., 2008).

The process for positioning something with

latitude, longitude and elevation is done by a

resection process, where range differences measured

to satellites are used, see figure 1. To relate this to

what is happening, the vector Q

relates to the center

of the earth (geocenter) of each satellite. The

geocentric position of the receiver on the ground is

defined by the vector Q

and is set to system time.

The geometric distance Q to each satellite could be

measured from recording the time required for the

satellite signal to reach the receiver. Using this

technique would yield in the unknowns, latitude,

longitude, and elevation, that could be determined

from the three range equations Q = ||Q

− Q

||.

(Hofmann-Wellenhof et al., 2008).

Figure 1: Principle of satellite based positioning

(Hofmann-Wellenhof et al., 2008).

2.1 Global Navigation Satellite Systems

The most oldest and most common GNSS system is

the American Global Positioning System (GPS).

Other GNSS systems are the Russian system

GLONASS, the European Union system Galileo,

and the Chinese system Beidou. GNSS satellites

orbit the earth at about 20,000 km altitude. Each

GNSS system has their own constellation of

satellites, providing the system with desired

coverage.

GNSS stands for global navigation satellite

system and consists of a number of satellites in

space that broadcast navigation signals. The

navigation signals can in its turn be picked up by a

GNSS receiver on earth to determine that receiver’s

position and velocity. GNSS is useful in

navigational applications and provides fairly

accurate position (2.5 metres) and velocity (0.03

metres/second). A GNSS receiver must have a clear

signal from at least 4 satellites to function. GNSS

satellite signals are weak and struggle to penetrate

through buildings and other objects obstructing view

of the sky. GNSS can also occasionally drop out due

to disturbances in the upper atmosphere.

2.2 Differential GNSS

The GNSS used in this test is a differential global

navigation satellite system (DGNSS). Differential

GNSS is an enhancement to a primary GNSS, using

a reference station with a accurately surveyed

position. The method takes advantage of the slow

variation with time and user position of the errors

due to ephemeris prediction, residual satellite clocks,

ionospheric and tropospheric delays. Starting from

the reference station the system broadcasts

corrections to the GNSS rover, see figure 2. The

rover needs to be enabled for receiving correction

signals and be connected to the same satellite as the

reference station in order to function (GMV, 2011,

Hofmann-Wellenhof et al., 2008).

Figure 2: System overview of a differential GNSS.

icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support

190

This technology results in a reduction of the

deviation of the measured position to the actual

position of the GNSS user receivers. The reference

station has the technical possibility to position itself

using different satellite systems, which leads to a

more accurate position. Variations of the technology

exist, where multiple reference stations are used,

leading to a higher accuracy for the rover. This

technology can be applied in order to cover a larger

area, using reference stations strategically placed in

order to have coverage on the correction signals.

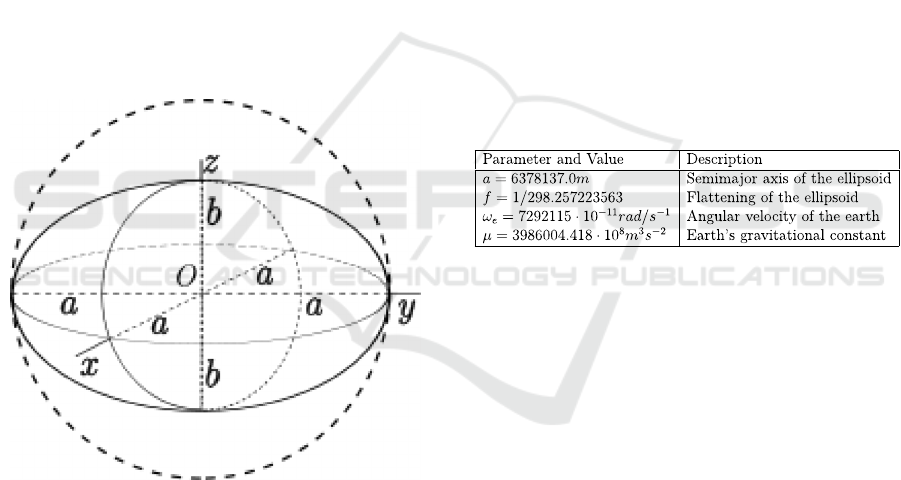
2.3 Data Processing

When processing the data coming from the units, the

error and standard deviation needs to be expressed in

an easy comparable unit. The unit of choice was

meters, to get a physical translation that is relatable.

This yields for transformations of the data.

According to Advanced Navigation, their procedure

was to do the transformation to Earth Centered Earth

Fixed (ECEF) (Orr, 2016).

Figure 3: A sphere of radius a compressed into ellipsoid.

This format is useful in calculation of Cartesian

coordinates when using a non- spherical form.

Converting in to Cartesian coordinates and considers

the earth as a sphere will yield in a systematic error

in the measurements, as the earth is not spherical,

see figure 3. This means that if calculating with

Cartesian coordinates and using the same radius for

all of the earth would yield in different errors at

different locations. Using ECEF conversion the earth

is considered an elliptical shape and the flattening of

the earth will be considered in the calculations. The

Cartesian coordinates calculated will have its origo

in the center of the earth. The geodetic coordinates

will be transformed from latitude and longitude into

X and Y coordinates while the altitude will be added

to the Z-component to get the altitude and the

change thereof. The altitude of the Z-component will

be expressed in meters above the reference ellipsoid.

World Geodetic System 1984 (WGS84) is a

terrestrial reference frame, a reference ellipsoid. The

reference ellipsoid is a mathematically defined way

of describing the surface of a geoid. Associated with

this frame is a geocentric ellipsoid of revolution,

originally defined by the parameters a, f, ω

and μ,

see table 1. WGS84 is globally considered accurate

within 1 meter (Hofmann-Wellenhof et al., 2008).

Using the Matlab command LLA2ECEF from

the aerospace toolbox, the geodetic coordinates

latitude, longitude and altitude where converted into

ECEF-format in meters. The LLA2ECEF command

is using WGS84 as default ellipsoid. The input

arguments for LLA2ECEF is [degree, degree,

meters], which is fitting for the data set that is

provided by the DGNSS examined (Statista, 2016).

Table 1: Parameters of the WGS-84 ellipsoid.

3 METHOD

In this section the research methodology is

described. The data collection design together with

data handling is described.

The measurement method where made with

accurately surveyed positions were calibrated on flat

ground and in a ski slope.

The flat ground testing was performed on

Vallhamra sports facilities (Sweden) and the ski

slope of choice was located in Ulricehamn

(Sweden).

By doing post-processing calculations using

Matlab and Microsoft Excel, the latitude, longitude

and altitude can be translated into meters.

The used points were accurately surveyed using

hired technology from Leica.

The surveyed points were then put on the form

fitted for comparison with the data points from the

tested product. By hiring the technology a reference

value could be established, and thereby minimize

sources of errors in reference.

Differential GNSS for Outdoor Sports - Testing of Applicability for Alpine Sports

191

By putting the GNSS antenna in the zigzag

pattern and allowing it to collect 180 samples the

point is considered accurately surveyed and the

position is known with 3mm + 0.1 ppm accuracy.

The tests carried out on Vallhamra sports

facilities where replicated in a slope at Ulricehamn

ski center. The proceed was the same using hired

technology from Leica to survey points in the slope,

marking out these and thereafter make a run on skis,

wearing the devices mounted on top of the helmet.

3.1 Data Collection

When processing the data coming from the units, the

error and standard deviation needs to be expressed

Physical testing have been performed on flat ground

and in a slope. The flat ground tests were performed

for getting a value where accuracy could be

calculated. This accuracy was then applied on the

tests in the ski slope as a proof of concept. The tests

were made with regard to finding absolute accuracy

and the relative accuracy. To get a value of the

absolute accuracy, accurately surveyed points on a

plane surface is being marked out using a levelled

Leica Viva GNSS GS14 together with a hand held

Leica CS20. Here the exact position can be

compared to the value from the GNSS unit. The

accurately surveyed points on the sport arena were

placed in a zigzag pattern. The points were marked

using orange spray paint and thereafter visited one at

a time. By holding the GNSS over the point for five

seconds, a visual trigger was provided for the post-

processing of data, providing the possibility to see

where the points are.

3.2 Data Analysis

Both the flat ground tests and the tests performed in

a ski slope were made using a calibrated starting

point and then 4 other points in a zigzag pattern. The

points are calibrated with the Leica Viva GNSS

GS14 mounted in the point, using averaging for 160

cycles, and thereafter marked out, using an orange

spray paint. The collection of data was made after

calibrating points. After this the devices where hand

held and walked across the field. At each point the

device was held still for five seconds to mark the

position in data. This yielded, with a sample rate of

20 Hz, 100 samples at the position, making it

possible to read out from the data sheet. By plotting

the data, an estimation of at what sample the

position is marked. This sample number is then

translated from its (latitude, longitude, altitude)-form

to an earth centered, earth fixed, ECEF-form. This

will yield in a format of the coordinates and the

movement can be given in a form of a regular

coordinate system (X, Y, Z). The movement given in

ECEF-form will then be used for creating a mean

value around the turning point. The mean value is

calculated around the minimal difference value

using 90 samples. From these values a standard

deviation and mean error for the accuracy was

calculated.

Investigating the accuracy between two devices

was made by putting two or more units on a fix

distance between the units. Here the recorded

distance can be compared to the actual distance. This

testing was only performed on flat ground. The

testing was performed using a plank attached to a

bicycle holder in the back of a car. This car was then

driven around a running track. The two units

attached to the plank were then observed and the

distance between them, 188 cm, could be observed

how it differed from the reality. From this data the

standard deviation and mean error can be calculated.

The recording of the distance between the devices is

made by using a plugin for the program recording

the data. Gmap.net and

mapprovider.projection.getDistance are the plugins

and functions that are used by the program.

4 RESULTS

For the flat ground test with calibrated points the test

was made using two different trackers. The data was

processed separately from that data set and thereafter

analysed. The accurately surveyed latitude and

longitude will be denoted CALLAT and CALLON.

The values used around the turning points when

doing the tests are denoted lat and the mean value

around that point is denoted ∆lat and ∆lon.

The columns ECEF means that the values have

been converted from lat, lon, alt into earth-centered

earth-fixed, ECEF-form. This was done using

Matlab and converts an input of ([rad], [rad], [m])

into ([m], [m], [m]). The Matlab code uses the

following values for WGS84 ellipsoid constants

(National Imagery and Mapping Agency, 2004). The

final column Diff is simply the difference between

the calibrated value and the mean value around the

turning point. This is the same as the distance from

the calibrated point (Table 2).

For tracker 2 the RMS values for the different

positions were 0.5274, 0.36026, 0.11289, 0.53633,

and 0.484 meters for each point. This results in a

standard deviation of 0.1773 m.

icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support

192

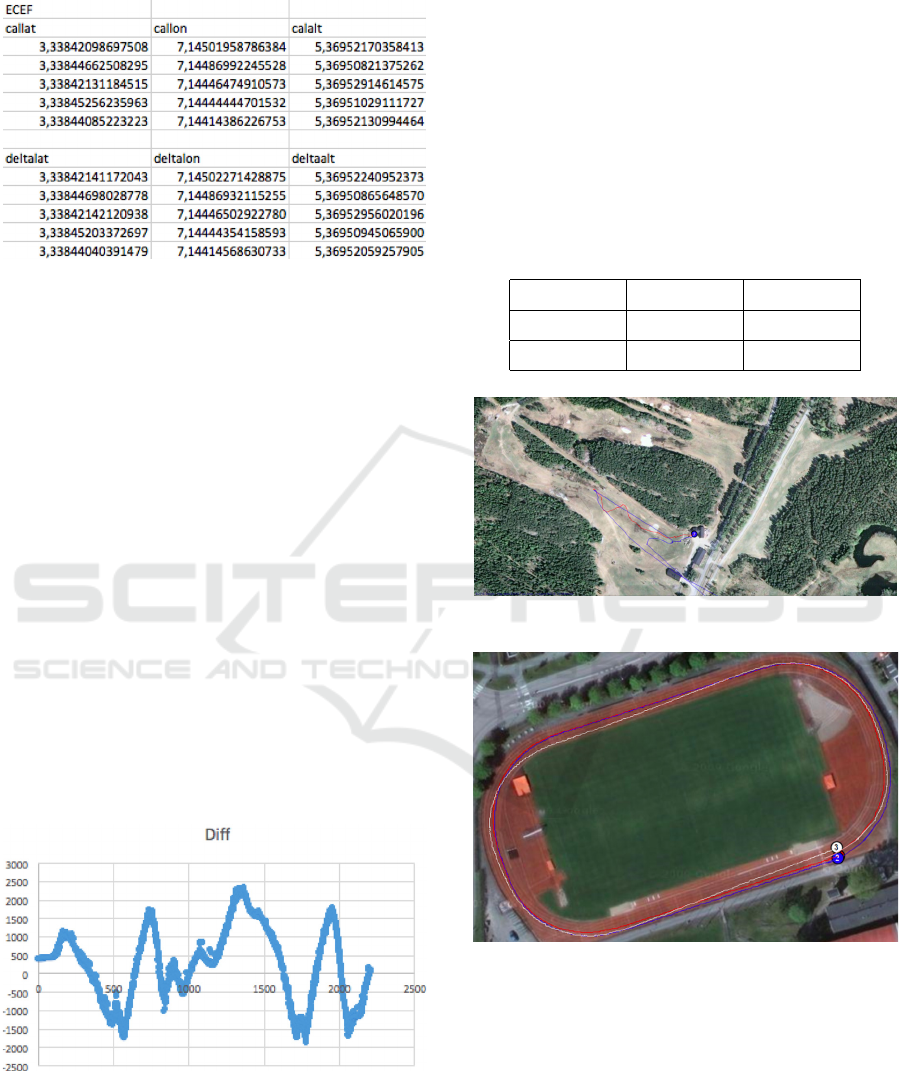
Table 2: ECEF values for tracker 2 at Vallhamra [m].

For tracker 3 the RMS values for the different

positions were 0.0768, 0.3877, 0.5563, 0.9203, and

0.4331 meters for each point. This results in a

standard deviation of 0.3053 m.

Tests on relative positioning error was also made

by putting two devices on a fix distance between

them and then driven around a running track with a

car. The physical distance between the devices was

1880 mm and in figure 4 the fluctuations in

difference can be seen over the 2200 samples.

The calculations from this gives a standard

deviation of 1.003 m, a mean value of 0.215 mm and

fluctuating values between -1.877 m and 2.321 m.

This means that mean of the two trackers results

in a standard deviation of 0.2413 m (Table 3). So,

with 68% certainty the data retrieved from the

tracking device is within a span of 0.2413 meters of

the observed position. With 95 % certainty the data

from the tracking device the device is within a span

of 0.4826 m of the observed position. With 99.7 %

certainty the data from the tracking device the

device is within a span of 0.7239 m of the observed

position.

Figure 4: Positioning error, distance [mm] between two

units over sample number [n].

Physical testing in the intended environment of

use was also made. This was made as a proof of

concept, that the device can be used for tracking an

alpine skier. In figures 5 and 6, a red and a blue line

can be observed. These lines are both representing a

rover carried by a skier. The red line is following the

track that was surveyed. The blue line is an other of

the rover, that drifted away and did not provide any

results of use. When riding the lift up for the ski

slope test, the connection was lost when going up

the lift and the devices needed to be restarted. After

this, the data collection could proceed and in the

peaks, the turns can be observed.

Table 3: Standard deviation of the measurements from

Vallhamra IP.

Figure 5: Run from ski slope in Ulricehamn.

Figure 6: Measurements from Vallhamra sports facilities.

5 DISCUSSION

The data collected, the collection method and the

handling of the data will be discussed. Along with

this, problems that manifested themselves during the

tests will be discussed. Technical outcomes from the

testing will be discussed.

1‡ 2‡ 3‡

68% 95% 99.7%

0.2413 m 0.4826 m 0.7239 m

Differential GNSS for Outdoor Sports - Testing of Applicability for Alpine Sports

193

5.1 Discussion of Measurements

After some research on methods of how to translate

the data available, it was decided to take the

approach using accurately surveyed points. Holding

the rovers laying flat in the palm of the hand, the

accurately surveyed points were marked one at a

time by holding the rover still for five seconds.

Mean error and standard deviation was than

calculated by taking the difference between this

point and the points close to the point. This could

yield in a better accuracy than reality, since the data

collection was allowed to run while being close to

the point. When calculating the mean error in this

case, the measurement is assumed to reach a steady

state with close to zero error. Therefore the outcome

from these results should be approached with

caution as they might leave a too promising

prognosis.

The accuracy from the tests was better than

expected. As earlier stated, the accuracy should be

approached with caution, as the method is not

verified. It is hard to further discuss whether the

accuracy is good enough or not, regarding what

requirements and future areas of use into a value to

aim for.

After performing the tests it was found that the

calibration of altitude should have been made before

commencing the collection of data but was not made

properly which resulted in a systematic error of 5.4

meters. This calibration is made with regard to the

height above the ground that the reference station is

put. This was handled when doing the post

processing of the data. The calculations were per-

formed with the systematic error subtracted in order

to not affect the data. The subtraction was made in

order to get a proper value of the altitude

measurements, as these are important when

measuring in a ski slope.

The values on the relative positioning error was

not as good as expected. Earlier measurements

performed by a company had shown more promising

results. The reason for this could be that there have

been a problem with getting a differential fix

between the reference station and the devices,

something that was experienced during the tests.

Earlier tests have shown standard deviations and

mean errors that were more in the range of 0.7 m

and 0.003 m in mean error according to the company

contact. This method of testing should however be

considered to be discarded. To calculate the error

between two unsure sources should not be

considered as a scientific way of proving

performance for a product like this. The way errors

occur for two rovers among them can be random and

if interference of the satellite signal occurs, it will do

so for both of them, causing unreliable results.

It is important outcome from the testing in the

ski slope, is that when connection is lost for the

device it is crucial to restart it and allow it to get a

differential fix before commencing the tests.

Reasons for the blue line in figure 5 can be because

of this problem. The rover has failed to get

differential fix and the collected data is useless. The

problem can also have appeared because of

problems with the software causing multi-path

errors. After the study, a software update has been

performed, targeting a number of weaknesses. A

follow up study showed considerably better results.

Alternative methods for measuring are present.

The most used method is continuous measurements

using a calibrated differential GNSS. Post

measurements data processing then needs to be

made using Matlab or software such as Justin from

Javad, where one can evaluate data from two

different input sources in double differential mode.

In a comparison of cost between choosing to go with

Matlab versus investing in Justin it differs 2800 SEK

between getting Justin from Javad. Matlab 18500

SEK + aerospace toolbox 9500 SEK = 28000 SEK

versus Justin from Javad 30800 SEK. (Javad, 2016,

Matlab, 2016).

The method using accurately surveyed points put

demands on post processing data handling that was

time consuming. The time consumption is not in

parity with the power of the results, as the method is

not verified when evaluating GNSS accuracies. This

is an other reason for investing in software for

facilitate quick evaluations of future updates in the

product.

The tests showed that the units where non robust

to rotation, something that caused the unit to loose

the differential fix. This needs to be evaluated in a

future requirement specification whether it will be a

problem when using.

6 CONCLUSIONS

Wearable tech is an expanding market and the rate

of emerging companies is high.

The similar products in the segment are many.

Ranging from GPS watches to ungainly differential

GNSS, the competition is extensive. By getting a

differential, wearable GNSS to show stable results, it

would be a completely new segment of tracking and

positioning devices. The wearable technology, using

differential GNSS with an accuracy that could pose

icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support

194

a threat to this product has chose to direct their

development focus towards virtual reality products.

It should be kept in mind that this kind of

technology is growing in many different areas of

technology and more spread.

By specifying what the product is going to be

used for, whether it is time measurement, line choice

of the skiers or measurements of velocity, etcetera.

The recommendation for the company when

pursuing the market of differential GNSS tracking of

athletes, is to standardize their testing method. Since

the product has not yet reached its final technology

and the implementation of real time kinematics, it

should be considered favourable to have a

standardized method for testing where

improvements can be confirmed. The standardized

method needs to be created in order to be able to

process data in a reasonable way where

improvements can be easily recorded. When using a

standardized method, it will also be easier to

evaluate the different settings and additional

functions that are available in the technology.

The next step when reaching a prototype that is

reaching the requirements for the product and testing

in different environments and possible sources of

error and most favourable conditions for testing. The

technical possibility for switching between antennas

is already implemented but not yet evaluated and

should therefor also be evaluated. This will be vital

to provide signal range for a full ski slope or a cross-

country ski slope.

At present there are several factors with the

devices that are not making it robust enough for

using. Tilting of the devices, calibration of height

over the ground and loss of differential fix when put

in a skip zone are all problems that is pointing

towards an unfinished product. These findings

should be put in the requirements specification if

they pose a threat to a functioning problem. The

earlier these problems can be resolved, the cheaper it

can be fixed rather than having to do late changes in

product development process.

6.1 Recommendations

When performing future accuracy evaluations, a

reference track should be used in order to

continuously evaluate updates. By having a

consistency in the evaluation method, the evaluation

gets reliable. The creation of the reference track

should be made simultaneously with the data

collection of the differential GNSS. There are two

reason for this, to be able to synchronize the data

sets and to ensure that the circumstances of the earth

is the same for the two different data sets.

When performing tests, it is important to make

everything at the largest extent possible, replicable.

Therefore it is suggested to use the same algorithm

for the process every time.

Other factors that might affect the measurements

that should be considered when collecting data are

the following:

• Collect data in clear weather in order to

ensure satellite coverage. Cloudy skies

might prohibit signal coverage.

• Collection of data to be analysed should be

made continuously, instead of around

accurately surveyed points.

• The rovers needs to be restarted and get

differential fix before commencing data

collection.

• The rovers must be carried with the right

side up, and with the correct side in front.

The rovers should not be rotated over 40

degrees in order to not loose contact with

the reference station.

• The reference station needs to be calibrated

in height over ground every time when

performing tests. This is important to

remember, otherwise it will result in a

systematic error in the altitude

measurements, something that is important

to do as accurate as possible when tracking

alpine skiers.

ACKNOWLEDGEMENTS

The authors wish to acknowledge the support from

New Century Information AB, with Bengt Julin,

Anders Yttergård and Klas Öberg. And Västra

Götalandsregionen via Regionutvecklingsnämnden

for financial support.

REFERENCES

Advanced Navigation (2015), Spatial,. URL

http://www.advancednavigation.com.au/product/spatia

l#applications. Accessed: 2016-05-26.

Advanced Navigation (2016) Spatial,. URL

http://www.advancednavigation.com.au/product/spatia

l#documentation. Accessed: 2016-05-30.

Bernhard Hofmann-Wellenhof, Herbert Lichtenegger, and

Elmar Wasle. GNSS – Global Navigation Satellite

Systems. Springer-Verlag Wien, 2008.

Differential GNSS for Outdoor Sports - Testing of Applicability for Alpine Sports

195

GMV (2011) DGNSS fundamentals,. URL http://www.

navipedia.net/index.php/DGNSS_Fundamentals.

Accessed: 2016-05-12.

Granby, P. (2016) Unpublished MSc. Thesis, Chalmers

University of Technology

Javad. Justin, (2016). URL http://www.javad.com/jgnss/

products/software/justin.html#. Accessed: 2016-06-05.

Matlab (2016). Pricing and licensing aerospace toolbox,.

URL http://se.mathworks.com/pricing-licensing/

index.html?prodcode=AT&s_iid=main_pl_AT_tb.

Accessed: 2016-06-05.

Mercator, P. (2016). Leica viva gs14 – gnss smart

antenna,. URL http: //leica-geosystems.com/products/

gnss-systems/smart-antennas/leica-viva-gs14.

Accessed: 2016-05-16.

Murray, S., (2014) Putting wearables into context with

low-power GNSS, URL http://www.broadcom.com/

blog/wireless-technology/putting-wearables-into-

context-with-low-power-gnss/. Accessed: 2016-05-09.

National Imagery and Mapping Agency (2004) World

geodetic system 1984. Technical Report NIMA

TR8350.2, Department of Defense.

Orr. X., (2016) Nci sports tracker project - the road

ahead... unpublished company material.

Statista (2016) Big data market size revenue forecast

worldwide from 2011 to 2026 (in billion U.S. dollars).

http://www.statista.com/statistics/254266/global-big-

data-market-forecast/. Accessed: 2016-02-29.

Spörri J., Limpach P., Geiger A., Gilgien, M., and Müller

E. (2014) The effect of different global navigation

satellite system methods on positioning accu- racy in

elite alpine skiing. Sensors, 14 (10), 18433-18453.

icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support

196