Qualitative Reasoning for Understanding the Behaviour of Complex
Biomolecular Networks
Ali Ayadi
1,2
, Cecilia Zanni-Merk
1
and Franc¸ois de Bertrand de Beuvron
1
1
ICUBE/SDC Team (UMR CNRS 7357)-Pole API BP 10413, Illkirch 67412, France
2
LARODEC Laboratory, Institut Sup
´
erieur de Gestion de Tunis, University of Tunis, Rue de la libert
´
e, Bardo 2000, Tunisia
Keywords:
Biomolecular Networks, Dynamical Modelling, Qualitative Reasoning, Qualitative Simulation.
Abstract:
Understanding the dynamical behaviour of cellular systems requires the development of effective modelling
techniques. The modeling aims to facilitate the study and understanding of the dynamic behaviour of these
systems, by the simulation of their designed models. Complex biomolecular networks are the basis of these
models. In this paper, we propose a method of qualitative reasoning, based on a formal logical modeling,
to qualitatively simulate the biomolecular network and interpret it behaviour over time. The power of our
approach is illustrated by applying it to the case study of the autoregulation of the bacteriophage T4 gene 32.
1 INTRODUCTION
In recent decades, the molecular biology has accu-
mulated a sum of knowledge about the details of
the molecular mechanisms in cells (Ingalls, 2012).
For many years the biological experiments have dis-
covered much knowledge about genes, proteins and
metabolites. Indeed, with the development of high-
throughput techniques, huge amounts of data has been
generated on several levels (Caporaso et al., 2010).
We talk about the genomics (the qualitative study of
genes), the proteomics (the quantitative study of pro-
teins) and the metabolomics (the quantitative study of
metabolites) (Forbus, 1997). A major problem, which
was immediately recognised, was to develop mecha-
nisms for analysing these data, interpret and deduce
important knowledge.
These advances given their advantages and disad-
vantages pave the way for a new discipline of molec-
ular biology which is called systems biology. This
integrative discipline aims to combine all informa-
tion (from different levels) in order to understand the
processes and behaviours of all cellular components
while studying the interactions that take place among
them. Indeed, these molecular components interact
with each other, thereby forming large networks that
are called complex biomolecular networks.
The complex biomolecular network consists of a
set of nodes, denoting the molecular components and
a set of edges, denoting the interactions among these
cellular components. They are considered as systems
that dynamically evolve from a state to another so that
the cell can adapt itself to changes in its environment.
The key motivation behind this work is to develop
a platform to simulate the state changes of the com-
plex biomolecular networks with the hope of under-
standing and steering their behaviour. This issue has
already been addressed in Wu et al. ’s research (Wu
et al., 2014b), which they introduce and define the
transittability of biomolecular as the idea of steer-
ing the complex biomolecular network from an un-
expected state to a desired state (Wu et al., 2014b).
In this paper, we propose a method of qualitative
reasoning. Indeed, biomolecular networks consist of
various subnetworks which themselves are composed
of several molecular components interacting in their
turn with each other, producing a complex global be-
haviour. Their complexity and large size have pre-
vented a fully quantitative simulation. We consider
that qualitative reasoning responds to the complex-
ity of calculating the quantitative reasoning methods,
which sometimes are impossible to implement (Field-
ing and Schreier, 2001).
The rest of the paper is organised as follows. In
Section 2, we give some background on biomolecu-
lar networks, we discuss our motivations and we de-
fine qualitative reasoning. In Section 3, we propose
a qualitative reasoning method and detail all its con-
struction steps. In section 4, we enrich and explain
this qualitative method with a concrete case study to
explain how this technique can be used in practice.
144
Ayadi, A., Zanni-Merk, C. and Bertrand, F.
Qualitative Reasoning for Understanding the Behaviour of Complex Biomolecular Networks.
DOI: 10.5220/0006065901440149
In Proceedings of the 8th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2016) - Volume 2: KEOD, pages 144-149
ISBN: 978-989-758-203-5
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 BACKGROUND AND RELATED
WORK
2.1 Biomolecular Networks
The cell is a complex system consisting of thou-
sands of diverse molecular entities (genes, proteins
and metabolites) which interact with each other phys-
ically, functionally and logically creating a biomolec-
ular network (Karp, 2010; Wu et al., 2014b).
The complexity of the biomolecular network ap-
pears by its decomposition into three levels: the
genome level models the genetic material of an organ-
ism, the proteome level describes the entire set of pro-
teins and the metabolism level contains the complete
set of small-molecule chemicals (Wu et al., 2014a;
Hayes et al., 1978). Figure 1 depicts these levels.
Figure 1: Multi-level modelling of a biomolecular network
from a real cell.
Depending on the type of its cellular elements
and their interactions, we can distinguish the three
basic types of networks: the Gene Regulatory net-
works (GRNs), the Protein-Protein-Interaction net-
works (PPINs) and the Metabolic networks (MNs),
that were logically and semantically formalized in
(Ayadi et al., 2016).
2.2 Qualitative Reasoning
The reasoning is a mental activity that humans prac-
tice to solve difficulties they confront in their life.
This reasoning is often performed in the lack of quan-
titative knowledge, which is called qualitative reason-
ing. In literature, we distinguish two types of rea-
soning, heuristic reasoning which is effective and the
causal reasoning based on a model (Trav
´
e-Massuy
`
es,
1997). This reasoning is based on a modeling of the
system (model-based reasoning), be it a human be-
ing, a machine, etc. Such reasoning is based on a
model of causal type because it combines the effects
and causes, such as a causal graph. It solves a prob-
lem by reasoning about the structure and function of
the object in an application environment and their be-
haviour over time (De Kleer and Brown, 1984; For-
bus, 1997).
3 QUALITATIVE REASONING
The explicit representation of the network behaviour
evolution, between two instants t
0
and t
n
is essen-
tial. We must then link the dynamic model defined in
(Ayadi et al., 2016) to a qualitative simulation mech-
anism. This simulation lets to execute the model in
order to simulate the network evolution and its com-
ponents over time.
We chose to use qualitative reasoning for two
reasons: (1) To understand the overall functioning
and properties of complex biomolecular networks,
through the analysis and simulation of the dynami-
cal model (explained in the previous section), and the
interpretation of the obtained knowledge. (2) To steer
these networks, in particular by allowing to evaluate
at any time their simulation in a discrete time.
3.1 Basic Concepts
In the following sections, we will define the basic
concepts of qualitative simulation (Trav
´
e-Massuy
`
es,
1997) and detail the major phases of construction.
3.1.1 The Causal Graph
The qualitative simulation model is based on the de-
velopment of a causal graph whose nodes denote vari-
ables which this simulation is concerned and edges
denote causality relations between these variables. By
analogy with the model presented in our previous
work (Ayadi et al., 2016), the causal graph is itself
the biomolecular network SR which its nodes repre-
sent causal states of network molecular components
and its edges represent the types of interactions that
can occur between these components.
3.1.2 Quantitative Variables & Quantity Space
A variable is a characteristic of interest. For exam-
ple, in our case the variables of the qualitative model
denote the state of the molecular components at a
given moment denoted by en(m,t). These variables
are qualitative because they are represented by quali-
ties (nominal or ordinal).
The set of these qualitative values and their cor-
responding intervals constitutes the quantity space
of the variable en(m, t), denoted by EQ
en(m,t)
.
Each variable en(m, t) takes its qualitative value
in its ordered set of qualitative values EQ
en(m,t)
=
{vq
1
, vq
2
, ..., vq
n
}. In fact, the quantity space is a
partition of the domain of a variable values into be-
haviour regions that are qualitatively homogeneous.
To resolve the conflicts of partitioning the
EQ
en(m,t)
, we present the following algorithm.
Qualitative Reasoning for Understanding the Behaviour of Complex Biomolecular Networks
145

Algorithm 1: Pseudocode of the EQ
en(m,t)
partitioning al-
gorithm.
Require: m ∈ M, oe(m), min
m
, max
m
, EQ
en(m,t)
←
/
0
Ensure: Partition of EQ
en(m,t)
1: if (m ∈ M
P
∪ M
M
) then
2: for all outgoing edges i ∈ oe(m) do
3: Read its T hreshold;
4: Sort the threshold values;
T hreshold
1
< T hreshold
2
<, ..., < T hreshold
n
5: Quantitative partitioning of EQ
en(m,t)
;
EQ
en(m,t)
= {[min
m
;T hreshold
1
],
[T hreshold
1
, T hreshold
2
], ·· · , [T hreshold
n
, max
m
]}
6: Translate quantitative measures into qualitative
values;
EQ
en(m,t)
= {vq
1
, vq
2
, ..., vq
n+1
}
Where: vq
1
≡ [min
m
, T hreshold
1
] and
||EQ
en(m,t)
|| = ||oe(m)|| + 1
7: end for
8: Return the quantity space
EQ
en(m,t)
= {vq
1
, vq
2
, ..., vq
n+1
}
9: else
10: if (m ∈ M
G
) then
11: Boolean partitioning of EQ
en(m,t)
;
EQ
en(m,t)
= {true, f alse}
12: Translate boolean measures into qualitative val-
ues;
EQ
en(m,t)
= {vq
1
, vq
2
}
Where: vq
1
≡ 0, vq
2
≡ 1 and ||EQ
en(m,t)
|| = 2
13: Return the quantity space
EQ
en(m,t)
= {vq
1
, vq
2
}
14: end if
15: end if
As defined in Algorithm 1, the partition of the
quantity space EQ
en(m,t)
depends on the type of node:
• If m ∈ M
G
: en(m,t) = {Deactivated, Activated},
its states can be ”Activated” or ”Deactivated”. So,
we assign to its EQ
en(m,t)
the qualitative values
0 and 1 meaning respectively ”Deactivated” and
”Activated”.
en(m,t) = {Deactivated, Activated}
⇒ EQ
en(m,t)
= {0, 1}
• If m ∈ M
P
∪ M
M
: EQ
en(m,t)
is calculated de-
pends on the outgoing arcs oe(m) that can have
the node m. In fact, for a quantity m of outgoing
arcs, there will be n + 1 qualitative values that are
defined by an order relation on EQ
en(m,t)
, creating
an ordered set of qualitative values EQ
en(m,t)
=
{vq
1
, vq
2
, ..., vq
n
}.
en(m,t) =
{[min
m
, T hreshold
1
[, [T hreshold
1
, T hreshold
2
[, · ·· , [T hreshold
n
, max
m
]}
⇒ EQ
en(m,t)
= {vq
1
, vq
2
, · ·· , vq
n
}
Figure 2 displays the execution of the EQ
en(m,t)
partitioning algorithm in both cases. In addition to the
quantity space of its variables, a qualitative reasoning
method also includes algebraic relations (constraints,
influences, etc.) that act among these quantity space.
3.1.3 Operations and Rules
The Operations. In (Trav
´
e-Massuy
`
es, 1997), the
authors define six operations for calculating the quan-
tity spaces of the variables. Among them, we were
just use the three unary operations as shown in Ta-
ble 1: the incrementation (incr), the decrementation
(decr) and the inverse (inv) of a qualitative variable
vq
i
.
Table 1: Unary operations on quantity spaces presented in
(Trav
´
e-Massuy
`
es, 1997).
Operations on EQ
Unary operations
∀[en(m,t)] ∈ EQ
en(m,t)
= {vq
1
, vq
2
, vq
3
, vq
4
, vq
5
}
and n ∈ N
Incrementation ”incr”
incr
0
([m]) = [en(m, t)]
[en(m,t)] : vq
1
vq
2
vq
3
vq
4
vq
5
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
incr
1
([en(m,t)]) : vq
2
vq
3
vq
4
vq
5
vq
5
incr
n
([en(m,t)]) = incr
n−1
(incr
1
([en(m,t)]))
Decrementation ”decr”
decr
0
([en(m,t)]) = [en(m, t)]
[en(m,t)] : vq
1
vq
2
vq
3
vq
4
vq
5
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
decr
1
([en(m,t)]) : vq
1
vq
1
vq
2
vq
3
vq
4
decr
n
([en(m,t)]) = decr
n−1
(decr
1
([en(m,t)]))
Inverse ”inv”
[en(m,t)] : vq
1
vq
2
vq
3
vq
4
vq
5
- - - - - - - - - - - - - - - - - - - - - - - - - - - - -
inv([en(m, t)]) : vq
5
vq
4
vq
3
vq
2
vq
1
Using these operators, we can combine several
variables together to create our own operations as a
specific combination table.
The Partition and Propagation Rules. Based on
the work presented in (Trav
´
e-Massuy
`
es, 1997), we
adapt qualitative reasoning mechanism to calculate
the qualitative value of the nodes. This mechanism is
based on both the partition rules and the propagation
rules (Figure 3). These rules are used to calculate the
value of the target variable (en(m,t + 1)) at the next
time t + 1 based on its qualitative value (en(m,t)) and
the value of its predecessors (en(Pred(m), t)) at the
current time t.
• Partition rules allow the translation of quantitative
measures of the variables (en(m, t)) into qualita-
KEOD 2016 - 8th International Conference on Knowledge Engineering and Ontology Development
146

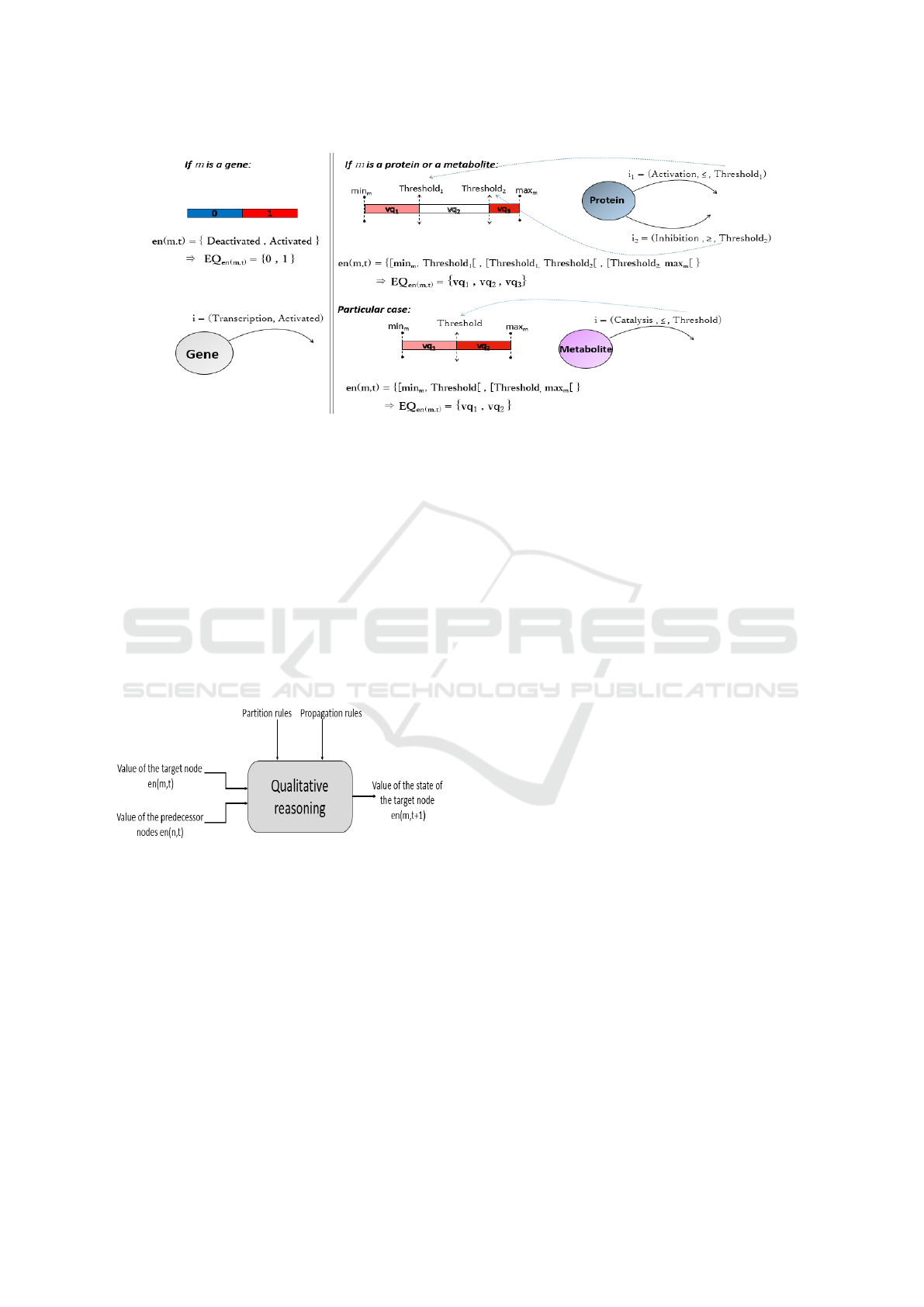
Figure 2: Description of the EQ
en(m,t)
partitioning algorithm.
tive values. They match a quantitative (real) inter-
val with its correspond qualitative value belonging
to the quantity space EQ
en(m,t)
. They are defined
by the pseudo code of the algorithm 1.
• Propagation rules calculate the propagation of the
qualitative values from the sources components to
the target components of the causal graph. They
are defined by the aggregate functions A
m
which
calculates the evolution of the node status be-
tween two successive instants of the simulation
(this function is detailed in (Ayadi et al., 2016)).
These rules are expressed by combining the oper-
ations presented in Table 1.
Figure 3: Qualitative reasoning mechanism.
4 AN EXAMPLE
Ribosomal proteins control its own level in the cell
by itself. We call them as ribosomal regulatory pro-
tein. The gene encoding the regulatory protein is it-
self a target of the protein which it produces. This
is so-called self-regulation or autoregulation when a
protein regulates its own production. We distinguish
two types of regulations:
• A negative self-regulation when the regulatory
protein represses the expression of its own gene
(inhibit the expression of its mRNA). This inhi-
bition occurs when there is an accumulation of
the protein concentration that exceeds a certain
threshold.
• A positive self-regulation, when the regulatory
protein activates the expression of its producing
gene. This activation occurs when there is a lack
of concentration of the protein which becomes
less than a certain threshold.
We choose a special case of self-regulating ribosomal
protein, the autoregulation of the bacteriophage T4
gene 32. Figure 4 displays the general model of this
example. This network consists of a gene G32 cod-
ing for a protein p32 and a metabolite m32 which can
catalyse the protein p32. Self-regulation of the bac-
teriophage T4 gene 32 depends on the concentration
of the protein p32. Indeed, the concentration of p32
is regulated by itself and normally should remain be-
tween S
p32
= 0.2 10
−6
Mol and S
p32
= 0.7 10
−6
Mol.
However, when the concentration of p32 exceeds the
threshold S
p32
= 0.7 10
−6
Mol, it inhibits the trans-
lation of its gene G32 making it inactive. Similarly,
when the concentration of p32 decreases and becomes
less than threshold S
p32
= 0.2 10
−6
Mol, it activates
the translation of its gene G32 making it active. De-
tails of this example can be found in (Lewin and
Sanlaville, 1998). For the sake of simplicity, we pro-
vide the step-by-step construction of the qualitative
simulation by appling it to the autoregulation of the
bacteriophage T4 gene 32.
4.1 The Variables
In the example presented in Figure 4, we have three
variables en(G32,t), en(p32,t) and en(m32, t) that
respectively represent the state of the gene G32, the
protein p32 and the metabolite m32.
Qualitative Reasoning for Understanding the Behaviour of Complex Biomolecular Networks
147

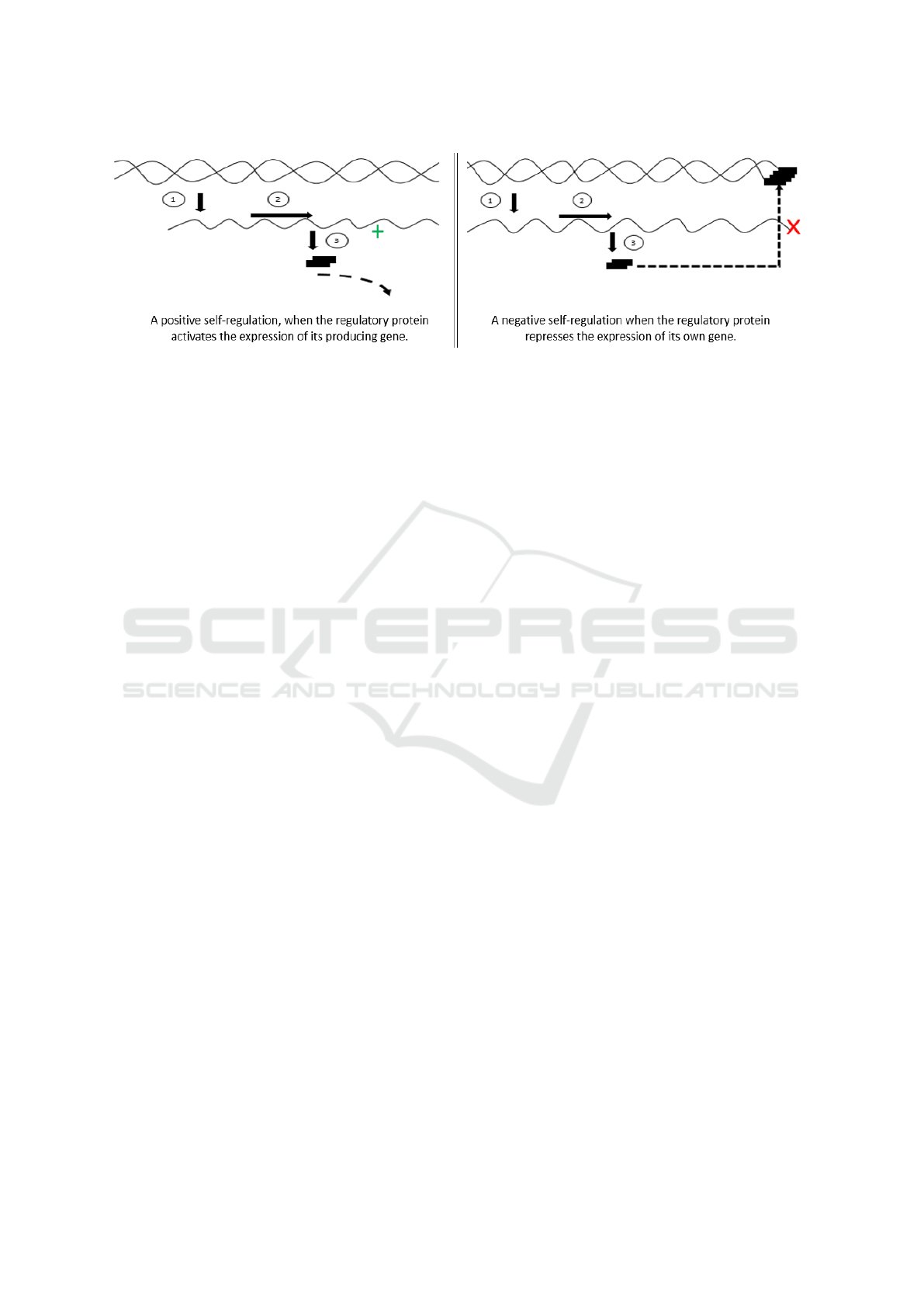
Figure 4: Autoregulation of the bacteriophage T4 gene 32.
4.2 The Causal Graph
We can use the structure of the biomolecular network
as the causal graph of our example.
4.3 The Partition Rules
en(G32,t) ∈ {Deactivated , Activated},
⇒ EQ
en(G32,t)
= {0 , 1}.
en(p32, t) ∈ {[min
p32
, 0.2[ , [0.2, 0.7[ , [0.7, max
p32
[},
⇒ EQ
en(p32,t)
= {vq
1
, vq
2
, vq
3
}.
en(m32,t) ∈ {[min
m32
, 0.8[ , [0.8, max
m32
[},
⇒ EQ
en(m32,t)
= {vq
1
, vq
2
}.
4.4 The Propagation Rules
For reasons of clarity, we note [m]
t
the qualitative
value of the state of the component m. It means that
the notation [m]
t
≡ [en(m,t)] ∈ EQ
en(m,t)
. Now, let us
define the aggregate rules of each variables.
For the variable G32:
[G32]
t+1
= A
G32
([G32]
t
, {i
1
, i
2
}, [p32]
t
)
i f ([p32]
t
= vq
1
) then
⇒ [G32]
t+1
= 1
else i f ([p32]
t
= vq
2
) then
⇒ [G32]
t+1
= [G32]
t
else i f ([p32]
t
= vq
3
) then
⇒ [G32]
t+1
= 0
For the variable p32:
[p32]
t+1
= A
p32
([p32]
t
, {i
3
, i
4
}, [G32]
t
, [m32]
t
)
i f ([m32]
t
= vq
1
) ∧ ([G32]
t
= 0) then
⇒ [p32]
t+1
= [p32]
t
else i f ([m32]
t
= vq
2
) ∧ ([G32]
t
= 0) then
⇒ [p32]
t+1
= decr([p32]
t
)
else i f ([m32]
t
= vq
1
) ∧ ([G32]
t
= 1) then
⇒ [p32]
t+1
= incr([p32]
t
)
else i f ([m32]
t
= vq
2
) ∧ ([G32]
t
= 1) then
⇒ [p32]
t+1
= [p32]
t
For the variable M32:
[m32]
t+1
= A
m32
([m32]
t
)
⇒ [m32]
t+1
= [m32]
t
4.5 The Simulation
Let us define the initial state of the network at t
0
:
ER(t
0
) = h[G32]
t
0
, [p32]
t
0
, [m32]
t
0
i.
We randomly choose the initial qualitative values of
the components as: ER(t
0
) = h0, vq
1
, vq
1
i.
Then, we have performed a series of simulations to
assesses the evolution of the network over time:
ER(t
0
+ 1) = h[G32]
t
0
+1
, [p32]
t
0
+1
, [m32]
t
0
+1
}
= h1, vq
1
, vq
1
i
ER(t
0
+ 2) = h[G32]
(t
0
+1)+1
, [p32]
(t
0
+1)+1
, [m32]
(t
0
+1)+1
i
= h1, vq
2
, vq
1
i
4.6 The Behaviour
CR
[t
0
,t
2
]
= {ER(0), ER(1), ER(2)}
= {h0, vq
1
, vq
1
i, h1, vq
1
, vq
1
i, h1, vq
2
, vq
1
i}
Figure 5 presents the possible simulation results.
5 CONCLUSION AND FURTHER
WORK
In this paper, we draw inspiration from the works
of (Trav
´
e-Massuy
`
es, 1997) to propose a qualitative
reasoning method to simulate the behaviour of the
KEOD 2016 - 8th International Conference on Knowledge Engineering and Ontology Development
148

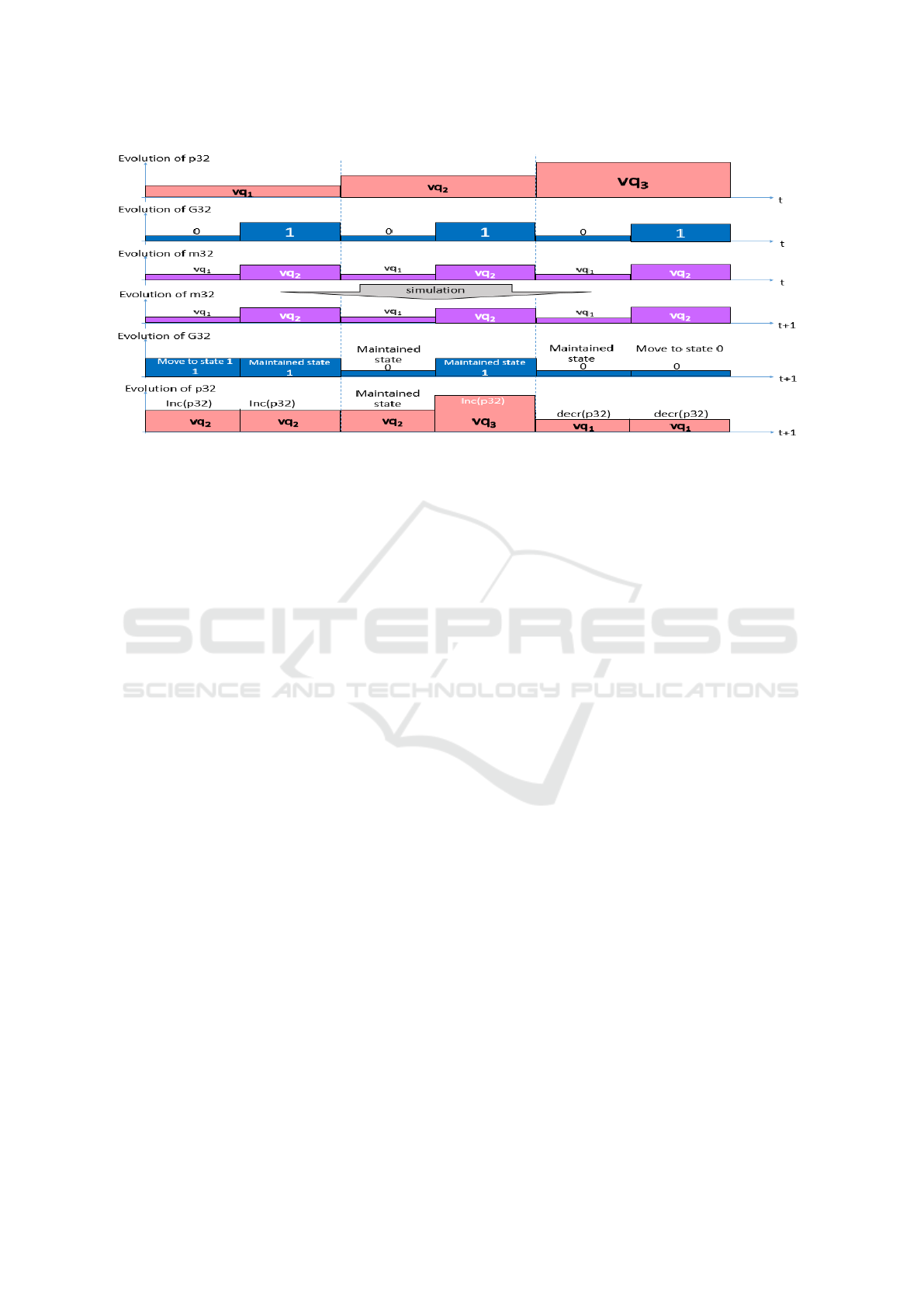
Figure 5: All possible simulation results of our example.
biomolecular network. This method is completely
based on the logical formalisation presented in our
previously research (Ayadi et al., 2016) that can be
assimilated to a causal model.
We have applied our approach to a comprehensive
model concerning the autoregulation of the bacterio-
phage T4 gene 32. In fact, the qualitative reasoning
presented here clearly demonstrates all the elements
that we need to understand the evolution of biomolec-
ular networks.
Further work includes the translation of this log-
ical formalism into ontologies where qualitative rea-
soning can be integrated to obtain an optimal model.
Simulation of these models along with optimization
algorithms will permit to obtain the best external stim-
uli to be applied to steer the network from its current
state to a desired state. These results will be compared
with the approach proposed by (Wu et al., 2014b).
REFERENCES
Ayadi, A., Zanni-Merk, C., de Bertrand de Beuvron, F., and
Krichen, S. (2016). Logical and semantic modeling of
complex biomolecular networks. Procedia Computer
Science, 96:475 – 484. Knowledge-Based and Intel-
ligent Information &amp; Engineering Systems: Pro-
ceedings of the 20th International Conference KES-
2016.
Caporaso, J. G., Kuczynski, J., Stombaugh, J., Bittinger,
K., Bushman, F. D., Costello, E. K., Fierer, N., Pena,
A. G., Goodrich, J. K., Gordon, J. I., et al. (2010).
Qiime allows analysis of high-throughput community
sequencing data. Nature methods, 7(5):335–336.
De Kleer, J. and Brown, J. S. (1984). A qualitative physics
based on confluences. Artificial intelligence, 24(1-
3):7–83.
Fielding, N. and Schreier, M. (2001). Introduction: On
the compatibility between qualitative and quantita-
tive research methods. In Forum Qualitative Sozial-
forschung/Forum: Qualitative Social Research, vol-
ume 2.
Forbus, K. D. (1997). Qualitative reasoning.
Hayes, P. J. et al. (1978). The naive physics mani-
festo. Institut pour les
´
etudes s
´
emantiques et cogni-
tives/Universit
´
e de Gen
`
eve.
Ingalls, B. (2012). Mathematical modelling in systems bi-
ology: An introduction.
Karp, G. (2010). Biologie cellulaire et mol
´
eculaire: Con-
cepts and experiments. De Boeck Sup
´
erieur.
Lewin, B. and Sanlaville, C. (1998). G
`
enes VI. De Boeck
Sup
´
erieur.
Trav
´
e-Massuy
`
es, L. (1997). Le raisonnement qualitatif
pour les sciences de l’ing
´
enieur (coll. diagnostic et
maintenance). Hermes Science Publications.
Wu, F., Chen, L., Wang, J., and Alhajj, R. (2014a).
Biomolecular networks and human diseases. BioMed
research international, 2014.
Wu, F.-X., Wu, L., Wang, J., Liu, J., and Chen, L. (2014b).
Transittability of complex networks and its applica-
tions to regulatory biomolecular networks. Scientific
reports, 4.
Qualitative Reasoning for Understanding the Behaviour of Complex Biomolecular Networks
149