
The Longest Common Subsequence Distance using a Complexity Factor
Octavian Lucian Hasna and Rodica Potolea
Computer Science Department, Technical University of Cluj-Napoca, Cluj-Napoca, Romania
Keywords:
Time Series, Classification, Longest Common Subsequence, Discretize, Complexity.
Abstract:
In this paper we study the classic longest common subsequence problem and we use the length of the longest
common subsequence as a similarity measure between two time series. We propose an original algorithm for
computing the approximate length of the LCSS that uses a discretization step, a complexity invariant factor
and a dynamic threshold used for skipping the computation.
1 INTRODUCTION
In the past decade there was a tremendous increase in
scientific interest in the field of time series and specifi-
cally on the subject of distance measures used to com-
pare two time series. According to (Bagnall et al.,
2016) the best results are obtained using the ensem-
ble classifier, Collective of Transformation Ensem-
bles (COTE), which aggregates 35 distances. Tested
on the datasets from (Chen et al., 2015), this classi-
fier outperforms other candidates in terms of accu-
racy at the cost of increasing the execution time. The
second best distance measure is the Dynamic Time
Warping (DTW) which was initially used in speech
recognition (Sakoe and Chiba, 1978). None of the
above presented methods yields the best accuracy for
all individual datasets. This motivates us to find a dis-
tance measure that gives the best results for a subset
of datasets. The subsets of datasets is decided based
on the results on the train set.
The similarity measure that we employed is the
Longest Common Subsequence (LCSS) between two
time series, first used in the field of time series in
(Vlachos et al., 2002). We propose a new approach
to compute LCSS by using the Symbolic Aggregate
aproXimation (SAX) (Lin et al., 2003) and a com-
plexity factor from (Batista et al., 2011) in order to
improve the similarity measure.
The rest of this paper is organized as follows.
In section 2 we define and present the properties of
time series. In section 3 we give an overview of the
strategies that are used in this work. In section 4 we
present the new LCSS based distances. In section 5
we present the results of the experiments conducted
on the datasets from (Chen et al., 2015). The final
section 6 contains the conclusions and the future di-
rections of this work.
2 TERMINOLOGY
A time series is also called a signal and can be defined
as a sequence of points at successive moments in time.
Formally it can be described as follows:
T S : R → R
n
, n ∈ N
∗
, TS(x) = y (1)
Based on the formula 1 the time series can be classi-
fied in one-dimensional if n = 1 or multi-dimensional
if n > 1. Also it is called discrete if the time domain
is discrete (in formula 1, x is from Z), otherwise it is
called continuous.
A window from a time series is defined as a se-
quence of points from the time series between two
moments in time, start and end. Formally it can be
defined as:
T S
start,end
= {T S(x)|start ≤ x < end} (2)
The process that transforms a continuous time se-
ries into a discrete time series is called sampling. The
sampled values are read from the continuous time
series at the frequency f
sampling
. According to the
Nyquist-Shannon theorem, f
sampling
should be at least
double the value of the continuous time series fre-
quency f
signal
so as to be able to reconstruct the con-
tinuous time series from the discrete time series. This
process that transforms a discrete time series into a
continuous time series is called interpolation.
From now on when we use the term time series,
we refer to the discrete and one-dimensional time se-
ries. Also we assume that all the time series are sam-
pled at the same frequency.
336
Hasna, O. and Potolea, R.
The Longest Common Subsequence Distance using a Complexity Factor.
DOI: 10.5220/0006067603360343
In Proceedings of the 8th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2016) - Volume 1: KDIR, pages 336-343
ISBN: 978-989-758-203-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

3 RELATED WORK
3.1 Longest Common Subsequence
The longest common subsequence is a classic prob-
lem in computer science. The task is to find the
longest subsequence common to the input sequences
(usually two sequences). The subsequence is formed
of one or more disjoint sequences. The formula
for computing the length of LCSS between two se-
quences A and B with discrete values is recursive. The
length of LCSS between A and B is dependent on the
length of LCSS between the tail of A and B in the fol-
lowing way:
0, if |A| = 0 ∨ |B| = 0
LCSS(tail(A), tail(B)) + 1, if A
1
= B
1
max{LCSS(tail(A), B), LCSS(A,tail(B))}
(3)
with
tail(V ) = {V
2
,V
3
, ...,V
n
} (4)
The formula 3 is transposed in the pseudo-code
from the algorithm 1. The length of A is m and the
length of B is n.
Algorithm 1: The length of LCSS recursive.
1: function lcss
1
(A, i, m, B, j, n)
2: if i ≥ m or j ≥ n then
3: return 0
4: else if A[i] = B[i] then
5: return 1 + lcss
1
(A, i + 1, m, B, j + 1, n)
6: s1 ← lcss
1
(A, i + 1, m, B, j, n)
7: s2 ← lcss
1
(A, i, m, B, j + 1, n)
8: if s1 > s2 then
9: return s1
10: else
11: return s2
The time complexity of the recursive algorithm is
exponential because the intermediate values are com-
puted more than once. The solution to this problem is
to store the intermediate values in a matrix. This tech-
nique is called memoization. Using this technique the
algorithm 2 has a quadratic time complexity, O(nm),
and it gives the possibility to extract the values of the
LCSS from the generated matrix.
The second algorithm has a disadvantage related
to the space complexity which increases from linear
to quadratic. A solution to this problem is to keep
only the last two rows of the matrix and so the space
complexity becomes linear, O(max{m, n}). Without
losing generality we assume that m ≥ n in algorithm
3.
Algorithm 2: The length of LCSS with memoization.
1: function lcss
2
(A, m, B, n)
2: v[0..m, 0..n] ← 0
3: for i ← 1, m do
4: for j ← 1, n do
5: if A[i] = B[ j] then
6: v[i, j] ← v[i − 1, j − 1] + 1
7: else
8: v[i, j] ← max(v[i − 1, j], v[i, j −1])
9: return v[m, n]
Algorithm 3: The length of LCSS with less space complex-
ity.
1: function lcss
3
(A, m, B, n)
2: v[0..n] ← 0
3: for i ← 1, m do
4: prev ← v
5: for j ← 1, n do
6: if A[i] = B[ j] then
7: v[ j] ← prev[ j − 1] + 1
8: else
9: v[ j] ← max(prev[ j], v[ j − 1])
10: return v[n]
The third algorithm computes only the length of
LCSS which is enough for computing the distance
between two sequences. We refer the reader to
(Hirschberg, 1975) where Hirschberg describes a lin-
ear space algorithm for computing the actual LCSS.
Algorithm 3 is not ready yet for comparing time
series because in the case of time series the values are
real numbers and not discrete symbols. The solution
provided by Vlachos in (Vlachos et al., 2002) is to
change the condition from line 6 with |A[i]−B[ j]| ≤ ε.
He recommends to use for ε the value of the standard
deviation of the values from the two time series.
Another contribution that is applied to the algo-
rithm 3 is to impose a given region on the matrix
where the values are compared. The idea comes from
Dynamic Time Warping (DTW) where Sakoe and
Chiba propose a rectangle region, symmetric to the
diagonal of the matrix, with a radius depending on
the length of the sequences (Sakoe and Chiba, 1978).
They also show that their rectangle region gives better
results compared to the parallelogram region pro-
posed by Itakura (Itakura, 1975). If we want to apply
these restrictions we need to assume that the length
of the two sequences are equal (n = m). If the lengths
of the two sequences are not equal then we need to
use a sliding window with the size of the smaller
sequences, compute all the distances with the longer
sequences and keep only the smallest distance. Algo-
The Longest Common Subsequence Distance using a Complexity Factor
337
rithm 4 computes the approximate length of the LCSS
with Sakoe and Chiba region.
Algorithm 4 : The approximate length of LCSS with Sakoe
and Chiba region.
1: function lcss
4
(A, B, n, radius)
2: w ← 2 ∗ radius + 1
3: k ← 1
4: v[0..w + 1] ← 0
5: for i ← 1, n do
6: prev ← v
7: k ← max(1, radius − i)
8: start ← max(1, i − radius)
9: start ← min(n, i + radius)
10: for j ← start, end do
11: if |A[i] − B[ j]| ≤ ε then
12: v[k] ← prev[k] + 1
13: else
14: v[k] ← max(prev[k + 1], v[k − 1])
15: k ← k + 1
16: return v[k − 1]
LCSS is giving information about the similarity
of the two time series, but we are interested in the
distance between the two time series. The distance
is a dissimilarity measure and according to (Vlachos
et al., 2002) can be compute using the following for-
mula:
dist
LCSS
(A, B) = 1 −
|LCSS(A, B)|
n
(5)
3.2 Symbolic Aggregate Approximation
The Symbolic Aggregate approXimation (SAX)
method consists of two phases. In the first phase,
SAX reduces the length of the time series using the
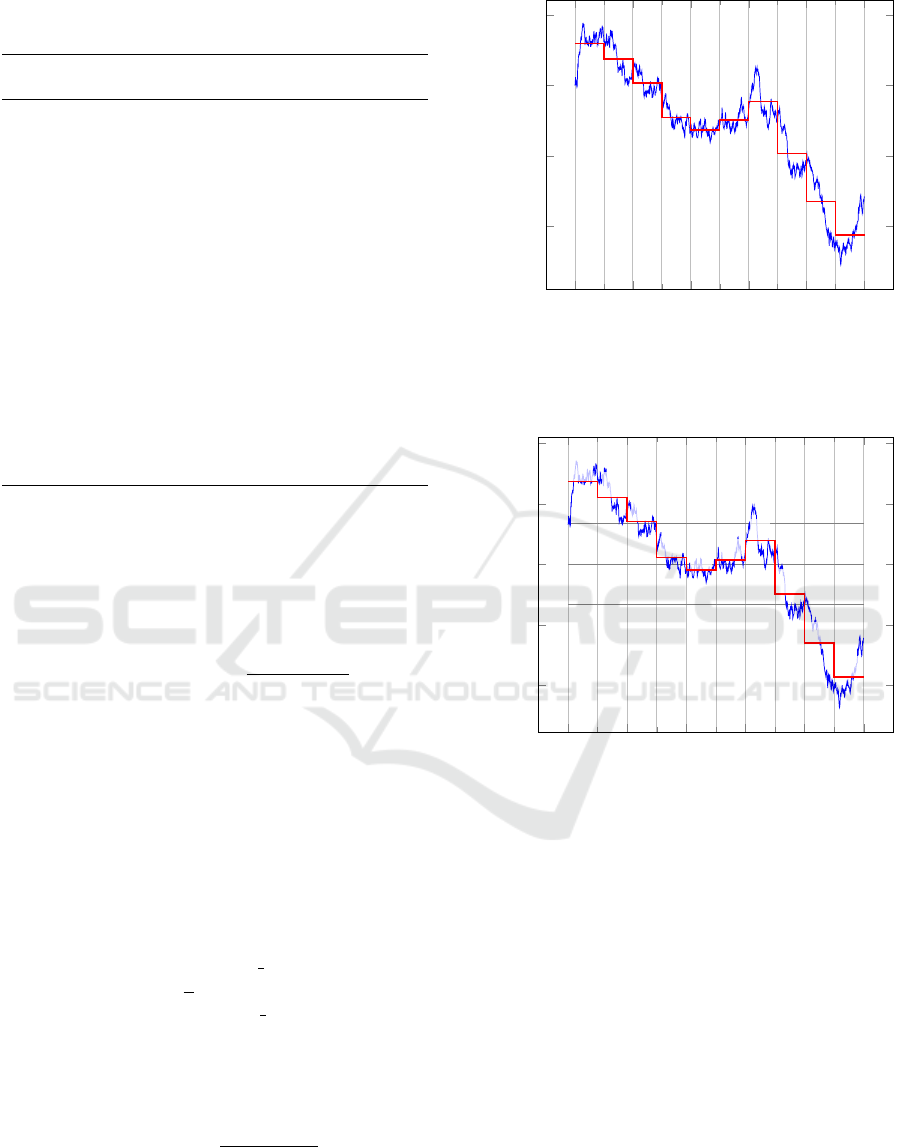
Piecewise Aggregate Approximation (PAA) (Figure
1) (Keogh et al., 2001). PAA divides a times series of
length n into k segments of equal size. Then it com-
putes the average value of the points inside each seg-
ment using the formula:
PAA(x) =
n
k
∗
(x+1)∗
n
k
−1
∑
i=x∗
n
k
T S(i) (6)
In the second phase, SAX performs a numeric re-
duction. In this phase, SAX normalizes the time se-
ries using the following formula:
ZNorm(x) =
T S(x) − µ
T S
σ
T S
(7)
After applying 7, the time series is normalized to
zero mean and unit standard deviation. In this case the
values have a Gaussian distribution. The next step is
0 200 400
600
800 1,000
−40
−20
0
20
Time
Values
Figure 1: The PAA representation of a time series. The ini-
tial time series of length 1000 is reduced to a representation
with 10 segments.
0 200 400
600
800 1,000
−2
−1
0
1
2
d
d
d
c
b
c
c
b
a
a
Time
Normalised values
Figure 2: The SAX representation of a time series with 10
segments and an alphabet of 4 symbols.
to compute the breakpoints that will divide the distri-
bution in intervals with equal probability. The num-
ber of intervals is equal to the size of the input al-
phabet. The breakpoints can be precomputed using
statistical tables. The final step is to label each seg-
ment based on the interval where the associated value
belongs. This step transforms the PAA representation
into a discrete representation (Figure 2).
3.3 Complexity Invariant Distance
Batista proposed a new invariance in (Batista et al.,
2011) based on the complexity property of the two
time series. Each of the known invariances deals with
a given aspect of the time series:
• amplitude/offset
KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval
338

• local scaling (warping)
• global (uniform) scaling
• phase (rotation)
• occlusion (outlier)
• complexity
Batista assumes that the complexity could refer to
the number of peaks and valleys and shows that in
many cases complex time series are closer to simple
time series because the peaks and the valleys are not
perfectly aligned. Because of this, he proposed a fac-
tor that will increase or decrease the distance between
two time series given theirs complexity. The next step
was to compute the complexity of a time series. For
this, he approximates the complexity by stretching the
time series and computing the length of the resulting
line using the formula:
CE(T S) =
s
n−1
∑
i=1
(T S(i) − T S(i + 1))
2
(8)
The complexity factor (CF) between two time se-
ries is computed as following:
CF(A, B) =
max{CE(A),CE(B)}
min{CE(A),CE(B)}
(9)
4 PROPOSED DISTANCE
By default, LCSS distance deals with the local scaling
invariance and with the occlusion invariance. The lo-
cal scaling invariance refers to finding similar points
from the two time series that are not locally aligned in
the time axis. The radius of the Sakoe and Chiba re-
gion represents the maximum allowed misalignment.
The occlusion invariance refers to skipping points
from one time series that are not similar with the
points from the other time series. This helps in dis-
carding outliers. To deal with the amplitude and off-
set invariance the two time series needs to be normal-
ized. If they are normalized with Z-Normalization
then the mean will become zero and the standard devi-
ation will become one. In this case, the recommended
value for ε will be always one, which cannot be the
best choice for every dataset. Also ε should depend
on the domain that contains the values of the com-
pared points. If the domain is rare then ε should be
greater so as to ignore small differences. Otherwise if
the domain is dense then ε should be smaller.
To deal with this problem we propose to use a
discretization technique before computing LCSS. The
discretization is similar to the second phase from
SAX. The values from the time series are transformed
into symbols from a finite alphabet. Two symbols are
considered equal if the absolute difference between
the associated integer values is less than or equal to
one.
The second improvement that we propose is the
addition of a threshold value. When the partially com-
puted distance is over the given threshold then we can
stop the rest of the computation and save time. In a
classification task the unlabelled time series is com-
pared to a set of labelled time series. The threshold
is dynamically set to the smallest distance found so
far between the unlabelled time series and a labelled
time series. The pseudo-code with the threshold is
presented in algorithm 5.
Algorithm 5 : The approximate length of LCSS with Sakoe
and Chiba region and threshold.
1: function lcss
5
(A, B, n, radius, threshold)
2: w ← 2 ∗ radius + 1
3: k ← 1
4: v[0..w + 1] ← 0
5: for i ← 1, n do
6: prev ← v
7: k ← max(1, radius − i)
8: start ← max(1, i − radius)
9: start ← min(n, i + radius)
10: for j ← start, end do
11: if |A[i] − B[ j]| ≤ 1 then
12: v[k] ← prev[k] + 1
13: else
14: v[k] ← max(prev[k + 1], v[k − 1])
15: if v[k − 1] + n − i ≤ threshold then
16: return −1
17: k ← k + 1
18: return v[k − 1]
5 RESULTS AND EVALUATION
For all the experiments that we run, we used the clas-
sifier k-nearest neighbours (KNN) with k=1 because
it is the most used in the field of time series (Rakthan-
manon et al., 2012). We choose the classifier imple-
mentation from Weka library (Hall et al., 2009). Also
the algorithms are implemented in Java based on the
description in their source articles. The source code
is available online at (Hasna, 2015).
In the first experiment we tried to find the best
value for the parameters of the proposed distances:
constrained LCSS (LCSS), constrained LCSS with
CID (CID-LCSS), discrete LCSS (dLCSS) and dis-
crete LCSS with CID (CID-dLCSS). For this experi-
ment we used the train instances from the benchmark
The Longest Common Subsequence Distance using a Complexity Factor
339
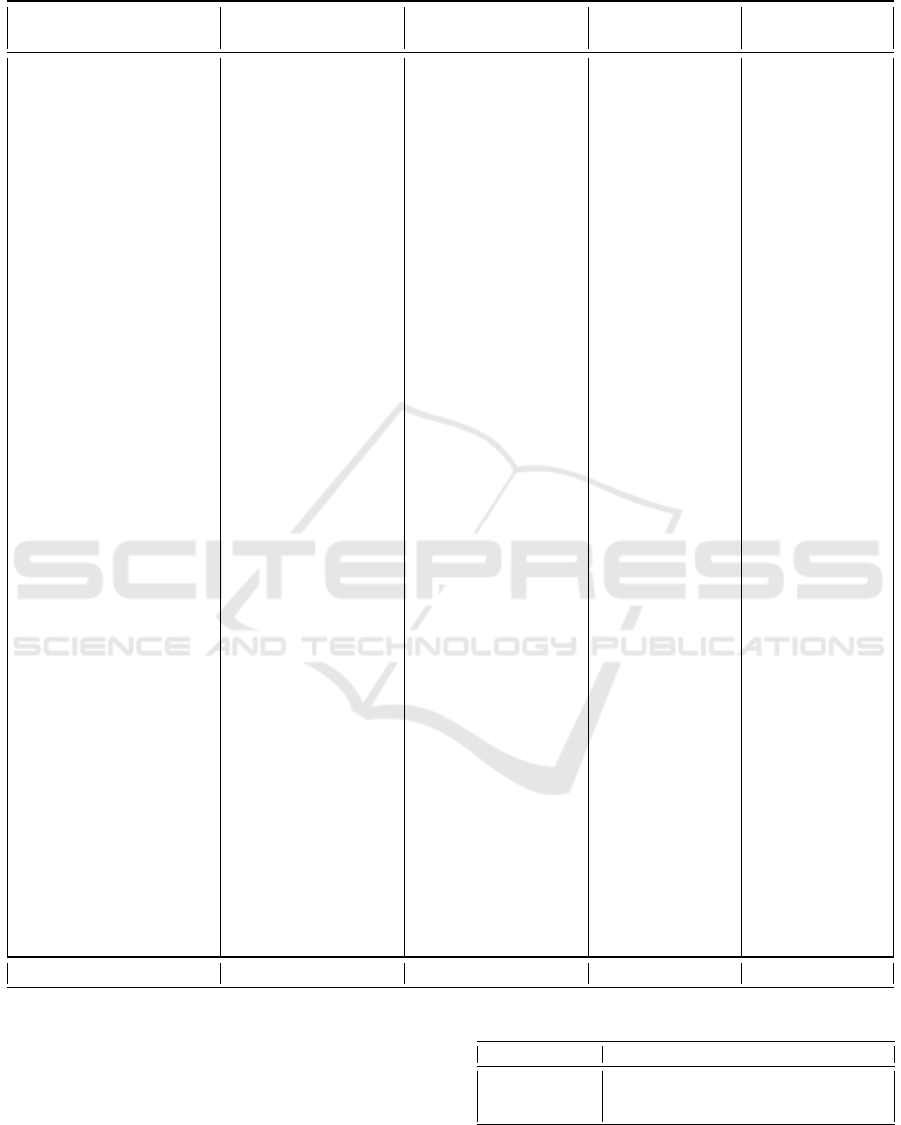
Table 2: The best value for the parameters with the corresponding classification error percentage for LCSS, CID-LCSS,
dLCSS and CID-dLCSS.
LCSS CID-LCSS dLCSS CID-dLCSS
Datasets R ε Error R ε Error R |A| Error R |A| Error
50words 10 0,2 21,11 10 0,2 20,44 10 32 22,22 10 16 21,33
Adiac 1 0,05 38,71 1 0,05 35,12 1 256 49,23 1 256 47,69
Beef 2 0,1 46,66 2 0,1 53,33 1 32 46,67 1 32 53,33
CBF 1 0,1 3,33 1 0,2 0 6 512 0 1 8 0
ChlorineConcentration 0 0,2 27,83 0 0,2 28,9 0 32 30,41 0 16 31,91
CinCECGtorso 1 0,8 10 2 0,8 7,5 2 16 12,5 1 16 12,5
Coffee 4 0,1 0 1 0,2 0 1 32 0 1 32 0
CricketX 9 0,4 22,56 5 0,4 20,51 9 16 23,59 6 16 21,03
CricketY 9 0,4 23,33 6 0,4 27,94 9 8 29,74 5 8 29,49
CricketZ 8 0,4 23,84 5 0,4 22,56 10 8 23,59 9 8 20,51
DiatomSizeReduction 1 0,00625 6,25 1 0,00625 6,25 1 32 6,25 1 32 6,25
ECG200 4 0,4 12 2 0,2 12 4 16 12 4 16 10
ECGFiveDays 8 0,0125 8,69 0 0,00625 8,69 0 8 17,39 0 8 17,39
FaceAll 6 0,8 2,14 9 0,4 1,78 6 8 1,79 5 8 2,32
FaceFour 1 0,2 4,16 1 0,2 8,33 1 8 4,17 6 8 0
FacesUCR 10 0,4 3,5 7 0,4 4 9 8 3 9 16 2,5
fish 7 0,05 13,14 5 0,025 13,14 4 32 14,86 3 64 16
GunPoint 1 0,2 2 2 0,2 2 3 32 0 2 32 0
Haptics 1 0,4 46,45 8 0,4 43,87 5 8 48,39 2 32 47,1
InlineSkate 5 0,2 48 9 0,00625 44 8 64 50 9 64 47
ItalyPowerDemand 5 0,1 7,46 5 0,025 2,98 5 64 4,48 5 8 5,97
Lighting2 1 0,1 16,66 3 0,1 16,66 9 32 16,67 1 16 21,67
Lighting7 10 0,4 27,14 1 0,1 24,28 1 16 31,43 2 32 31,43
MALLAT 1 0,4 1,81 1 0,4 1,81 1 8 9,09 3 64 5,46
MedicalImages 8 0,2 30,97 4 0,2 29,92 5 32 29,13 9 32 26,51
MoteStrain 4 0,0125 10 2 0,8 15 3 128 10 2 32 20
OliveOil 1 0,00625 6,66 1 0,00625 6,66 1 512 10 1 512 10
OSULeaf 10 0,2 18 10 0,2 19,5 10 32 18 10 16 19
SonyAIBORobotSurface1 2 0,4 10 0 0,00625 0 2 16 10 0 16 0
SonyAIBORobotSurface2 8 0,05 7,4 2 0,05 7,4 2 8 7,41 2 8 7,41
StarLightCurves 10 0,1 10,9 1 0,025 5 5 32 12,2 1 512 5,1
SwedishLeaf 4 0,2 10,8 3 0,2 10,6 10 16 15,2 10 16 13,4
Symbols 6 0,2 4 10 0,025 0 10 16 0 1 64 0
SyntheticControl 7 0,8 2,66 4 0,8 3 4 8 5,67 5 32 3
Trace 3 0,2 2 0 0,4 0 4 32 1 4 32 1
TwoLeadECG 7 0,2 4,34 7 0,1 4,34 3 32 4,35 7 32 4,35
TwoPatterns 9 0,8 0 10 0,2 0 7 16 0 8 8 0
uWaveGestureLibraryX 6 0,4 23,99 7 0,2 21,54 10 16 25 7 16 22,77
uWaveGestureLibraryY 4 0,4 28,01 8 0,4 25,44 7 32 27,68 6 32 26,23
uWaveGestureLibraryZ 8 0,4 26,56 8 0,4 24,44 8 16 28,35 9 32 27,01
wafer 1 0,2 0,1 2 0,2 0 1 4 0 1 4 0
WordsSynonyms 9 0,4 22,47 8 0,2 23,97 9 32 24,35 9 8 24,35
yoga 8 0,05 12 10 0,05 11,66 8 128 13 10 128 14
AVERAGE 15,06 14,29 16,25 15,69
datasets (Chen et al., 2015) and we apply the hold-
one-out validation i.e. one instance is used for testing
and the rest of the instances are used for training the
classifier.
The best values for the parameters are searched in
the intervals presented in Table 1. The chosen values
for the parameters and the corresponding classifica-
tion error percentage are shown in the Table 2.
Table 1: The tested values for the distances parameters.
Parameters Tested values
radius (R) 1%, 2%, 3%, 4%, 5%, 6%, 7%, 8%, 9%, 10%
alphabet size (|A|) 4, 8, 16, 32, 64, 128, 256, 512
epsilon (ε) 0.00625, 0.0125, 0.025, 0.05, 0.1, 0.2, 0.4, 0.8
Table 2 that for 36 from 43 datasets it is better
to apply the complexity invariant factor (CID) and
among them there are 15 cases where the results are
KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval
340

Table 3: The classification error percentage on the test instances for the 43 benchmark datasets.
Datasets DTW-full LCSS-full LCSS CID-LCSS dLCSS CID-dLCSS
50words 31,94 20,76 20,44 19,78 22,19 20,44
Adiac 39,66 75,84 38,61 35,55 48,84 46,03
Beef 50,3 45,7 26,66 26,66 23,33 23,33
CBF 0,67 1,67 12 1,77 1,44 2,77
ChlorineConcentration 35,45 30,13 28,17 29,16 31,97 30,75
CinCECGtorso 32,64 7,15 6,66 5,14 12,17 9,92
Coffee 1,11 2,11 7,14 0 10,71 10,71
CricketX 23,54 24,46 26,15 26,41 28,2 24,35
CricketY 26,2 24,3 22,05 24,35 26,92 25,38
CricketZ 22,82 23,39 24,35 24,87 28,97 23,33
DiatomSizeReduction 4,19 6,55 8,82 8,49 5,55 5,22
ECG200 20,13 14,15 9 10 11 13
ECGFiveDays 23,97 13,45 28,57 25,43 10,56 17,88
FaceAll 5,68 2,02 21,06 19,11 22,18 22,48
FaceFour 15,1 5,27 6,81 7,95 6,81 6,81
FacesUCR 10,15 4,44 4,63 5,56 4,82 6,73
fish 23,68 13,73 10,28 8 13,71 12,57
GunPoint 12,4 6,53 4 2,66 2 2
Haptics 60,99 59,44 65,9 62,66 63,63 61,68
InlineSkate 60,49 57,55 56,72 54,54 60,72 59,09
ItalyPowerDemand 7,74 6,26 13,31 15,74 10,78 7,67
Lighting2 17,7 24,51 14,75 16,39 18,03 18,03
Lighting7 30,16 34,22 32,87 35,61 31,5 34,24
MALLAT 5,78 7,07 10,06 9,42 13,81 8,31
MedicalImages 25,88 31,3 32,36 31,97 31,97 29,47
MoteStrain 16,79 12,18 18,53 14,29 17,33 18,69
OliveOil 13,93 60 16,66 16,66 13,33 13,33
OSULeaf 38,27 22,14 23,55 24,38 24,79 24,79
SonyAIBORobotSurface1 19,91 24,81 28,95 9,48 27,12 10,15
SonyAIBORobotSurface2 15,39 16,92 22,24 10,59 15,74 14,69
StarLightCurves 8,57 14,07 11,26 5,82 14,31 6,14
SwedishLeaf 21,36 11,11 11,04 11,2 14,88 12,64
Symbols 5,92 6,58 6,53 4,42 5,32 7,23
SyntheticControl 0,89 3,06 5,33 4,33 5,33 7,33
Trace 0,03 1,91 3 6 1 1
TwoLeadECG 8,17 11,73 10,88 8,78 18,96 8,95
TwoPatterns 0 0,14 0,07 0,2 0,07 0,1
uWaveGestureLibraryX 27,24 22,48 23,42 21,97 23,64 22,22
uWaveGestureLibraryY 37,68 31,07 31,29 28,42 31,63 29,34
uWaveGestureLibraryZ 34,35 30,61 30,43 28,53 31,74 29,87
wafer 1,6 0,39 0,92 0,82 0,35 0,4
WordsSynonyms 35,12 24,87 24,6 25,7 28,21 26,64
yoga 15,12 13,43 14 13,8 13,96 14,2
AVERAGE 20,66 19,75 18,93 17,27 19,29 17,9
significantly better (over 5% improvement). In 9
cases it is better to not use CID and this happens be-
cause the instances from the same class have different
levels of noise which implies different levels of com-
The Longest Common Subsequence Distance using a Complexity Factor
341

plexity.
In the second experiment we want to find out if the
assumptions made on the train instances are still valid
for the test instances. Also we want to compare the re-
sults for LCSS, CID-LCSS, dLCSS and CID-dLCSS
with the published results in (Bagnall et al., 2016) for
LCSS-full (no constraint region) and for the state of
the art DTW-full (no constrain region) and COTE. For
this experiment we used for the parameters of LCSS,
CID-LCSS, dLCSS and CID-dLCSS the values ob-
tain in the previous experiment. The classifier learns
from the train set and it is tested on the test set. The
split between test and train is already made on the
benchmark datasets. In Table 3 there are presented the
classification error percentages for the baseline meth-
ods: DTW-full and LCSS-full and for our methods:
LCSS, CID-LCSS, dLCSS and CID-dLCSS.
As we can see from the results, in 32 cases (75%)
the magnitude order between the errors of LCSS and
CID-LCSS on the test set remains the same as on the
train sets. In the case of dLCSS and CID-dLCSS there
are 29 datasets (67%) where the magnitude order is
preserved. When we compare CID-LCSS with the
baseline LCSS method (LCSS-full) there are 19 cases
(37%) where CID-LCSS is better than LCSS-full.
Among this cases there are 17 where the difference
is significant (more than 5% improvement). When we
compare CID-dLCSS with the baseline LCSS method
(LCSS-full) there are 32 cases (75%) where CID-
dLCSS is better than LCSS-full. Among this cases
there are the same 17 where the difference is signifi-
cant (more than 5% improvement).
In the third experiment (Table 4) we compare
the improvement made by the proposed threshold for
the distances: LCSS, CID-LCSS, dLCSS and CID-
dLCSS. We use the same classifier, train and test in-
stances and distances parameters as in the previous
experiment. We ran this experiment two times and
count the number of comparisons between the points
(line 11 from Algorithm 5). In the first run, the dis-
tances use the threshold (lines 15 and 15 from Algo-
Table 4: The number of benchmark datasets for which the
percentage of skipped comparisons is in the given interval.
Intervals LCSS CID-LCSS dLCSS CID-dLCSS
0-10 1 0 0 0
10-20 4 4 1 1
20-30 1 4 1 0
30-40 4 0 4 4
40-50 5 5 5 5
50-60 7 14 15 11
60-70 12 3 10 12
70-80 6 8 5 8
80-90 2 4 1 1
90-100 1 1 1 1
rithm 5) and in the second run the distances didn’t use
the threshold.
From the results presented in Table 4 we can see
that in the majority of the cases (> 50%), we skipped
between 50% and 70% of the comparisons. In more
than 65% of the cases we skipped at least 50% of the
comparisons. The number of comparisons is corre-
lated with the computation time and this means that
we doubled the computation speed in more than 65%
of the cases.
The computation time depends on internal factors
(ex: the similarity between the two time series, the
length of the time series etc.) and external factors
(ex: the language in which the algorithms are writ-
ten, the hardware of the machine where the experi-
ments are run etc.). Taking this into consideration,
for the first run, the smallest computation time is 0.04
ms (ItalyPowerDemand) and the longest computation
time is 315.42 ms (StarLightCurves). For the second
run, when we don’t use the threshold, the compu-
tation time is between 0.07 ms (ItalyPowerDemand)
and 1028.67 ms (StarLightCurves).
6 CONCLUSIONS
In this paper we have made a comparison between
different LCSS based distances and we have demon-
strated that applying a complexity factor to the LCSS
distance can improve the accuracy of the classifica-
tion. Also we showed that using a region constraint
and a threshold value for the distance not only im-
prove the speed of classification, but also reduce the
classification error rate.
All the distances used in the experiments
stretches/compress one time series so as to get the best
alignment with the second time series. The main dif-
ference between DTW and LCSS is the expressive-
ness of the distance value. In the case of DTW dis-
tance, we perform a sum of the distances between the
best aligned points from the two time series, but for
computing LCSS we perform a count of the similar
points. This implies that DTW distance is more sen-
sible to the differences between the two time series.
Whereas LCSS distance can skip more easily the out-
liers from the time series. This two properties are in
opposition and choosing the best distance depends on
the type of the datasets.
Like in other classification problems, the results
cannot be the best for each of the datasets. In the
above experiments we choose the distance that per-
forms the best in the training step. In the future we
want to search for the meta-features of the datasets
that will help us decide in which situation it is bet-
KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval
342

ter to use the proposed distances without running the
initial training step.
REFERENCES
Bagnall, A., Bostrom, A., Large, J., and Lines, J. (2016).
The Great Time Series Classification Bake Off: An
Experimental Evaluation of Recently Proposed Algo-
rithms. Extended Version.
Batista, G. E., Wang, X., and Keogh, E. J. (2011). A
Complexity-Invariant Distance Measure for Time Se-
ries. In SDM, volume 11, pages 699–710. SIAM.
Chen, Y., Keogh, E., Hu, B., Begum, N., Bag-
nall, A., Mueen, A., and Batista, G. (2015).
The UCR time series classification archive.
www.cs.ucr.edu/∼eamonn/time series data/.
Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann,
P., and Witten, I. H. (2009). The weka data min-
ing software: An update. SIGKDD Explor. Newsl.,
11(1):10–18.
Hasna, O. L. (2015). The time series math library.
github.com/octavian-h/time-series-math/.
Hirschberg, D. S. (1975). A linear space algorithm for com-
puting maximal common subsequences. 18(6):341–
343.
Itakura, F. (1975). Minimum prediction residual principle
applied to speech recognition. 23(1):67–72.
Keogh, E., Chakrabarti, K., Pazzani, M., and Mehrotra, S.
(2001). Dimensionality reduction for fast similarity
search in large time series databases. 3(3):263–286.
Lin, J., Keogh, E., Lonardi, S., and Chiu, B. (2003). A sym-
bolic representation of time series, with implications
for streaming algorithms. In Proceedings of the 8th
ACM SIGMOD Workshop on Research Issues in Data
Mining and Knowledge Discovery, pages 2–11. ACM.
Rakthanmanon, T., Campana, B., Mueen, A., Batista, G.,
Westover, B., Zhu, Q., Zakaria, J., and Keogh, E.
(2012). Searching and mining trillions of time se-
ries subsequences under dynamic time warping. In
Proceedings of the 18th ACM SIGKDD International
Conference on Knowledge Discovery and Data Min-
ing, pages 262–270. ACM.
Sakoe, H. and Chiba, S. (1978). Dynamic programming
algorithm optimization for spoken word recognition.
26(1):43–49.
Vlachos, M., Kollios, G., and Gunopulos, D. (2002). Dis-
covering similar multidimensional trajectories. In
Data Engineering, 2002. Proceedings. 18th Interna-
tional Conference on, pages 673–684. IEEE.
The Longest Common Subsequence Distance using a Complexity Factor
343
