Robust Fuzzy Modeling and Symbolic Regression for Establishing

Accurate and Interpretable Prediction Models in Supervising

Tribological Systems

Edwin Lughofer

, Gabriel Kronberger

, Michael Kommenda

, Susanne Saminger-Platz

Andreas Promberger

, Falk Nickel

, Stephan Winkler

and Michael Affenzeller

Heuristic and Evolutionary Algorithms Laboratory, School of Informatics, Communications and Media,

Softwarepark 11, 4232 Hagenberg, Austria

Department of Knowledge-Based Mathematical Systems, Johannes Kepler University Linz, 4040 Linz, Austria

Miba Frictec, Peter-Mitterbauer-Str., 4661 Roitham, Austria

Keywords:

Tribological Systems, Robust Fuzzy Modeling, Generalized Takagi-Sugeno Fuzzy Systems, Symbolic

Regression, Multi-objective Accuracy/Complexity Tradeoff, Enhanced Regularized Learning.

Abstract:

In this contribution, we discuss data-based methods for building regression models for predicting important

characteristics of tribological systems (such as the friction coefﬁcient), with the overall goal of improving and

partially automatizing the design and dimensioning of tribological systems. In particular, we focus on two

methods for synthesis of interpretable and potentially non-linear regression models: (i) robust fuzzy modeling

and (ii) enhanced symbolic regression using genetic programming, both embedding new methodological ex-

tensions. The robust fuzzy modeling technique employs generalized Takagi-Sugeno fuzzy systems. Its learning

engine is based on the Gen-Smart-EFS approach, which in this paper is (i) adopted to the batch learning case

and (ii) equipped with a new enhanced regularized learning scheme for the rule consequent parameters. Our

enhanced symbolic regression method addresses (i) direct gradient-based optimization of numeric constants

(in a kind of memetic approach) and (ii) multi-objectivity by adding complexity as a second optimization cri-

terion to avoid over-ﬁtting and to increase transparency of the resulting models. The comparison of the new

extensions with state-of-the-art non-linear modeling techniques based on nine different learning problems (in-

cluding targets wear, friction coefﬁcients, temperatures and NVH) shows indeed similar errors on separate

validation data, but while (i) achieving much less complex models and (ii) allowing some insights into model

structures and components, such that they could be conﬁrmed as very reliable by the experts working with the

concrete tribological system.

1 INTRODUCTION

Friction models have been studied for more than hun-

dred years (Berger, 2002) and are central for under-

standing and accurately describing tribological sys-

tems which occur in almost all mechanical systems.

The main difﬁculty in modeling friction is that it

is a very complicated phenomenon which depends

on a large variety of parameters including mechani-

cal properties (e.g. surface roughness and hardness,

lubrication), load (e.g. pressure, energy and slid-

ing speed), and environmental conditions (e.g. hu-

midity, temperature) (Berger, 2002). Additionally,

friction is a dynamic phenomenon as abrasive ef-

fects and material deterioration as well as tempera-

ture changes strongly inﬂuence friction characteristics

(De Wit et al., 1995).

Mathematical models of friction systems derived

solely from mechanical principles (De Wit et al.,

1995) are strongly simpliﬁed and therefore limited.

The forces acting in tribological systems on a micro-

and nano-level depend on the surface characteristics

of the friction materials as well as on the lubrication

and are difﬁcult to describe mathematically (Sellgren

et al., 2003) (Berger, 2002). Many of these factors

are hard to capture in a mathematical model based

solely on physical principles (Aleksendric and Car-

lone, 2015). In particular, we study friction systems

as applied in clutches employed in power-trains (Sen-

atore et al., 2011). Relevant inﬂuence factors include

Lughofer, E., Kronberger, G., Kommenda, M., Saminger-Platz, S., Promberger, A., Nickel, F., Winkler, S. and Affenzeller, M.

Robust Fuzzy Modeling and Symbolic Regression for Establishing Accurate and Interpretable Prediction Models in Supervising Tribological Systems.

DOI: 10.5220/0006068400510063

In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 2: FCTA, pages 51-63

ISBN: 978-989-758-201-1

the composition and mechanical properties of the em-

ployed friction material, the oil, or the geometry of

groovings on friction material.

The overall objective is the improvement of the

design process of these tribological systems by us-

ing accurate models for the most important charac-

teristics. These models should be included in an ex-

pert system for the virtual design and dimensioning

of friction systems to support engineers (Aleksendric

and Carlone, 2015), thus they should be not too com-

plex and interpretable.

1.1 State-of-the-Art

Friction models can be roughly categorized into an-

alytical models derived from physical principles and

purely empirical models (Berger, 2002). Analytical

models such as the one given by (De Wit et al., 1995)

are usually rather sophisticated and describe friction

forces based on surface characteristics of the fric-

tion materials. Drawbacks of these models are the

high complexity as well as the limited applicability

in real scenarios, because important effects such as

non-linear dynamics or abrasive effects are not cap-

tured by the models. Models based on ﬁnite elements

simulation, such as the model described in (Sellgren

et al., 2003), are computationally expensive and also

have the drawback that relevant effects in practical ap-

plications are not described accurately.

Empirical models have predictive capabilities but

do not provide a detailed, physically correct and gen-

eral description of friction. Depending on the simu-

lation objectives these empirical models can be rather

simple, such as the non-linear numerical model pre-

sented in (Loh et al., 2000) which estimates the co-

efﬁcient of friction based solely on load parameters.

An example for a more complex numerical model

that also include effects of surface characteristics is

given in (Xiao et al., 2007). In both of these cases,

the model structure has been manually (and not au-

tomatically) deﬁned based on experience and intu-

ition about the main effects and the parameters of the

model have been optimized to ﬁt the model to mea-

surements (which requires high development effort).

Recently, especially artiﬁcial neural networks

have been applied successfully in multiple occa-

sions for data-based modeling of tribological systems

(Aleksendric and Carlone, 2015). For example, neu-

ral networks have been used to predict wear of brake

friction materials where the complete formulation of

the friction material, important manufacturing condi-

tions, as well as load parameters, sliding velocity and

the temperature have been used as input for the net-

work (Aleksendri, 2010). Hosenfeldt and colleagues

describe that they trained an artiﬁcial neural network

model that “can predict the tribological behaviour

of camshaft and bucket tapped systems” (Hosenfeldt

et al., 2014), and state that they achieved “a deviation

of 8%” which “is a very good result, especially when

considering that the measurement error with reference

to friction is 5%” (Hosenfeldt et al., 2014). On the

other hand, ANNs deliver models which typically ap-

pear as black boxes with high structural complexity.

This makes them unattractive and not usable within

an interpretable expert system.

1.2 Our Approach

We design prediction models for a variety of nine

important system variables during the design and di-

mensioning of tribological systems: four different

measurements of the coefﬁcient of friction, two dif-

ferent measurements of wear, two temperature mea-

surements, vibration and harshness (NVH). We con-

centrated on two architectures for data-driven regres-

sion models, Takagi-Sugeno-type (TS) fuzzy systems

(Takagi and Sugeno, 1985), as recently introduced

in generalized form (Lemos et al., 2011), and sym-

bolic regression models containing functional terms

achieved through genetic progamming (GP) (Affen-

zeller et al., 2009), which both allow interpretation

and inspection of the resulting models, e.g., for gain-

ing better insights into the system behavior. We pro-

pose two major enhancements in our learning engines

to cope robustly with binary input variables and high

noise levels.

In case of (generalized) TS fuzzy systems, we in-

tegrate a convex combination of Lasso and ridge re-

gression for optimizing the linear consequent param-

eters. This is leaned on the concept of elastic net

regularization (Hastie et al., 2010) (Zou and Hastie,

2005), but adopted to the speciﬁc (locally weighted)

optimization problem for generalized Takagi-Sugeno

fuzzy systems for the ﬁrst time. Such a more so-

phisticated learning concept is expected to enhanced

the robustness of the solutions. For learning the

rule structure and the rules’ antecedent parts, we em-

ploy the Gen-Smart-EFS technique, originally devel-

oped for streaming data in (Lughofer et al., 2015),

which we adjust for the batch off-line case by spe-

ciﬁc two-stage iterative optimization procedure (see

Section 2.2.2). Joining rule antecedent and enhanced

regularized consequent learning, the new method is

termed as Robust-GenFIS (short for Robust General-

ized Fuzzy Inference Systems) and described in detail

in Section 2.2.2.

In case of symbolic regression models, the genetic

programming (GP) approach in (Affenzeller et al.,

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

2009) is extended by gradient-based optimization of

numeric constants (Kommenda et al., 2013) and by

multi-objective optimization of complexity and esti-

mation accuracy (Kommenda et al., 2016). These ex-

tensions are ﬁrstly combined to a joint enhanced op-

timization and applied to a real-world scenario in this

paper. In traditional GP-based symbolic regression

numeric constants are optimized side-by-side with the

model structure relying solely on evolutionary opera-

tors of crossover, mutation and selection to ﬁnd op-

timal constants. Incorporating a gradient-based op-

timizer for constants increases the efﬁciency of GP-

based symbolic regression and can thus improve ﬁnal

solution quality. A drawback of GP-based symbolic

regression in practical applications is the tendency

to produce very large (“bloated”) solutions (Langdon

et al., 1999). Selection in combination with crossover

operations has the effect that ineffective parts accu-

mulate in solution candidates and therefore the struc-

tural complexity of solution candidates increases. We

thus employ multi-objective optimization to produce

a set of Pareto-optimal solutions in the context of GP,

where one dimension corresponds to the model com-

plexity and the other to the model error — see Section

2.3.

In this article, we compare the newly extended

fuzzy and symbolic regression modeling approaches

with other state-of-the-art (SoA) techniques such as

support vector regression (Smola and Vapnik, 1997),

random forests (Breiman, 2001) or gradient boosted

trees (Friedman, 2001), as well as with related and

widely used fuzzy system extraction algorithms such

as LoLiMoT (Nelles, 2001), genﬁs2 (modiﬁed version

of it) (Chiu, 1994) and FLEXFIS (Lughofer, 2008), in

terms of predictive accuracy as well as model com-

plexity.

The major ﬁnding is that linear models are insuf-

ﬁcient for modeling the main characteristics of tri-

bological systems while the newly proposed robust

fuzzy modeling and enhanced symbolic regression

approaches produce signiﬁcantly more accurate mod-

els (Section 4.1), which satisfactory for the usage in

virtual design of tribological systems. The predictive

quality on separate test data indeed turned out to be

similar (similar error ranges) to the predictive qual-

ity achieved by related SoA methods. However, the

models produced with our methods have much lower

complexity (see Section 4.2) than those achieved by

related non-linear techniques. They also can be nat-

urally represented in form of linguistically readable

fuzzy rules and in form of symbolic, physically in-

terpretable terms; both can be casted into a tree-like

structure, achieving synergy on structural level, which

induces the possibility of a direct and transparent

Table 1: Variables in the preprocessed data set.

Number Type Identiﬁcation

22 continuous features x

. . . x

3 binary features representing the friction mat. type b

. . . b

2 binary features representing the test procedure Source

, Source

25 binary features representing the friction material Mat

. . . Mat

10 binary features representing the grooving type Gro

. . . Gro

11 binary features representing the oil Oil

. . . Oil

4 continuous measurements of coeff. of friction (target) Cf

. . . Cf

2 continuous measurements of wear (target) Wear

, Wear

1 ordinal rating of noise, vibration, and harshness (target) NVH

2 continuous measurements of temperature (target) Temp

, Temp

model comparison for operators and experts (Section

4.3).

2 METHODOLOGY

2.1 Data Acquisition and Preparation

The data used for modeling have been acquired

through extensive testing of many different friction

plates on tribological test benches. Each of the fric-

tion plates has been tested using one of two differ-

ent test programs. The ﬁrst test program is designed

to test and measure coefﬁcient of friction and wear

under different loads, the second test program is de-

signed to test noise and vibration characteristics. In

total, data from almost 1300 individual test runs are

considered. The combined data set contains measure-

ments from test procedures for many different com-

binations of friction materials and oils, whose major

inﬂuence factors are friction material, the oil, design

parameters of the friction plate as well as temperature.

In a preprocessing phase we cleaned the data set

by removing obvious measurement errors and incom-

plete test runs so that the resulting data set contains

only valid measurements for the most commonly used

combinations of friction material and oil. To prepare

for the modeling phase we created additional binary

indicator features for each friction material, grooving,

and oil. After preprocessing the dataset contains vari-

ables shown in Table 1. Depending on the target vari-

able the number of rows in the data sets is between

300 and 4000 rows.

2.2 Robust Fuzzy Modeling

2.2.1 Data-driven Fuzzy Modeling Architecture

The advantage of data-driven fuzzy systems among

other types of soft computing based model architec-

tures and machine learning techniques is their joined

characteristics of (i) universal approximation property

(Castro and Delgado, 1996), being able to model any

implicitly contained non-linear relationship with an

arbitrary degree of accuracy and (ii) linguistic inter-

pretability (Lughofer, 2013), allowing some insights

Robust Fuzzy Modeling and Symbolic Regression for Establishing Accurate and Interpretable Prediction Models in Supervising

Tribological Systems

into the system dependencies and variable interrela-

tions. While the antecedent parts of the rules embed

the linguistically interpretable description of feature

interrelations, there are various possibilities how to

design the consequent parts, inducing different types

of fuzzy systems (Lughofer, 2011).

For the robust modeling intentions in this paper,

we will employ the (recently introduced) generalized

version of TS fuzzy systems (Lemos et al., 2011),

which induced more compact rule bases with similar

or even less model errors than conventional TS fuzzy

systems during past studies (Lughofer et al., 2015) be-

cause of its ability to model piecewise local correla-

tions between variables in a more compact and accu-

rate way. In the generalized case, the rules are deﬁned

by:

IF ~x IS (about) µ

THEN l

(~x) = w

+ w

+ ... + w

(1)

where l

the hyper-plane deﬁning the consequent of

the ith rule, µ

denotes a high-dimensional kernel

function, which, in accordance to the basis function

networks spirit, is given by the multivariate Gaussian

distribution:

(~x) = exp(−

(~x −~c

)

−1

(~x −~c

)) (2)

with ~c

the center and Σ

−1

the inverse covariance ma-

trix of the ith rule, allowing any possible rotation and

spread of the rule.

The output of a (generalized) TS system consist-

ing of C rules is a weighted linear combination of the

outputs produced by the individual rules (through the

’s), thus:

f (~x) = ˆy =

∑

i=1

(~x) ·l

(~x) Ψ

(~x) =

(~x)

∑

j=1

(~x)

(3)

with µ

(~x) the rule ﬁring degree obtained through (2).

2.2.2 Our Robust Learning Engine for

Generalized TS Fuzzy Models

The learning engine is based on the generalized smart

evolving fuzzy systems approach, shortly termed

Gen-Smart-EFS (Lughofer et al., 2015), which has

been designed for (fast) streaming data, thus allow-

ing only a single-pass over incoming data samples for

expanding or shrinking the structure and recursively

updating the parameters. We thus adopt it here to

the batch, off-line case by performing multiple passes

over the entire (training) data set to optimize the po-

sitioning, shape and direction of the rules.

Rule Structure Elicitation and Initialization of

Non-linear Parameters. The ﬁrst phase performs

a single-pass over the whole data set in order to elicit

the optimal number of rules for the current problem

(data set) at hand. It follows the same procedure

as used in the Gen-Smart-EFS approach for the an-

tecedent parts by compactly applying the following

steps (with C = 0 initially) (see (Lughofer et al., 2015)

for detailed formulation and motivation of algorith-

mic parts):

1. Load a new sample ~x; if it is the ﬁrst one, Goto

Step 5 (there, ignoring the if-part);

2. Elicit the winning rule, i.e. the rule closest to

the current sample, which is then denoted as ~c

win

;

for the distance calculation, standard Mahalanobis

distance is used (as on the right hand side in (4)

below).

3. Check whether the following criterion is met (the

rule evolution criterion):

min

i=1,...,C

(~x −~c)

−1

(~x −~c) > r

= facp

√

1.0

(1 −1/(k

+ 1))

(4)

with p the dimensionality of the input feature

space and f ac an a priori deﬁned parameter, steer-

ing the tradeoff between stability (update of an old

cluster) and plasticity (evolution of a new cluster).

This is the only sensitive parameter and is var-

ied during the model evaluation phase, see Section

3.1.

4. If (4) is not met, the centre of the winning rule is

updated by

win

(N + 1) =~c

win

(N) + η

win

(~x −~c

win

(N)) (5)

and its inverse covariance matrix by (the index

win neglected due to transparency reasons):

−1

(k +1) =

−1

(k)

1 −α

−

1 −α

(Σ

−1

(k)(~x −~c))(Σ

−1

(k)(~x −~c))

1 + α((~x −~c)

−1

(k)(~x −~c))

(6)

with N the number of samples seen so far and

α =

win

with k

win

the number of samples seen

so far for which c

win

has been the winning rule

(cluster). The former stems from the idea in vec-

tor quantiﬁcation (Gray, 1984) by minimizing the

expected squared quantization error. The latter

is a recursive exact update, which is analytically

derived with the usage of the Neumann series

(Lughofer and Sayed-Mouchaweh, 2015).

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

5. If (4) is met, a new rule is evolved as covering a

new region in the feature space (i.e. having sufﬁ-

cient novelty content) by setting its center~c

C+1

the coordinates of ~x and initialize its inverse co-

variance matrix Σ

−1

win

by setting it to a diagonal

matrix with entries 1 divided by a small fraction

of the range; C = C + 1.

Optimizing Non-linear Parameters (New Exten-

sion #1). After the initial phase is ﬁnished, a ﬁne-

tuning phase is conducted which optimizes the cen-

ters and inverse covariance matrices of the rules as

initially formed in one single pass. This is achieved

over multiple iterations of the whole data set by suc-

cessively moving the centers and inverse covariance

matrices according to (5) and (6), with

win

iterations + 1

α =

iterations + 1

(7)

This is in accordance with the Robbins-Monroe con-

ditions and thus assures convergence to the optimal

solution in terms of the quantization error.

The iterations are performed as long as the stop-

ping criterion is not fulﬁlled. We have chosen the de-

gree of change between two cluster partitions from

two consecutive cycles t −1 and t; so, if the follow-

ing condition is met

∑

i=1

k~c

(t) −~c

(t −1)k < ε, (8)

with ε set to a small positive number, the optimization

iterations are stopped.

Robust Learning of Linear Consequent Parame-

ters (New Extension #2). Once the rule structure

and antecedent parts are obtained, the aim is to es-

timate the consequent parameters in a way to best

match predicted model outputs with observed target

values. Therefore, the least squares error criterion is

the most conventional choice in data-driven regres-

sion modeling as appropriate optimization problem.

We use its weighted version in order to induce a local

learning scheme, i.e. to estimate the parameters per

rule separately and independently due to robustness

and accuracy reasons (Lughofer, 2011) (Chapter 2).

The (locally) weighted least squares optimization

problem for consequent parameters in all C rules is

formalized as:

∑

k=1

(~x(k))e

(k) −→ min

i = 1, ...,C (9)

where e

(k) = y(k) − ˆy

(k) represents the error of the

local linear model in the kth sample. It can be solved

in closed analytical form:

= (R

−1

~y (10)

with R the regression matrix, additionally containing

a column of ones for the intercept, and Q

the diagonal

weighting matrix ∈ R

NxN

, containing the membership

degrees of all N training data samples to the ith rule.

Obviously, the solution in (10) may become unsta-

ble once the matrix R

R is of low rank or even sin-

gular. The likelihood for such an occurrence increase

with signiﬁcant noise levels and especially when bi-

nary variables (containing only either 0s and 1s) are

involved — both is the case in the application of tri-

bological systems, especially the usage of a particular

oil, grooving or friction material type results in bi-

nary inputs (compare with Figure 1). Therefore, it is

indispensable to perform a regularization of the opti-

mization problem in order to assure robust solutions.

The most convenient option is to integrate Tichonov-

type regularization, which leads to the form of classi-

cal ridge regression, see (Hastie et al., 2009) (Chapter

2), which has been also used before in fuzzy systems

training.

Here, we go one step further and employ a gen-

eralization of ridge regression, termed as elastic net

(Hastie et al., 2010), and adopt it for learning of con-

sequent parameters in fuzzy systems. It incorporates

a convex combination of Lasso and ridge regulariza-

tion term, thus its optimization problem in the context

of fuzzy systems consequent training is deﬁned as:

∑

k=1

(~x(k))e

(k) +λ

∑

j=1

(αw

i j

+ (1 −α)|w

i j

−→min

i = 1, ...,C (11)

with λ the regularization parameter and α a parameter

in [0,1], steering the degree of inﬂuence of the ’Lasso

term’

∑

j=1

i j

| versus the ’ridge term’

∑

j=1

i j

Obviously, the solution representation of the con-

sequent vector ~w

of (11) in a closed analytical form

is given by the (convex) combination of the represen-

tations obtained by Lasso and ridge regression, thus:

= (R

R + λ

−1

~y −

sign(~w

)), (12)

with λ

= λ ∗α and λ

= λ ∗(1 −α) which results

in a least squares problem with 2

p+1

inequality con-

straints, as there are 2

p+1

possible sign patterns ∈

{−1,1} for the entries in the consequent parameter

vector ~w

. This can be efﬁciently solved through a

quadratic programming approach, termed as LARS-

EN, see (Zou and Hastie, 2005).

2.3 Enhanced Symbolic Regression

Symbolic regression is a nonparametric regression

and function discovery method (Koza, 1992), where

Robust Fuzzy Modeling and Symbolic Regression for Establishing Accurate and Interpretable Prediction Models in Supervising

Tribological Systems

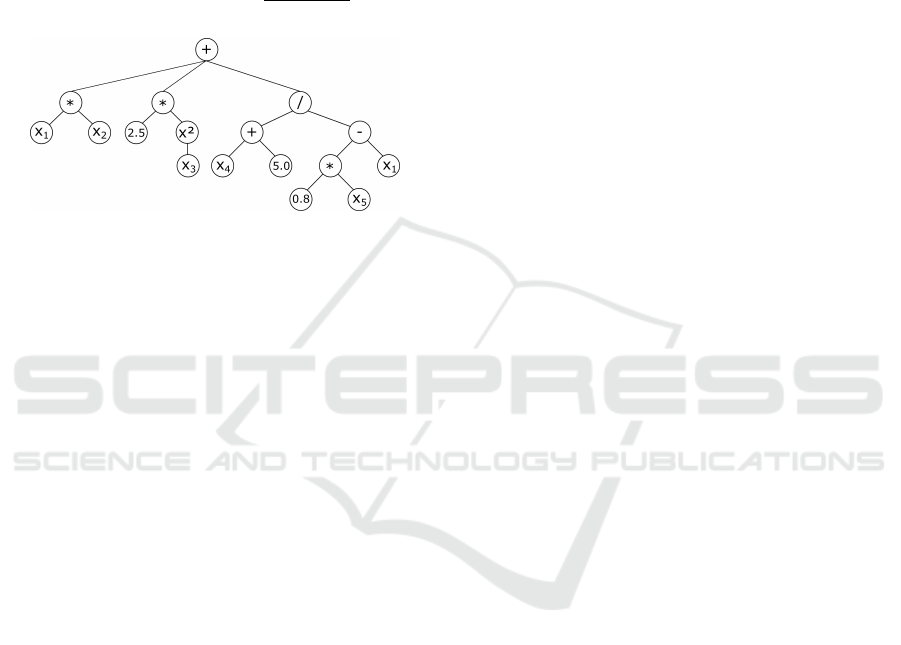
the generated prediction model is a mathematical ex-

pression. An advantage of symbolic regression is

that despite the generated models are able to ex-

press nonlinear relationships, they can be interpreted

and inspected by domain experts (Kronberger, 2011).

Furthermore, because the model is a mathematical

expression, it can be transformed and manipulated,

easily incorporated into expert systems (Affenzeller

et al., 2014) — see Figure 1 for an example.

f (x) = x

+ 2.5 x

+ 5.0

0.8 x

−x

Figure 1: Symbolic regression model represented as mathe-

matical expression and the equivalent symbolic expression

tree.

Tree-based genetic programming (GP) (Koza,

1992; Poli et al., 2008), an evolutionary meta-

heuristic optimization method, is commonly used to

solve symbolic regression problems. GP has been

originally developed to evolve solution candidates

that solve a given task without explicitly program-

ming them. In the case of symbolic regression, the

computer programs are mathematical expressions in

the form of a symbolic expression trees predicting the

dependent variable.

2.3.1 Constants Optimization in Symbolic

Regression

An advantage of symbolic regression compared to

other regression methods is that neither the model

structure nor its parameters nor the used variables are

predetermined. As a consequence, solving a symbolic

regression problem can be divided into three separate

but correlated subproblems:

• Selecting the appropriate variables

• Detecting the best suited model structure for the

selected variables

• Determining the numerical constants of a model

structure

Typical symbolic regression systems tend to solve

those three subproblems at the same time by combin-

ing variables, numerical constant and the functions

forming the model structure in the symbolic expres-

sion tree. This has the disadvantage that although the

appropriate model structure and variables are identi-

ﬁed, the model might have a high prediction error due

to wrong numerical constants. For example, when the

function y = 5 x

−x+ 2 should be identiﬁed, a possi-

ble candidate solution f (x) = −2 x

+ 2.4 x −3 using

the appropriate variables and model structure would

have a high prediction error due to the wrong numer-

ical constants ([−2,2.4,−3] instead of [5,−1,2]).

One of the ﬁrst attempts to diminish the effects of

wrong numerical constants has been the introduction

of linear scaling terms in symbolic regression (Kei-

jzer, 2003). For every generated model scaled pre-

dictions in the form of a ∗ f (x) + b instead of the raw

predictions f (x) are used for comparison with the de-

pendent variable. Therefore, it is not necessary any-

more to identify the correct scale and offset for the

prediction models, as these can be calculated by a

simple linear transformation. Other methods for de-

termining numerical constants in symbolic regression

range from using heuristic methods such as evolution

strategies (Alonso et al., 2009) or differential evo-

lution (Mukherjee and Eppstein, 2012) to gradient-

based optimization (Topchy and Punch, 2001).

We use a gradient-based optimization method,

similar to (Topchy and Punch, 2001), and combine

it with linear scaling for tuning numerical constants

of symbolic regression models (Kommenda et al.,

2013). The Levenberg-Marquardt algorithm is used

for tuning of numerical constants β by minimizing the

least squares functional: Q(β) =

∑

i=0

(y − f (x

,β))

Starting from an initial guess for β, which are the cur-

rent numerical values of the expression tree, the con-

stants are iteratively adapted using the current gradi-

ent information w.r.t β that can be efﬁciently calcu-

lated by automatic differentiation (Rall, 1981). The

Levenberg-Marquardt algorithm only ﬁnds a local op-

timum. In combination with evolutionary search, it

leads to a kind of memetic approach, where global

and local optimization is intervened to ﬁnd better so-

lutions more quickly. The ﬁnal results of symbolic

regression with constants optimization are more ac-

curate compared to symbolic regression without con-

stants optimization (Kommenda et al., 2013). The

rational behind it is that although fewer models are

generated and evaluated, the search direction for the

algorithm becomes clearer, because it can focus on

building the best suited model structure with appro-

priate variables.

2.3.2 Multi-objective Optimization of Accuracy

and Complexity

Symbolic regression is in general performed as a

single-objective optimization, where only the predic-

tion accuracy of the models is considered as an op-

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

Figure 2: Pareto-front evolved by NSGA-II showing the

trade-off between accuracy and complexity for symbolic re-

gression models.

timization objective. This may weaken the com-

pactness and transparency, therefore we switched

from single-objective to multi-objective optimization,

where next to the accuracy the complexity is opti-

mized as well. The result is a whole Pareto-front of

models that shows the trade-off between accuracy and

complexity (Smits and Kotanchek, 2005). An exem-

plary Pareto-front is depicted in Figure 2, where the

accuracy is measured as the correlation coefﬁcient be-

tween the dependent variable y and the model’s pre-

diction f (x) and the complexity is measures as the

symbolic expression tree length.

The non-dominated sorting genetic algorithm

(NSGA-II) (Deb et al., 2002) is used as multi-

objective optimization algorithm to generate the

Pareto-front of symbolic regression models. Similar

to standard genetic programming for single-objective

symbolic regression the models are encoded as ex-

pression trees and initialization, recombination and

mutation work in the same way. Before the prediction

accuracy of a model is evaluated its numeric constants

are improved (see Section 2.3.1) and afterwards its

complexity is calculated. The beneﬁts of this method

are that the generated models are in general simpler,

thus easier to interpret, and the occurrence of bloat

(Poli, 2003), an increase in tree length without accom-

panying accuracy improvement, is less likely.

3 EXPERIMENTAL SETUP

3.1 Test Protocol and Evaluation

Strategy

Cross-validation (CV) was used for validation of the

learning methods over all their tunable parameters

(see subsequent section), whereas a deterministic as-

signment of measurements to folds has been used. We

therefore ordered tests by time and assigned them to

ten folds using a round robin principle. This was nec-

essary in this case as simply shufﬂing the data would

have delivered a too optimistic CV performance.

The parameter setting achieving the minimal CV

error over the whole parameter grid (see below) was

applied to train a ﬁnal model on the whole training

data set and to test it on an independent test set —

this was repeated for each of the nine targets (listed in

Table 1).

We use the relative mean of absolute errors

Range(y)

∑

i=1

− ˆy

| to express model accurracy on

the separate test data sets. The separate test sets are

drawn from the complete data sets by using the latest

(timely recorded) 30% of all values.

3.2 Parameters for Fuzzy Methods

For the fuzzy modeling variants, the following

parametrization grids has been used within a 10-fold

CV procedure:

• For all methods: iteration over q = {1, ..., p} input

features, either in form of original variables or in

form of principal components (see below): in the

qth iteration, the ﬁrst q inputs are used for fuzzy

modeling from the ranked list.

• Rob-GenFIS (this paper): iteration over f ac =

{0.5,...,3.0} in step of 0.35 in order be more or

less conservative in rule evolution criterion; iter-

ation over α = {0, ...,1} in step of 0.1 to balance

lasso versus ridge regression in consequent learn-

ing.

• FLEXFIS (Lughofer, 2008): iteration over vigi =

{0.1,...,0.9} in order to be more or less conserva-

tive in rule evolution criterion.

• Genﬁs2 loc (Chiu, 1994) (Lughofer, 2011): it-

eration over radius = {0.1, ...,0.9} (denoting the

range of inﬂuence of rules) in steps of 0.1 in or-

der be more or less conservative in rule evolution

criterion.

• LoLiMoT (Nelles, 2001): iteration over

maxNumLL = {1,...,15} in steps of 1, i.e.

over the maximal number of local linear models

allowed as outcome of the splitting operation.

The dimensionality reduction of the (very) high-

dimensional input space (up to 60 inputs for the var-

ious targets) turned out to be indispensable for pre-

venting severe curse of dimensionality effects and

over-ﬁtting. Therefore, we conducted two variants,

one based on partial least squares (PLS) (Haenlein

and Kaplan, 2004), which transforms the input space

into a principal component space by successively

looking for directions in the data to best explain the

variance in the target, the other performs a ranking

Robust Fuzzy Modeling and Symbolic Regression for Establishing Accurate and Interpretable Prediction Models in Supervising

Tribological Systems

Table 2: Parameter settings for symbolic regression.

Settings Single-objective Symb. Regr. Multi-objective Symb. Regr.

Algorithm OSGA NSGA-II

Objective function maxR

maxR

, min complexity

Constants optim. 10 iterations 5 iterations

Maximum tree length 50 nodes 50 nodes

Allowed functions +, −, ∗, / +, −, ∗, /, e

, log(x)

Allowed terminals constant, constant ∗ variable constant, constant ∗ variable

Population size 1000 1000

Tree Initialization Probabilistic Tree Creator 2 Probabilistic Tree Creator 2

Parent selection Gender speciﬁc selection Crowded tournament selection

Crossover probability 100% 90%

Crossover operation Subtree swapping Subtree swapping

Mutation probability 25% 25%

Mutation operations

Change node, Shake node+tree, Change node, Shake tree,

Remove and replace branch Remove and replace branch

Termination

Generations > 50 Generations > 200

Selection pressure > 100

of the original features based on a modiﬁed variant of

forward selection — as also successfully used in (Cer-

nuda et al., 2011) in combination with fuzzy systems

training.

3.3 Parameters for Symbolic Regression

We have tested two variants of symbolic regression,

single-objective symbolic regression using an off-

spring selection genetic algorithm (OSGA) and multi-

objective symbolic regression solved by NSGA-II.

The algorithm parameters of both variants are de-

scribed in Table 2 and have been chosen according

to prior experience with the algorithms. The reason

that parameters have been manually chosen instead of

determining them by using grid-search in combina-

tion with cross validation is that due to the stochas-

tic nature of symbolic regression getting reliable es-

timates of the effects of parameters is hardly possi-

ble. The whole training partition has been used for

learning the symbolic regression models and 50 repe-

titions of each variant have been performed. The most

accurate models on the training partition have been

selected and manually simpliﬁed and pruned (Affen-

zeller et al., 2014).

3.4 Parameters for Standard Methods

In order to achieve a fair comparison with related SoA

methods in linear and non-linear regression model-

ing, such as partial least squares (Haenlein and Ka-

plan, 2004), elastic net (Hastie et al., 2010), random

forests (Breiman, 2001), Gaussian process regression

(Rasmussen and Williams, 2006), support vector ma-

chines (Smola and Vapnik, 1997), Gradient boosted

trees (Friedman, 2001) and Gradient boosted trees

(standard) (Friedman, 2001), we varied the most sen-

sitive learning parameters in each of these via a ﬁne

grid and performed the same cross-validation proce-

dure using exactly the same folds as in case of our

methods.

4 RESULTS AND DISCUSSION

4.1 Model Accuracy

Table 3 shows the results achieved for all modeling

methods The values are the relative mean of absolute

errors (MAE in percent) on separate validation data.

The best methods (with lowest perceptual MAE) for

each target over the linear SoA ones, over the non-

linear SoA ones as well as over our enhanced mod-

eling techniques are highlighted in bold font. From

this, it can be quite easily recognized that the linear

methods are outperformed by the non-linear methods

(state-of-the-art and our approaches), which has been

veriﬁed in statistical preference analysis tests using

Mann-Whitney test and a (default) signiﬁcance level

of α = 0.05 (Mann and Whitney, 1947). Furthermore,

the non-linear SoA methods seem to outperform our

proposed modeling techniques for most of the cases

— except for Temp

where there is a tie between en-

hanced symbolic regression employing NSGA-II and

gradient boosting, however for targets Wear

, CF

, and Temp

there is no statistical evidence for

the out-performance. It is also remarkable that in

four cases enhanced symbolic regression can outper-

form all fuzzy modeling variants, but in other four

cases the new method Rob-GenFIS produces the low-

est MAEs, whereas in two additional targets it also

produces lower MAEs than all other fuzzy modeling

variants.

From ﬁrst glance, the results seem not to be satis-

factory for our new proposed methods compared to

related state-of-the-art approaches, however an im-

portant issue in our application is to achieve some sort

of interpretability in the model outcomes. Thus, we

performed a deeper investigation of the results, based

on:

1. The compactness of the models measured by their

internal structural complexity (see Section 4.2),

which respects the number of inputs, the number

of components and the number of parameters.

2. The expressiveness power in interpretability of

model structures (Section 4.3).

4.2 Compactness of Models

We examined the compactness of all models achieved

by the various non-linear modeling variants listed in

Table 3. It is represented by the internal structural

complexity of the ﬁnal model and is elicited by:

• TS fuzzy models: C ∗(p ∗3 + 1) with C the num-

ber of rules and p the number of inputs; this is be-

cause each rule represents a structural component,

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

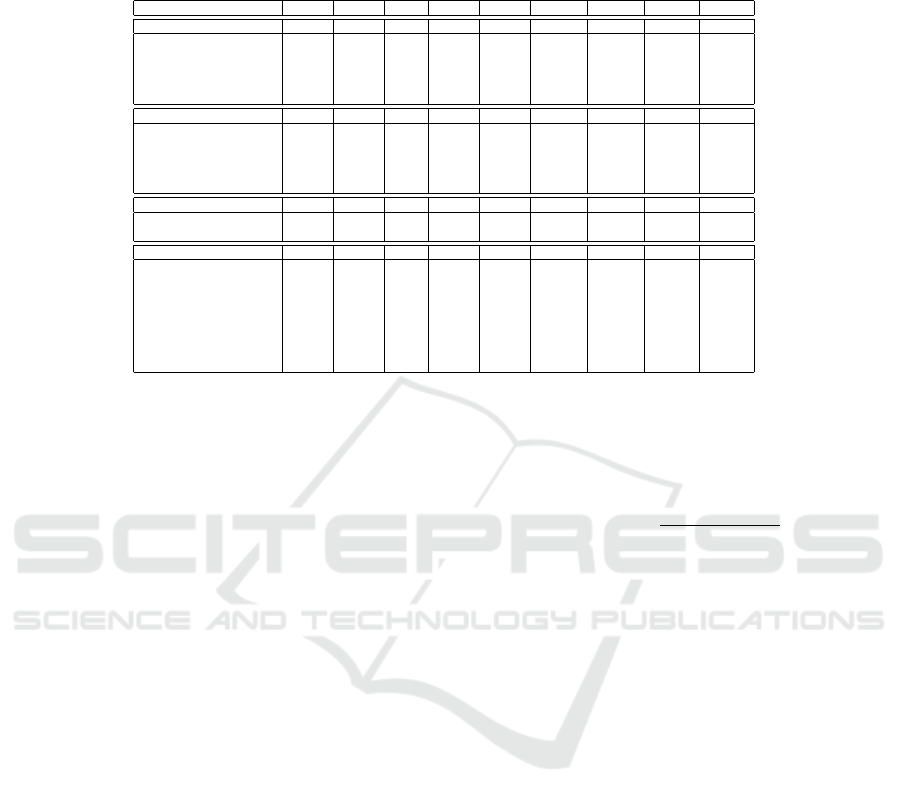
Table 3: Summary of results for all target variables and all methods that have been tested. The cell values are relative mean

of absolute errors (MAE in percent) on separate validation data; the best methods (with lowest MAE) for each target over the

linear SoA ones, over the non-linear SoA ones as well as over our enhanced modeling techniques are highlighted in bold font.

Algorithm CF

NVH Temp

Temp

Wear

Linear SoA Methods

Constant 17.22 11.99 9.99 11.57 31.18 4.82 16.51 8.46 5.27

Linear Regression 5.70 7.00 8.28 6.79 23.29 4.78 12.56 5.38 3.68

PLS 6.06 6.53 8.02 7.15 23.10 4.61 12.60 5.37 4.48

Elastic Net 5.85 6.83 8.46 7.82 23.90 4.80 13.40 5.24 4.32

Elastic Net + PLS 6.11 6.79 8.66 7.48 24.10 4.80 12.70 5.15 4.11

Non-Linear SoA Methods

SVM-RBF 4.97 5.04 6.90 5.89 16.65 3.78 11.37 5.18 3.52

Random Forest 4.19 5.05 7.22 5.90 17.83 4.20 11.70 4.73 3.32

GPR SEard 4.79 5.18 7.43 6.21 18.62 4.01 12.13 4.78 3.37

GBT 4.56 5.05 7.15 5.83 18.04 4.24 11.81 4.81 3.18

GBT standard 4.44 5.05 7.03 5.64 15.92 3.82 11.61 4.89 3.44

Enhanced Symb. Regr

Symbolic Regr. OSGA 5.34 6.95 8.05 6.72 20.56 4.12 12.08 5.64 3.28

Symbolic Regr. NSGA-II 5.34 6.64 7.75 6.11 20.74 4.42 11.75 5.44 3.18

Fuzzy Modeling Variants

FLEXFIS + FS 5.91 6.73 8.45 7.62 21.30 4.00 12.00 5.30 3.34

FLEXFIS + PLS 10.30 6.16 8.43 20.30 21.00 4.48 11.90 3.48

Rob-GenFIS + FS 5.79 5.56 9.31 7.54 21.90 4.19 14.40 5.92 3.93

Rob-GenFIS + PLS 5.01 5.53 7.94 7.08 19.40 3.94 11.90 5.60 3.36

Genﬁs2 loc + FS 5.52 5.76 8.73 8.79 24.60 4.19 5.13 3.32

Genﬁs2 loc + PLS 5.39 5.80 7.96 6.71 21.20 4.13 13.70 5.30 3.54

LoLiMoT +FS 5.85 5.85 8.46 6.34 21.30 4.39 12.10 5.19 3.20

LoLiMoT + PLS 5.61 5.88 7.69 6.93 19.60 4.61 12.60 5.40 3.41

whereas each of the p antecedent parts is com-

posed of two parameters (the input variable and

the assigned fuzzy set with its associated linguis-

tic term) and each consequent part is composed by

a hyper-plane with p +1 parameters (p inputs and

one intercept). This complexity deﬁnition shows

up in a structural representation of TS fuzzy mod-

els which is also in full accordance with the repre-

sentation obtained by symbolic regression, as will

be further analyzed in Section 4.3.

• Symbolic regression: the number of operators,

variables and constants in the tree (cf. with Figure

3).

• Support vector machines: C ∗ p with C the num-

ber of support vectors and the p the number of in-

puts; this is because each support vector can be in-

terpreted as one structural component (localizer)

similarly to one rule, whereas each support vec-

tor has only one parameter, namely in form of one

numeric coordinate value.

• Random forests:

∑

m=1

∗(2 ∗d

) with M the

number of trees in the forest, C

the number of

leaf nodes (=rules) and d

the depth of the mth

tree (i.e. the number of conditions from the root

to the leaves); in this way, it is also in accordance

to the TS fuzzy model and symbolic regression

tree complexity representation.

• Gradient boosted trees (GBT): the calculation is

done in the same way as for random forest.

• Gaussian process regression (GPR): same calcu-

lation as for support vector machines. The only

difference is that each row is considered as one

structural component (localizer).

In order to combine accuracy and complex-

ity within one value to represent a compact in-

dex for indicating a feasible tradeoff between accu-

racy and complexity, we also investigated an accu-

racy/complexity (A/C) index which is deﬁned by:

ind

100 −2 ∗MAE

log(C)

(13)

We applied this measure for the purpose of comparing

the compactness (and thus transparency) of the fuzzy

rule bases obtained by the fuzzy modeling approaches

against each other. In this sense, C denotes the num-

ber of rules plus the number of inputs and MAE the

mean absolute error achieved in the separate test data

set. This measure punishes the accuracy of more com-

plex models, thus the higher its value, the better the

method becomes in terms of representing a good ac-

curacy/complexity tradeoff.

Table 4 shows the internal structural complexity

across all methods, and also the A/C index values

for the fuzzy modeling and symbolic regression ap-

proaches after the slashes in each cell.

The interpretation of this table is obvious: the non-

linear state-of-the-art regression modeling techniques

produce models with extremely huge complexity (at

least a few thousands of parameters in all cases),

which makes them inapplicable for our purposes to

represent transparent and readable models to the ex-

perts. Compared to non-linear SoA methods, the

structural complexity of the symbolic regression mod-

els is much smaller and includes around 50 up to max-

imally 67 nodes for all target variables. The fuzzy

models produced by our new robust method Rob-

GenFIS (and also by FLEXFIS) are slightly larger

Robust Fuzzy Modeling and Symbolic Regression for Establishing Accurate and Interpretable Prediction Models in Supervising

Tribological Systems

Table 4: Summary of results for all target variables and all non-linear methods that have been tested. The cell values are

the values obtained from the internal structural complexity values as deﬁned in the text, the models with lowest complexity

for each target are highlighted in bold font; for the fuzzy modeling and the enhanced symbolic regression methods, after the

slashes the accuracy/complexity index as deﬁned by (13) is reported.

Algorithm CF

NVH Temp

Temp

Wear

Non-Linear SoA Methods

SVM-RBF 20265 120776 14473 10004 79827 13735 14350 33001 25600

RF 164010 506010 69860 78435 487475 53780 78055 153160 53210

GPR SEard 21385 129890 18040 17876 108035 17999 17876 39040 40896

GBT 267000 267000 267000 267000 267000 267000 267000 267000 267000

GBT standard 721814 745000 708128 703553 739721 709422 706279 744640 744748

Enhanced Symbolic Regr

Symbolic Regr. OSGA 26 / 27.41 48 / 22.24 41 / 22.59 46 / 22.61 43 / 15.65 38 / 25.23 46 / 19.81 42 / 23.74 28 / 28.04

Symbolic Regr. NSGA-II 43 / 23.75 67 / 20.62 36 / 23.58 56 / 21.81 44 / 15.46 47 / 23.68 48 / 19.76 50 / 22.78 49 / 24.06

Fuzzy Modeling Variants

FLEXFIS 96 / 17.40 128 / 18.07 104 / 17.90 144 / 11.95 208 / 10.87 182 / 17.49 130 / 15.65 50 / 23.78

Rob-GenFIS 104 / 19.37 130 / 18.27 21 / 27.63 144 / 17.27 70 / 14.41 182 / 17.70 130 / 15.65 38 / 24.41 48 / 24.10

Genﬁs2 loc 285 / 15.78 560 / 13.97 160 / 16.57 64 / 20.82 130 / 11.83 1444 / 12.61 95 / 15.94 185 / 17.13 95 / 20.40

LoLiMoT 57 / 21.96 780 / 13.25 301 / 14.83 125 / 17.84 364 / 10.31 10 / 39.43 152 / 14.89 150 / 17.80 171 / 18.12

and in the range of around 100 up to maximal 208

for all targets. The difference between fuzzy models

and symbolic regression are small, such that, together

with the error results in the table above, we can con-

clude that both perform almost equally.

In terms of the fuzzy modeling variants, when

comparing their achieved A/C index values, our

newly proposed method Rob-GenFIS is able to out-

perform the other methods for ﬁve targets, whereas

for CF

and Temp

LoLiMoT turns now out to be

the best option, although for these two targets Rob-

GenFIS produces the lowest MAEs. On the other

hand, Rob-GenFIS can signiﬁcantly outperform its

’predecessor’ FLEXFIS for 8 targets. This underlines

that the extension to generalized rules and to an im-

proved, more robust training of consequents (with the

usage of elastic net regularization) pays-off

4.3 Model Interpretation on Structural

Level — Gaining Insights

In case of the well-performing non-linear state-of-the-

art methods, no such insight on structural model level

is possible at all — all models generated by them are

rather appearing as black boxes.

In case of fuzzy models, the interpretable insight

can be achieved through the representation of fuzzy

rules in IF-THEN form (compare with (1)). This

yields some sort of linguistically readable (partial,

local) dependencies between the input variables and

the targets, which can then be associated with pre-

dominant system conditions in certain different op-

eration ranges/modes. This is possible as a fuzzy

model internally provides a granulated viewpoint on

the whole system behavior by partitioning all the in-

puts into several parts with the usage of fuzzy sets,

usually associated with linguistic terms such as LOW,

MEDIUM and HIGH, which are then combined to

form the antecedent parts of the rules. In case when

the fuzzy models are learned from data, the fuzzy

sets and rule antecedent parts can be obtained by the

projection concept (Lughofer et al., 2015) and typ-

ically by also applying some post-operating proce-

dure for removing redundant, signiﬁcantly overlap-

ping sets/rules (Lughofer, 2013).

We obtained the following ﬁve transparent fuzzy

rules with TS-type consequent hyper-planes after

removing three inputs whose partitioning resulted in

one global fuzzy set (which can be associated with

a don’t care part in all rules) and after projecting

the generalized rules to the axes (according to the

projection concept developed in (Lughofer et al.,

2015)) to form standard linguistic fuzzy partitions,

Finally, it ends up with only three antecedent parts

each and a maximum of two fuzzy sets per input

(ON/OFF resp. LOW/HIGH):

Rule 1: IF Source

is ON and x

is HIGH and Mat

is OFF THEN

y = 6.169 ∗Source

+ 0.00205 ∗x

−1.113 ∗Mat

−20.54

Rule 2: IF Source

is OFF and x

is LOW and Mat

is OFF THEN

y = 3.778 ∗Source

+ 0.00013 ∗x

−1.973 ∗Mat

+ 2.201

Rule 3: IF Source

is OFF and x

is HIGH and Mat

is OFF THEN

y = 5.705 ∗Source

+ 0.00013 ∗x

−2.335 ∗Mat

+ 1.811

Rule 4: IF Source

is ON and x

is LOW and Mat

is OFF THEN

y = 4.176 ∗Source

+ 0.00034 ∗x

−0.03488 ∗Mat

+ 1.784

Rule 5: IF Source

is OFF and x

is LOW and Mat

is ON THEN

y = 6.136 ∗Source

+ 0.0002029 ∗x

−2.399 ∗Mat

+ 2.069

where the variable y stands for the target ’Wear

’.

The consequents in this form may be interpretable

by experts if she/he is able to associate a physical

meaning of the weighted linear regression formula.

Alternatively, they can be even transferred to linguis-

tic terms as realized in the equivalent tree-structured

representation (Figure 3 left).

In order to obtain a direct valid comparison with

symbolic regression, we transformed this conven-

tional fuzzy rule base representation into a tree struc-

ture in accordance with the conventional tree structure

representation of symbolic regression by still keeping

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

model

if-then

and

Source

Off

Low

Mat

Off

Low

if-then

and

Source

High

Mat

Off

Medium

if-then

and

Source

Off

High

Mat

Off

Low

if-then

and

Source

Low

Mat

Off

Low

if-then

and

Source

Off

Low

Mat

Low

Mat

+ + c

* * c

Oil

Gooving

Figure 3: Tree-based model structures obtained through fuzzy modeling (left) and symbolic regression (right); all nodes and

assignments of parameters therein are counted to the internal structural complexity.

the correct semantic meaning of the rule base. For

the example above, the corresponding tree is shown

in Figure 3 (left), whereas in (right) the model tree for

the same target (Wear

) spanned by symbolic regres-

sion is shown.

In conventional notation the symbolic regression

model shown in Figure 3 (b) is:

Wear

= c

·x

+ c

·Mat

+ c

·x

+ c



·x

+ x

·Oil

·c



·(c

·x

+ c

·x

+ c

·Grooving

) + c

Comparing the two different models shown in Figure

3 it can be observed that the fuzzy model has more

nodes than the symbolic regression model. However,

when determining structural complexity we have not

counted the internal structural nodes ’IF-THEN’ and

’AND’ because they are ﬁxed and can not be changed

by the learning algorithm. In comparison, genetic

programming is free to combine the allowed opera-

tors, functions and their operands in any semantically

valid way. Therefore, we have also counted internal

nodes for symbolic regression models. The symbolic

regression model can be implemented rather easily in

any programming language as it only relies on stan-

dard operators. Implementing the fuzzy model is a

little bit more difﬁcult as it is also necessary to im-

plement the fuzzy inference algorithm which is nec-

essary to interpret the rules correctly.

5 CONCLUSIONS

We have for the ﬁrst time demonstrated that fuzzy

modeling and symbolic regression can be applied for

empirical modeling of wet tribological systems and

have shown that they can be used successfully for

modeling key metrics of tribological systems. The

errors achieved for nine important targets are signif-

icantly lower than those achieved by linear methods

and similar to those achieved by related non-linear

modeling regression methods. However, 1.) the struc-

tural complexity is much lower (around 100 versus a

few 1000s components) and 2.) the related methods

do not offer any interpretable meaning as appearing as

complete black boxes. Such a high complexity bears

the risk of signiﬁcant over-ﬁtting. Both of our meth-

ods, fuzzy modeling and symbolic regression can be

represented in tree-based structures, based on which

interpretation is pretty easy (we provided a concrete

example for target ”wear”). Upon such higher level

interpretation possibilities offer by our methods, the

experts and operators working with the system reach

a higher conﬁdence in the models.

ACKNOWLEDGEMENTS

The work described in this paper was done within

the COMET Project Heuristic Optimization in Pro-

duction and Logistics (HOPL), #843532 funded by

the Austrian Research Promotion Agency (FFG) and

within the project “Smart Factory Lab” funded within

the EU programme IWB 2020 by the provincial gov-

ernment of Upper Austria.

REFERENCES

Affenzeller, M., Winkler, S., Kronberger, G., Kommenda,

M., Burlacu, B., and Wagner, S. (2014). Gaining

deeper insights in symbolic regression. In Riolo, R.,

Moore, J. H., and Kotanchek, M., editors, Genetic

Programming Theory and Practice XI, Genetic and

Evolutionary Computation. Springer.

Affenzeller, M., Winkler, S., Wagner, S., and Beham, A.

(2009). Genetic Algorithms and Genetic Program-

ming: Modern Concepts and Practical Applications.

Chapman & Hall, Boca Raton, Florida.

Aleksendri, D. (2010). Neural network prediction of brake

friction materials wear. Wear, 268(12):117 – 125.

Aleksendric, D. and Carlone, P. (2015). Soft Computing

in the Design and Manufacturing of Composite Mate-

Robust Fuzzy Modeling and Symbolic Regression for Establishing Accurate and Interpretable Prediction Models in Supervising

Tribological Systems

rials: Applications to Brake Friction and Thermoset

Matrix Composites. Woodhead Publishing.

Alonso, C. L., Montana, J. L., and Borges, C. E. (2009).

Evolution strategies for constants optimization in ge-

netic programming. In 21st International Conference

on Tools with Artiﬁcial Intelligence, ICTAI ’09, pages

703–707.

Berger, E. (2002). Friction modeling for dynamic system

simulation. Applied Mechanics Reviews, 55(6):535–

577.

Breiman, L. (2001). Random forests. Machine learning,

45(1):5–32.

Castro, J. and Delgado, M. (1996). Fuzzy systems with

defuzziﬁcation are universal approximators. IEEE

Transactions on Systems, Man and Cybernetics, part

B: Cybernetics, 26(1):149–152.

Cernuda, C., Lughofer, E., Maerzinger, W., and Kasberger,

J. (2011). NIR-based quantiﬁcation of process param-

eters in polyetheracrylat (PEA) production using ﬂex-

ible non-linear fuzzy systems. Chemometrics and In-

telligent Laboratory Systems, 109(1):22–33.

Chiu, S. (1994). Fuzzy model identiﬁcation based on cluster

estimation. Journal of Intelligent and Fuzzy Systems,

2(3):267–278.

De Wit, C. C., Olsson, H., Astrom, K. J., and Lischinsky,

P. (1995). A new model for control of systems with

friction. Automatic Control, IEEE Transactions on,

40(3):419–425.

Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T. (2002).

A fast and elitist multiobjective genetic algorithm:

NSGA-II. Evolutionary Computation, IEEE Transac-

tions on, 6(2):182–197.

Friedman, J. H. (2001). Greedy function approximation: a

gradient boosting machine. Annals of statistics, pages

1189–1232.

Gray, R. (1984). Vector quantization. IEEE ASSP Maga-

zine, 1(2):4–29.

Haenlein, M. and Kaplan, A. (2004). A beginner’s guide

to partial least squares (PLS) analysis. Understanding

Statistics, 3(4):283–297.

Hastie, T., Tibshirani, R., and Friedman, J. (2009). The Ele-

ments of Statistical Learning: Data Mining, Inference

and Prediction - Second Edition. Springer, New York

Berlin Heidelberg.

Hastie, T., Tibshirani, R., and Friedman, J. (2010). Regu-

larized paths for generalized linear models via coordi-

nate descent. Journal of Statistical Software, 33(1).

Hosenfeldt, T., Schulz, E., Glerl, J., and Steinmetz, S.

(2014). Friction tailored to your requirements. In KG,

S. T. G. . C., editor, Solving the Powertrain Puzzle -

10th Schaefﬂer Symposium, chapter 23, pages 331 –

344. Springer Vieweg.

Keijzer, M. (2003). Improving symbolic regression with

interval arithmetic and linear scaling. In Ryan, C.,

Soule, T., Keijzer, M., Tsang, E., Poli, R., and Costa,

E., editors, Genetic Programming, Proceedings of Eu-

roGP’2003, volume 2610 of LNCS, pages 70–82, Es-

sex. Springer-Verlag.

Kommenda, M., Kronberger, G., Affenzeller, M., Win-

kler, S. M., and Burlacu, B. (2016). Evolving sim-

ple symbolic regression models by multi-objective ge-

netic programming. In Genetic Programming Theory

and Practice XIII (not yet published). Springer.

Kommenda, M., Kronberger, G., Winkler, S., Affenzeller,

M., and Wagner, S. (2013). Effects of constant op-

timization by nonlinear least squares minimization in

symbolic regression. In Proceedings of the 15th an-

nual conference companion on Genetic and evolution-

ary computation, pages 1121–1128. ACM.

Koza, J. R. (1992). Genetic Programming: On the Pro-

gramming of Computers by Means of Natural Selec-

tion. MIT Press, Cambridge, MA, USA.

Kronberger, G. (2011). Symbolic Regression for Knowledge

Discovery – Bloat, Overﬁtting, and Variable Interac-

tion Networks. Number 64 in Johannes Kepler Uni-

versity, Linz, Reihe C. Trauner Verlag+Buchservice

GmbH.

Langdon, W., Soule, T., Poli, R., and Foster, J. (1999). The

evolution of size and shape. In Advances in Genetic

Programming, volume 3, chapter 8, pages 163–190.

MIT Press.

Lemos, A., Caminhas, W., and Gomide, F. (2011). Mul-

tivariable gaussian evolving fuzzy modeling system.

IEEE Transactions on Fuzzy Systems, 19(1):91–104.

Loh, W.-Y., Basch, R. H., Li, D., and Sanders, P. (2000).

Dynamic modeling of brake friction coefﬁcients.

Technical report, SAE Technical Paper.

Lughofer, E. (2008). FLEXFIS: A robust incremental learn-

ing approach for evolving TS fuzzy models. IEEE

Transactions on Fuzzy Systems, 16(6):1393–1410.

Lughofer, E. (2011). Evolving Fuzzy Systems — Methodolo-

gies, Advanced Concepts and Applications. Springer,

Berlin Heidelberg.

Lughofer, E. (2013). On-line assurance of interpretability

criteria in evolving fuzzy systems — achievements,

new concepts and open issues. Information Sciences,

251:22–46.

Lughofer, E., Cernuda, C., Kindermann, S., and Pratama,

M. (2015). Generalized smart evolving fuzzy systems.

Evolving Systems, 6(4):269–292.

Lughofer, E. and Sayed-Mouchaweh, M. (2015). Au-

tonomous data stream clustering implementing incre-

mental split-and-merge techniques — towards a plug-

and-play approach. Information Sciences, 204:54–79.

Mann, H. and Whitney, D. (1947). On a test of whether one

of two random variables is stochastically larger than

the other. Annals of mathematical Statistics, 18:50–

60.

Mukherjee, S. and Eppstein, M. J. (2012). Differential

evolution of constants in genetic programming im-

proves efﬁcacy and bloat. In Rodriguez, K. and Blum,

C., editors, GECCO 2012 Late breaking abstracts

workshop, pages 625–626, Philadelphia, Pennsylva-

nia, USA. ACM.

Nelles, O. (2001). Nonlinear System Identiﬁcation.

Springer, Berlin.

Poli, R. (2003). A simple but theoretically-motivated

method to control bloat in genetic programming. In

Genetic programming, pages 204–217. Springer.

Poli, R., Langdon, W. B., and McPhee, N. F. (2008).

A ﬁeld guide to genetic programming. Published

FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications

via http://lulu.com and freely available at http://

www.gp-ﬁeld-guide.org.uk.

Rall, L. B. (1981). Automatic Differentiation: Techniques

and Applications, volume 120 of Lecture Notes in

Computer Science. Springer, Berlin.

Rasmussen, C. E. and Williams, C. K. (2006). Gaussian

processes for machine learning. The MIT Press.

Sellgren, U., Bjrklund, S., and Andersson, S. (2003). A

ﬁnite element-based model of normal contact between

rough surfaces. Wear, 254(11):1180 – 1188. Papers

presented at the 10th Nordic Conference on Tribology,

{NORDTRIB} 2002.

Senatore, A., D’Agostino, V., Giuda, R. D., and Petrone,

V. (2011). Experimental investigation and neural net-

work prediction of brakes and clutch material fric-

tional behaviour considering the sliding acceleration

inﬂuence. Tribology International, 44(10):1199 –

1207.

Smits, G. F. and Kotanchek, M. (2005). Pareto-front ex-

ploitation in symbolic regression. In O’Reilly, U. M.,

Yu, T., Riolo, R., and Worzel, B., editors, Genetic Pro-

gramming Theory and Practice II, volume 8 of Ge-

netic Programming, pages 283–299. Springer Verlag,

New York.

Smola, A. and Vapnik, V. (1997). Support vector regression

machines. Advances in neural information processing

systems, 9:155–161.

Takagi, T. and Sugeno, M. (1985). Fuzzy identiﬁcation of

systems and its applications to modeling and control.

IEEE Transactions on Systems, Man and Cybernetics,

15(1):116–132.

Topchy, A. and Punch, W. F. (2001). Faster genetic pro-

gramming based on local gradient search of numeric

leaf values. In Spector, L., Goodman, E. D., Wu,

A., Langdon, W. B., Voigt, H.-M., Gen, M., Sen, S.,

Dorigo, M., Pezeshk, S., Garzon, M. H., and Burke,

E., editors, Proceedings of the Genetic and Evolution-

ary Computation Conference (GECCO-2001), pages

155–162, San Francisco, California, USA. Morgan

Kaufmann.

Xiao, L., Bjrklund, S., and Rosn, B. (2007). The inﬂuence

of surface roughness and the contact pressure distribu-

tion on friction in rolling/sliding contacts. Tribology

International, 40(4):694 – 698. {NORDTRIB} 2004.

Zou, H. and Hastie, T. (2005). Regularization and variable

selection via the elastic net. Journal of the Royal Sta-

tistical Society, Series B, pages 301–320.

Robust Fuzzy Modeling and Symbolic Regression for Establishing Accurate and Interpretable Prediction Models in Supervising

Tribological Systems