Syllabification with Frequent Sequence Patterns
A Language Independent Approach
Adrian Bona, Camelia Lemnaru and Rodica Potolea
Technical University of Cluj-Napoca, Computer Science Department, Cluj-Napoca, Romania
Keywords:
Syllabification, Frequent Pattern Sequence, Language Independence, Graphs, Data Mining.
Abstract:
In this paper we show how words represented as sequences of syllables can provide valuable patterns for
achieving language independent syllabification. We present a novel approach for word syllabification, based
on frequent pattern mining, but also a more general framework for syllabification. Preliminary evaluations on
Romanian and English words indicated a word level accuracy around 77% for Romanian words and around
70% for English words. However, we believe the method can be refined in order to improve performance.
1 INTRODUCTION
The problem of splitting words by various criteria
has always presented high interest in a wide range
of fields, such as linguistics and artificial intelligence.
Text to speech systems and automatic end-of-line hy-
phenation in text editors could greatly benefit from an
efficient, language independent method for syllabifi-
cation.
In text to speech systems, for example, correct
syllabification is essential since humans pronounce
words not as sequences of letters, but as sequences
of syllables - the syllable being the atomic element
in spoken language. Starting from this observation,
our assumption is that the analysis of the words as se-
quences of syllables should provide a strong enough
foundation, not only from a linguistic perspective,
but also for an efficient and accurate syllabification
method. Also, we believe such a method to be generic
enough to be employed for a wide range of languages.
The rest of the paper explores, analyzes and eval-
uates the above mentioned assumptions: section 2
overviews the most prominent approaches for the syl-
labification problem available in literature. Section 3
places the more general problem of sequence pattern
mining in the present context - words as sequences
of syllables, whereas section 4 presents our algo-
rithms for syllabification, based on the principles of
sequence pattern mining. Section 5 presents the ex-
periments performed on Romanian and English syl-
labification, and section 6 discusses the concluding
remarks.
2 RELATED WORK
The literature acknowledges two main categories of
approaches for automatic syllabification: the rule-
based methods and the data-driven approaches (Marc-
hand et al., 2007).
The traditional approach to automatic syllabifica-
tion considers known grammatical rules or linguistic
principles to drive the syllabification process. For ex-
ample, there are three prevalent principles for syllab-
ification, as outlined in (Bartlett et al., 2009):
• the Legality Principle, which states that a syllable
cannot begin, or end, with a consonant group that
is not found at the beginning, or the end of some
word (Goslin and Frauenfelder, 2001).
• the Sonority Principle (Selkirk, 1984), which
states that the loudness with which a phoneme
is pronounced (given that the pitch and duration
are maintained constant) should increase from the
first phoneme of the onset to the syllable nucleus,
then fall off to the coda.
• the Maximal Onset Principle (Kahn, 1976),
which, as its name implies, favors long onsets at
the expense of the previous syllable’s coda, so
long as the legality principle is not broken.
Methods which apply these principles have been
investigated in (Bartlett et al., 2009) comparison
with data-driven approaches. The Sonority Principle
achieved the highest accuracy at word level, but data
driven methods outperformed these rule-based meth-
ods.
352
Bona, A., Lemnaru, C. and Potolea, R.
Syllabification with Frequent Sequence Patterns - A Language Independent Approach.
DOI: 10.5220/0006069703520359
In Proceedings of the 8th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2016) - Volume 1: KDIR, pages 352-359
ISBN: 978-989-758-203-5
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Another disadvantage of such approaches is that
they are language dependent, since the rules for syl-
labification differ for each language.
The data-driven methods are a relatively newer
approach to syllabification, with both supervised and
un-supervised techniques being investigated.
Syllabification by Analogy (SbA) (Marchand and
Damper, 2000) performs a full matching between a
new word and the dictionary entries, by means of a
directed graph, and identifies the best candidate syl-
labification by finding the shortest path between the
starting and the end node; ties are solved via sev-
eral scoring strategies. In (Daelemans et al., 1997)
the authors apply instance based learning to identify
the closest N-gram for each juncture. Different fea-
ture weighting functions are investigated, as well as
different N-gram sizes.
More recently, the task of syllabification has
been formulated as a structured classification problem
(Bartlett et al., 2008), which is solved via structured
Support Vector Machines (SVM-HMM). This prob-
lem formulation requires a tagging scheme, for the
relevant features to be marked. Positional tags (Not
Boundary, Boundary: NB) and structural tags (On-
set, Nucleus, and Coda: ONC) are investigated. Each
syllable is composed of a sequence of phones: a nu-
cleus (vowel), preceded by an onset (consonant) and
followed by a coda (consonant). From the phonetic
point of view, the nucleus and coda give the rhyme.
Probabilistic methods based on Conditional Random
Fields have also been investigated, modelling again
the problem as a sequence learning problem (Rogova
et al., 2013).
For the Romanian language, the authors of (Dinu,
2004) present the process of building a database of
the syllables in the language, while in (Barbu, 2008)
the authors introduce a dictionary for syllabification,
with morphological aspects. More recently, Condi-
tional Random Fields have been applied to Romanian
syllabification, in (Dinu et al., 2013), reaching an ac-
curacy of above 95% at word level.
3 SYLLABLE-BASED SEQUENCE
PATTERN MINING
This section presents the basic notions on which the
proposed syllabification solution is built, through an-
swering the following questions: What is a syllable?
Is it possible to syllabify words based on a strict set of
rules? What are frequent sequence patterns and how
could they be applied to words?
3.1 Syllable. Syllabification
Syllabification can be viewed as a procedure which
receives as input a word and outputs a sequence of
parts of that word, called syllables.
A syllable is a unit of organization for a sequence
of speech sounds. For example, the word water is
composed of two syllables: wa and ter. A syllable is
typically made up of a syllable nucleus (most often
a vowel) with optional initial and final margins (typi-
cally, consonants).
1
Note that the concept of syllable is not defined by
a rigid set of rules and there are even multiple types
of syllabifications possible. The root causes of this
ambiguity are the following:
1. languages are not rigid artificial constructs and
ambiguity is one attribute of natural constructs.
2. the use-cases for syllabification vary: phonetic
syllabification may differ from the orthographic
syllabification (also known as hyphenation).
The definition from above is rather a phonetic def-
inition of the syllable, for the orthographic rules might
have even aesthetic roots. To illustrate the difference,
let us consider the following example:
From a phonetic perspective, the Romanian word
inegal is split like i-ne-gal, but its hyphenated form is
in-e-gal.
3.2 Mining Frequent Sequence Patterns
Frequent sequence patterns are patterns that occur at
least a minimum number of times (minimum support)
within a collection of sequences.
We introduce the formal definition of such pat-
terns and then we show how syllabified words could
be mined for frequent sequence patterns.
Let I = {i
1
, i
2
, ..., i
n
} be an alphabet (a set of ele-
ments) for a collection of sequences. A sequence s is
defined as an ordered collection of elements from I:
< i
k
1
, i
k
2
, ..., i
k
m
>, where ∀k
j
, 0 ≤ j ≤ m, k
j
∈ I. (1)
For example: let I = {a, b, c, d}, a possible se-
quence is < b, b, a >.
A sequence dataset S
db
is a set of tuples of the
form (id, s), where id is a unique identifier and s - a
sequence.
For example, such a dataset is ilustrated in Table
1.
A sequence s
1
=< t
1
,t
2
, ...,t
n
> is contained by
s
2
=< l
1
, l
2
, ..., l
m
> if n ≤ m and ∃i, j so that t
1
=
l
i
,t
n
= l
j
and ∀k, i ≤ k ≤ j =⇒ t
k−i
= l
k
. We will use
s
1
⊆ s
2
to denote that s
2
contains s
1
.
1
https://en.wikipedia.org/wiki/Syllable
Syllabification with Frequent Sequence Patterns - A Language Independent Approach
353

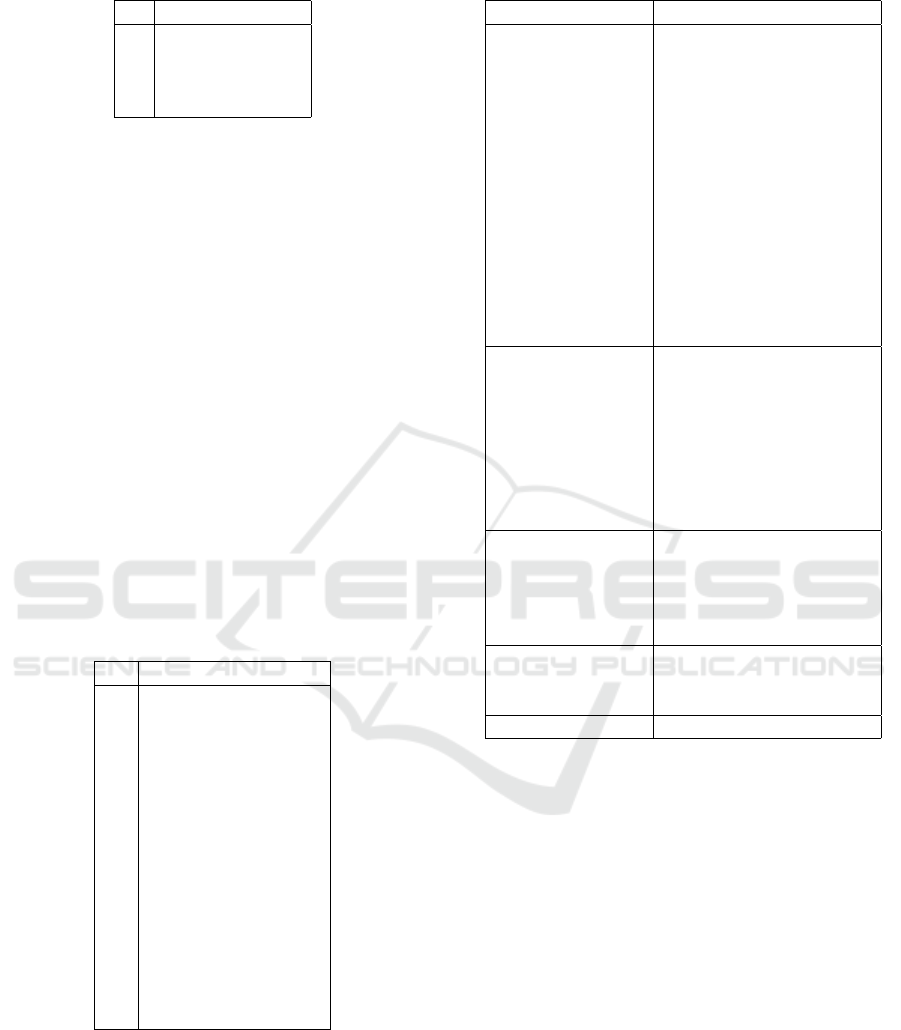
Table 1: Sequence dataset.
id s
1 < C, A, A, B,C >
2 < A, B,C, B >
3 < C, A, B,C >
4 < A, B, B,C, A >
Let S
db
a sequence dataset and T the set of all tu-
ples (id, s) from S
db
where for a certain s
0
we have
s
0
⊆ s. We define the support of s
0
within S
db
as |T |.
Informally, the support of a sequence is the number of
sequences from the dataset that contain it. We denote
the support of a sequence s within S
db
with sup
S
db
(s).
Having defined what a sequence and its support
are, a frequent sequence pattern is introduced as a
sequence contained within sequences from S
db
with a
support greater than a minimum threshold.
3.3 Frequent Syllable Sequence
Patterns
As mining frequent patterns is a domain agnostic
technique, it can also be applied to syllabification. In
this case, the alphabet used to define sequences is the
complete set of syllables of a language. Equivalent
to a sequence is a syllabified word. Such a sequence
dataset is illustrated in Table 2.
Table 2: Syllabified Romanian words dataset sample.
id sequence
1 < li, be, lu, l
˘
a>
2 < e, li, be, ra,tor >
3 < a, ma,tor >
4 < ar,ti, col >
5 < pro,gra, ma,tor >
6 < a, ni, ver, sa, re >
7 < vi, sa, re >
8 < gra, ma, ti, c
˘
a>
9 < e, va, da, re >
10 < ma, re, e >
11 < pro,gra, ma, re >
12 < g
ˆ
an, di, tor >
13 < e, li, t
˘
a>
14 < sa, re >
15 < e, li, cop, ter >
For the dataset in Table 2, we illustrate its frequent
sequence patterns and the associated support of each
pattern in Table 3. (s, sup) denotes a frequent pattern,
where s is a sequence and sup represents the support
of that pattern.
Table 3: Example of frequent syllable sequence patterns.
Minimum support Syllable sequence pattern
2 (< a >,2)
(< li, be >, 2)
(< pro, gra, ma >,2)
(< ma, re >, 2)
(< ma,tor >,2)
(< ti >,2)
(< e, li >,3)
(< gra, ma >, 3)
(< sa, re >, 3)
(< tor >, 4)
(< li >, 4)
(< e >,5)
(< ma >,5)
(< re >, 6)
3 (< e, li >,3)
(< gra, ma >, 3)
(< sa, re >, 3)
(< tor >, 4)
(< li >, 4)
(< e >,5)
(< ma >,5)
(< re >, 6)
4 (< tor >, 4)
(< li >, 4)
(< e >,5)
(< ma >,5)
(< re >, 6)
5 (< e >,5)
(< ma >,5)
(< re >, 6)
6 (< re >, 6)
4 FROM FREQUENT
SEQUENCES OF SYLLABLES
TO SYLLABIFICATION
In the previous section we introduced how words
can be represented as sequences of syllables. In
this section we will show how such a representa-
tion can be used to solve the syllabification problem,
in a generic way (without taking into account any
language-specific rules). The proposed method con-
sists in the following steps (described in more detail
later):
1. The identification of frequent syllable sequence
patterns
2. The identification of patterns with a high degree
of matching within the word to be syllabified
3. Classification of the matched patterns based on
KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval
354

the place where the match occurred (start, inner,
end).
4. Building a pattern graph where edges are defined
on overlapping between the word and the word to
be syllabified
5. (Optional) Pruning the graph of isolated inner
nodes
6. Find graph paths between start and end patterns,
and select the one with the highest probability to
produce the correct syllabification
4.1 Identifying Frequent Syllable
Patterns
Table 4 shows the number of patterns found in RoSyl-
labiDict (Barbu, 2008) (525486 Romanian syllabified
words), by varying the minimum support.
Table 4: The number of syllable patterns of a certain length
having a certain minimum support.
Supp. Len. 2 Len. 3 Len. 4 Len. 5
100 6754 2309 162 2
50 12671 7453 853 47
20 25731 28056 5384 674
10 41126 63388 17812 2940
5 63443 123429 52271 10553
2 104254 248227 186623 66915
For the pattern identification part we employed
an implementation of the gapBIDE algorithm (Li and
Wang, 2008). Note that selecting patterns with a small
minimum support might improve the syllabification
solution but it will also make it slower. Further anal-
yses will try to find the ”honey spot”, where a mini-
mum number of patterns are used to syllabify words
and the accuracy is still as high as possible. At this
step the high number of patterns can be compensated
with an indexing method for further matching. For
example, the patterns from Table 3 can be indexed
with a map where the keys represent the concate-
nated syllables of the pattern and the value represents
the pattern itself with its support. Example pairs of
keys and values are the following: (re, (< re >, 6)),
(programa, (< pro, gra, ma >, 2)).
4.2 Matching Syllable Sequence
Patterns within Words
Let w be a word composed of a sequence of letters
and Z
w
the set of all continuous subsequences of w,
with the associated indices.
Matching syllable patterns for the word w with
the associated Z
w
set refers to identifying those fre-
quent patterns which have their index included in Z
w
.
Let us denote by M
w
this set. Table 5 presents the
contents of M
amator
.
Table 5: Example of matched patterns for amator.
Pattern Matching indices
(< a >,2) [0, 1), [2, 3)
(< ma >,5) [2, 4)
(< ma,tor >,2) [2, 6)
(< tor >, 4) [4, 6)
The following algorithm can be used to find
matched patterns inside a certain word:
fi n dMa t che d Pat t er n s (IndexedPatterns, w)
P
w
=
/
0
S
w
= f indAllSubstringsWithIndices(w)
fo r indexedSubstring in S
w
s = substringFrom(indexedSubstring)
if hasKey(IndexedPatterns, s)
p = getPattern(IndexedPatterns, s)
i = indicesFrom(indexedSubstring)
P
w
= P
w
∪ {< p, i >}
retu r n P
w
After being able to identify patterns related to a
certain word, our method needs a preliminary classi-
fication of them based on the following categories:
• start patterns: (< a >,2)
• inner patterns: (< ma >,5), (< a >,2)
• end patterns: (< ma, tor >,2), (< tor >,4)
4.3 Frequent Syllable Patterns Graphs
We defined a matched pattern w.r.t a word w as a fre-
quent pattern associated with a start index and an end
index within w.
The core assumption of the method is that through
frequent sequence patterns we will be able to cor-
rectly syllabify words. Consequently, we need a way
to structure the patterns found for certain words. We
chose to employ graphs, since the patterns associated
with a word are highly related if we consider the over-
lapping of the indices where these are matched within
words.
4.3.1 Building Pattern Graphs
Consider p
1
and p
2
two patterns hs
1
, sup
s
1
, [i
s
1
, j
s
1
)i,
hs
2
, sup
s
2
, [i
s
2
, j
s
2
)i matched within w. p
1
y p
2
(p
1
is extended by p
2
) if i
s
1
ε [0, i
s
2
) and j
s
1
∈ the set of
indices where s
2
is split.
For the word amator, having the matched patterns
M
amator
presented in Table 5, we illustrate the pattern
extensions in Table 6.
Syllabification with Frequent Sequence Patterns - A Language Independent Approach
355

Table 6: Extensions of p
1
y p
2
w.r.t M
amator
.
p
1
p
2
h< a >,2, [0, 1)i h< ma >, 5, [1, 3)i
h< a >,2, [0, 1)i h< ma, tor >, 2, [1, 6)i
h< ma >,5, [1, 3)i h< tor >,4, [3, 6)i
h< a >,2, [2, 3)i h< tor >, 4, [3, 6)i
Let P
w
a set of patterns matched in w, then the set
of pair of patterns that represent extensions is defined
as:
E
w
= {hp
i
, p
j
i|p
i
, p
j
∈ P
w
∧ p
i
y p
j
} (2)
A graph of frequent syllable patterns for w is
then defined as G
w
= hP
w
, E
w
i.
In the following algorithm we sketch a simplified
procedure to obtain such a graph:
b u i ld M at ch e dP at t er nsG r ap h (P
w
)
E
w
=
/
0
C
P
w
= P
w
× P
w
fo r hp
1
, p
2
i in C
P
w
if p
1
y p
2
E
w
= E
w
∪ {hp
1
, p
2
i}
G
w
= hP
w
, E
w
i
retu r n G
w
4.3.2 Pattern Graph Minimisation
The number of matched sequences in the pattern
graph can be significantly large and finding all paths
between start and end nodes can therefore be compu-
tationally intensive.
Observing that inner nodes which are not con-
nected directly or indirectly by start and end nodes
are of no interest for the searched set path, we can
reduce the size of the graph by removing such nodes.
We illustrate this pruning method in the following
algorithm:
pr u neP a tt ern G rap h (G
w
)
isolatedVertices =
/
0
fo r v in V
w
if deg
−
(v) == 0 ∧ isNotStartNode(v)
isolatedVertices = isolatedVertices ∪ {v}
if deg
+
(v) == 0 ∧ isNotEndNode(v)
isolatedVertices = isolatedVertices ∪ {v}
if isolatedVertices ==
/
0
retu r n hV
w
, E
w
i
extraEdges =
/
0
fo r e in E
w
if e has n o d e in isolatedVertices
extraEdges = extraEdges ∪ {e}
V
0
w
= V
w
\ isolatedVertices
E
0
w
= E
w
\ extraEdges
retu r n hV
0
w
, E
0
w
i
4.4 Closed Chains of Syllable Sequence
Patterns
In order to extract, from the pattern graph, the syllab-
ification of a word, we identify the path having the
highest probability of being a correct syllabification.
Let I
w
be the interval that contains the indices
of all potential splitting points for the word w.
v
1
, v
2
, ..., v
n
is a sequence of vertices in G
w
, a pattern
graph, with v
x
like hp
x
, sup
x
, [i
x
, j
x
)i. We call such a
sequence a closed pattern chain if:
[
1≤x≤n
[i
x
, j
x
) = I
w
(3)
Informally, a closed pattern chain is a path con-
necting a start node and an end node.
The next procedure sketches a solution for closed
pattern chains identification:
fi n dC l os ed P a tt e rn Ch a i ns (G
w
)
L
w
=
/
0
SV
G
w
= f indStartVertices(G
w
)
EV
G
w
= f indEndVertices(G
w
)
T = SV
G
w
× EV
G
w
fo r hstartNode, endNodei in T
L
startNode−endNode
=
f indPathsBetween(startNode, endNode)
L
w
= E
w
∪ {L
startNode−endNode
}
retu r n L
w
}
Let l be a closed syllable pattern chain from L
w
and s
l
the syllabification of the word w based on l.
For example, considering the closed pattern chain h<
a >, 2, [0, 1)i, h< ma >, 5, [1, 3)i, h< tor >, 4, [3, 6)i,
its associated syllabification is a − ma −tor.
Multiple chains may actually lead to the same syl-
labification. We refer to such chains as equivalent
and denote this relation by ≡.
Let l
1
= h< a >, 2, [0, 1)i, h< ma,tor >, 4, [1, 6)i,
iar l
2
= h< a >, 2, [0, 1)i, h< ma >, 5, [1, 3)i, h< tor >
, 4, [3, 6)i. The associated syllabifications are s
l
1
=
a − ma −tor and s
l
2
= a − ma −tor, therefore l
1
≡ l
2
.
We denote the length of a closed chain of patterns
l with |l|. An example of a chain of length 2 is: h<
a >, 2, [0, 1)i, h< ma, tor >, 4, [1, 6)i.
4.5 Syllabification through Closed
Chains of Frequent Syllable
Patterns
From the set of potential syllabification solutions rep-
resented as closed pattern chains, we need to select
one as the predicted syllabification. In the following
we introduce three strategies to achieve this step.
KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval
356

4.5.1 Equivalent Classes based Strategy
The first strategy relies on the observation that there
are multiple closed pattern chains that actually rep-
resent the same solution. We define a strategy based
on the assumption that a syllabification is more likely
to be correct if it has a larger number of chains from
which it can be derived.
Let w be a word and L
w
− the set of closed chains
for w. The equivalence class of a certain chain e is:
[e] = {l ∈ L
w
|l ≡ e} (4)
We denote by E
L
w
the set of all equivalence
classes for L
w
and with S
L
w
− the set of all syllab-
ifications derived from L
w
.
In this context we use a relation f : S
L
w
→ E
L
w
that identifies for each syllabification its equivalence
class. Having this relation we can order syllabifica-
tions based on the number of chains associated with
each equivalence class.
4.5.2 Overlapping based Strategy
A second possible strategy comes from the obser-
vation that each closed chain may possess a certain
amount of overlapping between patterns and a higher
degree of overlapping increases the likelihood of that
chain giving the correct syllabification. Having two
patterns matched at the following indices: [i
p
1
, j
p
1
),
[i
p
2
, j
p
2
), we define an overlapping metric as:
ω(p
1
, p
2
) =

0, j
p
1
≤ i
p
2
max(i
p
2
, j
p
1
)
− min( j
p
2
, i
p
1
), j
p
1
> i
p
2
(5)
For example, considering the pattern p
1
matched
at [0, 6) and the pattern p
2
matched at [4, 8) we have
ω(p
1
, p
2
) = 2
Considering p
1
, p
2
, ..., p
n
a closed pattern chain
denoted by l, we define the overlapping on the entire
chain l as:
Ω(l) =
n−1
∑
i=1
ω(p
i
, p
i+1
) (6)
4.5.3 Chain Length based Strategy
The last strategy we propose is based on the obser-
vation that shorter chains contain longer patterns and
longer patterns have a higher probability of represent-
ing accurate syllabifications. Shorter chains might
also trigger a higher level of overlapping.
4.5.4 Complete Solution
As there are multiple possible strategies for selecting
the final solution, we present the complete algorithm
as a procedure where the chain selection strategy is
adjustable:
sp l i tW o rd (P, w, selectionStrategy)
M
w
= f indMatchingPatterns(P, w)
G
w
= buildMatchedPatternsGraph(M
w
)
Gp
w
= prune(G
w
)
L
w
= f indClosedPatternChains(Gp
w
)
retu r n pickSolution(L
w
, selectionStrategy)
5 EXPERIMENTAL EVALUATION
We have performed a series of evaluations for Ro-
manian syllabification. We have employed RoSyl-
labiDict (Barbu, 2008), a dictionary consisting of
more than 520,000 words and their syllabification
variants, together with lexical accents (in case there
are more accepted variants for a given word, the dic-
tionary also gives information about the morphologi-
cal aspects of words).
To estimate the performance, we have employed
approximately 200.000 words for the training stage
(i.e. to identify the frequent patterns) and we vali-
dated the model against 10.000 words, sampled ran-
domly from the rest of the dictionary.
To prove the generality of the approach, we have
also performed several evaluations for the syllabifica-
tion of English words, on a set of 187175 words
2
.
We have sampled randomly 5000 words for evalua-
tion, and the rest were employed for training.
We have considered two evaluation metrics: the
accuracy at word level, and the accuracy at split point
level. The accuracy at word level, m
w
, considers syl-
labification of a word as an atomic operation:
Definition 1. Given the word, w, s
p
a possible syllab-
ification of the word and s
e
its correct syllabification,
we define m
w
as:
m
w
(s
p
, s
e
) =

0, if s
p
= s
e
1, if s
p
6= s
e
(7)
There are cases in which a word presents different
correct syllabifications (e.g. homonyms). For such
situations, defining a metric with a smaller degree of
granularity is important. Consequently, we define the
accuracy at split point level, m
d
, as:
Definition 2. Let s be the syllabification of a word.
The set of split points associated to s, I
s
is the col-
lection of indices of the letters that have a hyphen be-
fore them in the syllabification (e.g. for a − ma − tor,
the set of split points is {1, 3}).
2
Moby Hyphenator: http://icon.shef.ac.uk/Moby/
mhyph.html
Syllabification with Frequent Sequence Patterns - A Language Independent Approach
357

Definition 3. Considering the set of split points I
s
p
associated to the syllabification s
p
, and I
s
e
the set of
split points associated to the correct syllabification of
the word, we define m
d
as:
m
d
(s
p
, s
e
) = 1 −
|I
s
e
\ I
s
p
|
2 · |I
s
e
|
−
|I
s
p
\ I
s
e
|
2 · |I
s
p
|
(8)
The value of m
d
depends on both the correctly and
the incorrectly predicted split points.
For example:
m
d
({1, 3, 5}, {2, 3, 6}) = 1 −
2
2 · 3
−
2
2 · 3
' 0.33 (9)
m
d
({1, 3, 5}, {2, 3, 5}) = 1 −
1
2 · 3
−
1
2 · 3
' 0.66
(10)
Figures 1 and 2 present the accuracy at word and
split point level, respectively, obtained by the three
different selection strategies, at varying levels of min-
imum support, for the Romanian language. As ex-
pected, split point accuracy values are higher than
word level values. The chain length based strategy
yields the highest accuracy levels, and seems to be
the least affected by the value established for the
minimum support, while the equivalent chains strat-
egy yields the poorest values. On a closer analysis
Figure 1: Word Accuracy - Romanian.
Figure 2: Split Point Accuracy - Romanian.
Figure 3: Word Accuracy - English.
Figure 4: Split Point Accuracy - English.
of several pattern graphs, we found that the equiva-
lent chains strategy favors shorter patterns, because
shorter patterns are better connected in the graph,
therefore generating a larger number of chains. This
is somehow in contradiction to the third strategy, but
also to the Maximum Onset principle.
Figures 3 and 4 present the results of the evalua-
tions performed on English syllabification. The best
word level accuracy is about 7% lower than for Roma-
nian. The chain length based strategy yields the best
results in this case as well, but the difference from
the overlap based strategy (which is second best) is
smaller than for Romanian.
Each strategy generates a certain number of errors;
we believe some of the errors could by corrected by
refining the selection strategy further − e.g. by taking
into account the pattern support at this step. However,
some errors are independent of the selection strategy
used − they are due to the fact that there are words
for which no path can be found between the start and
the end pattern, i.e. no closed chain can be found (un-
split words): between 2% and 9% for Romanian, and
between 2% and 32% for English (according to the
varying levels for the minimum support). Devising
alternative syllable boundary prediction strategies for
such cases should improve the accuracy at both word
and split point level.
KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval
358

6 CONCLUSIONS
This paper presents the syllabification problem and
shows how frequent syllable sequences can be identi-
fied in a syllabified corpus and then employed to pre-
dict the syllabification of a word in a language inde-
pendent manner.
We propose a formal framework for this entire
process, which consists of mining frequent pattern se-
quences, building the pattern graph, finding closed
pattern chains on the graph and then selecting the
most probable syllabification among several possi-
ble candidates. Preliminary evaluations performed on
both Romanian and English words indicate that the
method has potential. We believe that we can pro-
duce a significant boost in accuracy by providing a
solution for syllabifying words for which there is no
closed chain of patterns found. Also, none of the three
syllable boundary prediction strategies employs sup-
port information in the prediction process. We be-
lieve considering such information will further boost
the accuracy.
Furthermore, we intend to evaluate the solution on
a broader range of languages (Hungarian is one poten-
tial candidate, as it is not an Indo-European language)
and we are working on evaluating the impact of spe-
cial characters (such as diacritics in Romanian) on the
performance of our approach.
ACKNOWLEDGEMENT
The work presented in this paper is partially supported
by the Romanian Ministry of Education, under grant
agreement PN-II-PT-PCCA-2013-4-1660 (SWARA).
REFERENCES
Barbu, A.-M. (2008). Romanian lexical data bases: In-
flected and syllabic forms dictionaries. In Proceed-
ings of the Sixth International Conference on Lan-
guage Resources and Evaluation (LREC’08). Eu-
ropean Language Resources Association (ELRA).
http://www.lrec-conf.org/proceedings/lrec2008/.
Bartlett, S., Kondrak, G., and Cherry, C. (2008). Auto-
matic syllabification with structured svms for letter-
to-phoneme conversion. In ACL 2008, Proceedings of
the 46th Annual Meeting of the Association for Com-
putational Linguistics, June 15-20, 2008, Columbus,
Ohio, USA, pages 568–576.
Bartlett, S., Kondrak, G., and Cherry, C. (2009). On the
syllabification of phonemes. In Proceedings of Hu-
man Language Technologies: The 2009 Annual Con-
ference of the North American Chapter of the Asso-
ciation for Computational Linguistics, NAACL ’09,
pages 308–316, Stroudsburg, PA, USA. Association
for Computational Linguistics.
Daelemans, W., Van Den Bosch, A., and Weijters, T.
(1997). Igtree: Using trees for compression and clas-
sification in lazy learning algorithms. Artificial Intel-
ligence Review, 11(1):407–423.
Dinu, L. (2004). Despartirea automata in silabe a cuvintelor
din limba romana. aplicatii in constructia bazei de date
a silabelor limbii romane.
Dinu, L. P., Niculae, V., and Sulea, O.-M. (2013). Romanian
syllabication using machine learning. In Text, Speech,
and Dialogue, pages 450–456. Springer.
Goslin, J. and Frauenfelder, U. H. (2001). A comparison of
theoretical and human syllabification. Language and
Speech, 44(4):409–436.
Kahn, D. (1976). Syllable-Based Generalizations in English
Phonology. PhD thesis, Indiana University Linguis-
tics Club.
Li, C. and Wang, J. (2008). Efficiently mining closed sub-
sequences with gap constraints. In SDM, pages 313–
322. SIAM.
Marchand, Y., Adsett, C. R., and Damper, R. I. (2007).
Evaluating automatic syllabification algorithms for
english. In 6th International Speech Communication
Association (ISCA) Workshop on Speech Synthesis,
pages 316–321.
Marchand, Y. and Damper, R. I. (2000). A multi-strategy
approach to improving pronunciation by analogy.
Computational Linguistics, 26(2):195–219.
Rogova, K., Demuynck, K., and Van Compernolle, D.
(2013). Automatic syllabification using segmental
conditional random fields. Computational Linguistics
in the Netherlands Journal, 3:34–48.
Selkirk, E. O. (1984). On the major class features and syl-
lable theory.
Syllabification with Frequent Sequence Patterns - A Language Independent Approach
359