The Effect of Noise and Outliers on Fuzzy Clustering of
High Dimensional Data
Ludmila Himmelspach and Stefan Conrad
Institute of Computer Science, Heinrich-Heine-Universit
¨
at D
¨
usseldorf, 40225 - D
¨
usseldorf, Germany
Keywords:
Fuzzy Clustering, c-Means Models, High Dimensional Data, Noise, Possibilistic Clustering.
Abstract:
Clustering high dimensional data is still a challenging problem for fuzzy clustering algorithms because dis-
tances between each pair of data items get similar with the increasing number of dimensions. The presence
of noise and outliers in data is an additional problem for clustering algorithms because they might affect the
computation of cluster centers. In this work, we analyze the effect of different kinds of noise and outliers on
fuzzy clustering algorithms that can handle high dimensional data: FCM with attribute weighting, the multi-
variate fuzzy c-means (MFCM), and the possibilistic multivariate fuzzy c-means (PMFCM). Additionally, we
propose a new version of PMFCM to enhance its ability handling noise and outliers in high dimensional data.
The experimental results on different high dimensional data sets show that the possibilistic versions of MFCM
produce accurate cluster centers independently of the kind of noise and outliers.
1 INTRODUCTION
Clustering algorithms are used in many fields like
bioinformatics, image processing, text mining, and
many others. Data sets in these applications usually
contain many features. Therefore, there is a need
for clustering algorithms that can handle high dimen-
sional data. The hard k-means algorithm (MacQueen,
1967) is still mostly used for clustering high dimen-
sional data although it is comparatively unstable and
sensitive to the initialization. It is not able to distin-
guish data items belonging to clusters from noise and
outliers. This is another issue of the hard k-means
algorithm because noise and outliers might influence
the computation of cluster centers leading to inaccu-
rate clustering results.
In the case of low dimensional data, the fuzzy
c-means algorithm (FCM) (Bezdek, 1981), (Dunn,
1973) which assigns data items to clusters with mem-
bership degrees might be a better choice because it is
more stable and less sensitive to initialization (Kla-
wonn et al., 2015). The possibilistic fuzzy c-means
algorithm (PFCM) (Pal et al., 2005) partitions data
items in presence of noise and outliers. However,
when FCM is applied on high dimensional data, it
tends to produce cluster centers close to the cen-
ter of gravity of the data set (Winkler et al., 2011),
(Klawonn, 2013). In this work, we analyze three
fuzzy clustering methods that are suitable for cluster-
ing high dimensional data. The first approach is the
attribute weighting fuzzy clustering algorithm (Keller
and Klawonn, 2000) that uses a new attribute weight-
ing function to determine attributes that are impor-
tant for each single cluster. This method was rec-
ommended in (Klawonn, 2013) for fuzzy clustering
high dimensional data. The second approach is the
multivariate fuzzy c-means (MFCM) (Pimentel and
de Souza, 2013) that computes membership degrees
of data items to each cluster in each feature. The third
method is the possibilistic multivariate fuzzy c-means
(PMFCM) (Himmelspach and Conrad, 2016) which
is an extension of MFCM in a possibilistic cluster-
ing scheme. Additionally, we propose a new version
of PMFCM to enhance its ability distinguishing data
items belonging to clusters from noise and outliers
in high dimensional data. The main objective of this
work is to analyze the effect of noise and outliers on
fuzzy clustering algorithms for high dimensional data.
Our aim is to ascertain which fuzzy clustering algo-
rithms are resistant to which kind of noise and outliers
when clustering high dimensional data.
The rest of the paper is organized as follows: In
the next section we give a short overview of fuzzy
clustering methods for high-dimensional data. The
evaluation results on artificial data sets containing dif-
ferent kinds of noise and outliers are presented in Sec-
tion 3. Section 4 closes the paper with a short sum-
mary and the discussion of future research.
Himmelspach, L. and Conrad, S.
The Effect of Noise and Outliers on Fuzzy Clustering of High Dimensional Data.
DOI: 10.5220/0006070601010108
In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 2: FCTA, pages 101-108
ISBN: 978-989-758-201-1
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All r ights reserved
101

2 FUZZY CLUSTERING
ALGORITHMS
Fuzzy c-means (FCM) (Bezdek, 1981), (Dunn, 1973)
is a partitioning clustering algorithm that assigns data
objects to clusters with membership degrees. The ob-
jective function of FCM is defined as:
J
m
(U,V ; X) =
n
∑
k=1
c
∑
i=1
u
m
ik
d
2
(v
i
, x
k
), (1)
where c is the number of clusters, u
ik
∈ [0, 1] is the
membership degree of data item x
k
to cluster i, m > 1
is the fuzzification parameter, d(v
i
, x
k
) is the distance
between cluster prototype v
i
and data item x
k
. The
objective function of FCM is usually minimized in an
alternating optimization (AO) scheme (Bezdek, 1981)
under constraint (2).
c
∑
i=1
u
ik
= 1 ∀k ∈ {1, ...,n} and
n
∑
k=1
u
ik
> 0 ∀i ∈ {1, ..., c}.
(2)
The algorithm begins with initialization of cluster
prototypes with random values in the data space. In
each iteration of the algorithm, the membership de-
grees and the cluster prototypes are alternating up-
dated according to Formulae (3) and (4).
u
ik
=

d
2
(v
i
, x
k
)

1
1−m
c
∑
l=1
(d
2
(v
l
, x
k
))
1
1−m
, 1 ≤ i ≤ c, 1 ≤ k ≤ n.
(3)
v
i
=
n
∑
k=1
u
m
ik
x
k
n
∑
k=1
u
m
ik
, 1 ≤ i ≤ c . (4)
The iterative process continues as long as the cluster
prototypes change up to a chosen limit.
The FCM algorithm has several advantages over
the hard k-means algorithm (MacQueen, 1967) in low
dimensional data. It is more stable, less sensitive to
initialization, and is able to model soft transitions be-
tween clusters (Klawonn et al., 2015). However, the
hard k-means algorithm is still mostly used in real
world applications for clustering high dimensional
data because fuzzy c-means does not provide useful
results on high dimensional data. It usually computes
equal membership degrees of all data items to all clus-
ters which results in the computation of final cluster
prototypes close to the center of gravity of the entire
data set. This is due to the concentration of distance
phenomenon described in (Beyer et al., 1999). It says
that the distance to the nearest data item approaches
the distance to the farthest one with increasing num-
ber of dimensions.
2.1 Fuzzy Clustering Algorithms for
High Dimensional Data
In (Klawonn, 2013), the author recommended to
use the attribute weighting fuzzy clustering algorithm
(Keller and Klawonn, 2000) for clustering high di-
mensional data. This method uses a distance function
that weights single attributes for each cluster:
d
2
(v
i
, x
k
) =
p
∑
j=1
α
t
i j
(x
k j
− v
i j
)
2
, 1 ≤ i ≤ c, 1 ≤ k ≤ n,
(5)
where p is the number of attributes, t > 1 is a fixed
parameter that determines the strength of the attribute
weighting, and
p
∑
j=1
α
i j
= 1 ∀i ∈ {1, ..., c}. (6)
This approach works in the same way as FCM but
it circumvents the concentration of distance phe-
nomenon using a distance function that gives more
weight to features that determine a particular clus-
ter. The objective function of the attribute weighting
fuzzy clustering algorithm is defined as:
J
m,t
(U,V ; X) =
n
∑
k=1
c
∑
i=1
u
m
ik
p
∑
j=1
α
t
i j
(v
i j
− x
k j
)
2
. (7)
The attribute weights are updated in an additional it-
eration step according to Formula (8).
α
i j
=





p
∑
r=1




n
∑
k=1
u
m
ik
(x
k j
− v
i j
)
2
n
∑
k=1
u
m
ik
(x
kr
− v
ir
)
2




1
t−1





−1
1 ≤ i ≤ c, 1 ≤ k ≤ n.
(8)
The second approach that we analyze in this work
is the multivariate fuzzy c-means (MFCM) algorithm.
This fuzzy clustering method computes membership
degrees of data items to clusters for each feature (Pi-
mentel and de Souza, 2013). The objective function
of MFCM is defined as follows:
J
m
(U,V ; X) =
n
∑
k=1
c
∑
i=1
p
∑
j=1
u
m
ik j
(v
i j
− x
k j
)
2
, (9)
where u
ik j
∈ [0, 1] is the membership degree of data
object x
k
to cluster i for feature j. The objective func-
tion of MFCM has to be minimized under constraint
(10).
c
∑
i=1
p
∑
j=1
u
ik j
= 1 ∀k ∈ {1, ...,n} and
p
∑
j=1
n
∑
k=1
u
ik j
> 0 ∀i ∈ {1, ..., c}.
(10)
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
102

The multivariate membership degrees and the cluster
prototypes are updated in the iterative process of the
algorithm according to (11) and (12).
u
ik j
=


c
∑
l=1
p
∑
j=1

(x
k j
− v
i j
)
2
(x
k j
− v
l j
)
2

1
m−1


−1
1 ≤ i ≤ c, 1 ≤ k ≤ n, 1 ≤ j ≤ p.
(11)
v
i j
=
n
∑
k=1
u
m
ik j
x
k j
n
∑
k=1
u
m
ik j
1 ≤ i ≤ c, 1 ≤ j ≤ p. (12)
MFCM is not influenced by the concentration of dis-
tance phenomenon because it computes membership
degrees in each feature depending on the partial dis-
tances in single dimensions. Therefore, this approach
is suitable for clustering high dimensional data.
2.2 Possibilistic Clustering Algorithms
for High Dimensional Data
The fuzzy clustering algorithms described before are
not designed to cluster data in presence of noise and
outliers. They assign such data items to clusters in
the same way as data items within clusters. In this
way, noise and outliers might affect the computation
of cluster centers which leads to inaccurate partition-
ing results. There are different ways for avoiding this
problem. The mostly used method is determining out-
liers before clustering. There are different methods
for outlier detection but the most of them compare the
distances from data points to their neighbors (Kriegel
et al., 2009). Another method called noise cluster-
ing introduces an additional cluster that contains all
data items that are located far away from any of clus-
ter centers (Dave and Krishnapuram, 1997), (Rehm
et al., 2007). In this work, we extend the clustering
algorithms described in the previous subsection us-
ing the possibilistic fuzzy c-means (PFCM) clustering
model proposed in (Pal et al., 2005). This approach
extends the basic FCM by typicality values that ex-
press a degree of typicality of each data item to the
overall clustering structure of data set. The advan-
tage of using typicality values is that outliers get less
weight in the computation of cluster centers. The ob-
jective function of PFCM is defined as:
J
m,η
(U, T,V ; X) =
n
∑
k=1
c
∑
i=1
(au
m
ik
+ bt
η
ik
)d
2
(v
i
, x
k
)
+
c
∑
i=1
γ
i
n
∑
k=1
(1 −t
ik
)
η
,
(13)
where t
ik
≤ 1 is the typicality value of data item x
k
to
cluster i, m > 1 and η > 1 are user defined constants.
Similarly to FCM, the first term in (13) ensures that
distances between data items and cluster centers are
minimized, where constants a > 0 and b > 0 control
the relative influence of fuzzy membership degrees
and typicality values. The second term ensures that
typicality values are determined as large as possible.
The second summand is weighted by the parameter
γ
i
> 0. In (Krishnapuram and Keller, 1993), the au-
thors recommended to run the basic FCM algorithm
before PFCM and to choose γ
i
by computing:
γ
i
= K
n
∑
k=1
u
m
ik
d
2
(v
i
, x
k
)
n
∑
k=1
u
m
ik
1 ≤ i ≤ c, (14)
where the {u
ik
} are the terminal membership degrees
computed by FCM and K > 0 (usually K = 1). The
objective function of PFCM has to be minimized un-
der constraints (2) and (15).
n
∑
k=1
t
ik
> 0, ∀i ∈ {1, ..., c} (15)
In (Himmelspach and Conrad, 2016), we extended
the MFCM algorithm in the possibilistic clustering
scheme to make it less sensitive to outliers. Since
we considered outliers as data points that have a large
overall distance to any cluster, we did not compute
typicality values of data points to clusters for each
feature. The objective function of the resulting ap-
proach that we refer here as possibilistic multivariate
fuzzy c-means (PMFCM) is defined as
J
m,η
(U, T,V ; X) =
n
∑
k=1
c
∑
i=1
p
∑
j=1
(au
m
ik j
+ bt
η
ik
)(v
i j
− x
k j
)
2
+ p
c
∑
i=1
γ
i
n
∑
k=1
(1 −t
ik
)
η
.
(16)
The objective function of PMFCM has to be mini-
mized under constraint (17).
c
∑
i=1
u
ik j
= 1 ∀k, j and
n
∑
k=1
u
ik j
> 0 ∀i, j, and
n
∑
k=1
t
ik
> 0 ∀i.
(17)
In MFCM, the sum of membership degrees over all
clusters and features to a particular data item was con-
strained to be 1. Since we want to retain equal influ-
ence of membership degrees and typicality values, we
only constrain the sum of membership degrees over
all clusters to a particular data item to be 1.
The Effect of Noise and Outliers on Fuzzy Clustering of High Dimensional Data
103

The membership degrees and the typicality values
have to be updated according to (18) and (19). In PM-
FCM, the cluster centers are updated in a similar way
as in PFCM according to Formula (20).
u
ik j
=


c
∑
l=1

(x
k j
− v
i j
)
2
(x
k j
− v
l j
)
2

1
m−1


−1
1 ≤ i ≤ c, 1 ≤ k ≤ n, 1 ≤ j ≤ p.
(18)
t
ik
=


1 +
b
∑
p
j=1
(x
k j
− v
i j
)
2
γ
i
p
!
1
η−1


−1
1 ≤ i ≤ c, 1 ≤ k ≤ n.
(19)
v
i j
=
n
∑
k=1
(au
m
ik j
+ bt
η
ik
)x
k j
n
∑
k=1
(au
m
ik j
+ bt
η
ik
)
1 ≤ i ≤ c, 1 ≤ j ≤ p.
(20)
The membership degrees of data objects to clusters
can be computed in this model as the average of the
multivariate membership degrees over all variables,
u
ik
=
1
p
∑
p
j=1
u
ik j
.
Due to the concentration of distance phenomenon,
PMFCM might not produce meaningful typicality
values because it uses the Euclidean distances be-
tween data items and cluster prototypes. Since dis-
tances between data items within clusters and clus-
ter centers and distances between outliers and clus-
ter centers might be similar in high dimensional data,
the typicality values as they are computed in PMFCM
will not be helpful for distinguishing between data
items within clusters and outliers. Therefore, in this
work, we propose another version of PMFCM that
computes typicality values of data items to clusters in
each dimension. We refer this approach here as pos-
sibilistic multivariate fuzzy c-means for high dimen-
sional data (PMFCM HDD). The objective function
of PMFCM HDD is given in Formula (21).
J
m,η
(U, T,V ; X) =
n
∑
k=1
c
∑
i=1
p
∑
j=1
(au
m
ik j
+ bt
η
ik j
)(v
i j
− x
k j
)
2
+
c
∑
i=1
γ
i
n
∑
k=1
p
∑
j=1
(1 −t
ik j
)
η
.
(21)
The objective function of PMFCM
HDD has to be
minimized under constraint (22).
c
∑
i=1
u
ik j
= 1 ∀k, j and
n
∑
k=1
u
ik j
> 0 ∀i, j, and
n
∑
k=1
t
ik j
> 0 ∀i, j.
(22)
The membership degrees are updated in the same way
as in PMFCM according to Formula (18). The update
Formulae for typicality values and cluster centers are
given in (23) and (24).
t
ik j
=


1 +

b(x
k j
− v
i j
)
2
γ
i

1
η−1


−1
1 ≤ i ≤ c, 1 ≤ k ≤ n, 1 ≤ j ≤ p.
(23)
v
i j
=
n
∑
k=1
(au
m
ik j
+ bt
η
ik j
)x
k j
n
∑
k=1
(au
m
ik j
+ bt
η
ik j
)
1 ≤ i ≤ c, 1 ≤ j ≤ p.
(24)
The typicality values of data objects to clusters can
also be computed as average of the multivariate typi-
cality values over all variables, t
ik
=
1
p
∑
p
j=1
t
ik j
.
3 DATA EXPERIMENTS
We tested the four fuzzy clustering methods for high
dimensional data described in Sections 2 on artificial
data sets containing different kinds of noise and out-
liers. The main data set was generated similarly to
one that was used in (Keller and Klawonn, 2000). It is
a two-dimensional data set that consists of 1245 data
points unequally distributed on one spherical cluster
and three clusters that have a low variance in one of
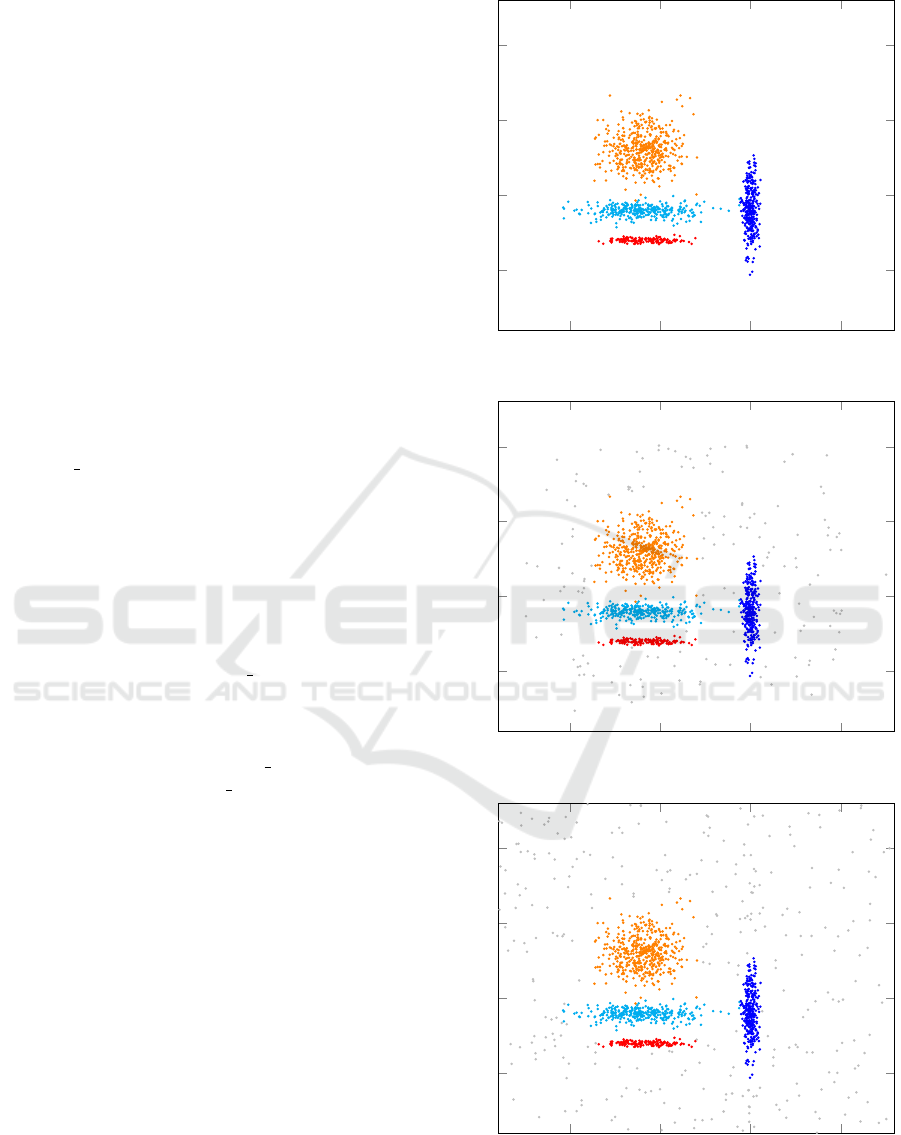
the dimensions. The data set is depicted in Figure 1.
We generated the second and the third data sets that
are depicted in Figures 2 and 3 by adding 150 and 300
noise points to the main data set.
In order to generate high dimensional data sets, in
the first experiment, we added 18 additional dimen-
sions containing feature values close to zero. Addi-
tionally, we generated the fourth data set by adding
300 noise points containing values different from zero
in all 20 dimensions. We had to modify PMFCM and
PMFCM HDD. Instead of running FCM at the begin-
ning, we only computed membership values to com-
pute γ
i
. If we ran FCM at the beginning, it output
cluster centers close to the center of gravity of the data
set which is a bad initialization for possibilistic clus-
tering algorithms. In order to provide the best starting
conditions for the clustering algorithms, in this pre-
liminary work, we initialized the cluster centers with
the original means of clusters in all experiments.
Table 1 shows the experimental results for FCM
with attribute weighting (FCM
AW), MFCM and its
possibilistic versions PMFCM and PMFCM HDD
for a = 0.5 and different values of b on the 20-
dimensional data set without noise and outliers. In
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
104

order to evaluate the experimental results, we com-
puted the Frobenius distance d
orig
between the origi-
nal cluster means and the cluster centers obtained by
the clustering algorithms. Moreover, we computed
the sum of distances d
means
between cluster centers
produced by the clustering algorithms. The most ac-
curate cluster centers were produced by MFCM. This
is indicated by a low d
orig
and high d
means
(good sep-
aration between clusters). The FCM algorithm with
attribute weighting produced the least accurate clus-
ter centers because it recognized the additional di-
mensions containing feature values close to zero as
the important ones and gave small weights to impor-
tant dimensions. This method was introduced by the
authors as a clustering algorithm that performs the
dimensionality reduction while clustering. Our re-
sults have shown that this method is not always able
to distinguish between important and unimportant di-
mensions. The second best results were produced
by the possibilistic clustering methods PMFCM and
PMFCM HDD for b = 1000. Tables 2 and 3 show
the experimental results on the second and the third
data sets with 150 and 300 noise points. The clus-
tering algorithms performed similarly as on the data
set without noise and outliers. Table 4 shows the
performance results of the algorithms on the fourth
data set where noise points contained values differ-
ent from zero in all features. MFCM produced clus-
ter centers that were farther from each other than the
real means of clusters. FCM AW produced cluster
centers that were not close to the center of gravity of
the entire data set anymore but they were too far from
each other. The most accurate cluster centers were ob-
tained by PMFCM and PMFCM HDD for b = 1000.
In all experiments, PMFCM HDD produced more ac-
curate results than PMFCM because the last uses the
Euclidean distances for computation of typicality val-
ues which is adversely in high dimensional domain.
In the second experiment, we distributed clusters
in the data space so that clusters were determined by
different features. For example, data items of the first
cluster had real values in the third and the fourth fea-
tures, data items of the second cluster had real val-
ues in the sevenths and the eighth features etc. Fur-
thermore, we completely distributed all noise points
among the dimensions so that each dimension pair
contained some noise points. Table 5 shows the exper-
imental results on the 20-dimensional data sets with
four clusters distributed among dimensions without
noise and outliers. The clustering algorithms simi-
larly performed as on the data set where data points
of all clusters had real values in the first two fea-
tures. Tables 6 and 7 show performance results of
the clustering algorithms on the same data set as in
4 cluster
0 5 10 15
0
5
10
15
1
Figure 1: Test data with four clusters.
4 cluster with 150 noise points
0 5 10 15
0
5
10
15
1
Figure 2: Test data with four clusters and 150 noise points.
4 cluster with 300 noise points
0 5 10 15
0
5
10
15
1
Figure 3: Test data with four clusters and 300 noise points.
the previous experiment but with 150 and 300 noise
points. As in the previous experiments, MFCM pro-
The Effect of Noise and Outliers on Fuzzy Clustering of High Dimensional Data
105

Table 1: Comparison between clustering methods on 20-dimensional data set with four clusters.
FCM AW: m = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
13.41 0.829 0.356 0.310
d
means
0.0004 32.58 32.05 31.82
MFCM: m = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
0.019 0.762 1.035 0.748
d
means
31.58 31.45 32.28 32.10
Table 2: Comparison between clustering methods on 20-dimensional data set with four clusters and 150 noise points.
FCM AW: m = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
13.67 0.853 0.655 0.376
d
means
0.0023 32.68 32.63 32.19
MFCM: m = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
0.031 2.456 0.911 1.051
d
means
31.61 27.34 32.05 32.36
Table 3: Comparison between clustering methods on 20-dimensional data set with four clusters and 300 noise points.
FCM AW: m = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
13.99 0.874 0.899 0.674
d
means
0.0004 32.67 32.82 32.67
MFCM: m = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
0.019 2.418 0.720 0.912
d
means
31.58 26.73 31.34 32.10
Table 4: Comparison between clustering methods on 20-dimensional data set with four clusters and 300 noise points contain-
ing values in all features.
FCM AW: m = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
95.24 2.501 2.273 0.709
d
means
90.86 26.46 27.52 32.15
MFCM: m = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
12.81 13.33 6.052 2.797
d
means
38.16 1.489 21.15 25.86
duced the most accurate cluster prototypes. Its possi-
bilistic versions PMFCM and PMFCM HDD also ob-
tained final cluster centers that were close to the actual
cluster means. Although FCM with attribute weight-
ing produced the least accurate cluster prototypes, its
performance was comparable to the performance of
the other methods. Due to noise points, all features
contained at least some values different from each
other. Therefore, FCM AW was able to correctly rec-
ognize features determining different clusters. In the
last experiment, we added 300 noise points that con-
tained values different from zero in all features. As in
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
106

Table 5: Comparison between clustering methods on 20-dimensional data set with four clusters distributed in data space.
FCM AW: m = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
27.47 1.333 0.495 0.460
d
means
0.0017 67.49 66.64 66.39
MFCM: m = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
0.072 0.753 0.959 0.701
d
means
65.97 65.34 65.33 65.79
Table 6: Comparison between clustering methods on 20-dimensional data set with four clusters and 150 noise points dis-
tributed in data space.
FCM AW: m = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
1.499 1.228 0.767 0.962
d
means
64.33 65.88 65.69 66.70
MFCM: m = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
0.104 0.665 0.731 0.924
d
means
66.00 65.07 65.48 65.37
Table 7: Comparison between clustering methods on 20-dimensional data set with four clusters and 300 noise points dis-
tributed in data space.
FCM AW: m = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
3.733 1.728 1.085 0.784
d
means
61.34 64.76 65.48 65.74
MFCM: m = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
0.072 0.983 0.680 0.787
d
means
65.97 64.25 65.34 65.47
Table 8: Comparison between clustering methods on 20-dimensional data set with four clusters distributed in data space and
300 noise points containing values in all features.
FCM AW: m = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2 PFCM HDD: m = 2, η = 2, t = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
36.42 12.61 5.016 0.949
d
means
127.20 56.79 61.93 65.24
MFCM: m = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2 PMFCM: m = 2, η = 2
a = 0.5, b = 100 a = 0.5, b = 400 a = 0.5, b = 1000
d
orig
12.42 11.21 1.595 0.699
d
means
73.79 55.25 62.92 64.89
the case of data set where data points within clusters
had real values in the first two dimensions, the most
accurate final cluster centers were obtained by PM-
FCM and PMFCM HDD for b = 1000. MFCM and
FCM AW produced cluster centers that were farther
from each other than the original means of clusters.
The Effect of Noise and Outliers on Fuzzy Clustering of High Dimensional Data
107

4 CONCLUSION AND FUTURE
WORK
Clustering high dimensional data is still a challeng-
ing problem for fuzzy clustering algorithms because
of the concentration of distance phenomenon. Noise
and outliers in data sets additionally make the parti-
tioning of data difficult because they affect the com-
putation of cluster centers. In this work, we analyzed
two fuzzy clustering algorithms for high dimensional
data from the literature and two possibilistic versions
of the MFCM algorithm in terms of correct determin-
ing final cluster prototypes in presence of noise. Our
experiments showed that MFCM produced the most
accurate cluster centers as long as data items had real
values in few features while its possibilistic versions
PMFCM and PMFCM HDD produced quite accurate
final cluster centers independently from the number
of features in that noise points had real values.
Although the performance results for PMFCM
seem to be promising, before applying this method
on real data sets, we plan to analyze the performance
of fuzzy clustering algorithms in terms of sensitivity
to different initializations because usually we do not
have any a priori knowledge about the distribution of
data in practical applications. In our future work, we
also plan to apply other possibilistic clustering models
to MFCM to make it less sensitive to outliers. Further-
more, we aim to apply fuzzy clustering algorithms for
clustering text and image data and compare their per-
formance with common crisp clustering algorithms.
REFERENCES
Beyer, K. S., Goldstein, J., Ramakrishnan, R., and Shaft,
U. (1999). When is ”nearest neighbor” meaningful?
In Proceedings of the 7th International Conference on
Database Theory, ICDT ’99, pages 217–235, London,
UK, UK. Springer-Verlag.
Bezdek, J. C. (1981). Pattern Recognition with Fuzzy Ob-
jective Function Algorithms. Kluwer Academic Pub-
lishers, Norwell, MA, USA.
Dave, R. N. and Krishnapuram, R. (1997). Robust cluster-
ing methods: A unified view. IEEE Transactions on
Fuzzy Systems, 5(2):270–293.
Dunn, J. C. (1973). A fuzzy relative of the isodata process
and its use in detecting compact well-separated clus-
ters. Journal of Cybernetics, 3(3):32–57.
Himmelspach, L. and Conrad, S. (2016). A possibilistic
multivariate fuzzy c-means clustering algorithm. In
Proceedings of the 10th International Conference on
Scalable Uncertainty Management, SUM 2016, pages
338–344.
Keller, A. and Klawonn, F. (2000). Fuzzy clustering with
weighting of data variables. International Journal
of Uncertainty, Fuzziness and Knowledge-Based Sys-
tems, 8(6):735–746.
Klawonn, F. (2013). What can fuzzy cluster analysis con-
tribute to clustering of high-dimensional data? In
Proceedings of the 10th International Workshop on
Fuzzy Logic and Applications, WILF2013, Genoa,
Italy, November 19–22, 2013., pages 1–14.
Klawonn, F., Kruse, R., and Winkler, R. (2015). Fuzzy clus-
tering: More than just fuzzification. Fuzzy Sets and
Systems, 281:272–279.
Kriegel, H., Kr
¨
oger, P., Schubert, E., and Zimek, A. (2009).
Outlier detection in axis-parallel subspaces of high di-
mensional data. In Proceedings of the 13th Pacific-
Asia Conference on Advances in Knowledge Discov-
ery and Data Mining, PAKDD 2009, pages 831–838.
Krishnapuram, R. and Keller, J. M. (1993). A possibilistic
approach to clustering. IEEE Transactions on Fuzzy
Systems, 1(2):98–110.
MacQueen, J. (1967). Some methods for classification and
analysis of multivariate observations. In Proceed-
ings of the Fifth Berkeley Symposium on Mathematical
Statistics and Probability, Volume 1: Statistics, pages
281–297, Berkeley. University of California Press.
Pal, N. R., Pal, K., Keller, J. M., and Bezdek, J. C. (2005).
A possibilistic fuzzy c-means clustering algorithm.
IEEE Transactions on Fuzzy Systems, 13(4):517–530.
Pimentel, B. A. and de Souza, R. M. C. R. (2013). A multi-
variate fuzzy c-means method. Applied Soft Comput-
ing, 13(4):1592–1607.
Rehm, F., Klawonn, F., and Kruse, R. (2007). A novel ap-
proach to noise clustering for outlier detection. Soft
Computing, 11(5):489–494.
Winkler, R., Klawonn, F., and Kruse, R. (2011). Fuzzy c-
means in high dimensional spaces. International Jour-
nal of Fuzzy System Applications, 1(1):1–16.
FCTA 2016 - 8th International Conference on Fuzzy Computation Theory and Applications
108