
Exploring the Neurosolver in Playing Adversarial Games
Andrzej Bieszczad
Computer Science, California State University Channel Islands, One University Drive, Camarillo, CA 93012, U.S.A.
Keywords: Neural Network, Neurosolver, General Problem Solving, State Spaces, Search, Adversarial Search, Temporal
Learning, Neural Modeling.
Abstract: In the past, the Neurosolver, a neuromorphic planner and a general problem solver, was used in several
exploratory applications, such as Blocks World and Towers of Hanoi puzzles, that in which we investigated
its problem solving capabilities. In all of them, there was only one agent that had a single point of view focus:
how to solve a posed problem by generating a sequence of actions to get the system from its current state to
some goal state. In this paper, we report on our experiments with exploring the Neurosolver’s capabilities to
deal with more sophisticated challenges in solving problems. For that purpose, we employed the Neurosolver
as a driver for adversary games. In that kind of environment, the Neurosolver cannot just generate a plan and
then follow it through. Instead, the plan has to be revised dynamically step by step in response to the other
actors following their own plans realizing adversarial points of view. We conclude that while the Neurosolver
can learn to play an adversarial game, to play it well it would need a good teacher.
1 INTRODUCTION
The goal of the research that led to the original
introduction of Neurosolver, as reported in
(Bieszczad et al., 1998), was to design a
neuromorphic device that would be able to solve
problems in the framework of the state space
paradigm. Fundamentally, in this paradigm, a
question is asked how to navigate a system through
its state space so it transitions from the current state
into some desired goal state. The states of a system
are expressed as points in an n-dimensional space.
Trajectories in such spaces formed by state transitions
represent behavioral patterns of the system. A
problem is presented in this paradigm as a pair of two
states: the current state and the desired, or goal, state.
A solution to the problem is a trajectory between the
two states in the state space.
The Neurosolver can solve such problems by first
building a behavioral model of the system and then
by traversing the recorded trajectories during both
searches and resolutions as will be described in the
next section.
In this paper, we report on our explorations of the
capabilities of the Neurosolver to construct a
behavioral model for carrying out more complex
tasks. For that purpose, we employed it as a controller
for playing an adversarial game. Specifically, we
used a variety of versions of the Neurosolver and
training techniques to construct automatically a driver
for the computer player in the game of TicTacToe.
The Neurosolver has proven itself as a reliable
problem solver finding trajectories in problem spaces
of several problems between the current system state
and the desired goal state (Bieszczad, 2006, 2007,
2011, 2015). In the application reported in here, the
Neurosolver confirms that it is a reliable tool for
producing sequences between two configurations of
the TicTacToe board. However, an adversarial game
is an interactive activity rather than a plan prepared a
priori and then followed through. Simply, adversaries
do not follow the same plan (and especially the plans
of their opponents!), so the Neurosolver must
recalculate the plan after each adversarial move. That
requires more time, but again it’s something that the
Neurosolver can handle well. Unfortunately, that is
not all; the rules of the game must be followed and
not all configurations are allowed to be successors of
a given move, even though they might be minimizing
the path to a goal (i.e., one of the winning game
configurations). That is a particularly unpleasant
challenge for automated training that uses randomly
generated games for training, since even if the game
ends with a winning configuration, it is difficult to
evaluate the player’s quality reliably.
The original research on Neurosolver modeling
was inspired by Burnod’s monograph on the
workings of the human brain (Burnod, 1988). The
Bieszczad, A.
Exploring the Neurosolver in Playing Adversarial Games.
DOI: 10.5220/0006070800830090
In Proceedings of the 8th International Joint Conference on Computational Intelligence (IJCCI 2016) - Volume 3: NCTA, pages 83-90
ISBN: 978-989-758-201-1
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
83

class of systems that employ state spaces to present
and solve problems has its roots in the early stages of
AI research that derived many ideas from the studies
of human information processing; among them on
General Problem Solver (GPS) (Newell and Simon,
1963). This pioneering work led to very interesting
problem solving (e.g. SOAR (Laird, Newell, and
Rosenbloom, 1987)) and planning systems (e.g.
STRIPS (Nillson, 1980).
The Neurosolver employs activity spreading
techniques that have their root in early work on
semantic networks (e.g., (Collins and Loftus, 1975)
and (Anderson, 1983)).
The Neurosolver is a network of interconnected
nodes. Each node is associated with a state in a
problem space. In the case of the TicTacToe game, a
state is associated with a single configuration of the
board. In its original application, the Neurosolver is
presented with a problem by two signals: the goal
associated with the desired state and the sensory
signal associated with the current state. In the context
of the TicTacToe game, the current state is the initial
broad configuration (i.e., an empty board), and the
desired state is one of the winning board
configurations. A sequence of firing nodes that the
Neurosolver generates represents a trajectory in the
state space. Therefore, a solution to the given problem
is a succession of firing nodes starting with the node
corresponding to the current state of the system, and
ending with the node corresponding to the desired
state of the system. In case of the TicTacToe game, a
sequence represents a winning game.
The node used in the Neurosolver is based on a
biological cortical column (references to the relevant
neurobiological literature can be found in (Bieszczad,
1998)). It consists of two divisions: the upper and the
lower, as illustrated in Figure 1. The upper division is
a unit integrating internal signals from other upper
divisions and from the control center providing the
limbic input (i.e., a goal or — using more psycholo-
gycal terms — a drive or desire). The activity of the
upper division is transmitted to the lower division
where it is subsequently integrated with signals from
other lower divisions and the thalamic (i.e., sensory)
input. The upper divisions constitute a network of
units that propagate search activity from the goal,
while the lower divisions constitute a network of
threshold units that integrate search and sensory
signals, and subsequently generate sequences of
firing nodes. A sequence of outputs of the lower
divisions of the network constitutes the output of the
whole node; a response of the network to the input
stimuli.
Figure 1: Neurosolver learning rule.
In the original Neurosolver, the strength of all
inter-nodal connections is computed as a function of
two probabilities: the probability that a firing source
node will generate an action potential in this
particular connection, and the probability that the
target node will fire upon receiving an action
potential from the connection.
An alternate implementation follows the Hebbian
approach that increments the strength of the
connection that carried the action potential that cause
the recipient to fire. In this approach, a certain small
value is added to the weight of a connection on each
successful pairing. To keep the values under control
all weights of afferent and efferent connections may
be normalized so their sum does not exceed 1. This
model approximates well the statistical model
described in the previous paragraph.
One other option for training is making all
weights the same (for example, equal to 1);
alternately, the weights may be ignored completely to
improve efficiency. In this approach, multiple
presentations of data do not affect the model. In such
implementation, the system produces optimized
(shortest) solution paths that are independent of the
frequency of sample presentations.
Figure 2: Learning state space trajectories through bi-
directional traces between nodes corresponding to
transitional states of the system.
TicTacToe (also know as “noughts and crosses”
or “Xs and Os”) is a very popular game that is very
NCTA 2016 - 8th International Conference on Neural Computation Theory and Applications
84
simple in its most fundamental form using a board of
9 squares that can be either empty or hold one of the
the two player symbols: a cross or a circle (or some
other markers) as shown in Figure 3.
Each of the two players is assigned one of the two
symbols: a cross (‘X’) or a circle (‘O’). The game
proceeds by placing players symbols on the still
empty board squares. The objective of the game is to
align 3 same symbols in a vertical, horizontal, or
diagonal line.
There are numerous variations of the game; e.g.,
larger boards can be used, including a border-less
version. As well, the number of symbols in a winning
arrangement may vary.
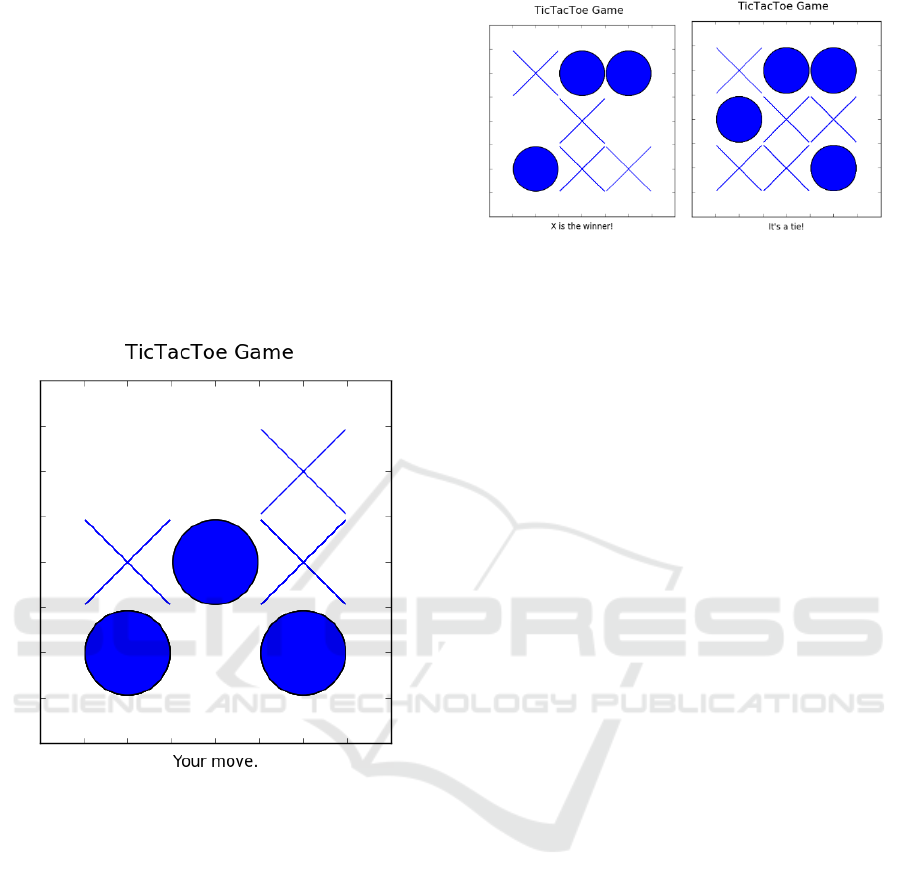
Figure 3. A TicTacToe board used in the experiments. The
board shows the configuration encoded as ‘001121202’ in
the implementation.
TicTacToe has been used extensively in research
on Artificial Intelligence (e.g., Russell et al., 2010),
because its problem space is manageable, so even an
exhaustive search can be used on today’s computers
in case of its simpler versions. For example, the
number of states in a 3-by-3 version used in the work
reported here is 3
9
=19,683 and the number of possible
games is 9!=362,880. Each game is a sequence of
moves from the the board with all empty squares to
one of the final configurations representing either a
win for ‘X’, or a win for ‘O’, or a tie. There are two
final configurations shown in Figure 4. Usually, the
problem space is considerably reduced by
preprocessing that reflects a number of observations
such as board symmetry, rotation, and player
symmetry.
Figure 4. Two board configurations showing a win for
crosses encoded as ‘122010211’ (left side) and a tie
encoded as ‘122211112’.
2 IMPLEMENTATION
2.1 Models
In this implementation, each state of the puzzle is
represented internally as as a 9-element string of
characters ‘0’, ‘1’, and ‘2’ representing the
configuration of the board. The string is constructed
by concatenating 3-element strings representing each
of the rows in the board. ’0’ represents and empty
square, ‘1’ - an ‘X’, and ‘2’ - an ‘O’. Using numbers
rather than letters helps internally as the game is
implemented in Python using the NumPy library, and
it’s easy to move a configuration to a NumPy array
for some flexible operations provided by that library.
There are some examples of the configuration
representation shown in Figures 4 and 5.
The Neurosolver consists of a collection of nodes
representing the configurations (states) of the board.
Each node has two dictionaries that represent efferent
and afferent connections with keys being string
representations of neighboring configurations (states)
and values representing the corresponding weights. A
node can be activated up to a certain platform
maximum that can be adjusted to control the time that
the Neurosolver is given to perform computations.
There are two activity thresholds that control activity
propagation for searching and for following solutions
as explained shortly.
2.2 The Neurosolver Operation
The Neurosolver requires three main stages to solve a
problem: training, searching, and solving.
These stages can be interwound in online learning
mode. In the offline learning mode the first stage is
separated from the two others.
Exploring the Neurosolver in Playing Adversarial Games
85

2.2.1 Training
As training sample games are presented to the
Neurosolver, nodes and connections are added to the
model. A node is added to the Neurosolver when a
corresponding configuration (state) is present as one
element of a training sample. Consecutive pairs of
board configurations represent transitions between
configurations; they constitute game moves. During
training, the Neurosolver is presented with all moves
in each training sample game. If not yet in the model,
a node representing a configuration is added when the
configuration represents the first element of the
sample pair, or when it is presented as the target of
the transition. Learning always affects two nodes: a
‘from’ node and a ‘to’ node. The dictionaries holding
references to nodes representing forward and
backward neighbors (successors and predecessors) in
the training sample are constructed in the process. In
the Hebbian model, the weights are adjusted
accordingly by incrementing them by a certain value
and normalizing. In the model with fixed cone-ctions,
just a fact of being a neighbor matters, so the weights
in that case are ignored and not adjusted.
The implementation includes offline and online
modes. In the online mode both a command line and
GUI interfaces were implemented. Figures 4 and 5
show the GUI interface. However, training - although
preferable due to the human involvement in
evaluating the quality of the training samples as
explained later - using such manual approach is very
time consuming. To make the process fast, a game
generator has been implemented. The generator
ensures that a valid game is generated by randomly
generating the next valid board configuration and
testing whether the most recently generated
configuration is one of the final states. If the final
state in the generated game is the winner or a tie, the
whole game is presented as a learning sample to the
Neurosolver. With the spirit of learning from
somebody else’s experience, a game won by the
adversary (the human player) the game is transitioned
to a form that represents exactly same sequence of
moves but with the computer as the winner and also
used as a training sample. The process merely substi-
tutes all ‘1s’ to ‘2s’ (i.e., ’Xs’ to ‘Os’) and vice versa.
The ties were added to the training because they
evidently improved the capabilities of the model as
shown in the section analyzing the experimental data.
2.2.2 Searching
After the training is complete, the Neurosolver will
have built a connection map between numerous states
of the problem domain. The next step is to activate
the node representing the goal state and allow the
propagation process to spread this search activity
along the connection paths in the direction that is
reverse to the flows of sample games used in training.
If there were only one game learned, then the flow
would be from the last configuration to the first.
There are however many training samples used in
training, so the activity spreads out as a search tree
looking for the node representing the starting state.
The extent of the search tree is controlled by imposing
a search threshold; a node that is a leaf in the search
tree is allowed to propagate its activity further only if
its activity exceeds the value of the search threshold.
The starting node is activated in preparation for
incoming search activity flow, so when that activity
reaches it the node may fire if its activity exceeds the
firing threshold. At that moment, the next stage of the
Neurosolver operation, solving, will start. That
process is explained in the next section.
A TicTacToe Game data set from UCI repository
was used as the basis of a data set to select the goals.
The UCI set only shows negative and positive
outcomes for ‘Xs’. Using the UCI set, a data set of all
non-loosing states was produced. Each game in the
new set was labeled with ‘1’ for ‘X’ winners, ‘2’ for
‘O’ winners, and with ‘3’ for ties. The new set was
used for two types of training sessions: one with ties
included and another one with ties excluded. The
section analyzing the results illustrates the impact of
using ties in the learning process.
2.2.3 Solving
The last stage of the Neurosolver is to actually use all
of the information collected thus far, and to generate
an actual solution from the given current state to the
specified goal state. Since all the nodes in the search
tree are activated, we may consider them in
anticipating state for the firing sequence. Therefore,
when the firing node projects its activity weighted by
the strength of the forward connections, the neighbor
that has the highest anticipatory activity will fir next,
That node is added to the solution, and then process
repeats itself until the goal state is reached. When that
happens, the solution to the problem has been
produced.
However, in contrast to the earlier experimental
application of the Neurosolver, in adversarial games
there are no single “solutions” that can be generated
once up front and then used as a recipe to “solve the
problem”. Hence, firstly there are many possible
goals, so all of them get activated to start the search.
In this way, the propagation process constructs
multiple search trees. Since they span the same
NCTA 2016 - 8th International Conference on Neural Computation Theory and Applications
86
network, the trees are not independent, so the activity
from one goal affects trees rooted in other goal states.
Secondly, the need arises to generate a single “next
state” rather than a complete solution. Accordingly,
the operation of the Neurosolver has been augmented
by facility to produce one configuration rather than
the whole sequence to one of the goal states. The
latter would be rather unusable, since the adversaries
usually do not follow each other advice.
The next move can be suggested quickly in the
model using Hebbian learning by following the
strongest connection from the node corresponding to
the current state. However, that approach just follows
the frequency of training moves (state transitions) and
is unreliable with automated training that uses
random training samples. A ore reliable approach is
to use the same activity propagation process as
described, however collecting only the first transition
rather than the complete solution. That process must
be repeated for every game turn of the computer
player. Hence, there are numerous solving processes
involved in playing a single game.
In the model with the fixed weights, activity spre-
ading is the only way to find suggested moves, since
there is no probabilistic model to take advantage of.
3 EXPERIMENTS
Measuring the quality of the model is a challenge due
to the difficulty is evaluating quantitatively the
quality of moves. A computer player controlled by the
Neurosolver can be evaluated qualitatively by an
adversary human player, but that is limited and
somewhat subjective.
To get some quantitative measure of the
Neurosolver capabilities, we used the data set from
UCI to create a test set that includes all possible
problems (games; i.e., sequences of moves) with the
original board configuration with all squares empty as
the current (start) state to a state representing every
possible winning (for a selected player; ‘X’ or ‘O’)
board configuration. We conducted several
experiments trying to select the best training strategy.
The following sections describe the results.
In each of the experiments, we created five
models of the Neurosolver-based TicTacToe
controller each trained with progressively increasing
number of sample games. Each game was generated
randomly by generating valid moves and testing for
the terminal state at every step. We experimented
with varied number of presentations of each game,
but ultimately decided that it’s better to spend the
same time on generating more variety of games rather
than reinforcing ones that were already presented.
Therefore, each game was presented only once when
generated. We allowed for repeats if the random
process happened to produce a game more than once.
The probability of that is not very high taking into
account the number of possible games.
3.1 Hebbian Learning with No Ties
and No Move Validation
In this experiments, we wanted to know if the
Neurosolver performs as in the past on the problems
that are solved by producing state transition paths
between the start state and the goal state in the state
space. In this session, we used only winning states as
the goal states, and we did not validate the generated
moves. We just wanted to confirm that the
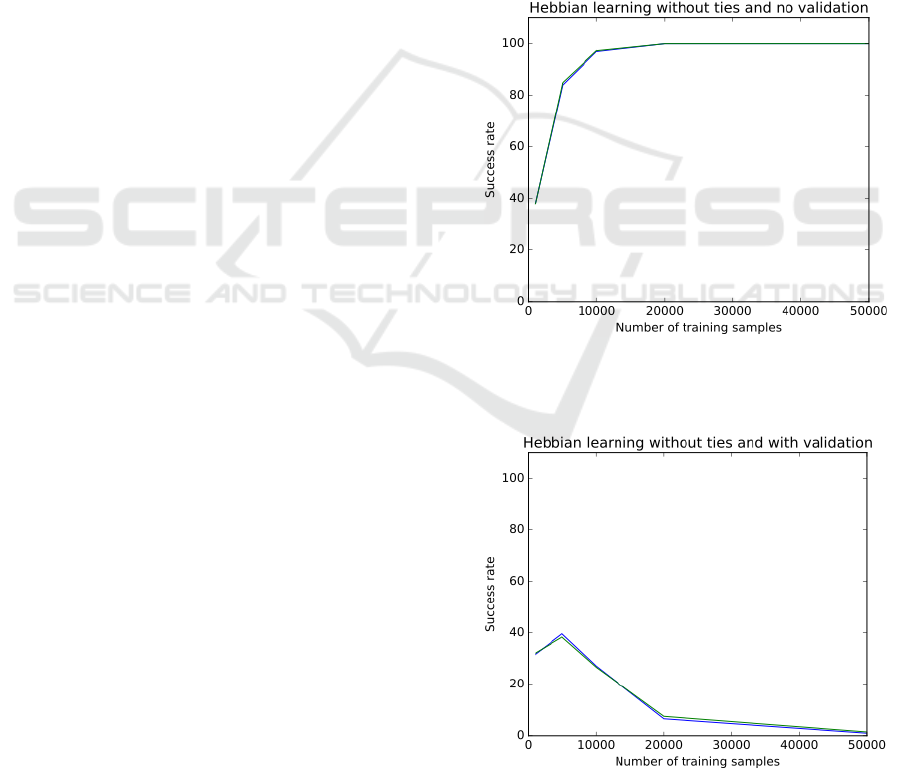
Figure 5: Success rate of the model built using the Hebbian
learning with ties excluded and the validation of moves
turned off.
Figure 6: Success rate of the model built using the Hebbian
learning with ties excluded and the validation of moves
turned on.
Exploring the Neurosolver in Playing Adversarial Games
87

Neurosolver behaves in the same way as in the past
applications.
It appears that the resulting model reliably
produces paths between the starting board
configurations and every winning terminal state as
shown in Figure 5. With 1000 training samples the
success rate measured as the percentage of successful
attempts to find a path between the start and the goal
is around 40%. With 10000 sample, the performance
starts to approach 100%, and with 20000 samples and
more the system is nearly perfect.
3.2 Hebbian Learning with No Ties
and with Move Validation
The results from the first experiment session were
very promising. To validate the games we built a
move validator that ensures that every move
generated by the Neurosolver is actually valid
according to the TicTacToe rules. In the following
session, we validated every game (i.e., every solution
path) generated by the Neurosolver. If a game did not
validate (i.e., if it included at least one invalid move),
the attempt was marked as a failure.
The results shown in Figure 6 illustrate the
problem with applying the Neurosolver in a context
in which not only the path, and even the path length,
matter, but also the “quality” of the solution that must
adhere to some externally-imposted standards. While
initially the success rate is similar to the previous
model, increasing the number of training samples
lowers the success rate dramatically. With 20000 or
more training samples, the model failed for most
posed problems.
3.3 Hebbian Learning with Ties and
with Move Validation
The results from the second experiment session were
not good to say the least. When playing against the
computer, we noticed that it was better being
offensive than defensive, so we decided to also use
the tying games in the training to teach the model
some defensive strategies; e.g., to block adversarial
moves. It was quite a surprise to see that including
ties actually improved the quality of solutions quite
dramatically.
As shown in Figure 7, the model built with a data
set that included the tying games brought the success
rate close to 80% already for 10000 training samples.
The rate changed minimally with increased number
of training samples. That is an important observation,
since increasing the number of training samples. The
rate changed minimally with increased number
Figure 7: Success rate of the model built using the Hebbian
learning with ties included and the validation of moves
turned on.
of training samples. That is an important observation,
since increasing the number of training samples
increases dramatically the time necessary for building
the model, and also - albeit not dramatically - the time
for producing a solution. The latter might be a bit
surprising, but the reason for that is that more samples
lead to larger search activity trees.
3.4 Fixed-weight Learning with No
Ties and No Move Validation
As we explained earlier, the Neurosolver models with
fixed connection weights are good optimizers
producing shortest paths. Since the drive to move to
a goal might be a good capability for suggesting
better, more aggressive moves, we also built two
models to test this hypothesis.
Figure 8. Success rate of the model built using the fixed-
weight learning with ties excluded and the validation of
moves turned off.
NCTA 2016 - 8th International Conference on Neural Computation Theory and Applications
88
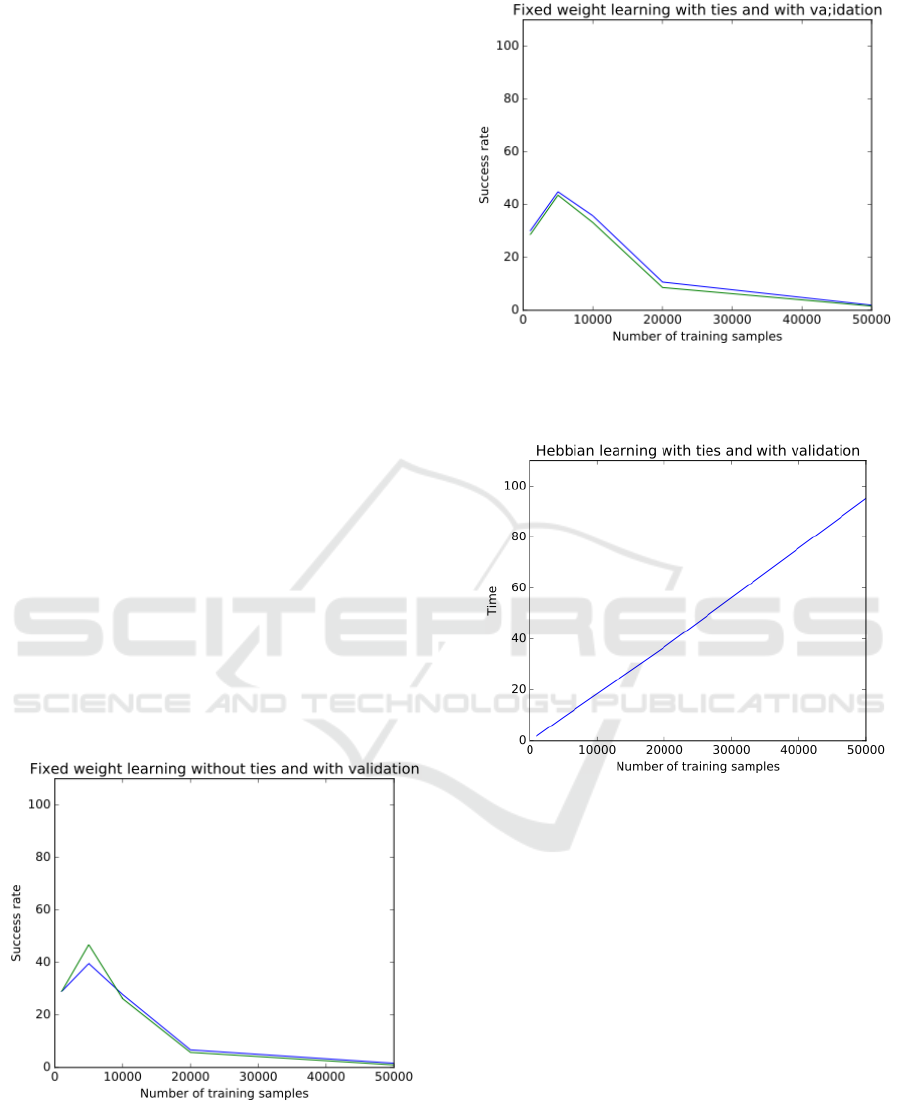
The first model was built with games ending in
tying configurations excluded and with no validation
of moves. As shown in Figure 8, this model
performed as well as the model crated using the
Hebbian learning. With 10000 training the success
rate approached 100%. We did not compare the
lengths of the produced games (i.e., the lengths of the
solution paths), but one could suspect that they would
tend to be shorter in this model.
3.5 Fixed-Weight Learning with No
Ties and with Move Validation
As with the models built with the Hebbian approach,
we wanted to evaluate the quality of the solutions, so
we used exactly same method that validated all moves
in each produced game.
As shown in Figure 9, the quality of the games is
as bad, and it goes down with the increasing number
of training samples.
3.6 Fixed-Weight Learning with Ties
and with Move Validation
To next question was whether including the tying
games in training would also improve the ability of
the fixed-weight model to generate quality games.
Unfortunately, as shown in Figure 10, the trick
that was so useful in the Hebbian model did not work
here. The success rate of the model built with the
tying games included in training is as bad as of the
model built without ties included.
Figure 9: Success rate of the model built using the fixed-
weight learning with ties excluded and the validation of
moves turned on.
Figure 10: Success rate of the model built using the fixed-
weight learning with ties included and the validation of
moves turned on.
Figure 11: Sample time necessary to construct the model
using the Hebbian learning.
3.7 Time to Build Models
The time necessary to build the models depends on
the computing platform, of course. Nevertheless,
looking at the trends might be informative.
Figure 11, includes a graph that shows how the
time required to train a Hebbian model (with ties
excluded, to be precise) increases as a function of the
training samples. As shown, the dependency is linear.
It is worth noting, that evidently that is the trend as in
one session the training time rose to close to 600
seconds for a training sample of 300000 games. That
would be an approximate value if the graph from
Figure 11 was used for extrapolation.
Exploring the Neurosolver in Playing Adversarial Games
89

3.8 Qualitative Evaluation
We played with the Neurosolver-driven computer
player numerous games. Although the current best
model (see Figure 7) shows some signs of decent
playing skills, it is far from satisfactory. The model
seems to be superior in offensive strategies, but
evidently does not acquire skills necessary to prevent
some obvious moves, like blocking placing the third,
winning, adversarial symbol in a line.
4 CONCLUSIONS
In the line of experiments reported in this paper, we
showed that the Neurosolver can find paths between
the starting TicTacToe board configuration and any
winning state with very high success just after
sampling 10000 out of 9! possible games. However,
finding a path is not sufficient in the application of
the Neurosolver as a controller for driving a computer
player in an adversarial game. In this application, the
quality of the game measured by its validity as well
as an ability to interactively produce “good” moves is
of paramount importance. The strategies used for
training the Neurosolver yielded only moderate
success. The main reason for that is the automated
process that can validate games, but cannot evaluate
the quality of individual moves.
The Neurosolver is a device that learns by being
told, so employing either a skillful human or
computer player, or a data set of “good” games, seems
to be necessary to acquire good playing skills. For
example, the common heuristic utility function for
TicTacToe configurations could be used to generate
more promising moves. The point of our experiments,
however, was to see if such heuristics can be
developed automatically. The current answer to that
question is a sound ‘no’.
Our next goal is to identify states from the raw
images of the TicTacToe board and to acquire the
behavior without explicit representation of the state
space. We hope to build a model from scratch by
putting together a deep learning front end (e.g.,
convolution networks (Lawrence at al., 1998)) with
the Neurosolver back end.
REFERENCES
Anderson, J. R., 1983. A spreading activation theory of
memory. In Journal of Verbal Learning and Verbal
Behavior, 22, 261-295.
Bieszczad, A. and Pagurek, B., 1998. Neurosolver:
Neuromorphic General Problem Solver. In Information
Sciences: An International Journal 105, pp. 239-277,
Elsevier North-Holland, New York, NY.
Bieszczad, A. and Bieszczad, K., (2006). Contextual
Learning in Neurosolver. In Lecture Notes in Computer
Science: Artificial Neural Networks, Springer-Verlag,
Berlin, 2006, pp. 474-484.
Bieszczad, A. and Bieszczad, K., (2007) Running Rats with
Neurosolver-based Brains in Mazes. In Journal of
Information Technology and Intelligent Computing,
Vol. 1 No. 3.
Bieszczad A., (2011). Predicting NN5 Time Series with
Neurosolver. In Computational Intelligence: Revised
and Selected Papers of the International Joint
Conference IJCCI 2009 (Studies in Computational
Intelligence). Berlin Heidelberg: Springer-Verlag, pp.
277-288.
Bieszczad, A., and Kuchar, S., (2015) The Neurosolver
Learns to Solve Towers of Hanoi Puzzles. In
Proceedings of 7th International Joint Conference on
Computational Intelligence (IJCCI 2015), Lisbon,
Portugal.
Burnod, Y., 1988. An Adaptive Neural Network: The
Cerebral Cortex, Paris, France: Masson.
Collins, Allan M.; Loftus, Elizabeth F., 1975. A Spreading-
Activation Theory of Semantic Processing. In
Psychological Review. Vol 82(6) 407-428.
Laird, J. E., Newell, A. and Rosenbloom, P. S., 1987.
SOAR: An architecture for General Intelligence. In
Artificial Intelligence, 33: 1--64.
Lawrence, S., et al., 1998. Face Recognition: A
Convolutional Neural-Network Approach. In IEEE
Transactions on Neural Networks, Vol 8(1), pp.98-113.
Newell, A. and Simon, H. A., 1963. GPS: A program that
simulates human thought. In Feigenbaum, E. A. and
Feldman, J. (Eds.), Computer and Thought. New York,
NJ: McGrawHill.
Nillson, N. J., 1980. Principles of Artificial Intelligence,
Palo Alto, CA: Tioga Publishing Company.
Russell, S. J., Norvig, P., 2010. Artificial Intelligence: A
Modern Approach (3rd ed.), Pearson.
Stewart, B. M. and Frame, J. S., 1941. Solution to Advanced
Problem 3819. In The American Mathematical
Monthly Vol. 48, No. 3 (Mar., 1941), pp. 216-219
NCTA 2016 - 8th International Conference on Neural Computation Theory and Applications
90
