
A Bayesian Approach for Weighted Ontologies and Semantic Search
Anna Formica
1
, Michele Missikoff
2
, Elaheh Pourabbas
1
and Francesco Taglino
1
1
National Research Council, Istituto di Analisi dei Sistemi ed Informatica ”Antonio Ruberti”,
Via dei Taurini 19 - 00185, Rome, Italy
2
National Research Council, Istituto di Scienze e Tecnologie della Cognizione,
Via S. Martino della Battaglia, 44 - 00185, Rome, Italy
Keywords:
Semantic Search, Similarity Reasoning, Weighted Reference Ontology, Bayesian Network.
Abstract:
Semantic similarity search is one of the most promising methods for improving the performance of retrieval
systems. This paper presents a new probabilistic method for ontology weighting based on a Bayesian approach.
In particular, this work addresses the semantic search method SemSim for evaluating the similarity among
a user request and semantically annotated resources. Each resource is annotated with a vector of features
(annotation vector), i.e., a set of concepts defined in a reference ontology. Analogously, a user request is
represented by a collection of desired features. The paper shows, on the bases of a comparative study, that the
adoption of the Bayesian weighting method improves the performance of the SemSim method.
1 INTRODUCTION
A weighted ontology is obtained by associating
a weight with each concept. The adoption of
such weights has proved to be beneficial in several
ontology-based applications and services that range
from ontology mapping to ontology-based decision
making, to semantic search. Our main research ob-
jectives lay in the area of Semantic Similarity Rea-
soning for advanced search, where weighted ontolo-
gies represent a primary base for our search engine,
called SemSim (Formica et al., 2013). There are var-
ious methods for weighting ontology concepts (see
Related Work Section) and this great variety also de-
pends on the meaning that such weights assume. In
SemSim the concept weight is used to derive the in-
formation content (IC) of a concept in a hierarchy ac-
cording to (Resnik, 1995), that represents the basis for
computing the concept similarity.
According to the semantics adopted in SemSim,
given a Universe of Digital Resources (UDR, i.e., the
search space) the IC of a concept is directly related to
its selectiveness and inversely related to the probabil-
ity that, randomly selecting an instance in the UDR,
such an instance belongs to the extension of the con-
cept (i.e., the set of its instances). In a retrieval per-
spective, a concept with higher IC is expected to be
more selective than a concept with lower IC, since
the former has a lower probability than the latter.
Furthermore, in an ontology, the concept weight de-
creases downward along the specialization hierarchy,
proceeding from the root (the most general concept,
e.g., Thing) towards the leaves, the most specific con-
cepts. This is because the extension of a more specific
concept is contained in the extension of a more gen-
eral concept, and consequently, the likelihood of the
former is lower than the likelihood of the latter. Sym-
metrically, the IC will progressively increase while
we move downward along the hierarchy. For exam-
ple, given a tourism domain, assuming that Farm-
house is a more specific concept of Accommodation,
the latter has a lower information content than the for-
mer. Accordingly, at ontology level, the weight of
concepts needs to be consistent with the set inclusion
semantics of the ISA hierarchy, as described above.
The main focus of this paper concerns a method
for assigning the weights to the concepts in the ontol-
ogy, used to compute their IC. It may seem a marginal
problem, but it is not, since a correct weighting strat-
egy can significantly improve the performance of the
semantic services based on weighted ontologies. In
the literature there are several proposals, as reported
in the Related Work Section.
In a previous work (Formica et al., 2013), we ex-
perimented two methods of concept weighting, both
following the IC approach. The two methods, called
frequency-based and probabilistic-based, differ for
the way the likelihood of a concept c is computed.
The frequency-based method is the most straightfor-
ward, it consists in counting the instances of each
Formica, A., Missikoff, M., Pourabbas, E. and Taglino, F.
A Bayesian Approach for Weighted Ontologies and Semantic Search.
DOI: 10.5220/0006073301710178
In Proceedings of the 8th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2016) - Volume 2: KEOD, pages 171-178
ISBN: 978-989-758-203-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
171

concept and then normalizing such a number over
the total number of instances of concepts. The
probabilistic-based method depends, in general, on
the characteristics of the application domain and the
structure of the taxonomy. Both approaches exhibit
pros and cons. The frequency-based method depends
on the number of UDR resources, and the more this
number increases the more the concept weights are
expected to be trustworthy. However, this method
can be expensive, since it is necessary to maintain
a count of the extensions of each concept in the on-
tology. This is only feasible in the Closed World
Assumption and in the presence of a relatively sta-
ble UDR, otherwise for each update it is necessary
to recompute a (more or less extensive) part of on-
tology weights. Conversely, the probabilistic-based
approach is valid for both Closed and Open World As-
sumptions and, with large UDR, tends to be more sta-
ble. In fact, UDR updates usually evolve according to
a given probability distribution (e.g., in a University,
the ratio of students to professors tend to be stable,
despite a significant number of new enrollments ev-
ery year). Here, the problem is to be able to guess
what are the more appropriate probabilities to be as-
sociated with each concept. In the perspective of ad-
dressing large application domains, in this paper we
adopt the probabilistic approach.
The SemSim similarity reasoning method is based
on semantic annotations in the form of Ontology-
based Feature Vectors (OFV), where each component
is a concept in a reference ontology (referred to as
feature when used for annotation). Each resource in
the UDR is associated with an annotation vector (re-
ferred to as AV) while the user request is represented
by a request vector (RV). The SemSim search engine
then computes the semantic similarity by contrasting
the RV against each AV, producing a ranked list of re-
sources.
In this paper, we present a new probabilistic
method for ontology weighting based on a Bayesian
Network (BN). The importance of integrating BN
into ontologies is discussed in (Grubisic et al., 2013),
where they are considered a valid support to experts
in the modeling of a specific problem domain. The
new Bayesian weighting method defined here can be
considered as an extension of the previous method
defined in (Formica et al., 2013), i.e., it starts with
the same probability assignments (w
p
) given in the
mentioned paper, used here as a priori probabilities.
Then, such probabilities are refined taking into con-
sideration the subsumption relations and the inherent
dependencies among concepts. To this end, we build
a BN isomorphic to the ISA hierarchy of the ontology
referred to as Onto-Bayesian Network (OBN). It is
constructed as follows: each concept in the ontology
corresponds to a node in OBN and each subsumption
relation corresponds to a probabilistic dependency.
Considering the above example, we assume that the
probabilistic weight of Farmhouse depends on the
weight of its subsumer Accommodation. The method,
referred to as SemSim-b, is illustrated in Section 3,
while Section 4 shows its validation, by examining the
correlation, precision, and recall and comparing them
with the experiment given in (Formica et al., 2013).
The results demonstrate that SemSim-b outperforms
the previous SemSim method. Finally, Section 5 con-
cludes the paper.
2 WEIGHTED ONTOLOGIES
In this section, we recall the probabilistic approach
defined in (Formica et al., 2010), (Formica et al.,
2013) in order to assign weights to a given ontology.
The UDR is the set of digital resources that are
semantically annotated with a reference ontology (an
ontology is a formal, explicit specification of a shared
conceptualization (Gruber, 1993)). In our work we
address a simplified notion of ontology, Ont, consist-
ing of a set of concepts organized according to a spe-
cialization hierarchy. In particular, Ont is a taxonomy
defined by the pair:
Ont =< C, ISA >
where C = {c
i
} is a set of concepts and ISA is the
set of pairs of concepts in C that are in subsumption
(subs) relation:
ISA = {(c
i
, c
j
) ∈ C ×C|subs(c
i
, c
j
)}
Given two concepts c
i
, c
j
∈ C, their least upper bound,
lub(c
i
, c
j
), is always uniquely defined in C (we as-
sume the hierarchy is a tree). It represents the least
abstract concept of the ontology that subsumes both
c
i
and c
j
.
Each resource in the UDR is annotated with an
OFV
1
, which is a vector that gathers a set of concepts
of the ontology Ont, aimed at capturing its semantic
content. The same also holds for a user request. It is
represented as follows:
ofv = (c
1
,...,c
n
), where c
i
∈ C, i = 1,...,n
Note that, when an OFV is used to represent the
semantics of a user request, it is referred to as seman-
tic Request Vector (RV) whereas, if it is used to rep-
resent the semantics of a resource, it is referred to as
1
The proposed OFV approach is based on the Term Vec-
tor (or Vector Space) Model approach, where terms are sub-
stituted by concepts (Salton et al., 1975).
KEOD 2016 - 8th International Conference on Knowledge Engineering and Ontology Development
172

semantic Annotation Vector (AV). They are denoted
as follows, respectively:
rv = {r
1
, . . . , r
n
},
av = {a
1
, . . . , a
m
},
where {r
1
, . . . , r
n
} ∪ {a
1
, . . . , a
m
} ⊆ C.
Finally, a Weighted Reference Ontology (WRO) is
defined as follows:
WRO =< Ont, w >
where w, the concept weighting function, is a proba-
bility distribution defined on C, such that given c ∈ C,
w(c) is a decimal number in the interval [0. . .1].
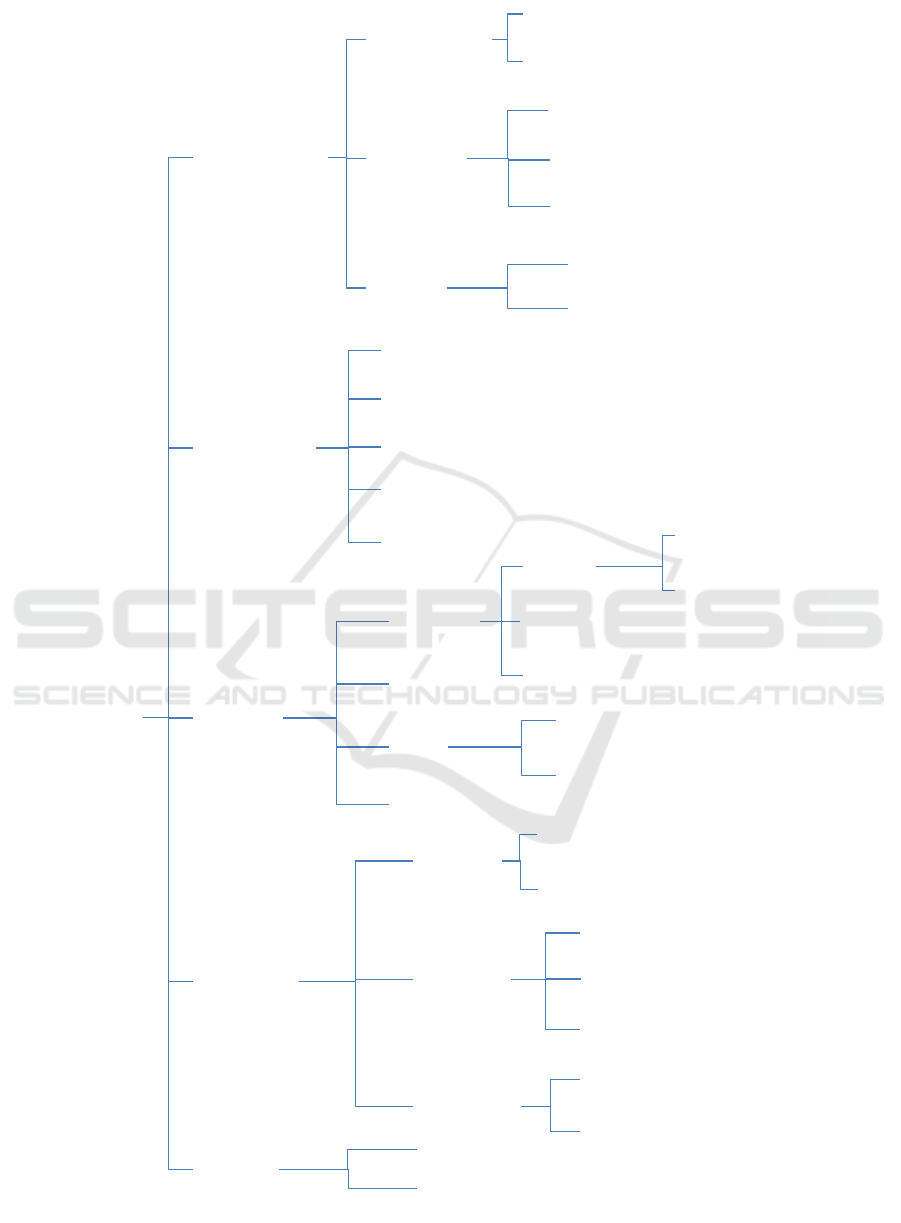
Figure 1 shows the WRO drawn upon the tourism
domain that will be used in the running example. In
this figure, the weights w
p
have been assigned ac-
cording to the probabilistic-based approach defined in
(Formica et al., 2013). In particular, the weight of
the root of the hierarchy, referred to as Thing is equal
to 1, and the weights of the concepts of the hierar-
chy are assigned according to a top-down approach,
as follows. Given a concept c, let c
0
be the parent of
c, w
p
(c) is equal to the probability of c
0
, divided by
number of the children of c
0
:
w
p
(c) =
w
p
(c
0
)
|children(c
0
)|
For instance, let us consider the concept
Salon. The associated w
p
is 0.05 because
w
p
(Attraction) = 0.2 and Attraction has four
children.
Below, the semantics of a feature vector OFV is
presented, by extending its first formulation given in
(Formica et al., 2008). When a concept is used in an
OFV to annotate a resource or to represent a RV , it is
referred to as a feature.
Consider an ontology Ont, a set of features F, F ⊆
C, let SPEC be the reflexive and transitive closure of
ISA. Then, the semantics of a feature a ∈ F is defined
as follows:
Γ(a) = {res ∈ UDR | feat(b, res), (b,a) ∈ SPEC}
where feat(b, res) means that the resource res ∈ UDR
is annotated by the feature b ∈ F. The semantics of
an ofv, say:
ofv = {a
1
,..., a
n
}
is therefore defined according to the Γ function as fol-
lows:
Γ(ofv) =
T
j
Γ(a
j
)
Overall, we emphasize the difference between the
concept semantics and feature semantics. A concept
denotes the set of the instances whose type is such a
concept; while, if a concept is used as a feature, it
denotes all the resources in the UDR annotated with
such a feature.
3 BAYESIAN NETWORKS FOR
WEIGHTED ONTOLOGIES
The core of the proposed solution is the adoption of a
Bayesian approach for ontology weighting.
Bayesian Networks (BN), also known as belief
networks, are probabilistic graphical models based
on DAGs. They have been defined in the late 1970s
within cognitive science and artificial intelligence as
the method of choice for uncertain reasoning (Pearl
and Russell, 2001). A BN is therefore a graphical
structure that allows us to represent and reason about
an uncertain domain. In particular, each node in the
graph represents a random variable, that can take dif-
ferent values associated with probabilities, while the
edges represent probabilistic dependencies of the cor-
responding random variables. In particular, an edge
from a node X
i
(parent node) to a node X
j
(child node)
indicates that a value taken by the variable X
j
de-
pends on the value taken by the variable X
i
or, roughly
speaking, the variable X
i
“influences” X
j
. Note that
nodes without parents (roots) are not influenced by
any node, nodes without children (leaves) do not in-
fluence any node, while any node affects its children.
Therefore, nodes that are not directly connected in the
BN represent variables that are conditionally indepen-
dent of each other. According to the global semantics
of BN, the full joint distribution is:
P(x
1
, ...,x
n
) =
∏
i
P(x
i
|pa
i
)
where x
i
is a value of the variable X
i
, pa
i
is a set of
values for the parents of X
i
, and P(x
i
|pa
i
) denotes the
conditional probability distribution of x
i
given pa
i
.
Therefore, in a BN, each node is associated with
a probability function that takes, as input, a particular
set of values for the node’s parent variables, and gives
(as output) the probability of the variable represented
by the node. These probability functions are specified
by means of (conditional) probability tables
2
, one for
each node of the graph.
In our approach, as mentioned in the Introduction,
we build a BN isomorphic to the ISA hierarchy, re-
ferred to as Onto-Bayesian Network (OBN). In the
OBN, according to the BN approach, the concepts are
boolean variables and the Bayesian weight associated
with a concept c, indicated as w
b
, is the probability P
that the concept c is True (T ), i.e.:
w
b
(c) = P(c=T )
As mentioned in the Introduction, in order to compute
the weights w
b
, conditional probability tables are de-
2
A (conditional) probability table is defined for a set
of (non-independent) random variables to represent the
marginal probability of a single variable w.r.t. the others.
A Bayesian Approach for Weighted Ontologies and Semantic Search
173
Thing
Accommodation
Transportation
Attraction
Gastronomy
Shopping
AlternativeAcc.
RegularAcc.
CozyAcc.
Campsite
FarmHouse
InternationalHotel
PrivateHouse
Pension
SeasideCottage
CountryResort
Flight
Train
Ship
CarRental
Bus
Exhibition
Museum
Salon
ArcheologicalSite
Concert
Theatre
Cinema
ClassicalConcert
RockConcert
PictureGallery
ArtGallery
LightMeal
EthnicMeal
RegularMeal
VegetarianMeal
MediterraneanMeal
ThaiMeal
IndianMeal
MexicanMeal
InternationalMeal
FrenchMeal
ShoppingCenter
Bazaar
w
p
= 0.20; w
b
= 0.20
w
p
= 0.07; w
b
= 0.014
w
p
= 0.03; w
b
= 0.042
w
p
= 0.03; w
b
= 0.00042
w
p
= 0.03; w
b
= 0.00042
w
p
= 0.02; w
b
= 0.00028
w
p
= 0.02; w
b
= 0.00028
w
p
= 0.02; w
b
= 0.00028
w
p
= 0.01; w
b
= 0.00001
w
p
= 0.01; w
b
= 0.00001
w
p
= 0.02; w
b
= 0.0002
w
p
= 0.03; w
b
= 0.0002
w
p
= 0.02; w
b
= 0.0002
w
p
= 0.07; w
b
= 0.014
w
p
= 0.07; w
b
= 0.014
w
p
= 0.04; w
b
= 0.008
w
p
= 0.04; w
b
= 0.008
w
p
= 0.04; w
b
= 0.008
w
p
= 0.04; w
b
= 0.008
w
p
= 0.04; w
b
= 0.008
w
p
= 0.05; w
b
= 0.010
w
p
= 0.05; w
b
= 0.010
w
p
= 0.05; w
b
= 0.010
w
p
= 0.05; w
b
= 0.010
w
p
= 0.03; w
b
= 0.0003
w
p
= 0.03; w
b
= 0.0003
w
p
= 0.07; w
b
= 0.014
w
p
= 0.03; w
b
= 0.00042
w
p
= 0.03; w
b
= 0.00042
w
p
= 0.07; w
b
= 0.014
w
p
= 0.07; w
b
= 0.014
w
p
= 0.02; w
b
= 0.00028
w
p
= 0.02; w
b
= 0.00028
w
p
= 0.02; w
b
= 0.00028
w
p
= 0.03; w
b
= 0.00042
w
p
= 0.03; w
b
= 0.00042
w
p
= 0.10; w
b
= 0.020
w
p
= 0.10; w
b
= 0.020
w
p
= 0.20; w
b
= 0.20
w
p
= 0.20; w
b
= 0.20
w
p
= 0.20; w
b
= 0.20
w
p
= 0.20; w
b
= 0.20
w
p
= 0.03; w
b
= 0.042
w
p
= 1; w
b
= 1
Figure 1: The WRO of our running example with the w
p
and w
b
concept weights.
KEOD 2016 - 8th International Conference on Knowledge Engineering and Ontology Development
174

Table 1: Probability table of Gastronomy.
Gastronomy
T F
0.20 0.80
Table 2: Conditional probability table of LightMeal.
LightMeal
Gastronomy T F
T 0.07 0.93
F 0 1
fined by using w
p
proposed according to the proba-
bilistic approach recalled in the previous section as a
priori weights. In particular, given two concepts c
1
,
c
2
, we assume that:
P(c
2
=T |c
1
=T )=w
p
(c
2
)
where c
1
is the parent of c
2
according to the ISA rela-
tion.
For instance, consider the concepts Gastronomy,
LightMeal, and VegetarianMeal of the ontology given
in Figure 1. Gastronomy (G for short) has as
parent T hing, which is always True (w
p
(T hing) =
w
b
(T hing) = 1), therefore the weight w
b
coincides
with the weight w
p
, i.e., w
b
(G) = w
p
(G), where
w
p
(G) = P(G=T |T hing=T ) = P(G=T) = 0.2, as
shown in Table 1. Consider now LightMeal (L). In
this case the conditional probability, which is given
in Table 2, depends on the True/False (T/F) values
of its father Gastronomy, and in particular w
p
(L) =
P(L=T |G=T ) = 0.07 (therefore P(L=F|G = T ) =
0.93). Then, the weight w
b
associated with L, w
b
(L)
= P(L=T ), is computed starting from the probability
of its parent Gastronomy as follows:
P(L=T ) =
∑
v∈{T,F}
P(L=T, G = v)
= P(L=T, G=T ) + P(L=T, G=F)
= P(L=T |G=T )P(G=T )
+ P(L=T |G=F)P(G=F)
= 0.07 × 0.2 + 0 × 0.8 = 0.014
taking into account the Kolmogorov definition for two
given variables A and B:
P(A, B) = P(A|B)P(B).
Therefore, the Bayesian weight w
b
(L) = P(L=T ) =
0.014, as shown in Table 4. Analogously, in Table 5
the probability of VegetarianMeal (V ) is given. The
weight w
b
(V ) has been computed by using the con-
ditional probabilities given in Table 3, and by taking
into account the weight w
b
(L) computed above (see
Table 4).
Table 3: Conditional probability table of VegetarianMeal.
VegetarianMeal
LightMeal T F
T 0.03 0.97
F 0 1
Table 4: Probability table of LightMeal.
LightMeal
T F
0.014 0.986
4 SemSim AND VALIDATION
The SemSim method has been conceived to search for
the resources in the UDR that best match the RV, by
contrasting it with the various AV, associated with the
searchable digital resources. This is achieved by ap-
plying the semsim function, which has been defined
to compute the semantic similarity between OFV.
In SemSim, the weights are used to derive the IC
of the concepts that, according to (Lin, 1998), repre-
sents the basis for computing the concept similarity.
In particular, according to the information theory, the
IC of a concept c, is defined as:
IC = −log(w(c))
The semsim function is based on the notion of sim-
ilarity between concepts (features), referred to as con-
sim. Given two concepts c
i
, c
j
, it is defined as follows:
consim(c
i
, c
j
) =
2×IC(lub(c
i
,c
j
))
IC(c
i
)+IC(c
j
)
where the lub represents the least abstract concept of
the ontology that subsumes both c
i
and c
j
. Given an
instance of RV and an instance of AV , say rv and av re-
spectively, the semsim function computes the consim
for each pair of concepts belonging to the set formed
by the Cartesian product of the rv, and av.
However, we focus on the pairs that exhibit high
affinity. In particular, we adopt the exclusive match
philosophy, where the elements of each pair of con-
cepts do not participate in any other pair. The method
aims to identify the set of pairs of concepts of the rv
Table 5: Probability table of VegetarianMeal.
VegetarianMeal
T F
0.00042 0.99958
A Bayesian Approach for Weighted Ontologies and Semantic Search
175

and av that maximizes the sum of the consim similar-
ity values (maximum weighted matching problem in
bipartite graphs (Dulmage and Mendelsohn, 1958)).
In particular, given:
rv = {r
1
,..., r
n
}
av = {a
1
,..., a
m
}
as defined in Section 2, let S be the Cartesian Product
of rv and av:
S = rv × av
then, P (rv, av) is defined as follows:
P (rv, av) = {P ⊂ S | ∀ (r
i
, a
j
), (r
h
, a
k
) ∈ P,
r
i
6= r
h
, a
j
6= a
k
, |P| = min{n, m}}.
Therefore, on the basis of the maximum weighted
matching problem in bipartite graphs, semsim(rv,av)
is given below:
semsim(rv, av) =
max
P∈P (rv,av)
∑
(r
i
,a
j
)∈P
consim(r
i
,a
j
)
max{n,m}
In (Formica et al., 2013), we defined semsim-p in
which the weights w
p
of the concepts in the WRO are
computed by using the probabilistic approach. Anal-
ogously, in this paper we introduce semsim-b where
the weights, w
b
, are defined by using a Bayesian Net-
work, as described in Section 3.
4.1 Validation
In order to validate semsim-b, we refer to the ex-
periment proposed in (Formica et al., 2013). In
that experiment, we considered four request vectors,
namely rv
i
, i = 1, ...4, which are recalled below:
rv
1
= {Campsite, EthnicMeal, RockConcert, Bus}
rv
2
= {InternationalHotel, InternationalMeal,
ArtGallery, Flight}
rv
3
= {Pension, MediterraneanMeal,Cinema,
ShoppingCenter}
rv
4
= {CountryResort, LightMeal, ArcheologicalSite,
Museum, Train}
and 22 annotated resources, represented by their
annotation vectors, namely av
1
, av
2
, ..., av
22
. Below,
only 10 of them are recalled for lack of space:
av
1
= {InternationalHotel, FrenchMeal,Cinema,
Flight}
av
2
= {Pension,VegetarianMeal, ArtGallery,
ShoppingCenter}
av
3
= {CountryResort, MediterraneanMeal, Bus}
av
4
= {CozyAccommodation,VegetarianMeal,
Museum, Train}
av
5
= {InternationalHotel, ThaiMeal, IndianMeal,
Concert, Bus}
av
6
= {SeasideCottage, LightMeal, ArcheologicalSite,
Flight, ShoppingCenter}
av
7
= {RegularAccommodation, RegularMeal,
Salon, Flight}
av
8
= {InternationalHotel,VegetarianMeal, Ship}
av
9
= {FarmHouse, MediterraneanMeal,
CarRental}
av
10
= {RegularAccommodation, EthnicMeal,
Museum}
...
For each request vector, we computed the sem-
sim value against the 22 annotation vectors, and then,
we calculated the Pearson correlation index (Corr)
against human judgment (HJ) scores. While the
original experiment demonstrated that SemSim out-
performs some of the most representative similarity
methods defined in the literature (i.e., Dice, Jaccard,
Cosine, and Weighted Sum (Formica et al., 2013)), in
this work, we show in Tables 6 and 7 that semsim-b
(SS-b) achieves a higher correlation with HJ with re-
spect to semsim-p (SS-p).
Furthermore, Table 8 reports the values of the Pre-
cision and Recall measures obtained by a threshold
fixed to 0.60. As we observe, the Precision achieved
by applying semsim-b is equal to 1 for all the four RV ,
and for three of them, namely rv
1
, rv
3
, and rv
4
, it is
higher with respect to the Precision obtained by ap-
plying semsim-p. We also observe that both semsim-b
and semsim-p achieve the same Recall (equal to 1) for
three out of four RV , while the Recall for the remain-
ing RV (i.e. rv
1
) by semsim-b is lower than the one by
semsim-p.
5 RELATED WORK
In this section, we first recall some of the existing pro-
posals concerning the weighting of the concepts of an
ontology. Successively, a second line of research is
recalled regarding the integration of BN and Ontolo-
gies.
5.1 Ontology Weighting Methods
In (Gao et al., 2015) an approach based on edge-
counting and information content theory for measur-
ing semantic similarities has been presented. In par-
ticular, different ways of weighting the shortest path
length are proposed, although they are essentially
based on WordNet frequencies. As also mentioned
in (Formica et al., 2008), we do not adopt the Word-
Net frequencies for several reasons. Firstly, because
KEOD 2016 - 8th International Conference on Knowledge Engineering and Ontology Development
176

Table 6: Correlation about rv
1
and rv
2
.
AV
rv
1
rv
2
HJ SS-p SS-b HJ SS-p SS-b
av
1
0.10 0.54 0.20 0.72 0.80 0.68
av
2
0.10 0.34 0.12 0.21 0.55 0.43
av
3
0.25 0.50 0.37 0.16 0.35 0.18
av
4
0.18 0.49 0.22 0.10 0.49 0.26
av
5
0.51 0.64 0.37 0.10 0.47 0.34
av
6
0.14 0.40 0.18 0.20 0.49 0.34
av
7
0.16 0.51 0.24 0.71 0.90 0.77
av
8
0.10 0.37 0.20 0.10 0.49 0.38
av
9
0.10 0.46 0.29 0.10 0.35 0.18
av
10
0.21 0.49 0.32 0.40 0.46 0.30
av
11
0.15 0.45 0.16 0.10 0.44 0.28
av
12
0.10 0.25 0.12 0.10 0.23 0.10
av
13
0.89 0.71 0.67 0.10 0.34 0.16
av
14
0.10 0.38 0.16 0.44 0.55 0.41
av
15
0.10 0.33 0.13 0.86 0.70 0.64
av
16
0.10 0.39 0.18 0.25 0.54 0.40
av
17
0.93 0.87 0.77 0.10 0.48 0.21
av
18
0.26 0.46 0.17 0.10 0.39 0.21
av
19
0.50 0.73 0.37 0.10 0.46 0.23
av
20
0.34 0.51 0.32 0.10 0.41 0.21
av
21
0.77 0.85 0.52 0.10 0.48 0.26
av
22
0.46 0.72 0.56 0.10 0.46 0.20
Corr 1.00 0.90 0.93 1.00 0.83 0.88
we deal with specialized domains (e.g., tourism), re-
quiring specialized domain ontologies and WordNet
is a generic lexical ontology. Secondly, there are con-
cepts in WordNet for which the frequency is not given
(e.g., accommodation), or is irrelevant, as in the case
of meal (the frequency is 20).
In (Rusu et al., 2014), the importance of measur-
ing semantic similarity between concepts of an ontol-
ogy is emphasized. In particular, the authors show
that their proposal improves the basic distance met-
ric, although the information content approach is not
addressed in the experiment.
The method proposed in (Seco et al., 2004) is
based on the assumption that the more descendants
a concept has the less information it expresses. Con-
cepts that are leaf nodes are the most specific in the
taxonomy and their information content is maximal.
Analogously to our proposal, in this method the infor-
mation content is computed by using only the struc-
ture of the specialization hierarchy. However, it forces
all the leaves to have the same IC, independently of
their depth in the hierarchy.
5.2 Ontology and Bayesian Networks
In (Rajput and Haider, 2011) a framework, called
BNOSA, has been proposed that uses an ontology to
conceptualize a problem domain. In this framework, a
BN has been adopted to predict missing values and/or
Table 7: Correlation about rv
3
and rv
4
.
AV
rv
3
rv
4
HJ SS-p SS-b HJ SS-p SS-b
av
1
0.10 0.55 0.43 0.10 0.39 0.21
av
2
0.62 0.80 0.68 0.10 0.36 0.23
av
3
0.29 0.36 0.30 0.45 0.48 0.41
av
4
0.10 0.44 0.26 0.88 0.75 0.68
av
5
0.10 0.38 0.25 0.10 0.38 0.21
av
6
0.31 0.56 0.43 0.50 0.66 0.58
av
7
0.10 0.45 0.29 0.10 0.43 0.27
av
8
0.10 0.38 0.26 0.10 0.37 0.25
av
9
0.12 0.36 0.30 0.10 0.37 0.25
av
10
0.18 0.45 0.29 0.14 0.42 0.33
av
11
0.78 0.85 0.70 0.14 0.40 0.30
av
12
0.38 0.52 0.33 0.16 0.34 0.25
av
13
0.10 0.39 0.16 0.18 0.48 0.29
av
14
0.42 0.63 0.40 0.20 0.42 0.33
av
15
0.10 0.28 0.17 0.10 0.29 0.16
av
16
0.31 0.47 0.39 0.31 0.59 0.51
av
17
0.10 0.51 0.24 0.10 0.49 0.32
av
18
0.18 0.43 0.30 0.84 0.86 0.75
av
19
0.10 0.49 0.32 0.32 0.57 0.46
av
20
0.22 0.40 0.30 0.36 0.71 0.55
av
21
0.10 0.53 0.37 0.21 0.50 0.37
av
22
0.10 0.50 0.23 0.29 0.58 0.44
Corr 1.00 0.81 0.86 1.00 0.88 0.93
to resolve conflicts of multiple values. In contrast, in
our approach the BN has been used to assign weights
to concepts of the reference ontology.
(Clark and Radivojac, 2013) applies BN for com-
puting the information content of concepts in a tax-
onomy and, more in general, of a sub-graph, by sum-
ming the information content of each concept in the
sub-graph. However, with respect to our work, it does
not focus on any specific way for building the con-
ditional probability tables of the BN, and such tables
are assumed to be given.
In (Yazid et al., 2014), a similarity measure for the
retrieval of medical cases has been proposed. This ap-
proach is based on a BN, where the a priori probabil-
ities are given by experts on the basis of cause-effect
conditional dependencies. As already mentioned, in
our approach the a priori probabilities are not given by
experts and rely on the probabilistic-based approach.
In (Jung et al., 2010), an ontology mapping-based
search methodology (OntSE) is proposed in order to
Table 8: Precision and Recall about the four request vectors.
Precision Recall
SS-b SS-p SS-b SS-p
rv
1
1.00 0.50 0.67 1.00
rv
2
1.00 1.00 1.00 1.00
rv
3
1.00 0.67 1.00 1.00
rv
4
1.00 0.50 1.00 1.00
A Bayesian Approach for Weighted Ontologies and Semantic Search
177

evaluate the semantic similarity between user key-
words and terms (concepts) stored in the ontology,
using a BN. Furthermore, in (Grubisic et al., 2013),
the authors emphasize the need of having a non-
empirical mathematical method for computing con-
ditional probabilities in order to integrate a BN in an
ontology. In particular, in the proposed approach the
conditional probabilities depend only on the structure
of the domain ontology. However, in the last two
mentioned papers, the conditional probability tables
for non-root nodes are computed starting from a fixed
value, namely 0.9.
In line with (Grubisic et al., 2013), we also pro-
vide a non-empirical mathematical method for com-
puting conditional probabilities, but our approach
does not depend on a fixed value as initial assumption.
In fact, in SemSim-b the conditional probabilities are
computed on the basis of the weight w
p
, which de-
pends only on the structure of the domain ontology,
i.e., the probability of the parent node divided by the
number of sibling nodes.
6 CONCLUSION
In this paper we presented a new approach to seman-
tic similarity reasoning based on the integration of
Bayesian Networks and Weighted Ontologies. Such
a solution improves the performance of the Sem-
Sim method proposed in (Formica et al., 2013). In
essence, the proposed approach is based on the con-
struction of a Bayesian Network, isomorphic to a
given ontology, referred to as OBN (Onto Bayesian
Network). Then, the OBN is used to compute the in-
formation content of each concept in the ontology. We
have shown that the SemSim method achieves better
performances by using the weights obtained from the
OBN rather than the ones achieved according to the
probabilistic-based approach. The SemSim method
has been conceived assuming that the ontology is or-
ganized as a tree-shaped taxonomy. In a future work,
we will focus on ontologies organized as DAG, there-
fore we will extend these results to ISA hierarchies
with multiple inheritance.
REFERENCES
Clark, W. T. and Radivojac, P. (2013). Information-
theoretic evaluation of predicted ontological annota-
tions. Bioinformatics, 29(13):i53–i61.
Dulmage, A. and Mendelsohn, N. (1958). Coverings of
bipartite graphs. Canadian Journal of Mathematics,
10:517 – 534.
Formica, A., Missikoff, M., Pourabbas, E., and Taglino,
F. (2008). Weighted Ontology for Semantic Search,
pages 1289–1303. Springer Berlin Heidelberg, Berlin,
Heidelberg.
Formica, A., Missikoff, M., Pourabbas, E., and Taglino,
F. (2010). Semantic search for enterprises competen-
cies management. In Proceedings of the International
Conference on Knowledge Engineering and Ontology
Development (IC3K 2010), pages 183–192.
Formica, A., Missikoff, M., Pourabbas, E., and Taglino,
F. (2013). Semantic search for matching user re-
quests with profiled enterprises. Computers in Indus-
try, 64(3):191 – 202.
Gao, J.-B., Zhang, B.-W., and Chen, X.-H. (2015). A
wordnet-based semantic similarity measurement com-
bining edge-counting and information content the-
ory. Engineering Applications of Artificial Intelli-
gence, 39:80 – 88.
Gruber, T. R. (1993). A translation approach to portable on-
tology specifications. Knowl. Acquis., 5(2):199–220.
Grubisic, A., Stankov, S., and Perai, I. (2013). Ontology
based approach to bayesian student model design. Ex-
pert Systems with Applications, 40(13):5363–5371.
Jung, M., Jun, H.-B., Kim, K.-W., and Suh, H.-W. (2010).
Ontology mapping-based search with multidimen-
sional similarity and bayesian network. The Interna-
tional Journal of Advanced Manufacturing Technol-
ogy, 48(1):367–382.
Lin, D. (1998). An information-theoretic definition of sim-
ilarity. In In Proceedings of the 15th International
Conference on Machine Learning, pages 296–304.
Morgan Kaufmann.
Pearl, J. and Russell, S. (2001). Bayesian networks. In
Arbib, M. A., editor, Handbook of Brain Theory and
Neural Networks, pages 157–160. MIT Press.
Rajput, Q. and Haider, S. (2011). Bnosa: A bayesian net-
work and ontology based semantic annotation frame-
work. J. Web Sem., 9(2):99–112.
Resnik, P. (1995). Using information content to evaluate se-
mantic similarity in a taxonomy. In Proc. of the 14th
Int. Joint Conference on Artificial Intelligence - Vol-
ume 1, IJCAI’95, pages 448–453, San Francisco, CA,
USA. Morgan Kaufmann Publishers Inc.
Rusu, D., Fortuna, B., and Mladenic, D. (2014). Measuring
concept similarity in ontologies using weighted con-
cept paths. Applied Ontology, 9(1):65–95.
Salton, G., Wong, A., and Yang, C. S. (1975). A vector
space model for automatic indexing. Commun. ACM,
18(11):613–620.
Seco, N., Veale, T., and Hayes, J. (2004). An intrinsic infor-
mation content metric for semantic similarity in Word-
Net. Proc. of ECAI, 4:1089–1090.
Yazid, H., Kalti, K., and Amara, N. E. B. (2014). A new
similarity measure based on bayesian network sig-
nature correspondence for braint2 tumors cases re-
trieval. Int. J. Computational Intelligence Systems,
7(6):1123–1136.
KEOD 2016 - 8th International Conference on Knowledge Engineering and Ontology Development
178
