
Anti-cancer Drug Activity Prediction by Ensemble Learning
Ertan Tolan and Mehmet Tan
Department of Computer Engineering, TOBB University of Economics and Technology, Ankara, Turkey
Keywords:
Cancer, Drug Activity, Ensemble Learning.
Abstract:
Personalized cancer treatment is an ever-evolving approach due to complexity of cancer. As a part of personal-
ized therapy, effectiveness of a drug on a cell line is measured. However, these experiments are backbreaking
and money consuming. To surmount these difficulties, computational methods are used with the provided
data sets. In the present study, we considered this as a regression problem and designed an ensemble model
by combining three different regression models to reduce prediction error for each drug-cell line pair. Two
major data sets were used to evaluate our method. Results of this evaluation show that predictions of ensemble
method are significantly better than models per se. Furthermore, we report the cytotoxicty predictions of our
model for the drug-cell line pairs that do not appear in the original data sets.
1 INTRODUCTION
It’s a known fact that personalized cancer treatment
and medicine are more effective methods than tradi-
tional therapies (Jackson and Chester, 2015). As a
part of personalized treatment, experiments on tumor
cells show how sensitive a tumor cell is to an anti-
cancer drug. On deciding whether a given drug will
be effective or not on the treatment of a certain can-
cer, experimental results on cancer cell lines are gen-
erally the starting point. However, large-scale screens
of chemical compound-cell line pairs do have a sig-
nificant cost due to large numbers potential drug can-
didates. To overcome this problem, computational
models to predict drug responses are designed instead
of performing wet-lab experiments for each drug re-
sponse on the tumor cell.
Building models to predict drug activity has be-
come possible due to the recent introduction of large-
scale drug response screens. These databases are
composed of the results of cytotoxicity experiments
of a large number of chemical compounds against
hundreds of cancer cell lines. The cell lines are char-
acterized in terms of several different data types such
as gene expression, DNA methylation and copy num-
ber variation data. Among these, gene expression data
is considered the most informative as also confirmed
by a recent DREAM challenge (Costello et al., 2014).
Models for prediction of half maximum inhibitory
concentration (IC
50
) and area under the dose-response
curve (AUC) consider this either as classification or a
regression problem. In comparison with binary classi-
fication (drug is sensitive or not), regression problem
is explicitly harder, nevertheless it gives much more
information on how drug affects tumor cell.
We define an ensemble model which combines
three distinctive methods; trace-norm regularized
multitask learning, kernelized Bayesian multitask
learning and gradient boosting regression to predict
drug responses. Since joint learning is a favorable
method for response prediction of cancer drugs due
to applicability of drugs as related tasks of multi-
task learning model , we choose two prominent and
publicly available multitask learning models . Also
GBR is chosen among single task learning models
by considering predictive power. To build our pre-
dictive model, we use hundreds of cell lines and drug
responses provided by genomics of drug sensitivity
in cancer(Yang et al., 2013) and cancer therapeutics
response portal(Seashore-Ludlow et al., 2015) (Rees
et al., 2015) data sets.
2 RELATED WORK
To predict drug responses,(Zhang et al., 2015) de-
veloped cell line similarity network (CSN) and drug
similarity network (DSN) based on similar cell lines
and similar drugs have similar responses. By combin-
ing these similarity networks with a linearly weighted
model they propose integrated network which out-
performs single-layer models. (Bansal et al., 2014)
Tolan, E. and Tan, M.
Anti-cancer Drug Activity Prediction by Ensemble Learning.
DOI: 10.5220/0006085704310436
In Proceedings of the 8th International Joint Conference on Knowledge Discovery, Knowledge Engineering and Knowledge Management (IC3K 2016) - Volume 1: KDIR, pages 431-436
ISBN: 978-989-758-203-5
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
431

show computational prediction of compound-pair ac-
tivity is possible by using single-compound perturba-
tion data. Another method to develop efficient can-
cer therapies taking advantage of synergistic effects
of different drugs is proposed by (Qin et al., 2015).
(Dong et al., 2015), unlike the other methods, com-
bine two different databases, Cancer Cell Line Ency-
clopedia and CGP, to build and evaluate their model.
Omissions of drug responses make data set
smaller. By using kernelized bayesian multitask
learning (Gonen and Margolin, 2014) off-target ef-
fects and experimental noise are eliminated and short-
comings of discarding missing values are compen-
sated. Learning model of Gonen is highly applicable
for drug response prediction and publicly available.
Feature selection is used to reduce dimension of
data to purify from irrelevant features. (Zhao et al.,
2013) develop their model with feature selection and
multiple instance learning. (Menden et al., 2013)
combine structural drug properties and genomic char-
acterizations of cell lines to build their model. Also
(Cort
´
es-Ciriano et al., 2015) use combination of the
chemical information of compounds and cell line pro-
filing data as input. By associating multivariate inter-
action of gene expression levels, (Riddick et al., 2011)
improve ability of drug response predictions. (Haider
et al., 2015) show that copula based multivariate ran-
dom forest framework enhances the accuracy and pro-
vides improved variable selection.
3 METHODS
We benefit from subset selection by the methods
given below. Also we includes determined singletask
and multitask learning methods to generate an ensem-
ble model. Parameters of these models are obtained
by using optimization algorithms. Moreover the way
of combination for ensemble model is detailed and il-
lustrated.
3.1 Feature Selection
As the number of genes is greater than the number of
samples, we applied a gene selection procedure that
exploits the MalaCards database (Rappaport et al.,
2013). From this database, one can get the list of
genes currently known to be related to the disease
of interest. We generated a set of keywords that are
based on the cancer types of the cell lines and down-
loaded the list of genes related to the cancer cell lines.
This constituted a list of 1545 genes. We used the in-
tersection of this list with the list of genes in the gene
expression data of the data sets used.
3.2 Gradient Boosting Regression
For regression problems, Gradient Boosting Regres-
sion (GBR) (Friedman, 2002) is a powerful machine
learning algorithm. GBR is an ensemble model com-
posed of many weak learners largely represented by
decision trees. By adding each weak learner iter-
atively to the existing model, shortcomings of the
current strong learner is compensated. As a part
of our ensemble model we use LSBoost which is
found in MATLAB Statistics and Machine Learning
Toolbox. We set Learners to Tree with default pa-
rameters. The other two important parameters for
GBR are NLearn, number of learners in the model,
and LearnRate, learning rate for shrinkage. We set
NLearn and Lear nRate to 100 and 0.1 which are the
popular choices for GBR. By utilizing GBR with de-
fined parameters we obtain good predictive model.
3.3 Trace-norm Regularized Multitask
Learning
Instead of training machine learning tasks individ-
ually, Multitask Learning (MTL) considers related
tasks simultaneously. Training tasks concurrently
help tasks be better learned (Caruana, 1998). To
benefit from MTL, tasks, such as various anti-cancer
drugs, should be related to each other.
Like the other regularization functions, trace-
norm regularization adjusts the learning models to
prevent over fitting by penalizing the complexity.
Trace-norm, also known as the nuclear-norm, is a fa-
miliar case of Schatten p-norm where p = 1. Based
on trace-norm, Trace-Norm Regularized Multitask
Learning(Ji and Ye, 2009) considers this problem:
min
W
n
∑
i=1
f (W ) + λkW k
∗
(1)
We used grid search to optimize regularization pa-
rameter, λ, from the list of 0.1, 1, 10, 100 for both
data sets. We used the MATLAB implementation of
MALSAR(Zhou et al., 2012) for TRMTL.
3.4 Kernelized Bayesian Multitask
Learning
(Gonen and Margolin, 2014) propose a method which
includes novelties such as using a shared subspace
for all tasks to eliminate noise and overcoming prob-
lem of missing values. This method, called kernel-
ized Bayesian multitask learning (KBMTL), is con-
venient for both binary classification and regression
problems. We use regression with the default param-
eters given at the implementation of KBMTL.
KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval
432
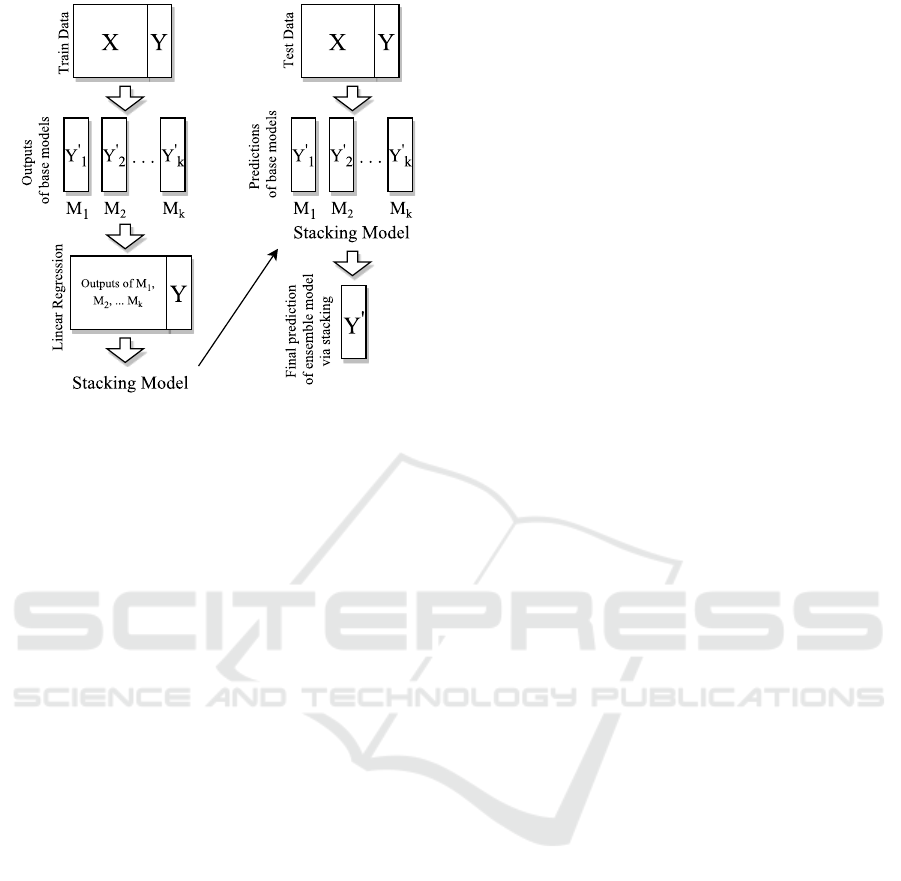
Figure 1: Stacking algorithm.
3.5 Ensemble Model
Ensemble learning is the way of combining various
machine learning algorithms to acquire better predic-
tions. There are several ensemble models such as av-
eraging, voting,stacking etc. (Sewell, 2008). We de-
sign an ensemble model which consists of the above
learning methods by stacked generalization(Wolpert,
1992). In stacking, outputs of base predictors and tar-
get values for training data are used to generate linear
combinations. By using predictions of base predictors
as feature vectors, stacking model with the obtained
coefficients is used to combine models (Figure 1).
As the stacking model, we experimented with both
linear regression and regression tree where we got
better results via linear regression. Although model
parameters are usually derived by 2-folds for stack-
ing, we used 5-folds where we achieved better perfor-
mance.
4 EXPERIMENTAL RESULTS
4.1 Data Sets
To evaluate our model we use two major data sets for
cell line-drug responses and gene expression data of
relevant cell lines.
Genomics of drug sensitivity in cancer (GDSC)
consists of 265 drugs, 1074 cell lines and 224,510
drug response values. Natural log of half maximal
inhibitory concentration (log(IC
50
)) and area under
the dose-response curve (AUC) values are provided
by GDSC thereby we evaluate our model with both
of them. Also gene expressions of cell lines are pre-
sented as RMA normalized basal expression profiles
with some deficiencies. After we removed those cell
lines without gene expression data, 1014 cell lines re-
main. Numbers of experimented cell lines for drugs
range between 363 and 940 .
Cancer therapeutics response portal (CTRP) con-
tains 481 drugs and 860 cell lines. Sensitivity
scores (AUC) of drug - cell lines and average log2-
transformed gene-expression values for each gene and
cancer cell line are used to evaluate our model. Anal-
ogously we removed cell lines with no gene expres-
sion data and 823 cell lines remain. Furthermore, for
some drugs, there are insufficient number of cell lines
with response value. To avoid this inadequacy, we
set a limit on the sample size of the drugs. Conse-
quently we discard drugs with less than 250 samples
and consider 439 drugs with sufficient response val-
ues. Among these 439 drugs , minimum and maxi-
mum numbers of experimented cell lines are 299 and
809 respectively.
4.2 Data Preprocessing
For TRMTL and KBMTL, data is split into train and
test , than we normalize train data to have zero mean
and unit standard deviation. And to normalize test
data, mean of train data is subtracted from test data
and divided by standard deviation of train data.
The process of dimensionality reduction lower the
number of attributes and applying kernel trick linear
models transform to non-linear models. For these pur-
poses, using the (Gaussian) radial basis function ker-
nel (RBF) is known method.
We choose parameter of σ by using internal 5-fold
grid search algorithm for each data set. Parameter
ranges are generated referring the mean of pairwise
Euclidean distances between data points (Gonen and
Margolin, 2014). As we obtain the ranges, [22, 24,
27, 31, 38, 55] and [25, 27,30,35,43,62] , 24 and 27
are selected for GDSC and CTRP data sets.
For tree-based algorithms such as GBR, normal-
ization doesn’t matter because of these methods only
care about whether a value is greater or lower. Also
there is no need to kernel trick for nonlinear learn-
ing models. Thereby, these processes are ignored for
Gradient Boosting Regression and data is given to the
model without normalization and using kernel.
In order to show that the ensemble model per-
forms better than other methods we evaluate learning
models with 10-fold cross validation and three dif-
ferent metrics, average of drugs’ mean squared er-
ror (AMSE) (2), weighted average of drugs’ mean
squared error (WAMSE) (3) and the number of drugs
Anti-cancer Drug Activity Prediction by Ensemble Learning
433

predicted best by each estimator (NDPB). AMSE and
WAMSE are calculated as
AMSE =
1
T
T
∑
t=1
1
n
t
n
∑
i=1
(
ˆ
Y
t
i
−Y
t
i
)
2
(2)
WAMSE =
1
∑
T
t=1
n
t
T
∑
t=1
n
∑
i=1
(
ˆ
Y
t
i
−Y
t
i
)
2
(3)
where T is the number of drugs and n is the num-
ber the sample size for each drug.
Table 1: Results for GDSC Data set (IC
50
).
GBR TRMTL KBMTL Ensemble
NDPB 26 4 6 229
AMSE 1.65 1.87 1.83 1.60
WAMSE 1.63 1.87 1.81 1.58
Table 2: Results for GDSC Data set (AUC).
GBR TRMTL KBMTL Ensemble
NDPB 160 18 4 83
AMSE 1.51 × 10
−2
1.84 × 10
−2
1.72 × 10
−2
1.51 × 10
−2
WMSE 1.51 × 10
−2
1.85 × 10
−2
1.71 × 10
−2
1.5 × 10
−2
Table 3: Results for CTRP Data set (AUC).
GBR TRMTL KBMTL Ensemble
NDPB 68 63 10 298
AMSE 2.07 2.38 2.32 2.03
WMSE 2.09 2.40 2.33 2.05
As it can be seen in the Tables 1 and 3, ensemble
model outperforms the other models for almost all the
drugs especially for GDSC data set. And error rates
decrease significantly for both of the data sets.
Individual MSE of anti-cancer drugs are presented
in the Figures 2(a) , 2(b) and 2(c) for IC50 and AUC
values on GDSC data set and AUC values on CTRP
data set respectively. Ensemble model outperforms
the base models for 229 out of 265 drugs on GDSC
data set and 298 out of 439 drugs on CTRP data set.
4.3 New Activity Predictions
After training our model, we predict non-
experimented drug-cell line pairs to define whether
a drug is sensitive on a cell line or not. We present
the drugs that are predicted to be most active (and
corresponding cell lines) in Tables 4 and 5.
With the model we designed, it is revealed which
cell line is sensitive to which drug in slico, (e.g.
Bortezomib is sensitive on SW756). Also we can re-
spond to the question of ’Which drug is more effec-
tive on a given cell line?’ (e.g., Epothilone B is more
active than Thapsigargin on IOSE-397).
Performed in vivo experiments confirm the pre-
dictions of our model on drug-cell line pairs indi-
cated at Table 4. For instance, Bortezomib is effi-
cacious on SW756 cells and among the other drugs
experimented, the combination of bortezomib with
eeyarestatin efficiently suppressed clonal growth of
SW756 cells (Brem et al., 2013). Also (Shi et al.,
2016) shows that docetaxel controls the progression
of tumor and docetaxel is conjugated via ester linkage
to improve the therapeutic efficacy in HSC-3 cells.
Similar experiments exist in the literature for the
given pairs at Table 5. For example, synergy is ob-
served by using LOR-253 with BRD-A05821830 or
BRD-A28746609 in sequential and concurrent treat-
ments on NCIH226 cells (Cukier et al., 2012).
Table 4: Predictions on GDSC Data set.
Compound Cell Line IC50
Bortezomib SW756 -7.50
Docetaxel HSC-3 -6.83
Epothilone B IOSE-397 -6.07
GSK2126458 RCH-ACV -5.86
AICAR A673 -5.68
SN-38 SUP-B15 -5.59
YM155 OCI-LY7 -5.31
Vinorelbine RCH-ACV -4.83
Thapsigargin IOSE-397 -4.79
Table 5: Predictions on CTRP Data set.
Compound Cell Line AUC
BRD-K13662825 D283MED 0.05
BRD-K27624156 TE14 1.69
BRD-A05821830 NCIH226 1.78
BRD-A28746609 NCIH226 2.05
BRD-K02130563 AMO1 2.11
BRD-K82109576 NCIH1793 2.50
BRD-K92428232 NCIH1793 3.00
BRD-K23547378 NCIH1793 3.08
BRD-K76674262 NCIH1793 3.16
5 CONCLUSION
In this study, we design an ensemble model which
combines three distinctive learning models, GBR,
TRMTL and KBMTL To validate our model we use
two largest accessible data sets for sensitivities on
drug cell line pairs. Cross validation results on these
data sets show that our model surpasses the others. In
the light of these results, we made new predictions for
pairs that are not available in the original data sets.
KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval
434
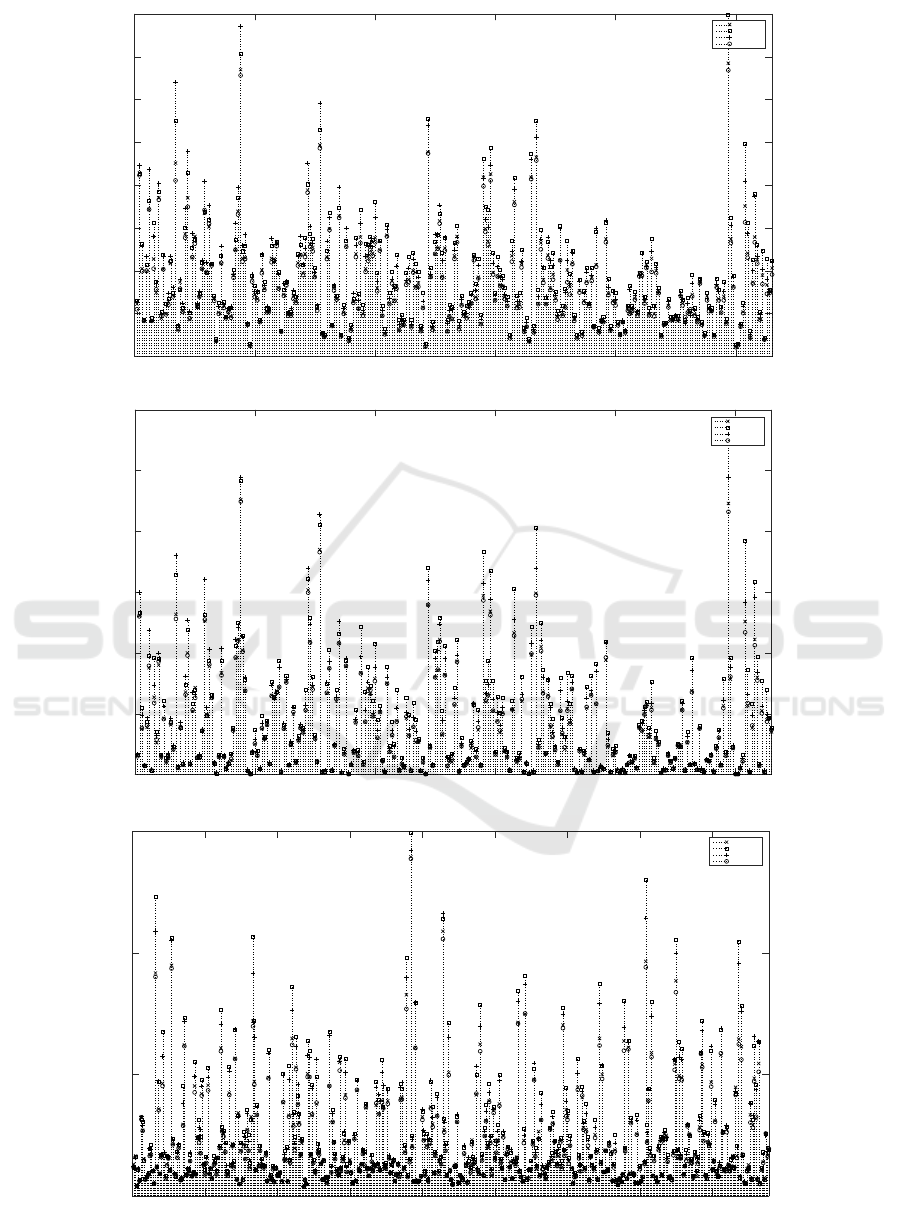
0 50 100 150 200 250
0
1
2
3
4
5
6
7
8
GBR
TRMTL
KBMTL
Ensemble
(a) GDSC (IC
50
0 50 100 150 200 250
0
0.02
0.04
0.06
0.08
0.1
0.12
GBR
TRMTL
KBMTL
Ensemble
(b) GDSC (AUC)
0 50 100 150 200 250 300 350 400
0
5
10
15
GBR
TRMTL
KBMTL
Ensemble
(c) CTRP (AUC)
Figure 2: MSE for each drug (Dataset (Metric)).
Anti-cancer Drug Activity Prediction by Ensemble Learning
435

Enhancement on the predictions of our model arises
from selecting proper models to combine and the way
of combination. We select three distinctive models,
and combine them by using stacked generalization.
There are several extensions that we plan to study.
First, designed ensemble model can be extended by
the other learning models or the other ways to com-
bine models. As stated, these selections play a key
role in ensemble models. Besides that, after overcom-
ing the matching problems of drugs or cell lines aris-
ing from varied denomination, model can be trained
by using more balanced data sets for each drug by
unifying different data sets. Furthermore, used fea-
tures are important for models. For drug response pre-
diction, traditional way is using gene expression data
but features can be extended via integration of drugs’
chemical information and other genomic features.
ACKNOWLEDGEMENTS
This study is supported by The Scientific and Tech-
nological Research Council of Turkey, Grant no:
115E274.
REFERENCES
Bansal, M., Yang, J., et al. (2014). A community computa-
tional challenge to predict the activity of pairs of com-
pounds. Nature Biotechnology, 32(2):1–3.
Brem, G. J., Mylonas, I., et al. (2013). Eeyarestatin causes
cervical cancer cell sensitization to bortezomib treat-
ment by augmenting ER stress and CHOP expression.
Gynecologic Oncology, 128:383–390.
Caruana, R. (1998). Multitask Learning. In Learning to
Learn, pages 95–133. Springer US, Boston, MA.
Cort
´
es-Ciriano, I., van Westen, G. J. P., et al. (2015). Im-
proved large-scale prediction of growth inhibition pat-
terns using the NCI60 cancer cell line panel. Bioinfor-
matics, 32(1):btv529.
Costello, J. C., Heiser, L. M., et al. (2014). A community
effort to assess and improve drug sensitivity prediction
algorithms. Nature Biotechnology, 32(12):1202.
Cukier, H., Peralta, R., et al. (2012). Preclinical dose
scheduling studies of lor-253, a novel anticancer drug,
in combination with chemotherapeutics in lung and
colon cancers. In AACR; Cancer Res, volume 72.
Dong, Z., Zhang, N., et al. (2015). Anticancer drug sensitiv-
ity prediction in cell lines from baseline gene expres-
sion through recursive feature selection. BMC cancer,
15(1):489.
Friedman, H. (2002). Stochastic gradient boosting. Compu-
tational Statistics and Data Analysis, 38(4):367–378.
Gonen, M. and Margolin, A. A. (2014). Drug suscepti-
bility prediction against a panel of drugs using ker-
nelized Bayesian multitask learning. Bioinformatics,
30(17):i556–i563.
Haider, S., Rahman, R., et al. (2015). A Copula
Based Approach for Design of Multivariate Random
Forests for Drug Sensitivity Prediction. PLOS ONE,
10(12):e0144490.
Jackson, S. E. and Chester, J. D. (2015). Personalised
cancer medicine. International Journal of Cancer,
137(2):262–266.
Ji, S. and Ye, J. (2009). An accelerated gradient method for
trace norm minimization. In Proceedings of the 26th
annual ICML, pages 457–464. ACM.
Menden, M. P., Iorio, F., et al. (2013). Machine Learning
Prediction of Cancer Cell Sensitivity to Drugs Based
on Genomic and Chemical Properties. PLoS ONE,
8(4):e61318.
Qin, Y., Chen, M., et al. (2015). A network flow-based
method to predict anticancer drug sensitivity. PLoS
ONE, 10(5):1–14.
Rappaport, N., Nativ, N., et al. (2013). MalaCards: an inte-
grated compendium for diseases and their annotation.
Database : the journal of biological databases and
curation, 2013:bat018.
Rees, M. G., Seashore-Ludlow, B., et al. (2015). Correlat-
ing chemical sensitivity and basal gene expression re-
veals mechanism of action. Nature Chemical Biology,
12(2):109–116.
Riddick, G., Song, H., et al. (2011). Predicting in vitro drug
sensitivity using Random Forests. 27(2):220–22410.
Seashore-Ludlow, B., Rees, M. G., et al. (2015). Harnessing
Connectivity in a Large-Scale Small-Molecule Sensi-
tivity Dataset. Cancer discovery, 5(11):1210–23.
Sewell, M. (2008). Ensemble learning. RN, 11(02).
Shi, L., Song, X.-B., et al. (2016). Docetaxel-conjugated
monomethoxy-poly(ethylene glycol)-b-poly(lactide)
(mPEG-PLA) polymeric micelles to enhance the ther-
apeutic efficacy in oral squamous cell carcinoma. RSC
Adv., 6(49):42819–42826.
Wolpert, D. H. (1992). Stacked generalization. Neural Net-
works, 5(2):241–259.
Yang, W., Soares, J., et al. (2013). Genomics of Drug Sen-
sitivity in Cancer (GDSC): a resource for therapeutic
biomarker discovery in cancer cells. Nucleic Acids
Research, 41(D1):D955–D961.
Zhang, N., Wang, H., et al. (2015). Predicting Anticancer
Drug Responses Using a Dual-Layer Integrated Cell
Line-Drug Network Model. PLoS computational bi-
ology, 11(9):e1004498.
Zhao, Z., Fu, G., et al. (2013). Drug activity predic-
tion using multiple-instance learning via joint instance
and feature selection. BMC Bioinformatics, 14 Suppl
1(Suppl 14):S16.
Zhou, J., Chen, J., and Ye, J. (2012). User’s Manual MAL-
SAR: Multi-tAsk Learning via StructurAl Regulariza-
tion. Arizona State University.
KDIR 2016 - 8th International Conference on Knowledge Discovery and Information Retrieval
436
