Modeling

V O

and

VCO

with Hammerstein-Wiener Models

Alexander Artiga Gonzalez

, Raphael Bertschinger

and Dietmar Saupe

Dept. of Computer and Information Science, University of Konstanz, Konstanz, Germany

Dept. of Sport Science, University of Konstanz, Konstanz, Germany

Keywords:

Mathematical Modeling, Simulation, Oxygen Dynamics, Hammerstein-Wiener Models.

Abstract:

V O

and

VCO

measurements are central to methods for assessment of physical ﬁtness and endurance ca-

pabilities in athletes. As measuring

V O

and

VCO

is difﬁcult outside a lab, models with good prediction

properties are necessary for online analysis and modeling in the ﬁeld. Easier to measure are heart rate and

during cycling also power. Thus, the here described models are based on either one of them or both. It is

commonly accepted that the relationship between power and

V O

VCO

and heart rate can be described

by a linear and a nonlinear component. The latter describes a drift over time without increase in workload.

Thus, block-structured systems such as Hammerstein-Wiener models with linear and nonlinear elements can

be employed for modeling and prediction. Modeling and prediction power of these models is compared with

a dynamic model based on physiological evidence. Our ﬁndings show that the simpler Hammerstein-Wiener

model performs slightly better for both modeling and prediction with the advantage of being easier to estimate

and evaluate. Overall, both models performed with errors smaller than the range of the natural variability of

the modeled quantities. Thus, such models allow for applications in the ﬁeld where

V O

and

VCO

cannot be

measured.

1 INTRODUCTION

Physiological quantities such as heart rate or respira-

tory gas exchange are important parameters to assess

the performance capabilities of athletes in competi-

tive sports. In particular the respiratory gas exchange

is a valuable source of information since it allows

for a non-invasive, continuous, and precise measure-

ment of the gross oxygen uptake and carbon dioxide

output of the whole body. Particularly in endurance

sports, the metabolic rates of this substantial fuel and

the degradation product of the exercising muscles are

reﬂected in that rate.

For endurance sports like cycling the models for

power demand due to mechanical resistance are well

understood by Martin et al. (1998). However, the indi-

vidual power supply model of an athlete is the bottle-

neck that has hindered the design of an individual ad-

equate feedback control system that guides him/her to

perform a speciﬁc task such as to ﬁnd the minimum-

time pacing in a race on a hilly track (Dahmen, 2012).

For such purposes, a model for the prediction of gas

exchange rates in response to load proﬁles given by a

particular race course would be beneﬁcial.

There are two kinds of approaches to get such a

model. The ﬁrst model type is directly based on con-

cepts of physiology, such as exponential saturation

functions with appropriate time-constants. Another

approach are black box models without relation to

physiology such as Hammerstein-Wiener models.

2 PREVIOUS WORK

A detailed review and historical account of the math-

ematical modeling of the

V O

kinetics for constant

work rate has recently been given by Poole and Jones

(2012), containing over 800 references. See also

Jones and Poole (2005) and, for a clariﬁcation, Ma

et al. (2010).

Artiga Gonzalez et al. (2015) generalized success-

fully the established constant work rate models to-

wards a dynamic model for variable work rate. The

result is a model that consists of two differential

equations based on a steady-state function for oxy-

gen demand. For completeness, we brieﬂy review

this dynamic model in the following and later com-

pare the performance of Hammerstein-Wiener models

with that of the dynamic model.

The steady-state oxygen demand is given by a

134

Gonzalez, A., Bertschinger, R. and Saupe, D.

Modeling

V O

and

VCO

with Hammerstein-Wiener Models.

DOI: 10.5220/0006086501340140

In Proceedings of the 4th International Congress on Sport Sciences Research and Technology Support (icSPORTS 2016), pages 134-140

ISBN: 978-989-758-205-9

constant baseline component, the ﬁrst, fast compo-

nent, and the second, slow component with ampli-

tudes

V O

2base

, A

(P), and A

(P), respectively. In

terms of formulas, the amplitudes are

(P) = min(s ·P,

V O

2max

−

V O

2base

)

(P) =



∆

·exp(−(P

−P)/∆) P ≤ P

V O

2max

−

V O

2base

−A

(P) P > P

where s is the slope (or gain) for the fast component,

denotes the critical power, V

∆

is the maximal am-

plitude of the slow component for exercise load up to

critical power, and ∆ is the corresponding decay con-

stant that governs the decay of the steady-state slow

component as the load is decreased from the critical

power.

The following equations describe the ﬁrst and sec-

ond component, x

(t), x

(t),

˙x

= τ

−1

(P) −x

), x

) = 0, k = 1,2

deﬁned for times t ≥ T

(and setting x

(t) = 0 for

t < T

). Here, the power demand is a function of time

P = P(t) and A

(P), k = 1,2, are the steady state am-

plitudes for the fast and slow components. The total

V O

accordingly is given by

V O

(t) =

V O

2base

+ x

(t) +x

(t).

The differential equations require the four parameters

,τ

, and T

In our previous work (Artiga Gonzalez et al.,

2015) this dynamic model was applied to oxygen con-

sumption

V O

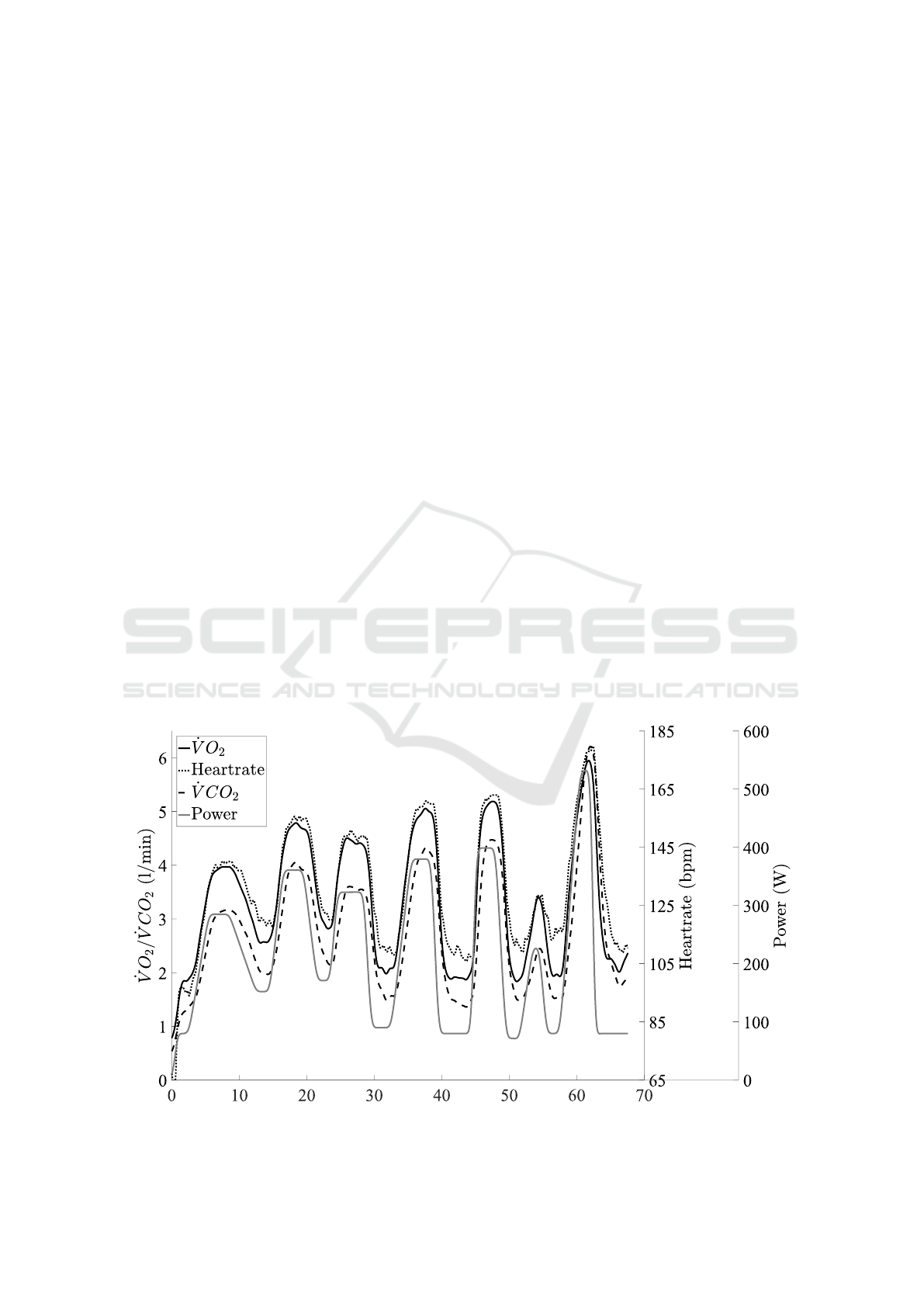
. Figure 1 shows that there is a strong

relationship between

V O

VCO

and heart rate and

thus, the model can be expected to work well also for

VCO

and heart rate. Corresponding results are given

below in Table 1.

Data Collection

The same dataset as in Artiga Gonzalez et al. (2015)

is taken to allow a comparison of methods for mod-

eling and prediction. For the sake of completeness

we give a short description of data collection and data

preprocessing.

Five healthy, recreational to well trained subjects

(age 37.8±14.8 yrs, height 180.4±10.1 cm, weight

75.2±7.6 kg) completed four different cycle ergome-

ter (Cylus2, RBM elektronik-automation GmbH,

Leipzig, Germany) tests with continuous breath-by-

breath gas exchange and ventilation measurements at

the mouth (Ergostik, Geratherm Respiratory GmbH,

Bad Kissingen, Germany). The tests featured a vari-

ety of load proﬁles in order to comprehensively eval-

uate the model prediction quality.

The testing procedure commenced with an incre-

mental step test starting at a workload of 80 W with

increments of 20 W every 3 minutes. In the initial

step the subjects were instructed to choose their pre-

ferred cadence between 80–100 rpm and were then

instructed to keep the cadence constant at that level

in all four test trials. The step test was terminated at

volitional exhaustion of the subject. After test termi-

nation subjects recovered actively at 80 W and at or

Figure 1: Measured

V O

VCO

and heart rate for the power proﬁle of the third test and one subject.

Modeling

V O

and

VCO

with Hammerstein-Wiener Models

135

near their self-selected cadence for ﬁve minutes.

The second ergometer test consisted of four

sprints of 6 s duration each and an incremental ramp

test. Two sprints were carried out before and two after

the ramp test to obtain the subjects’ maximal power

output and

V O

proﬁles in a recovered and a fatigued

state.

In the third test subjects had to complete a vari-

able step protocol. The steps varied in load and dura-

tion and alternated between low and moderate or se-

vere intensity. The linearly in- or decreasing intensity

between the steps was also varied in time. The load

proﬁle is illustrated in Figure 1.

For the ﬁnal ”synthetic hill climb test” the er-

gometer was controlled by our simulator software in

Dahmen et al. (2011). The load was deﬁned by the

mathematical model by Martin et al. (1998) to simu-

late the resistance on a realistic track. The gradient of

that track and the subjects’ body weight were the ma-

jor determinants of the load. While holding the same

cadence as before, the subjects were able to choose

their exercise intensity by gear shifting. (On the steep-

est section most subjects were not able to hold the ca-

dence even in the lowest gear.)

Data Preprocessing

In order to validate and compare the models, data se-

ries of time-stamped values of produced power and

resulting breath-by-breath oxygen consumption are

required for exercise intensities ranging from moder-

ate to severe. These time series from ergometer labo-

ratory experiments are typically very noisy, have dif-

ferent sampling rates and the samples may be irregu-

larly spaced.

Therefore, a combined smoothing and resampling

operator has to be applied. In this study we have

used the standard Gaussian smoothing ﬁlter with ker-

nel (σ

√

2π)

−1

exp(−0.5t/σ

) and σ = 20 s for respi-

ratory gas, heart rate and power measurements.

Dynamic Model

We have extended the dynamic model from Ar-

tiga Gonzalez et al. (2015) described above with

two more parameters. With these two additional pa-

rameters, a much smaller average root-mean-square

modeling error was obtained and also the predictive

power of the model was improved (details to be pub-

lished elsewhere). For a better comparison between

the dynamic model and Hammerstein-Wiener mod-

els, we also applied this modiﬁed dynamic model for

VCO

and heart rate modeling and prediction based

on power.

3 HAMMERSTEIN-WIENER

MODELS

The dynamical model for

V O

under variable work

rate (Artiga Gonzalez et al., 2015) described in Sec-

tion 2 is based on physiological evidence collected in

many years of research. Thus, in addition to the ap-

plication for modeling and prediction, the estimated

model parameters can be used as indicators for per-

formance capabilities of athletes or enhance the com-

prehension of physiological processes. For instance,

a deeper analysis of the second differential equation

might lead to a better understanding of the so called

slow component.

Black box models like Hammerstein-Wiener mod-

els do not offer the same understanding as physio-

logical models have, but they bring other advantages.

Detached from physiological evidence they are more

ﬂexible and can adjust better to data and therefore,

may deliver better ﬁtting results.

Though not derived by principles of physiology, it

is still important to select the right model type and

model settings to obtain good results. For this re-

search MATLAB



was used. The System Identiﬁca-

tion Toolbox

offers a large selection of models. Dif-

ferent linear (ARX, ARMAX, State-Space) and non-

linear (ARX, Hammerstein-Wiener) models from that

toolbox have been tested on selected data sets with

the System Identiﬁcation App. Best results have been

achieved with State-Space and Hammerstein-Wiener

models. In a direct comparison Hammerstein-Wiener

models have shown the best modeling results.

This outcome coincides with the knowledge that

there is a strong linear relationship between power

and

V O

(fast component) and a smaller nonlinear

relation (slow component), because Hammerstein-

Wiener models consist of nonlinear and linear ele-

ments. This holds also for the relationship between

power and

VCO

or heart rate.

Figure 2: Block diagram of Hammerstein-Wiener model.

icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support

136

In general Hammerstein-Wiener models consist

of the three elements shown in Figure 2. The ﬁrst

element is a static nonlinear function transforming

the input. MATLAB



offers seven options for

the nonlinearity (Piecewise linear function, Sigmoid

network, Wavelet network, Saturation, Dead zone,

One-dimensional polynomial, Unit gain, Custom net-

work). The input nonlinearity is followed by the sec-

ond element, a linear block that applies a discrete time

linear model (Transfer function model, Input-output

polynomial model, State-space model) to the output

of the ﬁrst element. The last element is again a static

nonlinear function modifying the result of the second

element. The same nonlinear functions as for the ﬁrst

block can be selected.

Different conﬁgurations of Hammerstein-Wiener

models have been tested and have resulted that for

modeling of

V O

VCO

and heart rate, we can omit

the ﬁrst element. Thus, our chosen model consists

only of a linear block followed by a nonlinear func-

tion. This model type is called a Wiener model.

Wiener models with a linear transfer model for the

linear block and a piecewise linear function for the

output nonlinearity performed best.

The Hammerstein-Wiener models were estimated

with the MATLAB



function nlhw. This function re-

quires, in addition to the input and target output data

for training, the orders of the linear transfer function.

Orders are the number of zeros, the number of poles

and the input delay. To cover a large range of possible

combinations for the orders, the Genetic Algorithm

ga from the Global Optimization Toolbox

was used

to search the best combination where all three values

have varied in the set {2,3,..,20}.

These models has also been estimated with heart

rate as input and with heart rate and power as com-

bined input for modeling and predicting

V O

and

VCO

4 RESULTS

The models were estimated for all four tests and ﬁve

subjects. For prediction, the models estimated for

each subject for Test 3 were applied on the other three

tests of the subject. The resulting average root-mean-

square error (RMSE) and the average mean absolute

percentage error (MAPE) for modeling and prediction

are given in Table 1 for the dynamic model and in

Table 2 for the Wiener models. The results for

V O

modeling and prediction are better than those reported

in (Artiga Gonzalez et al. (2015), ﬁrst data row in Ta-

ble 1) because the improved extended version with

two additional parameters was used.

The dynamic model has an average

V O

modeling

error of 0.09 l/min RMSE respectively 3.1 % MAPE.

The Wiener models that are also based on power, per-

form better with only 0.06 l/min RMSE and 1.8 %

MAPE. Figure 3 illustrates

V O

and power data and

the modeling result for Test 3 of Subject 1.

With heart rate as additional input, performance is

even better with 0.04 l/min RMSE and 1.3 % MAPE.

Figure 3:

V O

modeling results for Test 3 and Subject 1. Both models are based on power as independent variable. The noisy

grey signals are the original (unﬁltered) measurements.

Modeling

V O

and

VCO

with Hammerstein-Wiener Models

137

Figure 4:

V O

prediction results for Test 4 and Subject 1. Both models are based on power and trained on Test 3.

Table 1: Average modeling and predicting errors for

V O

VCO

and heart rate based on power with the dynamic

model.

Modeling Prediction

RMSE MAPE RMSE MAPE

l/min % l/min %

V O

(2015) 0.23 0.37

V O

0.09 3.1 0.30 8.8

VCO

0.12 4.7 0.41 12.6

Heart Rate 4.55 2.5 7.46 4.4

The Wiener models with only heart rate as input have

similar errors compared to the Wiener models with

power or power and heart rate as input.

For the dynamic model, a prediction error of 0.30

l/min RMSE respectively 8.8 % MAPE was observed.

With 0.27 l/min RMSE and 7.5 % MAPE the Wiener

model performed slightly better. Figure 4 visualizes

the prediction results for Subject 1 and Test 4 based

on power and models trained on Test 3. Predictive

power did not beneﬁt from heart rate as additional in-

put (0.28 l/min RMSE, 8.4 % MAPE).

As expected, estimation of

VCO

with Wiener

models works as well as estimation of

V O

, but pre-

diction is worse. Especially with combined input

of power and heart rate the Wiener models perform

poorly with 0.64 l/min RMSE and 17.6 % MAPE.

With the dynamic model similar results were obtained

for

VCO

based on power. The average modeling

root-mean-square error is 0.12 l/min or 4.7 % MAPE

while the average prediction error is 0.41 l/min RMSE

or 12.6 % MAPE.

Power based heart rate modeling and prediction

outperforms the Wiener models for

V O

and

VCO

with a MAPE of 0.9 % respectively 4.8 %. The

dynamic model also produces reliable results with a

modeling MAPE of 2.5 % and a MAPE of 4.4 % for

prediction.

5 DISCUSSION

Overall, the results show that Hammerstein-Wiener

models, respectively Wiener models with a linear

Table 2: Average modeling and predicting errors for

V O

and

VCO

based on power, heart rate and both with Wiener models.

Power Heart rate Power + Heart rate

RMSE MAPE RMSE MAPE RMSE MAPE

l/min % l/min % l/min %

Modeling

V O

0.06 1.8 0.09 2.8 0.04 1.3

VCO

0.08 2.9 0.07 2.5 0.04 1.6

Prediction

V O

0.27 7.5 0.34 10.0 0.28 8.4

VCO

0.44 14.2 0.43 13.3 0.64 17.6

icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support

138

Figure 5: Response of an estimated Wiener model applied on a synthetic power proﬁle with two ramps and two plateaus.

transfer function followed by a static piecewise non-

linear function, perform slightly better than the dy-

namic model. It should be noted that the steady-state

function for the dynamic model also consists of a lin-

ear component followed by a nonlinear increase. Fig-

ure 5 illustrates the linear relationship and the nonlin-

ear inﬂuence of an estimated Wiener model applied

on a synthetic power proﬁle with two ramps and two

plateaus.

In a small study (unpublished work) a grand av-

erage root-mean-square difference of 0.09 l/min be-

tween

V O

measurements of two identical tests of

the same subject was obtained. The corresponding

mean absolute percentage difference is 2.95 %. The

best one can expect from an optimal modeling is that

the accuracy is in the range of this natural variabil-

ity of the modeled quantities. For our results with

the Wiener models for

V O

consumption we have ob-

tained 0.06 l/min, 0.09 l/min and 0.04 l/min (see ﬁrst

row in Table 2) and with the dynamic model we have

obtained an error of 0.09 l/min (see Table 1).

Thus, both models are suitable and the choice

of the right model depends on other factors. For

example estimation and evaluation of Hammerstein-

Wiener models is much faster than parameter estima-

tion for the physiological model. But the latter offers

more insights into the physiological processes and

estimates parameters like critical power or

V O

2max

which can be used for further analysis.

The overall predictive power for both models is

not as promising as the modeling results. This is

most likely based on the big differences between the

four tests and the small data set per subject. Train-

ing on only one test may lead to overﬁtting and there-

fore weak predictive power. Figure 6 illustrates that

both models overestimate

VCO

in the severe domain.

The models may misbehave there, because Test 3 on

which they have been trained does not contain that

large parts in the severe intensity domain.

Moreover, there is evidence for an asymmetry be-

tween on- and off-transient dynamics (

Ozyener et al.,

2001) but neither model can distinguish between on-

and off-transient parts. This leads again towards over-

estimation, at least for the dynamic model (unpub-

lished work).

In addition to

V O

and

VCO

, heart rate was suc-

cessfully modeled with power based Hammerstein-

Wiener models and the dynamic model. In general,

heart rate prediction is not useful because heart rate

can easily be measured directly. But there are some

use cases, for example in medical applications where

it is important to control and predict heart rate (Cheng

et al., 2008). However, forecasting models that know

past values collected by a heart rate measurement de-

vice are expected to perform much better for control-

ling issues.

Our results indicate that heart rate based Wiener

models also perform well. This could be an inter-

esting alternative to power based prediction in the

ﬁeld as heart rate belts are much cheaper compared

to power meters. However there may arise compli-

cations because heart rate varies depending on train-

Modeling

V O

and

VCO

with Hammerstein-Wiener Models

139

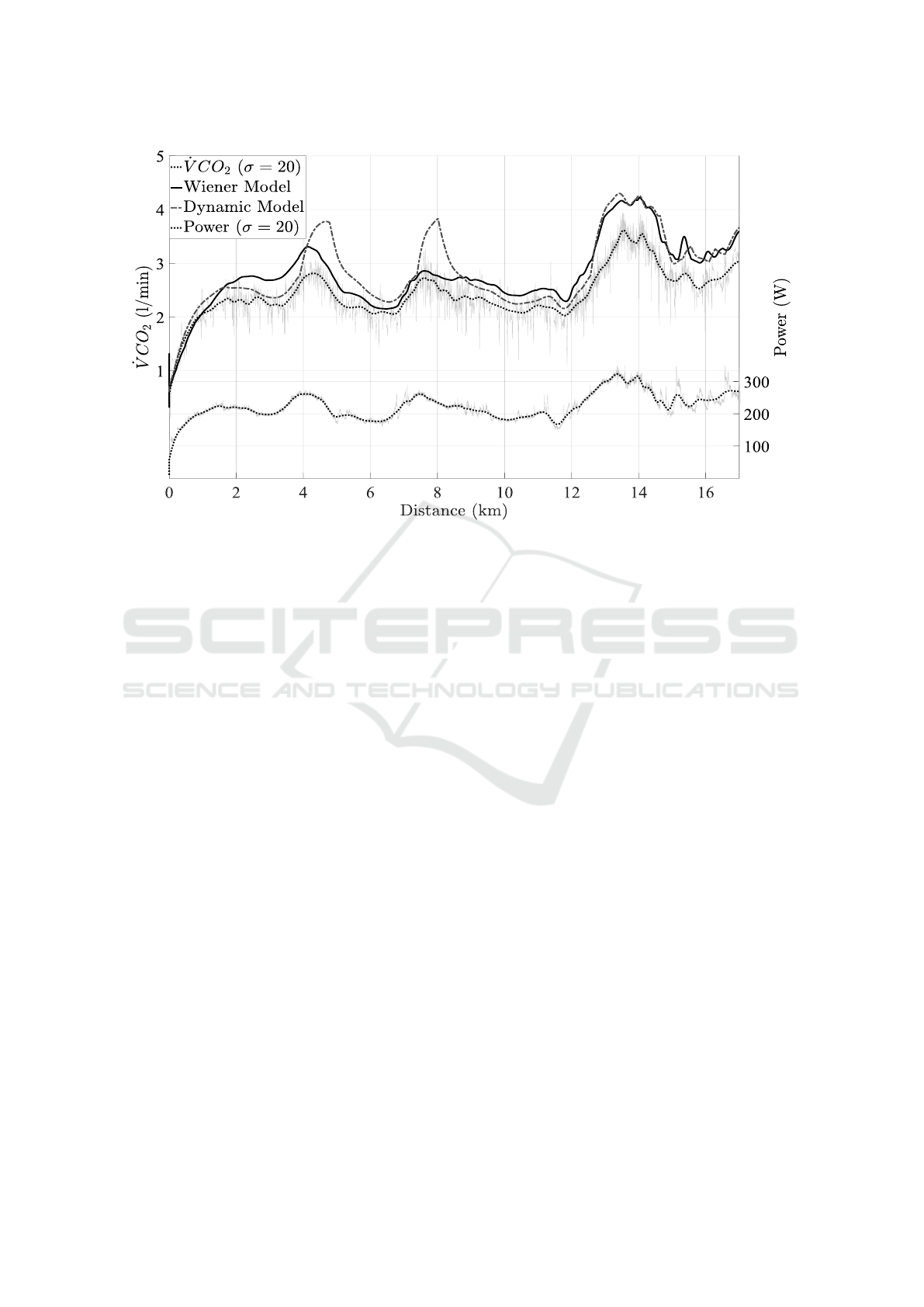
Figure 6:

VCO

prediction results for Test 4 Subject 1. Both models are based on power and trained on Test 3.

ing state, daily condition and environment conditions,

e. g. temperature.

6 CONCLUSIONS

We showed that Hammerstein-Wiener models are a

suitable tool for modeling and predicting

V O

VCO

and heart rate. They performed slightly better than the

dynamic model for

V O

under variable work rate (Ar-

tiga Gonzalez et al., 2015), that is based on physiolog-

ical evidence. Thus, both model types are suitable for

modeling and prediction.

We expect a better predictive power for both mod-

els when trained on a more suitable or bigger data set.

An alternative modeling approach that was not

discussed yet and could perform well or even better

are models based on neural networks.

REFERENCES

Artiga Gonzalez, A., Bertschinger, R., Brosda, F., Dahmen,

T., Thumm, P., and Saupe, D. (2015). Modeling oxy-

gen dynamics under variable work rate. In icSPORTS

2015: 3rd International Congress on Sport Sciences

Research and Technology Support, pages 198–207.

Cheng, T. M., Savkin, A. V., Celler, B. G., Su, S. W.,

and Wang, L. (2008). Nonlinear modeling and con-

trol of human heart rate response during exercise with

various work load intensities. IEEE Transactions on

Biomedical Engineering, 55(11):2499–2508.

Dahmen, T. (2012). Optimization of pacing strategies

for cycling time trials using a smooth 6-parameter

endurance model. In Proceedings Pre-Olympic

Congress on Sports Science and Computer Science in

Sport (IACSS), Liverpool, England, UK, July 24-25,

2012.

Dahmen, T., Byshko, R., Saupe, D., R

oder, M., and

Mantler, S. (2011). Validation of a model and a simu-

lator for road cycling on real tracks. Sports Engineer-

ing, 14(2-4):95–110.

Jones, A. M. and Poole, D. C. (2005). Introduction to oxy-

gen uptake kinetics and historical development of the

discipline. In Jones, A. M. and Poole, D. C., edi-

tors, Oxygen Uptake Kinetics in Sport, Exercise and

Medicine, pages 3–35. London: Routledge.

Ma, S., Rossiter, H. B., Barstow, T. J., Casaburi, R., and

Porszasz, J. (2010). Clarifying the equation for model-

ing of

V O

kinetics above the lactate threshold. Jour-

nal of Applied Physiology, 109(4):1283–1284.

Martin, J. C., Milliken, D. L., Cobb, J. E., McFadden, K. L.,

and Coggan, A. R. (1998). Validation of a mathemat-

ical model for road cycling power. Journal of Applied

Biomechanics, 14:276–291.

Ozyener, F., Rossiter, H. B., Ward, S. A., and Whipp, B. J.

(2001). Inﬂuence of exercise intensity on the on- and

off-transient kinetics of pulmonary oxygen uptake in

humans. The Journal of Physiology, 533(3):891–902.

Poole, D. C. and Jones, A. M. (2012). Oxygen uptake ki-

netics. Comprehensive Physiology, 2:933–996.

icSPORTS 2016 - 4th International Congress on Sport Sciences Research and Technology Support

140