The Modularity Matrix as a Source of Software Conceptual Integrity

Iaakov Exman

Software Engineering Dept., The Jerusalem College of Engineering – JCE - Azrieli, POB 3566, Jerusalem, Israel

Keywords: Conceptual Integrity, Modularity Matrix, Conceptual Lattice, Linear Software Models, Liskov Substitution

Principle, Abstract Mathematical Concepts, Standard Modularity Matrix, Software System Design.

Abstract: Conceptual Integrity has been declared the most important consideration for software system design.

However, the very concept of Conceptual Integrity remained quite vague, lacking a precise formal

definition. This paper offers a path to a novel definition of Conceptual Integrity in terms of the Modularity

Matrix, the basic structure of Linear Software Models. We provide arguments for the plausibility of the

Modularity Matrix as the suggested source of software system Conceptual Integrity, viz. the orthogonality

and propriety of the Matrix modules. Furthermore, the paper also reveals some new characteristic properties

of Software Conceptual Integrity.

1 INTRODUCTION

We can trace back the idea of conceptual integrity,

in the context of software, to Brooks in his well-

known book “The Mythical Man-Month” – in

Chapter 4, page 42 of the anniversary edition –

(Brooks, 1995). Already there, it is said that

conceptual integrity is the most important idea for

software system design. The idea has been proposed

and praised, but not exactly defined.

This paper offers a path to a formal definition of

conceptual integrity in terms of the Modularity

Matrix. This matrix is the basic algebraic structure

of Linear Software Models.

In this Introduction section we clarify the idea of

software conceptual integrity, as far as it has been

done since its initial presentation by Brooks, and

concisely review the basics of the Modularity

Matrix.

1.1 Software Conceptual Integrity

The idea of conceptual integrity, in the context of

software, has been reiterated in a more recent book

by Brooks “The Design of Design: Essays of a

computer scientist” – in Chapter 6, pages 69-70 –

(Brooks, 2010).

There, conceptual integrity is said to consist of

three principles referring to system functions. These

principles have been verbally formulated in a paper

by De Rosso and Jackson (De Rosso and Jackson,

2013) as follows:

 Orthogonality – individual functions

should be independent of one another;

 Propriety – the system should have only the

functions essential to its purpose and no

more;

 Generality – a single function should be

usable in many ways.

There are a few problems with these formula-

tions, but the most important one is that there is no

“algorithm” or “protocol” to make concrete usage of

these principles.

This work has as its aim to offer a formal path to

conceptual integrity, gaining in this process both a

deeper understanding of this idea and the basis for a

practical application of the above principles. Thus,

among other things, if the above principles are

indeed the essence behind conceptual integrity, then

they must follow as consequences of the offered

formal path.

1.2 Modularity Matrix

The Modularity Matrix – see e.g. (Exman, 2014) is a

representation of a hierarchical software system in

its several abstraction levels, through sub-systems,

down to indivisible basic modules. The matrix

columns, the structors, stand for architectural

structure units, generalizing classes. The matrix

Exman, I.

The Modularity Matrix as a Source of Software Conceptual Integrity.

DOI: 10.5220/0006098300270035

In Proceedings of the 7th International Workshop on Software Knowledge (SKY 2016), pages 27-35

ISBN: 978-989-758-202-8

rows, the functionals, stand for architectural

behavioural units, generalizing class methods.

Algebraic manipulations lead in the optimal case

to a standard square and block diagonal matrix, in

which the blocks along the diagonal are the modules

of the current matrix level. This is seen in the

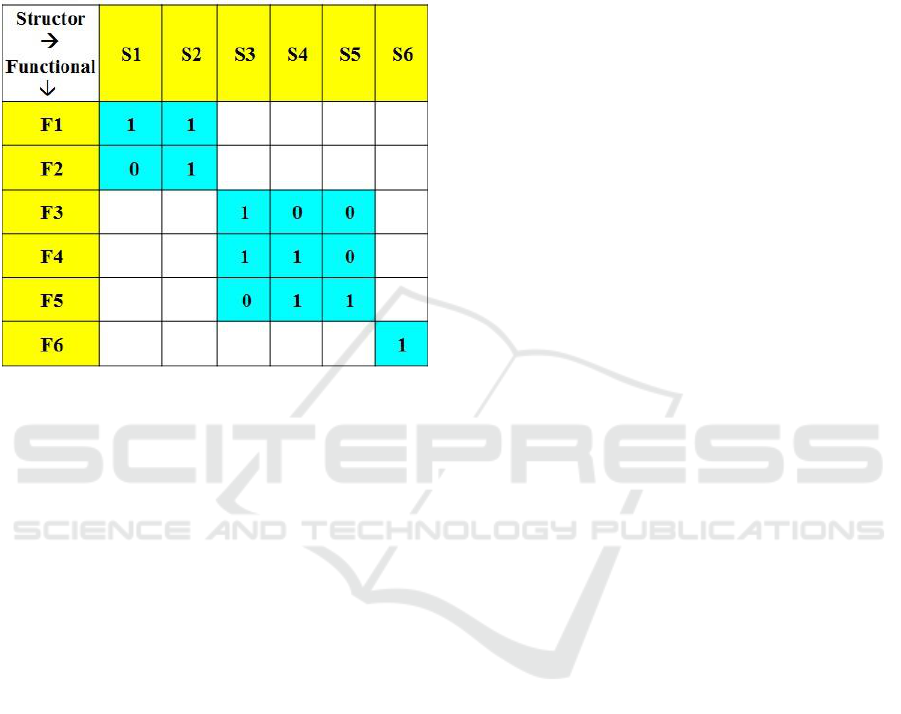
abstract Modularity Matrix displayed in Fig. 1.

Figure 1: An Abstract Standard Modularity Matrix – The

matrix is standard as it is strictly square and block-

diagonal. It has 6 structors (columns) and 6 functionals

(rows). Its 3 modules are the three blocks in the diagonal,

having 1 valued matrix elements (with light blue

background). Outside the modules (blank areas) there are

only zero-valued matrix elements. These values are

omitted for simplicity.

In case there remain some non-zero outlier

matrix elements, i.e. outside the diagonal modules,

these elements point out to undesirable couplings

among the modules. These couplings should be

resolved by moving structors/functionals among

modules or by adding/removing structors and/or

functionals, in the columns/rows containing the

outliers.

1.3 Related Work

In this concise review of the related literature we

mention works referring to Conceptual Integrity.

We also mention tools which support this notion,

particular discussions of orthogonality in this

context and different kinds of matrices used to

analyse software design, besides the Modularity

Matrix.

The origin of Conceptual Integrity ideas, as

already mentioned in the beginning of this

Introduction, is Brooks’ book originally published in

1975, with an extended edition 20 years later

(Brooks, 1995).

Jackson and co-workers have further elaborated

on the Brooks’ notions, say by means of cases

studies, see e.g. (De Rosso and Jackson, 2013).

Jackson also formulated a relevant Research Agenda

(Jackson, 2013). In a recent essay Jackson stresses

the importance of concepts for software systems,

and gives examples of arrangements of concepts in a

dependence graph, from which coherent subsets can

be extracted and analysed. But, these graphs have

not been formalized (Jackson, 2015).

Documents that explicitly refer to Conceptual

Integrity occasionally mention it, and often

formulate some vague statement about what this

means, see e.g. Beynon et al. in (Beynon, 2008).

Kazman and Carriere in page 31 of a Technical

Report (Kazman, 1997) describe the problem of

reconstructing the software architecture of a system.

Their guide to a good and meaningful architecture is

conceptual integrity. It should be built from a small

number of components connected in regular ways,

with consistent allocation of functionality to the

architecture’s components.

Clements et al. in their book (Clements, 2001)

refer to conceptual integrity as the underlying theme

that unifies the design of the system at all levels. The

architecture should do similar things in similar ways,

having a small number of data and control

mechanisms, and patterns throughout the system.

There are two points to be stressed in this statement:

a- they refer to the system at all levels; b- a possible

approach to a more precise definition would be

counting mechanisms and patterns.

The concept of orthogonality also appears

occasionally in the software development literature.

For instance, Krone and Snelting refer to it in a

paper using conceptual lattices inferred from source

code (Krone, 1994).

Another kind of works refers to software tools to

support software systems analysis and design. For

instance, (Kazman, 1996) describes a so-called

SAAMtool, with visualization capability.

Conceptual Integrity is estimated by the number of

primitive patterns that a system uses.

Finally, there are papers dealing with other

matrices, besides the Modularity Matrix, for

software systems design. The DSM (Design

Structure Matrix) is part of the Design Rules

approach (Baldwin and Clark, 2000) and adopted by

many works, appeared and has been applied outside

the software engineering context. For a set of

references to this approach see e.g. (Exman, 2014).

SKY 2016 - 7th International Workshop on Software Knowledge

1.4 Paper Organization

The remaining of the paper describes a formal path

to conceptual integrity (section 2); shows how

conceptual integrity principles follow from the

Modularity Matrix (section 3); characterize

properties of conceptual integrity (section 4); and

conclude with a discussion (section 5).

2 FORMAL PATH TO SOFTWARE

CONCEPTUAL INTEGRITY

We propose a formal path from an Abstract Domain

Conceptualization to Software Conceptual Integrity.

We claim that Conceptual Integrity exists, say in

abstract mathematics, before being formally defined.

We first overview the formal path, leading

through the Modularity Matrix to the main goal of

Software Conceptual Integrity. We then look in

more detail at each of the steps made in this path.

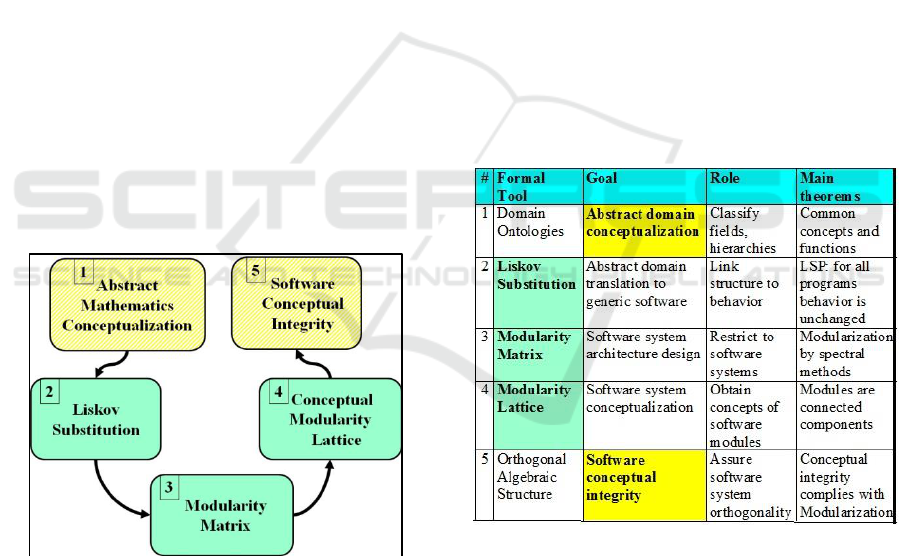
2.1 Overview of the Formal Path

A formal path from Abstract Conceptual Integrity to

Software Conceptual Integrity, passing through the

Modularity Matrix has 5 states with 3 intermediate

states in between. These are shown in Fig. 2.

Figure 2: From An Abstract Domain To Software

Conceptual Integrity – The five states are: the initial state

“Abstract Mathematics”; the goal state “Software

Conceptual Integrity”, and three intermediate states: a-

Liskov Substitution; b- Modularity Matrix; c- Conceptual

Modularity Lattice.

The meaning of the five states in the formal path

is as follows:

1. Abstract Mathematics Conceptualization –

due to its long history, concepts in

Mathematics were classified in fields and

sub-fields, within hierarchies obeying

conceptual integrity;

2. Liskov Substitution – it is an attempt to

translate abstract mathematics notions to

equivalent software notions; the central

idea here is to link “structure” to

“behavior”;

3. Modularity Matrix – the basic algebraic

structure of Linear Software Models, used

to guide software system design; it restricts

whole domains to a modularized class of

software systems;

4. Conceptual Modularity Lattice – this is a

particular case of conceptual lattices

(defined in FCA = Formal Concept

Analysis) derived from the Modularity

Matrix; it obtains the concepts of the

software system modules;

5. Software Conceptual Integrity – the

desired goal of the whole path, will assure

software system orthogonality and

propriety.

One can summarize the above states by their

roles, as shown in Fig. 3.

Figure 3: FORMAL PATH: TOOLS, GOALS, And

ROLES – This summarizes the properties of the Formal

Path states in terms of their formal tools, goals and roles.

See detailed discussion in subsequent subsections. LSP

means Liskov Substitution Principle.

2.2 Preliminary Definitions

Here we provide some preliminary definitions

needed to discuss in detail each of the above states.

Despite starting with an abstract mathematics

domain, the ultimate goal of the formal path refers to

software systems. Therefore, when talking about

The Modularity Matrix as a Source of Software Conceptual Integrity

structure and behavior we think in terms of software.

Here are the relevant definitions.

Definition 1 – Software Structure

Software Structure is a relation among software

architectural units (classes and their

generalization “structors”) involving the

following operators: sub-classing (sometimes

called “inheritance”) and composition.

It is not by chance that we are using the same

operators for software systems and for abstract

ontologies. We are just following common practice,

which emphasizes the analogies between abstract

concepts and their respective software classes.

Definition 2 – Software Behavior

Software Behavior is the performance of the

computation of a function (sometimes called a

method). The result of the function computation

is a change of state of a software system. We call

functions (and their generalization “functionals”)

software architectural units of behavior.

Functionals are provided by structors, but are not

necessarily invoked. Thus we often, by linguistic

license, refer to the functions themselves – without

the performance of a computation – as software

behavior.

2.3 Conceptual Integrity in Abstract

Mathematics

Mathematical concepts are classified by properties’

similarity in a hierarchical fashion. The hierarchy is

determined by which concepts are particular cases of

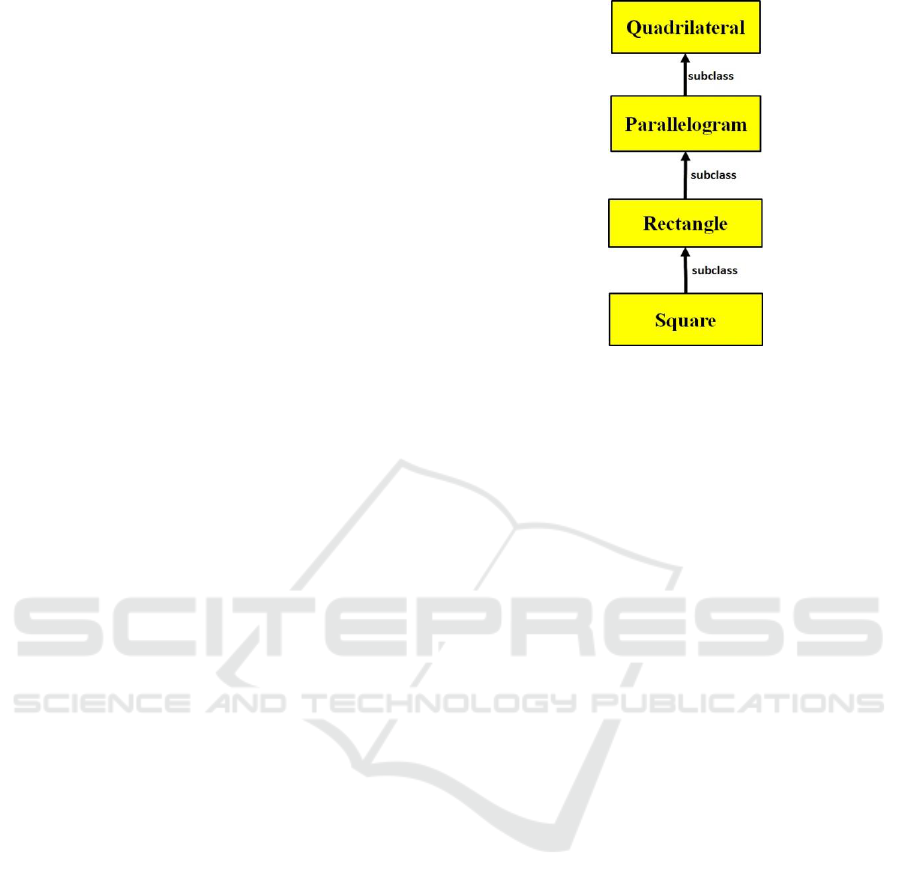
other ones. We clarify the idea with some examples.

A square is a subclass (particular case) of a

rectangle, which is a subclass of a parallelogram,

which in turn is a subclass of a quadrilateral. A

quadrilateral, the most general case in this small

hierarchy (in Fig. 4), is a polygon with four sides. A

parallelogram is a subclass of quadrilateral with

opposite sides parallel. A rectangle is a subclass of a

parallelogram with four right angles. A square is a

subclass of a rectangle with all four sides equal.

Each lower hierarchy class has all the properties

of the upper classes. A square has 4 sides (as the

quadrilateral), which are parallel (as in the

parallelogram), and 4 right angles (as the rectangle).

This is also true with respect of behavior, i.e. the

outcome of what the respective functions calculate

for each concept (or each class). For instance, the

perimeter of any of the classes in this hierarchy is

calculated in general by summing the length of the

four sides (which may be all different, partially

Figure 4: The Quadrilaterals Hierarchy – Each arrow

(meaning subclass or subtype of) points from the

particular class to the more general class. Quadrilateral is

the most general class of this hierarchy and Square is the

most specific class.

different or all equal).

A different hierarchy would have a circle as a

subclass of an ellipse. A third different hierarchy

would deal with 3-dimensional objects such as a

sphere as a subclass of an ellipsoid.

Each of the three referred hierarchies

(quadrilaterals, ellipses, 3-D ellipsoids) display

conceptual integrity, both intuitively and by some

specific well-defined characteristic. For example, all

quadrilaterals in Fig. 4 have linear segments as sides

of a polygon (literally meaning "multiple angles"),

while the ellipses have no linear segments and no

angles in between at all in their perimeters.

These hierarchies, such as that the quadrilaterals

in Fig. 4, are in fact small fragments of an ontology

of geometric figures, e.g. (Rovetto, 2011), which

may encompass the three referred hierarchies.

We summarize conceptual integrity in an abstract

domain such as mathematics by means of the

following theorem:

Theorem 1 – Conceptual Integrity in Abstract

Domain Hierarchy of Concepts

In a class hierarchy determined by sub-classing, in

an abstract domain, all the concepts of the

hierarchy have at least one common concept,

and one common function defined in the

most general member of the hierarchy. The

common concept and the common function

stand for the conceptual integrity.

SKY 2016 - 7th International Workshop on Software Knowledge

2.4 Liskov Substitution

The Liskov Substitution Principle (LSP) attempts to

translate, as precisely as possible, notions found in

Abstract Mathematics, as discussed above (in

subsection 2.3), to the realm of software. This is

possible since the ontology fragments (hierarchies)

in abstract mathematics are built upon the

subclassing operator, while it can be said that LSP is

an effort to define “inheritance” which is the

software term for subclassing.

The basic idea of Liskov Substitution which is

relevant to conceptual integrity is to link “structure”

to “behavior”, effectively transforming concepts in

an abstract (e.g. “mathematics”) domain into generic

software.

A formulation of the Liskov Substitution

Principle (Liskov, 1988) is shown in Fig. 5. A

corresponding class diagram illustrates it in Fig. 6.

The main principle conditions are marked in

bold: a- 'all programs P' assures that the principle

still is generic in terms of software, i.e refers neither

to a specific software system nor to a specific class

of software systems, but is not clear how to test it in

real systems; b- 'behavior of P is unchanged' is

particularly interesting, as a “structural” class

diagram (type T and its subtype S) is being linked to

a “behavioural” condition, which is precisely what

transforms an abstract domain to software concepts!

We summarize conceptual integrity within

Software – according to the Liskov Substitution

Principle – by the following theorem.

Theorem 2 – Conceptual Integrity in Liskov

Substitution

If by the Liskov Substitution Principle, a sub-class

object substitution by a parent class object,

causes no change of behavior of a system,

Conceptual Integrity is preserved, when one

passes from an abstract domain to a whole

domain of software systems.

Figure 5: Liskov Substitution Principle Formulation – The

significant terms of the principle are stressed in bold face:

“all programs P” for generality; “behavior is unchanged”

linking structure to behavior.

Figure 6: Liskov Substitution Principle Class Diagram –

This is a class diagram illustrating Liskov's principle. T is

a class (or type). S is subclass (or subtype) of T. Object o1

is of type S, and object o2 is of type T. This diagram is

analogous to an abstract hierarchy in Fig.4. The arrow-

head is white to conform to the UML convention.

2.5 Modularity Matrix

The Modularity Matrix of a software system is built

using structors (a class generalization) preserving

the notion of sub-classing. Thus, the Modularity

Matrix implicitly conveys the central ideas for which

the Liskov Substitution Principle was formulated.

The important contribution of the Modularity

Matrix, from the viewpoint of the argumentation

along the current Formal Path is to restrict the

complete generality of Liskov Substitution – i.e. for

all programs P, translated to for all software systems

P – into a limited set of software systems defined by

the Modularity Matrix structors and functionals.

This is summarized by the following theorem:

Theorem 3 – Conceptual Integrity in the

Modularity Matrix

If the Modularity Matrix is standard (square and

block-diagonal), then specific structors

provide related functionals within modules,

and the modules conceptual integrity is

preserved for the restricted set of software

systems represented by the Matrix.

2.6 Conceptual Modularity Lattice

The Conceptual Modularity Lattice – the last link

towards Conceptual Integrity – has been shown

(Exman and Speicher, 2015) to be equivalent to the

Modularity Matrix, in terms of information

conveyed about its software system modularity.

On the other hand, by its very definition - from

FCA (Ganter and Wille, 1998) – the Conceptual

Modularity Lattice is an algebraic structure

restricted to the concepts relevant to its software

system.

Summarizing, the role of the Conceptual

Modularity Lattice in our formal path, is by its

The Modularity Matrix as a Source of Software Conceptual Integrity

equivalence to the Modularity Matrix, and the

conceptual relevance, to enable to extract from the

Modularity Matrix the module concepts which may

be tested for Conceptual Integrity.

This is shown by the following theorem.

Theorem 4 – Conceptual Integrity in the

Modularity Lattice

Since the Modularity Lattice is software design

equivalent to its corresponding Modularity

Matrix, the concepts fitting to the Matrix

modules preserve conceptual integrity and

this can be explicitly tested for the restricted

set of software systems represented by the

Modularity Lattice.

3 CONCEPTUAL INTEGRITY

PRINCIPLES FROM THE

MODULARITY MATRIX

In this section we finally assign a formal definition

to two of the principles – referred to in sub-section

1.1 – behind Conceptual Integrity, viz. Orthogona-

lity and Propriety. The proposed definitions are

based on the Modularity Matrix properties.

3.1 Orthogonality

Orthogonality, as already stated (DeRosso and

Jackson, 2013) in section 1.1 is "individual functions

should be independent of one another". Based upon

the Modularity Matrix, this definition has two

associated meanings:

 Linear independence – among structors and

among functionals;

 Strict orthogonality – among modules, which

is also a consequence of linear independence,

is easily visually recognized in the diagonal

blocks of the Modularity Matrix.

So, orthogonality, from the Modularity Matrix, is

totally consistent with the earlier intuitive

formulation.

3.2 Propriety

Propriety reflects the fact that the Modularity Matrix

is the result of optimization of the number of linear

independent structors and their provided functionals.

In other words, linear independence of structors (and

linear independence of the corresponding function-

nals), means that there are no superfluous structors,

just the strictly necessary minimal number.

This is also consistent with the earlier intuitive

formulation, viz. "a system should only have the

functions essential to its purpose and no more".

See the Discussion sub-section 5.2 for

considerations on “Generality”.

4 CONCEPTUAL INTEGRITY

CHARACTERISTICS

In this section we go beyond the definitions based

upon the Modularity Matrix, suggesting additional

conceptual integrity characteristics that could

sharpen the understanding the nature of conceptual

integrity.

4.1 Conceptual Integrity Is Intensive

Here we suggest that conceptual integrity, besides a

property of a whole hierarchical software system, it

should be a recursive property of each of its

subsystems down to basic blocks. It is plausible that

if any subsystem does not have conceptual integrity,

the whole system cannot display it either.

Let us explain what are intensive versus

extensive quantities by an example. Suppose that our

system is a vehicle – a car or a truck. A family car

typically has 4 wheels. A truck may have a bigger

number of wheels.

The weight of a vehicle is an extensive quantity,

since the weight of the system is the sum of the

weights of its components. For instance, additional

wheels increase the weight of the vehicle.

On the other hand, the speed of a vehicle is an

intensive quantity. The speed of the system is not the

sum of the speeds of its components. All the parts of

a car move at the same speed. In particular, the

tangential speed of any of the wheels is the same as

the speed of the vehicle, irrespective of the number

of wheels.

We claim that Conceptual Integrity is an

intensive quantity. It is not the sum of the conceptual

integrities of the components of a system.

4.2 Increasing Conceptual Integrity by

Components Exchange among

Modules

Let us use another physical metaphor as a further

illustration for the idea of Conceptual Integrity being

intensive.

SKY 2016 - 7th International Workshop on Software Knowledge

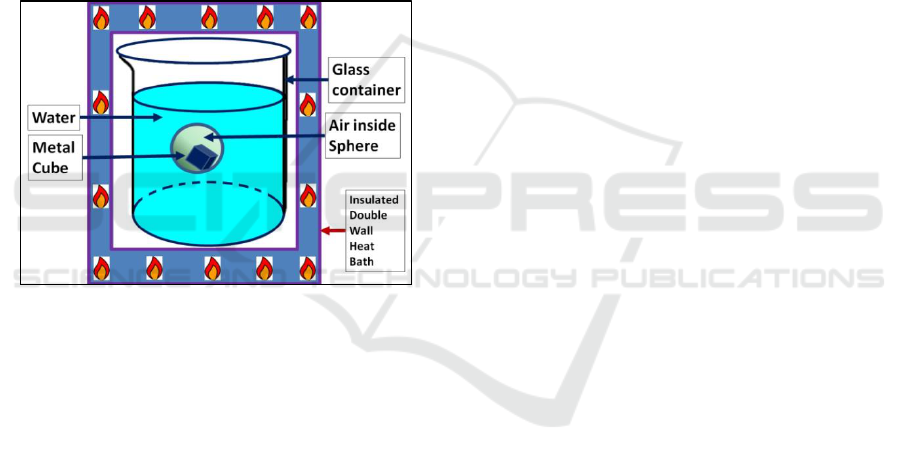
Assume a system composed of 4 sub-systems as

in Fig. 7:

1. glass container;

2. water contained by the glass;

3. sphere mostly filled with air partially

floating in the water;

4. small solid metal cube inside the sphere.

Heating the glass container by an external heat

bath, despite the different thermal conducting

properties of the sub-system materials (glass, water,

air, metal), heat energy will flow between the

different sub-systems from those with higher

temperatures to those with lower temperatures, until

the whole system reaches a uniform temperature.

The metaphor suggests that conceptual integrity

is not an extensive property, like heat energy, but an

intensive property, like temperature.

Figure 7: Physical System Metaphor – The system has 4

sub-systems: a- glass container; b- water inside the glass;

c- floating sphere filled with air; d- metal cube inside the

sphere. A heat bath heats the glass container until the

temperature is uniform, causing heat energy flow among

the sub-systems.

In a software system, each sub-system may have

different computation characteristics – one dealing

with data, another one with business logic, and so

on. But, moving some concepts (classes) from one

sub-system to another may increase conceptual

integrity in both sub-systems. As a consequence, one

could say that Conceptual Integrity in the whole

system is optimized by flow of concepts (classes)

among sub-systems. One should note, however, that

such flow and the hypotheses of conceptual integrity

being intensive, do not imply a single value of

conceptual integrity throughout a whole software

system.

5 DISCUSSION

We summarize the basic claim of this paper, discuss

fundamental issues, consider future work on open

issues and conclude with the main paper

contribution.

5.1 Basic Claim

Conceptual Integrity has been up to now, on one

hand been considered of fundamental importance for

software system design, on the other hand, only has

been vaguely defined.

The basic claim of this paper is that the

Modularity Matrix is a source of a formally defined

Conceptual Integrity. To this end we have provided

two lines of argumentation:

a. Formal Path from Abstract Domains

through the Modularity Matrix to

Conceptual Integrity – We started from the

accepted conceptual integrity of abstract

mathematics, made a transition to generic

software with the help of Liskov

Substitution, whose meanings are conveyed

by the Modularity Matrix to a restricted set

of software systems. Using the equivalence

to the Modularity Conceptual Lattice, we

returned to "conceptual" aspects, to finally

reach Conceptual Integrity.

b. Plausibility supported by the intuitive

Principles behind Conceptual Integrity –

We directly used the Modularity Matrix to

obtain the intuitive principles in a formal

way, viz. orthogonality and propriety.

Both these lines of argumentation deserve further

considerations.

The "formal path" transitions were formulated

into a series of reasonable theorems. But, in order to

have a really formal path, these theorems demand

rigorous demonstrations, or eventual reformulation

of the theorems.

The intuitive principles – at least the two first

ones, viz. orthogonality and propriety – have a very

neat definition by the Modularity Matrix properties.

We suggest inverting the situation: instead of trying

to derive the principles from the Matrix, take the

Modularity Matrix is the actual source of Conceptual

Integrity.

We may summarize the current situation, stating

that some promising progress has been achieved, but

additional investigation is needed to further clarify

the issues, as detailed in the next sub-section.

The Modularity Matrix as a Source of Software Conceptual Integrity

5.2 Fundamental Issues

a- Are hierarchies with conceptual integrity really

independent?

We have referred in sub-section 2.3 to two

independent hierarchies, one of polygons and

another one of ellipses, say a circle. However, one

may think of a circle as a regular polygon in the

limit of an infinite number of sides, enabling a

transition between two of the above hierarchies. One

can easily estimate the value of  in the perimeter of

a circle 2**Radius by taking the limit of the

perimeter of a polygon inscribed in the circle, when

the number of polygon sides goes to infinity.

b- Are conceptual hierarchies stable along time?

The situation is more complex than the naïve

view of Fig. 4 would suggest. One could say that

concepts evolve – see e.g. (Lakatos, 1976) in his

book on "Proofs and Refutations" which discusses

the empirical contribution to the concept evolution

of regular polyhedrons (from the initial five of

Euler). Concepts also can be said to expand along

time – see e.g. (Buzaglo, 2002) according to the

terminology of his book "The Logic of Concept

Expansion".

c- What is the origin of the conceptual integrity of

major software systems?

Brooks in his books has defended the position

that only a single brilliant mind, can provide

conceptual integrity to a major work of art, say an

architect of a cathedral, or similarly to a major

engineering enterprise such as a very large software

system.

Gabriel challenges Brooks' position that a single

mind is the best originator of Conceptual Integrity

(Gabriel, 2007).

In our opinion, Brooks' position is difficult to

rationally prove for real systems. But its main

drawback is that it leaves us depending on the

existence and the opportunistic presence of a single

brilliant mind. We obviously prefer a systematic

construction of formal tools, based upon conceptual

integrity ideas, as proposed in this paper.

d- Are the Liskov Substitution Principle specific

problems detrimental to our argumentation?

We can mention two problems of the Liskov

Substitution Principle. First, how to measure the lack

of change of behavior for all programs P? Second,

the well-known problem of setter functions for

subclasses: for instance, if a 'Square' class has

inherited from the 'Rectangle' class setter functions

(like 'SetWidth' and 'SetHeigth'), independent

application of these functions may distort a Square

object into a Rectangle object. Thus, software

inheritance has subtleties in addition to those within

abstract mathematical sub-typing.

We claim that from the point of view of

conceptual integrity we can ignore these subtle

problems, and our argumentation remains valid.

e- What are the difficulties to formally interpret the

Generality property of Conceptual Integrity?

Generality, has been described as the quality that

"a single function should be usable in many ways" in

the same system. This intuitive formulation seems so

vague that its more formal interpretation is not so

clear-cut.

One possible interpretation could be the

repeated provision of the same functional by two

different structors. This should not be allowed for

the same functional in different modules. But, such

interpretation, besides being obvious in case of

inheritance among classes, is not an interesting

contribution to the overall understanding of

conceptual integrity.

5.3 Future Work

Open issues for future work include, more strictly

formalization and more extensive investigation of

the implications of the formalization, providing case

studies, to exemplify the claims.

5.4 Main Contribution

The main contribution of this work is to propose a

path to a formal definition of Conceptual Integrity,

pointing to the Modularity Matrix as a possible

source of such definition.

REFERENCES

Baldwin, C.Y. and Clark, K.B., Design Rules, Vol. I. The

Power of Modularity, MIT Press, Cambridge, MA,

USA.

Beynon, W.M., Boyatt, R.C. and Chan, Z.E., 2008.

"Intuition in Software Development Revisited", in

Proc. of 20

Annual Psychology of Programming

Interest Group Conference, Lancaster University, UK.

Brooks, F.P., 1995. The Mythical Man-Month – Essays in

Software Engineering – Anniversary Edition,

Addison-Wesley, Boston, MA, USA.

Brooks, F.P., 2010. The Design of Design: Essays from a

Computer Scientist, Addison-Wesley, Boston, MA,

USA.

SKY 2016 - 7th International Workshop on Software Knowledge

Buzaglo, M., 2002. The Logic of Concept Expansion,

Cambridge University Press, Cambridge, UK.

Clements, P., Kazman, R, and Klein, M., 2001. Evaluating

Software Architecture: Methods and Case Studies.

Addison-Wesley, Boston, MA, USA.

DeRosso, S.P. and Jackson, D., 2013. “What’s Wrong

with Git? A Conceptual Design Analysis”, in Proc. of

Onward! Conference, pp. 37-51, ACM. DOI:

http://dx.doi.org/10.1145/2509578.2509584.

Exman, I., 2012a. “Linear Software Models”, Proc. GTSE

SEMAT Workshop on a General Theory of

Software Engineering, KTH Royal Institute of Tech-

nology, Stockholm, Sweden. http://semat.org/wp-con

tent/uploads/2012/10/GTSE_2012_Proceedings.pdf.

Exman, I., 2012b. “Linear Software Models”, video

presentation of paper (Exman, 2012a) at GTSE 2012,

KTH, Stockholm, Sweden, Web site:

http://www.youtube.com/watch?v=EJfzArH8-ls.

Exman, I., 2014. “Linear Software Models: Standard

Modularity Highlights Residual Coupling”, Int.

Journal of Software Engineering and Knowledge

Engineering, Vol. 24, pp. 183-210. DOI:

10.1142/S0218194014500089.

Exman, I. and Speicher, D., 2015. “Linear Software

Models: Equivalence”, in Proc. ICSOFT’2015 Int.

Conference on Software Technology, pp. 109-116,

ScitePress, Portugal. DOI = 10.5220/0005557701090

116

Gabriel, R.P., 2007. "Designed as Designer". In Essay

track, ACM SIGPLAN International Conference on

Object-Oriented Programming, Systems, Languages

and Applications, Montreal, Canada. Web site:

http://dreamsongs.com/DesignedAsDesigner.html.

Ganter, B. and Wille, R., 1998. Formal Concept Analysis:

Mathematical Foundations, Springer-Verlag, Berlin,

Germany.

Ganter, B., Stumme, G. and Wille, R., 2005. Formal

Concept Analysis - Foundations and Applications.

Springer-Verlag, Berlin, Germany.

Jackson, D., 2013. “Conceptual Design of Software: A

Research Agenda”, CSAIL Technical Report, MIT-

CSAIL-TR-2013-020. URL: http://dspace.mit.edu/bit

stream/ handle/1721.1/79826/MIT-CSAIL-TR-2013-

020.pdf?sequence=2

Jackson, D., 2015. "Towards a Theory of Conceptual

Design for Software", in Proc. Onward! 2015 ACM

Int. Symposium on New Ideas, New Paradigms and

Reflections on Programming and Software, pp. 282-

296. DOI: 10.1145/2814228.2814248.

Kazman, R., 1996. “Tool Support for Architecture

Analysis and Design”, in ISAW’96 Proc. 2

Int.

Software Architecture Workshop, pp. 94-97, ACM,

New York, NY, USA. DOI: 10.1145/243327.243618

Kazman, R. and Carriere, S.J., 1997. “Playing Detective:

Reconstructing Software Architecture from Available

Evidence.” Technical Report CMU/SEI-97-TR-010,

Software Engineering Institute, Carnegie Mellon

University, Pittsburgh, PA, USA.

Krone, M. and Snelting, G., 1994. "On the Inference of

Configuration Structures from Source Code, in Proc.

ICSE-16 16

Int. Conf. on Software Engineering.

DOI: 10.1109/ICSE.1994.296765.

Lakatos, I., 1976. Proofs and Refutations: The Logic of

Mathematical Discovery, Cambridge University Press,

Cambridge, UK.

Liskov, B., 1988. "Keynote address - data abstraction and

hierarchy". ACM SIGPLAN Notices. 23 (5): 17–34.

doi:10.1145/62139.62141

Rovetto, R., 2011. "The Shape of Shapes: an Ontological

Exploration", in Proc. SHAPES 1.0 1

Interdiscipli-

nary Workshop on Shapes, Karlsruhe, Germany.

The Modularity Matrix as a Source of Software Conceptual Integrity