Requirements Engineering: More Is Not Necessarily Better

Gonzalo Génova

Departamento de Informática, Universidad Carlos III de Madrid, Leganés, Spain

Keywords: Requirements Engineering, Software Development Process, Software Economics.

Abstract: We show that documenting requirements (and, in general, requirements engineering) is profitable for the

project, but not as profitable as to consider that “the more, the better”.

1 INTRODUCTION:

DOCUMENTING PROJECTS IS

THE “LESSER EVIL”

We often hear among practitioners the statement that

“documenting a project is a necessary evil”, or “the

lesser evil”. What lies behind this statement? To

answer this question, first let's recall something we

already know: the software development process,

including its classical activities (analysis, design,

implementation, testing, etc.), is not a linear process,

but rather a cyclic one.

In particular, it should be revealing to find out

that a project does not end when it is delivered, but

when it is retired. Indeed, if we think that a software

project has no future after delivery, then it is

reasonable to think that documentation is a lesser

evil. An evil you have to pass through in order to

avoid big failures or, in the worst case, to meet

bureaucratically with a standard process. If the

project ends when it is delivered, then it is best to

devote minimal effort to document it, because

documenting is a bad investment without a future.

We think the real benefit of project

documentation (starting with requirements),

considered as an essential part of software

engineering, can be seen only if we focus our look

on software maintenance activities. A good

documentation will make software maintenance not

only possible: it can make it extremely profitable.

Maintenance not only fully justifies the

documentation of projects; maintenance also gives

the right measure of effort that should be devoted

for project documentation to be maximally

profitable.

Documentation is then a must for all the

activities in the software development process, and

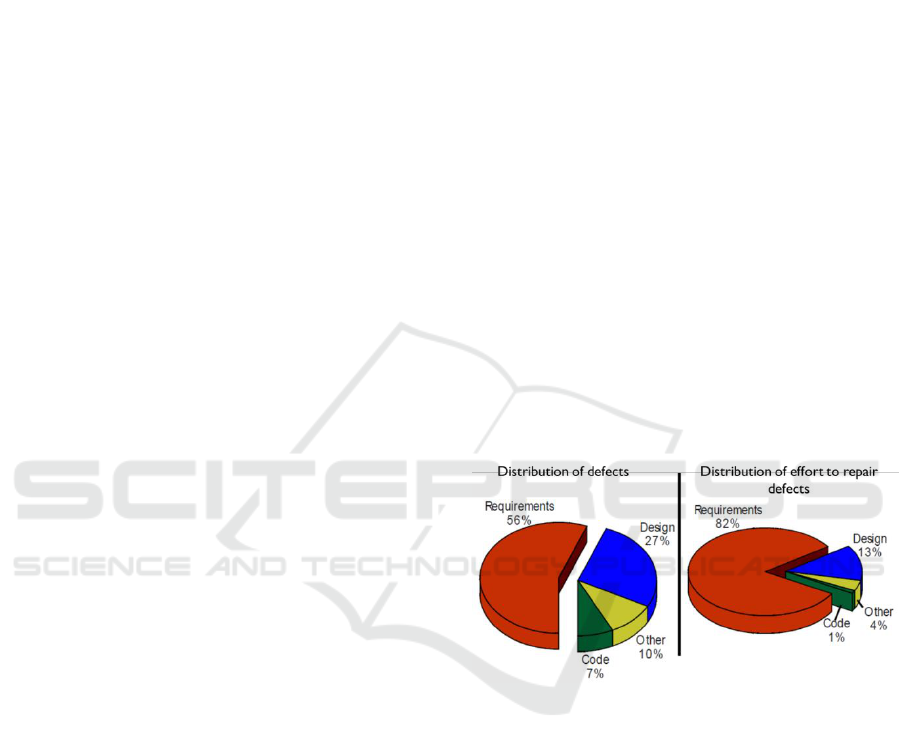
in particular for requirements engineering. A

classical study by James Martin (1984) showed that

more than a half of the defects found in software

projects are attributed to requirements problems and

over 80% of rework effort is spent on requirements

related defects (see Figure 1).

Figure 1: Distribution of defects and efforts to repair

defects in software projects.

But beware: stating that requirements

engineering can be very profitable does not imply

that the more effort is devoted, the bigger benefit

will be obtained.

2 THE BENEFITS OF INVESTING

IN REQUIREMENTS

ENGINEERING

Is it true that the more effort is dedicated to

requirements engineering (RE), the greater the

benefit for a software project?

Génova, G.

Requirements Engineering: More Is Not Necessarily Better.

DOI: 10.5220/0006099200650068

In Proceedings of the 7th Inter national Workshop on Software Knowledge (SKY 2016), pages 65-68

ISBN: 978-989-758-202-8

Let’s try to answer this question in an intuitive

manner. Suppose a retired engineer accomplishes the

RE activities in a given project, for free. What would

the cost of the project be, in terms of the RE effort?

Let’s represent the total cost of the project as a

function of the effort invested in requirements

engineering (see the blue curve in Figure 2).

Figure 2: Project cost as a function of the effort devoted to

requirements engineering, when RE effort is not included.

In general terms, the more effort this generous

engineer gives, the lower the cost of the project,

since it contributes to improve the performance of

other activities. Therefore, it will be a monotonically

decreasing function.

The decreasing rhythm need not be as regular

and smooth as it is depicted in Figure 2. The

function could have “bumps” as in Figure 3,

meaning that certain increments in the amount of RE

effort are not so productive as others.

Figure 3: Project cost as a function of the effort devoted to

requirements engineering, irregular decreasing rhythm.

However, if we consider the extreme cases, we

can assert that:

(a) As we approach zero RE effort, the total cost

of the project increases enormously, tending

to infinity. The situation of zero RE effort is

certainly unrealistic: it means nothing (really

nothing) is done to understand the project

requirements; it is like trying to satisfy the

requirements by pure chance. This situation is

unrealistic, because any feedback received in

a simple process of trial and error is an

elementary form of requirements engineering.

But, anyway, this fiction helps to state that

zero RE effort makes the total cost tend to

infinity.

(b) Obviously, the total cost of the project will

never become zero, no matter how much we

increase the RE effort, because there are

other costs involved. Therefore, we have a

monotonically decreasing function with a

lower bound.

However, it is not generally true that RE is free.

In fact, that would be a very strange case. Because

we cannot take RE effort for free any longer, let’s

represent its cost also graphically. Since the

horizontal axis represents precisely the effort

invested in RE, then the plot is a straight line (see

the green curve in Figure 4).

Figure 4: Cost of Requirements Engineering considered as

directly proportional to RE effort.

If we now add the cost of the project without RE

(the blue curve) to the cost of RE (the green straight

line), we obtain the total cost of the project (see the

red curve in Figure 5). Without a precise

mathematical analysis, it is clear that this is a

function with an absolute minimum.

Figure 5: Project cost as a function of the effort devoted to

requirements engineering, now including RE effort.

That is, the effort invested in RE initially entails

savings in the total cost of the project, but there is a

point beyond which the savings becomes waste:

more effort in requirements engineering does not

reduce the total cost, but increases it!

SKY 2016 - 7th International Workshop on Software Knowledge

Of course, the same rasoning can be applied to

any other activity of software engineering: analysis,

architecture, design, testing... In other words, any

software development process should be kept in the

region of savings through moderate effort in each of

the engineering activities, without actually crossing

the optimum point, so that the benefit of investing

effort in each activity (in particular, requirements

engineering) is perceived. Overexertion, perhaps due

to being too formalistic or exhaustive, comes to

undermine the progress of the project.

3 EMPIRICAL SUPPORT

Our intuition has in fact partial empirical support. In

March 2001 a project was initiated within the

International Council on Systems Engineering

(INCOSE) to collect and analyze data that would

quantify the value of systems engineering (Honour,

2004). Their analysis showed, within the limitations

of their research, that the ratio actual cost / planned

cost was minimal for a 15-20% of systems

engineering effort against the total project effort (see

Figure 6).

Figure 6: Cost performance as a function of systems

engineering (SE) effort (Honour, 2004).

The most usual SE budgets in the projects they

analyzed were around 3-8%, leading to frequent cost

overruns. In this context, recommending 15-20% is

always seen as “the more, the better”. Few projects

spent above 20% of the budget in SE, since that is

not the usual tendency among practitioners. In any

case, the data were enough to establish that the

minimum was below 20% of total project effort.

Summing up, these results do not fully support

our thesis, even though they provide a good

empirical indication that we are right.

4 DISCUSSION OF RELATED

CONCEPTS

4.1 Investment in Prototypes

When seeking an optimal level of effort to be spent

on a prototype, Eric Braude explains that, as the

expenditure on a prototype increases, its usefulness

increases, but so does its drain on the project’s

budget. As a result, there is a point at which the

payoff is optimal, and some point beyond which

funds are being squandered (see Figure 7).

Figure 7: Payoff from building prototypes, adapted from

(Braude, 2001, p. 162).

However, Braude does not give a detailed

explanation of the shape of this curve. Trying to

explain it was the driving force that inspired the

present paper.

4.2 Brooks’ Law

Frederick Brooks states in his famous and influential

The mythical man-month (Brooks, 1975) that adding

more human resources to a project may well delay

the schedule, instead of speeding it up. “The bearing

of a child takes nine months, no matter how many

women are assigned.”

The effect is somewhat similar, More is not

necessarily Better, but the causes are different. In

the case of Brooks’ Law the schedule’s worsening is

mainly due to overhead in communication among

workers and limited divisibility of tasks, both of

which make men and months not to be

interchangeable. In our case the misuse of budget is

due to the fact that benefit increases slower than

effort in the waste region.

4.3 Pareto’s Law

The 80/20 rule is usually stated as “80% of the

benefit is obtained with 20% of the effort”, “80% of

Requirements Engineering: More Is Not Necessarily Better

the effects come from 20% of the causes”, or some

variant of these. The law was first observed by

Italian economist Vilfredo Pareto in the late 19th

century, regarding distribution of wealth. This rule

of thumb has been empirically observed in many

natural phenomena that follow a particular

configuration of the power law distribution

(Newman, 2004).

The function depicted in Figure 2 might follow a

Pareto distribution, but in general we should not

expect a perfect mathematical relationship between

project cost and RE effort.

4.4 Production Functions

In economics, a production function relates the

achievable output of a system to the level of inputs

consumed (Boehm, 1981). A production function is

nondecreasing and nonnegative. Typically (though

not necessarily), a production function will be S-

shaped with three major segments (see Figure 8):

(a) An investment segment, in which inputs

are consumed without a great deal of

resuting output.

(b) A high payoff segment, in which

relatively small incremental inputs result

in relatively large increments in output.

additional inputs produce relatively little

increase in output.

The last segment represents software gold-plating,

i.e. features which make the job bigger and more

expensive, but which turn out to provide little help

to the user or maintainer when put into practice.

Figure 8: A typical production function for software

product features, adapted from (Boehm, 2001, p. 162).

Production functions are closely related to our thesis

that More is not necessarily Better. Only, as we have

argued before when discussing Figure 2, investment

in RE has a strong impact (big slope) just from the

start. As for the third segment, RE can also become

gold-plating: one can always do more RE for a

project, and no doubt it will improve the technical

quality of the product, but the payoff will be

progressively lower.

4.5 Logistic Functions

Production functions are related to the logistic

function (Kingsland, 1995) discovered by Pierre

François Verhulst in the mid-19th century, in

relation to population growth in a context of

competence for resources: the initial stage of growth

is approximately exponential when resources appear

to be unlimited, but then the growth slows as

saturation begins, and finally growth stops when

resources are exhausted.

5 CONCLUSION

As we have seen, our thesis that “more is not

necessarily better” is a well-known property of

economical systems. However, we think it is worth

to recall it because this principle is not so well

known by software engineering practitioners. Both

extremes are bad: the one that does not recognize the

value of requirements engineering, and the other that

wastes resources in being too formalistic or

exhaustive. Unfortunately, the frustrating results of

overexertion could increase the diffidence of

practitioners towards “big theories” in requirements

engineering.

REFERENCES

Boehm, B.W., 1981. Software Engineering Economics.

Prentice-Hall.

Braude, E.J., 2001. Software Engineering. An Object-

Oriented Perspective. John Wiley and Sons.

Brooks, F.P., 1975. The mythical man-month, Essays on

software engineering. Addison-Wesley.

Honour, E.C., 2004. Understanding the Value of Systems

Engineering. INCOSE International Symposium

14(1):1207-1222.

Kingsland, S.E., 1995. Modeling nature: episodes in the

history of population ecology. University of Chicago

Press.

Martin, J., 1984. An Information Systems Manifesto.

Prentice Hall.

Newman, M.E.J., 2005. Power laws, Pareto distributions

and Zipf's law. Contemporary Physics. 46(5):323–351.

SKY 2016 - 7th International Workshop on Software Knowledge