A Backpressure Framework Applied to
Road Traffic Routing for Electric Vehicles
Evangelos D. Spyrou and Dimitrios K. Mitrakos
School of Electrical and Computer Engineering, Aristotle University of Thessaloniki,
Egnatia Odos, Panepistimioupoli, Thessaloniki, Greece
{evang
Keywords:
Electric Vehicles, Routing, Backpressure Weight, Lyapunov.
Abstract:
Electric vehicles (EVs) emerged in the transport domain, due to their energy efficiency and clean energy that
they utilise. The electric vehicle routing problem is essentially a problem of selecting a set of minimum
cost routes, while the demand of the customers is achieved. Route cost metrics include energy consumption
and driving time. In this work, we model the electric vehicle routing problem using a wireless network
methodology, namely the backpressure framework. The penalty imposed to every route includes the driving
time of each road. We derive a weight as a function of the road queue backpressure and the driving time of a
car. The next route for our EV is the one that has the highest weight. It turns out that this methodology leads
to faster routes in that there are often roads with accidents or traffic jams, even though they are in the shortest
path of the route to the destination. We present results via simulations, which verify the fact that backpressure
is an efficient algorithm to be applied to electric vehicle routing.
1 INTRODUCTION
The use of electric vehicles (EVs) into the transport
sector has been introduced (Emadi, 2011) for two rea-
sons. Firstly, there is the need for energy efficiency
in transport, since the charging of the EV is not ex-
pensive as opposed to the internal combustion engine
vehicles. Secondly, there is the reduction of the CO
2
emissions due to the clean sources (battery) employed
for the production of electricity. On the other hand,
traditional vehicles are associated to the combustion
of fossil fuels. Thus, EVs provide a great alternative
as a next generation of the transport means in a city.
The main characteristics of EVs play a key role
on the design of algorithms utilised by route planners.
EV route planning exhibits certain differences from
conventional route planning. Initially, the limited ca-
pacity of the EV’s battery introduces the constraints
of driving ranges of approximately 100 km on aver-
age. Moreover, charging of EVs take place in stations
that do not exist in as many places as gas stations.
EV charging is a process that may take hours to com-
plete. Thus, routes may be determined in an economic
manner rather than just the fastest ot shortest. On the
other hand, there are cases where the state of the bat-
tery does not necessarily decrease when driving. All
of the above sum up to the fact that companies with
EV fleets, require their goods to be delivered on time
in often jammed road networks with potential uncer-
tainties, such as road accidents or road works.
The Vevhicle Routing Problem (VRP) was pro-
posed in (Dantzig and Ramser, 1959). Thereafter,
a plethora of extensions of the problem have been
suggested, which included real world constraints.Two
works that constitute the most widely investigated ex-
tensions are the Capacitated VRP (CVRP), where ve-
hicles have a limited freight capacity and the VRP
with Time Windows (VRPTW), where customers
have to be reached within a specified time interval
(Laporte, 2009) (Nagata et al., 2010). The Electric
Vehicle Routing Problem (EVRP) (Touati-Moungla
and Jost, 2012; Artmeier et al., 2010) has been for-
mulated as a problem of locating a set of minimum
cost routes, in order for the demand of the costumer
to be accomplished. Often, constraints related to the
capacity of the battery of the EV have been investi-
gated.
In this paper we deal with dynamic traffic routing
for electric vehicles. For our approach, we employ
a methodology ustilised in wireless networks, called
the Backpressure routing, which essentially builds the
routing without routes (Moeller et al., 2010). The aim
is to employ infrastructure, such as traffic cameras to
estimate the queues created at each traffic light road.
235
Spyrou E. and Mitrakos D.
A Backpressure Framework Applied to Road Traffic Routing for Electric Vehicles.
DOI: 10.5220/0006224302350240
In Proceedings of the Sixth International Symposium on Business Modeling and Software Design (BMSD 2016), pages 235-240
ISBN: 978-989-758-190-8
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

This will provide the driving time of each street and
we provide a penalty minimisation used in a weight to
be calculated for each road. We provide results based
on simulations to show the efficiency of our approach,
which results in the successful delivery of companies’
goods on a predefined schedule in a single depot. We
show the following:
• EV routing may be modelled with the backpres-
sure framework, which exhibits stable queues and
they are used to construct a weight to select the
next best route
• Road driving time is a metric that may act as a
penalty that is minimised.
• Backpressure application results in fastest routes,
avoiding any sudden road condition changes in a
real-time fashion.
• There are cases that backpressure outperformsDi-
jkstra’s shortest path algorithm in reaching a des-
tination via EV routing.
The paper is structured as follows: Section 2
presents the related work in electric vehicle routing,
section 3 provides a decription of the backpressure
framework utilised, section 4 explains the penalty to
be minimised, section 5 gives the simlations of our
proposed scheme and section 6 gives the conclusions
of our approach.
2 RELATED WORK
In (Afroditi et al., 2014), the authors investigate the
one-to-many vehicle routing and scheduling problem
in EVs. More specifically, problem formulation and
constraints in practical scenarios are examined. They
highlight that the EVRP is an NP-hard problem and
requires significant computational power for the lo-
cation of near optimal solutions in medium to large
scale scenarios. The authors provide a mathemati-
cal formulation to model the EVRP due to its ca-
pacity, time window and predefined charging level
constraints. Furthermore, EVRP trends are examined
providing significant information regarding future re-
search on real world scenarios and approximation al-
gorithms.
In (Bruglieri et al., 2015), the authors aim to find
the optimal route for EVs in a multi-customer sce-
nario considering recharging requirements during the
routes. They formulate routing as a Mixed Integer
Linear Programming problem. The battery recharg-
ing at every station is a variable, since flexible routes
are to be guaranteed. The proposed scheme opti-
mises total travel, waiting and recharging time as well
as the number of the EVs utilised. The problem is
solved using Variable NeighbourhoodSearch Branch-
ing (VNSB) in reasonable computational times.
In (Schneider et al., 2014), the authors intro-
duce the electric vehicle-routing problem with time
windows and recharging stations (E-VRPTW). The
model employs recharging at any of the predeter-
mined stations using a recharging scheme. Further-
more, they consider limited vehicle freight capaci-
ties in conjuction with customer time windows, which
constitute constraints in real-world transport applica-
tions. To solve the aforementioned problem, a hy-
brid heuristic is presented, which combines a variable
neighbourhood search algorithm with a tabu search
heuristic.
In (de Weerdt et al., 2015) the authors propose
an intention-aware routing system (IARS) for elec-
tric vehicles. The system provides the ability to EVs
to estimate a routing policy, which minimises jour-
ney time, while keeping track of other vehicles inten-
tions. Considering other vehicles’ intentions is signif-
icant since the driver may have to charge the vehicle
in the journeyand queueing time may be large, in case
other vehicles select the same stations. Thus, queue-
ing times are predicted based on the intentions of the
other EVs.
In (Abousleiman and Rawashdeh, 2014), the au-
thors attempt to tackle the problem of energy effi-
cient routing for EVs using Particle Swarm Optimi-
sation. They also show that EVs route optimization
techniques, such as negative edge costs, battery power
and capacity limits, as well as vehicle parameters that
are only available at query time, make the task of elec-
tric vehicle routing a challenging problem.
In (Baum et al., 2014) the authors investigate route
planning applicationsfor electric vehicles. They show
that such problems have to consider constraints such
as energy consumption. They indicate that recent ap-
proaches for EV routing focus on optimizing energy
consumption as a single variable. They provide pre-
liminary work towards a holistic framework for com-
puting shortest paths for electric vehicles with lim-
ited range. Their scheme comprises driving energy-
efficient speed adjustments, realistic modeling of bat-
tery charging and the integration of turn costs.
3 BACKPRESSURE
FRAMEWORK
The dynamic nature of the road network combined
with the unwanted but sometimes occuring bottle-
necks, provide the necessary means for the emergence
of a dnamic routing algorithm, where routing deci-
Sixth International Symposium on Business Modeling and Software Design
236

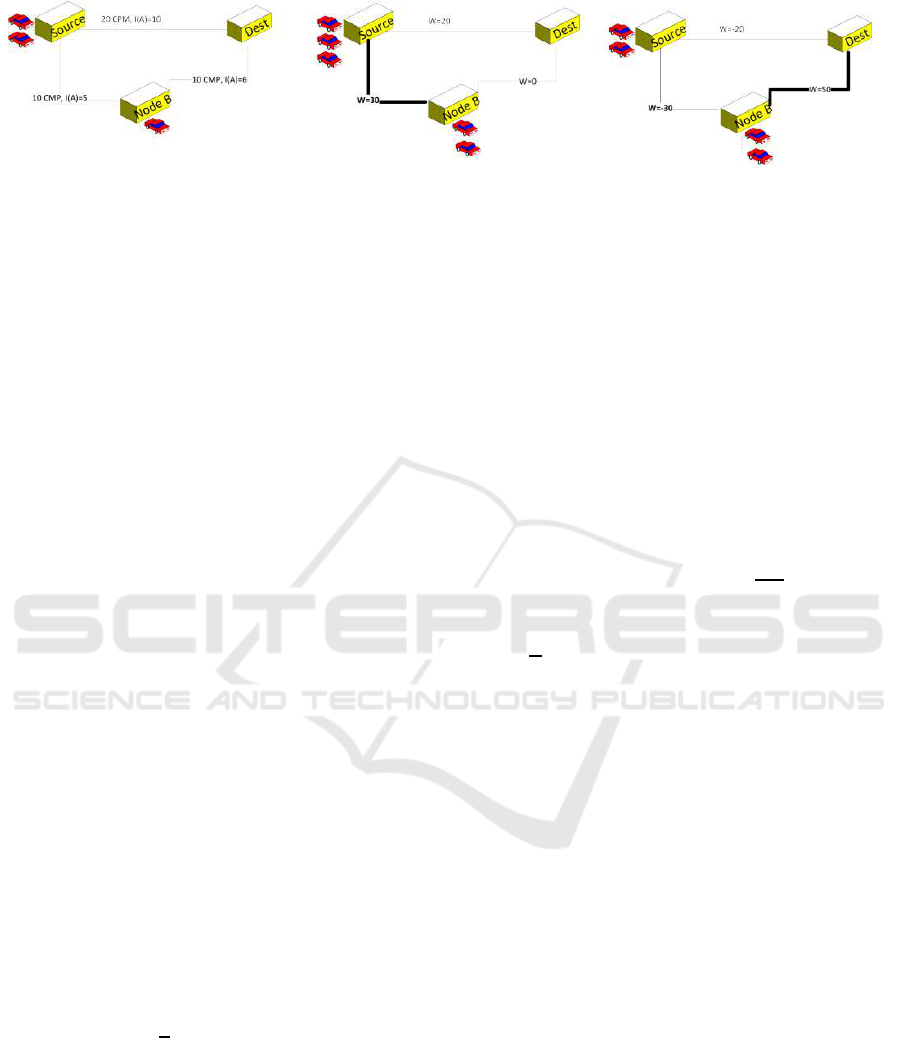
Figure 1: Backpressure operation.
sions will be made dynamically each time a car enters
a road leading to a junction. Hence, it is quite useful
to employ a wireless network routing algorithm that
performs this task, with respect to the road network
conditions. Modern road networks utilise traffic cam-
eras to monitor traffic and to prevent speeding above
the limit. Hence, it is quite reasonable to assume that
they may be used to calculate driving time and num-
ber of cars within a road. Furthermore, with the emer-
gence of the Internet of Things (Kopetz, 2011) and
Cyber-Physical Systems (Baheti and Gill, 2011), it is
clear that infotainment systems in cars maybe con-
nected to devices on junction traffic lights that may
exchange trafic information, resulting thus, to a wire-
less road network. Hence it may be promising to em-
ploy a dynamic routing algorithm in a road network, if
we consider it as a graph-theoretic entity (Bondy and
Murty, 1976) where vertices are considered as junc-
tions and edges as roads.
Backpressure routing does not operate like tradi-
tional routing mechanisms, meaning that it does not
locate an explicit path estimation from any source to
a destination. It performs routing decisions for each
car by calculating for each outgoing road a backpres-
sure weight. This weight is a function of localised
queue and link state information. In figure 1 we ob-
serve the backpressure functionality in a simple road
network. Note that Node B represents an intermediate
routing junction.
We will next provide a definition of a stable net-
work.
We denote the queue at junction i during time slot
t as Q
i
(t). A network of queue backlogs is defined as
strongly stable if:
limsup
t→∞
1
t
t=1
∑
τ=0
E[Q
i
(τ)] < ∞, ∀i (1)
Furthermore, we denote as f(~x(t)) the penalty,
which comes as an outcome of routing decisions be-
tween queues in time slot t. We assume that f is
non-negative,continuous, convexand entry-wise non-
decreasing, meaning, f(~x) ≤ f(~y) when ~x ≤ ~y entry-
wise. Let f (~x) be the penalty value of the function
that works on the average value of the ~x vector. We
formulate the road network as a stochastic optimi-
sation problem in which routing decisions minimise
function f and keeping strongly stable queues simul-
taneously. That is:
minimise: f(~x)
subject to: Strongly Stable
(2)
Assuming that f(~x) is a cost metric of the rout-
ing process, we can derive the solution of equation
(2) using the Utility Optimal Lyapunov Networking
framework (Neely et al., 2008; Neely and Urgaonkar,
2008). This can show that we may have the result
of routing decisions resulting in a backpressure rout-
ing policy. More specifically, each junction computes
the weight per outgoing road in every time-slot. The
weight is given below:
w
i, j
= (∆Q
i, j
− τθ
i, j
)
R
i, j
(3)
where ∆Q
i, j
= Q
i
− Q
j
is the queue backpressure
and Q
i
,Q
j
are the backlogs of junctions i, j respec-
tively,
R is the road car driving rate and θ
i, j
a road
usage penalty that depends upon the particulars of the
utility and penalty functions of (2). The parameter τ
is a constant trades system queue occupancy for min-
imising the penalty. We propose a decentralised ap-
proach where junction i calculates the backpressure
weight of all its neighbouring junctions. Thereafter, it
is used to determine independent routing. For exam-
ple, junction i locates the road (i, j
∗
), which has the
highest value of the backpressure weight as the next
route of the car. We assume, at this point, that the
weight is always larger or equal to 0. In the case that
the weights are equal, we adjusted the algorithm to
select the route with the shortest distance.
4 PENALTY MINIMISATION
The main challenge we are facing is to identify the
most suitable penalty function f(~x) in equation (2), in
order to provide efficient performance when we use it
in a real work road traffic network.
Initially, we give some preliminaries regarding the
road traffic network problem. We model the road net-
work using a directed graph G(V,A), where V rep-
resents the junctions and A represents the roads. As
A Backpressure Framework Applied to Road Traffic Routing for Electric Vehicles
237

we mentioned at a previous section, we assume that
each junction has traffic control cameras, or other de-
vices that may monitor and calculate the rate and driv-
ing time of each vehicle. The graph includes two at-
tributes on each road a ∈ A. The first is an estimate
before hand for its driving time for the solution we
request, and the second is the road performance func-
tion. We use the road performance function that has
been utilised in (Jahn et al., 2005). In particular, the
road performance function, I
α
, maps the traffic rate
x
α
, to its dricing time I
α
(x
α
).
The road performance functions, which will
serve as the penalty functions of (2) determine the
impedance of roads for a variety of congestion lev-
els. We wish our functions to be nondecreasing and
differentiable, as well as I
α
(x
α
) to be convex. In our
experiments we employ the function derived by the
U.S Bureau of Public roads (BUREAU, 1964)
I
α
(x
α
) := I
0
α
1+ α

x
α
c
α

β
!
(4)
where I
0
α
represents the travel time under no con-
gestion, α ≥ 0 and β ≥ 0 are tuning parameters, and
finally, c
α
is the practical capacity (Patriksson, 1994).
We employ the metric (4) to be minimised in the
backpressure framework and we have the following
penalty function in (2):
f(~z) =
∑
i
∑
j∈N
i
z
i, j
(t)
I
α
(5)
where N
i
is the set of neighbouring junctions of
junction i, I
α
is the road performance and z
i, j
(t) is the
number of routed cars over the road i → j. Notably,
f(~z) satisfies the properties of problem (2) and pro-
vides a backpressure weight, calculated by a junction
i to a neighbour j as follows:
w
i, j
= (∆Q
i, j
− τ
I
α
)x
i, j
(6)
5 SIMULATIONS
We produced a road network in MATLAB consisting
of 7 junctions that we assume they are traffic lights
equipped with traffic cameras. Furthermore, we have
10 roads connecting the junctions in a fashion that is
given in figure 2 (a). We also show the distance of the
roads between the junctions. This is since we wish to
compare our algorithm with Dijkstra’s shortest path
algorithm (Dijkstra, 1959).
The parameters that the backpressure algorithm
uses are given in table 1. More specifically, we pro-
vide the times that a car requires to pass from a road
and the queue backpressure for each junction. More-
over, the rate of each road is assumed to be equal,
notably 4 cars per round (traffic light green to red).
Finally, we set the paramater τ = 2. We assume that
there are certain roads that require more time to be
driven even though they are of longer distance, due to
more cars selecting these routes or by an occurance of
accidents.
Table 1: Time and Queue Backpressure per Junction.
Road Time Queues (i,j) Queue Backpressure
A-B 4 15-10 5
A-C 6 12-5 7
A-D 10 13-6 7
B-C 10 10-5 5
B-F 7 10-3 7
C-E 5 5-2 3
C-F 5 5-3 2
F-S 4 3-1 2
E-S 5 2-1 1
D-S 12 6-1 5
Initially, we run the algorithm computing the
shortest path for a car starting from junction A to the
destination S. We observe in figure 2 (b) that the route
computed is A → C → E → S. This can be easily seen
from the distances provides for each road.
Thereafter, we applied the backpressure algo-
rithm, where we see that the route selected by a car
starting from the origin A, in order to reach the desti-
nation S is different from the shortest path algorithm.
In figure 2 (c) we see that the car drives to junctions
A → C → F → S. Furthermore, the driving time of the
route using the backpressure as opposed to the short-
est path algorithm is shorter by 1 minute. We are pos-
itive that in other scenarios the time difference may
be longer.
In figure 3 (a) - (c) we present the steps of the
backpressure algorithm by showing the routes se-
lected by cars in different junctions. Each vertex
includes the letter of the junction and its respective
queue size i.e., A − 14. Furthermore, we provide the
backpressure weight in each edge of the graphs, in
order to make the route selections clear. Finally, we
converted the driving time from minutes to hours to
calculate the backpressure weights. Note that we as-
sume that the incoming cars to junction A = 3 and that
the junctions’ traffic lights work simultaneously,for
the sake of simplicity.
During the first round that the traffic lights become
green we have the following configuration, which ap-
pears in figure 3 (a). As we can see, the backpres-
sure weights that are given in the edges of the figure,
promote the cars to route from A − C, B−C, C − E,
D− S and F − S. Note that the routes to S occur, since
there are no other routes from the respective junctions.
Sixth International Symposium on Business Modeling and Software Design
238

(a) Distances of Road Configuration
(b) Shortest Path Algorithm of Route
Selection
(c) Backpressure Routing Road Selection
Figure 2: Routes of Backpressure, Shortest Path and initial configuration.
(a) Backpressure Round 1
(b) Backpressure Round 2
(c) Backpressure Round 3
Figure 3: Backpressure Routing Rounds.
Furthermore, we assume that cars routed to junction
C from junction A arrive first, since the driving time
of the road is less than than the road originated from
junction B.
In round 2 of the backpressure algorithm in figure
3 (b), we observe that the car that interests us moves
from junction C to junction F, since the backpressure
weight is higher than the one from C to E. Further-
more, the other routing decisions in this round consist
of B− F, A− D and F, E, D to the destination S, since
there are no other routes to select from. Moreover,
we observe that these routes have a weight of 0, since
it is the smallest value our algorithm may accept (the
weight has a negative value in our calculations).
In figure 3 (c), the car that we are routing, reaches
the destination S from junction F. We also see that
other routing decisions include A − C, B −C, C − E
and all the one hop junctions to the destination. Note
that the routing decision for the routing of the cars of
junction C to either F or E has been done using the
shortest path, since both the respective backpressure
weights are 0. The end of this round routes our car
from junction A to the destination S.
6 CONCLUSIONS
In this paper we applied a state-of-the-art routing pro-
tocol for wireless networks to electric vehicle rout-
ing. The backpressure routing is essentially routing
without routes. It calculates the next route of the
car dynamically based on the calculation of the back-
pressure weight and the strong stability of the formed
queues on the junctions. We utilised the driving time
of each road as a penalty to be minimised by every
car. The penalty is selected based on the necessity
of a company’s fleet to reach the clients’ addresses
within a given time window and in a sigle depot.
Our simulations showed that the backpressure al-
gorithm creates faster routes than Dijkstra’s shortest
path algorithm. This may be very useful, since roads
may have several problems such as traffic accidents,
road works or traffic jams, which may prolong their
driving times even if the distance between two junc-
tions is small. Hence the backpressure algorithm es-
tablishes an efficient routing mechanism.
Our future work includes the integration of the
electric vehicle battery to the penalty minimisation
process. This might provide a useful insight as to
the route selection problem, since the fastest route
may not be the most energy-efficient one. It is crucial
A Backpressure Framework Applied to Road Traffic Routing for Electric Vehicles
239

to compare our approach with state-of-the-art routing
potocols for EVs that take into consideration charg-
ing station locations and charging times. The back-
pressure framework provides us with the flexibility to
employ the penatly function of our liking, in order
to produce the backpressure weight. Hence we are
optimistic that it will perform well comparing other
routing schemes. Moreover, our approach is not re-
stricted to EVs only and it may be adjusted to operate
in cnventional vehicle routing as well. Finally, we aim
to put the backpressure algorithm to a more complex
road network, and perhaps to a real test.
REFERENCES
Abousleiman, R. and Rawashdeh, O. (2014). Energy effi-
cient routing for electric vehicles using particle swarm
optimization. Technical report, SAE Technical Paper.
Afroditi, A., Boile, M., Theofanis, S., Sdoukopoulos, E.,
and Margaritis, D. (2014). Electric vehicle routing
problem with industry constraints: trends and insights
for future research. Transportation Research Proce-
dia, 3:452–459.
Artmeier, A., Haselmayr, J., Leucker, M., and Sachen-
bacher, M. (2010). The optimal routing problem in
the context of battery-powered electric vehicles. In
Workshop CROCS at CPAIOR-10, 2nd International
Workshop on Constraint Reasoning and Optimization
for Computational Sustainability.
Baheti, R. and Gill, H. (2011). Cyber-physical systems. The
impact of control technology, 12:161–166.
Baum, M., Dibbelt, J., Gemsa, A., and Wagner, D. (2014).
Towards route planning algorithms for electric vehi-
cles with realistic constraints. Computer Science-
Research and Development, pages 1–5.
Bondy, J. A. and Murty, U. S. R. (1976). Graph theory with
applications, volume 290. Macmillan London.
Bruglieri, M., Pezzella, F., Pisacane, O., and Suraci, S.
(2015). A variable neighborhood search branching
for the electric vehicle routing problem with time
windows. Electronic Notes in Discrete Mathematics,
47:221–228.
BUREAU, O. P. R. (1964). Traffic assignment manual. US
Department of Commerce.
Dantzig, G. B. and Ramser, J. H. (1959). The truck dis-
patching problem. Management science, 6(1):80–91.
de Weerdt, M. M., Stein, S., Gerding, E. H., Robu, V., and
Jennings, N. R. (2015). Intention-aware routing of
electric vehicles.
Dijkstra, E. W. (1959). A note on two problems in connex-
ion with graphs. Numerische mathematik, 1(1):269–
271.
Emadi, A. (2011). Transportation 2.0. Power and Energy
Magazine, IEEE, 9(4):18–29.
Jahn, O., M¨ohring, R. H., Schulz, A. S., and Stier-Moses,
N. E. (2005). System-optimal routing of traffic flows
with user constraints in networks with congestion.
Operations research, 53(4):600–616.
Kopetz, H. (2011). Internet of things. In Real-time systems,
pages 307–323. Springer.
Laporte, G. (2009). Fifty years of vehicle routing. Trans-
portation Science, 43(4):408–416.
Moeller, S., Sridharan, A., Krishnamachari, B., and
Gnawali, O. (2010). Routing without routes: the back-
pressure collection protocol. In Proceedings of the
9th ACM/IEEE International Conference on Informa-
tion Processing in Sensor Networks, pages 279–290.
ACM.
Nagata, Y., Br¨aysy, O., and Dullaert, W. (2010). A penalty-
based edge assembly memetic algorithm for the vehi-
cle routing problem with time windows. Computers
& Operations Research, 37(4):724–737.
Neely, M. J., Modiano, E., and Li, C.-P. (2008). Fair-
ness and optimal stochastic control for heterogeneous
networks. Networking, IEEE/ACM Transactions on,
16(2):396–409.
Neely, M. J. and Urgaonkar, R. (2008). Opportunism, back-
pressure, and stochastic optimization with the wireless
broadcast advantage. In Signals, Systems and Com-
puters, 2008 42nd Asilomar Conference on, pages
2152–2158. IEEE.
Patriksson, P. (1994). The traffic assignment problem: mod-
els and methods.
Schneider, M., Stenger, A., and Goeke, D. (2014). The
electric vehicle-routing problem with time windows
and recharging stations. Transportation Science,
48(4):500–520.
Touati-Moungla, N. and Jost, V. (2012). Combinatorial op-
timization for electric vehicles management. Journal
of Energy and Power Engineering, 6(5).
Sixth International Symposium on Business Modeling and Software Design
240