
Efficiency of the Equivalent Slab Thickness of the Ionosphere to Set
Radio Wave Propagation Conditions
Olga Maltseva and Natalia Mozhaeva
Institute for Physics, Southern Federal University, Stachki, 194, Rostov-on-Don, Russia
mal@ip.rsu.ru
Keywords: GPS, Total electron content TEC, Ionospheric models, Equivalent slab thickness.
Abstract: Now the total electron content ТЕС is a key parameter characterizing conditions of the ionosphere. ТЕС is
widely used for an estimation of positioning accuracy, definition of index of ionospheric storm activity. Data
of TEC is very important for systems of satellite communication and navigation. The advantages of the TEC
measurement are the systems of a large number of receivers, the possibility of continuous global monitoring
of the ionosphere, the availability of data on the Internet. For many systems (HF-communication, HFDF,
HFGINT) it is necessary to know the maximum density of the ionosphere NmF2 or, that is equivalent, a
critical frequency foF2. To obtain NmF2, it is necessary to know the proportionality coefficient
τ=TEC/NmF2, which is the equivalent slab thickness of the ionosphere. Before occurrence of navigational
satellites, no special attention was given to this parameter and there were many inaccuracies in the papers
devoted to τ. The possibility of the global monitoring of NmF2 with use of ТЕС, measured by navigational
satellites, makes to give the more close attention to its study. In the present paper, data of more than 50
ionospheric stations and several global maps of ТЕС are used to investigate behavior of a median τ(med) of
the observational equivalent slab thickness τ(obs). Comparison of τ(med) with the equivalent slab thickness
τ(IRI) of the IRI model, τ(NGM) of the Neustrelitz global model and others has shown essential differences
between these values. Approaches for developing a global model of τ(med) are offered. The most amazing
are following results: (1) for a large amount of stations, the use of observational TEC and τ(IRI) worsens
values of foF2 compared to the initial IRI model, (2) there are no fundamental quantitative differences in the
use of τ(med) for all regions of the world, (3) the IRI model and maps of TEC (in the absence of GPS receivers)
for the most northern Nord station (Greenland) showed surprisingly good agreement with the experimental
values of foF2.
1 INTRODUCTION
The critical frequency of the ionosphere foF2 was the
main parameter determining the state of the
ionosphere and radio wave propagation conditions in
the last century. It is connected with the maximum
density NmF2 of the ionosphere by the relationship
NmF2 = 1.24
10
10xfoF2
2
and with the maximum
usable frequency MUF through the propagation
factor M(D): MUF = M(D)xfoF2. This frequency is
measured by ground ionosondes. In the 21st century,
the total electron content TEC becomes the main
parameter. TEC is measured by means of navigation
satellites in units of TECU = 1
10
16 e/m
2
. The
advantages of the TEC measurement are regional
systems of a large number of receivers, the possibility
of continuous global monitoring of the ionosphere,
the availability of data on the Internet. Naturally,
there was a proposal to use TEC to determine the
maximum density of the ionosphere NmF2 and foF2.
To do this, we need to know the proportionality
coefficient τ=TEC/NmF2, which is the equivalent
slab thickness of the ionosphere. Despite the fact that
the measurement of NmF2 was begun with the
invention of ionosondes (Breit and Tuve, 1926) and
TEC measurements were begun with the first
artificial satellite launch (Aitchison and Weekes,
1959), and the opportunity to use τ to obtain
knowledge of the ionosphere parameters and the
atmosphere was immediately appreciated, interest in
this parameter was increased only with the advent of
satellite navigation systems GPS, GLONASS,
allowing measurement of TEC. Despite the huge
amount of publications, unified picture of the
behavior of the experimental equivalent slab
thickness τ(obs) does not exist because different data
5
Olga M. and Mozhaeva N.
Efficiency of the Equivalent Slab Thickness of the Ionosphere to Set Radio Wave Propagation Conditions.
DOI: 10.5220/0006226600050014
In Proceedings of the Fifth Inter national Conference on Telecommunications and Remote Sensing (ICTRS 2016), pages 5-14
ISBN: 978-989-758-200-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

is used to determine TEC. Distinctions concern both
technical characteristics, and heights of satellites.
Traditionally the International Reference Ionosphere
model IRI (Bilitza, 2001; Bilitza et al., 2014) and its
equivalent slab thickness τ(IRI) are used to calculate
foF2. However, on one hand, τ(IRI) is not an
empirical model in a statistical sense, but, on the other
hand, almost nobody compared values of τ(obs) and
τ(IRI) and suggested the use of experimental median
τ(med) to calculate foF2. In (Maltseva et al. 2011), it
was proposed to use τ(med) together with the
experimental values TEC(obs) and it was shown that
this use allows to obtain foF2 closer to the
experimental value foF2(obs) than by means of
τ(IRI), and to fill gaps of the experimental data of
foF2.
The aim of this article is to estimate: (1) the
features of the behavior of the median equivalent slab
thickness, (2) the effectiveness of its use together with
the total electron content to obtain the critical
frequencies in comparison with the equivalent slab
thickness of current models of the ionosphere, (3) the
opportunity of developing a global model of τ(med).
2 EXPERIMENTAL DATA AND
CALCULATED VALUES
The feature of the current stage of research is the
availability of online databases of experimental data
that allows us to obtain the results on a global scale
(Maltseva, 2015). Data of foF2 of 56 ionosondes of
vertical sounding were used together with 5 global
maps JPL, CODE, UPC, ESA, IGS (Hernandez-
Pajares et al., 2009). The disadvantage of ionospheric
data is their sketchy character however there are
stations for which long-term measurements are
available. Data of foF2 was taken from the databases
SPIDR (http://spidr.ngdc.noaa.gov/spidr/index.jsp) and
DIDBase (http://ulcar.uml.edu/DIDB/). TEC values
were calculated from IONEX files
(ftp://cddis.gsfc.nasa.gov/pub/gps/products/ionex/).
As models, we used IRI2001, IRI2012 (Bilitza, 2001;
Bilitza et al., 2014), which have the upper limit of
2,000 km, and IRI-Plas (Gulyaeva, 2003; Gulyaeva
and Bilitza, 2012) located on the site
http://ftp.izmiran.ru/pub/izmiran/SPIM/ and allowed
determining N(h)-profile up to heights of navigation
satellites h(GPS) by taking into account a
plasmaspheric part of the profile. The magnitude of
the equivalent slab thickness τ is calculated in
accordance with the relationship τ = TEC/NmF2 for
the model and experimental parameters TEC and
NmF2. In this paper, values of τ(IRI) of the IRI model
and the median τ(med) of observational τ(obs) are
calculated and compared. To evaluate the
effectiveness of their use jointly with observational
TEC(obs) we have introduced corresponding
efficiency coefficients. These coefficients are
determined by using the deviations of calculated foF2
from the observational foF2(obs). The value of
|ΔfoF2(IRI)=|foF2(obs) - foF2(IRI)| is the difference
between the instantaneous values of the IRI model
and observational foF2(obs). Monthly averages were
calculated. This difference is in the denominators of
the efficiency coefficients. |ΔfoF2(τ(IRI))|=
|foF2(obs)-foF2(τIRI)| is the difference between the
values calculated using τ(IRI) and TEC(obs) and the
observational foF2(obs). Deviation |ΔfoF2(τ(med))|=
|foF2(obs)-foF2(τmed)| is the difference between
values calculated using τ(med) and TEC(obs) and
foF2(obs). Coefficient KτIRI =| foF2(ΔIRI|) /
|ΔfoF2(τ(IRI))| is the coefficient of efficiency of joint
use of τ(IRI) and TEC(obs). Coefficient
Keff=|ΔfoF2(IRI|)|/|ΔfoF2(τ(med))| is the coefficient
of efficiency of joint use of τ(med) and TEC(obs).
These coefficients are given together with the line K
= 1 to visually evaluate the effectiveness of using
TEC(obs): if the coefficient is 1, this means that the
use of TEC(obs) leads to the same results of foF2, as
the initial IRI model without TEC(obs). In this case
|ΔfoF2(IRI)|=|ΔfoF2(τ(IRI))|. If the coefficient > 1,
then the use of TEC(obs) leads to results better than
the initial model. If the coefficient is higher than 1,
then the use of TEC(obs) worsens the results of the
model. These values determine how strongly the
deviation of the initial model differs from the
deviation of values calculated using τ(IRI) and
τ(med) together with TEC(obs).
3 FEATURES OF τ BEHAVIOR
In the literature, there are certain disagreements in the
describing of such features of τ as: 1) diurnal
variation, 2) seasonal variation, 3) latitudinal
dependence 4) dependence on solar activity, 5)
behavior during disturbed conditions. The most
important disagreement is the absence or weakness of
the latitudinal dependence of τ, noted in many
publications (Kouris et al., 2008; Sardar et al., 2012;
Vryonides et al., 2012). Real situation is given in
Figure 1.
If the latitudinal dependence of τ(med) was
absent, the value of τ(med) for one station could be
used in obtaining foF2 with the observational TEC in
Fifth International Conference on Telecommunications and Remote Sensing
6
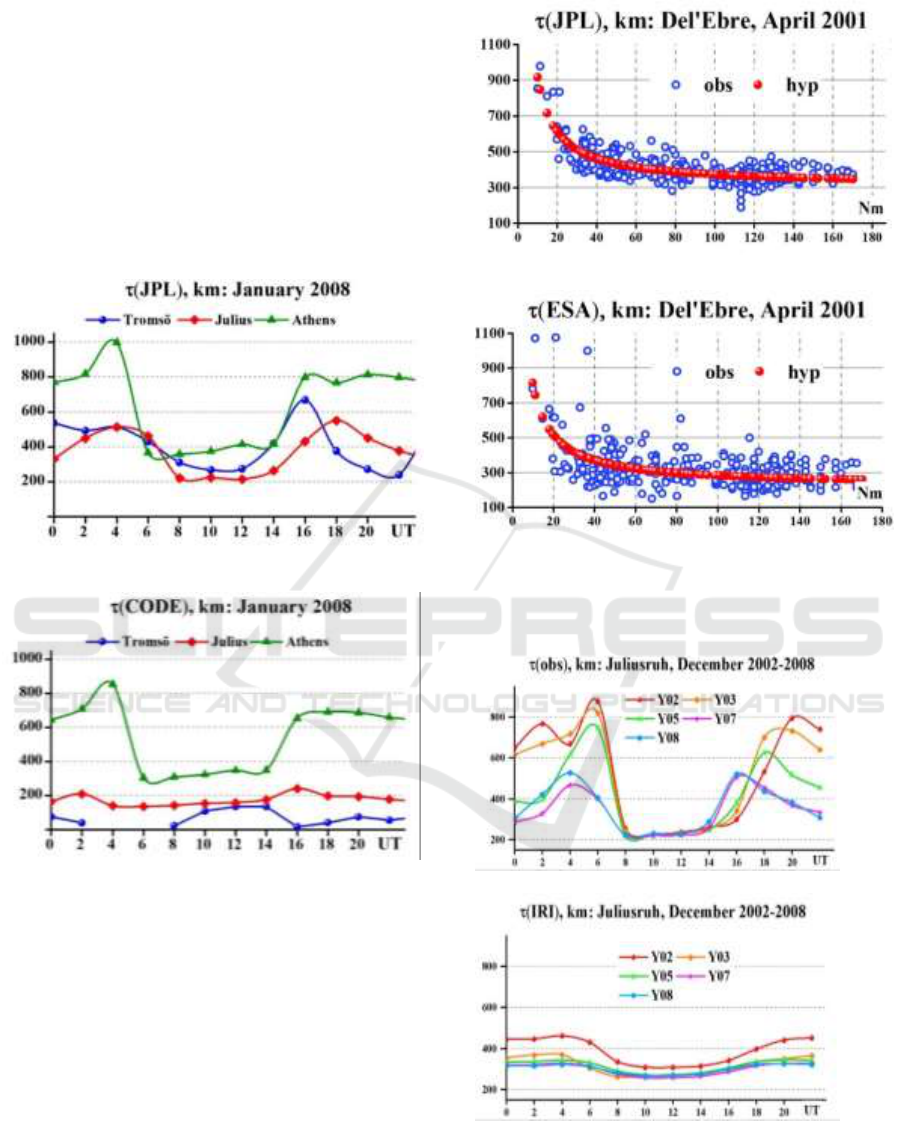
the whole region. Of particular importance is the
study of the behavior of τ(obs) during disturbances
because it is different from the behavior of τ(med). In
paper (Maltseva et al. 2011), a hyperbolic
approximation of τ was introduced as τ(hyp) = b0 +
B1/Nm to build a regression relation in which Nm =
foF2 * foF2 (foF2 in MHz). Such function is
calculated for each map. An example is shown in
Figure 2. Approximation of τ(hyp) was built for a
more accurate determination of τ during the
disturbances.
Figure 1. Example of the diurnal variation of τ(obs) for the
different latitude and two maps JPL and CODE.
The most important is the difference between
τ(IRI) and τ(med). Numerous examples are given in
papers (Maltseva and Mozhaeva, 2014, 2015) for
stations in all regions of the world with long-term
data. Example for the etalon station Juliusruh is
shown in Figure 3.
Large difference is seen not only in magnitude but
also in the diurnal variation. Namely this difference
determines the difference of the critical frequency
foF2(rec) reconstructed from the observational values
TEC(obs) using τ(med) and τ(IRI).
Figure 2: An example of a hyperbolic dependence of τ for
the disturbed month.
Figure 3: Differences of the model and the experimental
equivalent slab thicknesses in the example for the mid-
latitude station Juliusruh of European region and JPL map.
Efficiency of the Equivalent Slab Thickness of the Ionosphere to Set
Radio Wave Propagation Conditions
7

4 EFFICIENCY OF JOINT USING
τ(IRI) AND τ(MED) AND
TEC(OBS)
Figure 4 shows the deviation of the calculated values
of foF2 from foF2(obs) and efficiency coefficients for
stations with long-term observations: high- latitude
Thule, mid-latitude Juliusruh and equatorial
Kwajalein stations of the northern hemisphere and the
high-latitude Mawson station of the southern
hemisphere. Black dots show the results for the IRI
model, triangles present the results of joint using
τ(IRI) and TEC(obs), circles give the results of joint
using τ(med) and TEC(obs).
Figure 4: Deviations |ΔfoF2| and efficiency coefficients for the IRI model and two cases of using τ(IRI) and τ(med) together
with the TEC(obs).
It can be seen that the joint use of τ(IRI) and
TEC(obs) (K<1) can significantly worsen the
calculation of foF2 compared with the model (K <1).
By using τ(med) and TEC(obs) deviations |ΔfoF2| do
Fifth International Conference on Telecommunications and Remote Sensing
8
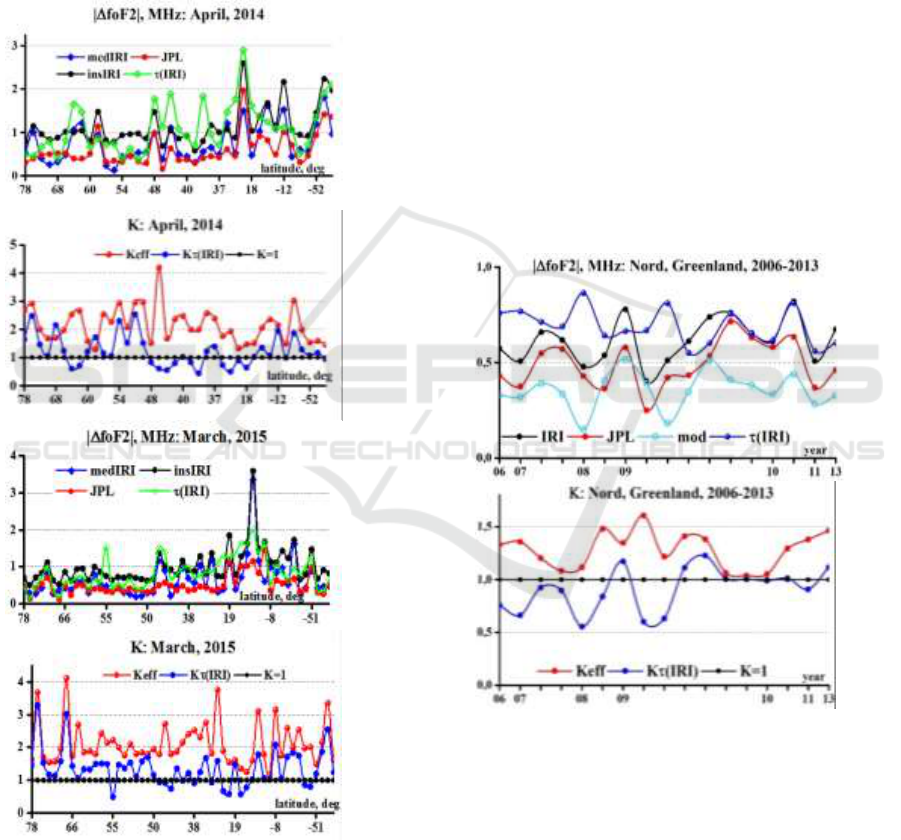
not exceed 1.0 MHz in most cases even in
problematic areas, such as high and equatorial
latitudes, and the coefficients are always exceed 1. In
the previous 2-3 years, a large amount of ionospheric
data has become available. This allows us to check
and compare the results simultaneously on many
stations on a global scale, in particular, to obtain these
results in the points in which they have not been
obtained and the IRI model was not tested itself. We
selected April 2014 and March 2015, because they
included geomagnetic disturbances.
Figure 5: Correspondence between the model and the
observational values of foF2 and efficiency coefficients on
a global scale in April 2014 and March 2015.
Figure 5 illustrates the effectiveness of using
τ(med) globally by example of data for April 2014
(minimum Dst = -81 nT) and March 2015 (minimum
Dst = -223 nT). The samples shown on the x axis are
with a variable step, as stations are located not
uniformly.
It is evident that in the northern hemisphere the
amount of stations is larger than in the southern one.
In all cases, the use of τ(med) and TEC(obs) improves
matching calculated foF2(rec) with foF2(obs)
compared with two options: using the initial IRI
model and joint using τ(IRI) and TEC(obs). Joint
using τ(IRI) and TEC(obs) may provide poor results
compared to the initial model. The best results were
obtained for mid-latitudes. For high latitudes they
were not worse, but in the equatorial latitudes
problems for the model are seen, although the joint
use of τ(med) and TEC(obs) mitigates these
problems. Figure 6 gives the results for the Nord
station (Greenland) which are of particular interest
because it is the most northern station. Unfortunately
data of this station in the DIDbase were downloaded
recently and in a very limited extent (a few months
and not each year).
Figure 6: Long-term statistics for the Nord station
(Greenland) for available months of years indicated on the
x axis.
The results are almost similar to the results for
Thule, Tromso and other lower high-latitudinal
stations. Since the critical frequency of the Nord
station has never been compared with the model the
upper-hand plot of Figure 6 presents the curve
showing the deviation of the model from the
experimental medians of foF2. Results indicate a
surprisingly good performance of the IRI model in
this region.
Efficiency of the Equivalent Slab Thickness of the Ionosphere to Set
Radio Wave Propagation Conditions
9

5 ABOUT THE CONSTRUCTION
OF A GLOBAL MODEL OF
τ(MED)
The mention of the opportunity to construct a model
of τ is practically absent in the papers, but in recent
years some articles were published on the use of TEC
and the ionospheric equivalent slab thickness τ to
determine NmF2, what confirms the importance of
this problem. In (Gerzen et al., 2013), the authors
have proposed the use of two Neustrelitz models of
TEC and NmF2 (Hoque and Jakowski, 2011;
Jakowski et al., 2011) for the calculation of foF2, but
without sufficient testing. We use these models under
one name NGM (from Neustrelitz Global Model). It
is obvious that authors of (Gerzen et al., 2013) have
also used the value of τ(NGM) = TEC(NGM)/NmF2,
which can serve as an empirical model of τ. However,
testing this model in (Maltseva et al., 2013, 2014)
showed that in many regions the value of τ(NGM) is
very different from the experimental τ(med). In
(Muslim et al., 2015), a model of the average values
of τ was proposed as expansion in Fourier series
according to the TEC of the global map CODE and
foF2 for 21 stations, however, the assumptions made
in constructing the model: (1) linear dependence of all
parameters of the TEC, foF2 and τ on solar activity,
(2) lack of longitudinal dependence of these
parameters at the same local time LT, (3) regularity
of τ in quiet and disturbed conditions need
confirmation. This allows drawing a conclusion about
the need to develop the model of τ. To build a model
of τ(med) on a global scale two approaches are
proposed: two-parameter model based on a
hyperbolic approximation τ(hyp) = b0 + b1/NmF2
and the use of the coefficient K(τ)= τ(med)/τ(IRI),
since the construction of the model using the values
themselves is not possible because of the large
variability of values (in particular, the pre-sunrise
peak on some latitudes). A hyperbolic dependence
and approximation coefficient K(τ) were calculated
for March 2015. The results are shown for two
regions 2 (15°E <λ <40°E) with 8 stations and 4
(110°E <λ <170°E) with 9 stations and two wider
zones (Lat1 and Lat2). Area Lat1 includes stations,
located mostly in American continent of northern and
southern hemispheres. Area Lat2 includes stations
from European, Siberian and South-Eastern regions.
Behavior of coefficients b0 and b1 is shown in Figure
7 for these regions.
The test results of this model are shown in
Table_1
Figure 7: Behavior of hyperbolic approximation
coefficients in various regions
Table 1 includes different deviations. Column 1
indicates the station name and the region to which it
belongs. The second column shows the coefficients
of the hyperbolic approximation of τ(obs) for the
corresponding station. The third column specifies
conditions to which the two rows of values belong.
The top line (full) indicates average for all days of the
month, the bottom line (dist) gives average for
disturbed days (from 16 to 21 March). The fourth
column shows the results for the initial IRI model, the
fifth column presents the absolute difference between
the foF2(obs) and the values calculated using τ(med)
and TEC(obs). Column 6 contains the frequency
deviation, calculated using the coefficients b0 and b1
of the hyperbolic approximation for a given station.
The remaining columns give results of using
coefficients of areas referred to in the line title. All of
these values should be compared with the values for
the IRI model in bold. This is a test of the
effectiveness of the model. It can be seen that all
values are higher in disturbed days and the largest
differences concern to the initial IRI model. It is seen
that frequencies of one region could be used to
calculate the coefficients for other region. This
demonstrates a global character of the model of
τ(med).
Another method of constructing a global model of
τ(med) would be to use the coefficients K(τ)=
τ(med)/τ(IRI). Definite advantage of this model
might be in the fact that its denominator is the value
of τ(IRI), which has a global character, and a small
change in K(τ) in areas with close latitudes.
The distinction is development of a model for
each hour. The degree of proximity of τ is better
Fifth International Conference on Telecommunications and Remote Sensing
10

illustrated in the circular diagram. An example of
some diagrams is shown in Figure 8 for region 4 for
UT = 0, 6, 12, and 18 on March 2015. The red line
shows the value of coefficient K(τ), green triangles
are the average values, the blue quadrates concern
circles with radius R = 1.
Table 1: Deviation of frequencies, calculated by the hyperbolic dependence, from the experimental values in March 2015.
1
2
3
4
5
6
7
8
9
10
station
b1, b0
IRI
rec
stat
reg2
reg4
Lat1
Lat2
Juliusruh
3295.5
full
0.73
0.41
0.43
0.68
0.67
1.03
0.57
reg2
273.2
dist
1.44
0.52
0.49
0.67
0.68
1.07
0.64
Athens
5929.3
full
0.91
0.36
0.46
0.56
0.48
0.52
0.58
reg2
253.2
dist
1.31
0.44
0.74
0.52
0.59
0.87
0.51
Grahamstown
3788.7
full
0.80
0.40
0.54
0.77
0.59
0.73
0.73
Lat2
293.2
dist
1.54
0.46
0.62
0.84
0.75
0.82
0.77
Longyearbyen
4947.1
full
0.70
0.43
0.62
0.60
0.58
0.82
0.58
Lat2
244.2
dist
0.69
0.49
0.73
0.69
0.69
1.01
0.63
Thule
692.7
full
0.51
0.14
0.15
0.56
0.42
0.47
0.59
437.6
dist
0.55
0.10
0.13
0.51
0.46
0.64
0.54
Millstonehill
4864.4
full
0.90
0.50
0.47
0.48
0.46
0.67
0.49
Lat1
265.4
dist
1.38
0.67
0.67
0.65
0.81
0.81
0.80
Bejing
5402.8
full
1.17
0.49
0.61
0.61
0.58
0.70
0.62
reg4
263.9
dist
1.99
0.42
0.64
0.45
0.51
0.84
0.45
Kokubunji
6176.7
full
1.29
0.47
0.65
0.61
0.69
0.85
0.62
reg4
228.4
dist
2.11
0.55
0.66
0.56
0.70
0.96
0.56
Niue Island
4874.7
full
1.85
1.15
1.36
1.35
1.28
1.43
1.29
reg4
285.0
dist
1.67
0.71
1.00
0.73
0.85
1.11
0.67
Cocos Island
5467.3
full
1.43
0.55
0.68
0.86
0.62
0.65
0.82
Lat2
267.8
dist
1.66
0.52
0.77
0.88
0.67
0.80
0.83
Mawson
1466.2
full
0.91
0.27
0.37
1.00
0.85
1.02
0.92
Lat2
386.8
dist
1.12
0.12
0.21
0.80
0.98
0.98
0.81
Efficiency of the Equivalent Slab Thickness of the Ionosphere to Set
Radio Wave Propagation Conditions
11

Figure 8: Illustration of charts for the coefficient K(τ).
The model is the average value K(mean). The
algorithm of its use is calculation of the new value
τ(Kτ) = K(mean) x τ(IRI) and the use of this new
value together with TEC(obs) to calculate foF2. To
test the efficiency of the algorithm, averages of
K(mean) were calculated for 7 stations for region
consisted of 8 stations and were used to calculate foF2
for the 8
th
station. Results are presented in Figure 9 as
deviations of the calculated values from observational
foF2(obs) for the four stations: Pruhonice,
Gorkovskaya, Tunguska and Ramey.
Table 2. Average deviations of calculated foF2 from
foF2(obs) using various options of models and τ.
station
IRI-
off
IRI-
on
τ(IRI)
new
τ(med)
Pruhonice
0.63
0.65
0.54
0.34
0.32
Gorkovsk
0.64
0.60
0.43
0.37
0.36
Tunguska
0.95
0.86
0.72
0.57
0.50
Ramey
0.78
0.85
1.36
0.78
0.58
Fifth International Conference on Telecommunications and Remote Sensing
12

All plots contain curves of deviations for the
initial model without the use of TEC. Since both
options (off and on) were used, the curves were
indicated by IRI-off and IRI-on. Curves with the icon
τ(IRI) show results of joint using of τ(IRI) and
TEC(obs).
Figure 9: Deviation of calculated foF2 values from
foF2(obs) using various options of τ.
The curves marked by “new” show test values for
the Kτ model. Asterisks present results for τ(med) and
TEC(obs). Most values of |ΔfoF2| do not exceed 1
MHz. Significant deviations are only visible to the
IRI model in disturbed days on March 18-21 for the
case τ(IRI) and for the Ramey station. Quantitative
characteristics are given in Table. 2.
6 CONCLUSIONS
Data of more than 50 ionospheric stations and several
global maps of ТЕС were used to study behavior of a
median τ(med) of the observational equivalent slab
thickness τ(obs) and comparisons with existing
models τ(IRI), τ(NGM) and others. Essential
differences between them, leading to the large
deviations of the calculated values of foF2 from the
experimental ones are shown. As a quantitative
estimation, the effectiveness coefficients of joint
using TEC(obs) and τ(med) in comparison with joint
using TEC(obs) and τ(IRI) are used. It is shown that
the effectiveness coefficients practically always
exceed 1 for joint using of TEC(obs) and τ(med).
There are several striking results: (1) for a large
amount of stations, the use of observational TEC and
τ(IRI) worsens values of foF2 compared to the initial
IRI model, (2) there are no fundamental quantitative
differences in the use of τ(med) for all regions of the
world, (3) the IRI model and maps of TEC (in the
absence of GPS receivers) for the most northern Nord
station (Greenland) showed surprisingly good
agreement with the experimental values of foF2. In
this sense, results of HF propagation modeling on
high-latitude paths based on the IRI model
(Blagoveshchensky et al., 2016) seem no longer
surprising. Two approaches for developing a global
model of τ(med) are offered.
ACKNOWLEDGEMENTS
The authors thank the scientists who provided data of
SPIDR and DIDBase, global maps of TEC, operation
and modification of the IRI model, Southern Federal
University for financial support (grant N 213.01-
11/2014-22).
REFERENCES
Aitchison, G.J., Weekes, K., 1959. Some deductions of
ionospheric information from the observations of
emissions from satellite 1957α2—I: The theory of the
analysis, J. Atm. Terr. Phys., 14(3–4), 236–243.
doi:10.1016/0021-9169(59)90035-2.
Efficiency of the Equivalent Slab Thickness of the Ionosphere to Set
Radio Wave Propagation Conditions
13

Bilitza, D., 2001. International Reference Ionosphere,
Radio Sci., 36(2), 261-275.
Bilitza, D., Altadill, D., Zhang, Y., Mertens, C., Truhlik, V.,
Richards, P., McKinnell, L.-A., Reinisch, B., 2014.The
International Reference Ionosphere 2012 – a model of
international collaboration, J. Space Weather Space
Clim., 4, A07, 12p. DOI: 10.1051/swsc/2014004.
Blagoveshchensky, D.V., Maltseva, O.A., Anishin, M.M.,
Rogov, D.D., Sergeeva, M.A., 2016. Modeling of HF
propagation at high latitudes on the basis of IRI, Adv.
Space Res., 57, 821–834.
Breit, G., Tuve, M.A., 1926. A test for the existence of the
conducting layer, Phys. Rev., 28, 554-575.
Gerzen, T., Jakowski, N., Wilken, V., Hoque, M.M., 2013.
Reconstruction of F2 layer peak electron density based
on operational vertical total electron content maps, Ann.
Geophys., 31, 1241-1249. doi:10.5194/angeo-31-1241-
2013.
Gulyaeva, T.L., 2003. International standard model of the
Earth’s ionosphere and plasmasphere, Astron. and
Astrophys. Transaction, 22, 639-643.
Gulyaeva, T., Bilitza, D., 2012. Towards ISO Standard
Earth Ionosphere and Plasmasphere Model, In: New
Developments in the Standard Model, (R.J. Larsen ed.).
NOVA, Hauppauge, New York, 1–48.
Hernandez-Pajares, M., Juan, J. M., Orus, R., Garcia-Rigo,
A., Feltens J., Komjathy, A., Schaer, S.C., Krankowski,
A. 2009. The IGS VTEC maps: a reliable source of
ionospheric information since 1998, J. Geod., 83, 263–
275.
Hoque, M.M., Jakowski, N., 2011. A new global empirical
NmF2 model for operational use in radio systems.
Radio Sci., 46, RS6015, 1-13.
Jakowski, N., Hoque M.M., Mayer C., 2011. A new global
TEC model for estimating transionospheric radio wave
propagation errors, J. Geod., 85(12), 965-974.
Kouris, S.S., Polimeris, K.V., Cander, L.R., Ciraolo L.,
2008. Solar and latitude dependence of TEC and SLAB
thickness, J. Atmos. Solar-Terr. Phys., 70, 1351-1365.
Maltseva, O.A., 2015. Usage of the Internet resources for
research of the ionosphere and the determination of
radio-wave propagation conditions. Proceedings of the
Fourth International Conference on
Telecommunications and Remote Sensing, Rhodes,
Greece, 17-18 September, 7-17.
Maltseva, O.A., Mozhaeva, N.S., 2014. Features of
behavior and usage of a total electron content in the
Indian region, International Journal of Engineering
and Innovative Technology,4(4), October 2014, 1-9.
www.ijeit.com, ISSN: 2277-3754.
Maltseva, O.A., Mozhaeva, N.S., 2015. Obtaining
Ionospheric Conditions according to Data of
Navigation Satellites, International Journal of
Antennas and Propagation. 1-16.
http://dx.doi.org/10.1155/2015/804791.
Maltseva, O.A., Mozhaeva, N.S., Glebova, G.M., 2011.
Global maps of TEC and conditions of radio wave
propagation in the Mediterranean area, PIERS
Proceedings, Marrakesh, MOROCCO, March 20-23,
1Р9_0422, 1-5.
Maltseva, O.A., Mozhaeva, N.S., Nikitenko, T.V., 2014.
Validation of the Neustrelitz Global Model according
to the low latitude Adv. Space Res., 54 () 463–472.
Maltseva, O.A., Mozhaeva, N.S., Nikitenko T.V., 2015.
Comparative analysis of two new empirical models IRI-
Plas and NGM (the Neustrelitz Global Model), Adv.
Space Res., 55, 2086–2098.
Maltseva, O., Mozhaeva, N., Vinnik, E., 2013. Validation
of two new empirical ionospheric models IRI-Plas and
NGM describing conditions of radio wave propagation
in space. Proceedings of Second International
Conference on Telecommunications and Remote
Sensing, Noordwijkerhout, The Netherlands, 11-12
July, 109-118.
Muslim, B., Haralambous, H., Oikonomou, Ch.,
Anggarani, S., 2015. Evaluation of a global model of
ionospheric slab thickness for foF2 estimation during
geomagnetic storm. Ann. Geophys., 58(5), A0551.
doi:10.4401/ag-6721.
Sardar, N., Singh, A.K., Nagar, A., Mishra, S.D., Vijay,
S.K., 2012. Study of Latitudinal variation of
Ionospheric parameters - A Detailed report, J. Ind.
Geophys. Union, 16(3), 113-133.
Fifth International Conference on Telecommunications and Remote Sensing
14
