
Bathymetric Mapping of Shallow Rivers with
UAV Hyperspectral Data
Valeria Gentile
1,2
, Marek Mrόz
3
, Marie Spitoni
2
, Jérôme Lejot
4
, Hervé Piégay
2
and Luca Demarchi
5
1
Dept. of Information, Electronics & Telecom. Eng. (DIET), Univ. of Rome “Sapienza”, via Eudossiana 18, Rome, Italy
2
Université de Lyon, UMR 5600 EVS, Ecole Normale Supérieure, Lyon Cedex 07, France
3
Dept. of Photogrammetry & Remote Sensing, Univ. of Warmia and Mazury in Olsztyn, ul. Oczapowskiego, Olsztyn, Poland
4
Université de Lyon, UMR 5600 EVS, Université Lumière Lyon 2, Campus Porte des Alpes, Bron Cedex, France
5
WarsawUniversity of Life Sciences Nowoursynowska 166, 02-787 Warsaw, Poland
valeria.gentile@uniroma1.it, {valeria.gentile, marie.spitoni, herve.piegay}@ens-lyon.fr,
marek.mroz@uwm.edu.pl, jerome.lejot@univ-lyon2.fr, demarchi.luca.ld@gmail.com
Keywords: Bathymetry, High spatial resolution, Hyperspectral images, Fluvial morphology, Remote sensing.
Abstract: Airborne images have long been used to support environmental monitoring due to their synoptic capability
to cover wide areas with high spatial and temporal resolution. The potential for bathymetric mapping by
airborne remote sensing has been addressed and demonstrated in several studies by means of imaging and
non-imaging techniques. In this paper we evaluate the potential to retrieve water depth of shallow river from
high resolution hyperspectral images using an empirical model, applicable under a range of specific field
conditions and in a definite interval of wavelengths.
1 INTRODUCTION
The necessity to preserve water resources and
ecosystems has led to an increasing interest in
monitoring the morphological status of water bodies.
Through a constant data collection on the long term,
it is possible to determine trends in monitored
parameters and to decide suitable strategies in order
to prevent river channel degradation or to restore its
original status.
Remote Sensing (RS) has long been used to
support environmental monitoring of fluvial
environments due to its synoptic capability to cover
wide areas with high spatial and temporal resolution
and to detect features that are not rapidly and easily
evaluable with in situ measurements. Remote
sensing techniques have been also widely applied to
assess bathymetry of water body (Carbonneau, Lane
and Bergeron, 2006, Fonstad and Marcus, 2005,
Lane, Westaway and Murray Hicks, 2003), being the
only effective alternative to measurements collected
by echo sounder mounted on boat, in very shallow
and braided rivers, impossible to be entirely
navigated. Furthermore ground surveys are
extremely time-consuming, require a consistent
deployment of manpower and provide a low spatial
sampling of acquired data despite to their accuracy.
As reviewed by Feurer, Bailly, Puech, Le Coarer
and Viau (2008), besides echo sounder and GPR
(Ground Penetrating Radar), both requiring ground
surveys, three remote sensing approaches exist for
mapping water depth through imaging and non
imaging techniques (Gao, 2009). These are spectral
methods, photogrammetry and bathymetric LIDAR
(Light Detection and Ranging). Spectral methods
exploit the attenuation of electromagnetic wave
through the water interface in order to derive water
depth. Their capability for mapping bathymetry has
been addressed in several studies, using data
acquired in the visible spectrum from UAV
platforms (Lejot et al., 2007, Feurer et al., 2008) or
Airborne Thematic Mapper data simulated from
ground based measurements collected through
spectroradiometer (Gilvear, Hunter ad Higgings
2007) or AISA (Airborne Imaging Spectrometer for
Applications) data (Legleiter, Roberts and
Lawrence, 2009).
43
Gentile V., MrÏ
ˇ
Nz M., Spitoni M., Lejot J., PiÃl’gay H. and Demarchi L.
Bathymetric Mapping of Shallow Rivers with UAV Hyperspectral Data.
DOI: 10.5220/0006227000430049
In Proceedings of the Fifth International Conference on Telecommunications and Remote Sensing (ICTRS 2016), pages 43-49
ISBN: 978-989-758-200-4
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

In our study we evaluate the potential to retrieve
water depth of shallow river from very high
resolution hyperspectral images, using a simple
empirical model, applicable under a range of
specific field conditions. In doing so, we take
advantages first from the capability of UAV
platforms to acquire very high resolution images,
combined with the possibility given by hyperspectral
sensors to investigate the model behaviour over a
wide range of wavelengths in addition to the visible
spectrum.
In our paper we provide a detailed description of
the study site in section 2. In section 3 is explained
the overall process to obtain the final results: the
acquisition campaign with used sensors and platform
is described in subsection 3.1, in subsection 3.2 the
entire processing chain to derive the final
orthomosaics from raw hyperspectral data cubes is
illustrated, in subsection 3.3 the physical model
adopted to derive the relation between the
radiometric pixel value and the water depth is
explained. In subsection 3.4 processing applied to
the final orthomosaics to establish the goodness of
the relation previously described is explained.
Results and conclusion follow in sections 4 and 5
respectively.
2 STUDY SITE
The acquisition campaign was carried out along a
channel reach of the Ain River in the south-east part
of France. The Ain River drains a watershed surface
of about 3700 km² along 200 km. It rises in the Jura
Mountains, then it flows through a steep
mountainous relief, before reaching its Lower Valley
(Liébault and Piégay, 2002). The river in its Lower
Valley flows through 50 km, in alluvial deposits
(Bravard, 1986) where it is free to laterally and
vertically adjust. Its depth ranges between 0 to 5 m
(Lejot et al., 2007). Its hydrology is dominated by
snowmelt mixed with rainfall. The mean annual
discharge is 120 m
3
s
-1
, ranging between 17 m
3
s
-1
to
1600 m
3
s
-1
(1-in-50 year flood) at Pont d’Ain and
Chazey-sur-Ain gauging stations according to the
banque HYDRO (http://www.hydro.eaufrance.fr/). A
chain of 5 main hydroelectric dams were built until
the 70's in its middle V-shape valley section. These
dams have undergone important changes in the
Lower Valley, e.g. reduction of peak flows and
channel narrowing or degradation (Liébault and
Piégay, 2002).
The study site (Figure 1), approximately 700 m
long, between Pont d’Ain and Priay, is located in the
Ain Lower Valley, northeast of the city of Lyon. It
was chosen because of its fairly morphological and
channel stability (paved riverbed and low lateral
mobility). Due to the lack of in situ water depth data
synchronous with imagery data, we used the
simulated hydrological parameters from the
numerical model developed by Paquier, Camenen,
Le Coz and Béraud (2014). This model runs over
ADCP and GPS cross-sectional surveys performed
in 2013 and 2014 (Naudet, Le Coz, Camenen and
Paquier, 2015). Riverbed changes were assumed to
be negligible on the study reach since the last 3
years (the mean absolute error for the modelled 2013
water level elevation is 15 cm).
Figure 1: Orthomosaic at the central wavelength λ=776nm
and geographical location of the study site; in yellow
sampling points of 2D hydraulic model.
3 METHODS
3.1 Data Collection
The study area was imaged twice on 28
th
September
2015 in the interval 12h00-12h54 (CEST) using two
coupled cameras mounted on the UAV md4-1000
quadrocopter (table 1):
digital RGB OLYMPUS EP-2 camera
Fifth International Conference on Telecommunications and Remote Sensing
44
Rikola 2D spectral sensor (Makelainen, Saari,
Hippi, Sarkeala and Soukkamaki, 2013).
The Rikola 2D imaging system is a VNIR sensor
based on the Piezo-Actuated Fabry-Perot
Interferometer (FPI), working in the spectral range
500 nm - 900 nm. This allows the user to select the
central wavelengths of the bands to be recorded by
setting up the appropriate “air gaps” in the
interferometer. The CCD/CMOS matrix consists of
1024x1024 detectors. Each sensing element has the
size of 5.5x5.5 μm. The camera is characterized by
FOV=37°, focal length f=9mm and F-number=2.8.
The ADC (analog-to-digital converter) is operating
in 12 bit mode. The system is equipped with GPS
receiver and hemispherical irradiance sensor. The
described camera model and software version permit
to acquire 16 bands in full-frame mode or 24 bands
in the half-frame mode (1024x648 pixels) for one
“hypercube” (single frame). The user can also
choose one of the two FWHMs (full width at half
maximum): narrow or wide. The precise values of
the FWHM for each band are determined by the
interferometer itself.
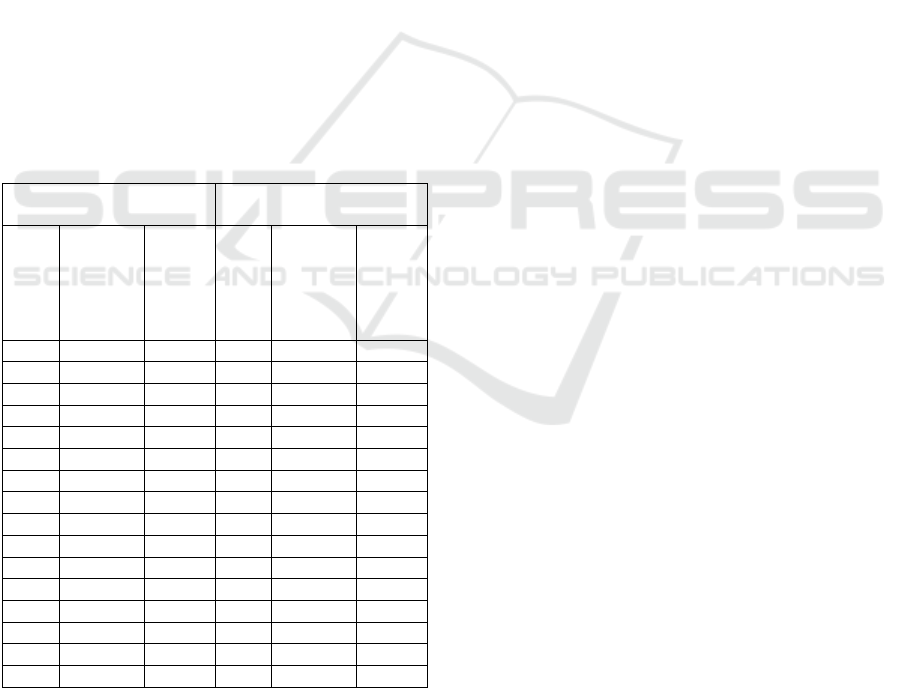
Table 1: Set of spectral bands recorded in the experiment.
First flight – Full frame
mode
Second flight – half frame
mode
Band no.
Central
wavelength
[nm]
FWHM
[nm]
Band no.
Central
wavelength
[nm]
FWHM
[nm]
1
500
15
1
500
13
2
523
20
2
516
13
3
546
19
3
532
11
4
569
18
4
548
10
5
591
18
5
564
11
6
614
19
6
580
13
7
643
13
7
596
15
8
661
19
8
612
14
9
684
17
9
628
18
10
707
18
10
644
13
11
730
18
12
676
13
12
753
17
13
692
11
13
776
18
14
708
11
14
799
17
15
724
12
15
822
19
16
740
12
16
845
18
-
-
-
The pictures were taken at the altitude
MHOG=100 m (mean height over ground) forming
regular blocks of strips with the end lap of 70% and
side lap of 30% for hyperspectral images. The mean
ground resolution of Rikola images was about 6 cm.
The Rikola camera takes the hypercubes with a
constant time interval Δt which was set in our
experiment at 5 s.
For each block of RGB images the overlapping
was bigger (80% and 40% respectively) and the
ground sampling distance (GSD) was about 2 cm.
The number of acquired hypercubes was bigger than
100 for each of two flights, and about 66 of RGB
pictures.
3.2 Data Pre-processing
Acquired RGB images underwent orthorectification
process with Agisoft Photoscan Professional
software. The process consisted of digital
aerotriangulation, image matching, 3D cloud point
and Digital Surface Model generation and the final
ortho-correction. The final RGB orthophotomap had
pixel size 5x5 cm and it was considered as a
background supporting the geometric processing of
acquired hyperspectral data.
The exposition time for Rikola camera is usually
set between 10 and 25 ms depending on sunlight
intensity. In our experiment the exposition was set at
15 ms. Such a value is suitable for taking non-
blurred pictures from moving platform but the
technology of image formation and recording on the
memory card leads to the situation where every band
of the given hypercube has a slightly different
position and external orientation. In these
circumstances there are two alternative ways for
further geometric processing:
to adjust all bands of the hypercube to a
common frame first and to produce in the next
step all spectral orthomosaics in one
photogrammetric run;
to split all bands of each hypercube and to
process all frames taken at the same
wavelength in separated photogrammetric
runs forming a set of independent spectral
mosaics.
We adopted the second way because the
automatic geometric adjustment/matching of the
bands taken in visible and infrared spectrum is very
problematic for the scenes without structural points.
Therefore hyperspectral frames were processed
similarly like RGB photos giving as a result a set of
monochromatic orthophotomaps at the resolution of
10 cm with, unfortunately, slightly different
georeferencing. The last step in geometric
processing was the adjustment of all spectral
orthophotomaps to the common frame by affine
transformation based on RGB orthophotomap.
Bathymetric Mapping of Shallow Rivers with
UAV Hyperspectral Data
45

Prior to the orthorectification at each spectral
band, the radiometric processing needed to be
performed. The first step was the radiometric
calibration of each hypercube to remove the
influence of the black current from measured
signals. The second step was the radiometric
normalization i.e. comparison of the recorded
spectral luminance for each band with the luminance
of the white standardized target. In our case the
Zenith Lite
TM
panel 50x50 cm covered by BaSO4-
based white paint was used. No other atmospheric or
radiometric corrections were applied. Some spectral
bands from second Rikola dataset taken in half-
frame mode were eliminated due to the encountered
errors in pictures recording.
3.3 Bathymetric Model
The spectral radiance observed at the remote sensor
detector L
T
(λ) for any wavelength λ is expressed as
the sum of four components (Legleiter et al., 2009):
L
T
(λ) = L
B
(λ) + L
C
(λ) + L
S
(λ) + L
P
(λ)
(1)
where L
B
(λ) is the radiance reflected from bottom,
L
C
(λ) is the radiance from water column, L
S
(λ) is the
radiance reflected from water surface and L
P
(λ) is
the path radiance from the atmosphere. Under the
conditions of homogeneous water properties,
shallow river, opportune viewing geometry, low
acquisition altitude, favourable atmospheric
conditions, highly reflective and homogeneous
streambed and relatively clear water, we can
consider negligible the radiance components L
C
(λ),
L
S
(λ), L
P
(λ) (Legleiter et al., 2009):
L
T
(λ) ≈ L
B
(λ)
(2)
where L
B
(λ) is (Philpot, 1989, Legleiter et al., 2009):
L
B
(λ)=E
d
(λ)C(λ)T(λ)(R
b
(λ)-R
c
(λ))exp(-k(λ)d)
(3)
E
d
(λ) is the downwelling solar irradiance, C(λ) is
a constant for transmission across air water
interface, T(λ) is the transmittance of atmosphere,
R
b
(λ) is the reflectance of river bottom, R
c
(λ) is the
volume reflectance of water column, k(λ) is an
attenuation coefficient that accounts for absorption
and scattering of light within the water column
(Maritorena, Morel, Gentili, 1994, Legleiter et Al.,
2009), d is the water depth. Solving with respect to
water depth, we obtain:
ln(L
B
)=ln(E
d
CT(R
b
-R
c
))-kd
(4)
where we have not considered the dependence on λ
to simplify the notation. The relation (4) suggests
that under the above-mentioned acquisition
conditions and for certain wavelengths, a relation
between the remotely sensed variable L
B
and the
water depth can be derived and used for mapping
river bathymetry. Replacing L
B
with the
corresponding value of digital number registered by
the sensor and opportunely calibrated, after several
adjustments we can rewrite (4) as a linear relation
between the natural logarithm of pixel values in the
image and the corresponding values of water depth:
d
i,j
= a
0,k
+a
1,k
lnP
i,j,k
(5)
where d
i,j
is the water depth in correspondence of
pixel i,j in the image, a
0,k
and a
1,k
are the coefficients
of linear relation related to k-th spectral band and
P
i,j,k
is the value of pixel i,j at k-th spectral band.
3.4 Data Processing
Before deriving coefficients a
0,k
and a
1,k
of linear
relation (5) for each orthomosaic, through a linear
regression, a median filter with a window of 5x5
was applied to remove residual noise after images
pre-processing.
For each spectral band, the pixel values were
extrapolated from orthomosaics, in correspondence
of the geographical coordinates of bathymetric
values given by the numerical model of Paquier et
al. (2014) applied to the Ain River (Naudet,
Camenen, Le Coz, Paquier and Piégay, 2014). This
2D hydraulic model provides the riverbed elevation,
the water level elevation and the water depth, based
on topographic cross-sections surveyed every 50 m,
increased to every 25 m where the riverbed
geometry rapidly changes.
The coefficients of the linear regression of the
empirical model were calculated with 70% of the
samples randomly extracted from the set of samples
derived in the previous step. The remaining 30% of
samples were used to assess the validity of the
model.
This method was repeated for each orthomosaic
at each spectral band. The goodness of fitting was
assessed by means of the coefficient of
determination calculated on the 70% of samples and
mean absolute error computed on the remaining 30%
of samples.
Fifth International Conference on Telecommunications and Remote Sensing
46

4 RESULTS
In Figures 2, 3, 4 and 5 a subset of results from the
first survey is shown. The sign of linear regression
slope changes from positive to negative values, as
wavelength increases. This behaviour is due to the
weak correlation between water depth values and
pixel values in the relation (5) at shorter
wavelengths, that increases at longer wavelengths
(Red and Near Infrared), when the absorption due to
water column becomes stronger compared to
reflectance. The increasing trend of correlation
versus wavelength is more evident in Figure 6 where
the coefficient of determination R
2
and the mean
absolute error with respect to spectral band are
shown.
Figure 2: Linear regression at λ = 614 nm.
Figure 3: Linear regression at λ = 642 nm.
Figure 4: Linear regression at λ = 730 nm.
Figure 5: Linear regression at λ = 776 nm.
The best correlations are obtained in the spectral
range from 700 nm to 800 nm.
Figure 6: Trend of coefficient of determination and mean
absolute error versus wavelength.
In Figures 7, 8, 9 and 10, a subset of results from
the second survey is shown. In Figure 11 trends of
coefficient of determination and mean absolute error
with respect to spectral band are shown, confirming
Bathymetric Mapping of Shallow Rivers with
UAV Hyperspectral Data
47
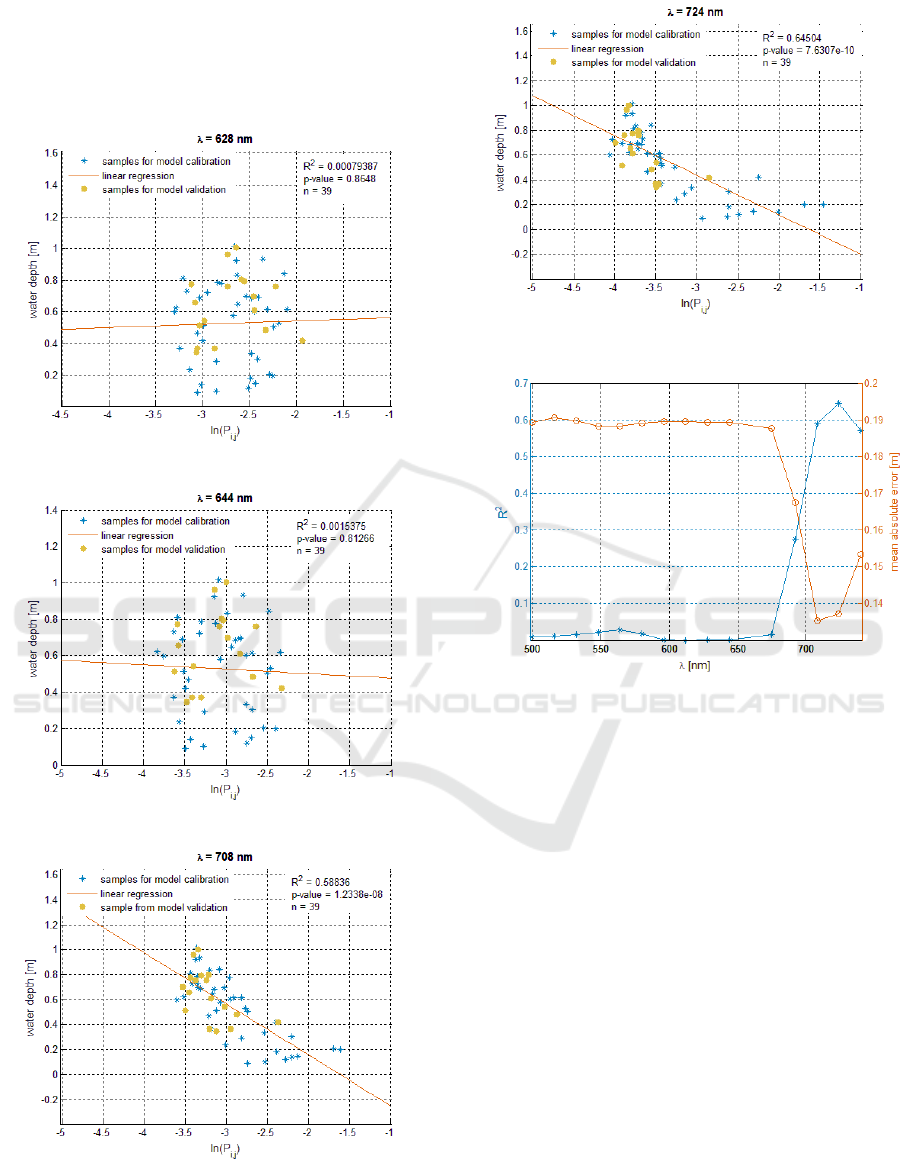
both the best values of correlation in the spectral
range from 700 nm to 750 nm and the increase of
correlation versus wavelength, obtained in the first
survey.
Figure 7: Linear regression at λ = 628 nm.
Figure 8: Linear regression at λ = 644 nm.
Figure 9: Linear regression at λ = 708 nm.
Figure 10: Linear regression at λ = 724 nm.
Figure 11: Trend of coefficient of determination and mean
absolute error versus wavelength.
5 CONCLUSIONS
The results show the potential of UAV hyperspectral
data for bathymetric mapping at centimetre
resolution. The empirical model fits well the water
depth values derived from the hydraulic model in the
spectral range from 700 nm to 800 nm with an
average error less than 0.13 m in the best case when
the water depth ranges from 0.09 m to 1.01 m.
In further studies we intend to apply the
proposed methodology over imagery acquired on
other longer reaches of the Ain River with a wider
range of water depth in order to confirm the model
behaviour with respect to wavelength, to investigate
its applicability over a range of wider environmental
conditions, such as changes in river bottom
morphology and composition, concentration in
suspended sediment, water deepness and finally to
examine obtained results on the basis of sensor
Fifth International Conference on Telecommunications and Remote Sensing
48

configuration and acquisition mode as pixel ground
resolution and bandwidth.
REFERENCES
Bravard, J. P. (1986). La basse vallée de l'Ain: dynamique
fluviale appliquée à l'écologie. Recherches
Interdisciplinaires sur les Ecosystémes de la Basse-
Plaine de l’Ain: Potentialitees Evolutives et Gestion.
Doc. Cartogr. Ecol, 29, 17-43.
Carbonneau, P. E., Lane, S. N., & Bergeron, N. (2006).
Feature based image processing methods applied to
bathymetric measurements from airborne remote
sensing in fluvial environments. Earth Surface
Processes and Landforms, 31(11), 1413-1423.
Feurer, D., Bailly, J. S., Puech, C., Le Coarer, Y., & Viau,
A. (2008). Very-high-resolution mapping of river-
immersed topography by remote sensing. Progress in
Physical Geography, 32(4), 403-419.
Fonstad, M. A., & Marcus, W. A. (2005). Remote sensing
of stream depths with hydraulically assisted
bathymetry (HAB) models. Geomorphology, 72(1),
320-339.
Gao, J. (2009). Bathymetric mapping by means of remote
sensing: methods, accuracy and limitations. Progress
in Physical Geography, 33(1), 103-116.
Gilvear, D., Hunter, P., & Higgins, T. (2007). An
experimental approach to the measurement of the
effects of water depth and substrate on optical and
near infra-red reflectance: A field-based assessment of
the feasibility of mapping submerged instream habitat.
International Journal of Remote Sensing, 28(10),
2241-2256.
Lane, S. N., Westaway, R. M., & Murray Hicks, D.
(2003). Estimation of erosion and deposition volumes
in a large, gravel‐bed, braided river using synoptic
remote sensing. Earth Surface Processes and
Landforms, 28(3), 249-271.
Lejot, J., Delacourt, C., Piégay, H., Fournier, T., Trémélo,
M. L., & Allemand, P. (2007). Very high spatial
resolution imagery for channel bathymetry and
topography from an unmanned mapping controlled
platform. Earth Surface Processes and Landforms,
32(11), 1705-1725.
Legleiter, C. J., Roberts, D. A., & Lawrence, R. L. (2009).
Spectrally based remote sensing of river bathymetry.
Earth Surface Processes and Landforms, 34(8), 1039-
1059.
Liébault, F., & Piégay, H. (2001). Assessment of channel
changes due to long-term bedload supply decrease,
Roubion River, France. Geomorphology, 36(3), 167-
186.
Makelainen, A., Saari, H., Hippi, I., Sarkeala, J., &
Soukkamaki, J. (2013). 2D Hyperspectral frame
imager camera data in photogrammetric mosaicking.
International Archives of the Photogrammetry,
Remote Sensing and Spatial Information Sciences,
263-267
Maritorena, S., Morel, A., & Gentili, B. (1994). Diffuse
reflectance of oceanic shallow waters: Influence of
water depth and bottom albedo. Limnology and
oceanography, 39(7), 1689-1703.
Naudet, G., Camenen, B., Le Coz, J., Paquier, A., &
Piégay, H. (2014, June). Numerical modelling
contribution to sedimentary redynamisation projects in
the Ain River. In Conférence Internationale IsRivers
2015.
Naudet, G., Le Coz, J., Camenen, B., Paquier, A. (2015,
Septembre). Modélisation numérique
hydrosédimentaire 1D et 2D de la basse vallée de
l'Ain. Technical report.
Paquier, A., Camenen, B., Le Coz, J., & Béraud, C.
(2014). Comparison of two models for bed load
sediment transport in rivers.
Philpot, W. D. (1989). Bathymetric mapping with passive
multispectral imagery. Applied optics, 28(8), 1569-
1578.
Bathymetric Mapping of Shallow Rivers with
UAV Hyperspectral Data
49
