
Improved Bacteria Foraging Optimization Algorithm for Solving
Flexible Job-Shop Scheduling Problem
Xingang Wang
1
, Pengfei Yi
2
1
Qilu university of technology, Jinan , China
2
Qilu university of technology, Jinan , China
wxg@spu.edu.cn, yipengfeiok@163.com
Keywords: Bacterial foraging algorithm; Flexible shop scheduling; Bacteria motor step; Stop condition.
Abstract: Bacterial foraging algorithm (BFO) is an emerging algorithm, which has been widely applied in many
fields by researchers . This paper designed an improved adaptive step and stop condition for solving local-
optimal and premature problems, and applied this improved algorithm to the flexible job-shop scheduling
Problem(FJSP). According to the changes of crowding lever between bacteria, step’s evaluation are divided
into three stages. Numerical simulation shows that the improved algorithm has avoided local optimal and
premature problems,and is superior to standard BFOA and genetic algorithm.
1 INTRODUCTION
Flexible job-shop Scheduling Problem (FJSP) is the
extension of JSP. It is a typical NP - hard problem to
optimize the allocation of production resources
(Jingjing Cui, Yanming Sun, Lanxiu Che, 2011). In
addition to take unprocessed process into account,
allows a process to choose on multiple machines
which have the ability to process. FJSP more
complex than JSP in combinatorial optimization
problem and more in line with the actual production
environment, so it has important theoretical
significance and practical value to study FJSP.
In recent years, there are a variety of intelligent
optimization algorithm be used to solve FJSP at
home and abroad, such as simulated annealing, ant
colony optimization and genetic algorithm, Waligora
G. propose the simulated annealing algorithm for
solving multi-objective scheduling problem
(Waligora G., 2014), achieved good effect. Qin Zhao
studied queuing theory in the application of shop
scheduling, and presents a detailed of theoretical
basis(Qin Zhao, Fuqing Zhao, 2013). Hongjun Liu
proposed a kind of new optimization genetic
algorithm
(Hongjun Liu, Shuai Zhao, 2011), blend
the idea of annealing strategy and tabu search into
genetic algorithm, combined with the simulated
annealing mechanism and tabu search mutation
mechanism, it is suitable for solving the workshop
scheduling problem. Moslehi G. Proposed improved
particle swarm optimization algorithm to solve
multi-objective characteristic on flexible job shop
scheduling problem (Moslehi G., Mahnam M.,
2011). The algorithm through fitness function to
judge the individual or group’s location weather is
the best, Bacteria foraging process can be described
as three processes: tendency, replication and
migration.
In this paper, based on original algorithm,
through analyzing foraging behavior of individuals
and populations, improved movement step and the
iteration stop condition, effectively improve
convergence rate and accuracy. Through compare
with the original algorithm, the progressive of the
algorithm be verified.
2 FLEXIBLE JOB SHOP
SCHEDULING
Suppose processing workshop with W artifacts and
M machines, each artifact contains one or more
processes, each working procedure can be performed
on one or more machine, the processing times on
each machine can be predetermined. Express
ij
p
as
the ith procedure of
artifact
i
W
, M
P
ij
said optional
machine set of process
ij
p
.
FJSP problem can be
simplified into two sub problems which are machine
63
Wang X. and Yi P.
Improved Bacteria Foraging Optimization Algorithm for Solving Flexible Job-Shop Scheduling Problem.
DOI: 10.5220/0006443800630067
In ISME 2016 - Information Science and Management Engineering IV (ISME 2016), pages 63-67
ISBN: 978-989-758-208-0
Copyright
c
2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
63

allocation and process order (Xiuli Wu, Zhiqiang
Zhang and Yanhua Du, 2015): Machine allocation
problem point that the process choose qualified
processing machine basis on the optimization goal;
Process scheduling problem refers to every process
allocated on each machine in what order processing.
In flexible manufacturing, there are many types of
the optimization goal, Tasks, for example, the
maximum completion time, the total load of the
machine and the total processing cost, it is unlikely
to achieve the optimal state of multiple targets at the
same time, the utmost pursuit of most businesses is
efficiency, namely, efficiently complete the general
assignment in the shortest possible time. This paper
set the maximum completion time as the
optimization goal. The objectives function as
follows:
))
c
(max(min
c
min
ijmax
= (1)
c
max
refers to the maximum completion time of
scheduling task,
c
ij
refers to completion time of
Process
o
ij
. In addition, during processing need
meeting some assumptions, as follows
:
0)1
y
)(
2
y
(
xx
)
p
cc
(
)1
y
)(
2
y
(
xx
)
p
cc
(
hgij
hgij
ijkhgk
hgk
ijhg
hgij
hgij
ijkhgk
ijk
hgij
≥+−−
+−−−
(2)
Formula 2 means there are two artifacts are not
processing on the same machine. Among them,
p
ijk
refers to the processing time of process
o
ij
on
machine k,
x
ijk
refers to the decision variable of the
machine allocation,
y
hgij
refers to the decision
variable of the order on process. Formula (4)
qualified procedure can only be completed in one
machine; (5), (6) limit the scope of the decision
variables.
⎪
⎩
⎪
⎨
⎧
=
elsewhere
machineonduneis
,0
k
o
if,1
x
ij
ijk
(3)
⎪
⎪
⎩
⎪
⎪
⎨
⎧
−=
otherwhere
adjacentandbehind
adjacentandbefore
,0
oo
,1
oo
,1
y
ijhg
ijhg
hgij
(4)
∑
∀∈= j,i,
s
k,1
x
ijijk
(5)
}{ 1,0
x
ijk
∈
(6)
}{ 1,0,1
y
hgij
−
∈
(7)
3 IMPROVED BACTERIAL
FORAGING ALGORITHM
3.1 Bacterial Foraging Optimization
Algorithm
BFOA abstracts from the biological foraging
behavior of bacterial. The foraging process was
described as three operation process, including
tendency, replication and migration. The optimal
performance is largely decided by numerous
parameters, such as bacteria population size, bacteria
movement step, tendency operations, the maximum
times of copy and transfer operation. Due to these
parameters have no adaptability, Its iterative times is
completely determined by the maximum times of
various operation, and no convergence criterion are
introduced, so it is difficult to ensure accuracy and
adding unnecessary iterative process. In this paper,
The improvement point on two aspect, there are
bacteria movement step and stop condition (Dalian
Yang, Xuejun Li and Lingli Jiang, 2012).
1)
Tendency operations: Mainly simulate the
motor processes, including move forward and move
towards. Assuming that flora size is S, With D
vector
),...,,(
pppp
i
n
ii
i 21
= represent the ith a
bacteria,
),,( lkjp
i
said the chemotactic operations
of bacteria i in the jth. The position after the kth
times copy operation and the ith times migration
operation means that a candidate solution of bacteria
i in the search space. The location updating formula
of the bacteria i after chemotactic operations as
follows:
)()()()( jicl,k,jpl,k,1jp
ii
ϕ+=+ (8)
Among them:
)(ic represent chemotaxis step length
of bacterial i ;
)( j
ϕ
represent a random direction
vector after bacteria i overturn
,
21T
iiij
/
)]()()/[()( θθθ=ϕ .
2)
Replication operations: Bacteria will be
divided after completed the sated tropism times, this
operation is mainly simulates the breeding process
of bacteria individual evolution.
Assumes that the
size of bacterial population is N,
),,( lkjF
i
as the
ith individual fitness value, first, for the fitness of
the whole population in descending order, The first
2N individuals will be survived which order by
ISME 2016 - Information Science and Management Engineering IV
64
ISME 2016 - International Conference on Information System and Management Engineering
64

fitness value, And make no difference to split in two,
the lower
2N individuals are eliminated, when
completed such a copy operation, the bacteria
population will remain the same size.
3)
Migratory operation: In order to improve
the global search ability of the algorithm, When a
problem's solution space have multiple extremum
points, its sociality make it easy to trap in local
extremum, the purpose of this process is to make the
new individual to replace the original individual,
Different from the copy operation, the occurrence of
migration is according to certain probability p,
When some bacteria can meet the conditions of the
migration, it will be randomly assigned to the
solution space.
3.2 Improved Bacteria Movement Step
Traditional algorithm using fixed chemotactic step
length, but BFOA is a dynamic process. The bacteria
activity will have a certain percentage of the decline
with each tendency operation. The greater step size
is, the more likely miss the optimal solution, it will
soon fall into local optimum. With the increase of
number of chemotactic, step length should make
appropriate adjustments, to maintain the searching
efficiency of the algorithm.
Through studying found that step length affected
by the number of nearby companions, namely
crowding level of population,
the more crowded the
higher demand for food, food consumption faster,
just search for this position, the individual fitness
may increase, but as more and more individual
learning to this position, the individual fitness
declines quickly, which requires quick to flee the
area, sat with adaptive step length to control the
residence time of an area, continue to look for a
better position. For above, this paper presents an
improved bacteria movement step for this problem.
congestion level of the region which Bacteria i in,
determined by the individual number and interval
length in this region,
lenncrowd = ;
t
j
Δ said the
difference of the fitness value between
)(
)(
lkj
ics
,,
and
)1(
)(
lkj
ics
,,
−
, represent the fitness
value of the bacteria i after the ith tendency
operation, the kth copy operation, the lth replication
operations.
)()(
)()(
l,k,jl,k,1j
j
icsics
t
−=Δ
−
(9)
Step length have three changes, the early stage of the
search in global optimization , Few bacteria around,
that within a certain range inadequate nutrition, sets
the chemotactic compensation to a larger value, be
helpful for global optimization, when looking for the
crowded degree of large scope, into local
optimization, set small step length, so as not to miss
the optimum solution, when the congestion is too
large and the growth rate of individual fitness
gradually smaller, step length will gradually increase,
so as not to fall into local optimization.
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
Δ<Δ∂>−
−
−
−
∂<
∂>
=
−
tt
crowd,
SS
1N
1N
S
crowd,
S
crowd,
S
iS
j1jminmax
i
max
min
max
且 ) (
)(
)(
(10)
Among them,
i
N represent the tendency times
have been executed in current, N represent total
times,
S
max
represent the maximum step length,
S
min
represent minimum step length. ∂ is the preset
threshold.
3.3 Improved Termination Condition
Appropriate termination condition can ensure to
obtain optimization results with reasonable accuracy,
and, reduce unnecessary computation. BFOA is
actually a process with constant iterations and
convergence, its goal is to improve convergence
speed and computational precision (J Q Li, Q K Pan
and K Z Gao, 2012). In practical applications, it is
unknown about the optimal solution. we can’t
determine whether to stop the iteration by judging
the magnitude of the error between current solution
and real solution, through above mentioned
analyzing, Population movement step can is the
basis of iterative stop. The step size smaller, the
bunching of bacteria more concentrated. The
iteration will stop until the following expression was
founded (ε is a smaller number) :
εMlkj(FlkjF
2
<
−
))],,min(()),,([max(( (11)
3.4 Algorithm Implementation Steps
The execution steps of the IBFO to solve the optimal
value as follows:
Step 1: Initialize parameter.
Step 2: Initialize bacteria position. Generate initial
solution randomly in the feasible region, The
according to formula (2) and (3) calculate individual
adaptive value. Always keep the ethnicity in a
reasonable range.
Step 3: Perform tendency operation. According to
the formula (3), (4), (5) adaptively adjust tendency
step. When the adaptive value rise, keep moving
direction. When adaptive value falls, rotate to select
Improved Bacteria Foraging Optimization Algorithm for Solving Flexible Job-Shop Scheduling Problem
65
Improved Bacteria Foraging Optimization Algorithm for Solving Flexible Job-Shop Scheduling Problem
65
new direction. If reach to the upper limit of tendency
operation, then step out the tendency, and perform
step 5.
Step 4: Perform replication operation.
Step 5: Perform tendency operation.
Step 6: Whether algorithm meet the convergence
conditions. If convergence, output the run results
and terminates the running process; otherwise, return
to step 3.
4 APPLICATION OF
EXPERIMENT
4.1 Experimental Environment
All experiments were paper processor for Intel (R)
Core (TM) i5-34700 CPU @ 3.20GHz, 4.00GB
RAM, Windows 7 systems under the.
4.2 Computational Results
To BFO algorithm, The most important impact of
the efficiency is the times of tendency, the more
times, the optimization ability in local is more subtle.
At the same time, with increasing complexity,
followed by the size of the bacteria, the more
bacteria involved in foraging individuals, the faster
to find the optimal solution, but the computational
cost will increase; Again is the influence of
migration dispel, this factor determines the global
search ability of the algorithm, it is easy to fall into
local optimization if the times is too small, therefore,
too many will increase the complexity of the
algorithm(Shiv P, Deo PV., 2014).Through
integrated balance, through many experiments to
obtain the optimal experimental parameters: Flora
scale
S = 100, Maximum Iterations N
iter
=
200,tendency times N
c
=50, maximum swimming
times
N
s
= 10,copy times N
re
= 10, migration times
N
ed
= 15.
Choose two instances make simulation
experiment: The 8 x 8 is part of the flexible
scheduling problem (P-FJSP), 10 x 10 is fully
flexible scheduling problem (T-FJSP)(Bagheri A.,
Zandieh M. and Mahdavi I.,2010).Compared IBFO
algorithm with standard BFO algorithm and the
improved genetic algorithm (IGA). Three algorithms
run 10 times respectively, the running results are
shown in table 2 and table 3.
Table 1 8 × 8 results by comparison
Algorithm Optimal Average
standard
deviation
BFO 17 19.0 2.31
IGA 13 16.1 1.23
IBFO 13 14.8 0.80
Table 2 10 ×10 results by comparison
Algorithm Optimal Average
standard
deviation
BFO 9 11.2 1.88
IGA 8 7.9 1.02
IBFO 8 7.4 0.71
Moreover, The experiment choose MK01
experiment(Brandimarte Paolo, 1993) to verified
which involved in Benchmark examples, 6 machine,
10 artifacts. In the number of 200 iterations the
experimental analysis was carried out on the three
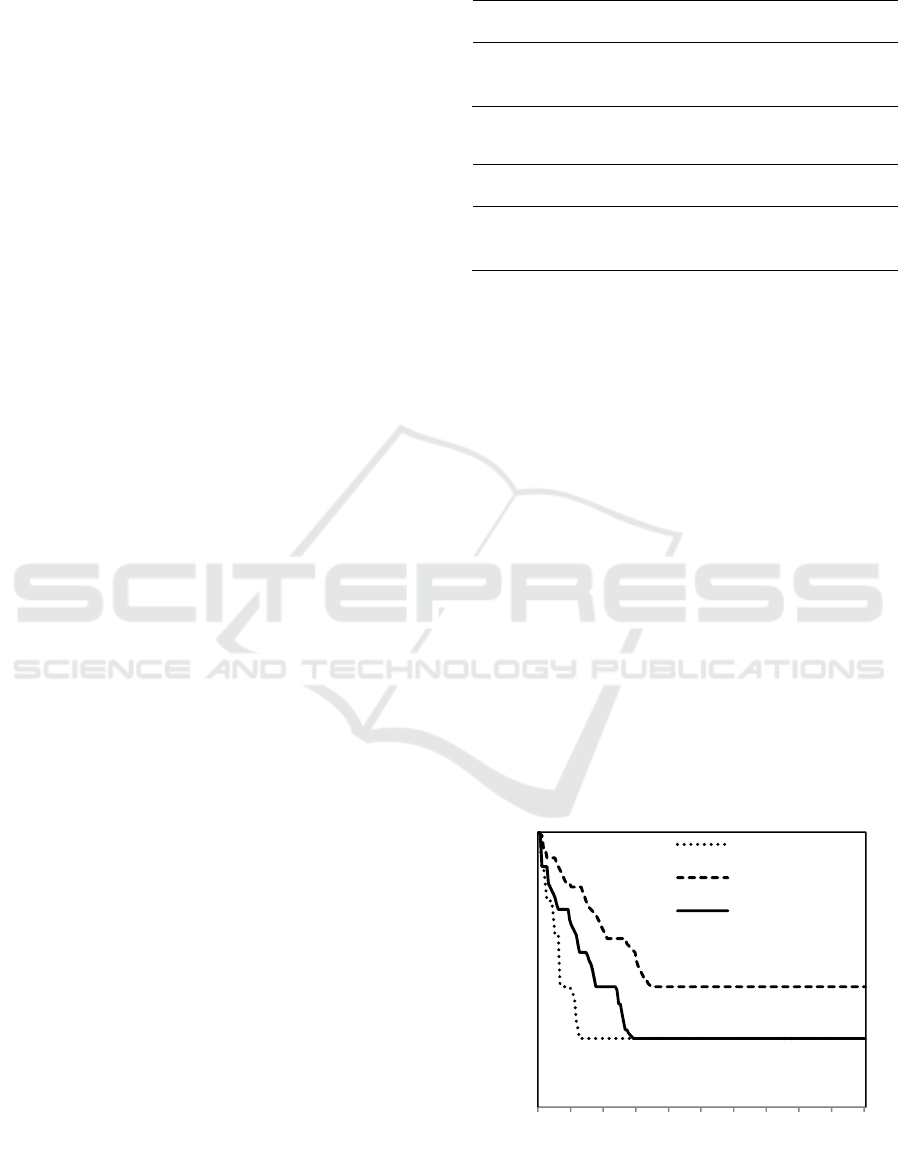
algorithms respectively. Figure 1 is the convergence
curves about the three algorithm, can be seen from
the diagram, In this paper, optimization algorithm
and the IGA algorithm can search to the optimal
solution 38, standard BFOA algorithm search to a
solution 41, although the two algorithms can get the
optimal solution, but the convergence speed of IGA
algorithm significantly slower than the improved
algorithm. Improved algorithm would find optimal
solution after 30 times in the iteration, and, IGA find
the optimal solution after 70 iterative times, so the
algorithm can more quickly find the optimal solution.
Figure 2 is the Gantt diagram of improved BFOA;
represent the scheduling scheme in the process of
convergence. The Y-axis means machine number.
The X-axis means execution time.
34
36
38
40
42
44
46
48
50
0 255075100125150175200
Improved BFOA
Standerd BFOA
IGA
Figure 1 Convergence curves
ISME 2016 - Information Science and Management Engineering IV
66
ISME 2016 - International Conference on Information System and Management Engineering
66

0 5 10 15 20 25 30 35 40
0
1
2
3
4
5
6
Processing time
Machine number
p(3,1)=6p(3,3)=2
p(2,2)=3p(2,4)=6
p(3,2)=4
p(2,6)=3p(2,2)=8
p(3,1)=5
p(5,6)=5
p(6,5)=3 p(6,5)=4
p(4,1)=5
p(1,3)=8
p(3,5)=5
p(1,6)=4 p(1,3)=8
p(4,2)=10
p(1,5)=3
p(4,4)=9
p(1,2)=3
p(6,1)=5
p(3,4)=5p(3,3)=6
p(1,5)=9
p(2,1)=5
p(1,6)=9
p(6,2)=8
p(3,1)=6p(3,3)=2
p(2,2)=3p(2,4)=6
p(3,2)=4
p(2,6)=3p(2,2)=8
p(3,1)=5
p(5,6)=5
p(6,5)=4
p(4,1)=5
p(1,3)=8
p(3,5)=5
p(1,6)=4 p(1,3)=8
p(4,2)=10
p(1,5)=3
p(4,4)=9
p(1,2)=3
p(6,1)=5
p(3,4)=5p(3,3)=6
p(1,5)=9
p(2,1)=5
p(1,6)=9
p(6,2)=8
p(2,6)=3
p(4,1)=5
p(1,5)=3p(1,2)=3
Figure 2 Optimal scheduling of Mk01 (The shortest
completion time is 38))
5 CONCLUSION
An improved bacterial foraging algorithm is
proposed in this paper,
and applied to search for the
optimal solution on FJSP. Compared with the
traditional algorithm, the optimization ability of this
method is more accurate. Compared with the
improved genetic algorithm, the improved method
can reduce the iterative time and greatly reduce the
solving time. But in view of the BFOA program is
running slightly slow, and have numerous
parameters, the present study mainly focus on the
single objective optimization, need to strengthen the
research for solving combinatorial optimization
problem.
ACKNOWLEDGMENT
I would like to express my gratitude to all those who
helped me during the writing of this thesis. My
deepest gratitude goes first and foremost to
Professor, my supervisor XinGang Wang, for his
constant encouragement and guidance. He has
walked me through all the stages of the writing of
this thesis. Without his consistent and illuminating
instruction, this thesis could not have reached its
present form.
REFERENCES
Bagheri, A., Zandieh, M., Mahdavi, I., 2010. An
artificialImmune algorithm for the flexible job-shop
scheduling problem. Future Generation Computer
System.
Dalian Yang, Xuejun Li, Lingli Jiang, 2012. Improved
algorithm of bacterium foraging and its application.
Computer Engineering and Applications.
Moslehi, G., Mahnam, M., 2011. A Pareto approach to
multi-objective flexible job-shop scheduling problem
using particle swarm optimization and local search.
International Journal of Production Economics.
Waligora, G., 2014. Simulated annealing and tabu search
for discrete-continuous project scheduling with
discounted cash flows. RAIRO-Operations Research.
Hongjun Liu, Shuai Zhao, 2011. Study on job-shop
scheduling based on hybrid genetic algorithm.
Manufacturing Automation.
Jingjing Cui, Yanming Sun, Lanxiu Che, 2011. Improved
bacteria foraging optimization algorithm for Job-Shop
scheduling problems. Application Research of
Computers.
J Q Li, Q K Pan, K Z Gao, 2012. Pareto-based discrete
artificial bee colony algorithm for multi-objective
flexible job shop scheduling problems. International
Journal of Advanced Manufacturing Technology.
Brandimarte, Paolo, 1993. Routing and scheduling in a
flexible job shop by tabu search. Annals of Operations
Research.
Qin Zhao, Fuqing Zhao, 2013. Research and application
on shop scheduling based on queuing theory. Lanzhou
University of Technology
Shiv, P., Deo, PV., 2014. A hybrid GABFO scheduling for
optimal makespan in computational grid. International
Journal of Applied Evolutionary Computation.
Xiuli Wu, Zhiqiang Zhang, Yanhua Du, 2015. Improved
bacteria foraging optimization algorithm for flexible
job shop scheduling problem. computer Integrated
Manufacturing Systems.
Improved Bacteria Foraging Optimization Algorithm for Solving Flexible Job-Shop Scheduling Problem
67
Improved Bacteria Foraging Optimization Algorithm for Solving Flexible Job-Shop Scheduling Problem
67
