Optimized Modal Research for a Manipulator using Bayesian based

Model Updating after Montecarlo-based Sensitivity Analysis

Bin Li

, Xi-fan Yao

,Shi-yong Chen

Department of Mechanical Engineering, Guangzhou Maritime Institute, Guangzhou, China

School of Mechanical & Auto Engineering, South China University of Technology, Guangzhou, China

Keywords: Model updating, Finite element model, Monte-Carlo, Bayesian, Sensitivity

Abstract: A procedure to identify the dynamic behavior of a 6 degree of freedom (6-DOF) Manipulator based on

modal data, has been developed in this paper. A ﬁnite element reference model with special emphasis on the

modeling of the joints has been built. The most uncertain parameters of the models are updated by minimiz-

ing the discrepancies between the analytical and the experimental natural frequencies of the model. The up-

dated models were tested using modal tests according to Monte-carlo based sensitivity analysis and Beyesi-

an based model reduction.

1 INTRODUCTION

In this paper, we investigate the application of the

Expectation Maximization (EM) algorithm to opera-

tional modal analysis of a 6-DOF manipulator. The

mechanical behavior of structures with multi- DOF

are idealized in the analysis as interconnected linear

elements. However, the response of the zone is more

complex and design-dependent, being directly af-

fected by a joint connection. In the past, joints were

considered as rigid. This assumption greatly simpli-

fies the analysis, but it does not accurately reflect the

true behavior of the joints. In practice, rigid joints

exhibit some flexibility. Therefore, adequate model-

ing and calibration of the joints is essential in the

structural design.

The mechanical behavior of the manipulator

can be obtained through detailed 3D finite element

(FE) models. Analytical models like the component

method are also extensively

used to characterize the

joints. These models should be validated or calibrat-

ed through data coming from experimental tests.

Thus, the joints are modeled as linear spring el-

ements for the analysis of the structural serviceabil-

ity limit state. This approach based only on the mo-

ment-rotation stiffness is adequate for static analysis.

In the dynamic case, however, it could give inaccu-

rate predictions. This is due to the fact that the ge-

ometry and inertia of the joint and the influence of

the connection on the mechanical properties of the

adjacent elements have a significant effect on the

structural response. Therefore, these features should

be considered in the joint modeling.

In the present work, a particular manipulator is

experimentally and analytically studied. The aim of

the paper is a proper modeling of the corresponding

joint by means of an FE model comprising beam

elements. It is intended to be understood as a whole,

considering not only the moment-rotation stiffness

of the joint but also its inertia, geometry and its in-

fluence on other elements. Once modeled, the aim is

to calibrate and validate the proposed models. In this

phase, the most uncertain parameters are selected

and updated on the basis of experimental data differ-

ent to those used in testing. For this purpose, two

different experimental models and testing proce-

dures are proposed. The first one consists of a cross-

like simple supported frame that is dynamically test-

ed in two different support configurations. The sec-

ond is a semi-portal frame that is statically tested.

One of the dynamic tests is used for updating, while

the other and the static test are used for testing. The

updating is proposed as the minimization of a given

fitting function, which accounts for the discrepancies

between the analytical and experimental models. A

novel adaptive sampling procedure based on values

of the fitting function is tried for minimization.

The portal axle is a gearbox that is specially de-

signed for off-road driving conditions. It is installed

between the wheel and the axle shaft to give higher

ground clearance to the vehicle. The

modeling and

257

Chen S., Li B. and Yao X.

Optimized Modal Research for a Manipulator using Bayesian based Model Updating after Montecarlo-based Sensitivity Analysis.

DOI: 10.5220/0006448602570262

In ISME 2016 - Information Science and Management Engineering IV (ISME 2016), pages 257-262

ISBN: 978-989-758-208-0

257

simulation of spur gears in portal axle is important to

predict the actual motion behavior. However, gear

train design in portal axle is difficult to study com-

prehensively due to their relatively low cost and

short product life cycle. In this study, modal analysis

of 6-DOF manipulator is simulated using finite ele-

ment method (FEM). Modal analysis is simulated on

three different combinations of gear train system

commonly designed for portal axle. FEM static

stress analysis is also simulated on three different

gear trains to study the gear teeth bending stress and

contact stress behavior of the gear trains in different

angular positions from 0° to 18°. The single and

double pair gear teeth contact are also considered.

This methodology serves as a novel approach for

gear train design evaluation, and the study of gear

stress behavior in gear train which is needed in the

small workshop scale industries.

2 MATHEMATICAL MODELS

The normal structural general equation of motion is

denoted by:

)}({}]{[}]{[}]{[ tFxKxCxM =++

(1)

Where

][M

is the mass matrix,

][K

stiffness ma-

trix,

][C

damping matrix,

][F

external incentives,

}{x

displacement matrix,

}{x

acceleration matrix.

Modal analysis in ANSYS software is linear (Wei,

2002), and any plastic、large deformation and non-

linear deformation are ignored, while the material of

the structure can be linear or non-linear, isotropic or

orthotropic, constant or temperature related, so for

linear structures, the Eq. (1) can be simplified as:

)cos(}{}{ tx

(2)

Where,

is the vibration mode (eigenvector);

is the natural circular frequency for vibration

type and the following equations can be obtained:

0)cos(}]{[

)cos(}]{[)cos(}]{[

+−

tCtM

iiiii

ωφ

ωφωφω

(3)

While

is insignificant, so Eq.(3) can be

simplified as follows:

[]

{} {} {}

[]

,,,

(4)

Through coordinate transformation for the nor-

mal mode matrix, the modal coordinates can be ex-

pressed as follows:

{}

[]

{} {}

∑

φλλφ

(5)

Where,

{}

is the weighting factor for the linear

superposition of main modes among

n-dimensional

space, and it can be proved to be orthogonal:

{} { }

λλλλ

,,,

(6)

Thus the kinetic energy of the system can be ex-

pressed as:

[] []

⎭

⎬

⎫

⎩

⎨

⎧

⎭

⎬

⎫

⎩

⎨

⎧

⎭

⎬

⎫

⎩

⎨

⎧

⎭

⎬

⎫

⎩

⎨

⎧

=Ε

•

••

•

λλ

(7)

While

[

]

{}

[

]

{}

φφ

Μ=Μ

(8)

And

φφ

Μ=

is the r-order modal mass,

that is its generalized mass for the corresponding

coordinates. Similarly, the system potential energy

can be expressed as:

{}

[]

{} {}

[]

{}

λλ

Κ=Κ=Ε

ΤΤ

(9)

While

[

]

{}

[]

{}

φφ

Κ=Κ

(10)

Where

φφκ

Κ=

is the r-order modal stiffness,

also the generalized stiffness for the corresponding

coordinate. Substitute it in the Lagrange equation

{} {}

{}

Ν=

∂

−

∂

−

∂

−

∂

λλ

)()(

ueue

(11)

Given generalized the force

{}

0=Ν

, then:

[] []

{}

0=+

⎭

⎬

⎫

⎩

⎨

⎧

••

λκλ

(12)

Converting it to independent expression:

ηλ

(13)

Where is the r-order system natural frequency.

Then, one particular solution of the free vibration

system would be:

{} {}

)sin(

(14)

With superposition, the solution of the whole system

would be:

{} {}

∑

iii

)sin(

θηφ

(15)

After transformation coordinate with regular

modal matrix, we can get the solution of the whole

system:

{}

[]

{}

(16)

ISME 2016 - Information Science and Management Engineering IV

258

ISME 2016 - International Conference on Information System and Management Engineering

258

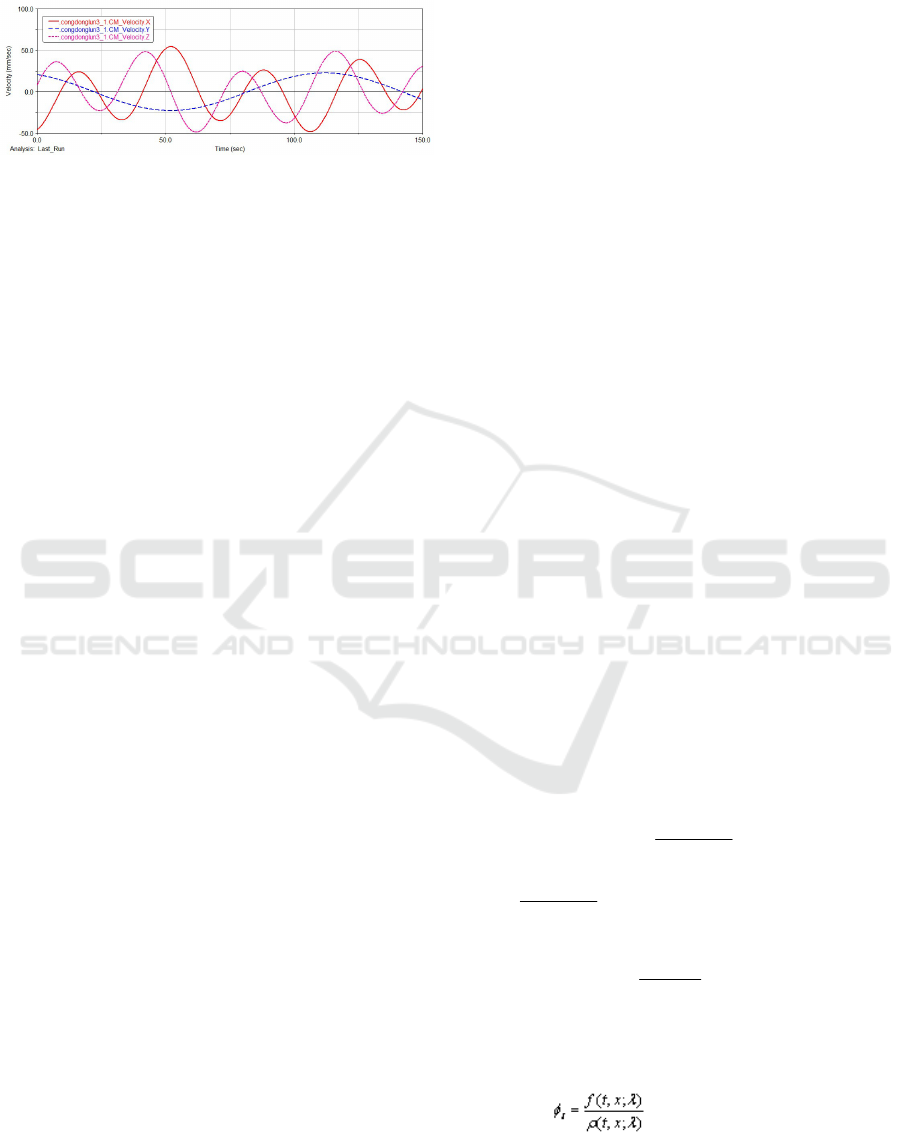
The test results for the manipulator using this

equator as following:

Figure 1: The velocity lines

3 MODEL UPDATING

Several methods of structural model updating have

been proposed and the topic is still under active

study in various areas. Most of these studies cen-

tered on approaches such as the optimal matrix up-

dating, eigen-structure assignment algorithms and

neural-networks updating methods. In this paper, the

model updating technique was described in detail

and updated parameters from the FE model were

compared to the original ones. It was presented the

theory of bayesian-based model updating with a

special focus on the properties of the solution that

result from the combination of montecarlo-based

sensitivity analysis with model reduction.

It should be attempted to assess the sensitivity

which can be attributed to various features of the

model. For example, joints and constraints could be

considered to be less accurately modeled, and there-

fore they are in greater need of updating. The pa-

rameterization of the inaccurate parts of the model is

important. The numerical predictions (e.g. natural

frequencies and

mode shapes) should be sensitive to

small changes in the parameters. Experimental re-

sults show that natural frequencies are often

signiﬁcantly affected by small differences in the

construction of joints in nominally identical test

pieces. However, it can be very difﬁcult to ﬁnd joint

parameters to which the analytical predictions are

sensitive. If the analytical response is insensitive to

changes in one or several updating parameters, then

updating will result in unrealistic values for rest of

updating parameters. The result, in this case, will be

an updated model which replicates the measure-

ments but lacks physical meaning.

Normally, the numerical model is incompatible

with the experimental modal one, therefore, in order

to make both of the two models more consistent, it is

necessary to modify the model by reducing the finite

element one, or by extending the experimental mod-

al one. And the reducing way will be much fast, so

here we use the reducing way. So the main goal for

the model update is to make the tolerance from the

errors between the frequencies obtained experimen-

tally and theoretically equal to zero. But, it is a

difﬁcult process because of the uncertainties from

the structural parameters such as the elasticity modu-

lus, mass density, boundary conditions, etc.

For this aim, this study denotes updating a ﬁnite

element model by following a process of following

substeps: (i) montecarlo-based sensitivity analysis;

(ii) bayesian based model updating.

3.1 Monte-Carlo based Sensitivity

Analysis

Sensitivity analysis includes local sensitivity analy-

sis methods and global sensitivity analysis. The first

one includes differential method, finite difference

method and perturbation method, which has clear

concept to facilitate the calculation. It has long been

widely used in engineering, but only being applied

in linear or non-strong nonlinear systems (Kang,

1990). But Global sensitivity analysis (Yu, 2004),

such as Monte Carlo method, also known as stochas-

tic simulation method, is a theory based on statistical

sampling, we random sample from probability dis-

tribution of an input known model to construct ran-

dom variables, then we get digital characteristics

resulting from its response (Zhou, 1997; Xiao, 2003;

Zhang, 2008), and which can be used for more com-

plex models, the analysis principle is outlined as

below:

Assuming that in the spatial domain

(Wang,

2003; Yan, 2003; Rulka, 2005), the system response

function

can be expressed as the integral of the

function f, and there exists an non-zero probability

density function

, as following:

)()

);,(

(

);,(

ΦΕ=Ε=

==Δ

∫∫

λρ

xtf

dxxt

xtf

dxxtf

(17)

Wherein:

);,(

λρ

xtf

=Φ

, t is the time,

),,,(

21 n

xxxX L=

the random input variable vec-

tor decided by a probability density function

, n

the

number of input variables,

a sys- tem parameter.

let, then

can be approxi-If

mately estimated by the mean

generated from N

random sample, that is:

Optimized Modal Research for a Manipulator using Bayesian based Model Updating after Montecarlo-based Sensitivity

Analysis

259

Optimized Modal Research for a Manipulator using Bayesian based Model Updating after Montecarlo-based Sensitivity Analysis

259

∑

≈Δ

(18)

The sensitivity of the system response function

Δ for the parameter

can be expressed as:

∑

∂≈Δ∂

λλ

(19)

3.2 Bayesian based Model Updating

Model modification is actually a mathematical in-

verse problem, there are several methods, and La-

grange multiplier method of direct correction matrix

has the following deficiencies:

①using experi-

mental modal vectors to correcting mass and stiff-

ness matrix. But Experimental modal vectors and the

number of DOF are much less than the calculated

model, so they must be extended;

② the error is

large normally;

③the sparsity from original mass

matrix and stiffness matrix may doesn’t exist any

longer;

④elements as zero may no longer be zero

from the original mass matrix and the stiffness ma-

trix, which may not be accordance with the actual

situation;

⑤ false modal (Spurious Modes) may

occur.

Therefore, the physical parameter modification

method based on sensitivity analysis is commonly

used in engineering, and there are two methods gen-

erally, such as: direct derivation and ad-joint struc-

ture method. Direct derivation, was first proposed by

Fox and Kappor. Adjoint structure method first pro-

posed by Van Bell and later improved by Van

Bonacker, it is coming from electronics (adjoint

network theory), which using the similarity between

Lurgan theorem (Tellegen's Theory) from electron-

ics and the virtual work principle from structural

mechanics. the structure sensitivity formula can be

obtained after analysis the original structure and the

accompanying one, through choosing dynamic char-

acteristics of the structural elements from the origi-

nal structure same as the one which has same topol-

ogy (structure) and geometry. But the calculation

with ad-joint structure method is more complex. So

this paper denotes a method combination with direct

derivation method.

There are three related requirements between the

finite element model and experimental modal model:

①modal frequencies must consistent; ②mode

shapes must consistent;

③frequency response must

consistent. These three factors can be weighted us-

ing Bayesian method when constructing the error

function based on the sensitivity analysis.

Bayesian approach lies in that using all known

information such as: the prior distribution of the

state and contact status, and also using the likelihood

function observed and of to construct the posterior

probability density for state variables of the system.

The main solution steps are as follows:

1) The first step, combined with a first-order

Markov process:

)(),(

1-1-:11- iiiii

xxxx ││ Ρ=ΚΡ

(20)

Priori probability density of the state space of the

system model:

11-:111-1-:1

)()()(

−−

Κ=ΚΡ

∫

iiiiiii

dxxpxxpx │││

(21)

2) The second step, using the nearest observation

for modifying the formula to obtain the posterior

probability density:

)(

)()(

)(

1-:1

iiii

xpxp

ΚΚ

=ΚΡ

│

││

│

(22)

The formula above is the optimal Bayesian esti-

mation, wherein,

x is the state for the system at the

moment

i ,

i:1

the observation sequence from the

initial moment to moment

)(

:1ii

x ΚΡ │

the likeli-

hood of the posterior probability density function.

Therefore, the linear model updating mathemati-

cal expressions:

{}{}

yx Δ=Δ

(23)

Wherein,

[]

sensitivity matrix of

nm ×

dimen-

sional;

{}

xΔ

the difference between model updating

parameters and the initial value;

{}

yΔ

the difference

between the eigenvalue tests from experiment model

and the calculated values of the finite element mod-

el, which containing the test errors

{}

and calcula-

tion errors, here ignored the calculation errors ,and

assumes

{}

xΔ

{}

obeys the normal distribution when

its mean is

,and they are independent on each oth-

er, here we have the following formula [24]:

{}{}

[

]

[]

σεε

=Ε

{}{}

[

]

[]

Uxx

=ΔΔΕ

{} { }

0=Δ

{}{}

[

]

{}

0=ΔΕ

(24)

Wherein,

[]

the covariance of

{}

xΔ

[

]

the

covariance of

{}

, and the joint probability density:

{}{}

[]

{}

[]

{}{}

[]

{}

⎥

⎦

⎤

⎢

⎣

⎡

+ΔΔ−

=ΔΡ

−Τ−Τ

)(

exp

)2(

),(

εε

UxUx

(25)

To have maximal value, first we need to solve the

following:

{}

[]

{}{}

[]

{}

)min(

εε

−Τ−Τ

+ΔΔ

UxUx

(26)

ISME 2016 - Information Science and Management Engineering IV

260

ISME 2016 - International Conference on Information System and Management Engineering

260

And substitute formula (24) to formula (26) into

it, and differentia it, then we get:

{} { } {}

Λ+=

(27)

Wherein,

{}

[]

{}

[] []

[]

)(

−Τ

−

−−Τ

Ζ+ΖΖ=Λ

yxy

UUU

(28)

Cause the correction model is the same im-

portant, we define three indicators to control its

quality: the average relative error of the modal fre-

quency

fΔ

, the maximum relative error

max

fΔ

, the

correlation coefficient of average modes

ℜ

, which

are indicated as follows:

∑

Δ=Δ

nkfMaxf

,,2,1),(

max

L=Δ=Δ

, (29)

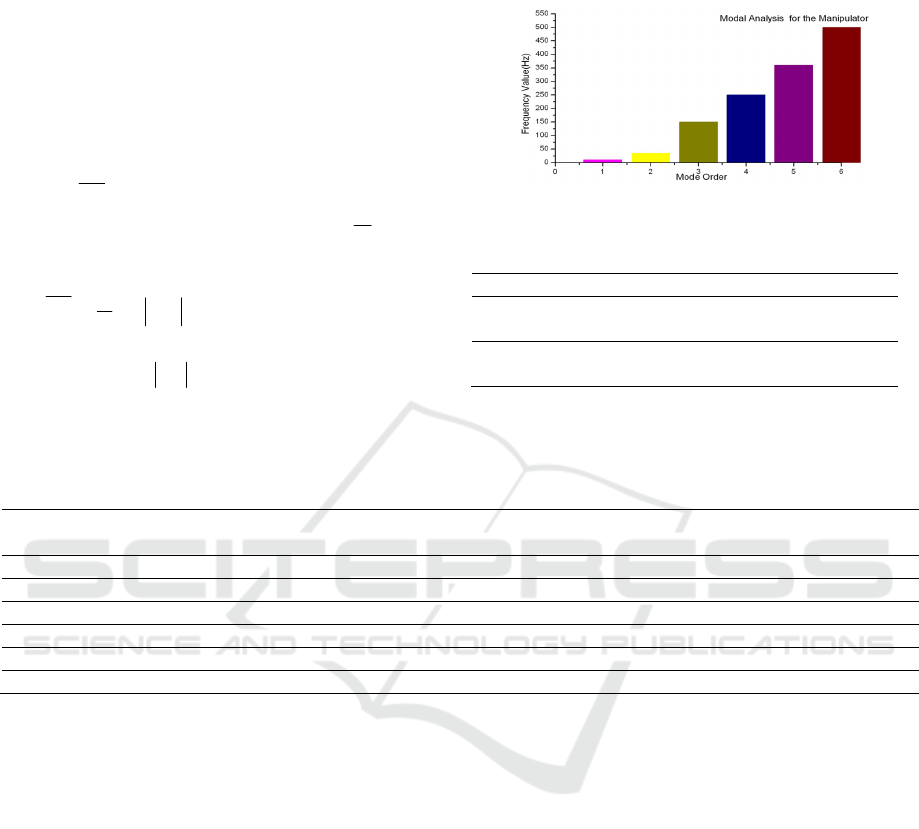
The proposed algorithm is tested on the model of

6-DOF manipulator. The results for both initial

model and revised model are shown in Fig 2, Table1

and 2.(here took six modes):

Figure 2: The Frequency Response

Table 1: The finite element model updating Controll index

rde

Δ (%)

max

(%)

ℜ

Before

revising

1~6 9.904 26.02 92.06

After

revising

1~6 0.817 3.29 89.31

Table 2: The comparison of the natural frequencies of the frame model before and after the update.

4 CONCLUSION

This paper addresses a method based on sensitivity

which is developed for modal analysis. For this pur-

pose, one example of a 6-DOF manipulator is select-

ed to demonstrate the efﬁciency of the proposed

method.

The model is investigated under ﬁve subtitles:

analytical modal analysis, experimental measure-

ment, comparison of the experimental and initial

analytical natural frequencies, application of the

developed modelupdating method using the platform

of Grid computing and comparison of the results.

It is observed that there are differences in the

natural frequencies obtained from experimental

measurement and initial analytical modal analysis of

the model because of the uncertain structural param-

eters. So, the model is updated using the proposed

model updating method.

According to the results of the study, the values

of each selected parameter are attained to reflect the

real condition of the models in terms of the dynamic

behavior. The average error in the natural frequen-

cies is decreased from 9.904% to 0.817% for the

DOF manipulator by using the developed model

updating method. In consequence, the proposed al-

gorithm gives better solutions for model updating

compared to the initial values.

ACKNOWLEDGEMENTS

The research was sponsored by the National Natural

Science Foundation of China (Project No.

51175187).

No. initial calculate

modal values=a

experimental

modal values=b

Difference=a-b

(confidence)

Correction

modal value=c

Difference=c-b

(confidence)

1 2.35 5.68 -3.33(36.2%) 3.39 -2.29(92.3%)

2 37.94 42.57 -4.63(89.6%) 43.94 -1.37(97.1%)

3 173.19 181.23 -7.04(93.6%) 178.35 .2.87(98.6%)

4 273.01 273.01 0(46.6%) 273.02 0.01(82.01%)

5 345.68 340.19 4.49(93.6%) 342.68 1.49(98.9%)

6 437.19 398.22 38.97(93.6%) 400.34 2.12(97.6%)

Optimized Modal Research for a Manipulator using Bayesian based Model Updating after Montecarlo-based Sensitivity

Analysis

261

Optimized Modal Research for a Manipulator using Bayesian based Model Updating after Montecarlo-based Sensitivity Analysis

261

REFERENCES

Kang, Z, Wang. Y, 1990, Sensitivity analysis method of

the dynamic optimal design for mechanical systems.

Journal of Vibration Engineering, China.

Rulka, W, Pankiewicz. E, 2005, MF3S approach to gen-

erate equations of motions for simulations in vehicle

dynamics,Multi-body System Dynamcis.

Smiths. F, Roussillie O. 2001, Sensitivity analysis in the

migration of radionuclides: differential Monte Carlo

versus double randomization. Mathematics and Com-

putersin Simulation.

Wang. Q, Liu. G, Wen.L, 2003, Reliability of crane struc-

ture based on Monte Carlo and finite element method

Journal of Wuhan University of Technology: Trans-

portation Science&Engineering.

Wei X., 2002,The finite element analysis software -ANSYS

Comprehension and Practice, China Water-Power

Press. BeiJing.

Xiao. G, Li H, 2003, Monte Carlo method in systematic

reliability Analysis, Science Press. Beijing, China.

Yan. B, Wang. L, Hu. J, 2003, Flexible model of multi-

axle vehicle ride comfort. Chinese Journal of Mechan-

ical Engineering.

Yu. J, Li. R, 2004,Application of Sobol' method to sensi-

tivity analysis of a non-linear passive vibration isola-

tors, Journal of Vibration Engineering, China.

Zhang. L, Bong. G, Shen. H, 2008, Robustness analysis of

planetary gear mechanism based on Monte Carlo

method. Journal of Mechanical Transmission.

Zhou. B, Dung. W, Tan. M, 1997,An analysis of addition-

al fluctuation of crankshaft torque and speed by using

Monte-Carlo simulation. Chinese Internal Combustion

Engine Engineering .

ISME 2016 - Information Science and Management Engineering IV

262

ISME 2016 - International Conference on Information System and Management Engineering

262