A Shrinkage Factor-based Iteratively Reweighted Least Squares
Shrinkage Algorithm for Image Reconstruction
Jian Zhao
1
*
, Chao Zhang
1
, Jian Jia
2
, Tingting Lu
1
, Weiwen Su
1
, Rui Wang
1
, Shunli Zhang
1
1 School of Information Science and Technology, Northwest University, Xian, PR China,710127 
2 Deparment of Mathematics, Northwest University, Xi’an, PR China,710127
Keywords: Compressed Sensing, IRLS, IRLS shrinkage, improved SIRLS.
Abstract: In order to improve convergence speed and reconstruction precision of IRLS shrinkage algorithm (SIRLS),
an improved iteratively reweighted least squares shrinkage algorithm (I-SIRLS) is proposed in this paper. A
Shrinkage factor is brought in each iteration process of SIRLS to adjust the weight coefficient to
approximate the optimal Lagrange Multiplier gradually. Put simply, the convergence speed is accelerated.
The proposed algorithm needs less measurements. It can also get rid of falling into local optimal solution
easily and the dependence on sparsity level. Simulations show that the I-SIRLS algorithm has faster
convergence speed and higher reconstruction precision compared to the SIRLS.
1 INTRODUCTION
Nyquist sampling theorem requires that signal could
be fully reconstructed only when the sampling rate is
2 times or more than 2 times the bandwidth.
However, with the rapid increase of information
demand, the bandwidth of the signal gets much
wider, which has brought great pressure to signal
processing. Compressed Sensing(CS)
theory(Donoho D.L,2006) proposed by Donoho
makes the sampling rate of signals exceed the
Nyquist limit, which presents a new method to
reconstruct the original signal from much fewer
measurements using the prior knowledge, and
compression and sampling are performed at the same
time. How to use the limited sampling value to
reconstruct the sparse signal with high accuracy, in
recent years, makes more scholars pay attention to
the sparse signal reconstruction(LC Jiao, SY Yang, F
Liu, 2011). Until now, researchers have proposed a
lot of algorithms to solve optimization problem(JH
Wang, ZT Huang, YY Zhou, 2012) in signal
reconstruction, including minimizing the norm(Van
Den etc 2008, Needell D, 2009, Cai T T, 2009 ),
minimizing the original signal norm(Chartrand R,
2007, Rodriguez P, 2006), matching pursuit
algorithm and other algorithms of CS.
Minimizing the norm can be regard as one of
convex optimization problems, thus making the
NP-hard simplified into linear programming. But the
norm-based signal reconstruction algorithm is still
not able to effectively remove great redundancy
between data. Chartrand R et.al(Chartrand R, 2007)
put forward a method minimizing the non-convex
norm of the original signal, which overcame the
shortcomings of minimizing the norm by changing
the nature of signal reconstruction. Not onlycan it
better approximate to the original signal
reconstruction andreduce data redundancy to a large
extent, but also greatly reduce the number of
observations which is needed to reconstruct the
original signal accurately.
The IRLS(Chartrand R, 2008) is a typical
non-convex of relaxation CS under RIP constraints,
transforming norm minimization into norm with
weights minimization(Daubechies I, 2010, Miosso C
J, 2009, Ramani S, 2010, Daubechies I, 2010), it
needs less measurements and it’s convergence speed
is often slow, and it is easy to fall into local optimal
solution.To solve the above drawbacks of IRLS, this
paper proposes an improved IRLS-based shrinkage
algorithm, the feasibility and effectiveness of the
improved algorithm is verified by experiments.
Compared with IRLS-based shrinkage algorithm, the
proposed method has a better reconstruction
accuracy and convergence speed.
289
Jia J., Zhao J., Zhang C., Lu T., Su W., Wang R. and Zhang S.
A Shrinkage Factor-based Iteratively Reweighted Least Squares Shrinkage Algorithm for Image Reconstruction.
DOI: 10.5220/0006449202890293
In ISME 2016 - Information Science and Management Engineering IV (ISME 2016), pages 289-293
ISBN: 978-989-758-208-0
Copyright
c
 2016 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
289

2 IMPROVED ITERATIVELY
REWEIGHTED LEAST
SQUARES SHRINKAGE
ALGORITHM
2.1 Compressed Sensing
In compressive sensing: the dimension measurement
vector can be obtained from the original real-valued
signal with the length:

yx ss=Φ =ΦΨ =Θ
 (1)
Where
Θ
is a
NN×
basis matrix, and
Φ
is a
NN×
measurement matrix. Here exists two
problems: (1) how to determine a stable basis
Θ
and
measurement; (2) how to recover the
N
dimension
vector
x when the sparsity is
K
. The first problem
can be solved when
M
K≥
.
That is, the matrix
Φ
must preserve the lengths of
these particular K-sparse vectors. A related condition
requires that the rows
{
}
j
ψ
of
Φ
cannot sparsely
represent the columns
{
}
j
ψ
of
Ψ
and vice versa.
The sparsest
x is chosen when it meets the least
nonzero. Zero norm of
x is,
:0
arg min || ||
xAx b
x
x
=
= (2)
Obviously, it is a NP-hard problem. It costs so
much and is impractical. So least square solution is
considered. Based on the above consideration,
(0 1)
p
lp<<
norm is chosen,

:
arg min
xAx b
p
x
x
=
=
%
 (3)
2.2 Iteratively Reweighted Least
Squares Shrinkage Algorithm
The basic idea of the improved algorithm is that the
non-convex
p
l
norm is replaced by
2
l norm, then
using the Lagrange multiplier method to seek the
iteration algorithm of optimal solution for formula
(3).In an iterative algorithm, given a current optimal
solution
1k
x
−
, set
||
q
kk
Xdiagx
−−
=
11
, if
k
X
−
1
is
reversible, then it satisfies the condition:

q
kk
q
X x diag x
−
−−
−
=
222
11
222
 (4)
If
/qp=−12is chosen, approximation
optimization problem is converted to solving the
p
l
norm, meaning solving
|| ||
p
p
x
. The equation is still
valid if
k
X
−
1
in formula (4) is converted to its pseudo
inverse matrix
k
X
+
−
1
. Following optimization problem
is obtained:

min
k
x
X
x
+
−
2
1
2
..st bAx=  (5)
To improve the sparseness, if there is a zero
element in
k
X
−
1
, following formula can be obtained:

.( )
T
k
b λ
−
=
AX A
2
1
05
⇒
()
T
k
b λ
−
−
= AX A
21
1
2
 (6)
The formula must solve the inverse matrix, so in
the practical application, selecting the pseudo
inverse matrix to instead the inverse matrix to
decrease the computational complexity:

()
TT
kk k
x
+
−−
= XAAXA b
22
11
 (7)
The SIRLS is in each iteration of IRLS,
A
and
T
A is used as the intermediate amount, while
shrinkage scalar is introduced minimize the objective
function. The algorithm is very effective in solving
the minimum problem of
()
f
x in the formula (8):

()
p
p
f
xx λ =+−xbA
2
2
1
2
 (8)
It is obvious that, choose the right
P
, we can
obtain the global optimal solution. Replace
|| ||
p
p
x
with,
.()
T
Wxx
−
x
1
05
, ()Wxis a diagonal matrix, the
diagonal value is
(,) . []/ ([])Wkk xk pxk=
2
05
, This
replacement is redundant for solving IRLS directly,
but when it is introduced into the iterative shrinkage
algorithm(like formula (13)), the result is desired:
() ()
p
T
p
f
xbx x bx Wx λλ
−
=− + =− +AAxx
22
1
22
11
22
(9)
Come to solve:

() ( ) ()
T
fx b x W xx λ
−
∇
=− − + =AA
1
0
 (10)
3 IMPROVED ITERATIVELY
REWEIGHTED LEAST
SQUARES SHRINKAGE
ALGORITHM
By solving the inverse matrix to obtain a new update
results. When
W
is fixed, updating x , the
approximation effect of the approximation solution
ISME 2016 - Information Science and Management Engineering IV
290
ISME 2016 - International Conference on Information System and Management Engineering
290

in this process is relatively poor, especially in the
treatment of high-dimensional signal. In order to
make the algorithm deal with high-dimensional data,
plus or minus to
cx
it. This is the shrinkage iterative
algorithm based on the IRLS algorithm.In order to
improve the convergence efficiency of the algorithm,
a shrinkage factor
c
is brought in each iteration
process of IRLS algorithm to minimize the objective
function. Meanwhile, the iteration speed is improved
and higher reconstruction precision is obtained.
()cc≥ 1 is a relaxation constant, put it into equation
(10)

()(())
TT
bcxWxcx λ
−
−+ − + + =AAAI I
1
0
 (11)
Rebuilding the iterative algorithm with
fixed-point iteration method, the result is:

()(())
TT
kkk
bcxWxcx λ
−
+
−−= +AAAI I
1
1
 (12)
Obtaining a new iterative equation:
(())( ( ))
TT
kk k
x
xbcx
ccc
λ
−−
+
=+−−WIAAAI
11
1
11
(( ))
T
kk
Sx
c
=⋅ − +Ab A x
1
(13)
Defining the diagonal matrix:

(())( ())()
kkk
Sx xx
cc
λλ
−− −
=+=+WI IWW
11 1
 (14)
Applying the matrix to formula (17):

.[]/([]) []
. [] / ( []) [] []
kk k
kk kk
xi xi xi
x
ixi xixi
cc
ρ
λλ
ρ
=
+
22
222
05
2
05
 (15)
It can be seen from the above equation, when
[]
k
x
i is very large, the equation (15) is close to 1,
when
[]
k
x
i is very small, the above equation is close
to 0, thus achieve the shrinkage effect. This is the
most important improvement relative to the previous
IRLS iteration shrinkage algorithm, this
improvement speeds up the convergence speed,
saves a lot of computation time, and gets higher
re-construction precision. Similarly, this algorithm
also requires the initial solution not be empty when
initialize.
4 EXPERIMENTAL RESULTS
AND DISCUSSION
4.1 Reconstruction of one-dimensional
random signal
The experiment is carried out in MATLAB R2010a
and it uses discrete-time signal with different
lengths, the sparsity data is set to 5. Figure 2 and
Figure 3 are results of signal with length 16 or 64;
Average values of 1000 times experimental results
with each length under the same conditions are
shown in Table.3.
The I-SIRLS algorithm has better performance
compared with the low measurement while
reconstructing discrete signal, as shown in Figure 1
and Table 2. When the reconstruction probability is
1, the I-SIRLS algorithm requires less measurements
than SIRLS algorithm. Meanwhile the reconstruction
probability of the I-SIRLS algorithm can achieve
0.8, even though the number of samples is low, but
the SIRLS algorithm probability can only get 0.6 or
lower. When the two algorithms reach the maximum
reconstruction probability, the I-SIRLS algorithm
maintains a maximum reconstruction probability, but
there is shocks in the performance of the SIRLS
algorithm, it illustrates that the I-SIRLS algorithm
has better shrinkage efficiency and stability. The
target of the improved IRLS is to find the optimal
solution
x
, making
()
p
p
f
xx λ =+−xbA
2
2
1
2
be
the minimum. Algorithm realization after initializing
(
k
=
0
, x
=
0
1,
k
rbAx
=
−
0
) can be generalized in
following steps:
(1) Back Projection: Calculate the residual
T
k
eAr
−
=
1
(2) Update shrinkage factor: Calculation of the
value of the diagonal matrix
(, ) ()/( ( []) [])
kkk
Sii x i x i x i
c
λ
ρ
=+
2
2
(3) Shrinkage computing: Calculate
(/)
sk
eSx ec
−
=+
1
(4) Linear search: Select the appropriate
μ
to
minimize the function
(())
ksk
fx e x μ
−−
+−
11
(5) Atomic map updater: Calculate
()
kk sk
x
xex μ
−−
=+ −
11
A Shrinkage Factor-based Iteratively Reweighted Least Squares Shrinkage Algorithm for Image Reconstruction
291
A Shrinkage Factor-based Iteratively Reweighted Least Squares Shrinkage Algorithm for Image Reconstruction
291

(6) Iteration stop condition: If
kk−
−xx
2
1
2
Less
than a given threshold value, Stop iteration;
Otherwise, jump to the iterative process step (1)
(7) Output
k
x
Table 1. Comparison of minimum number of
measurements in I-SIRLS and SIRLS.
Signal length Proposed method SIRLS
16 8 12
64 15 18
256 21 25
1024 30 33
Figure 1. Contrast of reconstruction probability: (a) Signal
length N=16; (b) Signal length N=64
4.2 Image Reconstruction
To further verify the reliability and effectiveness of
the proposed algorithm, we select a test image: Lena.
The original image is firstly transformed into DCT
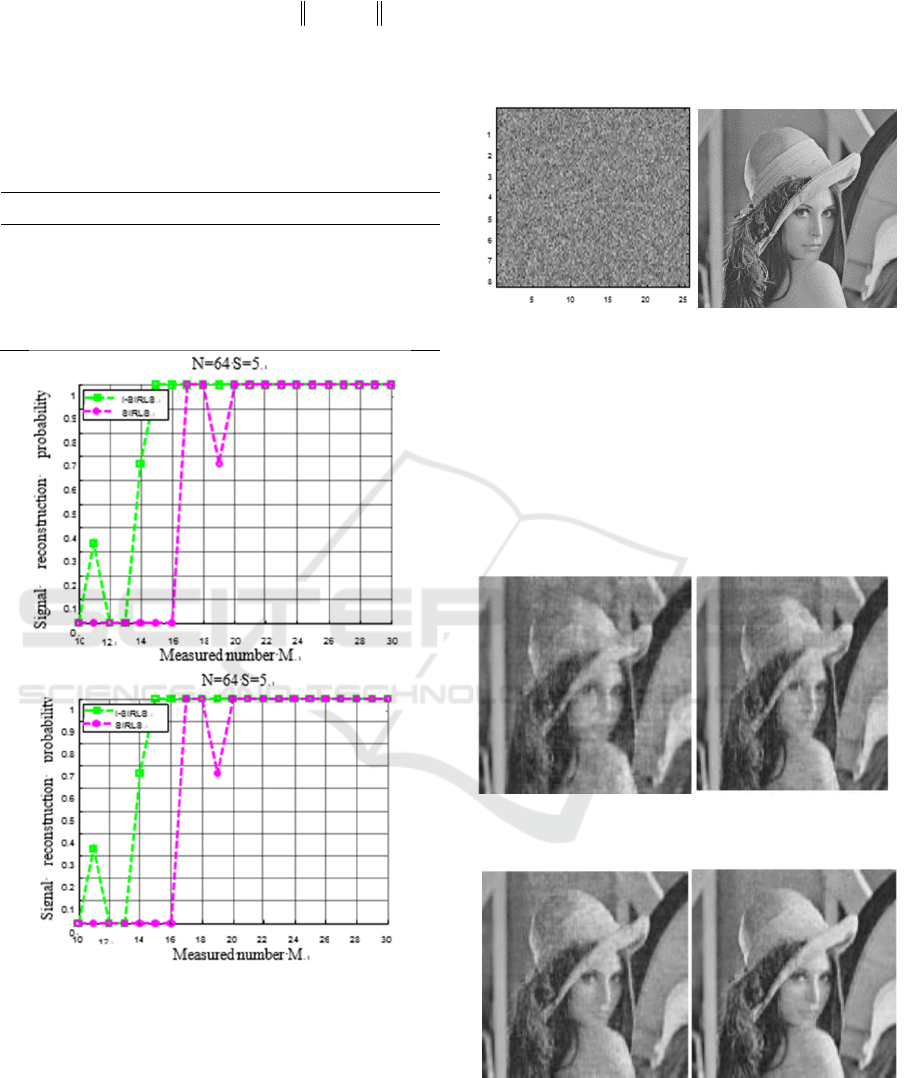
coefficients using DCT. The measurement matrix
and the original im-age are shown in figure 2. Based
on combination of CS theory, reconstructed images
using the proposed algorithm with compression ratio
is 0.3, 0.4 and 0.5, respectively. In the following, the
results of evaluating the proposed algorithm
compared with SIRLS algorithm are presented.
Figure 2. Measurement matrix and original Lena
According to results in Figure 3, Figure 4 and
Table 3: the image reconstruction quality is worse
with reducing sampling ratio, and the image even
cannot be recognized. From the above table it can be
seen that, the I-SIRLS algorithm has higher PSNR, it
shows that the effect of reconstruction is better; the
I-SIRLS algorithm has a smaller fluctuation range of
PSNR, it shows that the stability of the proposed
algorithm is superior to the SIRLS algorithm.
Figure 3.Reconstructed images of Lena: (a) SIRLS; (b)
I-SIRLS in thecase of compression ratio respectively 0.4

Figure 4.Reconstructed images of Lena: (a) SIRLS (b)
I-SIRLS in thecase of compression ratio respectively 0.5
ISME 2016 - Information Science and Management Engineering IV
292
ISME 2016 - International Conference on Information System and Management Engineering
292

Table 2. Comparison of PSNR values in proposed
reconstructed method and other methods.
Sampling rate SIRLS Proposed method
0.5 27.46 30.33
0.4 24.52 26.22
0.3 21.94 23.56
5 CONCLUSION
This article discusses the signal reconstruction based
on compressed sensing theory, solving the problem
that the convergence speed is not fast enough and the
reconstruction accuracy is not high enough in IRLS-
based shrinkage algorithm. Then the article presents
an improved IRLS shrinkage algorithm. Each
iteration process of SIRLS algorithm introduced a
shrinkage factor, which makes the convergence rate
and the reconstruction accuracy both better than the
previous algorithm. The simulation results show that
the improved algorithm has faster convergence rate
and higher reconstruction precision compared to the
previous algorithm.
ACKNOWLEDGEMENTS
This work was supported by National Natural
Science Foundation of China (No. 61379010 ，
61572400) and Natural Science Basic Research Plan
in Shaanxi Province of China (No.2015JM6293).
REFERENCES
Cai, T. T., Xu, G. and Zhang, J. (2009). On Recovery of
Sparse Signals Via
1
l Minimization. In IEEE
Transactions on Information Theory,
55(7):3388-3397.
Chartrand, R. (2007). Exact Reconstruction of Sparse
Signals via Nonconvex Minimization. In IEEE
Signal Processing Letters, 14(10):707-710.
Chartrand, R., and Yin, Wotao. (2008). Iteratively
reweighted algorithms for compressive sensing.
IEEE International Conference on Acoustics,
Speech and Signal Processing, pp. 3869-3872.
Daubechies, I., DeVore, R., Fornasier, M., & Güntürk, C.
S. (2010). Iteratively reweighted least squares
minimization for sparse recovery. Communications
on Pure and Applied Mathematics, 63(1):1-38.
Daubechies, I., DeVore, R., Fornasier, M., and Gunturk, S.
(2008). Iteratively Re-weighted Least Squares
minimization: Proof of faster than linear rate for
sparse recovery. Information Sciences and Systems,
pp. 26-29.
Donoho, D.L. (2006) Compressed sensing. In IEEE
Transactions on Information Theory,
52(4):1289-1306.
Ewout, V. D. B. and Friedlander, M. P. (2009). Probing
the pareto frontier for basis pursuit solutions. SIAM
Journal on Scientific Computing, 31(2), 890-912.
Forster, R. J. 2007. Microelectrodes—Retrospect and
Prospect. Encyclopedia of Electrochemistry.
Miosso, C. J., von Borries, R., Argaez, M., Velazquez, L.,
Quintero, C. and Potes, C. M. (2009). Compressive
Sensing Reconstruction With Prior Information by
Iteratively Reweighted Least-Squares. In IEEE
Transactions on Signal Processing,
57(6):2424-2431.
Needell, D. and Tropp, J. A. (2009). CoSaMP: Iterative
signal recovery from incomplete and inaccurate
samples. Applied and Computational Harmonic
Analysis, 26(3): 301-321.
Rodriguez, P. and Wohlberg, B. (2006). An Iteratively
Reweighted Norm Algorithm for Total Variation
Regularization. Fortieth Asilomar Conference on
Signals, Systems and Computers, pp. 892-896.
Ramani, S. and Fessler, J. A. (2010). An accelerated
iterative reweighted least squares algorithm for
compressed sensing MRI. IEEE International
Symposium on Biomedical Imaging: From Nano to
Macro, pp. 257-260.
Wang, J. H., Huang, Z. T., Zhou, Y. Y. and Wang, F. H.
(2012). Robust Sparse Recovery Based on
Approximate
0
l Norm. Chinese Journal of
Electronics, 40(6):1185-1189.
A Shrinkage Factor-based Iteratively Reweighted Least Squares Shrinkage Algorithm for Image Reconstruction
293
A Shrinkage Factor-based Iteratively Reweighted Least Squares Shrinkage Algorithm for Image Reconstruction
293