Simulation of Radar Signal Processing based on Matlab

Hanwen Wu

(Unit 92941 , Huludao liaoning 125000, China)

Key words: Signal processing; quadrature sampling, pulsed compression; echo accumulation.

Abstract: The simulation of radar signal processing is an important part of the simulation of the radar system. This

paper introduces a method of the simulation of radar signal processing based on Matlab, including the

simulation of radar echo and clutter, and researches the simulation method of important technologies in the

radar signal processing, including quadrature sampling, pulse compression, echo accumulation and CFAR

detector. The work in this paper can overcome the disadvantages such as difficulty and lengthiness and

show the convenience and simplicity of the simulation of radar signal processing based on MATLAB.

1 INTRODUCTION

The modern radar system is getting so complicated

that it can not be processed with simple analytical

methods. Thus people usually make use of

computer to simulate the functions and

performances of the system, which is featured by

great convenience, flexibility and low cost.

However, Matlab has provided a powerful

simulation platform which facilitates the operation

for the simulation of the majority radar system.

The typical radar is made up by antenna,

transmitter, receiver, signal processor, servo

system and terminal unit(Lufei Ding,1984). In the

paper, the authors mainly probe into the radar

signal processing part, and illustrate the application

of Matlab in the radar signal processing system

with the case of a certain pulsed compression radar

signal processing system.

2 GENERATION OF

SIMULATED SIGNAL

2.1 Generation of Radar Signal

The modern radar has diversified systems. The

form of signal can be selected according to the

radar system. In the following part, the method of

how to generate chirp signals in Matlab will be

introduced briefly.

Matlab provides the modulate function which

can generate chirp signals in a convenient manner.

The calling format for the modulate function is

shown as follows:

y = modulate (x, fc,fs, ‘method’,opt)

The parameter x represents the sequence of

modulating signal, fc represents the carrier

frequency, and fs represents the sampling

frequency. The ‘method’ is used to decide which

kind of modulation will be adopted. opt represents

the modulation sensitivity, that is, the stepping

coefficient of chirp signal.

A chirp signal, with the starting frequency of

10MHz, tuning bandwidth of 2MHz, sampling

frequency of 100MHz and pulse bandwidth of

10µs, is generated by a modulate function. The

output result is shown in Figure 1.

Figure 1. Chirp Signal with Carrier Wave of 10MHz and

Bandwidth of 2M

2.2 Generation of Noise and Clutter

In the real radar echo signals, there are not only

signals reflected from targets but also various

299

Wu H.

Simulation of Radar Signal Processing based on Matlab.

DOI: 10.5220/0006449402990304

In ISME 2016 - Information Science and Management Engineering IV (ISME 2016), pages 299-304

ISBN: 978-989-758-208-0

299

noises and clutters such as thermal noises from the

receiver, ground clutters, weather clutters and so

on. Noises and clutters can be analyzed only with

statistical properties because neither of them are

deterministic signals. In the following part, the

common method of generating noises and clutters

will be presented.

1) Thermal noises subject to Gaussian

distribution (random sequence): Matlab provides

the random function which is used to generate the

random number in standard Gaussian distribution.

random (m,n) can generate the m×n random

sequence matrix. Therefore, a random sequence

subject to Gaussian distribution can be easily

generated by a random function, as shown in

Figure 2.

Figure 2. Random Sequence Subject to Gaussian

Distribution

2) Generation of clutters in Rayleigh

distribution: The Rayleigh distribution is the most

frequently used and the earliest statistical model.

When there are many scatterers within the

discernible range of radar, the envelope amplitude

for synthesizing echo is subject to the Rayleigh

distribution according to the random characteristics

of the amplitude and phase position of scatterers. If

x represents the envelope amplitude of the clutter

echo subject to Rayleigh distribution, then its

probability density function can be expressed as

⎩

⎨

⎧

≥−

0,0

0),exp(

)(

σσ

(1)

In this formula, σ is the standard deviation of

clutter.

Matlab provides a raylrnd function which is

used to generate the random number in Rayleigh

distribution. In the raylrnd (B,m), B is the

parameter of Rayleigh distribution, and m is a

one-dimensional vector that contains two elements

which represent the line number and column

number of the random number matrix which is

subject to Rayleigh distribution respectively.

Generally, the line number is set as 1, and the

column number corresponds to the duration of

clutter. When the parameter of Rayleigh

distribution σ=2, the clutter generated with the

raylrnd function is shown as Figure 3.

Figure 3. Clutter in Rayleigh Distribution

3 SIMULATION OF SIGNAL

PROCESSING SYSTEM

The purpose of processing radar signals is to

remove the unwanted signals (such as clutter) and

the interference, and to extract and intensify the

echo signals generated by the target. The radar

signal processing provides many functions, and

functions of different radars also vary(You

He,1999). In this paper, a certain pulse

compression radar’s signal processing part is

simulated. The signal processing part of a typical

pulse compression radar mainly has the functions

of A/D sampling, quadrature demodulation, pulse

compression, video integration, constant false

alarm processing and so on. Hence, the simulation

model for the pulse compression radar’s signal

processing is as shown in Figure 4.

3.1 Quadrature Demodulation

Module

Before the pulse compression for radar ’ s

intermediate-frequency signals, it is necessary to

transform these signals into the I and Q quadrature

signals with the zero intermediate frequency.

The intermediate-frequency signals can be

expressed as

ISME 2016 - Information Science and Management Engineering IV

300

ISME 2016 - International Conference on Information System and Management Engineering

300

Figure 4. Simulation Model for Pulse Compression Radar’s Signal Processing

))(2cos()()(

ttftAtf

= (2)

In the formula, f

is the carrier frequency.

To set

⎩

⎨

⎧

)(sin)()(

)(cos)()(

ttATQ

ttATI

(3)

Then

tftQtftItf

IF 00

2sin)(2cos)()(

−

= (4)

In the simulation, all the signals are expressed as

discrete time series. Set the sampling period as T,

and then the intermediate-frequency signal will be

fIF (rT). Similarly, the local oscillating signals,

after being sampled, will be expressed as

)exp(

rTjf

local

−= (5)

The digitized intermediate-frequency signals and

local oscillating signals will turn into baseband

signals after they are multiplied and demodulated

and then pass the low-pass filter. The baseband

signal fBB (r) can be expressed as

{}

() ( )cos( ) ()

BB IF

r f rn rn Thn

−

=−− −

∑

{}

()sin() ()

frn rn Thn

−

−−

∑

(6)

Wherein, h(n) is the pulse response of the

low-pass filter which has an accumulated length of

According to the practical application, the

sampling using Nyquist sampling rate only will not

obtain good mixing signals and filtering results.

Generally, good real part and imaginary part of

signal can be obtained when the sampling

frequency fs is four times of the center

frequency(Yingle Fan,2001). When the sampling

frequency fs=4f

, and 2/

=T , the baseband

signal can be simplified as

() ( )cos( ) ()

BB IF

rn rn hn

−

⎧⎫

−− −

⎨⎬

⎩⎭

∑

()sin() ()

frn rn hn

−

⎧⎫

−−

⎨⎬

⎩⎭

∑

(7)

The steps for simulation of quadrature

demodulation using Matlab are shown as follows.

1) To generate the ideal chirp signal y;

2) To generate the I-channel local oscillating

signal and the Q-channel local oscillating signal.

Set f

as the center frequency of the local

oscillating signal, f

as the sampling frequency, n as

the length of the chirp signal’s time series, then the

I-channel local oscillating signal will be

)2cos(

n . Likewise, the Q-channel local

oscillating signal will be

)2sin(

n . When f

=4f

, the I-channel and Q-channel local oscillating

signals will be

)cos(

and )sin(

respectively.

3) Multiplying the chirp signal y by the double

local oscillating signal to obtain the I-channel

signal and the Q-channel signal.

4) The I-channel signal and the Q-channel signal

pass through the low-pass filter and filter off the

high-frequency component in order to get the final

result of demodulation(Haimang Hu,2004). Matlab

provides a convenient filter function filter(b,a,x),

in which x represents the input signal, and b and a

represent the coefficient vectors of the filter

transfer function’s numerator and denominator.

Figure 5 shows the simulation of chirp signal

with Matlab. Figure 6 and 7 show the demodulated

I-channel signal and Q-channel signal respectively.

Simulation of Radar Signal Processing based on Matlab

301

Simulation of Radar Signal Processing based on Matlab

301

Figure 5. Chirp Signal With the Carrier of 10MHz and

Bandwidth of 2MHz

Figure 6. I-channel Signal after Demodulating the Chirp

Signal

Figure 7. Q-channel Signal after Demodulating the Chirp

Signal

3.2 Pulse Compression Module

Before the pulse compression, it is necessary to

find a matched filter for signals transmitted by

radar(Yu Zhou,2004). In real projects, pulse

compression is usually done in the frequency

domain because it can improve the computation

speed by making use of the FFT algorithm. The

result of pulse compression can be obtained after

multiplying the radar echo by the matched filter’s

frequency domain response and then getting them

transformed with IFFT. Hence, convolution

processing has been replaced, thus greatly reducing

the amount of operation. Therefore, it is necessary

to firstly obtain the matched filter or pulse

compression coefficient for the pulse compression

when simulating the pulse compression. It is easy

to work out the chirp signal’s pulse compression

coefficient, which can be achieved by conjugating

and overturning the ideal chirp signal.

The steps for simulation of chirp signal’s pulse

compression using Matlab are shown as follows.

1) To generate the ideal chirp signal y;

2) To make quadrature demodulation for signals

in order to obtain the demodulated signals ;

3) To generate the ideal chirp compression

coefficient. To achieve this, you shall firstly find

out the matched filter for the signal fbb which has

been processed with quadrature demodulation, and

then work out the pulse compression coefficient by

making use of the discrete Fourier transform.

4) To generate the ideal echo signal and to

process the signal with quadrature demodulation.

The idea echo signal is the echo signal received by

radar within a pulse repetition period, and the

target is assumed to be a stationary-point target.

5) To make pulse compression. Firstly, make the

discrete Fourier transform for the echo signal in

order to obtain signal_fft, and then multiply the

signal_fft and the matched filter’s frequency

domain response, and then make inverse discrete

Fourier transform for it, thus obtaining the result of

pulse compression(Zewei Wang,2005). Assuming

the signals transmitted by radar are the chirp

signals, the relevant parameters are shown as

follows: bandwidth 10µs, center frequency 10MHz

and tuning bandwidth 2MHz. The frequency of

sampling radar’s echo signals is 40MHz. The

intermediate frequency is processed with

quadrature down-conversion. In Figure 8 and 9, the

oscillograms have shown the simulation of radar

pulse compression using Matlab.

Figure 8. Result Obtained after the Quadrature

Demodulation for Echo Signal

ISME 2016 - Information Science and Management Engineering IV

302

ISME 2016 - International Conference on Information System and Management Engineering

302

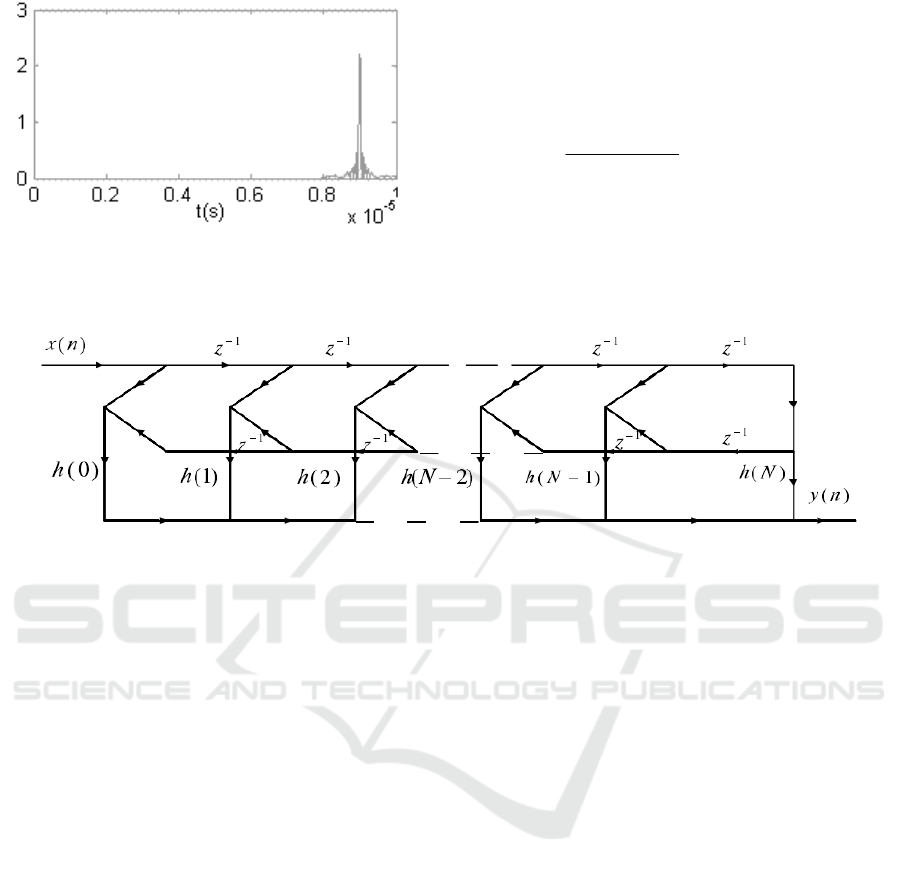
Figure 9. Result Obtained after the Pulse Compression

for Echo Signal

3.3 Echo Accumulation Module

The modern radars make detection based on

multi-pulse observation(). The integration of

multiple pulses can effectively improve the

sin ( )

()

(9)

Δθ represents the angle that the antenna has

swept across within a pulse repetition period. Such

integration can be realized by the FIR integrator,

with its structure shown in Figure 10.

Figure 10. Structural Diagram for FIR Accumulator

3.4 Constant False Alarm Rate

(CFAR) Processing Module

There are many methods to make constant false

alarm processing. In broad classification, there are

mean level CFAR, order statistics CFAR, clutter

map CFAR and so on. There are many ways to

realize the mean level CFAR, including cell

averaging, GO, SO and so on, all of which operate

under the same fundamental theory. The

procedures for simulation of CFAR using Matlab

are shown as follows.

1) To generate the point-target echo which has

superimposed the Rayleigh clutter and thermal

noise. In this step, the Gaussian thermal noise and

Rayleigh clutter are generated with the

above-mentioned method, and then are

superimposed with the point-target echo, during

which the amplitudes of Rayleigh clutter and

thermal noise shall be weighted.

2) To make constant false alarm processing for

the point-target echo which has superimposed

Rayleigh clutter and thermal noise. In this step, the

number of reference cells shall be determined

firstly. If the number of reference cells are 16, the

mean value of the first point noise for constant

false alarm processing will be decided by its

subsequent 16 points of noises, while mean value

of the noises from the second point to the 16

point will be jointly decided by the 16 points of

noises before and after it. The mean value of noises

on normal data points for constant false alarm

processing is determined by its former 16 points of

noises and its subsequent 16 noises, and the

constant false alarm processing for the last 16

points of noises is the same as that for the first 16

points of noises. The signal output lastly is the

ratio between the estimated mean values of each

detection unit and the clutter.

In the following part, we will simulate the

GO-CFAR using Matlab. The number of reference

cell is 16, and the radar’s pulse repetition period is

1ms. There are clutter echoes subject to Rayleigh

distribution in the range from 7.5 km to 30 km

away, and there is a point target 15km away. The

results of simulation are shown in Figure 11 and

Figure 12.

Simulation of Radar Signal Processing based on Matlab

303

Simulation of Radar Signal Processing based on Matlab

303

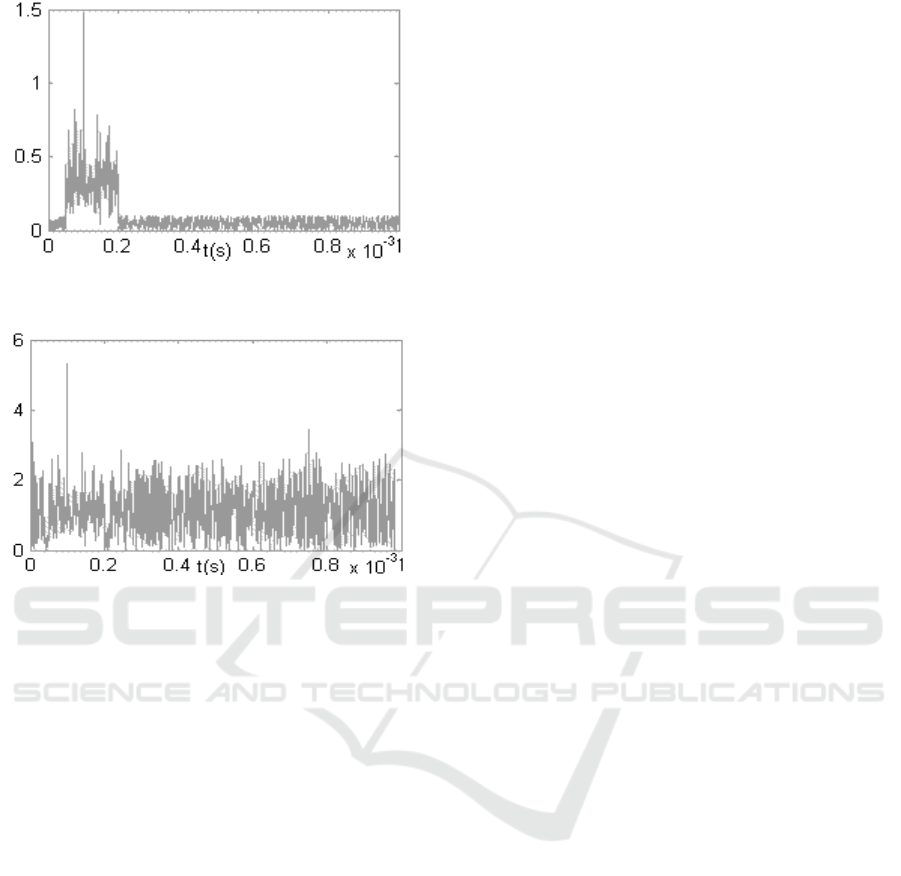
Figure 11. Target Echoes Which Have Superimposed

Clutters in Rayleigh Distribution and Thermal Noise

Figure 12. Outcome of GO-CFAR

4 CONCLUSIONS

In the simulation of radar signal processing system

using Matlab, a system model can be formed

rapidly, and your design concept can be reflected

in each little detail. It is featured by a short

modeling time and a high calculation accuracy.

The model formed is simple and clear. The model

and evaluation result can be revised, and the

system behavior can be verified at any phase of the

design. In this paper, the authors have take a

certain pulse compression radar as an example to

study the Matlab-based simulation of radar signal

processing, which achieves good outcome.

REFERENCES

Lufei Ding and Ping Zhang, 1984.Radar System. Xi’an:

Xidian University Press

You He, Jian Guan et al,1999.Radar Automatic

Detection and Constant False Alarm Processing.

Beijing: Tsinghua University Press.

Yingle Fan, 2001.Detailed Introduction of Application of

MATLAB-based Simulation. Beijing: Posts and

Telecom Press.

Yu Zhou, Linrang Zhang and Hui Tian, 2004. Radar

System Simulation Based on Matlab/ Simulink [J].

Computer Simulation.

Haimang Hu and Wanhai Yang, 2004. Simulink-based

Modeling and Simulation for Pulse Compression

Radar . Radar and Countermeasures.

Zewei Wang and Hongjin Jia,2005. Research on

Modeling and Simulation of Search Radar Radar and

Countermeasures.

ISME 2016 - Information Science and Management Engineering IV

304

ISME 2016 - International Conference on Information System and Management Engineering

304