A Convex Approach for Non-rigid Structure from Motion Via Sparse

Representation

Junjie Hu

and Terumasa Aoki

1,2

Graduate School of Information Sciences (GSIS), Tohoku University, Aramaki Aza Aoba 6-3-9, Aoba-ku, Sendai, Japan

New Industry Creation Hatchery Center (NICHe), Tohoku University, Aramaki Aza Aoba 6-6-10, Aoba-ku, Sendai, Japan

Keywords:

Non-rigid Structure From Motion, Sparse Representation, l1-norm Minimization.

Abstract:

This paper presents a convex solution for simultaneously recovering 3D non-rigid structures and camera mo-

tions from 2D image sequences based on sparse representation. Most existing methods rely on low rank as-

sumption. However, it will lead to poor reconstruction for objects with strong local deformation. Also, when

camera motion is unknown, there is no convex solution for non-rigid structure from motion (NRSfM). In order

to solve this problem, we estimate non-rigid structures by sparse representation. In this paper, we estimate

camera motions through a sparse spectral-norm minimization approach, and then a fast l1-norm minimization

algorithm is introduced to reconstruct 3D structures. Both of them are convex, therefore, our method gives

a global optimum. Our method can handle objects with strong local deformation and also doesn’t need low

rank prior. Experimental results show that our method achieves state-of-the-art reconstruction performance on

CMU benchmark dataset.

1 INTRODUCTION

Structure from Motion (SfM) is a well-known tech-

nology to simultaneously recover 3D structures and

camera motions of a rigid object from 2D correspond-

ing points. Although there are still some open prob-

lems such as real-time reconstruction, point match-

ing, large scale and dense reconstructions, the theory

has been well established over the past two decades

(Carlo and Kanade, 1992). Non-rigid Structure from

Motion (NRSfM) is an extension of SfM for non-rigid

objects. It’s also a fundamental problem in computer

vision. During the past decade, it has attracted lots of

researches and many different algorithms have been

proposed. However, there are still some problems to

be unsolved. The difﬁculty is mainly caused by the

inherently high number of degrees of freedom. For

rigid objects, the rigidity prior is enough to make the

problem well posed because well-known multi-view

relations are valid. However, this prior is not valid

for non-rigid deformable objects. For time-varying

observed 2D points, to obtain the corresponding 3D

points becomes ill posed.

Most existing methods have been attempted to

solve NRSfM by using additional constraints. For

instance, some approaches assume that the 3D non-

rigid structures can be modeled as a linear combi-

nation of several predeﬁned bases of shapes (Bre-

gler et al., 2000; Torresani et al., 2008; Xiao et al.,

2004). Also, other approaches attempt to represent a

3D point trajectory by using a ﬁxed set of discrete co-

sine transform (DCT) trajectory bases (Akhter et al.,

2008; Gotardo and Martinez, 2011; Park et al., 2010).

It also has been shown that it is a dual representation

to shape representation (Akhter et al., 2011). Gatardo

et al. combined these two concepts and proposed

an efﬁcient method that recover the trajectory using

DCT bases in a linear shape space (Gotardo and Mar-

tinez, 2011). Besides, Dai et al. proposed a well-

known rank minimization approach which minimizes

the rank of 3D structures based on nuclear minimiza-

tion algorithm and achieves one of the most remark-

able performance (Dai et al., 2014). The nuclear min-

imization based approaches then were also used to re-

construct 3D structures from realistic videos (Fragki-

adaki et al., 2014; Garg et al., 2013). These linear

representation based methods can achieve better re-

construction performance for some objects with small

deformation, but it is unable to handle strong defor-

mations such as complex human motions. Another

problem of these methods is that the number of bases

must be predeﬁned accurately, because the improper

number of bases will largely degrade the algorithm’s

performance. Unfortunately, the simple way to ﬁnd

Hu J. and Aoki T.

A Convex Approach for Non-rigid Structure from Motion Via Sparse Representation.

DOI: 10.5220/0006078603330339

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 333-339

ISBN: 978-989-758-227-1

333

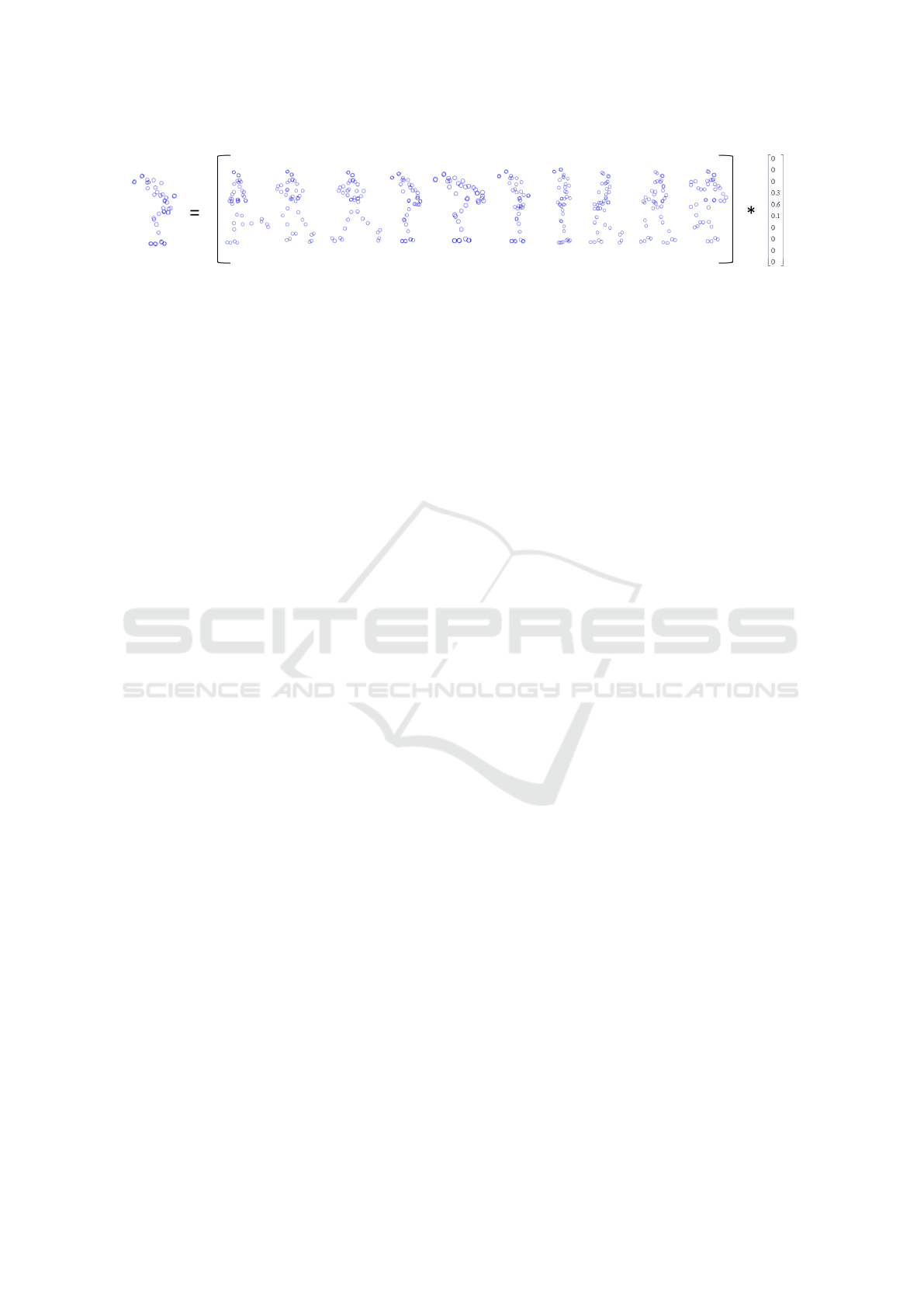
Figure 1: Illustration of the basic idea studied in this paper. The non-rigid 3D shape is represented as a linear combination of

some predeﬁned shape bases via sparse representation. We try to ﬁnd out a convex solution to estimate the sparse coefﬁcients

of the shape bases.

the optimal number of bases has not been discovered,

so we have to repeat numerous experiments to esti-

mate it.

The above limitations of existing methods

prompted us to think in another way. We thought

that the objects with complex deformation need to

be modeled by using more better bases of shapes or

trajectory. In order to avoid the problem of the esti-

mation of basis number, in this paper, we formulate

NRSfM as a sparse l1-norm minimization problem.

The 3D non-rigid structure is represented as a linear

combination of shape bases in the dictionary. One

beneﬁt of using shape basis is it allows to recover 3D

object in a sequential way which has recently been

paid many attentions (Agudo et al., 2014; Agudo and

Moreno-Noguer, 2015; Paladini et al., 2010). Due

to the fact that camera motion is unknown, the tradi-

tional sparse l1-norm minimization approach is non-

convex. Recently, Zhou et al. proposed a convex

approach to estimate camera motion based on sparse

spectral-norm minimization (Zhou et al., 2015) which

encourages us to solve sparse l1-norm minimization

problem in a convex way. As the fact that we learn

the better shape bases through dictionary learning

technique, our method can handle the objects with

complex deformation. Comparing to Zhu’s trajectory

learning method (Zhu and Lucey, 2015), our method

gives a convex solution to camera motion and also al-

lows to recover 3D structures in a sequential way. Ex-

periments demonstrate that our method could achieve

much more accurate reconstruction performance than

several existing well-known algorithms.

2 PREVIOUS WORKS

2.1 Batch Approaches

Batch approaches need to leverage the information of

all frames. After tracking 2D points over all frames,

these methods recover camera motions and 3D shapes

from 2D measurements. It can be represented as:

W = RS

s.t. R

= I

(1)

where R ∈ R

2F×3F

is the orthographic camera mo-

tion, and R

denotes the camera motion of f -th frame.

S ∈ R

3F×P

is the 3D non-rigid shapes matrix. W

∈ R

2F×P

, is the projections of S in a set of 2D images.

Due to the inherently high number of degrees of free-

dom, additional constraint is required to recover S,

such as modeling the 3D shapes as a linear combina-

tion of several predeﬁned bases of shapes:

W = RCB (2)

where B and C denote the predeﬁned shape bases

and the weight of these bases, respectively. Instead

of using predeﬁned shape bases or trajectory bases,

Dai et al. (Dai et al., 2014) formulate the following

rank minimization problem based on the assumption

of representing 3D shapes in a low rank space which

is convex and can be solved efﬁciently by minimizing

the nuclear-norm which is its convex approximation:

min rank(S)

s.t. W = RS

(3)

By such additional constraint, the non-rigid shape

can be recovered exactly. Apparently, it is necessary

to recover camera motions ﬁrstly. It has been proved

that the camera motion can be recovered uniquely and

accurately in a batch way only by using orthonormal-

ity constraints(Akhter et al., 2008; Dai et al., 2014).

But the camera motion can not be recovered for com-

plex deformable objects because the small deforma-

tion condition is essential for the recovery of camera

motion according to (Yezzi and Soatto, 2003; Zhang

and Hung, 2015).

2.2 Sequential Approaches

Sequential approaches recover 3D shape and camera

motion per frame. It can be represented as:

∑

f =1

= R

s.t. R

= I

(4)

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

334

where F denotes the total number of frames. S

are 3D shape and its 2D projection points for

f -th frame respectively. In order to solve the above

ill-posed problem, usually, camera motion and shape

deformation are considered to be smooth. Besides,

many additional conditions are also put to constrain

the deformation (Agudo et al., 2014; Agudo and

Moreno-Noguer, 2015; Paladini et al., 2010). The 3D

shape and camera motion can be solved by minimiz-

ing the following energy function:

min

∑

f =1

||W

− R

+ λ||R

− R

f −1

+µ||S

− S

f −1

(5)

where ||.||

denotes the Frobenius norm of matrix.

This optimization function is nonconvex and usually

it is solved by an alternating scheme (algorithm 1).

To date, in spite of all the efforts, the reconstruction

performance of sequential approaches is still not good

comparing with batch methods.

Algorithm 1: Sequential non-rigid structure from motion.

Input:

2D observations per frame W

Output:

camera motion R

and 3D non-rigid shape S

for each

frame

1: Initialize R

and S

;

2: while not converged do

3: update S

;

4: update R

;

5: end while

3 PROPOSED METHOD

Although small deformations can be modeled accu-

rately by a set of predeﬁned shape bases or trajectory

bases, more sufﬁcient bases should be prepared for

handling complex or strong deformations. It has been

shown that complex deformation can be modeled in

a nonlinear shape manifold (Tao and Matuszewski,

2013). Such nonlinear shape manifold can be approx-

imated well by sparse representation. Thus, in this

paper, we model the 3D non-rigid shape using a over-

complete dictionary. Such dictionary represents lots

of shape bases that learned from training data. As the

choice of bases is extremely important for NRSfM,

good basis should be assigned large weight; on the

other hand, bad basis should be abandoned. Thus, a

sparse solution is promising. Our method can be for-

mulated as the following optimization problem:

min

||W

− R

∑

i=1

+ λ||C||

(6)

where K is the total number of shape basis. B

rep-

resent the i-th shape basis in dictionary and its weight,

respectively. C is a vector contains the weight of each

shape basis C

. ||.||

denotes the l1-norm of vector

which is a convex relaxation of l0-norm minimiza-

tion. However, when R is unknown, the above mini-

mization problem is nonconvex. A common strategy

to solve Eq. (6) is to use the alternating scheme as de-

scribed in algorithm 1. However, the algorithm is not

convex, thus it may get stuck at local minimum. In

this paper, we aim at solving the above optimization

problem in a convex way; the steps of our algorithm

are summarized in algorithm 2.

3.1 Camera Motion Estimation

The ﬁrst task in our method is to estimate camera mo-

tion R accurately. Although Dai et al. introduced a

convex approach to recover R by semi-deﬁnite pro-

gramming (SDP). Their method recovers R in a batch

way and still need to be predeﬁned the number of

rank, so it can’t be employed to solve sequential

NRSfM. Therefore, we have to ﬁnd an efﬁcient solu-

tion to recover camera motion sequentially. As proved

in (Zhou et al., 2015), for each M

= R

, because

of the orthonormality of R:

= C

I (7)

such that:

||M

≤ |C

| (8)

where M

is a 2 × 3 matrix which contains camera

motion R

with weight of i-th shape basis. It’s a con-

vex relaxation to the constraint in Eq. (7), where ||.||

denotes the spectral-norm of matrix. Instead of solv-

ing Eq. (6), [16] introduced to solve the following

spectral-norm minimization problem:

min

||W

−

∑

i=1

+ λ||M||

(9)

Minimizing the above optimization function gives a

convex solution to M

and it can be solved efﬁciently

based on the algorithm of (Zhou et al., 2015). Next,

we solve the following bilinear factorization problem

to get R by the factorization algorithm of (Del Bue

et al., 2012).

min

R,C

||M − R

C||

s.t. R

= I

(10)

3.2 3D Shape Estimation

After recovering camera motion R, we will estimate

3D shape. The above spectral-norm minimization ap-

proach Eq. (9) and bilinear factorization algorithm

A Convex Approach for Non-rigid Structure from Motion Via Sparse Representation

335

Figure 2: Visualization of global optimum for l1-norm min-

imization.

Eq. (10) have already given a solution to camera mo-

tion R as well as the weights of shape bases C, it is

expected that if we can solve the original convex prob-

lem Eq. (6) we can achieve more accurate reconstruc-

tion performance. As seen in Figure 2, solving l1-

norm convex relaxation problem (spectral minimiza-

tion) can give a convex solution for camera motion R,

and when R is known, we solve the original sparse l1-

norm minimization problem Eq. (6) and ﬁnd a global

optimum for NRSfM by using a fast l1-norm mini-

mization algorithm (Lee et al., 2006). The ﬁnal de-

formable 3D shape is represented as:

∑

i=1

(11)

3.3 Shape Bases Learning

There are lots of dictionary learning algorithms. A

common strategy is to solve the following minimiza-

tion function:

min

B,L

∑

f =1

||S

−

∑

i=1

+ β||L||

s.t. ||B

≤ 1

(12)

where S

, B

, L

denote the f -th shape of training data,

a shape basis in the dictionary and its weight respec-

tively. The learned shape bases need to concisely rep-

resent the variability of training data. We use the al-

gorithm used in (Zhou et al., 2015) to learn our dic-

tionary.

Algorithm 2 : Convex sparse l1-norm minimization algo-

rithm for NRSfM.

Input:

2D observations per frame W

and shape bases dictio-

nary B

Output:

camera motion R

and 3D non-rigid shape S

for each

frame

1: Calculate M

by Eq. (9);

2: Recover camera motion R

by Eq. (10);

3: Estimate the weight C

of each shape basis in dictionary

by Eq. (11);

4: return S

∑

i=1

4 EXPERIMENTAL RESULTS

In this section, we compare our method against the

trajectory basis method (PTA) (Akhter et al., 2008),

Dai’s rank minimization method (BMM) (Dai et al.,

2014), and Zhou’s sparse spectral-norm minimization

method (Zhou et al., 2015) on the CMU motion cap-

ture database (Carnegie mellon university, ). This

database provides 41 landmark positions correspond-

ing to human motions. We selected ﬁve human mo-

tions with strong local deformations (Walking, Run-

ning, Jumping, Pickup, Marching) from this database.

For each motion, we selected three sequences as train-

ing data and one sequence for testing from the same

motion subject. For each testing data, we generated

2D projections of the 3D markers with the synthe-

sized orthographic camera around the subject for 360

degrees with the angle speed 5 per frame.

The size of the dictionary is set as 300. Since

PTA and BMM rely on low rank assumption, we set

the number of their low rank parameter from 3 to 13

and reported the best result. To compare the perfor-

mances, we measured the average 3D reconstruction

error using the same error metric as PTA and BMM

as follows:

σFn

∑

f =1

∑

n=1

f n

, σ =

∑

f =1

(σ

x + σ

y + σ

(13)

Figure 3: From ﬁrst row to last row: 3D shape of Walking,

Jumping, Marching and Pickup in 3 views recovered by the

proposed method, respectively. Recovered shapes are blue

circles and ground truth is dark dots.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

336

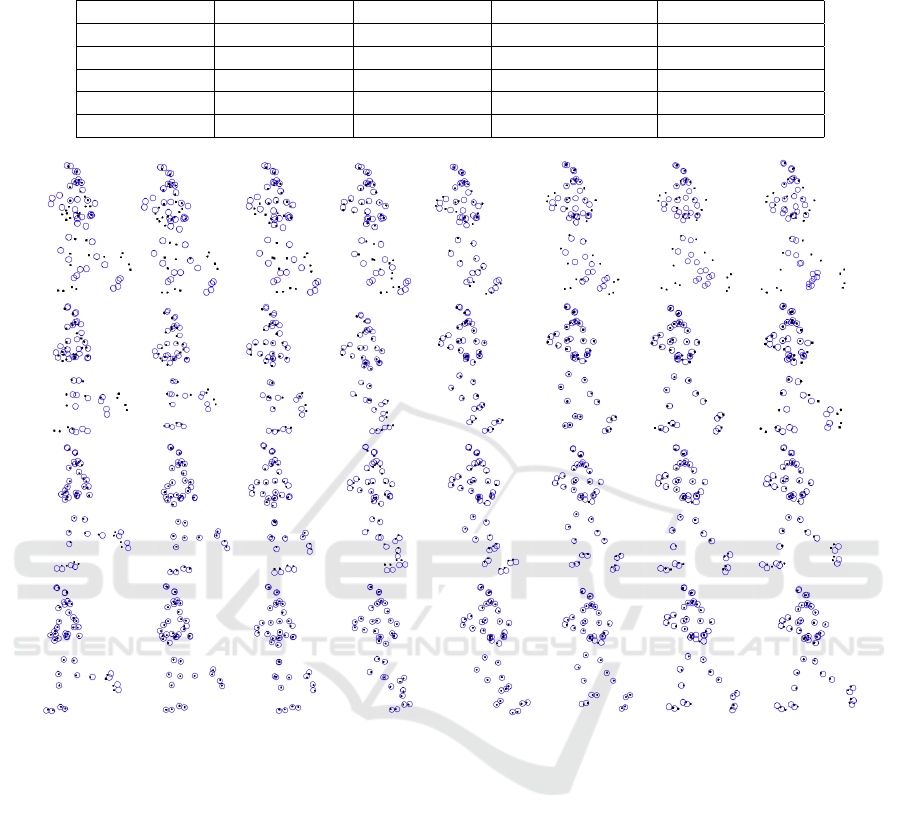
Table 1: Average 3D reconstruction error of PTA, BMM, Zhou’s method and proposed method. (K) denotes the rank number

which gave the smallest 3D error.

Dataset PTA(K) BMM(K) Zhou’s method Proposed method

Walking 0.1197(8) 0.1001(4) 0.0666 0.0394

Running 0.4212(3) 0.1638(5) 0.1093 0.0706

Jumping 0.2086(13) 0.1395(12) 0.1111 0.0728

Marching 0.1414(12) 0.1323(9) 0.1385 0.0731

Pickup 0.1211(13) 0.1412(12) 0.1163 0.0706

Figure 4: From ﬁrst row to last row: One view of 3D shapes of Running recovered by PTA, BMM, zhou’s method and the

proposed method, respectively. Recovered shapes are blue circles and ground truth is dark dots.

where σ

x, σ

y and σ

z are the standard deviations

of the X, Y and Z coordinates of the original shape in

frame f.

Table 1 shows the average 3D reconstruction er-

ror of different methods. It is seen that the pro-

posed method achieved the best performance on each

data. Figure 3 shows the 3 views of the reconstructed

shapes of Walking, Jumping, Marching, Pickup by

the proposed method. It is clear that our sparse l1-

norm minimization approach achived very accurate

reconstruction performance. Figure 4 shows the vi-

sual comparison between our method and other ap-

proaches on Running. Our method reconstructed the

legs (which is strongly deformed part of Running)

precisely than others. Also, Figure 5 (a) shows the

impact of the low rank to PTA and BMM while vary-

ing K on Running, this result proved that the per-

formance of low rank based methods largely rely on

the proper number of K. Figure 5 (b) shows the re-

sults of the proposed method with different size of

dictionary on Running. It can be observed that the

3D error decreases when the size of the dictionary in-

creases. In conclusion, experimental results show that

our method can handle non-rigid objects with strong

local deformation much better than several current

low rank based methods and Zhou’s sparse spectral-

norm minimization method. Since we don’t use the

time smoothness constraint, one more beneﬁt of the

proposed method is that it can be easily paralleled.

5 CONCLUSION

In this paper, we presented a convex solution for

NRSfM based on sparse representation. It does not

rely on low rank assumption and can reconstruct 3D

A Convex Approach for Non-rigid Structure from Motion Via Sparse Representation

337

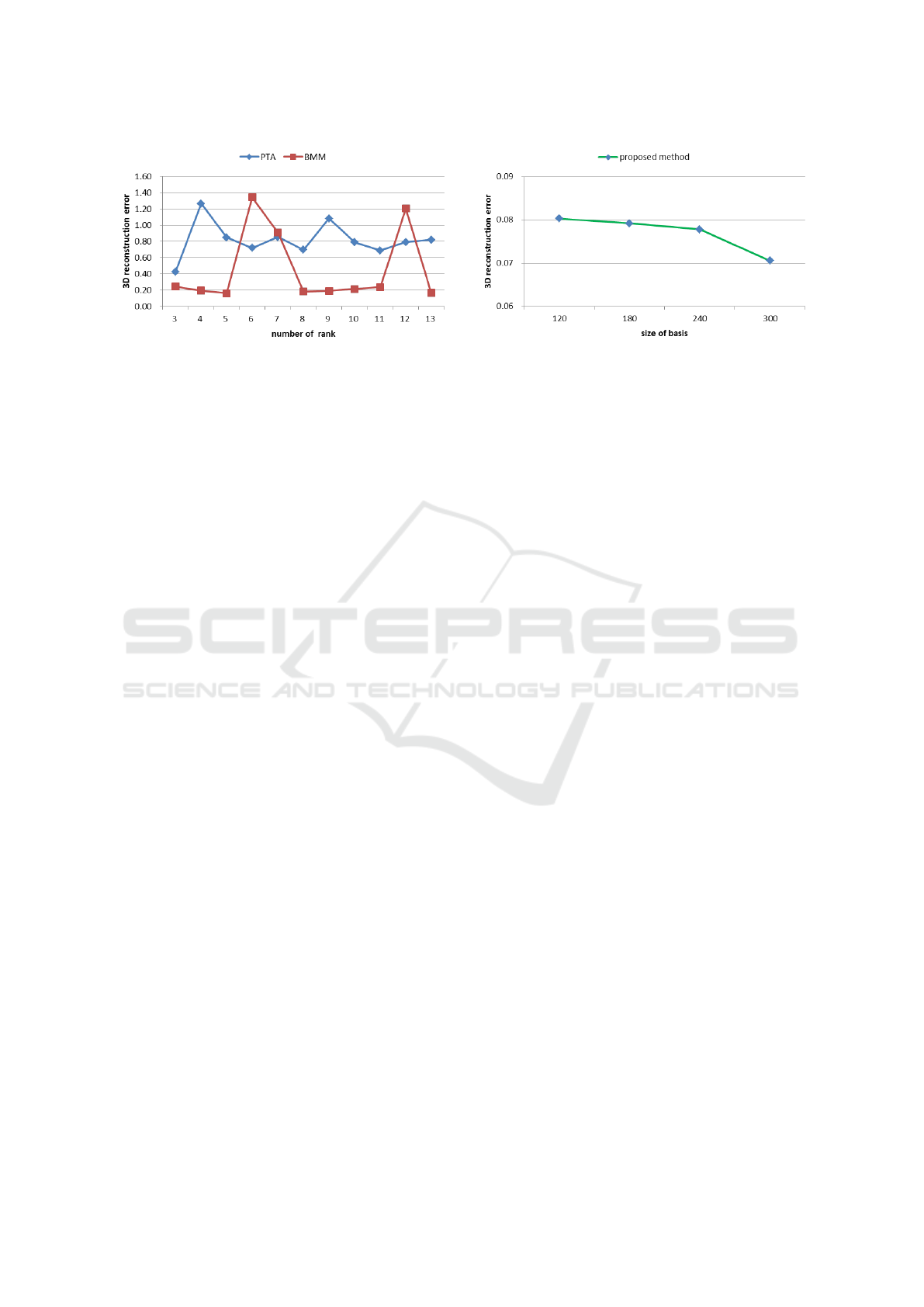
(a) (b)

Figure 5: The comparison of 3D reconstruction error between low rank based methods PTA , BMM with different rank and

our method with different dictionary size on Running.

shapes in a sequential way. As a result, we showed

that our method achieved the best reconstruction per-

formance on CMU database against several existing

methods. Unlike the low rank based methods such as

BMM and PTA, increasing the number of bases will

reduce reconstruction error for our method. We be-

lieve that our method is a reasonable choice for solv-

ing NRSfM when training data is available.

REFERENCES

Agudo, A., Agapito, L., Calvo, B., and Montiel, J. (2014).

Good vibrations: A modal analysis approach for se-

quential non-rigid structure from motion. In Proceed-

ings of the IEEE Conference on Computer Vision and

Pattern Recognition, pages 1558–1565.

Agudo, A. and Moreno-Noguer, F. (2015). Simultaneous

pose and non-rigid shape with particle dynamics. In

Proceedings of the IEEE Conference on Computer Vi-

sion and Pattern Recognition, pages 2179–2187.

Akhter, I., Sheikh, Y., Khan, S., and Kanade, T. (2008).

Nonrigid structure from motion in trajectory space. In

Advances in neural information processing systems,

pages 41–48.

Akhter, I., Sheikh, Y., Khan, S., and Kanade, T. (2011).

Trajectory space: A dual representation for nonrigid

structure from motion. Pattern Analysis and Machine

Intelligence, IEEE Transactions on, 33(7):1442–

1456.

Bregler, C., Hertzmann, A., and Biermann, H. (2000). Re-

covering non-rigid 3d shape from image streams. In

Computer Vision and Pattern Recognition, 2000. Pro-

ceedings. IEEE Conference on, volume 2, pages 690–

696. IEEE.

Carlo, T. and Kanade, T. (1992). Shape and motion from

image streams under orthography: a factorization

method. International Journal of Computer Vision,

9(2):137–154.

Carnegie mellon university, . Cmu graphics lab motion cap-

ture database. http://mocap.cs.cmu.edu/.

Dai, Y., Li, H., and He, M. (2014). A simple prior-

free method for non-rigid structure-from-motion fac-

torization. International Journal of Computer Vision,

107(2):101–122.

Del Bue, A., Xavier, J., Agapito, L., and Paladini, M.

(2012). Bilinear modeling via augmented lagrange

multipliers (balm). Pattern Analysis and Machine In-

telligence, IEEE Transactions on, 34(8):1496–1508.

Fragkiadaki, K., Salas, M., Arbelaez, P., and Malik, J.

(2014). Grouping-based low-rank trajectory comple-

tion and 3d reconstruction. In Advances in Neural In-

formation Processing Systems, pages 55–63.

Garg, R., Roussos, A., and Agapito, L. (2013). Dense

variational reconstruction of non-rigid surfaces from

monocular video. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 1272–1279.

Gotardo, P. F. and Martinez, A. M. (2011). Non-rigid struc-

ture from motion with complementary rank-3 spaces.

In Computer Vision and Pattern Recognition (CVPR),

2011 IEEE Conference on, pages 3065–3072.

Lee, H., Battle, A., Raina, R., and Ng, A. Y. (2006). Efﬁ-

cient sparse coding algorithms. In Advances in neural

information processing systems, pages 801–808.

Paladini, M., Bartoli, A., and Agapito, L. (2010). Sequential

non-rigid structure-from-motion with the 3d-implicit

low-rank shape model. In Computer Vision–ECCV

2010, pages 15–28. Springer.

Park, H. S., Shiratori, T., Matthews, I., and Sheikh, Y.

(2010). 3d reconstruction of a moving point from a

series of 2d projections. In ECCV, pages 158–171.

Tao, L. and Matuszewski, B. (2013). Non-rigid structure

from motion with diffusion maps prior. In Proceed-

ings of the IEEE Conference on Computer Vision and

Pattern Recognition, pages 1530–1537.

Torresani, L., Hertzmann, A., and Bregler, C. (2008).

Nonrigid structure-from-motion: Estimating shape

and motion with hierarchical priors. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

30(5):878–892.

Xiao, J., Chai, J., and Kanade, T. (2004). A closed-form

solution to non-rigid shape and motion recovery. In

ECCV, pages 573–587.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

338

Yezzi, A. J. and Soatto, S. (2003). Deformotion: Deforming

motion, shape average and the joint registration and

approximation of structures in images. International

Journal of Computer Vision, 53(2):153–167.

Zhang, P. B. and Hung, Y. S. (2015). Non-rigid struc-

ture from motion through estimation of blend shapes.

In Digital Image Computing: Techniques and Appli-

cations (DICTA), 2015 International Conference on,

pages 1–7. IEEE.

Zhou, X., Leonardos, S., Hu, X., and Daniilidis, K. (2015).

3d shape estimation from 2d landmarks: A convex re-

laxation approach. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 4447–4455.

Zhu, Y. and Lucey, S. (2015). Convolutional sparse cod-

ing for trajectory reconstruction. Pattern Analy-

sis and Machine Intelligence, IEEE Transactions on,

37(3):529–540.

A Convex Approach for Non-rigid Structure from Motion Via Sparse Representation

339