
Visual Odometry from Two Point Correspondences
and Initial Automatic Camera Tilt Calibration
Mårten Wadenbäck
1
, Martin Karlsson
2
, Anders Heyden
1
,
Anders Robertsson
2
and Rolf Johansson
2
1
Centre for Mathematical Sciences, Lund University, Lund, Sweden
2
Department of Automatic Control, Lund University, Lund, Sweden
Keywords:
Visual Odometry, Tilted Camera, Trajectory Recovery.
Abstract:
Ego-motion estimation is an important step towards fully autonomous mobile robots. In this paper we propose
the use of an initial but automatic camera tilt calibration, which transforms the subsequent motion estimation
to a 2D rigid body motion problem. This transformed problem is solved `
2
-optimally using RANSAC and a
two-point method for rigid body motion. The method is experimentally evaluated using a camera mounted
onto a mobile platform. The results are compared to measurements from a highly accurate external camera
positioning system which are used as gold standard. The experiments show promising results on real data.
1 INTRODUCTION
One of the fundamental problems in robotics research
is how to use various sensor data to estimate ac-
curately the position and motion of a mobile robot.
The solution to this problem will by necessity depend
heavily on various application specific considerations,
such as the type and quality of the sensors employed
and the environment in which the robot is intended
to operate. Many of the successful approaches to
this problem have been formulated in the framework
of Simultaneous Localisation and Mapping (SLAM),
where the robot estimates a map of its surroundings
as well as its own position with respect to this map.
What is considered a suitable representation of the
map is also application specific, and can range from
sparse clouds of feature points to dense and textured
3D models.
The early methods for SLAM were focused on
sensors such as wheel encoders and laser range find-
ers, and how to use statistical estimation and filtering
techniques to determine ego-motion and relative posi-
tion from such data. The probabilistic viewpoint has
proven to be a suitable framework for visual SLAM
as well, and has remained popular from pioneering
works such as those by Harris and Pike (1988) and by
Durrant-Whyte (1987) to more recent methods such
as the vSLAM system by Karlsson et al. (2005) and
the MonoSLAM system by Davison et al. (2007). In
this type of algorithms, Kalman filters and particle fil-
ters (Gustafsson, 2012) are popular choices, and are
often used e.g. to include a kinematic motion model
or to combine data from different sensors.
An important sub-problem in SLAM deals with
Loop Closure, where the goal is to join spatially close
but temporally distant areas of the map. Being able
to detect loops typically allows a drastic reduction in
the accumulated positioning error, as demonstrated by
e.g. Newman and Ho (2005) and Jones and Soatto
(2011). However, if the loops are allowed to be of ar-
bitrary length, the storage of, and comparison against,
an increasingly large map becomes inhibiting both in
terms of storage and computation time.
On the other end of the spectrum are the so called
odometry methods, in which the map comprises only
very recent information that is used for local estima-
tion of relative position. The study of these methods
is important because they must be used if no loop has
yet been detected, or if for some reason loop closure
is not a viable option. When cameras are the primary
sensors used in an odometry method, as in this present
paper, it is often referred to as Visual Odometry (VO).
In many practical cases, especially for ground ro-
bots in indoor environments, the motion of the ro-
bot is constrained to a plane parallel to the floor. By
considering methods which explicitly assume planar
motion, the vertical positioning error of the attached
sensors will automatically be bounded over arbitrarily
long motion sequences. This insight has successfully
been utilised in several visual navigation systems such
as Ortín and Montiel (2001), Hajjdiab and Lagan-
ière (2004), Liang and Pears (2002), Scaramuzza
(2011a,b), and Zienkiewicz and Davison (2015).
340
WadenbÃd’ck M., Karlsson M., Heyden A., Robertsson A. and Johansson R.
Visual Odometry from Two Point Correspondences and Initial Automatic Camera Tilt Calibration.
DOI: 10.5220/0006079903400346
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 340-346
ISBN: 978-989-758-227-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Sample images from the positioning experiments. We assume that there is some perceivable structure in the floor,
but otherwise no particular preparation of the environment is necessary. This is mainly a requirement for the feature detector,
rather than for the proposed method itself.
Ortín and Montiel consider the epipolar geometry
derived from planar camera motion, and propose both
a linear three-point method and a non-linear two-point
method to estimate this type of camera motion (Ortín
and Montiel, 2001). The method requires the camera
to be mounted with the y-axis vertical with high ac-
curacy, which is achieved by means of a spirit level.
Neither of the methods presented in their paper de-
termine the relative length of the translation, which
therefore must be determined in some other way.
Essentially the same motion parametrisation was
used in the approach proposed by Scaramuzza, but
with an additional nonholonomic constraint based on
the assumption that the local motion is a circular mo-
tion (Scaramuzza, 2011a,b). Because of this addi-
tional constraint, the local motion can be estimated
from only one point correspondence, which allows
for a very efficient outlier removal based on his-
togram voting. The approach is evaluated on rela-
tively long motion sequences captured from a camera
mounted onto a car. Despite its many advantages, the
method shares the same weakness as Ortín and Mon-
tiel (2001) that the camera orientation must be known,
and no efficient way to calibrate this is presented. Fur-
thermore, though the nonholonomic constraint may
be valid in automotive applications, it is not valid for
robots with omnidirectional wheels (e.g. robots such
as the Fraunhofer IPA rob@work platform shown in
Figure 3).
In contrast to the two previously mentioned meth-
ods, Zienkiewicz and Davison use a dense matching
of the whole image in order to determine the full
camera pose (Zienkiewicz and Davison, 2015). The
method is demonstrated to perform well under a large
number of different conditions. Since the camera pose
is computed during the registration of the images, no
effort must be spent in order to mount the camera in
a particular way. The method relies on an efficient
implementation on a GPU in order to cope with the
heavy computations involved in performing the dense
registration.
The problem addressed in the present paper is the
determination of orientation and position of a mobile
robot during a motion sequence. Our goal is to use
d
ϕ
Figure 2: Illustration of the two-dimensional rigid body mo-
tion under consideration. The motion of the platform is
described by a displacement d and a rotation an angle ϕ
around the plane normal.
images from a camera mounted onto a mobile robot
in an unknown but rigid downward direction, together
with the assumption of planar motion to provide accu-
rate estimates of the local robot motion. Our method
does not yet perform any filtering techniques or non-
linear optimisation over several frames, but focuses
entirely on estimating the local motion. Some sample
images captured by the camera under these conditions
are shown in Figure 1.
The idea presented in this paper is to transform
the motion of the feature points into a 2D rigid body
motion problem, which is solved `
2
-optimally using a
decoupling of the determination of rotation and trans-
lation proposed by Arun, Huang and Blostein (1987).
This transformation of the problem is achieved by
performing an initial determination of the camera tilt
using the method by Wadenbäck and Heyden (2014).
This initial and automatic tilt calibration allows the
camera to be mounted onto the robot in an arbitrary
downward direction, and allows the subsequent mo-
tion estimates to be computed directly from the fea-
ture points instead of from a homography or essential
matrix.
2 METHOD
Our method relies on corresponding feature points in
the images, which need to be reliably detected and
matched. The selection of algorithms for this particu-
lar sub-problem is beyond the scope of this paper. In
Visual Odometry from Two Point Correspondences and Initial Automatic Camera Tilt Calibration
341

our experiments we used SURF features (Bay, Tuyte-
laars and Van Gool, 2006), which were matched using
the approximate nearest neighbour matching (Muja
and Lowe, 2009, 2014). This selection is not based on
a thorough evaluation of the alternatives, but it does
provide sufficiently useful point correspondences for
the method we present.
2.1 Camera Parametrisation
Assuming the standard model of the pinhole perspec-
tive camera (see Hartley and Zisserman (2004) for
an in-depth discussion), with known and constant in-
trinsic parameters, the normalised camera projection
matrix associated with an image taken at position
d = (d
1
,d
2
,d
3
) will be
P = R(ψ,θ, ϕ)[I | − d]. (1)
Here, (ψ, θ,ϕ) are Tait-Bryan angles
1
defining the
orientation through the rotation matrix
R(ψ, θ,ϕ) = R
x
(ψ)R
y
(θ )R
z
(ϕ), (2)
where each of R
x
, R
y
, and R
z
denotes a rotation about
its corresponding coordinate axis. In this work ψ and
θ are unknown but constant, whereas ϕ and d may
vary from image to image. We furthermore assume
that the camera moves in the plane z = 0 (i.e. we al-
ways have d
3
= 0), and that the floor plane is z = 1.
These assumptions do not constrain the model, be-
cause they only reflect our choice of global coordinate
frame.
2.2 Tilt Estimation
In this section we present a brief review of the tilt es-
timation scheme in Wadenbäck and Heyden (2014).
Without loss of generality, the camera projection ma-
trices associated with two images may be written as
(
P = R
ψθ
[I | 0]
P
0
= R
ψθ
R
z
(ϕ)[I | − d],
(3)
where R
ψθ
= R(ψ, θ , 0) is the unknown camera tilt.
From (3) it follows that the inter-image homography
will be of the form
H = R
ψθ
R
z
(ϕ)(I − dn
T
)R
T
ψθ
, (4)
where n = (0,0, 1) is a normal to the floor. As a con-
sequence,
R
T
ψθ
H
T
HR
ψθ
= (I − dn
T
)
T
(I − dn
T
). (5)
1
In the whole of this paper we will consider angles as
equivalence classes, where angles differing with additive
multiples of 2π belong to the same class.
In this matrix equation, it turns out that some elements
depend only on ψ and θ . Denoting the left hand side
of (5) by L, one obtains two non-linear equations
L
11
− L
22
= 0
L
12
= 0.
(6)
Wadenbäck and Heyden proposed a coordinate
descent-like method where in each iteration (6) be-
came a linear system of equations in the trigonomet-
ric functions. This allows several homographies of
the type (4) to be used simultaneously in the estima-
tion by simply stacking the linear systems, which im-
proves robustness and accuracy.
For this tilt estimation method to succeed, it is
assumed that for most of the homographies used the
translation vector d and the angle ϕ are not both zero,
otherwise the tilt angles ψ and θ are not well defined.
If indeed d and ϕ are both zero, the homography ma-
trix will be a scalar multiple of the identity matrix,
and this case is thus easily and efficiently detected
by a separate check. This situation arises in practice,
since the robot may at times stop during the motion,
e.g. to await new commands or to avoid collision with
obstacles.
2.3 Motion Estimation
Suppose x
0
j
↔ x
j
, j = 1, . . . , N are point correspon-
dences between the first and second image, expressed
in homogeneous coordinates. These must satisfy
x
0
j
∼ Hx
j
⇔
R
T
ψθ
x
0
j
∼ R
z
(ϕ)(I − dn
T
)R
T
ψθ
x
j
.
(7)
After the tilt has been determined as explained in
Section 2.2, we consider R
ψθ
to be known. Introduc-
ing
y
j
∼ R
T
ψθ
x
j
and y
0
j
∼ R
T
ψθ
x
0
j
, (8)
and using the representation with last coordinate
equal to one, (7) becomes a planar rigid body motion
in terms of z
j
= πy
j
and z
0
j
= πy
0
j
. Here π denotes an
orthogonal projection onto the first two coordinates,
i.e.
π =
1 0 0
0 1 0
. (9)
If all point correspondences are correct, i.e. no out-
liers are present, this may be solved directly in a least
squares sense using an adaptation to 2D of the method
presented in Arun, Huang and Blostein (1987). The
2D version of this problem is well-posed if at least
two point correspondences are used, and the solution
gives an estimate of ϕ and d.
The least squares solution to the rigid body mo-
tion problem presented in Arun, Huang and Blostein
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
342

(1987) works by decoupling the translation and the
rotation involved. It is shown that by forming
q
j
= z
j
−
1
N
N
∑
k=1
z
k
and q
0
j
= z
0
j
−
1
N
N
∑
k=1
z
0
k
, (10)
the optimal rotation matrix is VU
T
, where M =UΣV
T
is a singular value decomposition of
M =
N
∑
j=1
q
j
(q
0
j
)
T
. (11)
The optimal estimate d
∗
2D
of the 2D translation vector
will then be
d
∗
2D
=
1
N
N
∑
k=1
z
0
k
−VU
T
1
N
N
∑
k=1
z
k
, (12)
and to get the 3D translation a zero should be ap-
pended as the third coordinate.
Since the point correspondences are found by au-
tomatically matching the feature points, there will
typically be many incorrect matches, and a robust
estimation framework should be used. For this rea-
son, we employ the RANSAC framework (Fischler
and Bolles, 1981) to fit the rigid body motion to ran-
dom samples containing two point correspondences.
In each RANSAC iteration, a motion model is deter-
mined from two point correspondences, and for all
other point correspondences the difference between
the forward mapped points and the points observed
in the second image are computed. Here, points with
a transfer error greater than a certain threshold, typi-
cally expressed in terms of the standard deviation, are
regarded as outliers. In our experiments, a threshold
of one standard deviation worked well for the outlier
removal. After a suitable inlier set has been deter-
mined, the final motion model is determined using the
rigid body motion estimation method described above
with all the inliers.
3 EXPERIMENTS
During the experiments, a mobile robot of model
Fraunhofer IPA rob@work (base platform) (Fraun-
hofer IPA, 2012) was used. The platform, shown in
Figure 3, has omnidirectional wheels, allowing it to
perform pure translations and pure rotations, as well
as combinations of these. A camera was attached
to the undercarriage, directed down towards the floor
plane and recording at approximately ten frames per
second.
The tilt angles were determined from the first few
non-identity homographies, on which the tilt estima-
tion described in Section 2.2 was applied, and were
Figure 3: The experiments were carried out on a mobile
robot of model Fraunhofer IPA rob@work (base platform).
10 20 30 40
−20
−10
0
Number of homographies
Angle (degrees)
Line Experiment
ψ
θ
Figure 4: The tilt estimation reached convergence after
about 15-20 frames (roughly 2 s of motion). Since the tilt
estimation problem is ill-posed for very small translations,
using fewer than five images did not give reasonable esti-
mates with the current frame rate and velocity.
used for the remainder of the motion sequence. Since
the camera was mounted slightly differently in the dif-
ferent experiments, the tilt calibration had to be per-
formed for each experiment. In our experience, the
tilt estimation reached convergence after about 15-20
frames (roughly 2 s of motion), as can be seen in Fig-
ure 4.
3.1 Evaluation Against Gold Standard
For the experiments presented in this section, a highly
accurate optical tracking system of model K600 from
Nikon Metrology (Nikon Corporation, 2011) was
used for reference and served as gold standard for the
platform position. This system provides an absolute
accuracy of less than 100 µm, and was sampled at the
rate 250 Hz. In addition to the camera shown in Fig-
ure 5(a), the tracking system consists of a number of
LEDs mounted on the robot, for the Nikon Metrology
camera to track.
Visual Odometry from Two Point Correspondences and Initial Automatic Camera Tilt Calibration
343

(a) Nikon Metrology K600 (b) Axis P3364-VE
Figure 5: The stationary Nikon Metrology K600 camera (a)
used to measure the gold standard positions in the experi-
ments. This is not to be confused with the (Axis Communi-
cations AB, 2012) (b) that was mounted on the mobile robot
and used for the VO.
During these positioning experiments, the mobile
robot moved in three different motion patterns de-
scribed below.
1. Translation along a straight line with constant ori-
entation.
2. Translation forward, followed by translation to the
right, in the robot’s own frame. Again, the ori-
entation was kept constant. This motion is pos-
sible due to the omnidirectional wheels of the
robot, and resembles an effective version of par-
allel parking.
3. Translation combined with rotation (light turn).
The robot moved forward in relation to its own
frame, while rotating to the right, which resulted
in a curved path.
The motion patterns may be viewed in Figure 6, and
the positioning errors in relation to travelled distance
are shown in Figure 7. The average absolute position
error was 2.3 mm, 5.0 mm and 8.7 mm, for the trials
consisting of a straight line, parallel parking, and turn,
respectively.
3.2 Evaluation on a Longer Sequence
We also tried a slightly longer motion sequence,
shaped approximately as an ellipse, with a total length
of about 5.75 m and in which the robot made a full
turn. The robot was driven in such a way so as to
introduce some small irregularities to the trajectory,
and such that the images at the starting position and
the final position were overlapping. Due to range and
workspace limitations in the Nikon system, there is
no gold standard data for this experiment. Instead,
the images from the starting position and the final po-
sition were used to determine the true final position,
which was then compared to the final positions esti-
mated by the VO approach.
The result from this experiment is shown in Fig-
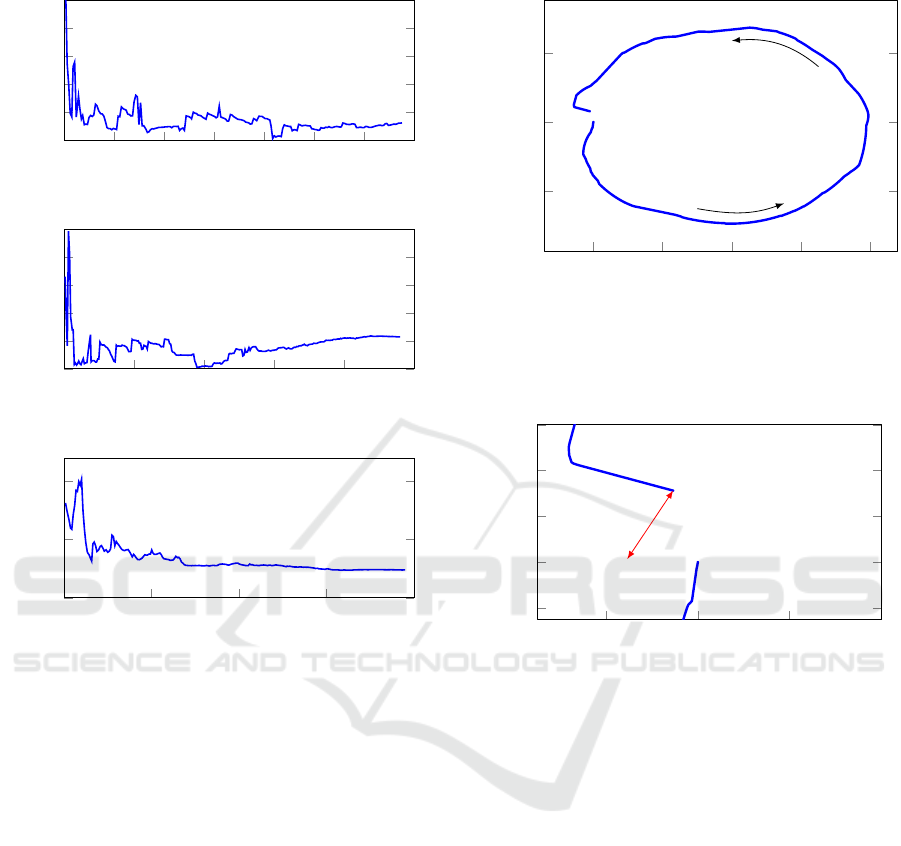
ure 8 and Figure 9. The position error in the final
0 100 200 300 400
500 600
−50
0
50
x (mm)
y (mm)
Line Experiment
Gold Standard Visual Odometry
0 100 200 300 400
0
100
200
300
400
x (mm)
y (mm)
Parallel Parking Experiment
Gold Standard Visual Odometry
0 100 200 300 400
500
−50
0
50
x (mm)
y (mm)
Turning Experiment
Gold Standard Visual Odometry
Figure 6: True and estimated positions, using VO. The fig-
ure shows the motions in the same order as they are de-
scribed in the text, i.e. straight line (top), parallel park-
ing (middle), and light turn (bottom). See also Figure 7,
where the position errors in relation to travelled distance
are shown.
position, as determined by comparing the first and fi-
nal image as explained above, was found to be 0.71 %
of the travelled distance.
4 DISCUSSION
The positioning provides good estimates locally, but
like all dead reckoning approaches, the accuracy de-
teriorates with the travelled distance. Sources of error
include inaccuracies in the intrinsic camera calibra-
tion, noise and outliers influence in the feature point
matching, as well as limited image resolution. Addi-
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
344
0
5
10
15
20
25
30
35
0.00
0.02
0.04
0.06
0.08
0.10
Time (s)
Relative error
Line Experiment
0 10 20 30 40
50
0.00
0.02
0.04
0.06
0.08
0.10
Time (s)
Relative error
Parallel Parking Experiment
0 10 20 30 40
0.00
0.05
0.10
Time (s)
Relative error
Turn Experiment
Figure 7: Relative estimation error, formed by dividing the
absolute error with travelled distance. The figure shows the
motions in the same order as they are described in the text
and in Figure 6.
tional sources are the carriage suspension and imper-
fections in the ground surface, which may invalidate
the planar motion assumption.
It remains as future work to extend this method
by considering map building parallel to the position-
ing in order to improve the performance over longer
distances, and to employ filtering techniques or non-
linear optimisation over several frames. Furthermore,
one could include sensors such as laser range finders,
to avoid the problem with pure dead reckoning.
5 CONCLUSIONS
In this paper we have proposed and evaluated a VO
approach based on 2D rigid body motion. The method
relies on an initial estimation of the camera tilt, which
we have demonstrated can be achieved from a short
automatic calibration process. After the tilt calibra-
0
500
1,000
1,500
2,000
−500
0
500
x (mm)
y (mm)
Closed Loop Experiment
Figure 8: Trajectory estimated using VO. Here the trajec-
tory has been scaled and is shown in the true scale, although
this scale cannot be determined from the images alone.
−100 0 100 200
−50
0
50
100
150
x (mm)
y (mm)
Closed Loop Experiment
True final
position
Estimated
final position
Initial
position
Figure 9: Close-up of the trajectory in Figure 8, showing
the initial and final position.
tion, a rigid body motion problem is solved robustly
using RANSAC and a two-point method, which fi-
nally gives an `
2
-optimal fit to the inliers. The method
has been evaluated experimentally, and was demon-
strated to achieve high positioning accuracy. This pa-
per additionally provided experimental verification of
the work in Wadenbäck and Heyden (2014) on real
image data.
ACKNOWLEDGMENTS
This work has been partly funded by the Swedish
Foundation for Strategic Research through the SSF
project ENGROSS (www.engross.lth.se). Among the
authors are members of the LCCC Linnaeus Center
and the ELLIIT Excellence Center at Lund Univer-
sity.
Visual Odometry from Two Point Correspondences and Initial Automatic Camera Tilt Calibration
345

REFERENCES
Arun, K. S., T. S. Huang and S. D. Blostein (1987). “Least
Squares Fitting of Two 3-D Point Sets”. In: IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence 9(5), pp. 698–700.
Axis Communications AB (2012). AXIS P3364-VE Net-
work Camera. URL: http://www.axis.com/global/en/
products/axis-p3364-ve (visited on 27/02/2016).
Bay, H., T. Tuytelaars and L. Van Gool (2006). “SURF:
Speeded Up Robust Features”. In: Proceedings of
the 9th European Conference on Computer Vision
(ECCV). Vol. 3951. in series Lecture Notes in Com-
puter Science. Graz, Austria: Springer-Verlag, pp.
404–417.
Davison, A. J., I. D. Reid, N. D. Molton and O. Stasse
(2007). “MonoSLAM: Real-Time Single Camera
SLAM”. In: IEEE Transactions on Pattern Analysis
and Machine Intelligence 29(6), pp. 1052–1067.
Durrant-Whyte, H. F. (1987). “Consistent Integration and
Propagation of Disparate Sensor Observations”. In:
The International Journal of Robotics Research 6(3),
pp. 3–24.
Fischler, M. A. and R. C. Bolles (1981). “Random Sample
Consensus: A Paradigm for Model Fitting with Ap-
plications to Image Analysis and Automated Cartog-
raphy”. In: Communications of the ACM 24(6), pp.
381–395.
Fraunhofer IPA (2012). Compact Drive Modules for
Omnidirectional Robot Platforms. URL: http://
www.care-o-bot.de/en/rob-work.html (visited on
26/02/2016).
Gustafsson, F. (2012). Statistical Sensor Fusion. Second
ed. Lund, Sweden: Studentlitteratur AB.
Hajjdiab, H. and R. Laganière (2004). “Vision-based Multi-
Robot Simultaneous Localization and Mapping”. In:
Proceedings of the 1st Canadian Conference on Com-
puter and Robot Vision (CRV). London, ON, Canada:
IEEE Computer Society, pp. 155–162.
Proceedings of the IEEE International Conference on
Robotics and Automation (ICRA) (2005). Barcelona,
Spain: IEEE Robotics and Automation Society.
Harris, C. G. and J. M. Pike (1988). “3D Positional Inte-
gration from Image Sequences”. In: Image and Vision
Computing 6(2), pp. 87–90.
Hartley, R. I. and A. Zisserman (2004). Multiple View Ge-
ometry in Computer Vision. Second ed. Cambridge,
England, UK: Cambridge University Press.
Jones, E. S. and S. Soatto (2011). “Visual-inertial naviga-
tion, mapping and localization: A scalable real-time
causal approach”. In: The International Journal of
Robotics Research 30(4), pp. 407–430.
Karlsson, N. et al. (2005). “The vSLAM Algorithm for Ro-
bust Localization and Mapping”. In: Proceedings of
the IEEE International Conference on Robotics and
Automation (ICRA). Barcelona, Spain: IEEE Robotics
and Automation Society, pp. 24–29.
Liang, B. and N. Pears (2002). “Visual Navigation using
Planar Homographies”. In: Proceedings of the IEEE
International Conference on Robotics and Automation
(ICRA). Vol. 1.Washington, DC, USA: IEEE Robotics
and Automation Society, pp. 205–210.
Muja, M. and D. G. Lowe (2009). “Fast Approximate Near-
est Neighbors with Automatic Algorithm Configura-
tion”. In: Proceedings of the Fourth International
Conference on Computer Vision Theory and Applica-
tions (VISAPP). Vol. 1. Lisbon, Portugal: INSTICC
Press, pp. 331–340.
Muja, M. and D. G. Lowe (2014). “Scalable Nearest Neigh-
bor Algorithms for High Dimensional Data”. In: IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence 36(11), pp. 2227–2240.
Newman, P. and K. Ho (2005). “SLAM- Loop Closing with
Visually Salient Features”. In: Proceedings of the
IEEE International Conference on Robotics and Au-
tomation (ICRA). Barcelona, Spain: IEEE Robotics
and Automation Society, pp. 635–642.
Nikon Corporation (2011). K-Series Optical CMM solu-
tions – supporting a variety of metrology apploca-
tions. URL: http://www.nikonmetrology.com (visited
on 26/02/2016).
Ortín, D. and J. M. M. Montiel (2001). “Indoor robot mo-
tion based on monocular images”. In: Robotica 19(3),
pp. 331–342.
Scaramuzza, D. (2011a). “1-Point-RANSAC Structure
from Motion for Vehicle-Mounted Cameras by Ex-
ploiting Non-holonomic Constraints”. In: Interna-
tional Journal of Computer Vision 95(1), pp. 74–85.
Scaramuzza, D. (2011b). “Performance Evaluation of 1-
Point-RANSAC Visual Odometry”. In: Journal of
Field Robotics 28(5), pp. 792–811.
Wadenbäck, M. and A. Heyden (2014). “Ego-Motion Re-
covery and Robust Tilt Estimation for Planar Motion
Using Several Homographies”. In: Proceedings of
the 9th International Conference on Computer Vision
Theory and Applications (VISAPP). Vol. 3. Lisbon,
Portugal: SCITEPRESS, pp. 635–639.
Zienkiewicz, J. and A. J. Davison (2015). “Extrinsics Au-
tocalibration for Dense Planar Visual Odometry”. In:
Journal of Field Robotics 32(5), pp. 803–825.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
346
