Coordination, Synchronization and Localization Investigations in a

Parallel Intelligent Robot Cellular Automata Model that Performs

Foraging Task

Danielli A. Lima

1,2

, Claudiney R. Tinoco

, Juan M. N. Viedman

and Gina M. B. Oliveira

Universidade Federal de Uberlandia UFU, Faculdade de Computacao, Avenida Joao Naves de Avila 2121,

Campus Santa Monica, Uberlandia, Minas Gerais, Brasil

Instituto Federal do Triangulo Mineiro IFTM, Departamento de Informatica, Avenida Liria Terezinha

Lassi Capuano 255, Chacara das Rosas, Patrocinio, Minas Gerais, Brasil

Keywords:

Cellular Automata, Multi-agents Control, Intelligent Swarms, Parallel Synchronization, Foraging Task,

Multi-objective Search.

Abstract:

Multiple agent systems can be applied to foraging tasks, thus solving this problem in a cooperative intelligent

approach using cellular automata modeling. The objective is to construct an algorithm that performs foraging

task correctly in Webots EDU simulation platform using robot architecture and also improves the individual

controller model of each intelligent agent, using e-Puck devices properly. The proposed communication model

has taken into account some cellular automata speciﬁcations, such as, the need for parallel synchronization,

localization and accuracy of information dependency. After several simulations in Webots EDU, evaluating

different approaches, the proposed communication model presented promising results on the parallel multi-

robot foraging performance being pertinent in intelligent swarm robotics context.

1 INTRODUCTION

Many collective biological systems have a higher

performance over a single agent, specially as many

agents can perform different kinds of tasks in par-

allel. This expectation associated with the poten-

tial advantages of using multi-agents over a single

agent have attracted the attention of many researchers.

However, the enormous potential associated with the

multi-agents system is achieved only if the respec-

tive coordination strategies are efﬁcient. There are

many suitable application approaches using multi-

agent systems, such as search and rescue operations

in a disaster (Kantor et al., 2006), garbage collection

(Vargas et al., 2012), and exploration and surveillance

(Calvo et al., 2014). The design process of coordina-

tion strategies algorithms for multiple agent systems

is a challenging problem in robotics, games, or any

other area that uses multiple agents. In this work, each

agent is a robot performing the foraging task.

Foraging task is one of the most studied tasks

for mobile robots, which is very relevant to collec-

tive intelligent robotics (Lima and Oliveira, 2016a).

This task can be studied as robot-robot cooperation

ﬁeld in multi-robot systems and this task is a repre-

sentation of other studied problems, such as cleaning

(Fortunati, 2016), search and rescue (Couceiro et al.,

2011), or surveillance (Lima et al., 2016). Two major

processes executed by a forager robot are searching

and homing, being that in the ﬁrst process the robot

needs to ﬁnd an object placed in unknown location

and in the second it has already collected the object

and needs to deposit it into nests.

Ants use different interactions depending on

the task being tackled and they can interact using

pheromone or direct communication, which produce

a network that represents the colony behavior, called

stigmergy (Beckers et al., 1994). An outgoing for-

ager ant does not go out unless it gets enough inter-

actions with returning foragers, because ants have a

mechanism that can indirectly count other ants near

the nests, as a density calculus (Gordon, 2014). There

are different types of pheromone, if a pheromone

trail is found and this pheromone type indicates

food, then more ants follow this trail, depositing

more pheromone and reinforcing the stimuli (Calvo

et al., 2014). An opposite behavior happens if the

pheromone is of the aversive type, indicating risk and

danger, in this case, they can use the pheromone to

spread out (Gordon, 2014).

Lima D., Tinoco C., Viedman J. and Oliveira G.

Coordination, Synchronization and Localization Investigations in a Parallel Intelligent Robot Cellular Automata Model that Performs Foraging Task.

DOI: 10.5220/0006081403550363

In Proceedings of the 9th International Conference on Agents and Artiﬁcial Intelligence (ICAART 2017), pages 355-363

ISBN: 978-989-758-220-2

355

Cellular Automata (CA) are totally discrete mod-

els and have been recently considered for robotics

ﬁeld (Lima et al., 2016), (Lima and Oliveira, 2016b),

(Ferreira et al., 2014), (Behring et al., 2001), (San-

toso et al., 2016). CA consist of a large number of

simple components with local connectivity. Despite

of the simplicity of their basic components, CA are

able to solve very complex problems in parallel such

as scheduling (Byun and Yu, 2014) and cryptography

(Silva et al., 2016). Because of CA features, the pro-

posed coordination model has to take in account that

the robot has to be centralized in such cell and also ex-

ecutes its movement synchronized with other robots,

avoiding collisions.

This work presents a coordination model for We-

bots simulator using intelligent swarm robots, includ-

ing localization and communication investigations.

The proposed model investigated herein is devoted to

Cellular Automata Ant Memory (CAAM) proposed

in (Lima and Oliveira, 2016a). These requirements

consider factors such as cellular automata speciﬁ-

cations, parallel synchronization, localization, accu-

racy of information dependency, and e-Puck architec-

ture in Webots simulator. The intelligent coordina-

tion model for multi-agents is divided into four parts:

(i) individual robot control proposed in (Lima and

Oliveira, 2016a), (ii) global robot control proposed

in (Lima and Oliveira, 2016a),(iii) smart grid con-

trol described ﬁrstly herein and, (iv) synchronization

and localization control presented and detailed ﬁrstly

herein. The Webots control model was used in the

results of (Lima et al., 2016), (Lima and Oliveira,

2016b), (Lima and Oliveira, 2016c) and it is de-

scribed, reﬁned and investigated ﬁrstly herein.

The major features of the model are: (i) cellu-

lar automata approach in the foraging task for multi-

robots, (ii) digital images processing for an object

detection, (iii) synchronization modeling for robot

parallel approach and coordination of the intelligent

swarm robotics, (iv) implementation of different lo-

calization approaches, (v) previous successful models

for cooperative robot swarms, including virtual obsta-

cles addition (Marchese, 2011). Besides that, the ap-

proach presented in this work can be used as a library

in other educational simulations in Webots for solv-

ing many multi-robots tasks, such as, surveillance or

search and rescue. More speciﬁcally, it can be used

when the simulation requires parallel and synchro-

nized techniques to solve swarm robots tasks based

on cell centralization using CA modeling strategy.

2 PROPOSED MODEL

Initially, the foraging task proposed in (Lima and

Oliveira, 2016a) was selected to be implemented as

a motivation of the investigations in educational sim-

ulations using Webots EDU and improved in (Lima

and Oliveira, 2016c) and (Lima and Oliveira, 2016b).

Any other task, like (Lima et al., 2016), that uses the

requirements - cellular automata used in swarm robots

context, which the movements have to be synchro-

nized and each robot has to be centralized into its cur-

rent cell - could be used in the investigations proposed

herein. The model is divided into four parts: individ-

ual robot control (Lima and Oliveira, 2016a), global

robot control (Lima and Oliveira, 2016c), (Lima and

Oliveira, 2016b), smart grid control and synchroniza-

tion and localization control proposed and investi-

gated herein. The individual robot coordination is

also reﬁned herein and improved using the robot cam-

era and image processing to identify food, different

from (Lima and Oliveira, 2016a), (Lima and Oliveira,

2016c), (Lima and Oliveira, 2016b), that have not

used this device. The robot camera usage turns the

model more realistic, but with a slower execution, be-

cause of the intelligent recognition stage.

2.1 Smart Grid

The bi-dimensional representation of the environment

structure is divided in squared regular cells of size l

and in three layers. The ﬁrst layer represents the en-

vironment, which each obstacle and the pheromone

are detailed. The second layer represents the robots

grid. The smart layer proposed herein is represented

by a regular grid with colored ball 90

upright sen-

sors, which represents the food grid. When a robot

passes on one sensor, then the sensor is turned off.

The smart grid is controlled by a ﬁle system through

server readings and writings. The last layer represents

the distance between each lattice cell and a nest. The

environment grid has to be constructed considering

that exists a passage from each cell. The obstacles

cells are represented in gray. In the Figure 1 (a) ex-

ample, the cells that are represented in white are free

and have a pheromone value. One robot, in the robot

smart grid, cannot overlaps another robot cell or a

wall cell, that means it is impossible two robots oc-

cupy the same cell. Each robot has to be centralized

in its current cell to avoid collisions with other robots

or obstacles/walls.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

356

Figure 1: Simulation smart environment world with  ob-

stacles and one nest A, the robot swarm is represented by

 and food units are represented by , the food sensor is

represented by ↑, and each food unit has a perpendicular

sensor.

2.2 Individual Behavior

The behavior model of each robot is controlled by an

individual ﬁnite state machine (FSM) that switches

over a 4-state cycle: Searching → Grabbing → Hom-

ing → Depositing → Searching; as shown in red in

Figure 2, reﬁned from (Lima and Oliveira, 2016a),

(Lima and Oliveira, 2016c), (Lima and Oliveira,

2016b) and improved herein adding more states into

the FSM. New states represent the image process-

ing steps for object identiﬁcation, such states brought

more realism and intelligence to the individual be-

havior. The environment is modeled as a cellular au-

tomata lattice formed by identical square cells. Each

state will be detailed for a better system understand-

ing. In this work, the moment that a certain amount of

time (T ) is passed, the task ends and all robots stop.

The Searching State represents the CAAM

searching model improvement and it is guided by the

repulsive pheromone (Calvo et al., 2011), (Lima et al.,

2016) - distributed by the robots over the environment

while they walking over it - and in a short-term indi-

vidual memory based on the Tabu search algorithm

(Glover, 1989), (Glover, 1990) and it is divided in

6 other states that are described below. The depo-

sition process state indicates the process where some

amount of pheromone δ is deposited in a central cell

and the amount of δ

is deposited in the correspond-

ing neighborhood. The identifying process state, im-

proved in this work, represents the robot camera us-

age. Each robot has a camera and a radius vision de-

noted by r

. To process the information captured by

the camera in the robot radius vision r

, the robot has

to turn in 360 and verify for each cell in the m-size

neighborhood if exists a food in its vision radius r

This process comprises the environment image pro-

cessing. The food is represented by an RGB blue [0

0 1] circle sensor ball. To simpliﬁcation, any other

object in the environment has the food’s color and the

camera has the rotation appointed to the ground ﬂoor.

To reduce the image processing time, the camera size

is conﬁgured as 1 × 14, which 14 represents the envi-

ronment cell size l. If a blue pixel is detected, then the

robot makes a movement and goes to the Grabbing

State, which consists in the single step that repre-

sents the picking up the detected object. On the other

hand, the robot continues in the Searching State and

goes to the pheromone detection to make a neigh-

borhood movement. The pheromone detection state

represents the environment pheromone reading pro-

cess. The pheromone is deposited in each grid cell x

i j

at each time (t). This reading comprises the Moore

neighborhood values m in the robot’s vision radius r

The neighborhood size is deﬁned as m = (2r

+ 1)

The robot keeps all the neighborhood cells x

i j

val-

ues, which have m size, in the robot’s vision radius

to make a movement decision. The robot veriﬁes in

its memory which is the lowest valued cell x

i j

that is

possible to movement. Then the robot makes the po-

sition decision based on pheromone and its memory.

This decision is a ﬁrst choice and it is based on the

inverted pheromone deposited in the neighborhood,

which avoids a robot return to a recently traveled path.

The movement state is the ﬁnal step that repre-

sents the robot’ transition to one cell x

i j

to cell in the

m-sized robot neighborhood. This action will be ac-

complished by the robots’ individual control, which

is responsible to decide how to control robot’s com-

ponents to make the desired step. The CA model in-

vestigated here is not standard since a transition robot

movement changes the state of two cells. The cell

occupied by the robot becomes a free cell, and a the

neighborhood free cell chosen by the robot, becomes

a cell occupied by the robot. Each robot movement

corresponds to change its current position to an adja-

cent cell and it is decided by a local rule which takes

in account the robot neighborhood. This update rule

changes the robot’s pheromone cell and its neighbor-

hood. Besides that, when a robot passes on a sen-

sor food cell, it changes its current state Searching →

Grabbing and the cell’s state occupied in food ﬂoor

state becomes a free cell.

The Homing State is devoted to the CAAM

model, which was inspired by previous CA-based

models of crowd dynamics during building evacua-

tion (Varas et al., 2007) and (Alizadeh, 2011). Each

robot chooses an optimal route to follow in homing,

by considering a static and dynamic ﬂoor ﬁeld, that

are merged using according to (Lima and Oliveira,

2016a). This merging ﬂoors prevents the formation

of rows close to the nests (Alizadeh, 2011), jamming

(Yamamoto et al., 2007), inertial behavior prevention

(Yang et al., 2005), as analyzed in (Lima and Oliveira,

Coordination, Synchronization and Localization Investigations in a Parallel Intelligent Robot Cellular Automata Model that Performs

Foraging Task

357

Figure 2: Individual behavior represented in a ﬁnite state machine that represents the cycle of each robot.

2016a). The homing process was inspired by pedes-

trian evacuation models previously investigated in the

literature (Varas et al., 2007), (Alizadeh, 2011), and

was proposed ﬁrstly in (Lima and Oliveira, 2016a).

The Depositing State represents the single step when

robot leaves the food into the nest.

2.3 Global Behavior

The global behavior comprehends two processes: the

evaporation process and the conﬂict avoidance pro-

cess (to regulate interactions among robots and their

neighboring obstacles and robots). The pheromone

evaporation process is a robot state inherent, it

means that at each time step t there is a global evapo-

ration process according to a constant β. Each cell

that is visited by a robot is receives an amount of

pheromone (6= 0), and each cell that is valued differ-

ent from zero is decreased.

Each robot tries to move to a neighborhood cell

depending on its movement radius r

. The model us-

ing the short term memory based on Tabu search and

the inverted pheromone permit an almost free con-

ﬂicts trajectory, but speciﬁc cases are solved by con-

ﬂicts avoidance process. Speciﬁc conﬂict case can be

solved the algorithm based on (Varas et al., 2007) and

adapted in (Lima and Oliveira, 2016a) as following: if

two robots try to move into the same cell, featuring a

conﬂict; a random value decides which robot will per-

form the movement, while the loser cannot move. If

one robot have two cells with the same lowest value to

chose, the robot selects one randomly. At each t some

time step a random decision is made to avoid robots in

different layers conﬂicts. As presented in (Lima and

Oliveira, 2016c), when two robots are in a perpendic-

ular crossing conﬂict, to solve this problem the move-

ment is made in two steps using a non-deterministic

method follows these steps: (a) the ﬁrst step one robot

is randomly chosen and makes its movement, then the

other robot realize its movement. (b) To solve a robot-

obstacle conﬂict problem, virtual obstacles (March-

ese, 2011) are inserted in the ﬂoor ﬁeld.

These interactions between robots and environ-

ment (pheromone ﬁeld), and by the robots and robots

(collision avoidance), emerges a complex behavior

that solves the foraging task by the robots swarm.

These interactions produce a robot-robot aversion in-

teraction, prevents collisions, and increases the explo-

ration and covered area.

2.4 Webots Controller and Localization

Approaches

Aiming to describe parallel synchronization and lo-

calization approach described ﬁrstly herein, all robots

have to accomplish their movements at the same time.

Another characteristic of the model is that all robots

have to be centralized in its current cell to avoid col-

lisions with robots or walls during their movements.

To synchronize the parallel robot team movement,

a global information was shared between the robots

through a server, as showed in ﬁnite state machine of

Figure 3. The messages were sent using text ﬁles,

which contains the robot matrix position and time

t. Initially, each robot sends its t time to the server,

which is responsible to read and process the next team

movement in the t +1 time. This server solves all con-

ﬂicts and sends back the message to the robots indi-

cating their next movement position. All robots reads

in parallel and independently the server ﬁle and search

for their robot number and execute their movement.

During each robot movement the server starts reading

continually the ﬁles from each robot verifying if the

robot ends its movement, which is indicated when the

robot write t + 1 in its ﬁle. If in all ﬁles are written

t + 1 time information, the server calculates the new

position.

Two approaches were considered in the robot lo-

calization. The ﬁrst one considers the odometry func-

tion usage (Oliveira et al., 2015). It is known that

the odometry propagates an error during the trajec-

tory path during the execution when it used without

any other correction mechanism (Martinelli, 2002).

The second uses a Global Positioning System (GPS)

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

358

Figure 3: Webots proposed controller represented in a ﬁnite

state machine to control the team of robots.

improvement for the localization precision, specially

when it was aggregated with the Webots EDU Iner-

tial Unit library to yaw reﬁnement. Besides that, it

is known that all robots execute their movements and

stop in a predeﬁned angle depending on the historical

of current and last cells, so a saved and an unsaved

robot turn angle were considered.

The ﬁrst approach using GPS proposed herein

considers that the robots execute their movements at

each time step. At each time step is calculated the

milliliter difference error e

, e

between the position

that the robot should be and the robot current posi-

tion, for each robot coordinate (x, y) respectively. The

error is increased at each time step. When the sum of

errors is bigger than a constant |ε

|, the robot adjust

its coordinate (x, y or both) according to the desired

position at that current step. If the robot has moved

more than the desired position, in the next step the

robot returns the extra distance. On the other hand, if

the robot has moved less than the desired position, in

the next step the robot progress the amount of missing

millimeters. But to control the errors in both coordi-

nates at the same time causes delays in the simula-

tion. To solve this problem, a solution is proposed

herein correcting the error just in the coordinate that

the robot realizes the next movement. For example, if

the robot has an error to correct in coordinate x, but

it is going to move in the next step forward the co-

ordination y, the robot will not correct its error. The

robot only corrects its own position in its movement

coordinate. On the other hand, if the robot is moving

diagonally, both coordinates are corrected.

Another orientation error that each robot has to

calculate is the robot yaw error e

. A yaw rotation

is a movement around the yaw axis that the robot per-

forms at each time step during its movements to the

neighborhood cells. At each time step the coordina-

tion system has the correct angle that the robot should

be and the current robot angle. Similarly to the coor-

dination error, the robot calculates the sum of rotation

errors during its path in radians, and when the error is

bigger than a constant |ε

|, the robot yaw is corrected.

3 EXPERIMENTS

The experiments are presented in this section were

conduct to show that investigations proposed herein

are capable of being implemented in a real simulator

Webots EDU using the e-Puck robot architecture for

swarm robots in foraging task with the synchroniza-

tion mechanism. The experiments were performed

using a simulator environment/grid of 20 × 30 cells

with two nests (showed in brown in Figure 4), each

cell has l = 14 cm size. To perform the task 6 robots

(N = 6 in green) and 6 units of food (F = 6 in blue)

were used to show the parallel behavior of the robots.

The ﬁrst instance of all experiments were conducted

using the conﬁguration shown in Figure 4 (a). The

ﬁrst experiment used the odometry function (Ferreira

et al., 2014) and at each time step t the robots have to

return to their initial angle (turn to 0

angle). Besides

that, the robot can rotate between one of the possible

angles {−135

, −90

, −45

, 0

, 45

, 90

, 135

}. The

results in Figure 4 (b) shows that although the robots

are executing the task using a parallel synchroniza-

tion, it is possible to observe that they are not cen-

tralized in their respective cells (provoking collisions

after t steps). This strategy of returning to the initial

angle provokes a delay in the simulation time. The

rotations accumulate errors in odometry function dur-

ing the robots navigation. To solve this problem an

approach that saves the current angle position in the

robot struct parameters was considered. After that,

two improvements were done: a faster processing

time and a lower error of position due to rotations.

Results obtained with this strategy are shown in Fig-

ure 4 (c).

Although the experiments using odometry and

saving the robot current position improved the per-

formance of the swarm, this approach also propagates

errors during the robot navigation process, avoiding a

robot centralization into its respective cell. Figure 5

(a) shows a partial solution for this problem using a

GPS slot in Webots EDU simulator. Each time step

the coordinate (x, y) was corrected by the robot when

it founds an error bigger than threshold |e

= 0.01|

for each x and y-axes. A robot also calculates previ-

ously its coordinate and correct its movement before

performing a movement action, increasing or decreas-

ing the movement step size. In this last case, the robot

moves more or less than the size of the cell to achieve

the correct coordinate at every |e

≥ 0.01|. However,

using only the coordinate error |e

= 0.01| the sys-

tem was not capable of accomplishing a good perfor-

mance due to the yaw error. Figure 5 (b) shows an

experiment that solves this problem the |e

| was used

to correct the turn angle of the robot every time its

Coordination, Synchronization and Localization Investigations in a Parallel Intelligent Robot Cellular Automata Model that Performs

Foraging Task

359

found an error, using our proposed controller model.

Finally, Figure 5 (c) shows the last experiment that

uses the robot camera sensor, another improvement

also investigated and proposed herein. Aiming the use

of this camera device correctly, at each time step the

robot has to turn in all 360 angles aiming to ﬁnd an

object into its radius vision r

. The camera device is

capable of capture images that are after treated by im-

age processing recognizing blue objects into robot’s

radius vision r

. In this case, robot also uses GPS and

Inertial unit slot to correct the robot team accuracy

into the lattice cells.

To compare the simulation time spent in Webots

Figure 4: Simulations in Webots EDU: (a) Initial conﬁgura-

tion. (b) Odometry without angle maintenance. (c) Odom-

etry with angle maintenance.

Figure 5: Simulations in Webots EDU: (a) GPS approach

without yaw correction. (b) GPS approach with yaw correc-

tion. (c) GPS approach without yaw correction and camera

device usage.

EDU platform a graphic shown in Figure 6 was plot-

ted to contrast the differences between each approach

implementation. The x-axis represents each time step

t of the task that are in the 0 ≥ t ≥ 7 and the x-axis rep-

resents the simulator time elapsed to conclude each

time step t. The ﬁrst implementation approach shown

in Figure 6 (a) represents one of the biggest Webots

simulator elapsed time to capture the ﬁrst object.

That fact can be explained due to the massive

amount of rotations each robot concludes turning

back to the initial angle. Figure 6 (b) refers to the sec-

ond implementation, that absents the rotation to initial

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

360

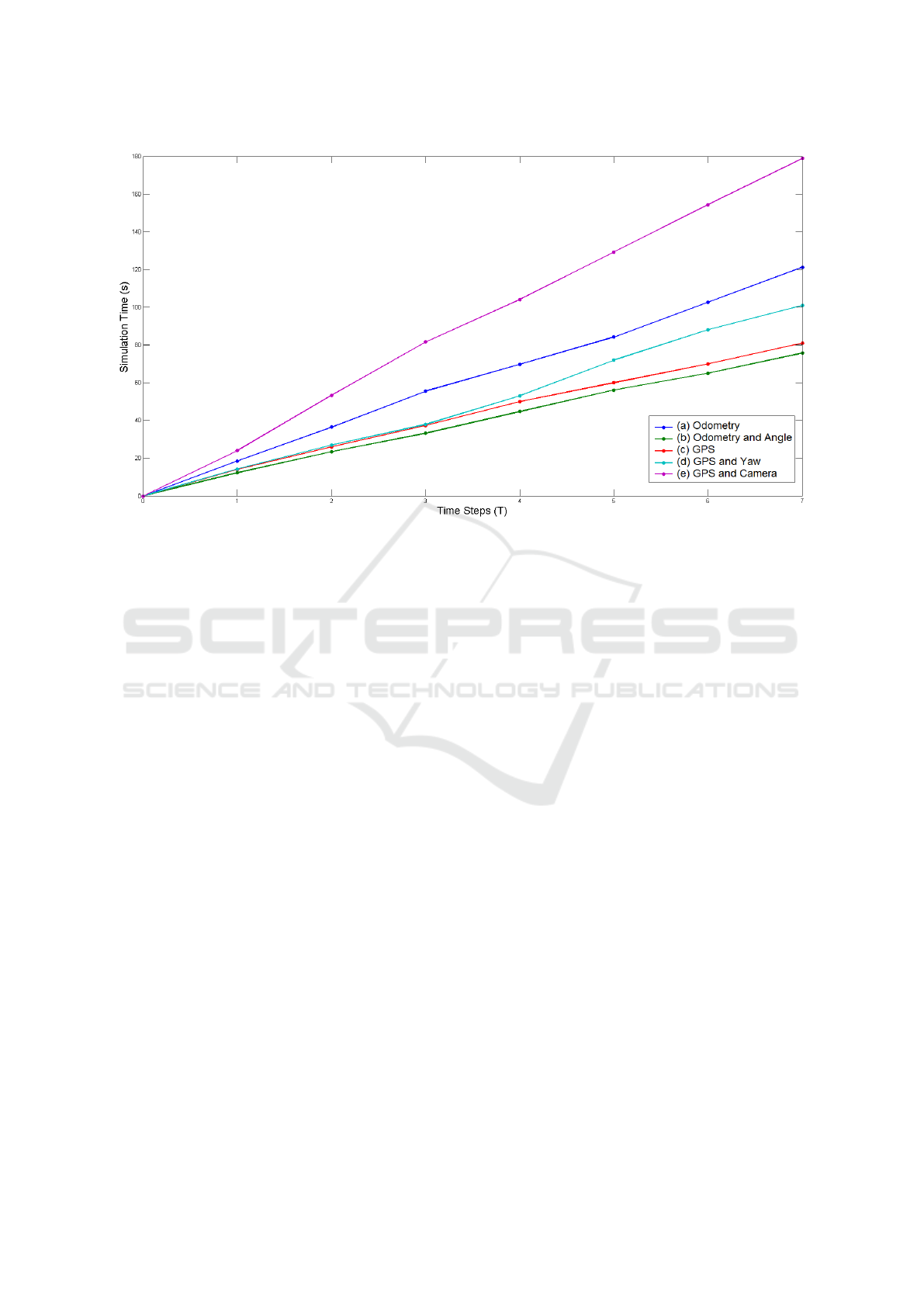
Figure 6: Different evaluations using: (a) Odometry approach without current angle maintenance. (b) Odometry approach

with current angle maintenance. (c) GPS approach without correction of the yaw. (d) GPS approach correcting of the yaw.

(e) GPS approach and correction of the yaw using the robot camera.

angle, and its resulted in the best simulation time, due

to the simplicity of the odometry calculus at each time

step. Figure 6 (c) shows the simulation results us-

ing the GPS localization and the processing simulator

time is closely to the odometry approach, that keeps

the current rotation angle. Figure 6 (d) shows the yaw

resolution, because of the correction being done at

each time step, this procedure increased the simula-

tion time. Finally, Figure 6 (e) uses the camera de-

vice returning the worst simulation performance, due

to the image processing that consumes high process-

ing capability and also because of the rotations. Al-

though some combinations are not resulting in good

simulations time, the accuracy in cell centralization is

most important aspect to be considered, so the pro-

posed coordination model uses the GPS yaw and co-

ordinates reﬁnement merged with the camera usage,

that is inherent to the foraging task.

4 CONCLUSIONS

Simulations were carried out in foraging task us-

ing the cellular automata model proposed in (Lima

and Oliveira, 2016a). The investigations proposed

herein used different implementation Webots EDU

approaches for a good adjustment of parameters and

a better comprehension of the model in terms of lo-

calization, devices usage and synchronization. The

best combination of mechanism and strategies pro-

posed herein comprehends: (a) the camera usage and

image processing, (b) the synchronization using text

ﬁles readings and writings, and (c) the localization al-

gorithm that both corrects the distance and yaw. The

scenario investigated of our model was foraging task,

which is very relevant to collective robotics (Falleiros

et al., 2015) due to it is a instance metaphor of a

broad class of problems, such as, search and rescue

and surveillance (Lima et al., 2016).

The requirements of the environment conﬁgura-

tion for the application of our model are: (i) the en-

vironment is modeled as a cellular automata lattice

formed by identical square cells; (ii) each robot is

controlled by an individual ﬁnite state machine; (iii)

the robot-robot conﬂicts avoidance are treated in a

non-deterministic way and also a crossing perpendic-

ular motion was detected; (iv) robots obstacles are

treated using virtual obstacles (Marchese, 2011); (v)

even the odometry localization presenting the best

processing time each time step, the GPS localization

model resulted in better accuracy of robot cell central-

ization. Using simulations on Webots EDU platform

it was possible to evaluate the proposed model in a

parallel architecture using e-Puck robots.

A forthcoming work is about the implementation

of other swarm robots tasks, such as, search and res-

cue and collective garbage collection, using the pro-

posed synchronization model in Webots EDU simu-

Coordination, Synchronization and Localization Investigations in a Parallel Intelligent Robot Cellular Automata Model that Performs

Foraging Task

361

lator. Besides that, the camera device can be used

not only for object identifying process but also in the

pheromone detection that can be used in the smart

grid adding a pen slot in the e-Puck. Additionally,

other device can also be used such as sensor IR de-

vices and camera image noise can be treated and in-

vestigated in a future work.

REFERENCES

Alizadeh, R. (2011). A dynamic cellular automaton model

for evacuation process with obstacles. Safety Science,

49(2):315–323.

Beckers, R., Holland, O., and Deneubourg, J.-L. (1994).

From local actions to global tasks: Stigmergy and col-

lective robotics. In Artiﬁcial life IV, volume 181, page

189.

Behring, C., Bracho, M., Castro, M., and Moreno, J. (2001).

An algorithm for robot path planning with cellular au-

tomata. In Theory and practical issues on cellular au-

tomata, pages 11–19. Springer.

Byun, H. and Yu, J. (2014). Cellular-automaton-based

node scheduling control for wireless sensor net-

works. Vehicular Technology, IEEE Transactions on,

63(8):3892–3899.

Calvo, R., de Oliveira, J. R., Figueiredo, M., and Romero,

R. A. (2014). Parametric investigation of a distributed

strategy for multiple agents systems applied to coop-

erative tasks. In Proceedings of the 29th Annual ACM

Symposium on Applied Computing, pages 207–212.

ACM.

Calvo, R., de Oliveira, J. R., Figueiredo, M., and Romero,

R. A. F. (2011). Bio-inspired coordination of multiple

robots systems and stigmergy mechanims to coopera-

tive exploration and surveillance tasks. In Cybernetics

and Intelligent Systems (CIS), pages 223–228. IEEE.

Couceiro, M. S., Rocha, R. P., and Ferreira, N. M. (2011). A

novel multi-robot exploration approach based on par-

ticle swarm optimization algorithms. In Safety, Secu-

rity, and Rescue Robotics (SSRR), 2011 IEEE Interna-

tional Symposium on, pages 327–332. IEEE.

Falleiros, E. L. S., Calvo, R., and Ishii, R. P. (2015).

Pheroslam: A collaborative and bioinspired multi-

agent system based on monocular vision. In Com-

putational Science and Its Applications–ICCSA 2015,

pages 71–85. Springer.

Ferreira, G. B., Vargas, P. A., and Oliveira, G. M. (2014).

An improved cellular automata-based model for robot

path-planning. In Advances in Autonomous Robotics

Systems, pages 25–36. Springer.

Fortunati, L. (2016). Moving robots from industrial sec-

tors to domestic spheres: A foreword. In To-

ward Robotic Socially Believable Behaving Systems-

Volume II, pages 1–3. Springer.

Glover, F. (1989). Tabu search part i. ORSA Journal on

computing, 1(3):190–206.

Glover, F. (1990). Tabu search part ii. ORSA Journal on

computing, 2(1):4–32.

Gordon, D. M. (2014). The ecology of collective behavior.

PLoS Biol, 12(3):e1001805.

Kantor, G., Singh, S., Peterson, R., Rus, D., Das, A., Ku-

mar, V., Pereira, G., and Spletzer, J. (2006). Dis-

tributed search and rescue with robot and sensor

teams. In Field and Service Robotics, pages 529–538.

Springer.

Lima, D. A. and Oliveira, G. M. B. (2016a). A cellular

automata ant memory model of foraging in a swarm

of robots (submitted to). Applied Mathematical Mod-

elling.

Lima, D. A. and Oliveira, G. M. B. (2016b). New bio-

inspired coordination strategies for multi-agent sys-

tems applied to foraging tasks. IEEE International

Conference on Tools with Artiﬁcial Intelligence (IC-

TAI), IEEE Artiﬁcial Intelligence Society, San Jose,

CA, United States, 6-8th November 2016.

Lima, D. A. and Oliveira, G. M. B. (2016c). A probabilis-

tic cellular automata ant memory model for a swarm

of foraging robots. 14th International Conference on

Control, Automation, Robotics and Vision (ICARCV

2016), IEEE Control Society, Phuket, Thailand, 13-

15th November 2016.

Lima, D. A., Tinoco, C. R., and Oliveira, G. M. B. (2016). A

Cellular Automata Model with Repulsive Pheromone

for Swarm Robotics in Surveillance, pages 312–322.

Cellular Automata: 12th International Conference on

Cellular Automata for Research and Industry, ACRI

2016, Fez, Morocco, September 5-8, 2016. Proceed-

ings, Springer International Publishing, Cham.

Marchese, F. (2011). Mrs motion planning: the spatiotem-

poral multilayered cellular automata approach. Intro-

duction to Modern Robotics. iConcept Press.

Martinelli, A. (2002). The odometry error of a mobile robot

with a synchronous drive system. Robotics and Au-

tomation, IEEE Transactions on, 18(3):399–405.

Oliveira, G. M., Vargas, P. A., and Ferreira, G. B. (2015). A

local decision making cellular automata-based path-

planning. The European Conference on Artiﬁcial Life

(ECAL 2015), Procedings, York, United Kingdom,

Monday, 20-24th July, 2015, Artiﬁcal Life Society.

Santoso, J., Riyanto, B., and Adiprawita, W. (2016). Dy-

namic path planning for mobile robots with cellular

learning automata. Journal of ICT Research and Ap-

plications, 10(1):1–14.

Silva, E. C., Soares, J. A. J. P., and Lima, D. A. (2016).

One-dimensional chaotic cellular automata with ﬁxed

border applied to a cryptosystem modeling for digital

images. Revista de Informatica Teorica e Aplicada,

23:250–276.

Varas, A., Cornejo, M., Mainemer, D., Toledo, B., Rogan,

J., Munoz, V., and Valdivia, J. (2007). Cellular au-

tomaton model for evacuation process with obstacles.

Physica A: Statistical Mechanics and its Applications,

382(2):631 – 642.

Vargas, P. A., Benhalen, A. M., Pessin, G., and Os

orio, F. S.

(2012). Applying particle swarm optimization to a

garbage and recycling collection problem. In Compu-

tational Intelligence (UKCI), 2012 12th UK Workshop

on, pages 1–8. IEEE.

ICAART 2017 - 9th International Conference on Agents and Artiﬁcial Intelligence

362

Yamamoto, K., Kokubo, S., and Nishinari, K. (2007). Sim-

ulation for pedestrian dynamics by real-coded cellular

automata (rca). Physica A: Statistical Mechanics and

its Applications, 379(2):654–660.

Yang, Z., Zhao, L., Li, J., and Fang, Y. (2005). Simulation

of the kin behavior in building occupant evacuation

based on cellular automaton. Building and Environ-

ment, pages 411 – 415.

Coordination, Synchronization and Localization Investigations in a Parallel Intelligent Robot Cellular Automata Model that Performs

Foraging Task

363