Reduction of Optical Rotation and Scattering in a Cholesteric Liquid

Crystal Layer

Mitsunori Saito and Junki Fujiwara

Department of Electronics and Informatics, Ryukoku University, Seta, Otsu 520-2194, Japan

Keywords: Liquid Crystal, Polarization, Optical Rotation, Scattering, Refractive Index.

Abstract: Cholesteric liquid crystal usually exhibits an optical rotation owing to its chirality. In the infrared region,

however, the optical rotation power disappears, since the light wavelength is too long to recognize the

refractive-index change of the nanometer-sized chiral structure. Consequently, the cholesteric liquid crystal

exhibits a polarization-independent refractive index in the long-wavelength infrared range. The effective

refractive index takes a value between the ordinary and extraordinary indices regardless of the polarization

direction. The refractive index decreases to the ordinary index, when a phase transition takes place by

application of an electric voltage (the electro-optical effect). This polarizer-free device operation, however,

used to be limited to the wavelength range beyond 4 μm, since the optical rotation remained in the short

wavelength range. In addition, a heavy scattering occurred during the phase transition process. In this study,

experiments were conducted to examine how the chiral pitch and the thickness of the liquid crystal layer

affected these optical characteristics. When a liquid crystal with a chiral pitch of 5 μm was enclosed in a cell

with a 3 μm gap, both the rotation power and scattering loss were reduced successfully in a wide spectral

range extending to 2 μm wavelength.

1 INTRODUCTION

Liquid crystals (LCs) are used widely in various

technical fields today (Khoo, 2007). Although LCs

exhibit efficient electro-optic effects, i.e., notable

changes in the refractive index or optical rotation

power by low-voltage application, they usually need

a polarizer that halves a light intensity. This problem

is serious in the infrared spectral range, in which

efficient, durable, low-cost polarizers are unavailable

due to opaqueness of ordinary glasses, crystals, and

polymers (Saito and Yasuda, 2010). Since the early

days of the LC device development, many researchers

have conducted experiments to attain polarization-

independent optical functions. A beam-splitting

method (Patel and Maeda, 1991), for example, was

used for creating a wavelength-division multiplexing

device (Hirabayashi et al, 1993) and an infrared Lyot

filter (Saito and Hayashi, 2013). A polarization-

insensitive hologram was realized by use of a quarter-

wave plate (Moore et al, 2008). A stack of

orthogonally-oriented LC layers, which yielded an

equivalent optical response for all polarization

directions, was used for creating an optical phase

modulator (Lin et al, 2005) or a tunable lens (Ye et al,

2006). An axially-symmetric director distribution

(Lee et al, 1999) and a complicated grating texture

(Provenzano et al, 2006) were also constructed by

coating special alignment films on the substrates.

Flat-panel displays use a twisted nematic LC, in

which molecules take a chiral texture. As a light beam

with a linear polarization propagates in this texture,

its polarization direction rotates according to the

director rotation (Saito et al, 2011). In a long-

wavelength range, however, the optical rotation

power decreases as the birefringence of the LC layer

decreases (Patel and Lee, 1991). Generally, a material

with a non-uniform structure exhibits uniform or

isotropic optical properties, if the structure is smaller

than the light wavelength (the effective medium

theory). This is the case with the blue phase LC

(Crooker, 2001), in which a nano-sized domain

texture induces an isotropic refractive index (Haseba,

2005). Although this characteristic is useful for

creating a polarization-independent optical device,

the blue-phase LC has to be stabilized in a polymer

matrix, and hence, needs a high voltage (~100 V) to

induce an index change of Δn=0.05. (Lin et al, 2010).

Saito M. and Fujiwara J.

Reduction of Optical Rotation and Scattering in a Cholesteric Liquid Crystal Layer.

DOI: 10.5220/0006089700220031

In Proceedings of the 5th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2017), pages 22-31

ISBN: 978-989-758-223-3

A cholesteric (chiral nematic) LC is another

selection to attain isotropic properties with a nano-

sized structure of the molecular orientation (Hsiao et

al, 2011). The chiral texture of the cholesteric LC is

similar to that of the twisted nematic LC but possesses

a shorter chiral pitch. The cholesteric LC, therefore,

induces an optical rotation only for a light beam

whose wavelength is sufficiently shorter than the

chiral pitch. If the chiral pitch is close to the

measurement wavelengths, a photonic band-gap

emerges in the transmission spectrum (Kopp et al,

1998), which is useful to create a tunable laser

(Furumi et al, 2003). In a longer wavelength range,

however, the dimension of the molecular rotation is

too small to be recognized by lightwave, and

consequently, the cholesteric LC exhibits an isotropic

index of refraction.

In a previous study, the authors examined infrared

transmission characteristics of a cholesteric LC in

order to realize a polarization-independent Fabry-

Perot filter (Saito et al, 2015). An isotropic refractive

index was attained in the infrared range beyond 2 μm

wavelength, and it decreased by 0.09 during

a voltage

application process (12‒18 V). The transmitted light,

however, exhibited a trace of optical rotation in the

wavelength range below 3 μm. In addition, the

transmittance decreased heavily in the midway of the

index change, which originated from the scattering in

the unstable phase transition process (Kim et al, 2010).

In this study, we conduct experiments to clarify how

the chiral pitch and the LC layer thickness affect the

transmission properties of the LC cell. On the basis of

the experimental results, we discuss a suitable design

of the LC cell to create a polarization-independent

device with a reduced scattering loss.

2 PRINCIPLE

Figure 1 illustrates various LC phases in a cell

together with polarization directions of propagating

lightwave. As Fig. 1(a) shows, ordinary cells align

Figure 1: Various molecular orientations in a LC cell (thickness d). The refractive indices of the LC are n

and n

for the

ordinary and extraordinary lightwaves (wavelength: λ), respectively. (a) A nematic LC that is oriented parallel to the substrate.

The light wavelength in the LC cell is λ/ n

or λ/n

depending on the polarization direction. (b) A homeotropic phase in which

LC molecules are oriented in the direction perpendicular to the substrates owing to an electric field. The light wavelength in

this LC cell is λ/n

regardless of the polarization direction. (c) A cholesteric LC that is oriented by an alignment coating on

the substrate surface. The director of the LC molecules rotates 360º with a chiral pitch, p. Accordingly, the polarization

direction of a light beam rotates with the same pitch as it propagates in this LC. The polarization direction of the transmitted

light can be analyzed by rotating an analyzer (polarizer) to find an angle Δθ that yields the maximum transmittance. (d) A

cholesteric LC in a cell with no alignment coating. The LC layer consists of multiple domains in which molecules form a

chiral structure. If the light wavelength is sufficiently long, this LC layer exhibits an effective refractive index, n

, that is

independent of the polarization direction. When an electric voltage is applied to the cells in (a), (c), and (d), they all turn to

the homeotropic phase in (b).

Reduction of Optical Rotation and Scattering in a Cholesteric Liquid Crystal Layer

nematic LC molecules in a fixed direction by the use

of an alignment coating on the substrates. This LC

orientation

exhibits an ordinary or extraordinary

refractive index, n

or n

, depending on the

polarization direction of incident light. Consequently,

a propagating beam takes a different wavelength, λ/n

or λ/n

, depending on the polarizer direction. As Fig.

1(b) shows, the LC molecules are reoriented in the

direction of the electric field, if a voltage is applied

between the substrates. In this phase, the LC exhibits

an ordinary index (n

) regardless of the polarization

direction, and accordingly, the light wavelength

becomes λ/n

. In other words, only the extraordinary

light suffers the change in the refractive index

(wavelength). No index change takes place for the

ordinary light. This is the reason that polarizers are

needed for tuning LC devices.

Figure 1(c) is a schematic illustration of the

cholesteric LC that is sandwiched between two

substrates with an alignment coating. The LC director

rotates 360° with a chiral pitch, p. A short-

wavelength beam changes its polarization direction

with the same pitch. Consequently, the polarization

direction of the output beam becomes different from

that of the input beam. The polarization state of the

beam can be analyzed by rotating an analyzer

(polarizer); i.e., if the polarization direction of the

beam rotates by ∆θ in the LC cell, the maximum

transmittance is attained at the same angle, ∆θ. If the

light wavelength is too long to recognize the chiral

texture, the refractive index becomes independent of

the polarization direction and takes an average of n

and n

. According to the effective medium theory

(Born and Wolf, 1980), the average has to be taken

for the dielectric constant, i.e., the square of the

refractive index. The average index is therefore

























2

⁄

. (1)

This average index is higher than n

, since n

usually higher than n

. When a voltage is applied, the

LC layer turns to the homeotropic phase in Fig. 1(b),

and hence, the refractive index decreases to n

The chiral texture of the cholesteric LC is affected

seriously by the substrate surface. If the alignment

coating on the substrate is removed, the regular

arrangement of the LC molecules is disturbed heavily,

and a domain texture emerges in the LC layer, as

shown in Fig. 1(d). In this texture, the refractive index

varies randomly in a small region, and consequently,

isotropic properties are readily attainable in the long

wavelength range. According to the effective medium

theory above, the refractive index of this texture is











2













3

⁄

, (2)

since one direction is parallel to the LC director

(extraordinary light) and the other two directions are

perpendicular to the director (ordinary light). A

voltage application causes the LC molecules to turn

to the electric field direction, and finally takes the

homeotropic phase in Fig. 1(b). In this manner, the

refractive index is adjustable between n

and n

independent of polarization. In the short wavelength

range, however, the LC does not act as a uniform,

isotropic medium, and hence the polarization state of

the incident beam is not maintained. The optical

scattering also increases as the wavelength becomes

shorter. The scattering loss is notable particularly in

the non-aligned cholesteric LC, since the molecular

arrangement is disturbed heavily in this phase.

3 SAMPLES AND EXPERIMENTS

Samples were prepared by injecting a cholesteric LC

into a gap between two silicon (Si) plates of 20 mm

square (Saito et al, 2007). The gap or the LC layer

thickness was adjusted between 3 and 20 μm by the

use of glass spheres. No alignment coating was

achieved on the substrate, since the polymer coating

caused an absorption in the infrared region. The LC

layer therefore took the domain texture shown in Fig.

1(d). The chiral pitch of the cholesteric LC (JNC

Corporation, JD-1036LA, JD-1036LB) was p=4.8 or

1.5 μm. The ordinary and extraordinary refractive

indices were n

=1.52 and n

=1.76, respectively.

According to Eq. (2), the effective index of the LC

layer was assumed to be n

=1.60. It was expected,

therefore, that the index change of ∆n≈0.08 was

attainable by voltage application.

Electric wires were soldered on the substrates for

voltage application. A sinusoidal signal of 1 kHz was

generated by an electric oscillator and an amplifier. A

peak voltage was adjusted between 0 and 100 V by

monitoring the signal with an oscilloscope. The

sample was mounted on the sample stage of a Fourier-

transformation infrared spectrometer (FTIR,

Shimadzu, IR Affinity-1) for spectral measurements.

No polarizers was used in regular transmittance

measurements. A polarization dependence of the

transmittance was examined by inserting a BaF

wire-

grid polarizer (Edmund, WGP8203) in front of the LC

cell. As Fig. 1(c) shows, another polarizer (analyzer)

was inserted on the output side, when the optical

rotation was examined. In all measurements,

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

transmittance was evaluated by taking the ratio of

transmitted light intensities that were measured

before and after mounting the LC cell on the stage.

The transmission characteristics of the polarizers

were therefore cancelled out in the measured

transmission spectra.

4 RESULTS

4.1 Conventional LC Cell

The first LC cell was prepared by using spheres of 20

μm diameter and the LC with a 4.8 μm pitch. The

black lines in Figs. 2(a)‒2(c) show the transmission

spectra that were measured before and during a

voltage application process. Interference peaks were

visible over the entire spectral range. This

interference was caused by the resonance in the LC

layer (between the Si substrates), since the Si surfaces

(the Si-LC boundaries) yielded a high reflectance

owing to the high index of refraction. The high

reflectance at the outer surfaces (the Si-air

boundaries) reduced the maximum transmittance to

~55%. The dips at 3.4 and 5.7 μm were attributed to

the absorption by the LC. The spectral disturbance at

4.3 μm was caused by carbon dioxide gas that was

contained in the atmosphere around the sample. The

voltage application caused a transmittance decrease

(20 V) as well as the peak shift toward shorter

wavelengths. When the voltage exceeded 20 V, the

peak shift stopped. The transmittance returned to the

original level at ~30 V, and thereafter no spectral

change was visible.

The gray lines in Figs. 2(a)‒2(c) indicate the peak

wavelengths in the interference spectrum, which were

calculated by assuming suitable values for

the

refractive index (n) and thickness (d) of the LC

layer; i.e., according to the thin-film interference

theory (Hecht, 1998), the peak wavelengths were

calculated by the use of the relation,



2 

⁄

1,2,3,⋯. (3)

(The height and amplitude of these fitting curves have

no meaning.) The peak-wavelength fitting was first

conducted for the measured spectrum in Fig. 2(c),

since the refractive index was presumed to be n

=1.52

in the voltage application process [Fig. 1(b)]. By

using this index value, the theoretical peak

wavelengths were calculated for various thicknesses

(d) to examine the coincidence of the measured and

calculated peak wavelengths (the black and gray

lines). The best fitting was attained when the

thickness was assumed to be d=20.1 μm, which was

close to the sphere (spacer) diameter. Then the peak

fitting was conducted for the other spectra by using

this thickness. The best-fit value was n=1.52 in Fig.

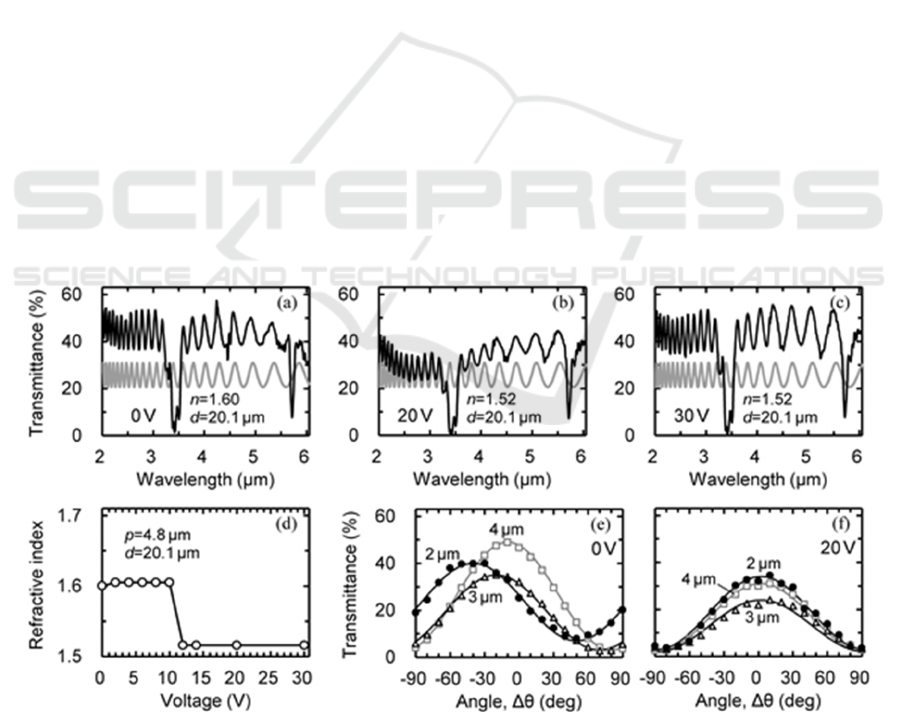
2(b) and 1.60 in Fig. 2(a). Figure 2(d) shows the

Figure 2: Optical properties of the LC with a chiral pitch of p=4.8 μm and an evaluated thickness of d=20.1 μm. (a–c) The

black lines show the transmission spectra. The gray lines show the fitting curves that assume the refractive index of 1.52 at

30 V. (d) Evaluated refractive indices as a function of the applied voltage. (e, f) Transmittance change by the rotation (Δθ) of

the analyzer. Measurements were conducted at 0 and 20 V.

Reduction of Optical Rotation and Scattering in a Cholesteric Liquid Crystal Layer

refractive indices that were evaluated in this manner.

The refractive index decreases rapidly at around 10 V,

and thereafter becomes constant. The transition to the

homeotropic phase [Fig. 1(b)] takes place in this

voltage range. A slight structural adjustment to

complete the homeotropic orientation seems to

continue until ~30 V, since the scattering remains

even at a voltage exceeding 20 V. In the initial phase

at 0 V, the evaluated refractive index is 1.60. This

value

closer

=1.60

than

=1.64, which

are

calculated by using Eqs. (2) and (1), respectively,

with n

=1.52 and n

=1.76. This fact confirms the

assumption that the current LC initially takes the

domain texture of Fig. 1(d).

The optical rotation in the LC cell was evaluated

by using two polarizers, as shown in Fig. 1(c). Figures

2(e) and 2(f) show the transmittances that were

measured as rotating the analyzer. During the voltage

application process (20 V), the transmittance

becomes the maximum at ∆θ=0° (parallel Nicols) and

the minimum at ±90° (crossed Nicols). This result

indicates that the light beam suffers no polarization

rotation in this phase. In the initial phase at 0 V,

however, the maximum angle shifts heavily at short

wavelengths, indicating that the polarization direction

rotates in the LC cell; e.g., 40° at 2 μm wavelength.

As mentioned in Section 2, light with a short

wavelength recognizes a fine index distribution, and

consequently, the polarization direction rotates

according to the molecular chirality.

4.2 LC with a Short Chiral Pitch

In the experiments above, the LC cell exhibited both

the scattering loss and the optical rotation. These

problems could be solved by using an LC with a short

chiral pitch (a fine structure). An LC with a 1.5 μm

pitch was therefore used to fabricate the next sample.

The glass spheres of the same diameter (20 μm)

were

used

spacer.

The

black

lines

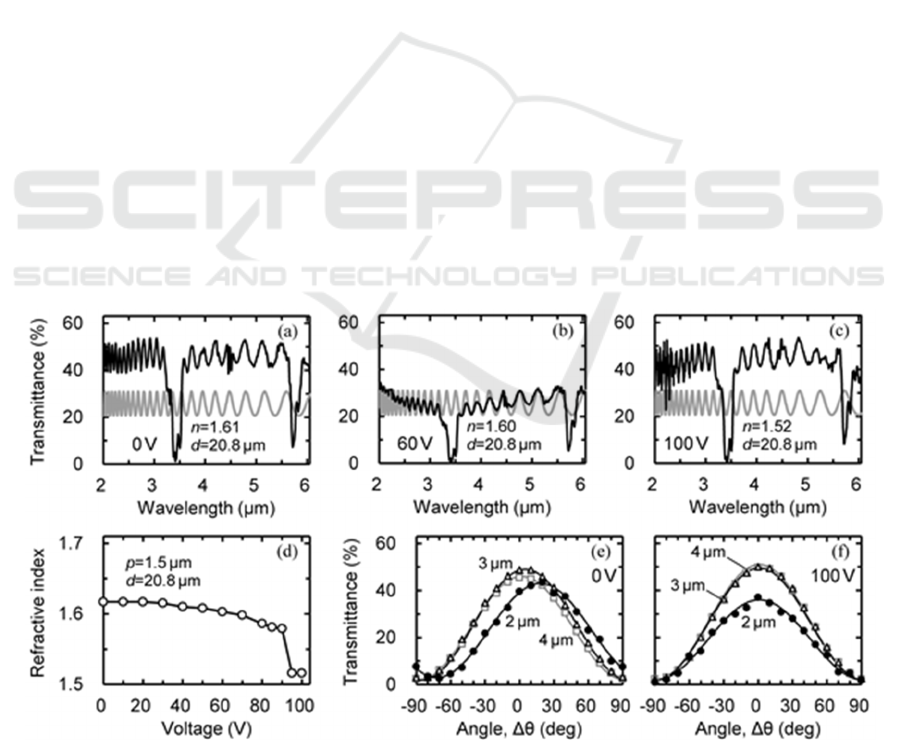
Figs. 3(a)‒3(c)

show the transmission spectra. Although the spectra

were similar to those of the first sample, a high

voltage was needed to induce the peak shift. A

notable decrease in transmittance was also visible at

around 60 V. The peak-wavelength fitting was

conducted by drawing theoretical curves (gray lines)

below the measured spectra. The LC layer thickness

was evaluated to be d=20.8 μm from the spectrum in

Fig. 3(c). The evaluated indices were 1.60 at 60 V and

1.61 at 0V. Figure 3(d) shows the refractive index as

a function of the applied voltage. The refractive index

of the initial phase (0 V) is 1.61, which is close to both

the result of the first sample [Fig. 2(d)] and the

predicted value (n

) [Eq. (2)]. The refractive index

decreases gradually to 1.58 as the voltage rises to 90

V, and then drops rapidly to 1.52. The cholesteric LC

is a mixture of nematic and chiral LCs. Increase in the

concentration of the chiral agent seems to raise a

voltage that is needed to induce the reorientation.

Figure 3(e) shows the polarization state of the

light beam that passed through the LC of the initial

Figure 3: Optical properties of the LC with a chiral pitch of p=1.5 μm and an evaluated thickness of d=20.8 μm. (a–c) The

black lines show the transmission spectra. The gray lines show the fitting curves that assume the refractive index of 1.52 at

100 V. (d) Evaluated refractive indices as a function of the applied voltage. (e, f) Transmittance change by the rotation (Δθ)

of the analyzer. Measurements were conducted at 0 and 100 V.

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

Figure 4: Optical properties of the LC with a chiral pitch of p=1.5 μm and an evaluated thickness of d=3.8 μm. (a–c) The

black lines show the transmission spectra. The gray lines show the fitting curves that assume the refractive index of 1.52 at

30 V. (d) Evaluated refractive indices as a function of the applied voltage. (e, f) Transmittance change by the rotation (Δθ) of

the analyzer. Measurements were conducted at 0 and 10 V.

phase. As expected, the optical rotation became

smaller in comparison with the result in Fig. 2(e). At

2 μm wavelength, however, a slight rotation still

remained. As Fig. 3(f) shows, no optical rotation

occurred in the homeotropic phase at 100 V.

These results indicate that decreasing the chiral

pitch neither eliminates the optical rotation and

scattering

nor

reduces

the

operation

voltage. We

therefore reduced the LC layer thickness in the

following experiment. Figures 4(a)‒4(c) show the

transmission spectra of the LC cell with a reduced

thickness. The thickness was evaluated to be d=3.8

μm by fitting the theoretical curve to the spectrum in

Fig. 4(c). In comparison with the spectra of the thick

cells (Figs. 2 and 3), the spectral curve changes gently

creating a smaller number of interference peaks. This

happens because the peak interval extends as the

optical thickness, nd, of the resonance cavity

decreases [Eq. (3)]. The interference peaks shift to

shorter wavelengths as the voltage increases. No

notable transmittance decrease is visible during the

voltage application process. Figure 4(d) shows the

voltage dependence of the refractive index. The

refractive index of the initial state (0 V) is 1.64. This

index is higher than those of the former LC cells [Figs.

2(d) and 3(d)] and coincides with the theoretical value

) of Eq. (1). The LC seems to take a regular chiral

texture [Fig. 1(c)] rather than a domain texture [Fig.

1(d)] when it is confined in a small volume. The

refractive index decreases gradually when the voltage

rises exceeding 6 V.

Figure 4(e) shows the polarization state of the

output beam. As regards a light beam of 3 μm

wavelength or longer, no polarization rotation is

visible. At 2 μm wavelength, however, a slight optical

rotation still remains (10°). As Fig. 4(f) shows, the

optical rotation becomes negligible when the LC is

reoriented by the voltage application.

4.3 Reduction of the LC Thickness

As the experiments in the last section clarified, both

the scattering loss and the optical rotation could be

eliminated more effectively by decreasing the LC

layer thickness than the chiral pitch. It was therefore

assumed that the cholesteric LC of 4.8 μm pitch could

also exhibit improved optical properties if it was

confined in a thin cell. To confirm this assumption,

we conducted experiments by using the long-pitch LC

again.

The black lines in Figs. 5(a)‒5(c) show the

transmission spectra of the LC cell whose chiral pitch

and thickness were p=4.8 and d=7.2 μm, respectively.

The thickness was determined by the peak-

wavelength fitting for the spectrum in Fig. 5(c). As

Fig. 5(b) shows, this LC cell still exhibited a

transmittance decrease during the phase transition

process. The LC layer thickness was therefore

Reduction of Optical Rotation and Scattering in a Cholesteric Liquid Crystal Layer

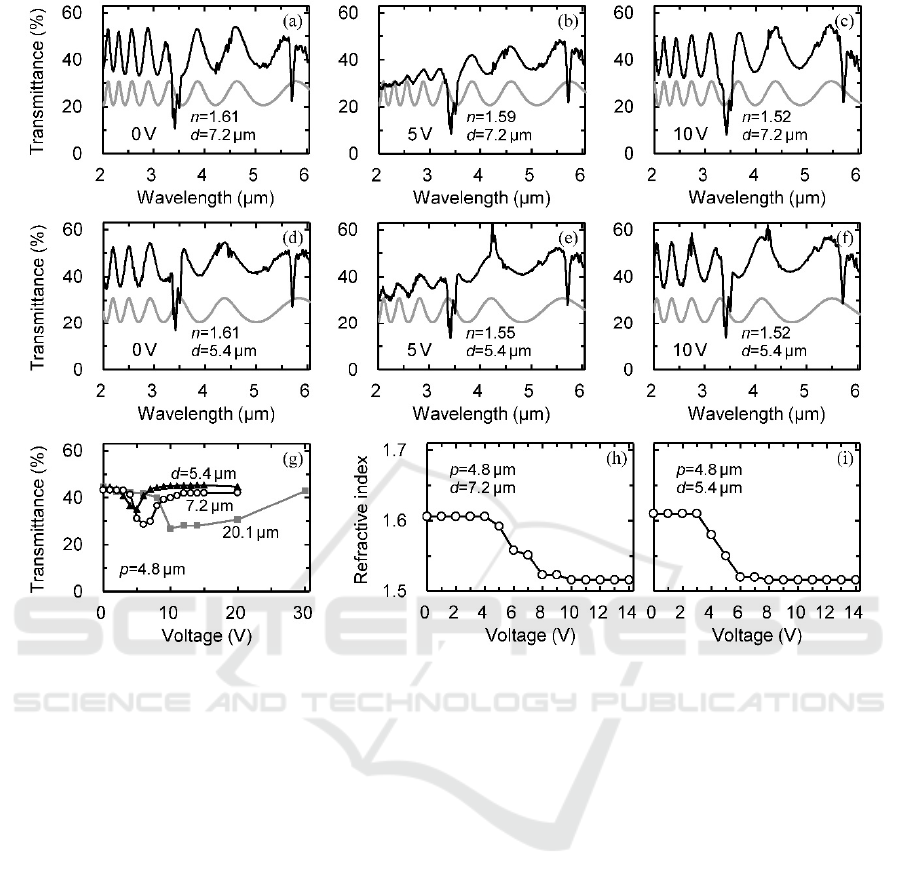
Figure 5: (a–f) Transmission spectra of the LC with a chiral pitch of p=4.8 μm and an evaluated thickness of d=7.2 or 5.4 μm.

The black lines show the measured spectra. The gray lines show the fitting curves. The peak-wavelength fitting was conducted

by assuming the refractive index of 1.52 at 10 V. (g) Average transmittance in the 2–3 μm range as a function of the applied

voltage. The data were taken from the spectra that were exemplified in (a–f) and Fig. 2. (h, i) Evaluated refractive indices as

a function of the applied voltage.

reduced further to 5.4 μm. Figures 5(d)‒5(f) show the

transmission spectra of this LC cell. The thickness

was still too large to reduce the scattering loss. Figure

5(g) shows voltage dependences of the transmittance,

which were plotted by using the spectral data in Figs.

2(a)‒2(c) and 5(a)‒5(f). Since the transmittance

changed heavily due to the interference, an average

was taken over the 2‒3 μm range. When the thickness

was 20.1 μm, the scattering occurred in the 8‒30 V

range. The scattering

range decreased to 4‒10 V in

the 7.2 μm cell, and 3‒6 V in the 5.4 μm cell. The

scattering strength also decreased as the thickness

decreased.

Figure 5(h) shows the refractive indices that were

evaluated for the cell of 7.2 μm thickness. The

refractive index in the initial phase (0 V) is close to

the theoretical value, n

[Eq. (2)]. The index

decreases gradually in the 4‒8 V range. This range

coincides with the heavy-scattering range. As Fig.

5(i) shows, the LC cell of 5.4 μm thickness also

exhibits a refractive index that is close to n

. The

index decreases to 1.52 in the 3‒6 V range. In

comparison with the thick LC cell [Fig. 2(d)], these

thin cells exhibit a gentle index change with the

increase of the applied voltage.

Finally, the LC cell of 2.9 μm thickness was

prepared. Figures 6(a)‒6(c) show the transmission

spectra. The peak interval became large, since the

optical thickness was small; i.e., nd=4.7 at 0 V and

4.4 at 10 V. As expected, no notable scattering was

visible

during the voltage application process. In

addition, the absorption bands at 3.4 and 5.7 μm

wavelengths became smaller owing to the reduction

of the optical thickness.

Figures 6(d)‒6(f) show the transmission spectra

that were measured by using a linearly-polarized light

beam. The probe beam of the spectrometer was

polarized in the direction that was horizontal or

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

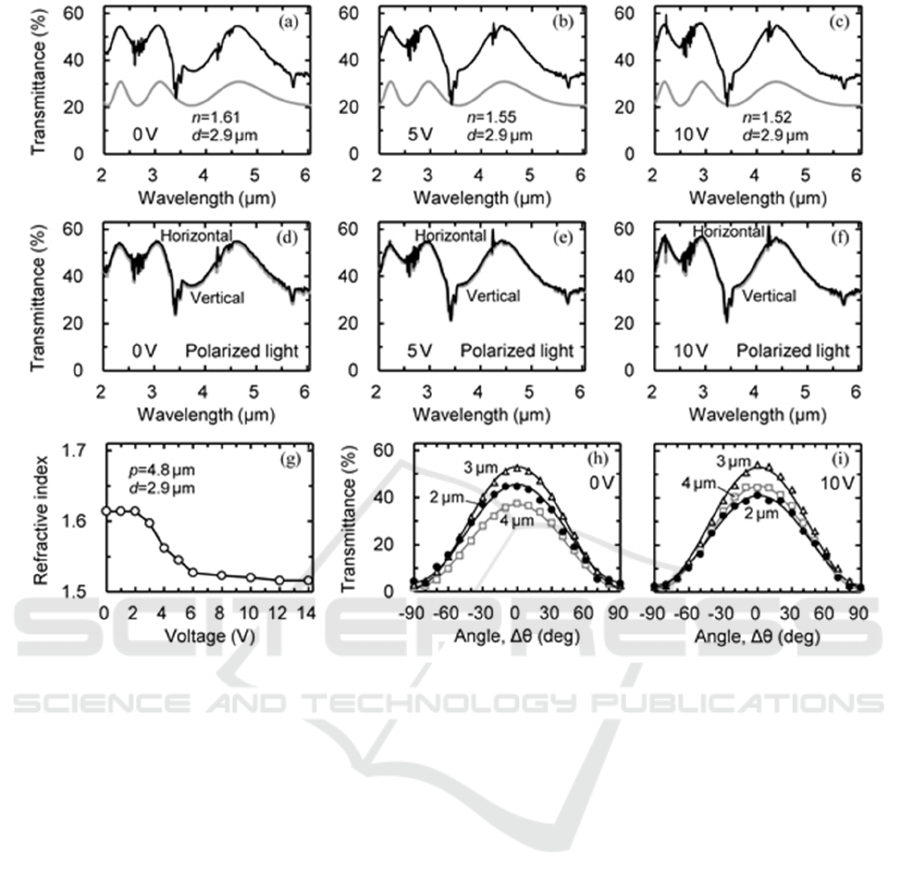
Figure 6: Optical properties of the LC with a chiral pitch of p=4.8 μm and an evaluated thickness of d=2.9 μm. (a–c) The

black lines show the transmission spectra. The gray lines show the fitting curves that assume the refractive index of 1.52 at

10 V. Measurements were conducted by using non-polarized light. (d–f) The black and gray spectra (overlapping) were

measured by using a probe beam that was linearly polarized in the horizontal or vertical direction. (g) Evaluated refractive

indices as a function of the applied voltage. (h, i) Transmittance change by the rotation (Δθ) of the analyzer. Measurements

were conducted at 0 and 10 V.

vertical to the ground. As described in Section 3, the

efficiency of the polarizer was cancelled out in the

measured transmission spectra. The two spectra (the

black and gray lines) corresponding to the horizontal

and vertical polarizations overlap with one another in

the entire spectral range. They also coincide with the

spectra in Figs. 6(a)‒6(c) that were measured with

non-polarized light.

Figure 6(g) shows the refractive indices that were

evaluated by the peak-wavelength fitting in Figs.

6(a)‒6(c). The refractive index at 0 V was 1.61, which

was close to the theoretical value, n

. The index

started

decrease

lower

voltage

in this

cell than the former ones. It decreased slightly in the

6‒12 V range, and thereafter became constant

=1.52).

Figure 6(h) shows the polarization state of the

beam that passed through the LC layer of the initial

phase. The transmittance took the maximum at ∆θ=0°

and the minimum at ±90° even at 2 μm wavelength.

That is, reduction of the optical rotation was

successful in the entire spectral range. As Fig. 6(i)

shows, the homeotropic phase at 10 V, of course,

exhibited no trace of the optical rotation.

5 DISCUSSION

In our previous study, we evaluated the LC layer

thickness or the cell gap (d) by using a transmission

spectrum of the empty cell before injecting the LC.

The cell gap, however, seemed to shrink during the

injection process probably due to the surface

tension. If this is the case, the inaccuracy of the

thickness causes an error in the evaluation of the

refractive index, since the peak-wavelength fitting

Reduction of Optical Rotation and Scattering in a Cholesteric Liquid Crystal Layer

determines only the optical thickness (nd). The

evaluation error becomes more serious as the

thickness (gap) decreases. In this work, therefore, we

evaluated the LC layer thickness from the spectrum

of the reorientation state by assuming that the LC took

the ordinary index (n

=1.52) in this state [Fig. 1(b)].

This evaluation method seems successful, since

evaluated indices are reproducible and plausible with

reference to the theoretical prediction. The evaluated

index change was ∆n=1.61‒1.52=0.09, and hence, the

relative index change was ∆n/n

=0.09/1.52=0.06

(6%). Although this relative evaluation is accurate,

the actual refractive index may be slightly lower than

the evaluated value, since the ordinary index (n

) is

possibly lower than the assumed value (n

=1.52 at

0.59 μm) because of the wavelength dispersion (Saito

and Yasuda, 2003). Further analysis is needed to

evaluate the refractive index more accurately.

The reduction of the LC layer thickness was

effective to decrease the optical rotation, the

scattering loss, the absorption loss (3.4 and 5.7 μm),

and the operation voltage. This is an expected result,

since these physical quantities change in proportion

to the thickness. In addition to this proportional effect,

a change in the microstructure (director distribution)

seems to affect the optical properties, since both the

surface tension and narrow space restrict the behavior

of LC molecules.

6 CONCLUSIONS

A cholesteric LC with a chiral pitch of 4.8 μm

exhibited a polarization-independent refractive index

in the infrared region (>2 μm). The index change of

∆n=0.09 was attainable by application of 10 V. Both

the optical rotation and the scattering loss were

eliminated successfully by enclosing this LC in a cell

of 2.9 μm thickness. This LC will be useful to create

polarizer-free devices for the infrared optical systems.

REFERENCES

Khoo, I. C., 2007. Liquid Crystals, Wiley. New York, 2

edition.

Saito, M., Yasuda, T., 2010. An infrared polarization switch

consisting of silicon and liquid crystal. J. Opt. 12(1). p.

015504-1–6.

Patel, J. S., Maeda, M. W., 1991. Tunable polarization

diversity liquid-crystal wavelength filter. IEEE Photon.

Technol. Lett. 3(8). p. 739–740.

Hirabayashi, K., Tsuda, H., Kurokawa, T., 1993. Tunable

liquid-crystal Fabry-Perot interferometer filter for

wavelength-division multiplexing communication

systems. J. Lightwave Technol. 11(12). p. 2033–2043.

Saito, M., Hayashi, K., 2013. Integration of liquid crystal

elements for creating an infrared Lyot filter. Opt.

Express, 21(10). p. 11984–11993.

Moore, J., Collings, N., Crossland, W. A., Davey, A. B.,

Evans, M., Jeziorska, A. M., Komarčević, M., Parker,

R. J., Wilkinson, T. D., Xu, H., 2008. The silicon

backplane design for an LCOS polarization-insensitive

phase hologram SLM. IEEE Photon. Technol. Lett.

20(1). p. 60–62.

Lin, Y.-H., Ren, H., Wu, Y.-H., Zhao, Y., Fang, Ge, J. Z.,

Wu, S.-T., 2005. Polarization-independent liquid

crystal phase modulator using a thin polymer-separated

double-layered structure. Opt. Express, 13(22). p.

8746–8752.

Ye, M., Wang, B., Sato, S., 2006. Polarization-independent

liquid crystal lens with four liquid crystal layers. IEEE

Photon. Technol. Lett. 18(3). p. 505–507.

Lee, J.-H., Kim, H.-R., Lee, S.-D., 1999 Polarization-

insensitive wavelength selection in an axially

symmetric liquid-crystal Fabry-Perot filter. Appl. Phys.

Lett. 75(6). p. 859–861.

Provenzano, C., Pagliusi, P., Cipparrone, G., 2006. Highly

efficient liquid crystal based diffraction grating induced

by polarization holograms at the aligning surfaces. Appl.

Phys. Lett. 89(12). p. 121105-1–3.

Saito, M., Yoshimura, K., Kanatani, K., 2011. Silicon-

based liquid-crystal cell for self-branching of optical

packets. Opt. Lett. 36(2). p. 208–210.

Patel, J. S., Lee, S.-D., 1991. Electrically tunable and

polarization insensitive Fabry-Perot étalon with a

liquid-crystal film. Appl. Phys. Lett. 58(22). p. 2491–

2493.

Crooker, P. P., 2001. Blue Phases. Kitzerow, H., Bahr, C.,

eds., Chirality in Liquid Crystals. Springer, New York.

Haseba, K., Kikuchi, H., Nagamura, T., Kajiyama, T., 2005,

Large electro-optic Kerr effect in nanostructured chiral

liquid-crystal composites over a wide temperature

range. Adv. Mater. 17. p. 2311–2315.

Lin, Y.-H., Chen, H.-S., Lin, H.-C., Tsou, Y. S., Hsu, H.-

K., Li, W.-Y., 2010. Polarization-free and fast response

microlens arrays using polymer-stabilized blue phase

liquid crystals. Appl. Phys. Lett.

96(11). p. 113505-1–3.

Hsiao, Y.-C., Tan, C.-Y., Lee, W., 2011. Fast-switching

bistable cholesteric intensity modulator. Opt. Express,

19(10). p. 9744–9749.

Kopp, V. I., Fan, B., Vithana, H. K. M., Genack, A. Z., 1998.

Low-threshold lasing at the edge of a photonic stop

band in cholesteric liquid crystals. Opt. Lett. 23(21). p.

1707–1709.

Furumi, S., Yokoyama, S., Otomo, A., Mashiko, S., 2003.

Electrical control of the structure and lasing in chiral

photonic band-gap liquid crystals. Appl. Phys. Lett.

82(1). p. 16–18.

Saito, M., Maruyama, A., Fujiwara, J., 2015. Polarization-

independent refractive-index change of a cholesteric

liquid crystal. Opt. Mater. Express, 5(7). p. 1588-1597.

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

Kim, K.-H., Jin, H.-J., Park, K.-H., Lee, J.-H., Kim, J. C.,

Yoon, T.-H., 2010. Long-pitch cholesteric liquid crystal

cell for switchable achromatic reflection. Opt. Express,

18(16). p. 16745–16750.

Born, M., Wolf, E., 1980. Principles of Optics, Pergamon.

Oxford. Chapter 2.

Saito, M., Takeda, R., Yoshimura, K., Okamoto, R.,

Yamada, I., 2007. Self-controlled signal branch by the

use of a nonlinear liquid crystal cell. Appl. Phys. Lett.

91(14), p. 141110-1–3.

Hecht, E., 1998. Optics. Addison-Wesley. Reading, MA.

Chapter 9.

Saito, M. Yasuda, T., 2003. Complex refractive-index

spectrum of liquid crystal in the infrared. Appl. Opt.

42(13). p. 2366–2371.

Reduction of Optical Rotation and Scattering in a Cholesteric Liquid Crystal Layer