
Narrow Band Pressure Computation for Eulerian Fluid Simulation
Aditya Prakash and Parag Chaudhuri
Department of Computer Science and Engineering, Indian Institute of Technology Bombay, Mumbai, India
Keywords:
Eulerian Fluid Simulation, Narrow Band Pressure Solve, Fluid Animation.
Abstract:
An Eulerian fluid simulation for incompressible fluids spends a lot of time in enforcing incompressibility
by solving a large Poisson’s equation. This involves solving a large system of equations using a solver like
conjugate gradients. We introduce a way of accelerating this computation by dividing the grid domain of
the fluid simulation into a narrow band of high resolution grid cells near fluid-solid boundaries and a coarser
grid everywhere else. Judiciously reducing the number of high resolution grid cells significantly lowers the
cost of the pressure projection step, while not sacrificing the simulation quality. The coarse grid values are
upgraded to a finer grid before advecting the fluid surface so that enough degrees of freedom are available
to resolve surface detail. We present and analyse two methods to perform this upgradation, namely, velocity
interpolation and pressure field smoothing. We discuss the merits and demerits of each and quantify the errors
introduced in the simulation as a function of size of the narrow band. Finally, since we are primarily interested
in visualizing the fluid animation, we produce rendered fluid simulation output to also validate the visual
quality of the simulations.
1 INTRODUCTION
Eulerian fluid simulation involves solving the Navier-
Stokes equations on a fixed grid. An incompressible
fluid solve on a regular rectilinear grid is a common
example of this kind of simulation. Even in its sim-
plest setting this a computationally intensive task, and
a major proportion of this computation is spent in the
pressure projection stage that enforces fluid incom-
pressibility (Lentine et al., 2010; Prakash and Chaud-
huri, 2015). This is done by solving a Poisson’s equa-
tion using an iterative or direct solver.
A lot of earlier research has attempted to in-
crease the speed of pressure projection on fixed grids.
These methods are either not tailored for visual liq-
uid simulation (Montijn et al., 2006), or use specific
complicated grid structures (Ferstl et al., 2014), or
treat the fluid free surface differently from rest of
the fluid volume (Autodesk, ). Dimension reduction
techniques (Treuille et al., 2006) and different ba-
sis functions (De Witt et al., 2012) have also been
used for this purpose. The problem however, remains
challenging for liquids simulation as the fluid vol-
ume topology changes rapidly and enforcing correct
boundary conditions is difficult.
We specifically focus on visual fluid (liquid) ani-
mation and present a technique to accelerate the pres-
sure solve by creating a very coarse grid for the en-
tire fluid simulation, except for a narrow band of fine
grid cells around the boundary. This grid structure
is statically determined and does not require runtime
re-gridding. It perfectly enforces both Dirichlet and
Neumann boundary conditions at the fluid free sur-
face and fluid-solid boundary. We avoid the pitfalls of
the previous methods while still managing to main-
tain enough degrees of freedom in the final velocity
field of the fluid simulation so as to be able to gener-
ate adequate surface detail. Our specific contributions
are as follows:
1. We present a simple, flexible method to reduce the
size of the pressure projection problem by using a
coarser grid and a narrow band fine grid. We show
how to couple these together to enforce both free
surface and fluid-solid boundary conditions.
2. We show how to upgrade values from the coarse
grid back to a fine grid to get adequate degrees of
freedom in the velocity field to represent surface
detail using two techniques, namely, velocity in-
terpolation and pressure field smoothing.
3. We rigorously compare the speedups obtained
in computation while using the two upgradation
strategies. We also quantify the errors introduced
due to our methods, and the visual quality of the
simulation thus produced, in both 2D and 3D.
Prakash A. and Chaudhuri P.
Narrow Band Pressure Computation for Eulerian Fluid Simulation.
DOI: 10.5220/0006090200170026
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 17-26
ISBN: 978-989-758-224-0
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
17

These ideas substantially reduce the computa-
tional cost of the pressure solve without compromis-
ing on simulation quality. Our method is also easy to
parallelize and works perfectly on multi-core archi-
tectures.
We start by looking at existing literature in the
concerned area in Section 2. We briefly discuss the
details of the Navier-Stokes equation and the Pois-
son’s equation that requires most of the computational
effort to solve during the simulation in Section 3.
We follow this up with a detailed description of our
narrow band pressure solve method and all the algo-
rithms in Section 4. We compare the performance of
our algorithms, the visual and timings results obtained
and the errors involved in Section 5. We conclude in
Section 6 with a brief summary and discussion about
limitations of the current system and possible future
directions.
2 BACKGROUND
Grid-based Eulerian simulation of incompressible flu-
ids is commonly used for visual fluid animation in
computer graphics and scientific visualization. Many
authors have presented systems that present visually
compelling results from fluid simulations on Eulerian
grids (Stam, 1999; Foster and Fedkiw, 2001; Enright
et al., 2002), however, the size of the grids that these
techniques can use is limited by computational power
available.
As a consequence of this, many authors have
looked at adding details to these simulations by
adding various kinds of noise, like Kolmogorov
noise (Larmorlette and Foster, 2002; Rasmussen
et al., 2003) or curl noise (Bridson et al., 2007). Some
techniques (Schechter and Bridson, 2008) determine
where to add the noise and couple it to the Navier-
Stokes equations. However, these are not physically
realistic techniques and do not produce convincing
details in all situations.
Another approach is to improve the original sim-
ulation by the particular choice of the methods used
to solve each stage depending on accuracy, stability
and computational cost. E.g. semi-Lagrangian ad-
vection, proposed by Stam et al. (Stam, 1999) is un-
conditionally stable but has only first order accuracy,
whereas Selle et al. (Selle et al., 2008) used a modified
McCormack scheme to give second order accuracy to
the advection step. Another way is to try and main-
tain certain invariants like energy (Mullen et al., 2009)
during the simulation. These methods increase accu-
racy and fidelity of the simulation, but they involve
more expensive computation and are still limited by
the grid resolution on which the simulation is per-
formed. In order to increase grid resolution without
too much computational cost, some authors have in-
troduced adaptive grid techniques like AMR (Berger
and Oliger, 1984) and octrees (Losasso et al., 2004),
however, these complicated data structures are diffi-
cult to update during simulation and robust numerical
solutions are difficult to design on such grids.
Lentine et al. (Lentine et al., 2010) present a
method of using a multi-resolution grid to speedup
the pressure projection step. They also require the ve-
locity field to be interpolated from a lower resolution
to a higher one. We show in this paper that velocity
interpolation is a poorer speedup strategy as forcing
the velocity field to be divergence free is harder post
interpolation and leads to lower speedups than other
methods.
Other authors have presented multigrid techniques
for efficiently solving Poisson problems (McAdams
et al., 2010; Chentanez and M
¨
uller, 2011; Jung et al.,
2013). Though theoretically multigrid techniques are
very efficient, they require precise discretization and
complicated data-structures for correctly converging
on regular grids (Ferstl et al., 2014). Our method is
much easier to apply and is guaranteed to converge.
Ando et. al (Ando et al., 2015) describe the work
that is closest to ours in spirit. They also describe a
dimension reduction strategy for simplifying the pres-
sure solve. Their work uses an up-sampling matrix
to interpolate the pressure to a higher resolution grid
during the pressure solve. They enforce Dirichlet
boundary conditions by using a surface aware pres-
sure basis to make the pressure zero at the free sur-
face. Our method is closely related to this work in
that we too present a dimension reduction strategy in
that interpolates pressure to a higher resolution grid,
after the linear pressure solve. In addition we com-
pute pressure at higher resolution in a narrow band
around the fluid-solid boundary. This gives a better
solution in this boundary region. Our method is also
easier to understand and implement.
Authors have also investigated hybrid Eulerian-
Lagrangian methods to achieve speedup in fluid sim-
ulation computations. Chentanez et. al (Chentanez
et al., 2014) couple a Eulerian solver, a shallow water
solver and a Lagrangian SPH solver within a simula-
tion. The material point method (MPM) combines a
grid-based Eulerian simulation with marker particles
to simulate a range of materials like snow (Stomakhin
et al., 2013) and foams (Yue et al., 2015). Ferstl et.
al (Ferstl et al., 2016) present a solution for accelerat-
ing FLIP advection in Eulerian grid-based fluid simu-
lations by using FLIP particles only in a narrow band
around the free surface of the fluid.
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
18
Some authors have also experimented with addi-
tion of high resolution detail to low-resolution simu-
lations (Threy et al., 2010; Kim et al., 2013) but these
are largely orthogonal to the techniques presented in
this paper.
3 THE NAVIER-STOKES
EQUATIONS
The Navier-Stokes for inviscid, incompressible fluids
is given by the pair of equations given below. These
equations govern the conservation of momentum and
mass of the fluid.
∂u
∂t
+ u · ∇u = −
1
ρ
∇p + f (1)
∇ · u = 0, (2)
where ρ is the density, u the velocity, p the pres-
sure, and f the acceleration due to an external force,
such as gravity. We solve these equations by operator
splitting. For any given iteration, n, and correspond-
ing fluid velocity, u
n
, first the advection step is solved
and an intermediate velocity, u
∗
, is computed. ∆t is
the timestep of the solver.
u
∗
− u
n
∆t
+ u
n
· ∇u
n
= f. (3)
The pressure is computed next by solving a Pois-
son system of the form
∇ ·
∆t
ρ
∇p = ∇ · u
∗
. (4)
Subsequently, the pressure forces are added to
compute the velocity for the next iteration, i.e., u
n+1
.
u
n+1
− u
∗
∆t
= −
1
ρ
∇p. (5)
The domain in which Equations 3, 4 and 5 are
solved is tracked by a distance field φ, where φ < 0 for
regions that contain the fluid. The level-set is evolved
with the fluid by solving
∂φ
∂t
= −u · ∇φ. (6)
Solving the Poisson system (in Equation 4) is
a substantial computational component of the entire
fluid solve (Lentine et al., 2010; Prakash and Chaud-
huri, 2015). Therefore, solving this on a coarse grid
reduces computational complexity substantially. A
coarse grid, however, cannot capture adequate fluid
surface detail, thus making high resolution or finer
grids essential.
We solve the Poisson system on a coarse grid
for almost the entire fluid domain, except in a nar-
row band around the fluid-solid boundary, where it is
solved at a finer resolution. The coarser solution is
then upgraded to a finer grid everywhere in the fluid
domain, while correctly enforcing all boundary con-
ditions. In the next section we explain the basic ideas
behind the narrow band pressure solve and the upgra-
dation strategies.
4 NARROW BAND PRESSURE
SOLVE
There are two regions in the fluid where resolving the
fluid accurately is essential. The first of these is the
fluid-solid boundary. In order to resolve the details at
such boundaries, we create a narrow band of fine grid
cells around all solid boundaries. Examples of this are
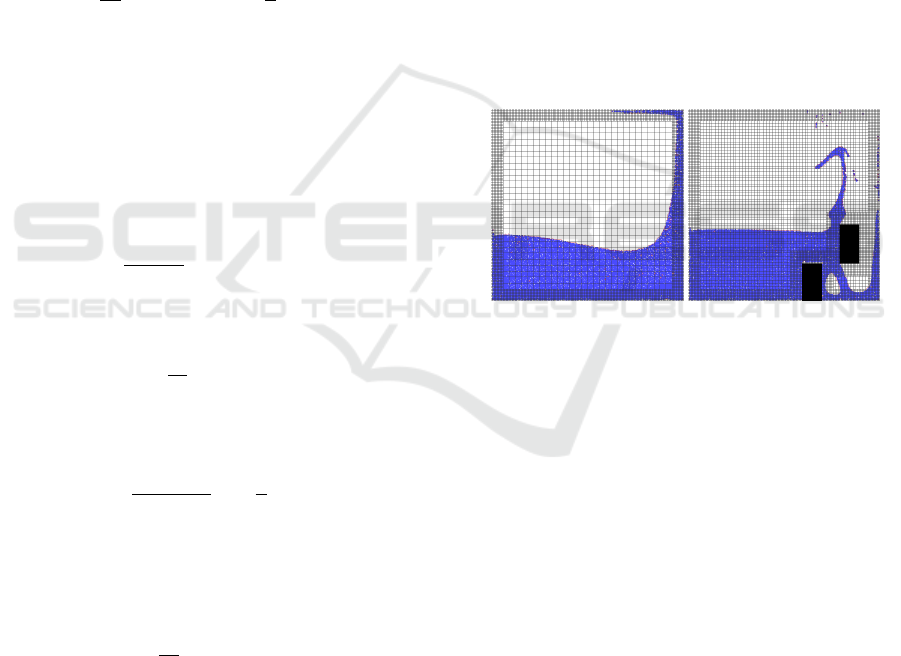
shown in Figure 1.
(a) (b)
Figure 1: The narrow band of fine grid cells can be seen
around all solid boundaries. 1(a) shows the coarse grid with
1 coarse grid cell equal to 16 fine grid cells and narrow band
of fine cells that is 8 fine grid cells wide. 1(b) shows the
coarse grid with 1 coarse grid cell equal to 4 fine grid cells
and narrow band of fine cells that is 8 fine grid cells wide.
Here the narrow band can be seen around the solid obstacles
as well.
Post velocity advection, the Poisson equation is
solved on the coarse and narrow band fine grid us-
ing a preconditioned conjugate gradients solver. Any
other solver of choice can also be used for this step.
If these two grids are used directly to advect the fluid
surface, the coarse grid is not able to resolve the fluid
surface accurately due to its Nyquist limit. This is the
second region where the fluid needs to be accurately
resolved, else all visual details are lost. In order to do
this, the coarse grid has to be upgraded to a finer grid
everywhere in the fluid domain, post the narrow band
pressure solve.
The fundamental idea behind the need for upgra-
dation here is to get velocity on a finer grid every-
where before the fluid surface is advected. This al-
Narrow Band Pressure Computation for Eulerian Fluid Simulation
19

lows the velocity field to have enough degrees of free-
dom to accurately resolve free surface detail. This ve-
locity field also has to be divergence free to enforce
mass conservation in the fluid.
We tried two methods for performing the upgrada-
tion. We call these methods upgradation by velocity
interpolation and by pressure field smoothing. We de-
scribe both below.
4.1 Upgradation by Velocity
Interpolation
The first method upgrades the velocity field in the
coarse grid, after the pressure solve. We create a
new fine grid everywhere in the fluid domain. At the
boundary between the coarse and the narrow band fine
grid, velocity is interpolated between the narrow band
values and the coarse grid values from the neighbour-
ing cells and the interpolated value is copied to the
new fine grid. Everywhere else, the value from the
underlying grid (coarse or narrow band fine) is copied
as is. Now, the final velocity field is available in a fine
grid everywhere in the fluid domain before the liquid
surface is advected and there are enough degrees of
freedom present to compute adequate surface detail.
Algorithm 1 explains what happens in one simulation
step when using this method.
Algorithm 1: Single time step algorithm with velocity field
interpolation.
1: Advect u
n
to u
∗
using Equation 3 on the fine grid
everywhere in the fluid domain.
2: Solve Poisson system given by Equation 4 on the
coarse grid.
3: Solve Poisson system given by Equation 4 on the
narrow band fine grid.
4: Compute velocity u
n+1
on the coarse and narrow
band fine grids using Equation 5.
5: Interpolate the velocity field across the coarse and
narrow band fine grid boundary.
6: Copy interpolated velocity to the new fine grid.
7: Extrapolate velocity from the fine grid.
8: Compute the distance field φ using Equation 6
and advect the liquid surface.
This method is easy to compute as the interpola-
tion adds minimal overhead to the computation cost.
We, however, found that when the narrow band is
smaller in width than a fourth of the original (i.e., non-
coarse) grid size, the fluid loses mass rapidly, as errors
in the velocity field dominate. The maximum speedup
obtained is thus limited when using this upgradation
method. It is also harder to ensure that the final up-
graded velocity field on the fine grid is divergence
free. Therefore, the method suffers from mass loss
errors.
4.2 Upgradation by Pressure Field
Smoothing
In our next method instead of upgrading the velocity
field, we upgrade the pressure field itself. In order
to do this, the pressure field is interpolated across the
coarse and narrow band fine grid boundary. Then the
pressure field is regularized by running 1 − 3 Jacobi
iterations on it. We start by intializing the iteration
using the interpolated pressure field on the fine grid
and then solve Equation 4 using the Jacobi iterations.
This ensures that the interpolated field is free from
divergence, as is the subsequent velocity field com-
puted from it. This is then used to advect the liquid
surface. This method does not suffer from significant
mass loss like the velocity interpolation method, and
with careful implementation the Jacobi iteration does
not pose too much of an additional computational bur-
den. Algorithm 2 presents the steps involved in this
method.
The pressure smoothing technique allows us to get
large speedups over a conjugate gradient solve every-
where on a fine grid, without sacrificing the fluid sur-
face details. This makes it very suitable for visual
fluid simulation.
Algorithm 2: Single time step algorithm with pressure field
smoothing.
1: Advect u
n
to u
∗
using Equation 3 on the fine grid
everywhere in the fluid domain.
2: Solve Poisson system given by Equation 4 on the
coarse grid.
3: Solve Poisson system given by Equation 4 on the
narrow band fine grid.
4: Interpolate the pressure field across the coarse
and narrow band fine grid boundary.
5: Copy interpolated pressure to the new fine grid.
6: Run upto 3 Jacobi iterations on the pressure field
in the fine grid to regularize it.
7: Compute velocity u
n+1
on the fine grid using the
regularized pressure field using Equation 5.
8: Extrapolate velocity from the fine grid.
9: Compute the distance field φ using Equation 6
and advect the liquid surface.
4.3 Boundary Conditions
There are usually two kinds of boundaries in a free
surface fluid simulation. The boundary between the
fluid and the solid requires a Neumann boundary con-
dition, which is enforced for all cells in the nar-
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
20

row band when the narrow band Poisson equation is
solved. The free surface requires a Dirichlet bound-
ary condition, which is carefully enforced for all cells
on the fluid surface during the Poisson solves and
the interpolation done for the pressure field smooth-
ing. A third boundary is introduced in the simulation
due to partitioning the fluid domain in coarse and nar-
row band fine cells. Fluid is allowed to move freely
across this boundary so that this boundary appears
completely porous to the fluid during advection.
5 EXPERIMENTAL RESULTS
AND ANALYSIS
We have performed a number of experiments to cat-
alog the efficacy of our methods and also to deter-
mine the kind of errors introduced in the simulation
due to its use. We have performed all our experiments
on a machine with a 16 core Intel 2.60 GHz Xeon
processor with 32 GB of RAM. We solve the Navier-
Stokes by splitting the equations, using operator split-
ting, into advection and pressure projections stages.
The pressure projection step needs to solve a large
linear system at each time step of the simulation. An
incomplete Cholesky preconditioned conjugate gradi-
ent technique is used to solve the voxelized Poisson
equation in this stage (Bridson, 2008). We use this
solver as a base solver in all our simulations. Our
base fluid simulator is parallelized using OpenMP,
with the exception of the preconditioned conjugate
gradient pressure solver, which is implemented seri-
ally. This same solver is used for the Poisson solves
in our narrow band simulator as well.
5.1 Performance with Velocity
Interpolation
We applied velocity interpolation based upgradation
(see Section 4.1) to grids with fine narrow bands of
width 64 and 128 cells. Average iteration time, av-
eraged over every 500 frame window, is plotted and
shown in Figure 2 for the narrow band width of 64. It
should be noted that narrow band widths are always
measured in number of fine grid cells. The original
base simulation is a simple dam-break simulation, run
on a 512×512 fine grid. In the coarse grid, the coarse
grid cell size used is double the size of the fine grid
cell size in either dimension. The speedup obtained in
total simulation time is 22.9% and 20.0% for the 64
and 128 sized narrow bands respectively. Reducing
the narrow band grid size below 64 pushes errors in
velocity beyond acceptable limits.
Figure 2: Performance of the fluid simulation when using
the velocity interpolation method with a narrow band of
width 64.
5.2 Performance with Pressure Field
Smoothing
Next, we applied pressure field smoothing upgrada-
tion (see Section 4.2) to grids with fine narrow bands
of widths ranging from 8 to 64. The pressure field
smoothing method allows much thinner narrow bands
of fine grid cells with less error, thereby offerring
much larger speedups. The original base simulation
is the same as the one used above. Average iteration
time, averaged over every 500 frame window, is plot-
ted and shown in Figure 3. In each case, 3 Jacobi iter-
ations were run to regularize the interpolated pressure
field.
Figure 3: Performance of the fluid simulation when using
the pressure field smoothing method. Here 1 coarse grid
cell is equal to 4 fine grid cells.
We further pushed the amount of speedup that can
be obtained with our technique by making the coarse
grid cells larger to contain 16 fine grid cells instead
of the earlier 4. The average iteration time is plotted
as before in Figure 4. The speedup obtained in total
simulation time in each case is shown in Table 1. The
second column of the table gives the speedup when 1
coarse grid cell contains 4 fine grid cells, and the third
column when 1 coarse grid cell contains 16 fine grid
cells.
Figure 5 shows a comparison of the per itera-
tion performance of the original simulator with the
Narrow Band Pressure Computation for Eulerian Fluid Simulation
21

Figure 4: Performance of the fluid simulation when using
the pressure field smoothing method with larger coarse grid
cells. Here 1 coarse grid cell is equal to 16 fine grid cells.
Table 1: Percent speedup obtained in total simulation time
over the original base simulation for different narrow band
widths.
Width of Speedup Speedup
narrow band (Coarse 4) (Coarse 16)
8 57.5% 64.4%
16 48.9% 55.1%
24 42.1% 47.7%
32 35.5% 41.5%
64 21.9% 26.8%
fastest velocity smoothing case and the fastest pres-
sure smoothing case, for the first 100 iterations of the
simulation. This is comparison of raw per iteration
timing data, without the averaging done in the pre-
vious cases. It can be clearly seen that the pressure
field smoothening method gives very large speedups
in comparison to the velocity interpolation method,
for the same original base simulation. We will see
later that is also produces less error in the simulation.
We compare the visual quality of the simulations pro-
duced next.
Figure 5: Comparison of performance of various implemen-
tations of the fluid simulator for first 100 iterations.
5.3 Visual Quality Comparison
Figure 6 shows rendered frames from the original 2D
simulator, and the same frames from the simulators
implemented with velocity interpolation and pressure
field smoothing at different coarse grid resolutions. It
can be seen that the pressure field smoothing results
are visually closer to the original, unaccelerated sim-
ulator. The velocity interpolation method introduces
artefacts in the simulation in the form of additional
air gaps in the fluid volume and also, mass loss. The
size of the narrow band is 64 with velocity interpola-
tion and 8 with pressure field smoothing. Between the
two pressure smoothing cases some difference can be
seen, owing to the difference in size of the coarse grid
cells.
We also show some more frames from another
simulation that had additional solid obstacles in the
fluid domain in Figure 7. The narrow band also exists
around the obstacles. It can be seen that our method
correctly resolves all simulation details even around
the obstacles.
Comparison videos of these simulations can be
seen in the supplementary video submitted with the
paper.
5.4 3D Simulation
We performed similar experiments on a 3D fluid sim-
ulator. The methods introduced in this paper work
perfectly in 3D too. The speedup in total simulation
time obtained with pressure field smoothing over an
original base dam break simulation on a grid size of
128 × 128 ×128 is 38.0%. This is with a narrow band
size of 24 and with 1 coarse grid cell equal to 8 fine
grid cells. Sample rendered frames of the simulation
can be seen in Figure 8. Visual quality of the results
generated by the pressure field smoothed simulator is
comparable to the original unaccelerated simulator.
5.5 Error Analysis
We compute the error introduced in the simulation
due to the approximation introduced by the coarse
grid. We show the difference in velocity in the hor-
izontal and vertical directions in the fluid field in Fig-
ure 9, for a single frame. Warmer colors represent
higher error. It can be seen that the velocity interpo-
lation method introduces more error in the fluid than
the pressure smoothing case. Errors also increase as
the coarse grid cell size increases and narrow band
width decreases (see Figure 10). Visual fidelity of
the simulation and error have to balanced against the
speedup obtained during simulation based on compu-
tational requirements and costs.
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
22

(a) (b) (c) (d)
(e) (f) (g) (h)
Figure 6: Comparison of visual quality of the simulation produced. 6(a) and 6(e) are two different frames from the original
simulation, 6(b) and 6(f) are the same frames from the simulator implemented with velocity interpolation, 6(c) and 6(g) are
frames from the simulator implemented with pressure field smoothing on coarse grid cell size equal to 4, 6(d) and 6(h) are
frames with pressure field smoothing on coarse grid cell size equal to 16 fine grid cells.
Figure 7: Comparison of visual quality of the simulation
produced with obstacles in the fluid. The top row shows
frames from the original simulation on a 256 × 256 grid.
The bottom row shows the same frames from the simulator
with pressure field smoothing, with 1 coarse grid cell size
equal to 4 fine grid cells and a narrow band of width 8.
Figure 8: Comparison of visual quality of the simulation
produced in 3D. The top row shows frames from the orig-
inal simulation on a 128 × 128 × 128 grid. The bottom
row shows the same frames from the simulator with pres-
sure field smoothing on a coarse grid with a narrow band of
width 24.
Narrow Band Pressure Computation for Eulerian Fluid Simulation
23

Figure 9: Comparison of error in fluid velocity. The first column shows frames 1000, 2000, 3000 and 4000 from the original
simulation, the second and third columns show error in the horizontal component of velocity for velocity interpolation and
pressure smoothing, the fourth and fifth columns show error in vertical component of velocity for velocity interpolation and
pressure smoothing respectively. Blue represents 0 error and red represents maximum error.
6 CONCLUSIONS
We have presented a method to accelerate the pres-
sure projection step in an Eulerian fluid simulator by
solving the Poisson’s equation only in a narrow band
around fluid-solid boundaries. We solve this system
of equations on a coarser grid everywhere else in the
fluid domain and then upgrade this result to a finer
grid to obtain enough degrees of freedom to track
the fluid surface accurately. We present two methods
of performing the upgradation, namely velocity inter-
polation and pressure field smoothing. We compare
the pros and cons of each, giving extensive results
about the visual quality of simulations produced, er-
rors introduced in the simulation and the computation
speedup obtained. We conclude that the pressure field
smoothing method performs better on all metrics and
is a better way to perform the upgradation than veloc-
ity interpolation. We also show that the same methods
work in a 3D fluid simulator also.
The behaviour of the narrow band computation in
the presence of more complicated, non-grid aligned
obstacles needs more analysis. The role of the size of
the obstacle with respect to the grid size also needs
to be carefully understood. Currently, we have used
a small and conservative timestep size in the narrow
band simulator. We would like to investigate adaptive
timestepping for such simulators as well.
We would like to explore adaptive grid coarsening
during every step of the simulation so that adequate
degrees of freedom are always available at the fluid
surface to resolve detail. This will help us avoid the
grid upgradation step and may lead to better perfor-
mance. We also want to explore the use of our method
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
24
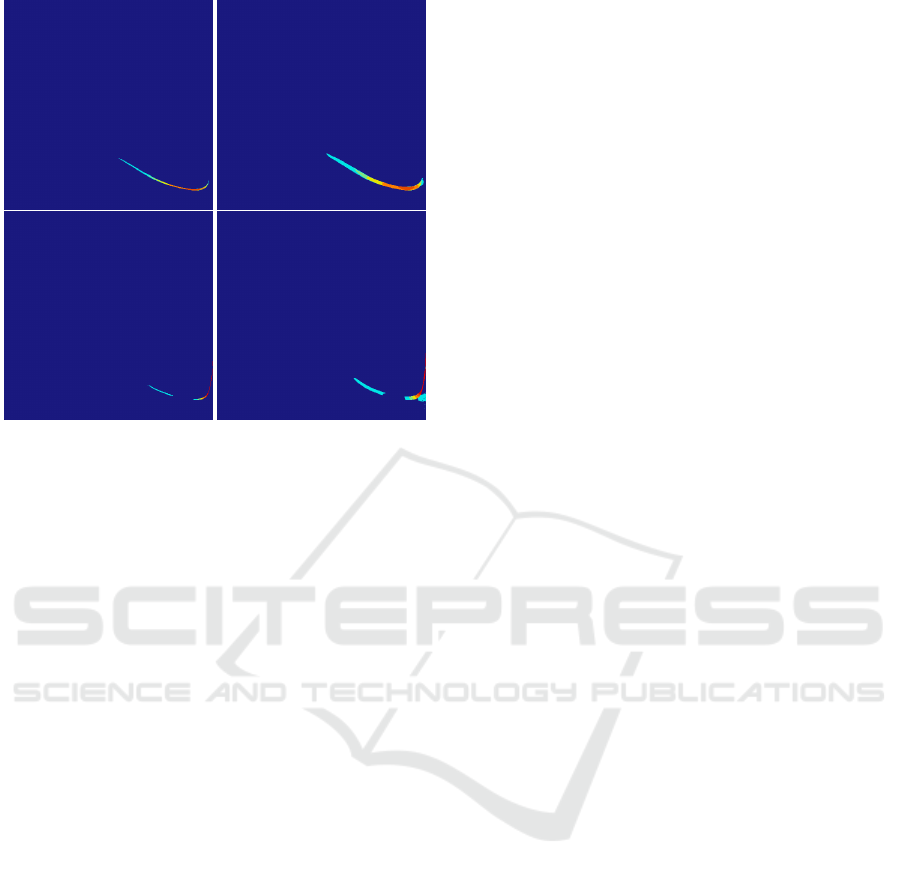
Figure 10: Comparison of error in fluid velocity be-
tween different coarse grid resolutions when using pressure
smoothing. The first column shows error in horizontal and
vertical components of velocity when 1 coarse grid cell con-
tains 4 fine grid cells, the second column shows the same
errors when 1 coarse grid cell contains 16 fine grid cells.
The error regions are wider for coarser grids.
in accelerating other fluids simulations such as smoke
and fire.
REFERENCES
Ando, R., Thuerey, N., and Wojtan, C. (2015). A
dimension-reduced pressure solver for liquid simula-
tions. Computer Graphics Forum, 34(2):473–480.
Autodesk. Deep adaptive fluid simulation in Maya 2016.
http://www.autodesk.com/products/maya/features/
dynamics-and-effects/deep-adaptive-fluid-simulation.
Last accessed on 8/6/2016.
Berger, M. and Oliger, J. (1984). Adaptive mesh refinement
for hyperbolic partial differential equations. Journal
of Computational Physics, 53:484–512.
Bridson, R. (2008). Fluid Simulation for Computer Graph-
ics. Taylor & Francis.
Bridson, R., Houriham, J., and Nordenstam, M. (2007).
Curl-noise for procedural fluid flow. ACM Transac-
tions on Graphics, 26(3).
Chentanez, N. and M
¨
uller, M. (2011). Real-time eulerian
water simulation using a restricted tall cell grid. In
ACM Transactions on Graphics, volume 30, page 82.
Chentanez, N., M
¨
uller, M., and Kim, T.-Y. (2014). Coupling
3d eulerian, heightfield and particle methods for in-
teractive simulation of large scale liquid phenomena.
In Proceedings of the ACM SIGGRAPH/Eurographics
SCA, pages 1–10.
De Witt, T., Lessig, C., and Fiume, E. (2012). Fluid simu-
lation using laplacian eigenfunctions. ACM Transac-
tions on Graphics, 31(1):10:1–10:11.
Enright, D., Marschner, S., and Fedkiw, R. (2002). Anima-
tion and rendering of complex water surfaces. ACM
Transactions on Graphics, 21(3):736–744.
Ferstl, F., Ando, R., Wojtan, C., Westermann, R., and
Thuerey, N. (2016). Narrow band FLIP for liquid sim-
ulations. Computer Graphics Forum (Eurographics),
35(2):to appear.
Ferstl, F., Westermann, R., and Dick, C. (2014). Large-scale
liquid simulation on adaptive hexahedral grids. IEEE
Transactions on Visualization and Computer Graph-
ics, 20(10):1407–1417.
Foster, N. and Fedkiw, R. (2001). Practical animation of
liquids. In Proceedings of SIGGRAPH, pages 23–30.
Jung, H. R., Kim, S.-T., Noh, J., and Hong, J.-M. (2013). A
heterogeneous CPUGPU parallel approach to a multi-
grid poisson solver for incompressible fluid simula-
tion. Computer Animation and Virtual Worlds, 24(3-
4):185–193.
Kim, T., Tessendorf, J., and Threy, N. (2013). Closest point
turbulence for liquid surfaces. ACM Transactions on
Graphics, 32(2):15:1–15:13.
Larmorlette, L. and Foster, N. (2002). Structural modeling
of flames for a production environment. ACM Trans-
actions on Graphics, 21(3):729–735.
Lentine, M., Zheng, W., and Fedkiw, R. (2010). A novel al-
gorithm for incompressible flow using only a coarse
grid projection. ACM Transactions on Graphics,
29(4).
Losasso, F., Gibou, F., and Fedkiw, R. (2004). Simulating
water and smoke with an octree data structure. ACM
Transactions on Graphics, 23(3):457–462.
McAdams, A., Sifakis, E., and Teran, J. (2010). A
parallel multigrid poisson solver for fluids simula-
tion on large grids. In Proceedings of ACM SIG-
GRAPH/Eurographics SC, pages 65–74.
Montijn, C., Hundsdorfer, W., and Ebert, U. (2006). An
adaptive grid refinement strategy for the simulation
of negative streamers. Journal of Computational
Physics, 219(2).
Mullen, P., Crane, K., Pavlov, D., Y., T., and Desbrun, M.
(2009). Energy-preserving integrators for fluid anima-
tion. In Proceedings of SIGGRAPH, pages 1–8.
Prakash, A. and Chaudhuri, P. (2015). Comparing per-
formance of parallelizing frameworks for grid-based
fluid simulation on the cpu. In Proceedings of the
8th ACM India Computing Conference, Compute ’15,
pages 1–7.
Rasmussen, N., Nguyen, D., Geiger, W., and Fedkiw, R.
(2003). Smoke simulation for large scale phenomena.
ACM Transactions on Graphics, 22(3):703–707.
Schechter, H. and Bridson, R. (2008). Evolving sub-grid
turbulence for smoke animation. In Proceedings of
the ACM SIGGRAPH/Eurographics SCA, page 17.
Selle, A., Fedkiw, R., Kim, B., Liu, Y., and Rossignac,
J. (2008). An unconditionally stable maccormack
method. Journal of Scientific Computing, 35(2-
3):350–371.
Stam, J. (1999). Stable fluids. In Proceedings of SIG-
GRAPH, pages 121–128.
Narrow Band Pressure Computation for Eulerian Fluid Simulation
25

Stomakhin, A., Schroeder, C., Chai, L., Teran, J., and Selle,
A. (2013). A material point method for snow simu-
lation. ACM Transactions on Graphics, 32(4):102:1–
102:10.
Threy, N., Wojtan, C., Gross, M., and Turk, G. (2010).
A multiscale approach to mesh-based surface tension
flows. ACM Transactions on Graphics, 29(4).
Treuille, A., Lewis, A., and Popovi, Z. (2006). Model re-
duction for real-time fluids. ACM Transactions on
Graphics, 25(3):826–834.
Yue, Y., Smith, B., Batty, C., Zheng, C., and Grinspun, E.
(2015). Continuum foam: A material point method for
shear-dependent flows. ACM Transactions on Graph-
ics, 34(5):160:1–160:20.
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
26
