
Search-and-Fetch with 2 Robots on a Disk
Wireless and Face-to-Face Communication Models
Konstantinos Georgiou
1,∗
, George Karakostas
2,∗
and Evangelos Kranakis
3,∗
1
Department of Mathematics, Ryerson University, 350 Victoria St., Toronto, ON, M5B 2K3, Canada
2
Dept. of Computing & Software, McMaster University, 1280 Main St. West, Hamilton, Ontario L8S 4K1, Canada
3
School of Computer Science, Carleton University, 1125 Col. By Dr., Ottawa, ON K1S 5B6, Canada
Keywords:
Search & Fetch, Distributed Algorithm, Rendevouz, Exploration, Face-to-Face Model, Wireless Model.
Abstract:
We introduce and study treasure-evacuation with 2 robots, a new problem on distributed searching and fetch-
ing related to well studied problems in searching, rendezvous and exploration. The problem is motivated by
real-life search-and-rescue operations in areas of a disaster, where unmanned vehicles (robots) search for a
victim (treasure) and subsequently bring (fetch) her to safety (the exit). One of the critical components in
such operations is the communication protocol between the robots. We provide search algorithms and contrast
two standard models, the face-to-face and the wireless model. Our main technical contribution pertains to
the face-to-face model. More specifically, we demonstrate how robots can take advantage of some minimal
information of the topology (i.e., the disk) in order to allow for information exchange without meeting. The
result is a highly efficient distributed treasure-evacuation protocol which is minimally affected by the lack of
distant communication.
1 INTRODUCTION
We introduce the study of a new distributed problem
on searching and fetching called treasure evacuation.
Two robots are placed at the center of a unit disk,
while an exit and a treasure lie at unknown positions
on the perimeter of the disk. Robots search with max-
imum speed 1, and they detect an interesting point
(either the treasure or the exit) only if they pass over
it. The exit is immobile, while the treasure can be car-
ried by any of the robots. The goal of the search is for
at least one of the robots to bring (fetch) the treasure
to the exit, i.e. evacuate the treasure, in the minimum
possible completion time. The robots do not have to
evacuate, rather they only need to co-operate, possi-
bly by sharing information, so as to learn the locations
of the interesting points and bring the treasure to the
exit. Contrary to previous work, this is the first time
an explicit ordering on the tasks to be performed is
imposed (first the treasure, then the exit). This makes
the problem inherently different in nature and more
difficult than similarly looking results.
Finding an optimal algorithm turns out to be a
challenging task even when the robots have some
knowledge, e.g., the arc-distance α between the exit
∗
Research supported in part by NSERC.
and the treasure. We propose treasure-evacuation pro-
tocols in two communication models. In the wireless
model robots exchange information instantaneously
and at will, while in the face-to-face model informa-
tion can be exchanged only if the robots meet. We aim
at incorporating this knowledge into our algorithm de-
signs. We offer algorithmic techniques such as plan-
ning ahead, timing according to the explicit task or-
dering, and retrieval of unknown information through
inference and not communication.
Part of our contribution is that we demonstrate
how robots can utilize the knowledge of the arc-
distance α between the interesting points. We pro-
pose protocols that induce worst case evacuation time
1 + π − α/2 + 3sin(α/2) for the wireless model and
1+π−α+4 sin(α/2) for the face-to-face model. The
upper bound in the face-to-face model, which is our
main contribution, is the result of a non-intuitive evac-
uation protocol that allows robots to exchange infor-
mation about the topology without meeting, effec-
tively bypassing their inability to communicate from
distance. Finally, we complement our results above
by showing that any algorithm in the face-to-face
model needs time at least 1+π/3+4sin (α/2), if α ∈
[0,2π/3] and at least 1+ π/3 +2 sin(α) +2sin (α/2),
if α ∈ [2π/3,π].
Georgiou K., Karakostas G. and Kranakis E.
Search-and-Fetch with 2 Robots on a Disk - Wireless and Face-to-Face Communication Models.
DOI: 10.5220/0006091600150026
In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 15-26
ISBN: 978-989-758-218-9
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
15

1.1 Contributions
Rendezvous, treasure hunting and exploration have
been subjects of extensive research in the broad area
of distributed and online computing (see related work
below). Challenges in each of these fundamental
tasks arise from different computation, communica-
tion or knowledge limitations, with admittedly nu-
merous variations. The novel distributed problem of
treasure-evacuation that we introduce and study in
this work combines in a complex way challenges from
all these fundamental tasks. As such, progress to-
wards solving generic treasure-evacuation-like prob-
lems will unavoidably touch on state-of-the-art tech-
niques of achieving these tasks.
In treasure-evacuation, two stationary targets (a
treasure and an exit that we call interesting points)
are hidden on a specific domain. At first, robots need
to (a) perform treasure hunting in this online envi-
ronment. Interestingly, the knowledge of the loca-
tion of one of these targets may or may not reveal
the location of the other. In particular, the task of the
robots does not end when both interesting points are
located, rather, only when the treasure-holder learns
(and finds) the location of the exit as well. Given
communication limitations, the latter can be accom-
plished efficiently only if (b) a sufficient portion of the
environment is explored before both interesting points
are found, or (c) if information can be exchanged be-
tween robots. In case (b), robots “invest” in domain
exploration in an attempt to expedite treasure evacua-
tion once the interesting points are found. In case (c),
robots may need to attempt to rendezvous (not very
late in the time horizon) so that the distributed sys-
tem becomes cognitive of the environment and con-
sequently completes the given task. Clearly, in order
for a distributed system to accomplish treasure evac-
uation efficiently, robots need to perform and balance
all tasks (a),(b),(c) above, i.e to perform treasure hunt-
ing, while learning the environment either by explo-
ration or by rendezvous. A unique feature of treasure-
evacuation is that only the treasure has to be brought
to the exit.
The last observation gives some first evidence
of the difficulty of solving treasure-evacuation, even
when the domain is a disk. Can a robot choose a tra-
jectory (maybe staying far from the exit) to help the
treasure-holder expedite evacuation? If a robot dis-
covers the treasure, is it a good strategy to become
the treasure holder and greedily search for the exit?
Should robots learn the environment by investing on
exploration or on rendezvous and hence on message
exchange? Finally, is it possible in a non-wireless en-
vironment for robots to exchange information without
meeting? An efficient algorithm should somehow ad-
dress all these questions.
From the discussion above, it is not a surprise that
plain vanilla algorithms cannot be efficient. Indeed,
our algorithms (for both the wireless and face-to-face
models) adapt their strategies, among others, with re-
spect to the distance of the interesting points. On
one hand, there are configurations where the evac-
uation protocols are simple and greedy-like. How-
ever, the reader can verify from our analyses that, had
we followed such simplistic approach for all config-
urations, the evacuation time would have been much
worse than our upper bounds. The simplest example
of this kind will be transparent even in the analysis of
the wireless model, in which robots can exchange in-
formation at will. To achieve our upper bound, robots
choose different trajectories (still greedy-like) for var-
ious distances of the interesting points. Nevertheless,
the analysis in this case is relatively simple.
Our main technical contribution pertains to the
face-to-face model where robots can exchange infor-
mation only if they meet. In particular, we explic-
itly exhibit distributed strategies that allow robots to
exchange information even from distance. At a high
level, and given that interesting points are located by
robots at some (carefully defined) critical intervals in
the time horizon, robots choose (occasionally) highly
non-intuitive trajectories, not in order to locate the re-
maining interesting points, rather to potentially meet
their fellow robots. The trajectories are carefully cho-
sen so that a robot may deduce information, using
an involved protocol, as to what the other robot has
found, and hence learn the environment regardless of
whether the rendezvous is realized or not. For the
treasure-holder, this would result in learning the loca-
tion of the exit. For the other robot(s), this would be
an altruistic attempt to help the fellow treasure-holder.
In particular, that could result in that the non treasure-
holder never finds the exit, still expediting the treasure
evacuation time. We note that once the trajectories
are determined (which is the heart of our contribu-
tion) correctness and performance analysis is a matter
of an exhaustive and technical case analysis. Inter-
estingly, the efficiency of our algorithm for the face-
to-face model is only slightly worse than the solution
for the wireless case (but significantly better than the
naive solution for the face-to-face model), indicating
that lack of communication can be compensated by
clever algorithms.
Finally, we complement our results by proving
some lower bounds for treasure evacuation with 2
robots for the face-to-face model. That concludes the
first attempt to study distributed problems of this kind,
i.e. optimization treasure hunting problems where the
distributed systems learn the online environment by a
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
16

combination of exploration and rendezvous, a feature
which, to the best of our knowledge, is also novel.
1.2 Related Work
Traditional search is concerned with finding an ob-
ject with specified properties within a search space.
Searching in the context of computational prob-
lems is usually more challenging especially when
the environment is unknown to the searcher(s) (see
(Ahlswede and Wegener, 1987; Alpern and Gal,
2003; Stone, 1975)). This is particularly evident in
the context of robotics whereby exploration is taking
place within a given geometric domain by a group
of autonomous but communicating robots. The ulti-
mate goal is to design an algorithm so as to accom-
plish the requirements of the search (usually locat-
ing a target of unknown a priori position) while at
the same time obeying the computational and geo-
graphical constraints. The input robot configuration
must also accomplish the task in the minimum possi-
ble amount of time (Berman, 1998).
Search has a long history. There is extensive and
varied research and several models have been pro-
posed and investigated in the mathematical and theo-
retical computer science literature with particular em-
phasis on probabilistic search (Stone, 1975), game
theoretic applications (Alpern and Gal, 2003), cops
and robbers (Bonato and Nowakowski, 2011), classi-
cal pursuit and evasion (Nahin, 2012), search prob-
lems as related to group testing (Ahlswede and We-
gener, 1987), searching a graph (Koutsoupias et al.,
1996), and many more. A survey of related search
and pursuit evasion problems can be found in (Chung
et al., 2011). In pursuit-evasion, pursuers want to
capture evaders who try to avoid capture. Examples
include Cops and Robbers (whereby the cops try to
capture the robbers by moving along the vertices of
a graph), Lion and Man (a geometric version of cops
and robbers where a lion is to capture a man in ei-
ther continuous or discrete time), etc. Searching for
a motionless point target has some similarities with
the lost at sea problem, (Gluss, 1961; Isbell, 1967),
the cow-path problem (Beck, 1964; Bellman, 1963),
and with the plane searching problem (Baeza-Yates
and Schott, 1995). This last paper also introduced the
“instantaneous contact model”, which is referred to as
wireless model in our paper. When the mobile robots
do not know the geometric environment in advance
then researchers are concerned with exploring (Al-
bers and Henzinger, 2000; Albers et al., 2002; Deng
et al., 1991; Hoffmann et al., 2001). Coordinating the
exploration of a team of robots is a main theme in
the robotics community (Burgard et al., 2005; Thrun,
2001; Yamauchi, 1998) and often this is combined
with the mapping of the terrain and the position of
the robots within it (Kleinberg, 1994; Papadimitriou
and Yannakakis, 1989).
Evacuation for grid polygons has been studied in
(Fekete et al., 2010) from the perspective of con-
structing centralized evacuation plans, resulting in the
fastest possible evacuation from the rectilinear envi-
ronment. There are certain similarities of our prob-
lem to the well-known evacuation problem on an in-
finite line (see (Baeza Yates et al., 1993) and the re-
cent (Chrobak et al., 2015)) in that the search is for
an unknown target. However, in this work the adver-
sary has limited possibilities since search is on a line.
Additional research and variants on this problem can
be found in (Demaine et al., 2006) (on searching with
turn costs), (Kao et al., 1996) (randomized algorithm
for the cow-path problem), (Kao et al., 1998) (hybrid
algorithms), and many more.
A setting similar to ours is presented in the re-
cent works (Czyzowicz et al., 2014; Czyzowicz et al.,
2016; Czyzowicz et al., 2015a; Czyzowicz et al.,
2015b) where algorithms are presented in the wire-
less and non-wireless (or face-to-face) communica-
tion models for the evacuation of a team of robots.
The “search domain” in (Czyzowicz et al., 2014; Czy-
zowicz et al., 2016; Czyzowicz et al., 2015a) is a
unit circle (while in (Czyzowicz et al., 2015b) the
search domain is a triangle or square), however, un-
like our search problem, in these papers all the robots
are required to evacuate from an unknown exit on the
perimeter. Moreover, in none of these papers is there
a treasure to be fetched to the exit.
Our work is also an attempt to analyze theoreti-
cally search-and-fetch problems that have been stud-
ied by the robotics community since the 90’s, e.g.
see (Jennings et al., 1997). A scenario similar to
ours (but only for 1 robot) has been introduced by
Alpern in (Alpern, 2011), where the domain was dis-
crete (a tree) and the approach/analysis resembled that
of standard search-type problems (Alpern and Gal,
2003). In contrast, our problem is of distributed na-
ture, and our focus is to demonstrate how robots’
communication affects efficiency.
1.3 Problem and Model Motivation
Our problem is motivated by real-life surveillance and
search-and-rescue operations where unmanned vehi-
cles, e.g. drones, search for victims in areas of a disas-
ter. Indeed, consider a group of rescuer-mobile-agents
(robots), initially located strategically in a central po-
sition of a domain. When alarm is triggered and a
distress signal is received, robots need to locate a vic-
Search-and-Fetch with 2 Robots on a Disk - Wireless and Face-to-Face Communication Models
17

tim (the treasure) and bring her to safety (the exit).
Our problem shares similarities also with classic and
well-studied cops-and-robbers games; robots rest at a
central position of a domain (say, in the centre of a
disk as in our setup) till an alarm is triggered by some
“robber” (the treasure in our case). Then, robots need
to locate the stationary robber and subsequently bring
him to jail (the exit). Interestingly, search-and-fetch
type problems resemble also situations that abound
in fauna, where animals hunt for prey which is then
brought to some designated area, e.g. back to the
lair. As such, further investigation of similar problems
will have applications to real-life rescue operations, as
well as to the understanding of animal behavior, as it
is common in all search problems.
From a technical perspective, our communication
models are inspired by the recent works on evac-
uation problems (Czyzowicz et al., 2014; Czyzow-
icz et al., 2015a; Czyzowicz et al., 2015b). No-
tably, the associated search problems are inherently
different than our problem which is closer in nature
to search-type, treasure-hunt, and exploration prob-
lems. Also, our mathematical model features (a)
a distributed setting (b) with objective to minimize
time, and (c) where different communication mod-
els are contrasted. None among (a),(b),(c) are well
understood for search games, and, to the best of our
knowledge, they have not been studied before in this
combination.
Specific to the problem we study are the number
of robots (2 and not arbitrarily many - though our
results easily extend to swarms of robots), the do-
main (disk), and the fact the robots have some knowl-
edge about the interesting points. Although extend-
ing our results to more generic situations is interest-
ing in its own right, the nature of the resulting prob-
lems would require a significantly different algorith-
mic approach. Indeed, our main goal is to study how
limitations in communication affect efficiency, which
is best demonstrated when the available number of
robots, and hence computation power, is as small as
possible, i.e. for two robots. In fact, it is easy to ex-
tend our algorithms for the n-robot case.
Notably, search-and-fetch problems are challeng-
ing even for 1 robot as demonstrated in (Georgiou
et al., 2016b). In particular, the work of (Georgiou
et al., 2016b) implies that establishing provably op-
timal evacuation protocols for 2-robots is a difficult
task, even when the domain is the disk. Nevertheless,
we view the domain that we study as natural. Indeed,
a basic setup in search-and-rescue operations is that
rescuer-robots inhabit in a base-station, and they stay
inactive till they receive a distress signal. As it is com-
mon in real-life situations, the signal may only reveal
partial information about the location of a victim, e.g.
its distance from the base-station, along with the dis-
tance between the points. When there are more than
one interesting points to be located, this kind of infor-
mation suggests that the points lie anywhere on co-
centric circles. When the points are equidistant from
the base-station, robots need only consider a disk, as
it is the case in our problem. We believe that with
enough technical and tedious work, our results can
also extend to non-equidistant points, however the al-
gorithmic significance of the proposed distributed so-
lutions may be lost in the technicalities.
In order to demonstrate that robots with primitive
communication capabilities are in fact not much less
powerful than in the wireless model, it is essential to
assume that robots have some knowledge of the dis-
tance between the interesting points. The reader may
also view this piece of advice as an algorithmic chal-
lenge in order to bypass the uncertainty regarding the
locations of the interesting points. Notably, our algo-
rithms adapt strategies as a function of the distance of
the interesting points, trying to follow protocols that
would allow them to detect the actual positions of the
points without necessarily visiting them. As an easy
example, note that if a robot has explored already a
contiguous arc of length α+ ε, the discovery of an in-
teresting point reveals the location of the other α-arc
distant away interesting point (our algorithm makes
use of distance α in a much more sophisticated way).
As a result, had we assumed that distances are un-
known, robots may not be able to deduce such im-
portant information about the topology using partial
exploration, and the problem would require an inher-
ently different algorithmic approach. Apart from that,
partial knowledge of the input is also interesting due
to the efficiency-information tradeoffs that are natu-
rally induced by the problem, which is also a standard
theme in competitive analysis, e.g. see (Hipke et al.,
1999) and (Georgiou et al., 2016b).
Admittedly, the model we introduce is simple but
natural, general, and complex enough to require non-
standard algorithmic solutions. Most importantly, our
model allows us to demonstrate in a relatively clean
way a couple of novel algorithmic techniques for at-
tacking challenging and newly introduced types of
distributed problems. We anticipate that the ideas in-
troduced in this work will initiate new research direc-
tions towards solving a family of problems that are
not yet understood from a theoretical perspective.
1.4 Notation & Organization
A treasure and an exit are located at unknown posi-
tions on the perimeter of a unit-disk and at arc dis-
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
18
tance α (in what follows all distances will be arc-
distances, unless specified otherwise). Robots start
from the center of the disk, and can move anywhere
on the disk at constant speed 1. Each of the robots
detects the treasure or the exit only if its trajectory
passes over that point on the disk. Once detected, the
treasure can be carried by a robot at the same speed.
We refer to the task of bringing the treasure to the
exit as treasure-evacuation. We use the abbreviations
T,E for the treasure and the exit, respectively. For
convenience, in the sequel we will refer to the loca-
tions of the exit and the treasure as interesting points.
For an interesting point I on the perimeter of the disk,
we also write I = E (I = T ) to indicate that the exit
(treasure) lies in point I. For a point B, we also write
B = null to denote the event that neither the treasure
nor the exit is placed on B.
We focus on the following online variations of
treasure-evacuation with 2 robots, where the exact
distance α between T,E is known, but not their po-
sitions. In 2-TE
w
(Section 2), information between
robots is shared continuously in the time horizon,
i.e. messages between them are exchanged instanta-
neously and at will with no restrictions and no addi-
tional cost or delays. In 2-TE
f 2 f
(Section 3), the com-
munication protocol between the robots is face-to-
face (non-wireless)—abbreviated F2F (or f2f), where
information can be exchanged only if the robots meet
at the same point anywhere. We give two algorithms:
in the former case we prove a 1 + π − α + 4sin (α/2)
and in the latter case a 1+π−α/2+3 sin(α/2) upper
bound, resp., on the treasure evacuation time, where α
is the arc distance between treasure and exit. Finally
in Section 4 we provide a lower bound for treasure-
evacuation with 2 robots in the F2F model.
Any omitted proofs, due to space limitations, can
be found in the full version of the paper (Georgiou
et al., 2016a).
2 WIRELESS MODEL
As a warm-up we present in this section an upper
bound for the wireless model, which will also serve
as a reference for the more challenging face-to-face
model. The algorithmic solution we propose is sim-
ple and it is meant to help the reader familiarize
with basic evacuation trajectories that will be used in
our main contribution pertaining to the face-to-face
model.
Theorem 2.1. For every α ∈ [0, π], problem 2-TE
w
can be solved in time 1 + π − α+4sin (α/2).
To prove Theorem 2.1, we propose Algorithm 1
that achieves the promised bound. Intuitively, our al-
gorithm follows a greedy like approach, adapting its
strategy as a function of the distance α of the interest-
ing points. If α is small enough, then the two robots
move together to an arbitrary point on the disk and
start exploring in opposing directions. Otherwise the
two robots move to two antipodal points and start ex-
ploring in the same direction. Exploration continues
till an interesting point is found. When that happens,
the robot that can pick up the treasure and fetch it to
the exit in the fastest time (if all locations have been
revealed) does so, otherwise remaining locations are
tried exhaustively. Detailed descriptions of the evac-
uation protocol can be seen in Algorithm 1, comple-
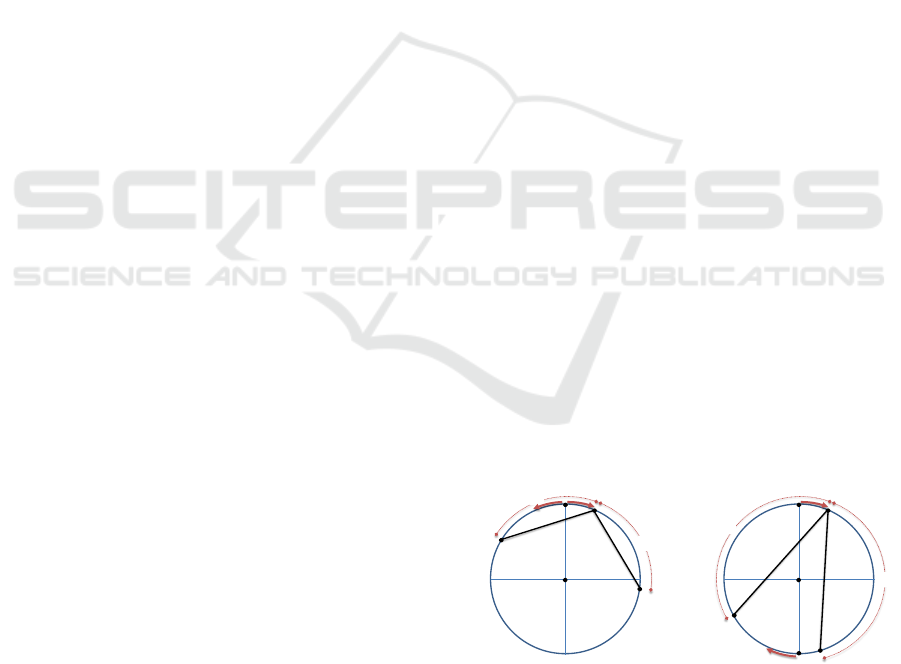
mented by Figure 1.
Noticeably, the performance analysis we give is
tight, meaning that for every α ≥ 0, there are con-
figurations (placements of the interesting points) for
which the performance of the algorithm is exactly
1 + π − α+4sin (α/2). Most importantly, the perfor-
mance analysis makes explicit that naive algorithms
that do not adapt strategies together with α are bound
to perform strictly worse than our upper bound. Also,
the achieved upper bound should be contrasted to
the upper bound for the face-to-face model (which is
achieved by a much more involved algorithm), which
at the same time is only α/2 − sin (α/2) more costly
than the bound we show in the wireless model.
Algorithm 1 takes advantage of the fact that robots
can communicate to each other wirelessly. This also
implies that lack of message transmission is effec-
tively another method of information exchange. In
what follows point A will always be the starting point
of R
2
, and A
0
denotes its antipodal point. For the sake
of the analysis and w.l.o.g. we will assume that R
2
is
the one that first finds an interesting point I = {E,T },
say at time x := AI
_
. We call B,C the points that are at
clockwise and counter-clockwise arc-distance α from
I respectively. Figure 1 depicts the interesting points
encountered.
′
≤ 2/3
> 2/3
Figure 1: The points of interest for our Algorithm 1.
The description of Algorithm 1 is from the per-
spective of the robot that finds first an interesting
point, that we always assume is R
2
. Next we assume
that the finding of any interesting point is instanta-
Search-and-Fetch with 2 Robots on a Disk - Wireless and Face-to-Face Communication Models
19

neously transmitted and received by the two robots.
Also, if at any moment, the positions of the interesting
points are learned by the two robots, then the robots
attempt a “confident evacuation” using the shortest
possible trajectory. This means for example that if the
treasure is not picked up by any robot, then the two
robots will compete in order to pick it up and return it
to the exit, moving in the interior of the disk.
Algorithm 1: Wireless Algorithm.
Step 1. If α ≤ 2π/3, then the two robots move to-
gether to an arbitrary point on the ring and start
moving in opposing directions, else they move to
arbitrary antipodal points A,A
0
on the cycle and
start moving in the same direction.
Step 2. Let I be the first interesting point discov-
ered by R
2
, at time x := AI
_
. Let B,C be the points
that are at clockwise and counter-clockwise arc-
distance α from I respectively.
Step 3. If x ≥ α/2 then robots learn that the other
interesting point is in B, else R
2
moves to B, R
1
moves to C.
Step 4. Evacuate
Correctness of Algorithm 1 is straightforward,
since the two robots follow a “greedy-like evacuation
protocol” (still, they use different starting points de-
pending on the value of α). Also, the performance
analysis of the algorithm, effectively proving Theo-
rem 2.1, is a matter of a straightforward case-analysis.
We note that our worst-case analysis is tight, in that
for every α ≥ 0 there exist configurations in which the
performance is exactly as promised by Theorem 2.1.
Moreover, we may assume that α > 0 as otherwise the
problem is solved when one interesting point is found.
Note that our algorithm performs differently when
α ≤ 2π/3 and when α > 2π/3. Let x := AI
_
be the
time that R
2
first discovers interesting point I. Then
it must be that x ≤ α/2 and x ≤ π − α for the cases
α ≤ 2π/3 and α > 2π/3 respectively (see also Fig-
ure 1). This will be used explicitly in the proof of
the next two lemmata. We also assume that R
2
al-
ways moves clockwise starting from point A. R
1
either moves counter-clockwise starting from A, if
α ≤ 2π/3, or it moves clockwise starting from the an-
tipodal point A
0
of A, if α > 2π/3. In every case, the
two robots move along the perimeter of the disk till
time x when R
2
transmits the message that it found an
interesting point.
The performance of Algorithm 1 is described in
the next two lemmata which admit proofs by case
analyses. Each of them examines the relative posi-
tion of the starting point of robot R
2
(which finds an
interesting point first) and the two interesting points.
Lemma 2.2. Let A be the starting point of R
2
which
is the first to discover an interesting point I. Let also
the other interesting point be at C, where CI
_
= α. If A
lies in the arc CI
_
, then the performance of Algorithm
1 is 1 + π − α+4sin (α/2), for all α ∈ [0,π].
Lemma 2.3. Let A be the starting point of R
2
which is
the first to discover an interesting point I. Let also the
other interesting point be at B, where IB
_
= α. If A lies
outside the arc IB
_
, then the performance of Algorithm
1 is 1 + π − α+4sin (α/2), for all α ∈ [0,π].
It is clear now that Lemmata 2.2, 2.3 imply that for
all α ∈ [0, π], the overall performance of Algorithm 1
is no more than 1 + π − α + 4 sin(α/2) concluding
Theorem 2.1.
3 F2F MODEL
The main contribution of our work pertains to the
face-to-face model and is summarized in the follow-
ing theorem.
Theorem 3.1. For every α ∈ [0,π], problem 2-TE
f 2 f
can be solved in time 1 + π − α/2 +3sin (α/2).
Next we give the high-level intuition of the pro-
posed evacuation-protocol, i.e. Algorithm 2, that
proves the above theorem (more low level intuition,
along with the formal description of the protocol ap-
pears in Section 3.1).
Denote by β the upper bound promised by the
theorem above. It should be intuitive that when the
distance of the interesting points α tends to 0, there
is no significant disadvantage due to lack of com-
munication. And although the wireless evacuation-
time might not be achievable, a protocol similar to
the wireless case should be able to give efficient so-
lutions. Indeed, our face-to-face protocol is a greedy
algorithm when α is not too big, i.e. the two robots try
independently to explore, locate the interesting points
and fetch the treasure to the exit without coordination
(which is hindered anyways due to lack of communi-
cation). Following a worst case analysis, it is easy to
see that as long as α does not exceed a special thresh-
old, call it α
0
, the evacuation time is β, and the analy-
sis is tight.
When α exceeds the special threshold α
0
, the lack
of communication has a more significant impact on
the evacuation time. To work around it, robots need
to exchange information which is possible only if they
meet. For this reason (and under some technical con-
ditions), robots agree in advance to meet back in the
center of the disk to exchange information about their
findings, and then proceed with fetching the treasure
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
20
to the exit. Practically, if the rendezvous is never re-
alized, e.g. only one robot reaches the center up to
some time threshold, that should deduce that interest-
ing points are not located in certain parts of the disk,
potentially revealing their actual location. In fact, this
recipe works well, and achieves evacuation time β, as
long as α does not exceed a second threshold, which
happens to be 2π/3.
The hardest case is when the two interesting points
are further than 2π/3 apart. Intuitively, in such a case
there is always uncertainty as to where the interesting
points are located, even when one of them is discov-
ered. At the same time, the interesting points, hence
the robots, might be already far apart when some or
both interesting points are discovered. As such, meet-
ing at the center of the disk to exchange informa-
tion would be time consuming and induces evacuation
time exceeding β. Our technical contribution pertains
exactly to this case. Under some technical conditions,
the treasure-finder might need to decide which of the
two possible exit-locations to consider next. In this
case, the treasure-holder follows a trajectory not to-
wards one of the possible locations of the exit, rather
a trajectory closer to that of its peer robot aiming for
a rendezvous. The two trajectories are designed care-
fully so that the location of the exit is revealed no mat-
ter whether the rendezvous is realized or not.
3.1 Algorithm & Correctness
In our main Algorithm 2, robots R
1
,R
2
that start from
the centre of the circle, move together to an arbi-
trary point A on the circle (which takes time 1). Then
they start moving in opposing directions, say, counter-
clockwise and clockwise respectively till the locate
some interesting point.
In what follows we describe only the trajectory
of R
2
which is meant to be moving clock-wise (R
1
performs the completely symmetric trajectory, and
will start moving counter clock-wise). In particular
all point references in the description of our algo-
rithm, and its analysis, will be from the perspective
of R
2
’s trajectory which is assumed to be the robot
that first visits either the exit or the treasure at posi-
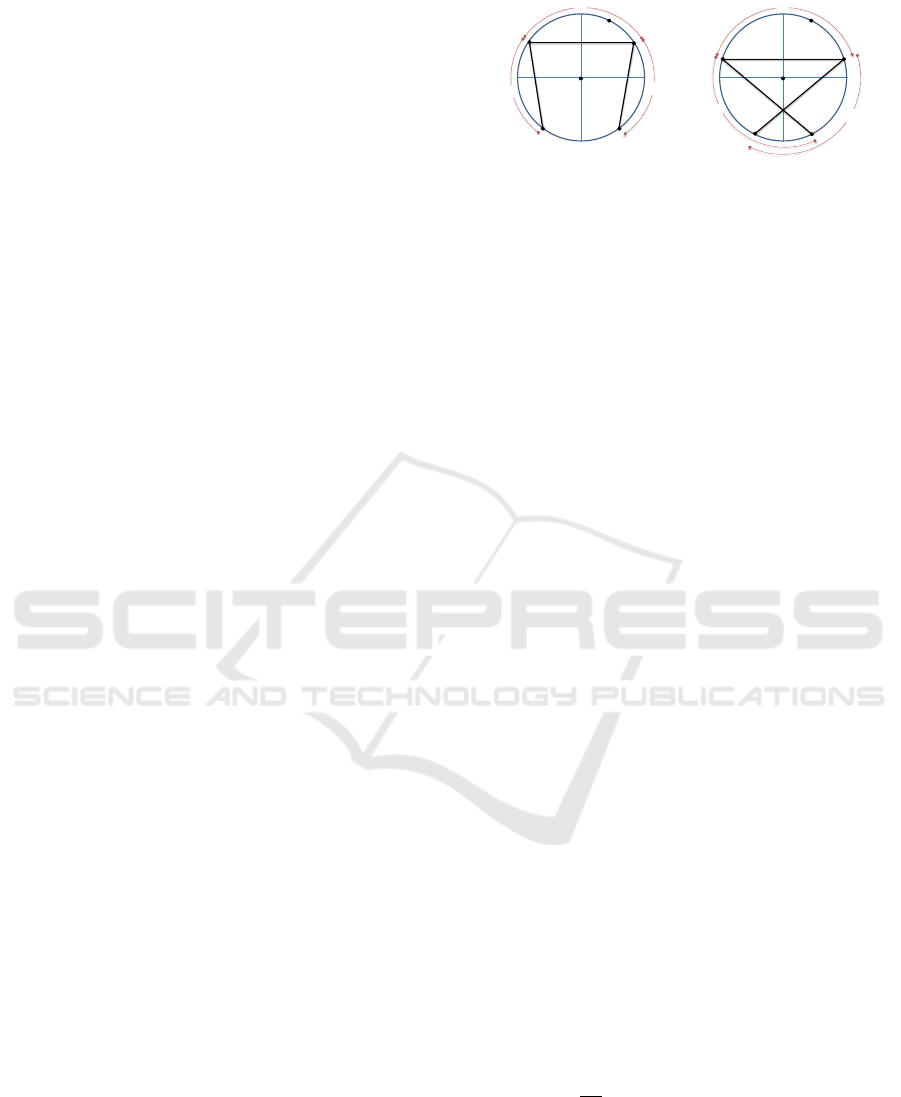
tion I. By B,C, D we denote the points on the circle
with DC
_
= CI
_
= IB
_
= α (see Figure 2). As before, and
in what follows, I ∈ {E,T } represents the position on
the circle that is first discovered in the time horizon
by any robot (in particular by R
2
), and that holds ei-
ther the treasure or the exit. Finally, O represents the
centre of the circle, which is also the starting point of
the robots.
According to our algorithm, R
2
starts moving
from point A till it reaches an interesting point I at
O
B
A
C
D
I
O
D
A
C
B
I
Figure 2: The points of interest from the perspective of R
2
,
when α ≤ 2π/3 on the left, and when α ≥ 2π/3 on the right.
time x := AI
_
. At this moment, our algorithm will de-
cide to run one of the following subroutines with input
x. These subroutines describe evacuation protocols,
in which the treasure must be brought to the exit. Oc-
casionally, the subroutines claim that robots evacuate
(with the treasure) from points that is not clear that
hold an exit. As we will prove correctness later, we
comment on these cases by writing that “correctness
is pending”.
A
1
(x) (Figure 3 i): If I = T , pick up the treasure and
move to B along the chord IB. If B = E evacuate,
else go to C along the chord BC and evacuate.
(Figure 3 ii): If I = E move to B along the chord
IB. If B = T , pick up the treasure, and return to
I along the chord BI and evacuate. If B = null,
then go to C along the chord BC. If the treasure
is found at C, pick it up, and move to I along the
chord CI and evacuate (else abandon the process).
A
2
(x) (Figure 3 iii): At the moment robots leave
point A, set the timer to 0.
If I = T , pick up the treasure and go to the cen-
tre O of the circle. Wait there till the time t
0
:=
max{x,α − x + 2sin (α/2)} +1. If R
1
arrives at O
by time t
0
, then go to C and evacuate (correctness
is pending). Else (if R
1
does not arrive at O by
time t
0
) go to B and evacuate (correctness is pend-
ing).
(Figure 3 iv): If I = E, move to B along the chord
IB. If B = T , pick up the treasure, and return to I
along the chord BI and evacuate. If B = null, then
go to the centre O and halt.
A
3
(x) (Figure 3 v): If I = T pick up the treasure.
If R
1
is already at point I go to C and evacu-
ate (correctness pending). If R
1
is not at point
I, then move along chord ID for additional time
y := α/2 − x + sin(α/2) + sin (α), and let K be
such that IK = y. If R
1
is at point K, then go to B
and evacuate (correctness is pending), else (if R
1
is not at point K) go to C and evacuate (correct-
ness pending).
(Figure 3 vi): If I = E, move to B along the chord
IB. If B = T , pick up the treasure, and return to I
along the chord BI and evacuate. If B = null, then
Search-and-Fetch with 2 Robots on a Disk - Wireless and Face-to-Face Communication Models
21

move along chord BC until you hit C (or you meet
the other robot- whatever happens first) and halt
at the current point, call it K.
It is worthwhile discussing the intuition behind the
subroutines above. First note that if a robot ever finds
a treasure, it picks it up. The second important prop-
erty is that each robot simulates A
1
either till it finds
the treasure or till it fails to find the treasure after find-
ing the exit. At a high level, A
1
greedily tries to evac-
uate the treasure. This means that if the treasure is
found first, then the robot tries successively the pos-
sible locations of the exit (using the shortest possible
paths) and evacuates. If instead the exit is found, then
it successively tries the (at most) two possibilities of
the treasure location, and if the treasure is found, it
returns it to the exit.
A
2
and A
3
constitute our main technical contribu-
tion. Both algorithms are designed so that in some
special cases, in which the exact locations of the in-
teresting points are not known, the two robots sched-
ule some meeting points so that if the meeting (ren-
dezvous) is realized or even if it is not, the treasure-
holder can deduce the actual location of the exit. In
other words, we make possible for the two robots to
exchange information without meeting. Indeed after
finding the treasure, in A
2
, R
2
goes to the centre of
the ring and waits some finite time till it makes some
decision of where to move the treasure, while in A
3
,
R
2
moves along a carefully chosen (and non-intuitive)
chord, and again for some finite time, till it makes a
decision to move to a point on the ring. If instead the
exit is found early, then the trajectories in A
2
, A
3
are
designed to support the other robot which might have
found the treasure in case the latter does not follow
A
1
.
The next non-trivial and technical step would be
to decide when to trigger the subroutines above. Of
course, once this is determined, i.e. once the trajecto-
ries are fixed, correctness and performance analysis is
a matter of exhaustive analysis.
We are ready to define our main non-wireless al-
gorithm. We remind the reader that the description is
for R
2
that starts moving clockwise. R
1
performs the
symmetric trajectory by moving counter-clockwise.
Our main algorithm uses parameter
x(α) := 3α/2 − π − sin (α/2) + 2sin(α) , which
we abbreviate by x whenever α is clear from the
context. By Lemma Aa, α
0
≈ 1.22353 is the unique
root of x(α) = 0, while x is positive for all α ∈ (α
0
,π)
and negative for all α ∈ [0,α
0
).
Lemma 3.2. For every α ∈ [0,π], Algorithm 2 is cor-
rect, i.e. a robot brings the treasure to the exit.
Algorithm 2: Non-Wireless Algorithm.
Step 1. Starting from A, move clockwise until an
interesting point I is found at time x := AI
_
.
Step 2. Proceed according to the following cases:
• If α > 2π/3 and I = T and α > x ≥ α − x, then
run A
3
(x).
• If α > 2π/3 and I = E and x ≤ x, then run
A
3
(x).
• If α
0
≤ α ≤ 2π/3 and I = T and α > x ≥ α −x,
then run A
2
(x).
• If α
0
≤ α ≤ 2π/3 and I = E and x ≤ x, then run
A
2
(x).
• In all other cases, run A
1
(x).
Proof. First, it is easy to see that the treasure is al-
ways picked up. Indeed, if the first interesting point I
that is discovered (by any robot) is the treasure, then
the claim is trivially true. If the first interesting point
I found, say, by R
2
is an exit, then R
2
(in all subrou-
tines) first tries the possible location B for the trea-
sure, and if it fails it tries location C (in other words
it always simulates A
1
till it fails to find the treasure
after finding the exit). Meanwhile R
1
moves counter-
clockwise on the ring, and sooner or later will reach
C or B. So at least one of the robots will reach the
treasure first. In what follows, let R
2
be the one who
found first the treasure (and picks it up). We examine
three cases.
If R
2
is following subroutine A
1
, then the treasure
is brought to the exit. Indeed, in that case R
2
expects
no interaction from R
1
and greedily tries to evacuate
(see subcases i,ii in Figure 3).
If R
2
is following subroutine A
2
, then it must be
that α
0
≤ α ≤ 2π/3, that α − x ≤ x < α, and that
it has not found any other interesting point before
(by Lemma Aa we have α − x < α and x > 0 for all
α > α
0
). Figure 3 subcase iii depicts exactly this sce-
nario, where I = T . Note that from R
2
’s perspective,
the exit can be either in B or in C, and R
2
chooses to
go to the center. This takes total time x+ 1. If the exit
was at point C, then R
1
would have found it in time
α −x ≤ x and that would make it to follow A
2
. So, R
1
would first check point D (where the treasure is not
present), and that would make it to go to the centre
arriving at time α−x + 2sin (α/2)+1 (an illustration
of this trajectory is shown in Figure 3 subcase iv, if
R
1
was moving clockwise). R
2
is guaranteed to wait
at the center till time t
0
(which is the maximum re-
quired time that takes each robot to reach the centre).
In that case, R
2
meets R
1
at the center (because R
1
did
find the exit in C), and R
2
correctly chooses C as the
evacuation point. Finally, if instead the exit was not in
C, then R
1
would not make it to the centre by time t
0
.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
22
=
B =
=
=
=
=
B =
=
=
=
1
2
3
(Subfigure )
(Subfigure )
(Subfigure )
(Subfigure )
(Subfigure )
(Subfigure )
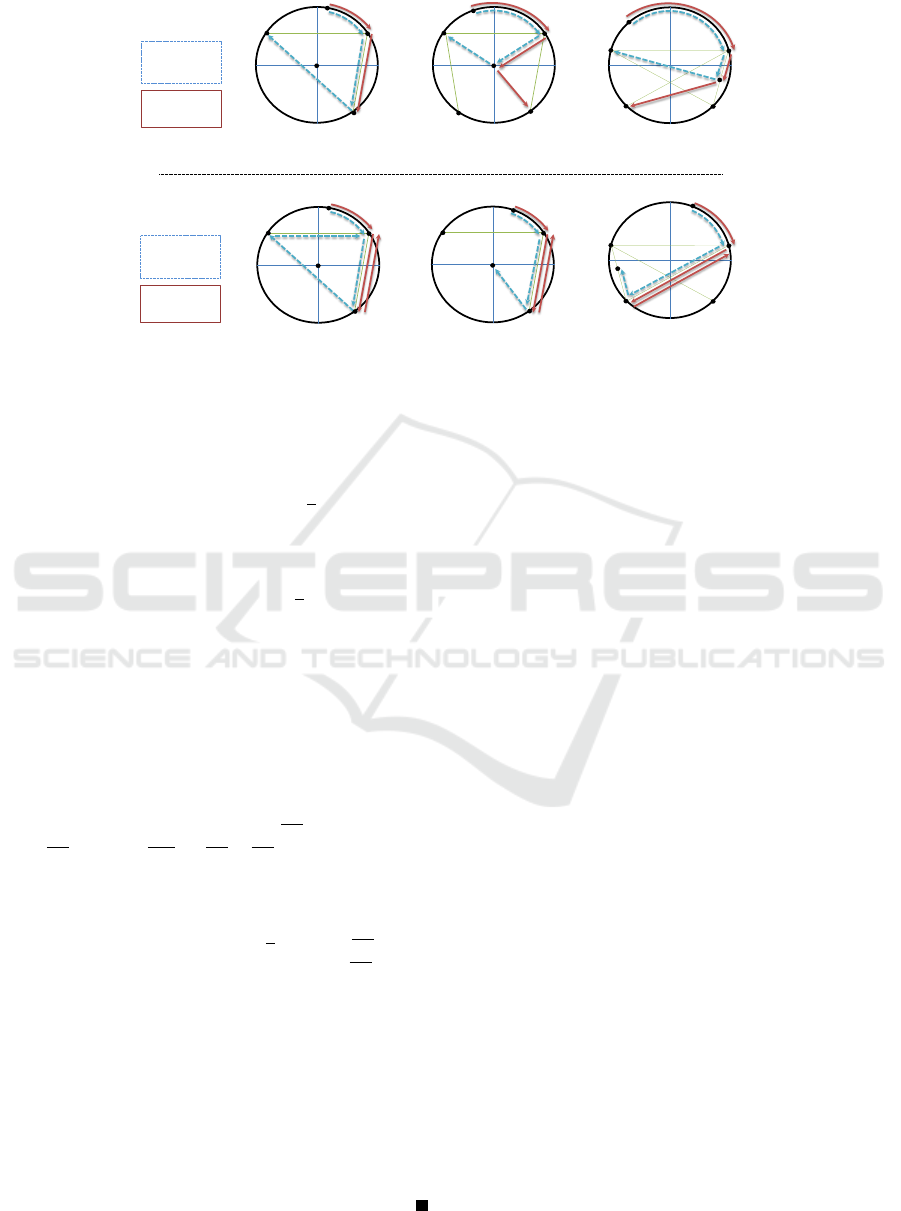
Figure 3: The non-wireless algorithm for two robots with performance π − α/2 +3 sin(α/2).
That can happen only if the exit is at point B, and once
again R
2
makes the right decision to evacuate from B.
In the last case, R
2
is following subroutine A
3
, and
so it must be that α > 2π/3, that α − x ≤ x < α, and
that it has not found any other interesting point before.
Figure 3 subcase v depicts this scenario. Note that the
exit could be either in C or in D.
If the exit is in C, then α − x ≤ x, and R
1
would
follow A
3
too. This means, R
1
would go to point D
(where there is no treasure), and that would make it
travel along the chord DI (an illustration of this tra-
jectory is shown in Figure 3 subcase vi, if R
1
was
moving clockwise). If R
1
reaches I, it waits there,
and when R
2
arrives in I, R
2
makes the right deci-
sion to evacuate from C. Otherwise R
1
does not reach
I, and it moves up to a certain point in the chord ID
similarly to R
2
. Note that the meeting condition on
a point K on the chord, with y = IK, would be that
AI
_
+ IK = CA
_
+ CD + (DI − IK), which translates
into y = x + sin(α/2) + sin(α) − α/2, i.e. the ex-
act segment of ID that R
2
traverses before it changes
trajectory. The longest R
2
could have traveled on the
chord ID would be when x = α−x, but then IK would
be equal to α − π + 3sin (α) ≤ 2 sin(α) = ID for all
α > 2π/3. Therefore, the two robots meet indeed in
somewhere in the chord ID. Note also that in this
case, R
2
makes the right decision and goes to point C
in order to evacuate.
If instead the exit is in B, then again R
2
travels
till point K (which is in the interior of the chord ID).
But in this case, R
1
will not meet R
2
in point K as it
will not follow A
3
. Once again, R
2
makes the right
decision, and after arriving at K it moves to point B
and evacuates.
3.2 Algorithm Analysis
In this section we prove that for all α ∈ [0,π], the evac-
uation time of Algorithm 2 is no more than 1 + π −
α/2 + 3sin (α/2), concluding Theorem 3.1. In the
analysis below we provide, whenever possible, sup-
porting illustrations, which for convenience may de-
pict special configurations. In the mathematical anal-
ysis we are careful not to make any assumptions for
the configurations we are to analyze.
It is immediate that when a robot finds the first
interesting point at time x ≥ α after moving on the
perimeter of the disk, then that robot can also deduce
where the other interesting point is located. In that
sense, it is not surprising that, in this case, the trajec-
tory of the robots and the associated cost analysis are
simpler.
Lemma 3.3. Let x be the time some robot is the first to
reach an interesting point I ∈ {E,T } from the moment
robots start moving in opposing directions. If x ≥ α,
then the performance of the algorithm is at most 1 +
π − α/2 + 3sin (α/2). Also, x ≥ α is impossible, if
α > 2π/3.
Proof. Note that 1 is the time it takes both robots
to reach a point, say A, on the ring. So we will
tailor our analysis to the evacuation time from the
moment robots start moving (in opposing directions)
from point A.
Let x be the time after which R
2
(without loss
of generality) is the first to find an interesting point
I ∈ {E,T }. Let also B be the other interesting point
{E, T } \ I. For R
2
to reach first I, it must be the case
that R
1
does not have enough time to reach B, and
Search-and-Fetch with 2 Robots on a Disk - Wireless and Face-to-Face Communication Models
23

hence x ≤ 2π − α −x, that is x ≤ π − α/2. Since also
x ≥ α, we conclude that α ≤ 2π/3.
Next we examine the following cases. For our
analysis, the reader can use Figure 2 as reference (al-
though A is depicted in the interior of the arc CI, we
will not use that AI
_
≤ α).
Case 1 (I = T ): R
2
picks up the treasure
and moves along the chord IB = 2 sin (α/2).
The worst case treasure-evacuation time then
is max
α≤x≤π−α/2
{
x + 2 sin(α/2)
}
= π − α/2 +
2sin (α/2).
Case 2 (I = E): According to the algorithm, R
2
moves towards the treasure point B along the
chord IB, and reaches it in time x + 2 sin (α/2).
R
1
moves counter-clock wise and will reach the
position of the treasure in time 2π − α − x. Who-
ever finds the treasure first will evacuate from the
exit, paying additional time 2 sin(α/2). Hence,
the total cost can never exceed
min
{
x + 2 sin(α/2) ,2π − α−x
}
+ 2 sin(α/2)
≤π − α/2 + 3sin(α/2) (by Lemma Ab)
It is easy to see that in both cases, the cost of the al-
gorithm is as promised.
By Lemma 3.3 we can focus on the (much more
interesting) case that R
2
, which is the first robot that
finds an interesting point, arrives at I at time x :=
AI
_
< α. A reference for the analysis below is Fig-
ure 3 which is accurately depicting point A at most
α arc-distance away from I. For the sake of better
exposition, we examine next the cases α ≤ 2π/3 and
α ≥ 2π/3 separately. Note that in the former case
robots may run subroutines A
1
or A
2
, while in the lat-
ter case robots may run subroutines A
1
or A
3
. For
both lemmata below, the reader may consult Figures 2
and 3.
Lemma 3.4. Let x be the time some robot is the first to
reach an interesting point I ∈ {E,T } from the moment
robots start moving in opposing directions. If x < α,
then the performance of the algorithm is at most 1 +
π − α/2 + 3sin(α/2), for all α ∈ [0,π].
Proof. As before, we omit in the analysis below the
time cost 1, i.e. the time robots need to reach the pe-
riphery of the disk. We examine the following cases
for R
2
, which is the robot that finds I.
(I = T, B = E,C = null): If R
2
runs A
1
, then it must
be that x ≤ α − x, so the cost is x + 2 sin(α/2) ≤
α − x + 2sin (α/2) ≤ π − α/2 + 3 sin(α/2) (see
Figure 3 i).
If R
2
runs A
2
, then it must be that α − x ≤ x < α
and α ≤ 2π/3, and the robot goes to the cen-
tre in order to learn where the exit is (see Fig-
ure 3 iii). Independently of where the exit is,
and by Lemma 3.2, R
2
makes the right deci-
sion and evacuates in time 1+max
α−x≤x<α
{x,α−
x+2sin (α/2)}+1 ≤ max{α,x +2 sin(α/2)}+ 2
which, by Lemma Ac, is at most π − α/2 +
3sin (α/2) for all α ≤ 2π/3. Note that the analy-
sis of this case is valid, even if I = T is not the first
interesting point that is discovered, and it is from
the perspective of the robot that finds the treasure.
If R
2
runs A
3
, then it must be that α − x ≤ x < α
and α > 2π/3. Then the trajectory of R
2
is as in
Figure 3 v, and the exit is found correctly due to
Lemma 3.2. For the sake of the exposition, we
will do the worst case analysis for both cases B =
E and C = E now (i.e. we only insist in that I = T
and that R
2
runs A
3
).
The total time for the combined cases is AI
_
+
IK +
max{
KB,KC}, where IK = y (see definition of
A
3
). Since as we have proved, K lies always in
chord ID, and since DB
_
= 3α − 2π we have that
BK ≤ max{BI,BD}
≤max{2 sin(α/2) ,2 sin(3α/2 − π)}
≤2sin (α/2)
We also have that KC ≤ CI = 2 sin (α/2). So the
cost becomes no more than
x + y + 2sin(α/2) = α/2 + 3sin (α/2) +sin(α)
≤π − α/2 + 3sin(α/2) (by Lemma Ad)
for all α ∈ [0,π].
(I = T, B = null,C = E): Since I is found first, we
must have x ≤ α/2, hence both robots run A
1
, see
Figure 3 i. Robot R
2
that finds the treasure will
evacuate in time no more than x + 2 sin(α/2) +
2sin (α) ≤ α/2 + 2sin (α/2) + 2 sin(α) < π −
α/2 + 3 sin(α/2) for all α ∈ [0,π].
(I = E,B = T,C = null): If R
2
is the first to find the
treasure, then this case is depicted in Figure 3
i. This happens exactly when x + 2sin (α/2) ≤
2π − x − α, so that the total evacuation time is
x +4sin (α/2) ≤ π− α/2 +3sin (α/2) for all α ∈
[0,π].
Otherwise x > π − α/2 − sin(α/2), and R
1
is the
robot that reaches the treasure first. If R
1
de-
cides to run A
1
, then the cost would be 2π −
x − α +2sin (α/2) < π − α/2 + 3sin (α/2) for all
α ∈ [0,π]. Finally, if R
1
decides to run A
2
or A
3
,
then we have already made the analysis in case
I = T, B = E,C = null above.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
24

(I = E,B = null,C = T ): Note that in all cases, both
robots will run the same subroutine. In particular,
if robots run either A
2
or A
3
, then we have already
done the analysis in case I = T,B = E,C = null
above.
Finally, if both robots run A
1
, it must be either
because α ≤ α
0
, or because x ≥ x, while the cost
is always α−x+2sin (α/2)+2 sin(α) (the case is
depicted in Figure 3 ii, with reverse direction). If
α ≤ α
0
, then the evacuation cost would be at most
α +2sin (α/2)+ 2 sin(α) which by Lemma Ah is
at most π − α/2 + 3 sin(α/2), for all α ∈ [0,α
0
].
If x ≥ x, then the cost would be at most α − x +
2sin (α/2) + 2 sin(α) = π − α/2 + 3sin (α/2).
Note that Lemmata 3.3, 3.4 imply that the perfor-
mance of Algorithm 2 is, in the worst case, no more
than 1 + π − α/2 + 3sin (α/2), concluding also The-
orem 3.1.
3.3 Extension to n Robots
We can easily extend our 2-robot algorithms to the
n-robot case (when n is even, otherwise we ignore
one robot) by splitting the robots into pairs, defining
points in intervals of length 4π/n on the cycle, assign-
ing each pair of robots to each such point, and letting
them run the corresponding 2-robot algorithm.
4 LOWER BOUNDS
We conclude the study of treasure evacuation with 2
robots by providing the following lower bound per-
taining to distributed systems under the face-to-face
communication model.
Theorem 4.1. For problem 2-TE
f 2 f
, any algorithm
needs at least time 1 + π/3 + 4 sin(α/2) if 0 ≤ α ≤
2π/3, or 1 + π/3 + 2sin (α) + 2sin (α/2) if 2π/3 ≤
α ≤ π.
For the proof, we invoke an adversary (not neces-
sarily the most potent one), who waits for as long as
there are three points A, B,C with AB = BC = α on the
periphery such that at most one of them has been vis-
ited by a robot. Then depending on the moves of the
robots decides where to place the interesting points.
5 CONCLUSION
In this paper we introduced a new problem on search-
ing and fetching which we called treasure-evacuation
from a unit disk. We studied two online variants of
treasure-evacuation with two robots, based on differ-
ent communication models. The main point of our ap-
proach was to propose distributed algorithms by a col-
laborative team of robots. Our main results demon-
strate how robot communication capabilities affect
the treasure evacuation time by contrasting face-to-
face (information can be shared only if robots meet)
and wireless (information is shared at any time) com-
munication.
There are several open problems in addition to
sharpening our bounds. These include problems on
1) the number of robots, 2) other geometric domains
(discrete or continuous), 3) differing robot starting
positions, 4) multiple treasures and exits, 5) limited
range wireless communication, 6) robots with dif-
ferent speeds, 6) different a priori knowledge of the
topology or partial information about the targets, etc.
In particular, we anticipate that nearly optimal algo-
rithms for small number of robots, e.g. for n = 3, 4,
or any other variation of problem we consider will re-
quire new and significantly different algorithmic ideas
than those we propose here, still in the same spirit.
REFERENCES
Ahlswede, R. and Wegener, I. (1987). Search problems.
Wiley-Interscience.
Albers, S. and Henzinger, M. R. (2000). Exploring un-
known environments. SIAM Journal on Computing,
29(4):1164–1188.
Albers, S., Kursawe, K., and Schuierer, S. (2002). Explor-
ing unknown environments with obstacles. Algorith-
mica, 32(1):123–143.
Alpern, S. (2011). Find-and-fetch search on a tree. Opera-
tions Research, 59(5):1258–1268.
Alpern, S. and Gal, S. (2003). The theory of search games
and rendezvous. Springer.
Baeza Yates, R., Culberson, J., and Rawlins, G. (1993).
Searching in the plane. Information and Computation,
106(2):234–252.
Baeza-Yates, R. and Schott, R. (1995). Parallel searching in
the plane. Computational Geometry, 5(3):143–154.
Beck, A. (1964). On the linear search problem. Israel Jour-
nal of Mathematics, 2(4):221–228.
Bellman, R. (1963). An optimal search. SIAM Review,
5(3):274–274.
Berman, P. (1998). On-line searching and navigation. In
Fiat, A. and Woeginger, G. J., editors, Online Algo-
rithms: The State of the Art, pages 232–241. Springer.
Bonato, A. and Nowakowski, R. (2011). The game of cops
and robbers on graphs. AMS.
Burgard, W., Moors, M., Stachniss, C., and Schneider,
F. E. (2005). Coordinated multi-robot exploration.
Robotics, IEEE Transactions on, 21(3):376–386.
Search-and-Fetch with 2 Robots on a Disk - Wireless and Face-to-Face Communication Models
25

Chrobak, M., Gasieniec, L., T., G., and Martin, R. (2015).
Group search on the line. In SOFSEM 2015. Springer.
Chung, T. H., Hollinger, G. A., and Isler, V. (2011). Search
and pursuit-evasion in mobile robotics. Autonomous
robots, 31(4):299–316.
Czyzowicz, J., Gasieniec, L., Gorry, T., Kranakis, E., Mar-
tin, R., and Pajak, D. (2014). Evacuating robots from
an unknown exit located on the perimeter of a disc. In
DISC 2014, pages 122–136. Springer, Austin, Texas.
Czyzowicz, J., Georgiou, K., Dobrev, S., Kranakis, E., and
MacQuarrie, F. (2016). Evacuating two robots from
multiple unknown exits in a circle. In ICDCN 2016.
Czyzowicz, J., Georgiou, K., Kranakis, E., Narayanan, L.,
Opatrny, J., and Vogtenhuber, B. (2015a). Evacuat-
ing robots from a disc using face to face communica-
tion. In CIAC 2015, pages 140–152. Springer, Paris,
France.
Czyzowicz, J., Kranakis, E., Krizanc, D., Narayanan, L.,
Opatrny, J., and Shende, S. (2015b). Wireless au-
tonomous robot evacuation from equilateral triangles
and squares. In ADHOC-NOW 2015, Athens, Greece,
June 29 - July 1, 2015, Proceedings, pages 181–194.
Demaine, E. D., Fekete, S. P., and Gal, S. (2006). Online
searching with turn cost. Theoretical Computer Sci-
ence, 361(2):342–355.
Deng, X., Kameda, T., and Papadimitriou, C. (1991). How
to learn an unknown environment. In FOCS, pages
298–303. IEEE.
Fekete, S., Gray, C., and Kr
¨
oller, A. (2010). Evacuation of
rectilinear polygons. In Combinatorial Optimization
and Applications, pages 21–30. Springer.
Georgiou, K., Karakostas, G., and Kranakis, E. (2016a).
Search-and-fetch with 2 robots on a disk: Wire-
less and face-to-face communication models. CoRR,
abs/1611.10208.
Georgiou, K., Karakostas, G., and Kranakis, E. (2016b).
Search-and-fetch with one robot on a disk. In 12th
International Symposium on Algorithms and Experi-
ments for Wireless Sensor Networks.
Gluss, B. (1961). An alternative solution to the lost at
sea problem. Naval Research Logistics Quarterly,
8(1):117–122.
Hipke, C., Icking, C., Klein, R., and Langetepe, E. (1999).
How to find a point on a line within a fixed distance.
Discrete Appl. Math., 93(1):67–73.
Hoffmann, F., Icking, C., Klein, R., and Kriegel, K. (2001).
The polygon exploration problem. SIAM Journal on
Computing, 31(2):577–600.
Isbell, J. R. (1967). Pursuit around a hole. Naval Research
Logistics Quarterly, 14(4):569–571.
Jennings, J. S., Whelan, G., and Evans, W. F. (1997). Coop-
erative search and rescue with a team of mobile robots.
In ICAR, pages 193–200. IEEE.
Kao, M.-Y., Ma, Y., Sipser, M., and Yin, Y. (1998). Opti-
mal constructions of hybrid algorithms. J. Algorithms,
29(1):142–164.
Kao, M.-Y., Reif, J. H., and Tate, S. R. (1996). Searching
in an unknown environment: An optimal randomized
algorithm for the cow-path problem. Information and
Computation, 131(1):63–79.
Kleinberg, J. (1994). On-line search in a simple polygon.
In SODA, page 8. SIAM.
Koutsoupias, E., Papadimitriou, C., and Yannakakis, M.
(1996). Searching a fixed graph. In ICALP 96, pages
280–289. Springer.
Nahin, P. (2012). Chases and Escapes: The Mathematics of
Pursuit and Evasion. Princeton University Press.
Papadimitriou, C. H. and Yannakakis, M. (1989). Short-
est paths without a map. In ICALP, pages 610–620.
Springer.
Stone, L. (1975). Theory of optimal search. Academic Press
New York.
Thrun, S. (2001). A probabilistic on-line mapping algo-
rithm for teams of mobile robots. The International
Journal of Robotics Research, 20(5):335–363.
Yamauchi, B. (1998). Frontier-based exploration using mul-
tiple robots. In Proceedings of the second interna-
tional conference on Autonomous agents, pages 47–
53. ACM.
APPENDIX
Lemma A. a) There exists some α
0
∈ (0,π) such
that 3α/2−π−sin (α/2)+2sin (α) is positive for
all α ∈ (α
0
,π) and negative for all α ∈ [0,α
0
). In
particular, α
0
≈ 1.22353.
b) min
{
x + 2 sin(α/2) ,2π − α−x
}
+ 2 sin(α/2) ≤
π − α/2 + 3sin(α/2) , ∀α ∈ [0,π].
c) max{α, x + 2 sin (α/2)} + 2 ≤ π − α/2 +
3sin (α/2) for all α ∈ [0, 2π/3].
d) α +sin(α) ≤ π for all α ∈ [0, π].
e) α −sin(α/2) + 2 sin(α) ≤ π for all α ∈ [0,π].
f) α/2 + 2 sin(α) ≤ π − α + 2 sin (α/2) , ∀α ∈
[0,2π/3]. .
g) max
0≤x≤π−α
{sin(π/2 −α/2 − x)} ≤
sin(α/2) , ∀α ∈ [2π/3,π]
h) max
0≤x≤α/2
{x +2 sin(α/2 − x)}+2sin (α) ≤ π −
α + 4 sin(α/2), ∀α ∈ [0,2π/3].
i) max
0≤x≤π−α
{x+2 sin (π/2 − α/2 − x)} ≤ π−α+
2sin (α/2), ∀α ∈ [2π/3,π]
j) sin (α) ≤ sin(α/2), ∀α ∈ [0,2π/3], and
sin(α) ≥ sin (α/2), ∀α ∈ [2π/3, π].
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
26
