
Adaptive Rendering based on Adaptive Order Selection
Hongliang Yuan
1,2
, Changwen Zheng
1
, Quan Zheng
1,2
and Yu Liu
1,2
1
Institute of Software, Chinese Academy of Sciences, Beijing, China
2
University of Chinese Academy of Sciences, Beijing, China
Keywords:
Adaptive Rendering, Adaptive Order Selection, Monte Carlo Ray Tracing, Mean Squared Error.
Abstract:
We propose a new adaptive sampling and reconstruction method based on a novel, adaptive order polynomial
fitting which can preserve various high-frequency features in generated images and meanwhile mitigate the
noise efficiently. Some auxiliary features have strong linear correlation with luminance intensity in the smooth
regions of the image, but the relationship does not hold in the high-frequency regions. In order to handle
these cases robustly, we approximate luminance intensity in the auxiliary feature space by constructing local
polynomial functions with order varying adaptively. Firstly, we sample the image space uniformly. Then
we decide the order of fitting with the least estimated mean squared error (MSE) for each pixel. Finally,
we distribute additional ray samples to areas with higher estimated MSE if sampling budget remains. We
demonstrate that our method makes significant improvement in terms of both numerical error and visual quality
compared with the state-of-the-art.
1 INTRODUCTION
Monte Carlo (MC) ray tracing (Kajiya, 1986) is the
commonly acknowledged efficient algorithm to syn-
thesize photo-realistic images from 3D models. How-
ever, the rendered images generated by MC ray trac-
ing at low sampling rate are noisy, and generating
noise-free images needs dozens of hours. In order to
synthesize satisfactory images in reasonable time, re-
moving MC noise in image-space has been actively
studied recently. The model of filtering MC noise can
be formulated as:
y = m(x) +ε (1)
where y is a scalar response variable, x = (x
1
, ..., x
d
)
T
is a d-dimensional vector of explanatory variables and
ε represents MC noise.
From the perspective of rendering, m(x) and y de-
note an unknown ground truth image and a noisy im-
age, respectively. The vector x contains spatial and
range components of the image, as well as additional
geometric information including surface normal, tex-
ture color and direct illumination visibility and so on.
The additional geometric information, which is also
called the auxiliary features, is computed at every
pixel where we average out geometries collected from
multiple sample rays.
Image-space denoising locally approximates the
color value of a pixel c as a weighted average of its
neighbors:
ˆm(x
c
;H) =
∑
i∈Ω
c
y
i
K
H
(i, c)
∑
i∈Ω
c
K
H
(i, c)
(2)
where ˆm(x
c
;H) is the filtered color value of pixel c, y
i
is the input color value of pixel i, Ω
c
is a local window
centered on c and K
H
(·) denotes a nonnegative weight
function with a bandwidth matrix H. The equation
is called Nadaraya-Watson (Nadaraya, 1964; Watson,
1964) estimator which is the weighted least square so-
lution of the following optimization problem:
min
α
∑
i∈Ω
c
(y
i
− α)
2
K
H
(i, c) (3)
i.e., ˆm(x
c
;H) =
ˆ
α. The solution can be also expressed
as follows:
ˆ
α = e
T
(X
T
WX)
−1
X
T
WY
= L
T
(x
c
)Y
(4)
where e = (1)
T
, Y = (y
1
, ..., y
n
)
T
and n represents
the number of pixels within a filtering window cen-
tered on c, W = diag(K
H
(1, c), ..., K
H
(n, c)) and X =
(1, ..., 1)
T
. L
T
(x
c
) is called equivalent kernel. The
bilateral filter (Tomasi and Manduchi, 1998) is an
example of Nadaraya-Watson estimator. The weight
K
H
(i, c) is defined as:
K
H
(i, c) = exp
−ki − ck
2
2σ
2
s
exp
−ky
i
− y
c
k
2
2σ
2
r
(5)
Yuan H., Zheng C., Zheng Q. and Liu Y.
Adaptive Rendering based on Adaptive Order Selection.
DOI: 10.5220/0006093100370045
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 37-45
ISBN: 978-989-758-224-0
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
37

so that the bandwidth matrix H =
diag(σ
s
, σ
s
, σ
r
, σ
r
, σ
r
). The non-local means
(NL-Means) filter (Buades et al., 2008) is also a
generalization of Nadaraya-Watson estimator where
the weight is computed based on small patches.
From the Equation 4, we know the Nadaraya-Watson
estimator
ˆ
α is a locally weighted average of the
response variables in the neighborhood of the given
pixel c.
The Nadaraya-Watson estimator converges more
slowly at the boundary and its conditional variance
is larger in practice for points on the boundary than
for points on the interior. Moon et al. (Moon et al.,
2014) introduces a local linear estimator to remove
MC noise:
min
α,β
∑
i∈Ω
c
(y
i
− α −β
T
(x
i
− x
c
))
2
K
H
(i, c) (6)
Its solution is also expressed as the Equation 4, but
e = (1, 0, ..., 0)
T
is a (d + 1)-dimensional vector and
the ith row of X is set as (1, (x
i
− x
c
)
T
).
Intuitively it is clear that in the smooth region
of the image the Nadaraya-Watson estimator or lo-
cal linear estimator is preferable, whereas in the high-
frequency region due to MC effects such as motion
blur and depth-of-field, polynomials of higher or-
der such as local cubic estimator is recommendable.
Hence, the order of local polynomial fitting should be
varied to reflect the local curvature of the unknown
ground truth image.
Based on previous analysis, we present a novel,
adaptive order polynomial fitting based adaptive sam-
pling and reconstruction method to effectively han-
dle various MC rendering effects (e.g., motion blur,
depth-of-field, soft shadow, etc). Given a fixed spatial
bandwidth, our method estimates an unknown func-
tion based on a data-driven variable order selection
procedure. Our core idea is to develop a robust esti-
mate of the MSE of each pixel and to use this estimate
as a criterion for adaptive order selection (AOS), i.e.
varying the order of the Taylor series approximation.
Our idea is based on obvious observations that a ref-
erence image in the area of motion blur no longer has
a linear correlation with given auxiliary features (e.g.,
textures). Specifically, we make the following techni-
cal contributions: For a given fixed spatial bandwidth
and each order (i.e., local linear estimator and local
cubic estimator), our method estimates the MSE of
each pixel which is decomposed into estimation of
bias and variance terms. The local optimal order is
selected with the least MSE.
2 PREVIOUS WORK
Adaptive sampling and reconstruction was pioneered
by Kajiya (Kajiya, 1986). The key of adaptive sam-
pling is to develop a robust error metric which can
guide where we need to allocate more ray sam-
ples. Common error metrics includes Stein’s Unbi-
ased Risk Estimator (SURE) (Stein, 1981), contrast
metric (Mitchell, 1987), median absolute deviation
(MAD) (Donoho and Johnstone, 1994), MSE which
can be decomposed into variance plus the square of
bias and so on. We will review the most recent adap-
tive renderings based on previous analysis and clas-
sify them into Nadaraya-Watson estimator, local lin-
ear estimator and higher order estimator.
Nadaraya-Watson Estimator. Li et al. (Li et al.,
2012) leverage cross-bilateral filter to filter MC noise.
They compute the weight between two pixels similar
to the Equation 5 as well as considering auxiliary fea-
tures. Sen et al. (Sen and Darabi, 2012) also use cross-
bilateral filter, but utilizing mutual information to
measure the relation between feature differences and
filter weights. Rousselle et al. (Rousselle et al., 2013)
adopt SURE to estimate MSE of three cross-bilateral
filters with the same spatial support, but different their
other parameters. Moon et al. (Moon et al., 2013) use
a virtual flash image as a stopping function to com-
pute the weight of a cross-bilateral filter. Rousselle et
al. (Rousselle et al., 2012) exploit NL-Means filter for
adaptive rendering, while Delbracio et al. (Delbracio
et al., 2014) propose a multi-scale NL-Means filter
for adaptive reconstruction. Kalantari et al. (Kalan-
tari et al., 2015) present a machine learning approach
to reduce MC noise. These methods are all the cases
of the Nadaraya-Watson estimator.
Local Linear Estimator. Moon et al. (Moon et al.,
2014) construct local linear estimator to estimate the
color value of each pixel. Moon et al. (Moon et al.,
2015) propose to approximate the color value of each
pixel in a prediction window with multiple, but sparse
local linear estimators. Bitterli et al. (Bitterli et al.,
2016) study existing approaches and present nonlin-
early weighted first-order regression for denoising
MC noise, which is also the case of local linear es-
timator, but computing the weight based on small
patches.
High Order Estimator. Most recently, Moon et al.
(Moon et al., 2016) locally approximate an image
with polynomial functions and the optimal order of
each polynomial function is estimated so that multi-
stage reconstruction error can be minimized. How-
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
38
ever, they construct polynomial functions only con-
sidering pixel position (2D). In contrast, we construct
higher order regression functions considering all aux-
iliary features and present a bias estimation leveraging
Taylor expansion.
There are some adaptive renderings which do
not belong to these categories. For example,
multi-dimensional adaptive rendering proposed by
Hachisuka et al. (Hachisuka et al., 2008), and adaptive
wavelet rendering presented by Overbeck et al. (Over-
beck et al., 2009).
3 LOCAL POLYNOMIAL
FITTING
Local linear estimator can locally estimate image
functions efficiently when non-linearity in the 2D im-
age space becomes nearly linear in the auxiliary fea-
ture space. This is definitely true in smooth region
of a noisy image, but in rendering, some MC effects
such as glossy highlights and defocused areas can be
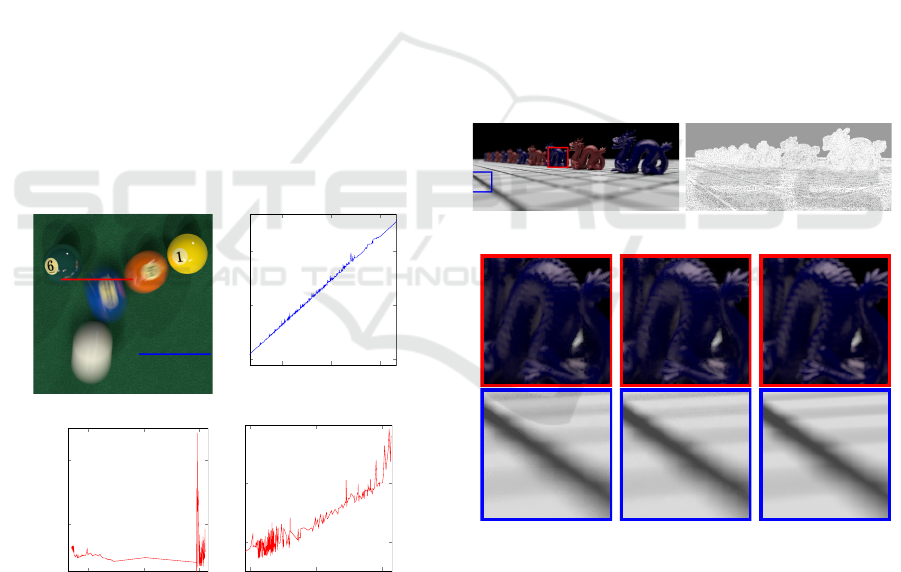
nonlinear as shown in Fig. 1. In such cases, we had
better select higher order of regression function to re-
duce bias due to the curvature of the signal being re-
constructed.
(a) Reference
0.6 0.9 1.2
0.3
0.6
0.9
Texture intensity×10
Reference intensity×10
(b) Intensity on texture
0.94 0.96 0.98
0.1
0.2
Depth
Reference intensity
(c) Intensity depth
0.5 1.5 2.5
0.5
1.5
2.5
Texture intensity×10
Reference intensity×10
(d) Intensity on texture
Figure 1: The reference image (a) is POOL scene gener-
ated with 32K ray samples per pixel. Intensity on texture
plot (b) is drawn from data in blue line of (a) which shows
strong linear correlation, where blue line is in smooth re-
gion. Intensity on depth plot (c) and on texture plot (d) are
drawn from data in red line of (a) respectively which shows
non-linearity, where red line covers smooth and motion blur
regions.
Based on our observations, we propose an adap-
tive order polynomial fitting based method to recon-
struct smooth and high-frequency areas adaptively
and efficiently with fixed spatial bandwidth. Bias will
increase and variance will decrease as bandwidth in-
creases. On the contrary, bias will decrease and vari-
ance will increase as bandwidth decreases. This is the
famous bias-variance trade-off issue. Bandwidth ro-
bustification can be explained as follows. If the given
spatial bandwidth is too large, our method will choose
a higher order fitting to reduce the bias. On the con-
trary, if the given spatial bandwidth is too small, our
method will select a lower order fitting to reduce vari-
ance. As a result, this procedure adapts to smooth and
high-frequency regions of a MC input image.
Weighted local regression (WLR) proposed by
Moon et al. (Moon et al., 2014) uses local linear
estimator to approximate the nonlinear effects in a
high dimensional auxiliary feature space. It is sus-
ceptible to oversmooth the regions with high curva-
ture, even though they suggest a sophisticated two-
step optimization procedure. Fig. 2 demonstrates that
our method can improve the image quality compared
with WLR.
(a) OUR: 1500×636 (b) Adaptive order selection
(c) WLR 32 spp
rMSE 0.00045
(d) OUR 32 spp
rMSE 0.00037
(e) Reference
64K spp
Figure 2: Adaptive order selection image (b) is generated
when reconstructing our image (a), it is clear that in smooth
region (e.g., black region in (a)) local linear estimator indi-
cated by grey is optimal choice. Whereas, in high-frequency
regions (e.g., red and blue rectangle in (a)), local cubic esti-
mator indicated by white can preserve details efficiently, see
details comparison with WLR. Even though relative MSE
(rMSE defined in Sec. 7) of WLR and our method is at
same order of magnitude, our method has an advantage over
WLR at the high-frequency regions from the perspective of
visual quality.
In order to perform AOS, we need fit a high or-
Adaptive Rendering based on Adaptive Order Selection
39

der multivariate regression function. For the sake of
reducing computational overhead, we bring in partial
local polynomial regression. For example, we will use
the following design matrix for a local polynomial of
order v:
X =
1 (x
1
− x
c
)
T
. . . (x
1
− x
c
)
vT
.
.
.
.
.
.
.
.
.
.
.
.
1 (x
n
− x
c
)
T
. . . (x
n
− x
c
)
vT
(7)
where (x
i
−x
c
)
vT
= ((x
i1
−x
c1
)
v
, ..., (x
id
−x
cd
)
v
)
T
, i =
1, ..., n. The design matrix is only used for deciding
which order of fitting can minimize the MSE at each
pixel. Once it is selected, we then estimate color value
and MSE which can guide the additional sampling.
Then, the optimization problem of higher order re-
gression can be written as follows:
min
β
n
∑
i=1
(y
i
− β
0
−
p
∑
v=1
β
T
v
(x
i
− x
c
)
v
)
2
K
H
(x
i
− x
c
) (8)
where p is the order of the polynomial function,
β = (β
0
, β
T
1
, ..., β
T
p
)
T
, β
v
= (β
v1
, ..., β
vd
)
T
and (x
i
−
x
c
)
v
= ((x
i1
− x
c1
)
v
, ..., (x
id
− x
cd
)
v
). K
H
(i, c) =
exp
−ki−ck
2
2h
2
, since we only optimize the order of
local polynomial function, we select fixed spatial fil-
tering window h. Solving (8) by the least squares
method provides the solution:
ˆ
β(x
c
) = (X
T
WX)
−1
X
T
WY (9)
whose conditional mean and variance are:
E(
ˆ
β(x
c
)|x
1
, ..., x
n
) = (X
T
WX)
−1
X
T
Wm
= (X
T
WX)
−1
X
T
W(Xβ + r)
= β + (X
T
WX)
−1
X
T
Wr
(10)
var(
ˆ
β(x
c
)|x
1
, ..., x
n
) = (X
T
WX)
−1
(X
T
W
2
X)
×(X
T
WX)
−1
σ
2
(x
c
)
(11)
where m = (m(x
1
), ..., m(x
n
))
T
denotes the unknown
ground truth image and r = m − Xβ represents bias
image between the unknown ground truth image and
estimated image. Since r contains unknown term m,
we need to estimate it (Sec. 4).
4 ADAPTIVE ORDER
SELECTION
Fan et al. (Jianqing Fan, 1995a) proposed to use the
estimated MSE as a criterion to opt for the best or-
der of regression function, but their method can only
apply to regression function with one response vari-
able. Motivated by the previous work, we present
MSE estimation for multivariate regression. We in-
troduce bias estimation first.
Bias Estimation. We estimate bias vector r = m −
Xβ = (r
1
, ..., r
n
)
T
via Taylor expansion
r
i
≈
p+a
∑
v=p+1
β
T
v
(x
i
− x
c
)
v
≡ ξ
i
(12)
where a is an order which is greater than the approx-
imation order p. Fan et al. (Jianqing Fan, 1995b) dis-
cuss the choice of the approximation order, who sug-
gest to use a = 2 for practical implementation. In this
paper, we follow this recommendation. The unknown
bias in ξ = (ξ
1
, ..., ξ
n
)
T
can be estimated by fitting
a local polynomial with the order p + a and the spa-
tial bandwidth h defined previously. Let
ˆ
β
∗
p+1
,...,
ˆ
β
∗
p+a
be the locally weighted least squares estimation, then
ˆ
ξ
i
=
∑
p+a
v=p+1
ˆ
β
∗T
v
(x
i
−x
c
)
v
. Bias at pixel c is estimated
by
d
bias
p
(x
c
) = (X
T
WX)
−1
X
T
W
ˆ
ξ (13)
Variance Estimation. After fitting a local poly-
nomial with order p + a, the estimation result
ˆm(x
c
;H) can be expressed by
∑
n
i=1
l
i
(x
c
)y
i
, where
l
i
(x
c
) is the item of row 0 and column i of matrix
(X
∗T
W
∗
X
∗
)
−1
X
∗T
W, then
ˆ
σ
∗2
(x
c
) =
n
∑
i=1
(l
i
(x
c
))
2
σ
2
(y
i
) (14)
where X
∗
and W
∗
are the design matrix and weight
matrix respectively for the local (p + a)th order poly-
nomial fitting. σ
2
(y
i
) is the mean sample variance at
pixel i. Substituting (14) into (11) produces an ap-
proximated variance matrix:
c
var
p
(x
c
) = (X
T
WX)
−1
(X
T
W
2
X)
×(X
T
WX)
−1
σ
∗2
(x
c
)
(15)
MSE Estimation. Equation (13) is a (d × p +1)×1
bias vector for β, the first item is the estimated
bias of β
0
, denoted by
d
bias
p
[0]. Equation (15) is a
(d × p + 1) × (d × p + 1) covariance matrix for β,
c
var
p
(x
c
)[0][0] is the estimated variance of β
0
. Hence,
the MSE of ˆm(x
c
) is estimated by
[
MSE
p
(x
c
;H) =
c
var
p
(x
c
)[0][0] + (
d
bias
p
(x
c
)[0])
2
(16)
Algorithm of AOS. With the estimated MSE in
equation (16), algorithm 1 describes the procedure of
AOS-based MSE estimation, sampling map generat-
ing and color value estimation for each pixel.
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
40

Algorithm 1: AOS-based adaptive rendering.
Input:
Local polynomial fitting of order p
max
= 3 and
order increment a = 2, Auxiliary feature vector
x
i
and intensity y
i
generated by renderer
Output:
Sampling density for next iteration or final fil-
tered image
1: for each pixel do
2: Dimension reduction by truncated singular
value decomposition (Moon et al., 2014);
3: Fit a local polynomial function of order p
max
+
a;
4: for each order l ∈ {1, 3} do
5: Get coefficients for a local polynomial fit-
ting of order l + a from step 3;
6: Estimate
[
MSE
l
(x
c
;H) by equation (16);
7: end for
8: Choose order l for this pixel with the least esti-
mated
[
MSE
l
(x
c
;H);
9: For each channel, compute ˆm(x
c
;H) using lo-
cal polynomial fitting with order l;
10: end for
11: if Sampling budget remains then
12: return a sampling density based on
∆rMSE(x
c
)(Sec. 5);
13: else
14: return ˆm(x
c
;H);
15: end if
5 ADAPTIVE SAMPLING
The state-of-the-art adaptive rendering methods ((Li
et al., 2012), (Rousselle et al., 2013) and (Moon et al.,
2014; Moon et al., 2015)) adopt a common iterative
approach to distribute additional ray samples to the
regions with higher estimated MSE. In this paper, we
implement that iterative model. To guide our adaptive
sampling, we uniformly distribute a small number of
ray samples (e.g., four ray samples per pixel) at the
first iteration. Then we estimate
[
MSE(x;H) by our
AOS-based reconstruction method with fixed spatial
bandwidth and predict an error reduction ∆MSE(x) =
[
MSE(x;H) × n(x)
−4
d+4
for each pixel, where the error
reduction factor n(x)
−4
d+4
is derived in (Moon et al.,
2014) and n(x) is the number of ray samples which
has been already allocated.
Rousselle et al. (Rousselle et al., 2011) suggest
relative MSE which is based on human visual percep-
tion that is more sensitive to darker areas. Since then,
most of adaptive rendering methods (e.g., (Li et al.,
2012), (Rousselle et al., 2012; Rousselle et al., 2013)
and (Moon et al., 2014; Moon et al., 2015)) adopt
that suggestion. The relative MSE is computed as fol-
lows: ∆rMSE(x) =
∆MSE(x)
ˆm
2
(x;H)+ε
, ε is a small number,
e.g., 0.0001, which is used to avoid a divide-by-zero.
If sampling budget still remains, we allocate ray sam-
ples per pixel which are proportional to ∆rMSE(x).
6 IMPLEMENTATION DETAIL
We implement our AOS-based adaptive rendering
method using CUDA on top of PBRT2 (Pharr and
Humphreys, 2010). The auxiliary features contain 10
dimensions: 2D pixel position, 1D depth, 3D texture,
3D normal and 1D direct illumination visibility. We
normalize auxiliary features to the range [0,1]. We
find that the direct illumination visibility is very noisy
at low sampling rate, so we prefilter direct illumina-
tion visibility leveraging a non-local means filter in
an 10 × 10 window with patch size 6 × 6 as was done
in Rousselle et al. (Rousselle et al., 2013) and Kalan-
tari et al. (Kalantari et al., 2015). Even though other
features have less noise than visibility, we also apply
non-local means filtering for them.
In order to continue to reduce the noise and mit-
igate the curse of dimensionality in multivariate re-
gression, we apply the truncated singular value de-
composition (Moon et al., 2014) to auxiliary features
within given filtering window. In all our tests, we use
a 11×11 filtering window in the iterative steps and
19×19 filtering window in the final step. The reason
why we use smaller filtering windows in the iterative
stage is that we only estimate relative MSE. This de-
cision has only a slight effect on adaptive sampling.
We opt for a small number of iterations (i.e., 3) for
adaptive sampling.
We tested two orders of local polynomial fitting,
one order is 1 which leads to local linear estimator and
the other is 3 which leads to local cubic estimator. All
the choice of the order of fitting is odd-order, because
the asymptotic variance becomes large when moving
from an odd-order estimation to its consecutive even-
order estimation.
7 RESULTS AND DISCUSSIONS
We test our method using a mobile workstation
with Intel Core i7-4700MQ CPU @2.40GHz, and
NVIDIA Quadro K1100M with CUDA 7.5 SDK
for accelerating our proposed reconstruction method
based on adaptive order selection (AOS). We com-
pare our method with low discrepancy (Dobkin et al.,
Adaptive Rendering based on Adaptive Order Selection
41

1996) (LD) and the state-of-the-art adaptive render-
ing methods including WLR (Moon et al., 2014),
APR (Moon et al., 2016) and LBF (Kalantari et al.,
2015). To evaluate the WLR and LBF method, we use
the source code provided by authors and set param-
eters recommended by their corresponding papers.
Since the authors of APR method didn’t make their
source code public, we implemented their algorithm
on the CPU using the Eigen 3 library for efficient
matrix operations. Even though our implementation
might not reach the same image quality as in their
original paper, it demonstrates that locally changing
polynomial function order can generate high-quality
image.
For purpose of comparing image quality gener-
ated by different methods in terms of a quantitative
measure, we introduce the relative mean squared er-
ror (rMSE) (Rousselle et al., 2011) which is defined
as:
1
n
∑
n
i=1
( ˆm(x
i
)−m(x
i
))
2
m(x
i
)
2
+ε
, where ε = 0.001 prevents a
divide by zero, m(x) refers to the ground truth image.
We also use the structural similarity (SSIM) (Wang
et al., 2004) index to measure the similarity between
two images.
We evaluate our method on rendering following
scenes: POOL (1024×1024), SANMIGUEL (1024×
1024), SIBENIK (1024 × 1024) and TEAPOT
(1024 × 1024). These scenes include a variety of MC
effects, e.g., motion blur, depth-of-field, soft shadow,
glossy reflection and so on. For each comparison,
we adopt equal-sample comparison with LBF and
WLR method, and equal-time comparison with LD
method. Our method and WLR implement adaptive
sampling, while LBF method only implement uni-
form sampling. Considering this case, all methods
adopt uniform sampling for SANMIGUEL scene.
Motion Blur Scene Comparison. The POOL
scene, in which three billiard balls have different mo-
tion directions, is used to compare motion blur effect
for different methods. Fig. 3 shows comparison re-
sults. LD generates noisy result even with larger ray
samples than other methods. LBF leaves artifacts in
the motion blur regions (blue box). The reason is
that LBF does not implement adaptive sampling and
rendering motion blur effect needs more ray samples.
APR method can preserve high-frequency edge while
WLR gives oversmoothed it (red box). Our method
not only generates a high-quality reconstruction re-
sult on the motion blurred regions but also preserves
soft shadows clearly. In addition, our method obtains
a lower rMSE and higher SSIM than other methods.
Complex Scene Comparison. The SANMIGUEL
scene has complex geometric structure with more
than 10 million triangles due to the use of object in-
stancing and is widely used for adaptive rendering
techniques. Fig. 4 illustrates comparison results. LD
method produces a very noisy image. Our method
preserves the edge and textures on wall (closeup in
red box) and the foliage details as well as the small di-
rect soft shadows (closeup in blue box). APR method
can preserve high-frequency edge and also the foliage
details. WLR fails to preserves edge and LBF tends
to blur textures on wall and the foliage details. Over-
all, our method generates more visual pleasing images
than other techniques.
Depth-of-field Scene Comparison. Fig. 5 illus-
trates depth-of-field effect comparison using the
SIBENIK scene, which has an environment light
which can be seen by refraction through the win-
dows. LBF and WLR produces an over-blurred fence
(closeup in blue box). Our method, on the other hand,
preserves the fence as on the reference image.
Glossy Reflection Scene Comparison. The
TEAPOT scene (Fig. 6) with glossy reflection and
high-frequency bump mapping on the floor is rec-
ognized as a challenging scene. LD produces noisy
image even with more than two times ray samples
than ours. All methods fail to reconstruct the bump
map (closeup in blue box) well. In addition, our
method preserves glossy highlights more accurately
than WLR which is inclined to oversmooth glossy
regions (closeup in red box).
Convergence Comparison. We also plot conver-
gence rate for the POOL and SANMIGUEL scenes
comparing with LD, LBF and WLR methods, see
Fig. 7. Our method and WLR adopt adaptive sam-
pling for the POOL scene. Considering that LBF
method does not implement adaptive sampling, all the
methods use uniform sampling for the SANMIGUEL
scene.
8 CONCLUSIONS
We have proposed a novel, adaptive order polyno-
mial fitting based adaptive rendering approach for
efficiently denoising images with diverse MC ef-
fects. Given fixed spatial bandwidth, we handle bias-
variance trade-off by varying order of polynomial fit-
ting. For the given two choices of the order of fit-
ting, we estimate the MSE for each pixel and select
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
42

(a) OUR
rMSE:
SSIM:
(b) LD
118 spp (175 s)
0.00883
0.947
(c) LBF
32 spp (169 s)
0.00109
0.959
(d) APR
32 spp (967 s)
0.00032
0.984
(e) WLR
32 spp (216 s)
0.00049
0.978
(f) OUR
32 spp (178 s)
0.00034
0.984
(g) Reference
64K spp
Figure 3: Motion blur scene comparison.
(a) OUR
rMSE:
SSIM:
(b) LD
196 spp (861 s)
0.03057
0.721
(c) LBF
128 spp (892 s)
0.0102
0.879
(d) APR
128 spp (1883s)
0.0070
0.939
(e) WLR
128 spp (883 s)
0.0098
0.890
(f) OUR
128 spp (865 s)
0.0076
0.936
(g) Reference
64K spp
Figure 4: Complex scene comparison.
(a) OUR
rMSE:
SSIM:
(b) LD
56 spp (175 s)
0.01043
0.863
(c) LBF
16 spp (163 s)
0.00083
0.960
(d) WLR
16 spp (185 s)
0.00106
0.947
(e) OUR
16 spp (171 s)
0.00067
0.973
(f) Reference
64K spp
Figure 5: Depth of field scene comparison.
the order of fitting with the least estimated MSE adap-
tively. We also distribute additional ray samples to the
regions with higher estimated MSE iteratively. We
compare our method with the state-of-the-art meth-
ods on a wide variety of MC distributed effects. The
comparison shows that our method enhances the im-
age quality in terms of both numerical error and visual
quality over the previous methods. In the future, we
Adaptive Rendering based on Adaptive Order Selection
43

(a) OUR
rMSE:
SSIM:
(b) LD
156 spp (243 s)
0.0409
0.724
(c) LBF
64 spp (246 s)
0.0388
0.761
(d) WLR
64 spp (289 s)
0.0391
0.760
(e) OUR
64 spp (247 s)
0.0313
0.778
(f) Reference
64K spp
Figure 6: Glossy reflections scene comparison.
16 32 64 128
0.19
0.76
2.64
11.6
Ray samples per pixel
rMSE×1e-3
LD
LBF
W LR
OU R
(a) POOL
16 32 64 128
0.01
0.02
0.04
0.08
0.16
Ray samples per pixel
rMSE
LD
LBF
W LR
OU R
(b) SANMIGUEL
Figure 7: Convergence plots in LD, LBF, WLR and our
method. Our method outperforms other three methods
across all the tested ray samples per pixel.
will explore extension of AOS-based adaptive render-
ing to handle animated images.
REFERENCES
Bitterli, B., Rousselle, F., Moon, B., Guiti
´
an, J. A. I., Adler,
D., Mitchell, K., Jarosz, W., and Nov
´
ak, J. (2016).
Nonlinearly weighted first-order regression for de-
noising Monte Carlo renderings. Comput. Graph. Fo-
rum, 35(4):107–117.
Buades, A., Coll, B., and Morel, J.-M. (2008). Nonlocal
image and movie denoising. Int. J. Comput. Vision,
76(2):123–139.
Delbracio, M., Mus
´
e, P., Buades, A., Chauvier, J., Phelps,
N., and Morel, J.-M. (2014). Boosting Monte Carlo
rendering by ray histogram fusion. ACM Trans.
Graph., 33(1):8:1–8:15.
Dobkin, D. P., Eppstein, D., and Mitchell, D. P.
(1996). Computing the discrepancy with applica-
tions to supersampling patterns. ACM Trans. Graph.,
15(4):354–376.
Donoho, D. L. and Johnstone, I. M. (1994). Ideal spa-
tial adaptation by wavelet shrinkage. Biometrika,
81(3):425–455.
Hachisuka, T., Jarosz, W., Weistroffer, R. P., Dale, K.,
Humphreys, G., Zwicker, M., and Jensen, H. W.
(2008). Multidimensional adaptive sampling and re-
construction for ray tracing. In ACM SIGGRAPH
2008 Papers, SIGGRAPH ’08, pages 33:1–33:10,
New York. ACM.
Jianqing Fan, I. G. (1995a). Adaptive order polynomial
fitting: Bandwidth robustification and bias reduction.
Journal of Computational and Graphical Statistics,
4(3):213–227.
Jianqing Fan, I. G. (1995b). Data-driven bandwidth selec-
tion in local polynomial fitting: Variable bandwidth
and spatial adaptation. Journal of the Royal Statistical
Society. Series B (Methodological), 57(2):371–394.
Kajiya, J. T. (1986). The rendering equation. In Pro-
ceedings of the 13th Annual Conference on Computer
Graphics and Interactive Techniques, SIGGRAPH
’86, pages 143–150, New York. ACM.
Kalantari, N. K., Bako, S., and Sen, P. (2015). A machine
learning approach for filtering Monte Carlo noise.
ACM Trans. Graph., 34(4):122:1–122:12.
Li, T.-M., Wu, Y.-T., and Chuang, Y.-Y. (2012). SURE-
based optimization for adaptive sampling and recon-
struction. ACM Trans. Graph., 31(6):194:1–194:9.
Mitchell, D. P. (1987). Generating antialiased images at low
sampling densities. In Proceedings of the 14th An-
nual Conference on Computer Graphics and Interac-
tive Techniques, SIGGRAPH ’87, pages 65–72, New
York. ACM.
Moon, B., Carr, N., and Yoon, S.-E. (2014). Adaptive
rendering based on weighted local regression. ACM
Trans. Graph., 33(5):170:1–170:14.
Moon, B., Iglesias-Guitian, J. A., Yoon, S.-E., and Mitchell,
K. (2015). Adaptive rendering with linear predictions.
ACM Trans. Graph., 34(4):121:1–121:11.
Moon, B., Jun, J. Y., Lee, J., Kim, K., Hachisuka, T., and
Yoon, S. (2013). Robust image denoising using a vir-
tual flash image for monte carlo ray tracing. Comput.
Graph. Forum, 32(1):139–151.
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
44

Moon, B., McDonagh, S., Mitchell, K., and Gross, M.
(2016). Adaptive polynomial rendering. ACM Trans.
Graph., 35(4):40:1–40:10.
Nadaraya, E. A. (1964). On estimating regression. Theory
of Probability & Its Applications, 9(1):141–142.
Overbeck, R. S., Donner, C., and Ramamoorthi, R. (2009).
Adaptive wavelet rendering. In ACM SIGGRAPH Asia
2009 Papers, SIGGRAPH Asia ’09, pages 140:1–
140:12, New York. ACM.
Pharr, M. and Humphreys, G. (2010). Physically Based
Rendering: From Theory to Implementation. Morgan
Kaufmann Publishers Inc., San Francisco.
Rousselle, F., Knaus, C., and Zwicker, M. (2011). Adaptive
sampling and reconstruction using greedy error mini-
mization. ACM Trans. Graph., 30(6):159:1–159:12.
Rousselle, F., Knaus, C., and Zwicker, M. (2012). Adaptive
rendering with non-local means filtering. ACM Trans.
Graph., 31(6):195:1–195:11.
Rousselle, F., Manzi, M., and Zwicker, M. (2013). Robust
denoising using feature and color information. Com-
put. Graph. Forum, 32(7):121–130.
Sen, P. and Darabi, S. (2012). On filtering the noise from the
random parameters in Monte Carlo rendering. ACM
Trans. Graph., 31(3):18:1–18:15.
Stein, C. M. (1981). Estimation of the mean of a multi-
variate normal distribution. The Annals of Statistics ,
9(6):1135–1151.
Tomasi, C. and Manduchi, R. (1998). Bilateral filtering for
gray and color images. In Proceedings of the Sixth
International Conference on Computer Vision, ICCV
’98, pages 839–, Washington, DC, USA. IEEE Com-
puter Society.
Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli,
E. P. (2004). Image quality assessment: From error
visibility to structural similarity. Trans. Img. Proc.,
13(4):600–612.
Watson, G. S. (1964). Smooth regression analysis. Sankhy:
The Indian Journal of Statistics, Series A (1961-2002),
26(4):359–372.
Adaptive Rendering based on Adaptive Order Selection
45
