Persistence-based Interest Point Detection for 3D Deformable Surface

Xupeng Wang

1,3

, Ferdous Sohel

, Mohammed Bennamoun

, Yulan Guo

4,3

and Hang Lei

School of Information and Software Engineering, University of Electronic Science and Technology of China,

Chengdu, China

School of Engineering and Information Technology, Murdoch University, Perth, Australia

School of Computer Science and Software Engineering, University of Western Australia, Perth, Australia

College of Electronic Science and Engineering, National University of Defense Technology, Changsha, China

Keywords:

3D Deformable Shapes, Interest Point Detection, Persistent Homology, Diffusion Geometry, Heat Kernel

Signature Function.

Abstract:

Several approaches for interest point detection on rigid shapes have been proposed, but few are available for

non-rigid shapes. It is a very challenging task due to the presence of the large degrees of local deformations.

This paper presents a novel method called persistence-based heat kernel signature (pHKS). It consists of two

steps: scalar ﬁeld construction and interest point detection. We propose to use the heat kernel signature

function at a moderately small time scale to construct the scalar ﬁeld. It has the advantage of being stable

under various transformations. Based on the predeﬁned scalar ﬁeld, a 0-dimensional persistence diagram is

computed, and the local geometric and global structural information of the shape are captured at the same time.

Points with local maxima and high persistence are selected as interest points. We perform a comprehensive

evaluation on two popular datasets (i.e., PHOTOMESH and Interest Points Dataset) to show the effectiveness

of our method. Compared with existing techniques, our interest point detector achieves a superior performance

in terms of repeatability and distinctiveness.

1 INTRODUCTION

With the increasing availability of low-cost 3D sen-

sors (e.g., Microsoft Kinect), there is a growing de-

mand for 3D surface analysis (Biasotti et al., 2015).

The representation of 3D surfaces is a challenging

task due to the presence of noise, occlusion, clutter

and a wide range of shape transformations (Guo et al.,

2013b)(Bronstein et al., 2011)(Litman and Bronstein,

2014).

A popular approach to measure the similarities of

3D surfaces is based on a collection of local features

(Guo et al., 2014a)(Guo et al., 2016). Local feature-

based approaches (Guo et al., 2013a)(Guo et al.,

2013d)(Guo et al., 2013c)(Guo et al., 2014b)(Wang

et al., 2016)(Wang et al., 2015) have been actively

investigated for the past two decades and are com-

monly used in many applications including 3D object

recognition, 3D reconstruction, 3D shape retrieval,

registration and tracking. Local feature based sur-

face description generally consists of two steps: inter-

est point detection and feature description (Tombari

et al., 2013). Prominent points on a shape with re-

spect to a particularly deﬁned saliency or interest are

ﬁrst detected based on surface analysis. Then, the lo-

cal surface around each interest point is described us-

ing a 3D surface descriptor. Finally, the descriptors

around the interest points are properly assembled to

map the surface into a feature space.

Interest point detection is a fundamental step be-

cause it identiﬁes a collection of 3D structures for

further surface description (Guo et al., 2014a). A

number of 3D interest point detectors have been pro-

posed, and most of them are designed for rigid sur-

faces (Pratikakis et al., 2010)(Mian et al., 2010)(Godil

and Wagan, 2011) (see (Guo et al., 2014a) for a re-

cent survey). In recent years, several studies (Sun

et al., 2009)(Zaharescu et al., 2012) have been pro-

posed for non-rigid shape analysis. In particular, dif-

fusion geometry achieves a superior performance be-

cause of its ability to reﬂect the intrinsic property

of a shape (Bronstein et al., 2011). The heat ker-

nel signature function, also known as the auto dif-

fusion function, was proposed as a local surface de-

scriptor (Sun et al., 2009) or a deﬁnition of the scalar

ﬁeld (Gbal et al., 2009). This function has been suc-

Wang X., Sohel F., Bennamoun M., Guo Y. and Lei H.

Persistence-based Interest Point Detection for 3D Deformable Surface.

DOI: 10.5220/0006093800580069

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 58-69

ISBN: 978-989-758-224-0

cessfully applied for surface matching (Sipiran and

Bustos, 2013)(Ganapathi-Subramanian et al., 2016),

shape retrieval (Bronstein et al., 2011) and shape seg-

mentation (Skraba et al., 2010). Our method takes

advantage of the heat kernel signature function for its

intrinsic property to describe a surface.

Distinctiveness and repeatability are considered as

two major characteristics of a 3D detector (Tombari

et al., 2013)(Dutagaci et al., 2012). Repeatability

measures the capability of an interest point detector

to ﬁnd the same set of interest points under various

nuisances, such as sensor noise, missing parts and

transformations. Distinctiveness measures the abil-

ity to detect the most salient and representative points

on the shape for feature description. Since distinc-

tiveness is a rather global property of a shape, it is

quite challenging to effectively achieve this property

by current 3D interest point detectors, because they

are based on the analysis of local surfaces (Tombari

et al., 2013).

Inspired by the recent advances in persistent ho-

mology for the characterization of function behavior

(Li et al., 2014)(Carri

ere et al., 2015), we propose a

framework to combine persistent homology with the

heat kernel signature function for interest point detec-

tion. First, the scalar ﬁeld is constructed using the

heat kernel signature function at a moderately small

time scale. The heat kernel signature function (Sun

et al., 2009) is originated from diffusion geometry,

and the signature is robust to isometric transforma-

tions. When computed at a small time scale, it is di-

rectly related to surface curvature and has been shown

to be informative (Bronstein et al., 2011). Second,

a 0-dimensional persistence diagram is computed to

capture the global structural information of a surface.

The saliency of a point is considered as its promi-

nence from the view of topological persistence. Due

to the intrinsically global property of the persistent

homology to describe the surface variations, our pro-

posed interest point detector is highly distinctive.

The main contribution of this paper is two-fold.

First, a new interest point detector is proposed for

non-rigid 3D surface analysis. Second, persistence

homology is used for interest point detection to

achieve high repeatability and strong distinctiveness.

The remainder of this paper is organized as fol-

lows. Section 2 discusses the related work and em-

phasizes on our contribution to achieve repeatable and

distinctive interest point detection on non-rigid sur-

faces. Section 3 introduces our proposed persistence-

based interest point detector. Section 4 presents a

comprehensive performance evaluation of our pro-

posed method and comparisons with the state-of-the-

art. Section 5 concludes the paper.

2 RELATED WORK

Over the past decades, a large number of 3D interest

point detection methods have been proposed for shape

analysis. Most existing interest point detectors for 3D

shapes concentrated on the stability under rigid sur-

face transformations (Tombari et al., 2013)(Guo et al.,

2014a).

In order to deal with shapes undergoing non-rigid

deformations, detectors that are invariant to isometric

transformations have also been proposed. The sim-

plest interest point detection method is fastest point

sampling in the geodesic metric space, which is quite

popular in this ﬁeld (Aubry et al., 2011)(Litman and

Bronstein, 2014)(Xie et al., 2016). However, this

method fails to detect qualiﬁed interest points, espe-

cially in terms of informativeness. This is because

that it gives no consideration to the richness of the dis-

criminative information of the detected interest points

(Guo et al., 2014a).

Several approaches have been proposed to extend

interest point detectors developed in the 2D images

to the 3D ﬁeld. Inspired by the SIFT method (Lowe,

2004), Difference-of-Gaussians (DOG) was used as a

saliency measure for interest point detection for 3D

shapes (Zaharescu et al., 2012)(Liu et al., 2016). The

scalar ﬁeld on a shape was deﬁned using a photomet-

ric or a geometric attribute and was convolved with

a set of Gaussian kernels. Then, DOG calculations

were performed on the convolution results and Mesh-

DOG interest points were selected as the maximum

points in the DOG scale space. This method is able

to detect a sufﬁcient number of repeatable interest

points. However, it is sensitive to varying mesh reso-

lutions (Guo et al., 2014a). The popular Harris de-

tector for 2D image analysis (Harris and Stephens,

1988) was extended to 3D meshes in (Sipiran and

Bustos, 2011). The ‘Harris 3D’ detector ﬁrst derives a

quadratic surface from the neighborhood of one point.

Derivatives were calculated by smoothing over the

surface, and these derivatives were used to calculate

the Harris response. A ﬁxed fraction of points with

the largest response were selected as interest points.

This method is shown to be robust to several transfor-

mations. However, it uses a ﬁxed-scale of the neigh-

borhood, and does not fully exploit the scale informa-

tion encoded in the local geometric structures (Guo

et al., 2014a).

The diffusion geometry has been applied for in-

terest point detection and achieved a good perfor-

mance. It is invariant to isometric transformations and

remains stable under surface pertubations. In (Sun

et al., 2009), the heat kernel function was restricted

to the temporal domain and used the local maximum

Persistence-based Interest Point Detection for 3D Deformable Surface

(a) Input shape

(b) Scalar field

definition

computation

(d) detected keypoints

Figure 1: An illustration of the proposed persistence-based interest point detector. (a) An input 3D model of Armadillo. (b)

The scalar ﬁeld generated for the shape using the auto diffusion function with a particular time scale. (c) The 0-dimensional

persistence diagram of the predeﬁned real-valued function. (d) Interest points extracted using our proposed interest point

detector.

of the function to ﬁnd interest points. The local max-

imum is obtained by comparing each point with its

2-ring neighborhoods. This method is able to detect

highly distinctive interest points, but it depends on the

mesh resolution (Guo et al., 2014a). Our method ex-

ploits the heat kernel signature function by combining

it with the concept of persistent homology, which is

more robust than the method proposed in (Sun et al.,

2009).

All these interest point detectors are proposed

based on the analysis of the local surface, and they

tend to detect points with local maximums using a

saliency measure. As a result, they are not highly dis-

tinctive (Tombari et al., 2013). Our work is motivated

by the recent advances in topological data analysis,

i.e., the theory of persistent homology (Edelsbrunner

and Harer, 2010)(Chazal et al., 2013). Persistence

homology summarizes the structure of a topological

space in a compact and provably stable way using a

persistence diagram (Carri

ere et al., 2015). This ap-

proach has been proved to be stable (Chazal et al.,

2009) and has been successfully applied to cluster-

ing (Chazal et al., 2013), shape segmentation (Skraba

et al., 2010), shape matching and retrieval (Carri

ere

et al., 2015)(Garro and Giachetti, 2016).

3 PROPOSED METHOD

Assume M is a compact 2D manifold embedded in

without boundary and mesh M is a discrete repre-

sentation of M . M consists of n

vertices, n

edges

and n

convex polygons (i.e. facets). M can be

viewed as a connectivity graph G= (V ,E), where the

set of vertices V = {v

,...,v

} represents sam-

ples on the manifold, E = {(v

)} represents the re-

lationship between adjacent vertices. Each vertex v

is associated with a 3D point in the Euclidean space,

i.e., v

∈ R

. M may undergo a non-rigid transforma-

tion. Our goal is to develop an interest point detector

which identiﬁes 3D interest points from M with a high

repeatability, strong distinctiveness and a good invari-

ance to isometric deformations.

An illustration of the proposed 3D interest point

detection method is shown in Fig. 1. Our inter-

est point detection method follows a typical pipeline

(see (Zaharescu et al., 2012) for example) and com-

prises two steps: scalar ﬁeld construction and inter-

est point detection. For an input shape, the ﬁrst and

important step is the scalar function deﬁnition, since

its accuracy directly affects the subsequent processing

steps. Since our method is designed for deformable

surface analysis, this deﬁnition should be stable un-

der isometric deformations. We use the heat kernel

signature function (Gbal et al., 2009) with a moder-

ately small time scale for its remarkable resistence to

extrinsic and intrinsic shape variations. Figs. 1(a) and

(b) represent the original shape and the corresponding

scalar ﬁeld, respectively. Then the 0-dimensional per-

sistence diagram of this real-valued function is com-

puted, where the prominence of the salient points is

encoded, as shown in Fig. 1(c). Finally, interest

points are selected as points with a local maximum

value and a high persistence (as shown in Fig. 1(d)).

3.1 Scalar Field Construction

3.1.1 Heat Diffusion Process

Imagine that there is an initial heat distribution over

M , and then heat starts to propagate. This heat diffu-

sion process over M is governed by the heat equation:

∂

∂t

)u(x,t) = 0, (1)

where the solution u(x,t) represents the amount of

heat at a point x ∈ M at time t, and 4

denotes

the positive semi-deﬁnite Laplace-Beltrami operator

on M , a Riemannian equivalent of the Laplacian.

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

Given an initial heat distribution f : M → R, the

heat operator applied to f describes the distribution

of the heat over M at time t. That is, H

f = u(·,t)

with u(·,0) = f , where H

represents the heat opera-

tor.

For a square integrable function f , there always

exists a function h

(x,y) : R

×M × M → R satisfying

f (x) =

(x,y) f (y)dy, (2)

where dy is the differential form of y ∈ M . The min-

imum function h

(x,y) satisfying Eq. 2 is called the

heat kernel. It measures the amount of heat that gets

transferred from x to y at time t with a unit heat source

initially located at x.

Since the heat operator is compact, self-adjoint

and positive semi-deﬁnite (Dey et al., 2010), it has

a discrete spectrum 1 = λ

≥ λ

≥ ... ≥ 0 with H

. According to the Spectral Theorem, the heat ker-

nel has the following eigen-decomposition:

(x,y) =

∞

∑

i≥1

−λ

(x)Φ

(y), (3)

where λ

and Φ

are the ith eigenvalue and eigenfunc-

tion of the heat kernel, respectively.

The heat diffusion kernel function has a number

of properties making it suitable for surface descrip-

tion as a point signature (Sun et al., 2009). First, it

is isometrically invariant due to the invariance of the

Laplace-Beltrami operator. It can therefore be used

to analyze shapes under non-rigid deformations. Sec-

ond, it is informative as it captures all the intrinsic

geometric information of a shape. Consequently it

is able to fully characterize shapes up to isometry.

Third, it captures the geometric information around

an interest point with multiple scales. Since heat dif-

fuses progressively to larger neighborhoods, the time

parameter provides an intuitive notion of scale to de-

scribe the local surface. Speciﬁcally, the heat kernel

(x,·) with a small t encodes the local properties of

the surface around x. As heat dissipates from the in-

terest point to the rest of the shape, the scale of the

neighborhood is increased.

3.1.2 Heat Kernel Signature

To make the heat kernel concise and measurable, the

heat kernel function was restricted to the temporal do-

main only, that is:

HKS(x,t) =

∞

∑

i≥1

−λ

(x), (4)

which is known as the heat kernel signature (Sun

et al., 2009). This signature has also been proved to

inherit many useful properties from the heat kernel.

Particularly, there is an asymptotic expansion of the

heat kernel signature function as t approaches 0, that

is:

HKS(x,t) = (4πt)

−d/2

∞

∑

i=0

, (5)

where a

= 1 and a

s(x) with s(x) being the

scalar curvature at point x. For a 2D manifold, s(x) is

referred to as the Gaussian curvature at point x. This

formula corresponds to the well-known property of

the heat diffusion process, that is, heat tends to dif-

fuse faster at points with low curvature, and slower

at points with high curvature. Moreover, the heat dif-

fusion process at an early stage is dominated by the

intrinsic curvature of the manifold. Besides, the heat

kernel signature parameterized by a small t provides

a meaningful notion of curvature for the local surface

around x.

3.1.3 Scalar Field Construction

We use the heat kernel signature with a small time

scale to construct the scalar ﬁeld. Examples are

shown in the top row of Fig. 3. Note that, areas with

high and low Gaussian curvatures correspond to large

and small values of HKS(x,t), respectively. In addi-

tion, the scalar ﬁeld remains stable on the two horses

with non-rigid transformations.

Note that this scalar ﬁeld construction approach is

also suitable for incomplete and partial shapes (Dey

et al., 2010)(Ovsjanikov et al., 2010), since the heat

kernel signature with small time scales represents the

properties of a local surface. To further enhance its

stability, edge points and outliers with extremely high

values compared to its neighborhood are removed.

3.1.4 Computation

In practice, the underlying manifold is unknown as

a sample of the shape, and it is usually given in the

form of a triangular mesh. In order to obtain the heat

kernel signature, the Finite Elements Method (Reuter

et al., 2006) is used to compute the eigenvalues and

eigenvectors of the Laplace-Beltrami operator associ-

ated with the shape.

3.2 Interest Point Detection

3.2.1 Persistence Diagram

Let f be a real-valued function deﬁned on the nodes

of G, f : V → R. A node v ∈ V is called a peak

if its function value is a local maximum in its local

neighborhood, i.e., for all u with (u,v) ∈ E, f (v) ≥

Persistence-based Interest Point Detection for 3D Deformable Surface

s’

p’

q’

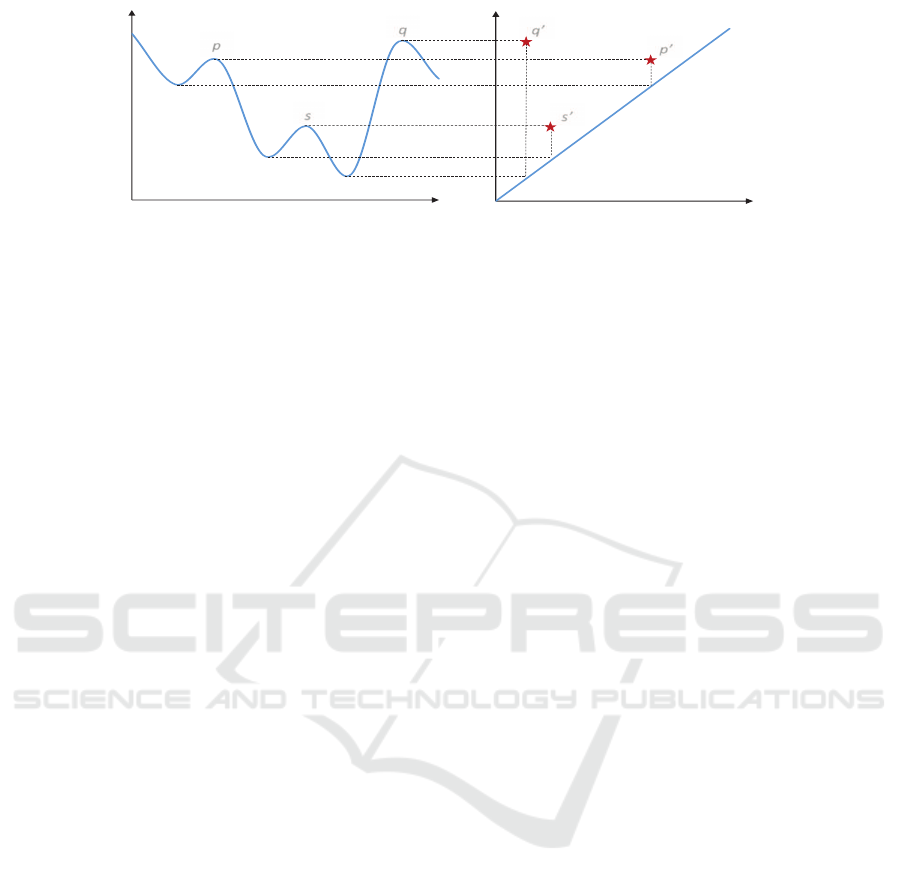
Figure 2: An illustration of the 0-dimensional persistence diagram computation. Left: a smooth function with three local

maximums. Right: 0-dimensional persistence diagram of the function.

f (u). The 0-dimensional persistence diagram en-

codes the topological changes of the sub-level sets

= f

−1

([α,+∞)) as α decreases from +∞ to −∞.

Let C(v,α) be a connected subgraph, C (v,α) ∈ F

∈

G, where α ≤ f (v) and f (v) is the largest value. The

subgraph is claimed to be born at v, or v represents

the component. The inﬁmum of α with which f (v)

remains to be the global maximum in the component

is called the death of C (v,α). As α continues to de-

crease, the subgraph C (v, α) is merged into another

component.

The lifespan of a component is thus determined

by its birth f (v) and death values f (u) ≤ f (v). This

allows us to project each component onto a point

( f (u), f (v)) on a 2D plane. Persistence or promi-

nence of the component is deﬁned as its lifespan, P =

f (v) − f (u) ≥ 0. The 0-dimensional persistence dia-

gram of f is computed by collecting all these points

together. In the diagram, all points live in the half

space above x

= x

, and their persistence can easily

be calculated as the vertical distance from the point

( f (u), f (v)) to this diagonal line (Edelsbrunner and

Harer, 2010). Figure 2 shows an illustration of the 0-

dimensional persistence diagram computation. It can

be seen that the topological information of a smooth

function can be captured by the 0-dimensional persis-

tence diagram.

3.2.2 Interest Point Detection

Similar to existing 3D feature detectors, interest

points are selected by considering local extrema of a

saliency measure. The saliency measure determines

the type of local surface to be selected by the detector,

and it is signiﬁcantly important to the distinctiveness

and repeatability of the detector. We consider that the

saliency of a point is not only determined by its abso-

lute saliency measure, but also by its relative signif-

icance as compared to its neighboring points. From

the view of topological data analysis, interest points

are determined as those points with local maxima and

in particular, high persistence.

Since each component is represented by a peak,

the 0-dimensional persistence diagram can be ex-

plained in another way (Li et al., 2014). That is, the

persistence diagram encodes the relative prominence

of different peaks of a given function by considering

the connectivity information in the domain, as shown

in Fig. 2. Based on the predeﬁned scalar function

(i.e., heat kernel signature with a small time scale),

the persistence diagram is able to select several peaks

with a high persistence, all of them are distinctive

points on a shape (as shown in Fig. 1(d)).

In addition, the persistence diagram has several

important properties and it is therefore highly suitable

for interest point detection. First, it is stable under

perturbations of the scalar function (Carri

ere et al.,

2015)(Chazal et al., 2009). Consequently, the persis-

tence diagram is highly robust to noise. Besides, it

is invariant to translation, rotation, scaling and non-

rigid transformations (as shown in Fig. 3), as long as

the scalar functions are consistent across shapes.

3.2.3 Computation

In practice, the 0-dimensional persistence diagram

can be computed using the Union-Find algorithm

(Cormen, 2009). It ranks the nodes of the graph with

respect to their scalar function values, and keeps track

of the evolution of the corresponding connected com-

ponents. In this paper, DIPHA (Bauer et al., 2014) is

used to compute the persistence diagram.

4 EXPERIMENTS

A comprehensive evaluation is performed to test our

interest point detector under two different scenarios.

Section 4.1 shows its performance evaluation on the

PHOTOMESH dataset (Zaharescu et al., 2012) in

terms of repeatability. In section 4.2, the performance

of our proposed interest point detector is compared

with several state-of-the-art methods on the Interest

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

Figure 3: An illustration of the scalar ﬁelds on three shape modes from the TOSCA dataset (two horses with non-rigid

transformations and a cat), and their corresponding 0-dimensional persistence diagram. Top: Heat kernel signature with a

small and ﬁxed time scale computed on these models. Note that values of the heat kernel signature function increase while

the color on the shape changes from blue to green and then to red. Bottom: The corresponding persistence diagram computed

from the real-valued function.

Points dataset (Dutagaci et al., 2012) in terms of dis-

tinctiveness, i.e., to measure how much the extracted

points are compatible with human perception.

4.1 Performance on The PHOTOMESH

Dataset

4.1.1 Dataset

The PHOTOMESH dataset consists of three base

shapes, so called null shapes. The simulated trans-

formations applied to these null shapes can be clas-

siﬁed into two categories: photometric transforma-

tions (Scalar-noise and Scalar-shot noise) and geo-

metric transformations (noise, shot noise, rotation,

scale, local scale, sampling, holes, micro-holes, topol-

ogy and isometry). Five levels of strength are applied

to each transformation. Totally, 65 shapes are pro-

duced for each null shape, and there are 135 shapes in

the dataset. Since our method is designed to encode

the geometric information, the shapes with photomet-

ric transformations were not considered in this exper-

iment. Examples of all possible transformations are

shown in Fig. 4.

4.1.2 Evaluation Methodology

Experiments were conducted on this dataset to test

the repeatability of each feature detector. The per-

formance was quantitatively measured by compar-

ing the interest points detected on each transformed

shape M

and its corresponding null shape M

. For

a point v on a shape M, its local neighborhood within

geodesic radius r is deﬁned as

(v) = {p ∈ M|gd(v, p) ≤ r}, (6)

where gd(v, p) represents the geodesic distance be-

tween v and p.

Suppose the ground-truth one-to-one correspon-

dence (M

= GT (M

)) is known as a prior, a point

v extracted from a transformed model M

is con-

sidered to be correctly detected if its corresponding

point GT (v) is located within the geodesic ball de-

ﬁned by N

), where v

is an interest point detected

on M

. Repeatability is calculated as the percentage

of correctly detected interest points. In this experi-

ment, we used the same setting as (Zaharescu et al.,

2012), where r was set to be 1% of the surface area.

We used the ﬁrst 100 eigenvalues and eigenvectors of

the Laplace-Beltrami operator on each shape to com-

pute the heat kernel signature, and the time parame-

ter was set to 0.1. Five interest points with the high-

est prominence on two hands, feet and head were de-

tected, which were considered as representatives of

the human shape by our method. For a fair compari-

son, the results achieved by the MeshDOG approach

(Zaharescu et al., 2012) are also reported since this

method achieves a good performance in terms of re-

peatability on the PHOTOMESH dataset. The Mesh-

DOG interest point detector was implemented with

three different scalar ﬁelds deﬁned over the mani-

folds, including color intensity, mean curvature and

Gaussian curvature.

Persistence-based Interest Point Detection for 3D Deformable Surface

(a) (b) (c) (d) (e) (f)

(g) (h) (i) (j) (k) (l)

Figure 4: Examples of all possible transformations of a null shape on the PHOTOMESH dataset. (a) Scalar-noise (b) Scalar-

shot noise (c) Noise (d) Shot noise (e) Holes (f) Micro-holes (g) Isometry (h) Local scale (i) Rotation (j) Sampling (k) Scale

(l) Topology.

4.1.3 Results and Discussion

Comparative results on the repeatability of theses de-

tectors are presented in Tables 1-4.

In the cases of noise, shot noise and sampling, the

performance of MeshDOG is decreased as the level

of transformation increases, especially for the Mesh-

DOG detectors generated with geometric scalar ﬁelds

(i.e., mean curvature and Gaussian curvature). In con-

trast, our method achieves better results. The repeata-

bility achieved by our pHKS method remains to be

1 under all levels of noise, shot noise and sampling

transformations. This is because the scalar ﬁeld used

in our method is more stable than the scalar ﬁeld used

in MeshDOG.

For the transformations of rotation, scale, local

scale and isometry, both MeshDOG and pHKS in-

terest point detectors can successfully ﬁnd the same

set of interest points. Those results clearly show that

MeshDOG and pHKS methods are invariant to rigid

and non-rigid transformations.

Both holes and micro holes transformations de-

crease the performance of MeshDOG linearly. In con-

trast, our method produces good results since the con-

structed scalar ﬁeld is able to handle partial and in-

complete shapes. In some cases, our approach cannot

produce a full repeatability of 1.00 because several in-

terest points are missing due to the presence of holes.

Table 1: Repeatability of MeshDOG (photometric).

Strength

Transform. 1 < 2 < 3 < 4 < 5

Noise 1.00 1.00 1.00 0.99 0.99

Shot Noise 1.00 0.99 0.99 0.99 0.98

Rotation 1.00 1.00 1.00 1.00 1.00

Scale 1.00 1.00 1.00 1.00 1.00

Local Scale 1.00 1.00 0.99 0.99 0.99

Sampling 0.96 0.96 0.95 0.90 0.94

Holes 1.00 1.00 0.99 0.99 0.97

Micro-Holes 1.00 1.00 0.99 0.99 0.99

Topology 0.93 0.86 0.82 0.82 0.78

Isometry 0.95 0.97 0.97 0.93 0.96

Table 2: Repeatability of MeshDOG (mean curvature).

Strength

Transform. 1 < 2 < 3 < 4 < 5

Noise 0.96 0.93 0.91 0.90 0.89

Shot Noise 0.99 0.98 0.96 0.95 0.94

Rotation 1.00 1.00 1.00 1.00 1.00

Scale 1.00 1.00 1.00 1.00 1.00

Local Scale 0.99 0.98 0.97 0.96 0.96

Sampling 0.92 0.89 0.91 0.88 0.92

Holes 0.99 0.99 0.99 0.98 0.98

Micro-Holes 1.00 1.00 0.99 0.99 0.98

Topology 0.90 0.83 0.75 0.62 0.76

Isometry 0.95 0.96 0.94 0.94 0.93

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

(a) (b) (c) (d) (e) (f) (g)

Figure 5: An illustration of interest points detected by different algorithms on Armadillo from Interest Points Dataset B (a)

ground-truth points (b) Mesh saliency (c) Salient points (d) 3D-Harris (e) SD-corners (f) HKS (g) pHKS.

Table 3: Repeatability of MeshDOG (Gaussian curvature).

Strength

Transform. 1 < 2 < 3 < 4 < 5

Noise 0.97 0.93 0.87 0.83 0.79

Shot Noise 0.99 0.98 0.97 0.96 0.92

Rotation 1.00 1.00 1.00 1.00 1.00

Scale 1.00 1.00 1.00 1.00 1.00

Local Scale 0.98 0.98 0.97 0.96 0.95

Sampling 0.88 0.88 0.91 0.94 0.92

Holes 0.99 0.99 0.99 0.97 0.97

Micro-Holes 1.00 0.99 0.99 0.98 0.97

Topology 0.85 0.70 0.65 0.58 0.64

Isometry 0.95 0.96 0.95 0.92 0.93

Table 4: Repeatability of the proposed method (pHKS).

Strength

Transform. 1 < 2 < 3 < 4 < 5

Noise 1.00 1.00 1.00 1.00 1.00

Shot Noise 1.00 1.00 1.00 1.00 1.00

Rotation 1.00 1.00 1.00 1.00 1.00

Scale 1.00 1.00 1.00 1.00 1.00

Local Scale 1.00 1.00 1.00 1.00 1.00

Sampling 1.00 1.00 1.00 1.00 1.00

Holes 0.80 1.00 1.00 0.60 1.00

Micro-Holes 1.00 1.00 1.00 1.00 1.00

Topology 1.00 1.00 0.60 1.00 1.00

Isometry 1.00 1.00 1.00 1.00 1.00

In the presence of topological transformations, the

performance of MeshDOG is signiﬁcantly decreased.

For example, the repeatability achieved by MeshDOG

with a Gaussian curvature is 0.85 under the ﬁrst level

of topological transformation. Its repeatability is then

decreased to 0.64 under the ﬁfth level of topological

transformation. In contrast, our approach achieves a

very high repeatability, as shown in Table 4. This

is mainly due to the deﬁnition of saliency of inter-

est point, which is not only a local maximum but also

has a large persistence, i.e., a strong contrast as com-

pared to its neighborhood in a connected topological

space. Therefore, although the whole shape is trans-

formed into several structures, the peaks remain the

same under our scalar ﬁeld construction. The interest

points are successfully selected as long as their per-

sistences are not greatly changed. In some cases (e.g.,

with the third level of topological transformation), the

result is not satisfactory because the persistences of

some peaks are destroyed by the topological transfor-

mations.

4.2 Performance on the Interest Points

Dataset

4.2.1 Dataset

This dataset consists of two sub-datasets (dataset A

and B) (Dutagaci et al., 2012). It is reported that

the performance of existing algorithms is consistent

across the two datasets (Dutagaci et al., 2012), so only

dataset B is used in this paper as it is much larger. In

dataset B, there are 43 models manually marked by

16 humans. Ground-truth points are constructed from

the human-marked points based on two criteria: ra-

dius of an interest region σ and the number of users n

who marked a point within the radius. In addition to

the location, the prominence of a ground-truth point is

included as the number of humans who have marked

it within its local neighborhood. An example of in-

terest points detected on a model from dataset B are

shown in Fig. 5.

4.2.2 Evaluation Methodology

On this dataset, evaluation was performed to test the

compatibility of each algorithm with human percep-

tion. This experiment is designed to test an inter-

est point detector in terms of distinctiveness, which

demonstrates the ability of an interest point to de-

tect representative and characteristic points on a sur-

face. Our evaluation was performed on each single

instance of the model using human generated ground-

truth. Three measures are used as in (Dutagaci et al.,

2012), i.e., false positive errors (FPE), false negative

errors (FNE) and weighted miss error (WME). Let

(n,σ) be the set of ground-truth points on a model

M and D

be the set of interest points detected by an

Persistence-based Interest Point Detection for 3D Deformable Surface

(a) σ = 0.03 and n = 2

(b) σ = 0.03 and n = 8

(d) σ = 0.05 and n = 8

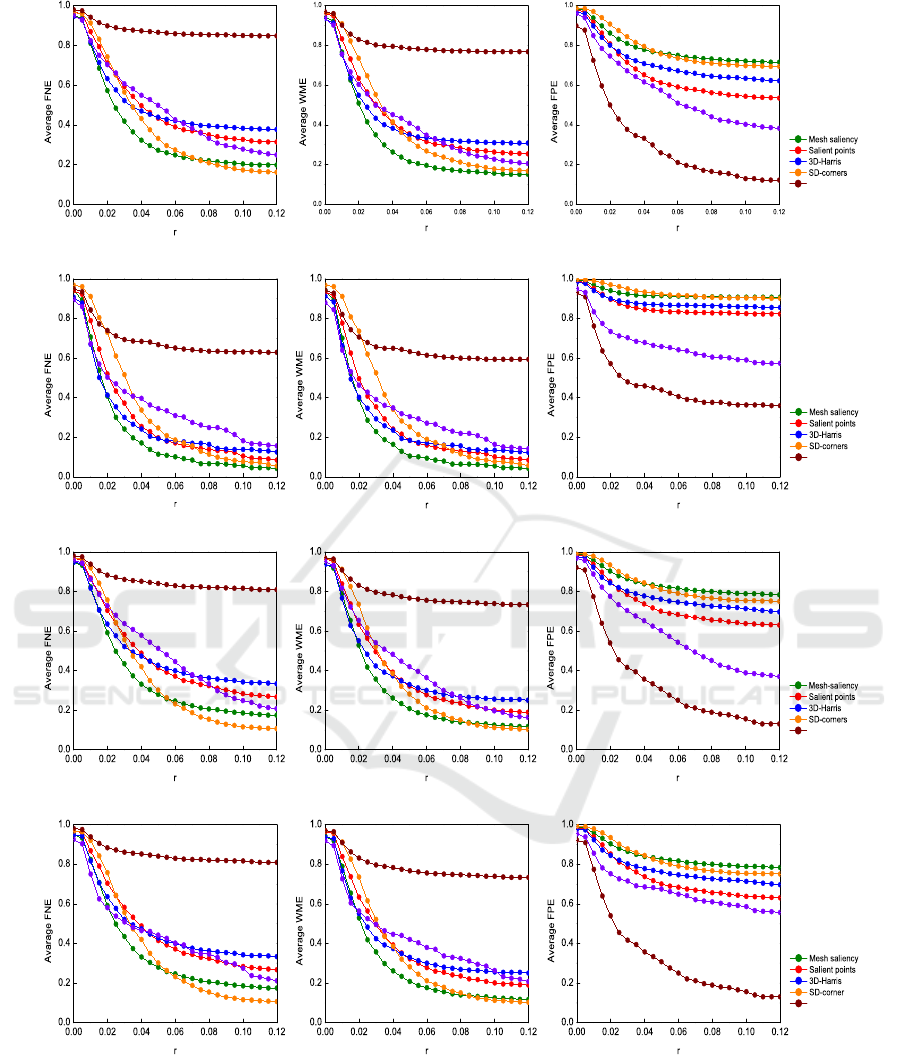
Figure 6: Performance on Dataset B (43 Models, 16 Subjects) of the Interest Points Dataset. False negative error (ﬁrst

column), weighted miss error (second column), and false positive error (third column) are shown in the ﬁgure. The settings

for ground-truth generation are given under the plots, where r stands for the localization error tolerance.

algorithm. A point v is considered to be ‘correctly de-

tected’ if there is a detected point within the geodesic

ball N

(v), where the parameter r is the localization

error tolerance. Given the number of ground-truth

points N

, the points detected by an algorithm N

and the correctly detected points N

, FNE, FPE and

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

W ME are deﬁned as follows:

FNE(r) = 1 −

, (7)

FPE(r) =

− N

, (8)

W ME(r) = 1 −

∑

i=1

∑

i=1

δ, (9)

where δ

is set to 1 if the ground-truth point is de-

tected. Otherwise, it is set to 0. n

is deﬁned as the

prominence of an interest point v

, which is equal to

the number of humans voting for that point.

In this experiment, we used the ﬁrst 100 eigenval-

ues and corresponding eigenvectors of the Laplace-

Beltrami operator to compute heat kernel signature

and its time parameter was set to 0.001. For compar-

ison, we present the results achieved by ﬁve state-of-

the-art methods including mesh saliency (Lee et al.,

2005), salient points (Godil and Wagan, 2011), 3D-

Harris (Pratikakis et al., 2010), SD-corners (Novat-

nack and Nishino, 2007) and HKS (Sun et al., 2009).

4.2.3 Results and Discussion

The comparative results are presented in Fig. 6. It can

be seen from the results that mesh saliency, salient

points, 3D-Harris, SD-corners and HKS are able to

achieve low FNE and WME measures at the cost of

a high FPE. Particularly, when σ = 0.03 and n = 8,

these methods can ﬁnd almost 80% of the ground-

truth points. However, 90% of their detected points

are false. In contrast, the average FNE and WME

measures achieved by HKS are extremely high, which

means that a large percentage of the ground-truth in-

terest points are not detected by the HKS method. On

the other hand, HKS performs the best on FPE. For

example, when σ = 0.05 and n = 2, the FNE and

WME scores of HKS are about 0.8, and the average

FPE is as low as 0.2. This is because HKS tends to

select the extremities of the models, which are often

of great interest to humans.

Our approach produces an overall good perfor-

mance as a trade-off is achieved between FNE, FPE

and WME. As the localization error tolerance r in-

creases, our proposed pHKS can detect about 80%

of the whole ground-truth points with far less false

positives as compared to the other methods. This

means that the set of points detected by pHKS is more

concise and effective. This result corresponds to the

fact that humans usually mark interest points corre-

sponding to extremities of 3D shapes (Dutagaci et al.,

2012). Although the points detected by HKS usually

have high prominence, the number of detected inter-

est points is too limited. That is because HKS selects

points with large values and as local maxima, and the

scale of points has to be predeﬁned (Sun et al., 2009).

Our pHKS method is able to detect more points, be-

cause we select interest points with a strong contrast

to their neighborhood and the scale of the neighbor-

hood is adaptively determined using topological data

analysis.

5 CONCLUSION

In this paper, we present a method for interest point

detection on 3D non-rigid shapes using topological

persistence. Our approach simultaneously captures

the local geometric and global structural information

of the surface. It extracts interest points with a high

repeatability and a strong distinctiveness. Our exper-

iments on two public datasets have clearly demon-

strated the effectiveness of our approach. In the fu-

ture, we will combine our interest point detector with

a local surface descriptor and test it on applications

such as surface registration, shape tracking and shape

retrieval of non-rigid objects.

ACKNOWLEDGEMENTS

This research is supported by a China Scholarship

Council (CSC) scholarship (No. 201406070059),

Australian Research Council grants (DE120102960,

DP150100294 and DP150104251), the National Nat-

ural Science Foundation of China (Nos. 61602499

and 61471371) and the Innovative Postdoctoral Tal-

ent Program of China (No. 182707).

REFERENCES

Aubry, M., Schlickewei, U., and Cremers, D. (2011). The

wave kernel signature: A quantum mechanical ap-

proach to shape analysis. In Computer Vision Work-

shops (ICCV Workshops), 2011 IEEE International

Conference on, pages 1626–1633. IEEE.

Bauer, U., Kerber, M., and Reininghaus, J. (2014). Dis-

tributed computation of persistent homology. In Pro-

ceedings of the Meeting on Algorithm Engineering

& Expermiments, pages 31–38. Society for Industrial

and Applied Mathematics.

Biasotti, S., Cerri, A., Bronstein, A., and Bronstein, M.

(2015). Recent trends, applications, and perspec-

tives in 3d shape similarity assessment. In Computer

Graphics Forum. Wiley Online Library.

Bronstein, A. M., Bronstein, M. M., Guibas, L. J., and Ovs-

janikov, M. (2011). Shape google: Geometric words

Persistence-based Interest Point Detection for 3D Deformable Surface

and expressions for invariant shape retrieval. ACM

Transactions on Graphics (TOG), 30(1):1.

Carri

ere, M., Oudot, S. Y., and Ovsjanikov, M. (2015). Sta-

ble topological signatures for points on 3d shapes. In

Computer Graphics Forum, volume 34, pages 1–12.

Wiley Online Library.

Chazal, F., Cohen-Steiner, D., Glisse, M., Guibas, L. J., and

Oudot, S. Y. (2009). Proximity of persistence modules

and their diagrams. In Proceedings of the twenty-ﬁfth

annual symposium on Computational geometry, pages

237–246. ACM.

Chazal, F., Guibas, L. J., Oudot, S. Y., and Skraba, P.

(2013). Persistence-based clustering in riemannian

manifolds. Journal of the ACM (JACM), 60(6):41.

Cormen, T. H. (2009). Introduction to algorithms. MIT

press.

Dey, T. K., Li, K., Luo, C., Ranjan, P., Safa, I., and Wang,

Y. (2010). Persistent heat signature for pose-oblivious

matching of incomplete models. In Computer Graph-

ics Forum, volume 29, pages 1545–1554. Wiley On-

line Library.

Dutagaci, H., Cheung, C. P., and Godil, A. (2012). Eval-

uation of 3d interest point detection techniques via

human-generated ground truth. The Visual Computer,

28(9):901–917.

Edelsbrunner, H. and Harer, J. (2010). Computational

topology: an introduction. American Mathematical

Soc.

Ganapathi-Subramanian, V., Thibert, B., Ovsjanikov, M.,

and Guibas, L. (2016). Stable region correspondences

between non-isometric shapes.

Garro, V. and Giachetti, A. (2016). Scale space graph rep-

resentation and kernel matching for non rigid and tex-

tured 3d shape retrieval. IEEE transactions on pattern

analysis and machine intelligence, 38(6):1258–1271.

Gbal, K., Bærentzen, J. A., Aanæs, H., and Larsen, R.

(2009). Shape analysis using the auto diffusion func-

tion. In Computer Graphics Forum, volume 28, pages

1405–1413. Wiley Online Library.

Godil, A. and Wagan, A. I. (2011). Salient local 3d features

for 3d shape retrieval. In IS&T/SPIE Electronic Imag-

ing, pages 78640S–78640S. International Society for

Optics and Photonics.

Guo, Y., Bennamoun, M., Sohel, F., Lu, M., and Wan, J.

(2014a). 3d object recognition in cluttered scenes

with local surface features: a survey. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

36(11):2270–2287.

Guo, Y., Bennamoun, M., Sohel, F., Lu, M., Wan, J., and

Kwok, N. M. (2016). A comprehensive performance

evaluation of 3d local feature descriptors. Interna-

tional Journal of Computer Vision, 116(1):66–89.

Guo, Y., Bennamoun, M., Sohel, F. A., Wan, J., and Lu,

M. (2013a). 3d free form object recognition using ro-

tational projection statistics. In Applications of Com-

puter Vision (WACV), 2013 IEEE Workshop on, pages

1–8. IEEE.

Guo, Y., Sohel, F., Bennamoun, M., Lu, M., and Wan, J.

(2013b). Rotational projection statistics for 3d local

surface description and object recognition. Int J Com-

put Vision, 105(1):63–86.

Guo, Y., Sohel, F., Bennamoun, M., Wan, J., and Lu, M.

(2014b). An accurate and robust range image registra-

tion algorithm for 3d object modeling. IEEE Transac-

tions on Multimedia, 16(5):1377–1390.

Guo, Y., Sohel, F. A., Bennamoun, M., Lu, M., and Wan,

J. (2013c). Trisi: A distinctive local surface de-

scriptor for 3d modeling and object recognition. In

GRAPP/IVAPP, pages 86–93.

Guo, Y., Sohel, F. A., Bennamoun, M., Wan, J., and Lu,

M. (2013d). Rops: A local feature descriptor for 3d

rigid objects based on rotational projection statistics.

In Communications, Signal Processing, and their Ap-

plications (ICCSPA), 2013 1st International Confer-

ence on, pages 1–6. IEEE.

Harris, C. and Stephens, M. (1988). A combined corner and

edge detector. In Alvey vision conference, volume 15,

page 50. Citeseer.

Lee, C. H., Varshney, A., and Jacobs, D. W. (2005). Mesh

saliency. In ACM transactions on graphics (TOG),

volume 24, pages 659–666. ACM.

Li, C., Ovsjanikov, M., and Chazal, F. (2014). Persistence-

based structural recognition. In The IEEE Conference

on Computer Vision and Pattern Recognition (CVPR).

Litman, R. and Bronstein, A. M. (2014). Learning spec-

tral descriptors for deformable shape correspondence.

IEEE transactions on pattern analysis and machine

intelligence, 36(1):171–180.

Liu, X., Liu, L., Song, W., Liu, Y., and Ma, L. (2016). Shape

context based mesh saliency detection and its applica-

tions: A survey. Computers & Graphics, 57:12–30.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. International journal of computer

vision, 60(2):91–110.

Mian, A., Bennamoun, M., and Owens, R. (2010). On the

repeatability and quality of keypoints for local feature-

based 3d object retrieval from cluttered scenes. In-

ternational Journal of Computer Vision, 89(2-3):348–

361.

Novatnack, J. and Nishino, K. (2007). Scale-dependent 3d

geometric features. In 2007 IEEE 11th International

Conference on Computer Vision, pages 1–8. IEEE.

Ovsjanikov, M., M

erigot, Q., M

emoli, F., and Guibas, L.

(2010). One point isometric matching with the heat

kernel. In Computer Graphics Forum, volume 29,

pages 1555–1564. Wiley Online Library.

Pratikakis, I., Spagnuolo, M., Theoharis, T., and Veltkamp,

R. (2010). A robust 3d interest points detector based

on harris operator. In Eurographics workshop on 3D

object retrieval, volume 5. Citeseer.

Reuter, M., Wolter, F.-E., and Peinecke, N. (2006).

Laplace–beltrami spectra as shape-dnaof surfaces and

solids. Computer-Aided Design, 38(4):342–366.

Sipiran, I. and Bustos, B. (2011). Harris 3d: a robust exten-

sion of the harris operator for interest point detection

on 3d meshes. The Visual Computer, 27(11):963–976.

Sipiran, I. and Bustos, B. (2013). A fully hierarchical

approach for ﬁnding correspondences in non-rigid

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

shapes. In Proceedings of the IEEE International

Conference on Computer Vision, pages 817–824.

Skraba, P., Ovsjanikov, M., Chazal, F., and Guibas,

L. (2010). Persistence-based segmentation of de-

formable shapes. In 2010 IEEE Computer So-

ciety Conference on Computer Vision and Pattern

Recognition-Workshops, pages 45–52. IEEE.

Sun, J., Ovsjanikov, M., and Guibas, L. (2009). A concise

and provably informative multi-scale signature based

on heat diffusion. In Computer graphics forum, vol-

ume 28, pages 1383–1392. Wiley Online Library.

Tombari, F., Salti, S., and Di Stefano, L. (2013). Perfor-

mance evaluation of 3d keypoint detectors. Interna-

tional Journal of Computer Vision, 102(1-3):198–220.

Wang, X., Sohel, F., Bennamoun, M., and Lei, H. (2015).

Binary descriptor based on heat diffusion for non-rigid

shape analysis. In Paciﬁc-Rim Symposium on Image

and Video Technology, pages 751–761. Springer.

Wang, X., Sohel, F., Bennamoun, M., and Lei, H. (2016).

Heat propagation contours for 3d non-rigid shape

analysis. In 2016 IEEE Winter Conference on Appli-

cations of Computer Vision (WACV), pages 1–7. IEEE.

Xie, J., Wang, M., and Fang, Y. (2016). Learned bi-

nary spectral shape descriptor for 3d shape corre-

spondence. In Proceedings of the IEEE Conference

on Computer Vision and Pattern Recognition, pages

3309–3317.

Zaharescu, A., Boyer, E., and Horaud, R. (2012). Key-

points and local descriptors of scalar functions on 2d

manifolds. International Journal of Computer Vision,

100(1):78–98.

Persistence-based Interest Point Detection for 3D Deformable Surface