
Confidence-Aware Probability Hypothesis Density Filter for Visual
Multi-Object Tracking
Nicolai Wojke and Dietrich Paulus
Active Vision Group, Institute for Computational Visualistics, University of Koblenz-Landau, 56070 Koblenz, Germany
Keywords:
Visual Tracking, Multi-Object State Estimation.
Abstract:
The Probability Hypothesis Density Filter (PHD) filter is an efficient recursive multi-object state estimator that
systematically deals with data association uncertainty. In this paper, we apply the PHD filter in a tracking-by-
detection framework. In order to mimic state-dependent false alarms, we introduce an adapted PHD recursion
that defines clutter generators in state space. Further, we integrate detector confidence scores into the measure-
ment likelihood. This extension is quite effective yet simple, which means that it requires few changes to the
original PHD recursion, that it has the same computational complexity, and that there exist few parameters that
must be adapted to the individual tracking scenario. Our evaluation on a popular pedestrian tracking dataset
demonstrates results that are competitive with the state-of-the-art.
1 INTRODUCTION
Visual multi-object tracking is a key challenge in
many computer vision applications. The problem is
well studied and numerous approaches have been pro-
posed. However, due to the combinatorial nature of
data association, the problem remains challenging.
Within the last decade, it has become increas-
ingly popular to formulate multi-object tracking as
tracking-by-detection, where plausible object trajec-
tories are found through global optimization. Zhang
et al. (2008) provide a prominent formulation using
a min-cost flow network. They create a graph on
the set of all measurements and find globally opti-
mal trajectories using a push-relabel algorithm. This
formulation has been adopted by others in order to
obtain better run-times: Pirsiavash et al. (2011) in-
troduce a greedy path search based on dynamic pro-
gramming, Berclaz et al. (2011) apply k-shortest path
search. Others have extended the model to incorpo-
rate more structural information. For example, De-
hghan et al. (2015) integrate identity-specific associ-
ation costs and propose a Lagrangian relaxation opti-
mization.
Conventional multi-object tracking systems usu-
ally contain three components: state estimation, data
association, and track handling. Therefore, these sys-
tems estimate the underlying object state, e.g., po-
sition and velocity, and perform association of mea-
surements to objects on a frame-by-frame basis. Re-
cently, a number of such conventional methods have
been revisited and shown competitive performance.
Notably, Kim et al. (2015) show that the classical
multiple hypothesis tracking algorithm (Reid, 1979)
can achieve state-of-the-art results when integrating
online-learned appearance information into the asso-
ciation likelihood and Rezatofighi et al. (2015) have
investigated an efficient solution to the joint proba-
bilistic data association that, combined with a heuris-
tic track handling scheme, achieves competitive re-
sults in dense tracking scenarios with substantial oc-
clusions, false alarms, and missed detections. Relat-
edly, Segal and Reid (2013) use a novel parametriza-
tion of the classical data association problem to for-
mulate a switching linear dynamical system that al-
lows efficient inference in a message passing frame-
work. Further, their formulation explicitly infers the
number of objects and classifies detections into ob-
ject and clutter categories. For this purpose, they use
the detector confidence score as an additional obser-
vation. Integration of detector confidence scores has
also been investigated Breitenstein et al. (2011) and
Poiesi et al. (2013). Both integrate the detector con-
fidence score as observations into a particle filtering
framework.
The Probability Hypothesis Density (PHD) fil-
ter (Mahler, 2003) is a set-valued state estimator that
is based on a relatively new, specialized theory for
multi-object information fusion (Mahler, 2007). This
theory provides comprehensive means of modeling
132
Wojke N. and Paulus D.
Confidence-Aware Probability Hypothesis Density Filter for Visual Multi-Object Tracking.
DOI: 10.5220/0006095801320139
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 132-139
ISBN: 978-989-758-227-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

multi-object phenomena and the PHD recursion it-
self deals with all notable sources of uncertainty in-
volved in multi-object state estimation, including pro-
cess and measurement noise as well as the uncertainty
involved in data association. However, successful ap-
plication of the PHD filter requires knowledge of the
clutter process and the performance of the filter is
known to degrade substantially if these parameters
are chosen incorrectly. Therefore, a number of exten-
sions have been proposed to learn the clutter process
over time (Maggio and Cavallaro, 2009; Mahler et al.,
2011). While the PHD filter does not provide track
identities itself, it has recently been shown how these
can be recovered in a network flow formulation (Wo-
jke and Paulus, 2016).
In this paper, we explore the PHD filter in a
tracking-by-detection framework. Therefore, our
work builds upon the min-cost flow formulation of
Wojke and Paulus (2016). Our contributions are as
follows: First, we extend the standard PHD filter to
mimic state-dependent false alarms. This is neces-
sary, because in visual tracking scenarios clutter is de-
pendent on the multi-object state. More specifically,
due to localization inaccuracies, the object detector
may fire false alarms in the surrounding of the true
object location. In this paper, we present an adapted
recursion that increases the accuracy of the cardinal-
ity estimate and reduces the number of false alarm
tracks. Second, we provide a practical Sequential
Monte-Carlo (SMC) implementation of a reformu-
lated PHD recursion in terms of single-object track
hypotheses (Wojke and Paulus, 2016). Our imple-
mentation is general, i.e., we make no a priori as-
sumptions about the location of appearing objects and
assume constant detection and survival probabilities.
However, extension to more specific tracking scenar-
ios is straight forward.
The remainder of this paper is organized as fol-
lows. In Section 2 we give a brief introduction to
random finite sets and set-valued state estimation. In
Section 3 we outline our adapted PHD recursion that
accounts for confidence detector scores and describe
a practical SMC implementation. In Section 4 we de-
scribe our experimental evaluation and we conclude
in Section 5.
2 MULTI-OBJECT STATE
ESTIMATION
In this section we give a brief overview of random
finite sets and multi-object Bayesian filtering. For
a more complete introduction to methods described
here, we refer the reader to (Mahler, 2003, 2007).
Finite set statistics (FISST) provides a set-
theoretical foundation for information fusion that ad-
dresses many of the difficulties that arise in multi-
object Bayesian filtering with unknown data asso-
ciation and unknown object appearance and disap-
pearance. For this purpose, the theory provides a
toolbox of mathematical procedures to systematically
deal with set-valued random variables that have an
unknown number of members, which are themselves
random. The statistics of such a random finite set
(RFS) can be described by two probability distribu-
tions: a discrete probability distribution for the cardi-
nality of the set and a joint probability for the individ-
ual members of the set, given its cardinality.
Let X be a RFS that draws its instantiations from
the hyperspace of all finite subsets F (X ) of some
space X . The first-order moment of X is a non-
negative function v(x) defined on X which integrates
to the expected number of elements in X that are also
present in S for any closed subset S ⊆ F (X ):
Z
S
v(x)dx = E[
|
X ∩ S
|
]. (1)
This function is called the probability hypothesis den-
sity (PHD) or simply intensity of X. The PHD pro-
vides a useful connection between set-valued and
vector-valued random variables: The intensity v(x) of
RFS X describes the zero-probability event P(x ∈ X)
that x is contained in X (Mahler, 2007).
For multi-object Bayesian filtering, the set of all
object states X
k
and measurements Z
k
at time k are
reconceptualized as single set-valued random vari-
ables
X
k
= {x
k,1
,...,x
k,N
k
}, (2)
Z
k
= {z
k,1
,...,z
k,M
k
}, (3)
where no specific ordering on the respective collec-
tions of object states and measurements exists. In-
dividual objects follow a single-object motion model
x
k
= f
k|k−1
(x
k−1
), and a single-object measurement
model z
k
= g
k
(x
k
) describes the measurement gener-
ation process.
The RFS model for evolution of multi-object state
X
k
incorporates object motion, disappearance, and ap-
pearance:
X
k
=
[
x∈X
k−1
S
k
(x)
∪
[
x∈X
k−1
T
k
(x)
∪ B
k
, (4)
where S
k
(x) is a Bernoulli RFS that takes on either
{ f
k|k−1
(x)} if object x survives from time k − 1 to k
or
/
0 otherwise, T
k
(x) is a RFS of targets that origi-
nate from x—this may be used to model, e.g., object
splitting—and B
k
is the RFS of spontaneous object
Confidence-Aware Probability Hypothesis Density Filter for Visual Multi-Object Tracking
133

appearances. According to the standard multi-object
measurement model (Mahler, 2007), measurements
are either generated by a true object or clutter:
Z
k
=
"
[
x∈X
k
ϒ
k
(x)
#
| {z }
Θ
k
(X
k
)
∪C
k
, (5)
where ϒ
k
(x) is a Bernoulli RFS that takes on {g
k
(x)}
if x is detected and
/
0 otherwise. The RFS C
k
is the set
of clutter measurements at time k.
Based on FISST, it is possible to derive an opti-
mal multi-object Bayes filter that propagates multi-
object densities. This Bayes filter is, however, gen-
erally computationally intractable (Mahler, 2007). In
this work, we focus on the PHD filter (Mahler, 2003).
The PHD filter is a computationally efficient alterna-
tive to the multi-object Bayes filter that propagates
first-oder moments, instead.
3 CONFIDENCE-AWARE PHD
FILTER
We present an adapted PHD recursion that mimics
state-dependent false alarms through state-space clut-
ter generators that survive for one time step only. The
underlying idea is related to a recent extension of the
PHD filter where the parameters of the clutter process
are learned over time (Mahler et al., 2011). We follow
this idea and present an alternative to the measure-
ment model for state-dependent clutter proposed by
Mahler (2014), which requires exhaustive summation
over measurement partitions and is, therefore, compu-
tationally more demanding. Our model is much sim-
pler, but requires detector confidence scores to guide
the cardinality estimate of the PHD.
3.1 State-Space Clutter Generators
In what follows we use an augmented state space
where each single-object state w
T
= (x
T
,β)
T
contains
a kinematic component x, e.g., position and velocity,
and an object class identifier β ∈ {0,1} that is 0 for
clutter and 1 for objects. The purpose of this augmen-
tation is to mimic state-dependent false alarms us-
ing state-space clutter generators. Let b
k
(x,β) denote
the intensity of appearing objects B
k
, τ
k
(x,β | x
0
,β
0
)
the intensity of spawning objects T
k
(x
0
,β
0
), v
k−1
(x,β)
the posterior intensity at time k − 1, p
S
(x,β) a state-
dependent probability of survival, and p
k|k−1
(x | x
0
)
the single-object motion model that is independent of
object class. Then, the predicted intensity at time k is
v
k|k−1
(x,1) = b
k
(x,1) +
hp
S
(·,1) p
k|k−1
(x | ·),v
k−1
(·,1)i,
(6)
v
k|k−1
(x,0) = N
FA
v
k|k−1
(x,1), (7)
where N
FA
is the expected number of false alarms that
are generated by the object detector for a given true
object. Note that throughout the paper we use the
inner product notation h f ,vi =
R
f (x)v(x)dx. Equa-
tion 6 is the standard PHD prediction (Mahler, 2003)
for β = 1 without spawning objects, i.e., τ
k
(x,1 |
x
0
,β) = 0. Equation 7 can be established as follows:
For each new-born object and for every object that
survives from previous times, create a Poisson clutter
RFS with expected mean cardinality N
FA
and set the
probability of survival p
S
(x,0) = 0, such that the RFS
of surviving clutter is empty (i.e., clutter survives for
one time step only). Then, the clutter birth intensity
is a scaled version of the object birth intensity, the
intensity of spawned clutter is a scaled version of the
intensity of surviving objects, and the intensity of sur-
viving clutter is zero. Note that, since the predicted
clutter intensity (7) is a scaled version of the object
intensity, it is not necessary to compute this term ex-
plicitly.
Now, let z
T
= (y
T
,s)
T
denote a single-object mea-
surement that contains a spatial component y and a
detector confidence score s. Then, we assume the
single-object measurement model factorizes into a
spatial density conditional on object state and a prob-
ability density over the confidence score conditional
on object class:
p(y,s | x,β) = p(y | x )p(s | β), (8)
where, in the following, we abbreviate
p(s | β) =
(
P
fg
(s) β = 1,
P
bg
(s) otherwise.
(9)
Following Mahler et al. (2011), we can now compute
the posterior for each object class separately. Let the
detection probability be independent of object class
p
D
(x,β) = p
D
(x). Then, the posterior intensity of ob-
jects becomes:
v
k
(x,1) = [1 − p
D
(x)]v
k|k−1
(x,1) +
∑
z
k, j
∈Z
k
v
k
(U)
(z
k, j
,x,1)
(10)
with
v
k
(U)
(z
k, j
,x,1) =
P
fg
(s
k, j
)p
D
(x)p
k
(y
k, j
| x)v
k|k−1
(x,1)
P
bg
(s
k, j
)
c
k
(y
k, j
) + N
FA
τ
k
(y
k, j
)
+ P
fg
(s
k, j
)τ
k
(y
k, j
)
,
(11)
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
134

where τ
k
(y
k, j
) = hp
D
p
k
(y
k, j
| ·),v
k|k−1
(·,1)i is the in-
tensity mass that accounts for the likelihood that y
k, j
has been generated by an object in X
k|k−1
and where
c
k
(y
k, j
) is the intensity of state-independent clutter.
Again, it is not necessary to write down the update
equation for clutter objects, because they survive for
one time step only.
Equations 6 and 10–11 represent our adapted PHD
recursion. The derivation follows directly from our
specific choice of clutter model. In the denomina-
tor of Equation 11, N
FA
transfers intensity mass from
the prior object intensity to the clutter intensity. For
the cardinality estimate, this scaling factor controls
how much emphasis should be put on the detector
confidence score compared to the filtering process.
Equation 10 collapses to the default PHD update for
P
fg
(s
k, j
) = P
bg
(s
k, j
) with N
FA
= 0.
3.2 Sequential Monte Carlo
Implementation
We now describe a practical SMC implementation of
the modified PHD recursion where we make use of
two extensions that are complementary to the pro-
posed clutter model: (i) We use an adapted sampling
scheme for appearing objects that is more efficient
when the birth intensity is uninformative (Ristic et al.,
2012), (ii) we use a reformulation of the PHD recur-
sion in terms of single-object hypotheses that can be
mapped into a min-cost flow network to solve for tar-
get trajectories (Wojke and Paulus, 2016). Therefore,
let Z
1:k
denote the set of measurements up to time
k. Then, we partition the multi-object intensity into
single-object track hypotheses
v
k
(x) =
∑
Z
t,i
∈Z
1:k
q
t,i
v
(t,i)
k
(x), (12)
where v
(t,i)
k
(x) is an intensity partition corresponding
to the i-th measurement at time t and where q
t,i
is
a scaling parameter.
1
Following Wojke and Paulus
(2016), intensity v
(t,i)
k
(x) is proportional to the dis-
tribution over hypothetical object state x
(t,i)
k
that has
generated measurement z
t,i
at time t and has since
then not been detected. The scaling parameter q
t,i
accounts for the probability that z
t,i
has indeed been
generated by an object in X
t
, i.e., is not clutter. In our
SMC implementation, we approximate each partition
using a set of L
T
samples and associated importance
1
Note that in contrast to Wojke and Paulus (2016) we
have no partition for the set of undetected targets. This
is, because in the adapted sampling scheme of Ristic et al.
(2012) it is assumed appearings objects are always detected.
weights:
Q
(t,i)
k
=
n
(w
(t,i,n)
k
,x
(t,i,n)
k
)
o
L
T
n=1
, (13)
v
(t,i)
k
(x) ≈
L
T
∑
n=1
w
(t,i,n)
k
δ(x − x
(t,i,n)
k
). (14)
From this particle approximation we can reconstruct
the full multi-object intensity using (12). For no-
tational brevity, we refer to this particle representa-
tion of the full multi-object intensity at time k as
Q
k
= {w
(n)
k
,x
(n)
k
}
L
k
n=1
.
The following implementation consists of two
steps: First, we propagate all legacy track hypothe-
ses from the previous to the current time step. Then,
we initialize a new measurement-induced track hy-
pothesis for each newly arrived measurement. In
terms of the PHD recursion, track propagation cor-
responds to prediction (6) and the missed detection
case of update (10). Track initialization accounts for
the measurement-corrected terms in update (10). At
all times, the full multi-object intensity can be recov-
ered from individual partitions using (12). Further,
note that in the following implementation we use un-
informed priors for spatial clutter and birth densities.
In particular, we assume that state-independent clut-
ter is Poisson with mean cardinality λ
c
and uniform
spatial density p
C
t
(y) = 1/V , where V is the volume
of the measurement space. Likewise, we assume no
prior knowledge about the location of appearing ob-
jects. Therefore, we assume the birth intensity is
Poisson with mean cardinality λ
b
and place a uni-
form prior on appearing objects in measurement space
p
B
k
(y) = 1/V . It is, however, easy to adapt the pre-
sented algorithm to scene-specific layouts using more
informed densities (e.g., higher birth probability at
image borders).
Track Propagation. Assume at time k we are given
particles Q
(t,i)
k−1
that approximate individual partitions
of the posterior intensity at time k − 1. Then, we
propagate these legacy track hypotheses to time k as
outlined in Listing 1. In lines 1–3 we multiply im-
portance weights by the state-dependent probability
of survival and sample from the single-object mo-
tion model to obtain a particle approximation Q
(t,i)
k|k−1
(c.f. Equation 6). In lines 4–6 we multiply importance
weights by one minus the state-dependent probabil-
ity of detection to account for the missed detection
case of update (10) and obtain a particle approxmia-
tion Q
(t,i)
k
.
Track Initialization. Assume at time k we are
given measurement set Z
k
as well as particle set
Confidence-Aware Probability Hypothesis Density Filter for Visual Multi-Object Tracking
135

Listing 1: Track propagation for a single legacy track
v
(t,i)
k−1
(x).
1: for n = 1,...,L
T
do
2: {Prediction}
w
(t,i,n)
k|k−1
= p
S
(x
(t,i,n)
k−1
)w
(t,i,n)
k−1
x
(t,i,n)
k|k−1
= p
k|k−1
(· | x
(t,i,n)
k−1
)
3: end for
4: for n = 1,...,L
T
do
5: {Update}
w
(t,i,n)
k
=
h
1 − p
D
(x
(t,i,n)
k−1
)
i
w
(t,i,n)
k|k−1
x
(t,i,n)
k
= x
(t,i,n)
k|k−1
6: end for
Q
k|k−1
that approximates the predicted multi-object
intensity. For each measurement z
k, j
∈ Z
k
we create
a single-object track hypotheses as outlined in List-
ing 2. First, we update importance weights to ac-
count for the single-object measurement likelihood
and state-dependent probability of detection (lines 1–
3). Then, we draw samples from the birth intensity
(line 4–6). Loosely following Ristic et al. (2012), we
draw samples from
p
k
(y
k, j
| x)b
k
(x) = p
k
(y
k, j
| x)p
B
k
(x)λ
b
, (15)
= p
k
(x | y
k, j
)p
B
k
(y)λ
b
, (16)
= p
k
(x | y
k, j
)
λ
b
V
, (17)
where we assume the RFS of appearing objects is
Poisson with expected number of objects λ
b
and uni-
form spatial prior on measurement space p
B
k
(y
k, j
) =
1/V . Consequently, we draw samples from an inverse
measurement model and set weights uniform such that
they sum up to b
k
(z
k, j
) = λ
b
V
−1
. In practice, sam-
pling from the inverse measurement model is more
efficient when the birth intensity is uninformative, be-
cause birth samples are placed in areas where the
measurement likelihood has high probability mass. In
lines 7 and 8 we compute the probability that mea-
surement z
k, j
has been generated by an object in X
k
.
Finally, in line 9 we resample to obtain L
T
new parti-
cles with uniform weights.
Pruning and Data Association. Due to partition-
ing the intensity according to (12), the number of
particles scales linearly with the number of measure-
ments. However, only few track hypotheses contribute
high intensity mass to the overall multi-object inten-
sity. Therefore, at each time step, we prune track hy-
potheses with intensity mass below a given threshold.
Listing 2: Track initialization for measurement z
k, j
∈ Z
k
.
1: for n = 1,...,L
k−1
do
2: Update weights of predicted intensity v
k|k−1
(x)
w
(k, j,n)
k
= p
D
(x
(n)
k|k−1
)p(y
k, j
| x
(k, j,n)
k|k−1
)w
(n)
k|k−1
x
(k, j,n)
k
= x
(n)
k|k−1
3: end for
4: for n = 1,...,L
T
do
5: Draw birth samples from inverse measurement
model
w
(k, j,L
k−1
+n)
k
=
λ
b
V
−1
L
T
x
(k, j,L
k−1
+n)
k
∼ p(· | y
k, j
)
6: end for
7: Compute
τ
k
(y
k, j
) =
L
k−1
+L
T
∑
n=1
w
(k, j,n)
k
8: Compute
q
k, j
=
P
fg
(s
k, j
)τ
k
(y
k, j
)
P
bg
(s
k, j
)
λ
c
V
−1
+ N
FA
τ
k
(y
k, j
)
+ P
fg
(s)τ
k
(y
k, j
)
9: Resample
n
w
(k, j,n)
k
,x
(k, j,n)
k
o
L
k−1
+L
T
n=1
to obtain
1
L
T
,x
(k, j,n)
k
L
T
n=1
Further, to recover object trajectories, the adapted
PHD recursion presented in this paper can be directly
applied to the min-cost flow network of Wojke and
Paulus (2016). The only parameter that is affected
by our adaption is the probability of existence that
is computed during track initialization (line 8). This
term can be directly plugged into the original formu-
lation. We refer the reader to the original publica-
tion (Wojke and Paulus, 2016) for further details on
this part.
4 EXPERIMENTS
Evaluation has been carried out on the popular
PETS’09 dataset (Ferryman and Shahrokni, 2009).
For fair comparison, we used publicly available detec-
tions and ground truth provided by Andriyenko et al.
(2012). Most of the sequences that we have evalu-
ated on are medium or densly crowded scenarios with
substantial occlusions, missed detections, and false
alarms. Tracking was performed in 3D using a con-
stant velocity motion model. Detections have been
projected onto the ground plane using known camera
calibration parameters. During all experiments, we
used a single set of parameters. The motion model
adds isotropic noise with standard deviation ∆t ·0.5 m
for the position and ∆t · 1 m/s for the velocity, where
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
136

Table 1: Evaluation on PETS’09 dataset Ferryman and Shahrokni (2009): MT = Mostly Tracked, ML = Mostly Lost, ID =
Number of ID switches.
Dataset MOTA MOTP GT MT ML ID Rec. Prec.
S1L1-2 61.8 68.0 44 22 12 8 64.3 96.5
Milan et al. (2013) 60.0 61.9 44 21 11 22 64.9 93.7
Rezatofighi et al. (2015) 63.5 64.5 44 17 9 13 66.7 95.8
S1L2-1 27.5 33.2 42 7 22 34 32.3 88.7
Milan et al. (2013) 29.6 58.8 42 2 21 42 30.9 98.3
Rezatofighi et al. (2015) 32.8 57.6 42 5 15 76 38.6 89.9
S2L1 86.2 77.5 19 18 0 6 96.0 90.8
Milan et al. (2013) 90.1 74.3 19 18 1 22 96.8 94.1
Rezatofighi et al. (2015) – – – – – – – –
S2L2 58.6 59.2 43 10 2 139 64.6 93.3
Milan et al. (2013) 58.1 59.8 43 11 1 167 65.1 92.4
Rezatofighi et al. (2015) 58.2 58.5 43 11 0 143 69.8 87.2
S2L3 44.5 69.0 44 11 20 13 46.2 96.9
Milan et al. (2013) 39.8 65.0 44 8 19 27 43.0 94.2
Rezatofighi et al. (2015) 48.0 62.3 44 13 18 23 52.2 93.4
∆t = 1/7 is the time gap between consecutive frames.
The measurement model adds isotropic noise with
standard deviation 0.2 m. When sampling from the
inverse measurement model, the unobserved velocity
was drawn from a normal distribution with standard
deviation 1m/s. Further, we used λ
c
= 1.0, λ
b
= 0.5,
N
FA
= 0.2, p
D
(x) = 0.7, and p
S
(x) = 0.95. The class-
conditional likelihood of detector confidence scores
P
fg
(s) and P
bg
(s) has been learned from data us-
ing Kernel Density Estimation with Gaussian kernel.
For training, we used sequences S1L1-1 and S1L2-2
which have been excluded from evaluation.
We used the MOT challenge evaluation
software (Leal-Taix
´
e et al., 2015) to compute
CLEAR MOT metrics (Bernardin and Stiefelhagen,
2008). All methods that we compare against use
the same detections, ground truth, and evaluation
criteria. Therefore, evaluation was carried out in 3D
using a matching threshold of 1 m. The results of our
evaluation are summarized in Table 1. Overall, the
presented method performs well in terms of tracking
precision, with consistently high ranked precision and
MOTP scores. This underlines the state estimation
capabilities of the PHD filter, even in dense tracking
scenarios with substantial amount of false alarms.
In terms of tracking accuracy, MOTA scores of our
method are usually lower than those of Rezatofighi
et al. (2015), but higher than those of Milan et al.
(2013). At the same time, our method produces
considerable fewer ID switches on all sequences. We
observed that lower MOTA scores are mostly due to
a larger number of false negatives. In crowded scenes
with high number of detector failures, our tracker
produced less, but stable tracks. Therefore the lower
MOTA scores, but competitive performance in terms
of ID switches and track statistics (MT/ML).
In a second experiment we have compared our
confidence-aware PHD recursion against the original
formulation of Wojke and Paulus (2016) to investi-
gate our contribution on overall results. Using se-
quence S2L1 only, we exhaustively searched for op-
timal clutter parameters, while leaving all others pa-
rameters untouched. Plots of several tracking statis-
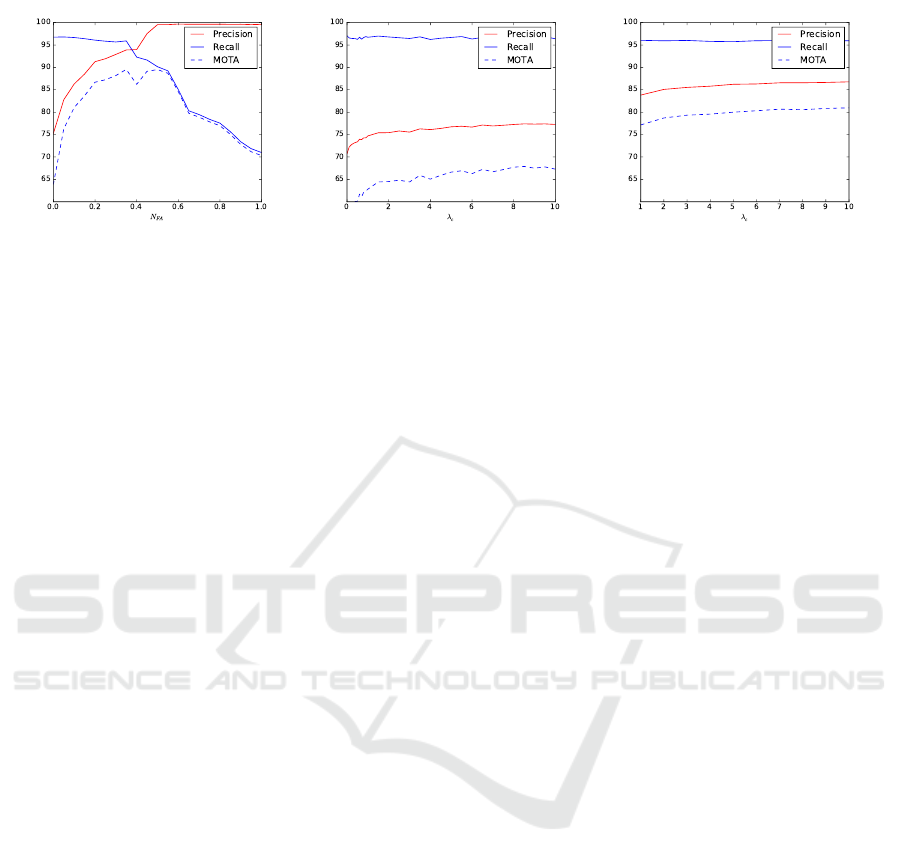
tics against clutter parameters are shown in Figure
1. With a MOTA score of 89.5 we found the opti-
mal value for state-dependent clutter at N
FA
= 0.35.
Using P
fg
(s) = P
bg
(s) and N
FA
= 0, i.e., applying
the standard PHD recursion with uniform clutter, we
found the optimal value for the expected number of
false alarms at λ
c
= 10.0 with a MOTA score of
67.3. Applying additional non maxima suppression,
the MOTA score increases to 81.0. While the artifi-
cially high clutter rate alone suggests that the uniform
distribution does not describe the false alarm process
accurately, we see substantial improvement in track-
ing accuracy due to integration of detector confidence
values.
5 CONCLUSIONS
The PHD filter provides a mathematically rigorous
framework for multi-object state estimation that is
relatively unexplored in the context of visual object
Confidence-Aware Probability Hypothesis Density Filter for Visual Multi-Object Tracking
137
(a) N
FA
(without non maxima suppres-
sion)
(b) λ
c
(without non maxima suppres-
sion)
(c) λ
c
(with non maxima suppression)
Figure 1: Clutter parameter analysis on S2L1: (a) with detector confidence scores, (b), (c) without detector confidence scores.
tracking. In this paper, we have presented an adapted
PHD recursion that incorporates detector confidence
scores to mimic state-dependent false alarms as well
as a practical SMC implementation that can be in-
tegrated into the min-cost flow network formulation
of Wojke and Paulus (2016). Our experiments re-
vealed that integration of detector confidence scores
has considerable impact on overall applicability of
the PHD filter and, in general, our approach achieves
results competitive with the current state of the art.
FISST and the PHD filter may help to solve open
multi-object tracking problems and there is ample op-
portunity for future work, e.g., integration of appear-
ance information, application of more complex global
data association formulations, and object group track-
ing.
REFERENCES
Andriyenko, A., Schindler, K., and Roth, S. (2012).
Discrete-continuous optimization for multi-target
tracking. In CVPR, pages 1926–1933.
Berclaz, J., Fleuret, F., T
¨
uretken, E., and Fua, P. (2011).
Multiple object tracking using k-shortest paths opti-
mization. IEEE Trans. Pattern Anal. Mach. Intell.,
33(9):1806–1819.
Bernardin, K. and Stiefelhagen, R. (2008). Evaluating mul-
tiple object tracking performance: The CLEAR MOT
metrics. EURASIP J. Image Video Process, 2008.
Breitenstein, M. D., Reichlin, F., Leibe, B., Koller-Meier,
E., and Van Gool, L. (2011). Online multiper-
son tracking-by-detection from a single, uncalibrated
camera. IEEE Trans. Pattern Anal. Mach. Intell.,
33(9):1820–1833.
Dehghan, A., Tian, Y., Torr, P. H., and Mubarak, S. (2015).
Target identity-aware network flow for online multiple
target tracking. In CVPR, pages 1146–1154.
Ferryman, J. and Shahrokni, A. (2009). An overview of the
PETS 2009 challenge. In PETS.
Kim, C., Li, F., Ciptadi, A., and Rehg, J. M. (2015). Mul-
tiple hypothesis tracking revisited. In ICCV, pages
4696–4704.
Leal-Taix
´
e, L., Milan, A., Reid, I., Roth, S., and Schindler,
K. (2015). MOTChallenge 2015: Towards a bench-
mark for multi-target tracking. arXiv:1504.01942
[cs].
Maggio, E. and Cavallaro, A. (2009). Learning scene con-
text for multiple object tracking. IEEE Trans. Image
Process., 18(8):1873–1884.
Mahler, R. (2003). Multitarget Bayes filtering via first-order
multitarget moments. IEEE Trans. Aerosp. Electron.
Syst., 39(4):1152–1178.
Mahler, R. (2007). Statistical Multisource-Multitarget In-
formation Fusion. Artech House, Norwood, MA,
USA.
Mahler, R. (2014). Advances in statistical multisource-
multitarget information fusion. Artech House, Nor-
wood, MA, USA.
Mahler, R., Vo, B.-T., and Vo, B.-N. (2011). CPHD filtering
with unknown clutter rate and detection profile. IEEE
Trans. Signal Process., 59(8):3497–3513.
Milan, A., Schindler, K., and Roth, S. (2013). Detection-
and trajectory-level exclusion in multiple object track-
ing. In CVPR, pages 3682–3689.
Pirsiavash, H., Ramanan, D., and Fowlkes, C. C. (2011).
Globally-optimal greedy algorithms for tracking a
variable number of objects. In CVPR, pages 1201–
1208.
Poiesi, F., Mazzon, R., and Cavallaro, A. (2013). Multi-
target tracking on confidence maps: An applica-
tion to people tracking. Comput. Vis. Image Und.,
117(10):1257–1272.
Reid, D. B. (1979). An algorithm for tracking multiple tar-
gets. IEEE Trans. Autom. Control, 24(6):843–854.
Rezatofighi, S., Milan, A., Zhang, Z., Shi, Q., Dick, A., and
Reid, I. (2015). Joint probabilistic data association
revisited. In ICCV, pages 3047–3055.
Ristic, B., Clark, D., Vo, B.-N., and Vo, B.-T. (2012).
Adaptive target birth intensity for PHD and CPHD fil-
ters. IEEE Trans. Aerosp. Electron. Syst., 48(2):1656–
1668.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
138

Segal, A. and Reid, I. (2013). Latent data association:
Bayesian model selection for multi-target tracking. In
ICCV, pages 2904–2911.
Wojke, N. and Paulus, D. (2016). Global data association
for the probability hypothesis density filter using net-
work flows. In ICRA, pages 567–572.
Zhang, L., Li, Y., and Nevatia, R. (2008). Global data asso-
ciation for multi-object tracking using network flows.
In CVPR, pages 1–8.
Confidence-Aware Probability Hypothesis Density Filter for Visual Multi-Object Tracking
139
