Measuring Human-made Corner Structures with a
Robotic Total Station using Support Points, Lines and Planes
Christoph Klug, Dieter Schmalstieg and Clemens Arth
Institute for Computer Graphics and Vision, Graz University of Technology,
Inffeldgasse 16/II, 8010 Graz, Austria
Keywords:
Robotic Total Station, Reflectorless Electrical Distance Measurement.
Abstract:
Measuring non-planar targets with a total station in reflectorless mode is a challenging and error-prone task.
Any accurate 3D point measurement requires a fully reflected laser beam of the electronic distance meter and
proper orientation of the pan-tilt unit. Prominent structures like corners and edges often cannot fulfill these
requirements and cannot be measured reliably.
We present three algorithms and user interfaces for simple and efficient construction-side measurement cor-
rections of the systematic error, using additional measurements close to the non-measurable target. Post-
processing of single-point measurements is not required with our methods, and our experiments prove that
using a 3D point, a 3D line or a 3D plane support can lower the systematic error by almost a order of magni-
tude.
1 INTRODUCTION
Total stations are commonly used for measuring an-
gles, distances and 3D points in surveying and build-
ing construction (Uren, 2010). A robotic total sta-
tion, which can be remotely controlled, is equipped
with an electronic distance meter (EDM), which uses
a laser signal for accurate distance measurements
1
.
The simplified and calibrated geometric model of a
common robotic total station without parallax effects
between EDM and camera is shown in Fig. 1. In
the ideal case, all coordinate systems are perfectly
aligned: The EDM is aligned with the principal ray
of the camera; the local spherical coordinate system
of the instrument is aligned with the camera coordi-
nate system, and the camera center is at the origin of
the instrument coordinate system. Adjustment screws
on the device allows an approximation of the ideal
model, but for accurate measurements, an extended
geometric model and device calibration is necessary.
Such calibration includes camera parameters, temper-
ature compensation and EDM corrections
2
.
1
Details about EDM types can be found in (Amann
et al., 2001).
2
Details about extended geometric models, environmen-
tal influences and calibrations of total stations can be found
in (Schulz, 2007; Uren, 2010; Nichols and Beavers, 2003;
Coaker, 2009; Reda and Bedada, 2012; Martin and Gatta,
2006).
vertical angle
(D, , )
horizontal angle
z
cam
x
cam
y
EDM
z
instr
(zenith)
y
inst
x
instr
x
img
y
img
z
EDM
x
EDM
principal point
(, )
y
cam
EDM distance D
Figure 1: Simplified geometric model for a calibrated
robotic total station with azimuth angle θ, polar angle φ
and radial distance D. In this simplified version the coor-
dinate system of the EDM is aligned with the camera co-
ordinate system as well as the spherical coordinate frame
robotic total station. Real-world devices require six degrees
of freedom (DOFs) pose conversations between the coordi-
nate frames as well as further corrections.
For standard measurements, reflective measurement
targets with known calibration parameters are used.
Modern total stations also support reflectorless mea-
surements using the diffuse reflection of natural sur-
faces. This is often referred to as measuring nat-
ural targets. Common natural targets in surveying
and building construction should have a high recall
value, thus, preferred targets are corners and edges
of human-made structures. Influences of the laser
Klug C., Schmalstieg D. and Arth C.
Measuring Human-made Corner Structures with a Robotic Total Station using Support Points, Lines and Planes.
DOI: 10.5220/0006096800170027
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 17-27
ISBN: 978-989-758-227-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
17

r
lb
d
1
d
0
EDM
r
lb
b)
Projected laser dot
a)
Figure 2: For a common refectorless measurement target
with one visible approximately planar surface, the laser dot
must be fully reflected by the surface to get reliable distance
results, precluding direct targeting of the corner. The mini-
mum vertical and horizontal measurement error e is approx-
imately defined by e = d
0
+ r
lb
, where d
0
is the safety dis-
tance between the edges of the target and the laser pointer,
and r
lb
is the radius of the projected laser beam (approx-
imating the elliptical projection of the laser through a cir-
cle). d
0
is influenced by user experience, image resolution,
focal length of the camera, image blur due to out-of-focus
problems, back light conditions and other effects.
beam divergence of the EDM, angular resolution of
the theodolite, inaccurate targeting and optical limi-
tations are reasons why direct measurements of non-
planar targets are critical and error-prone tasks. Sur-
veyors often use post-processing methods to increase
the accuracy of such measurements.
The wide variety of measurement conditions, the
demanding requirements for the results of the mea-
surement procedure regarding accuracy and reliabil-
ity, and the aim to perform single-view metrology
(Criminisi et al., 2000; Hartley and Zisserman, 2003)
make multi-view photogrammetric algorithms largely
inapplicable in realistic scenarios. Practical applica-
tions in indoor and outdoor environments can suf-
fer from problems caused by sunlight and strong
back-light, shadows, large distance measurements
and partly occluded targets. All these issues are not
fully solved problems in Computer Vision in general
per se. Eventually the absence of multiple measure-
ments and observations from multiple camera poses
prohibits the usage of classic photogrammetry algo-
rithms as such.
In this work, we therefore address the problem of
reflectorless measuring targets with at least one quasi-
planar surface visible to the total station (see Fig. 2),
using three different methods. Post-processing and
high density 3D point cloud scans are avoided to keep
the measurement effort as low as possible. Since the
projected laser dot should be fully located within the
planar surface to avoid distance measurement errors,
a systematic angular and distance error occurs, which
depends on the projected laser dot size, the observa-
tion angle of the surface and other parameters
3
. With
3
See Juretzko (Juretzko, 2004) for an extensive discus-
our algorithms, it is possible to reduce the systematic
measurement error by applying image-based correc-
tions directly in the field. As a side effect, the ap-
proach proposed simplifies the overall measurement
procedure, such that even non-experts in the field can
perform reliable and robust measurements. This is
proven by the results of our pilot study.
2 RELATED WORK
In the following, we shortly review related work about
using total stations for measuring.
The book by Uren (Uren, 2010) provides an ex-
tensive description of GPS measurements, total sta-
tions and laser range meters, explaining basic survey-
ing and measurement methods, surveying hardware,
software and tools, possible sources of errors and er-
ror propagations. Image-based measurement correc-
tions are not described, however. Coaker (Coaker,
2009) investigated accuracy, precision and reliabil-
ity of reflectorless total station measurement methods,
also mentioning the problem of direct measurements
of corners and edges. Similarly, Zeiske (Zeiske, 2004)
describes basic surveying methods and offline correc-
tions for 2D corner measurements using simple ge-
ometry. However, no online method or image-based
geometric correction are mentioned.
Many modern total stations are already equipped
with image-based measurement methods, like steer-
ing the total station to selected pixels, selecting and
visualizing 3D targets in the image or visualizing
metadata. Scherer et al. (Scherer, 2001; Scherer and
Lerma, 2009) investigated possible benefits of image-
based features for architectural surveying. The de-
vice of Topcon (Topcon Corporation, 2011) supports
an image-based measurement feature for not directly
measurable targets like corners and edges, but with-
out providing any mathematical details or evaluation
of the methods.
Ehrhart et al. (Ehrhart and Lienhart, 2015) investi-
gate image processing methods for deformation mon-
itoring. In their work they detect movements of com-
plete regions by comparing image patches acquired
with the camera of a total station, however, without
explicitly performing any structural analysis of build-
ing corners or edges.
Siu et al. (Siu et al., 2013) describe a close range
photogrammetric solution for 3D reconstruction and
target tracking by combining several total stations and
cameras. Jadidi et al. (Jadidi et al., 2015) use im-
age based modelling to reconstruct 3D point clouds
sion of this problem.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
18

and register as-built data to as-planned data. Fathi et
al. (Fathi and Brilakis, 2013) generate 3D wire dia-
grams of a roof using video streams from a calibrated
stereo camera set. Their algorithm combines feature
point matching, line detection and a priori knowledge
of roof structures to a structure from motion pipeline.
Even if the results of these approaches are quite im-
pressive, none of them can be applied for measur-
ing corner and edge structures from a single position.
Fathi et al. further notes accuracy problems of the re-
constructed models.
Closely related to our approach is the work by Ju-
retzko (Juretzko, 2004), who provides conceptional
descriptions for not directly measurable target using
intersections of 3D rays, lines and planes. How-
ever, no comparative study between the methods,
no detailed mathematical description and no suitable
user interface is provided. Furthermore, the author
mentions only minimal measured point sets for each
method without any model fitting approach.
To the best of our knowledge, we are the first to
proper describe such measurement techniques with
a detailed mathematical formalism, together with a
comparative study. Moreover we are the first to in-
vestigate the measurement concept in detail in an out-
door scenario, giving results and insights into the is-
sues arising outside of laboratory conditions in a prac-
tical working environment.
3 TEST HARDWARE AND
LIMITATIONS
The total station we used for our experiments (see
Fig. 3) had been fully calibrated by the manufacturer.
It provides a closed source driver for controlling the
device, for retrieving the camera image and for trans-
lating between all coordinate systems. As common
for commercially available systems, there is no direct
access to the raw data of the sensors, the geometric
model and the related parameters. The applied cor-
rection algorithms are confidential and kept secret by
manufacturers. While in our case the available API
does not provide a projection matrix, it offers a com-
plete API for coordinate system conversions. There-
fore, we use the simplified geometric model, which is
shown in Fig. 1, for a calibrated robotic total station
to explain our methods.
Note that whether or not it is theoretically pos-
sible to perform full manual calibration for a single
instance of a device at hand, it is neither reasonable
to assume that every device is shipped with a calibra-
tion by the manufacturer that is perfect for each possi-
ble measurement situation, nor is manual calibration
Figure 3: Robotic Total Station and mobile PC used in our
experiments. The communication between the devices is
done wirelessly over WLAN.
easily possible given the level of access provided by
APIs. Thus our assumption to work with the stock
calibrated device as is and employing our simplified
geometric model is plausible.
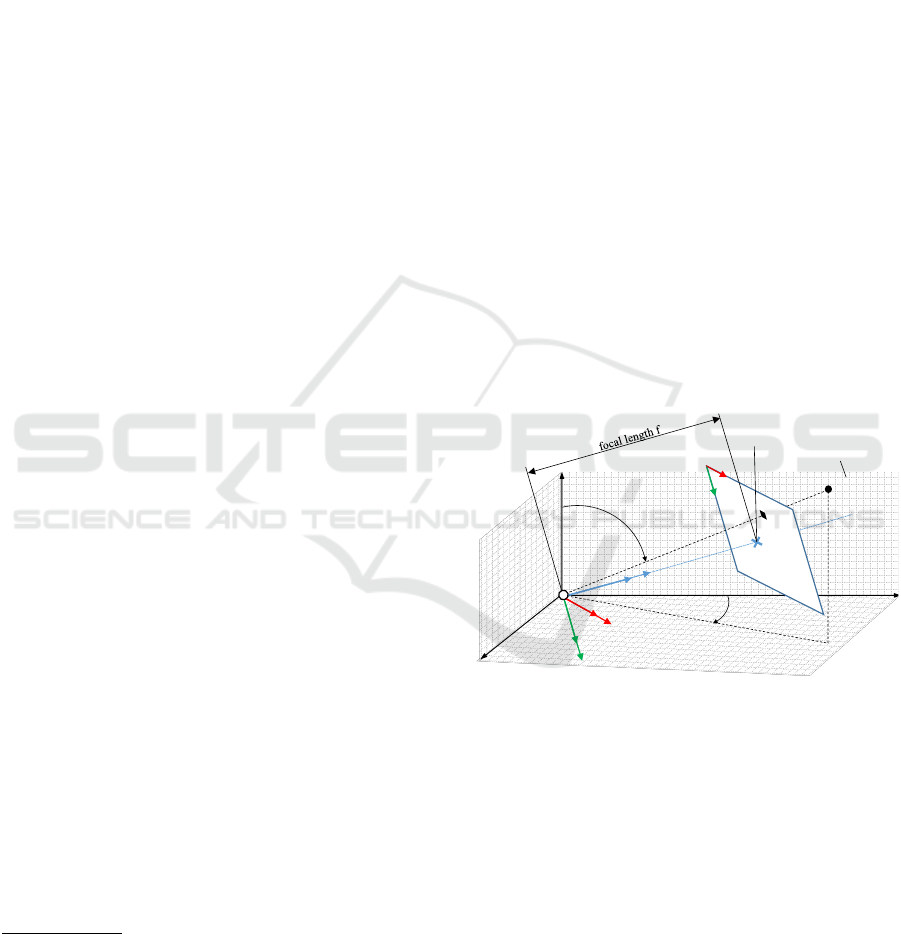
4 CONCEPT
We use the standard single point measurement
method as reference method and define three new
measurement methods, which integrate in-the-field
corrections for corner and edge measurements:
(a) Direct reflectorless target measurement
(b) Reflectorless target measurement using a support
point
(c) Reflectorless target measurement using a support
line
(d) Reflectorless target measurement using a support
plane
Figure 4 shows the direct measurement method as
well as the support point, support line and support
plane method. Details about the methods are provided
in following sections.
4.1 Standard Method
When measuring a corner directly in reflectorless
mode, the laser dot must be fully reflected by an at-
tached surface. Fig. 1 shows the simplified geometric
model for a single point measurement, while Fig. 2
shows the systematic error introduced by the afore-
mentioned constraint.
Measurement Flow. The simple measurement flow
is defined by following steps:
1. Use the pan/tilt control interface, until the target-
of-interest is visible in the image
2. Define target-of-interest in the image
Measuring Human-made Corner Structures with a Robotic Total Station using Support Points, Lines and Planes
19

a)
)
b)
)
c)
)
d)
)
Figure 4: Four different measurement methods of a cor-
ner with a single visible adjacent area: direct method (a),
support point method (b), support line method (c), support
plane method (d). The numbers in the image indicate the
minimum measurement count and the respective order used
in our algorithms.
3. Calculate the 3D position of the target-of-interest
by measuring the angle and distance at the se-
lected image point
Calculating the Point. A total station defines a lo-
cal spherical coordinate system. A point is defined by
the horizontal angle ϕ, the vertical angle θ and the
distance D. The simplified relation between spherical
and Euclidean coordinates for our test device is given
by following equations:
F(x, y, z) =
D
θ
ϕ
=
q
x
2
i
+ y
2
i
+ z
2
i
arctan
x
y
= atan2(x, y)
arccos
z
√
x
2
i
+y
2
i
+z
2
i
(1)
with
D ≥ 0 −π ≤ θ < π 0 ≤ ϕ < π (2)
Note that the azimuth angle ϕ is measured clockwise
and is related to the Cartesian y direction rather than
counterclockwise and related to to the Cartesian x di-
rection. This leads to swapped x and y variables in the
expression atan2(x, y) in Eqn. 1.
The inverse operation can be generalized to a 3D Eu-
clidean rotation for a right-handed coordinate system:
Q(θ, ϕ) = R
z
(−θ) ·R
y
(0) ·R
x
(−ϕ) (3)
p =
p
x
p
y
p
z
= G(D, θ , ϕ) = Q(θ , ϕ) ·
0
0
D
(4)
where p describes a 3D point in Euclidean coordi-
nates and (D, θ , ϕ) describes a 3D point in spherical
coordinates; R
x
, R
y
, R
z
are 3D rotation matrices in
the Euclidean right-handed coordinate system around
the x-axis, y-axis and z-axis, respectively. Q(θ, ϕ) is
the combined rotation matrix which converts an angle
measurement to an Euclidean space direction, here
used for translating between local instrument coordi-
nate system and camera coordinate system
4
. Eqn. 4
can easily be extended to non-aligned coordinate sys-
tems using homogeneous coordinates
5
.
We use spherical coordinates for storing selected 2D
image positions to support rotation-invariant opera-
tions in the image space. Fig. 5 shows an image-based
selection of a target in two different poses of the to-
tal station. To convert an image space coordinate to
spherical coordinates, we first back-project the pixel
coordinate into the camera space as view ray, convert
to the instrument space and then apply Eqn.1 with
D = 1. The instrument space is the local coordinate
system. For our simplified model, the conversion is
simply the inverse pose of the camera
6
.
The 3 ×4 camera projection matrix P can be split
into the 3 ×3 matrix M and the 3 ×1 vector m
P = [M|m] (5)
The back-projected ray X can be written as
X(λ , u) = P
†
·u + λ ·C (6)
where P
†
is the pseudo-inverse of the projection ma-
trix P, u defines a 2D image coordinate and C is the
camera center. For finite cameras, the following ex-
pression can be used, which avoids the calculation of
the P
†
X(µ, u) = µ
M
−1
·u
0
+
−M
−1
·m
1
(7)
This equation avoids a possible singularity of P
†
for
camera center C = 0.
For our simplified model, the projection matrix as
follows is calculated by
P = Q(−θ , −ϕ) ·[K,C] (8)
where θ, ϕ define the pose of the camera, K is defined
by the intrinsic parameters of the camera and C is the
camera center:
K =
f
x
0 u
0
0 f
y
v
0
0 0 1
C =
0
0
0
(9)
Note that the camera center C is aligned with the ori-
gin; f
x
and f
y
describes the focal length of the camera,
u
0
and v
0
specify the principal point.
4
A definition for the rotation matrices R
x
, R
y
, R
z
can be
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
20
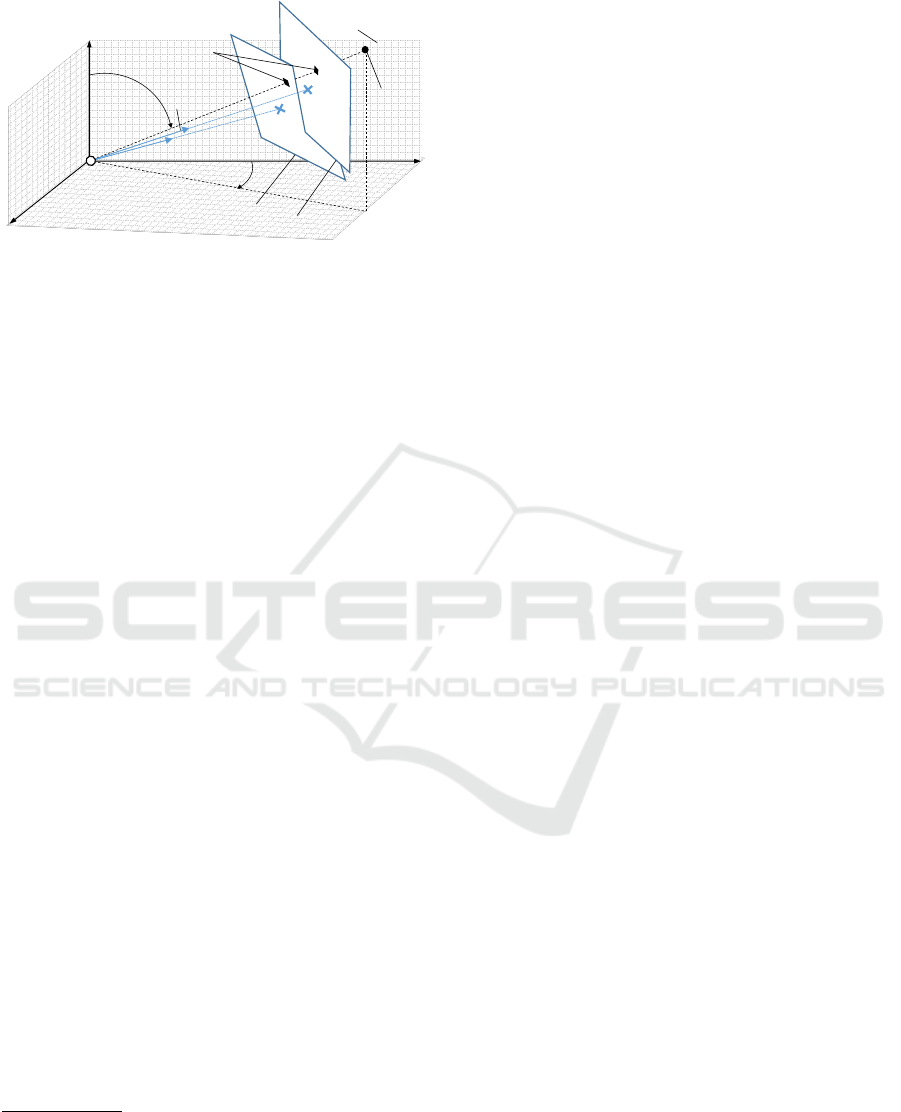
(D, , )
z
instr
y
inst
x
instr
z
1,EDM
distance D
(, )
z
2,EDM
image plane 1
image plane 2
3D target
Figure 5: Using Spherical coordinates for image pixels en-
ables rotation-invariant selection of 2D targets.
4.2 Support Point Method
To get the 3D coordinates of a building corner, the
image pixel of the corner and a support point near
the corner is defined, where the distance of the sup-
port point can be measured safely. Afterwards, the
corner itself can simply be defined in the 2D im-
age. The 3D coordinate of the target of interest is ap-
proximated by using the back-projected pixel of the
first point and the measured distance of the support
point. The approximation error becomes reasonable
small for certain applications when following condi-
tions hold: reasonable distance between the measure-
ment device and the target, a perpendicular arrange-
ment of the view ray and the measured surface, a
small distance between the corner and the measured
3D point.
An offline version of this method is commonly used
by surveying engineers (Coaker, 2009; Scherer, 2004;
Juretzko, 2004). With the support point method, the
minimal measurement count for a 3D point is N
min
=
1. Fig. 4 shows the support point concept.
Measurement Flow. The simple measurement flow
is defined by following steps:
1. Use the pan/tilt control interface, until the target-
of-interest is visible in the image
2. Define target-of-interest in the image
3. Define support point with a single distance mea-
surement
4. Calculate the 3D position of the target-of-interest
by using the angle of the image point and the dis-
tance of the support point measurement
found in (Schneider and Eberly, 2003).
5
In (Schneider, 2009; Schulz, 2007) a detailed descrip-
tion of the conversions is given.
6
A robust method for calculating the ray given a 3 ×4
camera projection matrix is described in (Hartley and Zis-
serman, 2003).
Calculating the Point. In the user interface, two 2D
image points are defined: the pixel coordinates of the
target-of-interest u
1
and the pixel coordinates of the
support point u
2
.
First both image points, u
1
and u
2
, are converted to
spherical coordinates using Eqn. 6 with distance µ =
1 and Eqn. 1 to get the control values for the EDM
pose of the total station,
r
1
=
r
1,x
r
1,y
r
1,z
= X(1, u
1
) r
2
=
r
2,x
r
2,y
r
2,z
= X(1, u
2
)
(10)
1
θ
1
ϕ
1
= F(r
1,x
, r
1,y
, r
1,z
)
1
θ
2
ϕ
2
= F(r
2,x
, r
2,y
, r
2,z
)
(11)
where r
1
and r
2
defines a back-projected point at dis-
tance µ = 1.
Then the distance D
2
is measured with the EDM
at the angle (θ
2
, ϕ
2
) using the API of the total station.
Finally, we estimate the Euclidean 3D point x
1
of the
back-projected image point u
1
using Eqn. 4 and the
measured distance D
2
:
x
1
≈ G(D
2
, θ
1
, ϕ
1
) (12)
4.3 Support Line Method
Several 3D points on the visible wall are measured by
the user to estimate an 3D line which intersects the
corner of interest. The corner itself can then simply
be defined in the 2D image. The related 3D target
is calculated by finding the intersection point of the
back projected view ray with the previous estimated
3D doing with an least square approximation.
With support lines, the minimal measurement count
for 3D points is N
min
= 2. When using more than
two points, a robust estimation like RANSAC based
least square 3D line fitting can be applied (Fischler
and Bolles, 1981). Fig. 4 shows the support line con-
cept.
Measurement Flow. The simple measurement flow
is defined by following steps:
1. Use the pan/tilt control interface, until the target-
of-interest is visible in the image
2. Define target-of-interest in the image
3. Define support line with N ≥ 2 measurements
4. Calculate the 3D position of the target-of-interest
by intersecting the back-projected view ray with
the support line
Measuring Human-made Corner Structures with a Robotic Total Station using Support Points, Lines and Planes
21

Calculating the Support Line. For N = 2 the 3D
support line can be written directly as Eqn. 19. Fitting
the 3D line for N > 2 can be separated into two steps:
fitting the 3D line position and fitting the 3D line di-
rection. First, the center of mass of the 3D points is
subtracted:
x
i
=
(x
i
,y
i
,z
i
)
T
|
i=0...N−1
¯x =
1
N
·
N−1
∑
i=0
x
i
(13)
x
0
i
= x
i
− ¯x|
i=0...N−1
(14)
with ¯x as center of mass of the 3D point set. The trans-
lated 3D points x
0
i
are now centered around 0. Then,
the 3D points are normalized:
k = max(|x
0
x,i
|, |x
0
y,i
|, |x
0
z,i
|)|
i=0...N−1
(15)
x
00
i
=
x
0
i
k
|
i=0...N−1
(16)
and the 3D line orientation is calculated by stacking
points and solving the maximization problem:
A
00
=
x
00
x,0
x
00
y,0
x
00
z,0
x
00
x,1
x
00
y,1
x
00
z,2
.
.
.
x
00
x,N−1
x
00
y,N−1
x
00
z,N−1
max
||n||=1
(||A
00
·n||)
(17)
The solution is the eigenvector which belongs to the
largest eigenvalue and can be calculated by using
SVD (Klasing et al., 2009). The line orientation is
normalized for reasons of convenience:
n
0
=
n
||n||
=
n
0
x
n
0
y
n
0
z
(18)
A 3D line is fully specified by an arbitrary point on the
line and the orientation. For consistent calculations,
the 3D orientation can be interpreted as 3D direction
vector. Using the center of mass ¯x and the normalized
line direction n
0
, the fitted 3D line L in leased square
sense is given by
L (t) = ¯x +t ·n
0
(19)
Intersecting the View Ray with the Support Line.
First the 2D coordinate is back-projected to a 3D view
ray using Eqn. 6. The best approximation for 3D line
intersection can be found using Pl
¨
ucker coordinates
(Hartley and Zisserman, 2003). However, we imple-
mented 3D line intersection for two lines based on
simple vector math (Schneider and Eberly, 2003).
4.4 Support Plane Method
To get the 3D coordinates of a building corner, the
user measures several 3D points on the visible wall
to estimate an planar approximation of this wall. The
corner of interest can simply be defined in the 2D im-
age. The related 3D target is calculated by intersect-
ing the back-projected view ray with the previous es-
timated plane. The measurement concept is shown in
Fig. 4. The target-of-interest can be moved freely on
the plane.
Measurement Flow. The simple measurement flow
is defined by following steps:
1. Use the pan/tilt control interface, until the target-
of-interest is visible in the image
2. Define target-of-interest in the image
3. Define support plane with N ≥ 3 measurements
4. Calculate the 3D position of the target-of-interest
by intersecting the back-projected view ray with
the support plane
Calculating the Support Plane. In the easiest case
the plane can be estimated by estimating the non-
trivial solution of the linear homogeneous equation
system
A · p = 0 A =
x
x,0
x
y,0
x
z,0
1
x
x,1
x
y,1
x
z,2
1
.
.
.
x
x,N−1
x
y,N−1
x
z,N−1
1
(20)
where A is a matrix of stacked homogeneous 3D
points with a 3D point count N = 4. The plane pa-
rameters a, b, c and d of the implicit plane equation
are given by the 4 ×1 vector
p =
a
b
c
d
p
T
·
x
x
x
y
x
z
1
= 0 (21)
where x
x
, x
y
, x
z
are the coordinates of a 3D point on
the plane.
Solving for p in Eqn. 20 for N ≥4 becomes a con-
strained least squares minimization problem
min
||p||=1
(||A · p||) (22)
and can be solved with SVD (Klasing et al., 2009).
A more robust plane estimation encounters some ad-
ditional aspects:
• Minimal point set N ≥ 3 instead of N ≥ 4
• Normalization before computation for numerical
stability
• RANSAC optimization for robustness against out-
liers in case of N > 3
For minimal point set, we must estimate the plane di-
rection (rotation) and the plane translation separately.
This procedure is analogous to the one for the sup-
port line, following Eqns. 13-18, but solving for the
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
22

eigenvector which belongs to the smallest eigenvalue.
Finally, the implicit plane representation is given by
p =
n
0
x
n
0
y
n
0
z
−n
0T
· ¯x
(23)
This method requires at least N
min
= 3 measured 3D
points.
Intersecting the View Ray with the Support Plane.
First, the 2D coordinate is back-projected to a 3D
view ray using Eqn. 6. The target-of-interest is given
by the plane-ray intersection
t =
−(n
0T
·C + d)
n
0T
·n
ray
(24)
x
target
= C +t ·n
ray
(25)
with n
ray
as ray direction of the back projected im-
age point, C = 0 as camera origin and d = p(4) as
distance between the origin and the intersection point
(Schneider and Eberly, 2003). If the denominator of
Eqn. 24 is zero, the ray is either parallel to the plane
or lies directly on the plane.
5 EXPERIMENTS
We implemented the four methods described above
and created a graphical user interface for a tablet com-
puter, seamlessly interfacing the total station. The
GUI shown in Fig. 6 is used to conveniently access the
implementation and to enable even novice and non-
expert users to use the methods in an intuitive way.
Training time to introduce the concepts of measuring
and the individual methods was thereby reduced to
only around 10 minutes. After selection of the given
method, the operator is automatically guided through
the process to fulfill the measuring task, with a final
result given at the end.
We defined a simple evaluation setup for prove-of-
concept without the need of a laboratory for surveying
and measurement. This setup can be applied in con-
trolled indoor and in selected outdoor environments.
Our analysis does not follow the ISO 17123 standard
(ISO 17123-3:2001, 2001), since we conduct only a
comparative studies of the proposed methods, where
non-direct measurable targets are measured. We per-
formed two different types of measurements, namely
distance measurements and area measurements, and a
number of laboratory and outdoor real-world experi-
ments as follows.
Get Image
Mouse Modes
TS Direct Control
a) Define 2D Points (direct)
b) Define 2D Points (support point)
c) Define 2D Points (support line)
d) Define 2D Points (support plane)
Move Estimated 3D Point
Move 2D Point
c) Move 2D Point & Adjust Line
c) Move 2D Point on Line
Turn To Pixel
Joystick
Optical Zoom
3
Measure & Save
Measurement
Point_0
Point_1
Point_2
Point_3
...
Focus
Enable Laser
Face
1
Prototype GUI: Direct Measurement vs. Support Point/Line/Plane Method
File
Device
View
Settings
Help
Calibrate
Load File ...
Load Predefined (Points/Angles/Views)
Run Stationing
Point_0
Point_1
Point_2
Point_3
...
EDM
Crosshair
Image coordinates
Live view of TS
camera
TS pose control
Image based zoom and optical zoom
Face control: left/right
Digital Zoom
Measurement method
Image based
adjustments
3D based adjustment
3D measurements
and calculations
Estimated 3D
points (red stars)
Predefined
TS poses
1b
2b
x
y
1a
4d
1d
2d
3d
1b
2b
1c
2c
3c
Figure 6: GUI used in our system. It enables intuitive se-
lection of the method to use and guides the operator through
the measurement process.
Measurement Setup. We measured the distance
between two corners of a flat surface, whereby only
the front face of the surface is fully visible. This is
achieved by appropriately positioning the target and
the total station:
• Approx. same height of target center and camera
center
• Approx. perpendicular laser beam direction for
laboratory experiments and outdoors for ground
truth measurements
• Approx. perpendicular laser beam direction for
ground truth measurements and 45
◦
direction for
outdoor evaluation
The measurement setup is shown in Fig. 7. The dis-
tance between the total station and the measurement
target is about 5m in all experiments. The distance be-
tween the two top corners of the measurement indoor
target is about 0.6m.
Measurement Strategy. For Euclidean distance
evaluation, a single set measurement consists of the
measured 3D position of the first and the second cor-
ner of the target
7
. All measurements where converted
to Euclidean coordinates using the API of the device
driver. The result is given in the confidence interval
of ±2
ˆ
σ
d
, with
ˆ
σ
d
as unbiased standard deviation as-
suming unbiased normal distribution of the measure-
ments:
The Euclidean distance of measurement i between
two points p
i,0
and p
i,1
is calculated by
d
i
= ||p
i,1
−p
i,0
|| = ||
x
i,1
y
i,1
z
i,1
−
x
i,0
y
i,0
z
i,0
|| (26)
and the average distance
¯
d and the unbiased standard
7
Note that we use a half-set for our evaluations, since
we do not use the second telescope face (face right).
Measuring Human-made Corner Structures with a Robotic Total Station using Support Points, Lines and Planes
23

a)
planar surface (ref)
b)
planar
target
l
ref
l
corners
c)
laser dot
(ref)
d)
e)
f)
h)
g)
i)
laboratory environment
outdoor environment, survey
j)
Figure 7: Measurement setups for laboratory conditions and
for outdoor scenarios: a) measurement of the reference dis-
tance between the two top corners of the portable target,
b) portable target used to measure the distance between two
corners in laboratory conditions, c) detailed view of the pro-
jected laser dot during the reference measurement, d) refer-
ence measurement of a window in indoor and outdoor con-
ditions using perpendicular viewing angle, e) the same win-
dows measured with a viewing angle of 45 degree, f) and h)
the modelling clay for reference measurements, i), j) and k)
the outdoor window, the portable laboratory target and the
robotic total station.
deviation
ˆ
σis given by
¯
d =
∑
N−1
i=0
d
i
N
ˆ
σ =
s
∑
N−1
i=0
(d
i
−
¯
d)
2
N −1
(27)
For outlier removal, at least N = 3 sets must be
measured. Outliers are removed using median abso-
lute deviation (MAD) with ±3
ˆ
σ interval on distances
(Leys et al., 2013). The statistic evaluation is repeated
on the reduced data set.
We calculate the distance error between two points
d using
∆d = |
¯
d
re f
−
¯
d|±2 ·
q
ˆ
σ
re f
2
+
ˆ
σ
1
2
(28)
with
¯
d
re f
±2
ˆ
σ
d
re f
as reference distance and
¯
d ±2
ˆ
σ as
measured distances between two corners.
For area measurements, the area of a window in an
outdoor environment was used as second method for
indirect accuracy evaluation. A single set measure-
ment for the area of the window consists of the the
four measured 3D positions of the window corners.
The area of an polygon in 3D can be calculated using
the surveyor’s area (Braden, 1986). For the four point
case the calculation can be simplified to
A
i
=
1
2
(||(p
i,1
−p
i,0
) ×(p
i,2
−p
i,0
)||+
||(p
i,2
−p
i,0
) ×(p
i,3
−p
i,0
)||) (29)
where A
i
is the estimated area of the i
th
measurement
set and p
i, j
is the j
th
estimated window corner of set
i. We applied the same statistics on the areas A
i
as
provided for the distances d
i
.
For measuring the ground truth, we employed two
different approaches. For the laboratory target, we
aligned it with a planar surface and measured the dis-
tance using the total station. Note that this method
is suitable for portable targets and outer corners only.
For ground truth estimation of immovable targets like
windows, we filled the corners with modelling clay
to create a quasi-planar surface around the corners,
which could be measured by the total station. This
method is suitable for fixed and portable targets and
is well suited for inner corners
8
.
5.1 Laboratory Measurements
First, we conducted two experiments with the
portable target. We measured the ground truth dis-
tance between the two top corners as shown in Fig. 7
a) and b). Then we used the four different methods
to perform the measurement again, giving results as
listed in the first group of rows in Tab. 1. The support
line and support plane methods either outperform the
others or perform on par.
In a second experiment, we measured the same
distance again with the total station pointing at the
target at an angle of approximately 45
◦
. The results,
given in the second group of rows in Tab. 1, indicate
that the support line and support plane based methods
achieve considerably better results than the standard
method and the support point method.
Given a window as seen from the interior of a
building, we performed four more experiments with
a perpendicular and a viewing angle of 45
◦
. First,
we measured the distance between the two corners,
then we measured the area of the window as shown in
Fig. 7 d) and e). The results are given in group 3 and
4 of Tab. 1 and group 1 and 2 of Tab. 2 respectively.
Overall, the support line and support plane based
methods achieve considerably better results than the
standard method and the support point method, or per-
form at least on par.
5.2 Outdoor Measurements
We conducted four outdoor experiments, where we
measured the extents and the area of a window from a
perpendicular and a 45
◦
point of view. We measured
8
Note that we performed the ground truth measurements
immediately before the experiments, to ensure that errors
due to changes in environmental conditions are negligible.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
24

the ground truth distance and area as shown in Fig. 7
d), f) and h). Then, we applied the four measurement
methods again. The results are shown in in group 5
and 6 of Tab. 1 and group 3 and 4 of Tab. 2. The
support line and the support plane methods are overall
more suitable and give better results, or perform at
least on par.
5.3 Pilot Study
We asked a group of eight novice users and one expert
user to perform all different methods on the task of
measuring the distance of the upper two corners of
an outdoor window and the area of the window, in
analogy to the experiment described above. All users
were introduced to the system, and all measurements
with all methods were repeated three times.
Even for novice users with a short introduction to the
system, the results for the support line and support
plane method clearly outperform the standard method
and the support point method, as indicated by the re-
sults listed at the bottom of Tab. 1 and Tab. 2 respec-
tively.
The results in terms of the accuracy of the individual
methods for the distance and the area measurements
is depicted in Fig. 8. The line and the support plane
method consistently and considerably outperform the
standard and support point method, and, more impor-
tantly, all measurements have a considerably smaller
variation.
The users were asked to complete a short question-
aire about the overall usability and the intuitiveness
of the GUI and the overall approaches. The questions
and the answers given by the users are summed in
Tab 3. At a glance, users mainly voted for the support
line and support plane method to be favorable over
the standard and the support point method in terms of
ease of use. Being asked about the usefulness of the
three methods introduced in this work, users tended to
favor the support line and the support plane method
over the support line method. Concerning the accu-
racy and rapidness of the measurements, users pre-
ferred the plane support and the line support method,
respectively.
6 DISCUSSION AND
CONCLUSION
In this work, we have described different methods for
indirect measurements using a total station. Based on
the results of the experiments conducted, our methods
consistently outperform the standard method, even
when applied by novice users. One reason for the
Table 1: Distance measurements for experiments and meth-
ods: ground truth (r), direct targeting (a), support point (b),
support line (c), support plane (d).
Record Meth. d [m]
ˆ
σ
d
[m] N d
re f
[m] ∆d [m]
lab.
90
◦
(r) 600.191e-3 82.942e-6 4.000 600.191e-3 0
(a) 586.664e-3 273.151e-6 4.000 600.191e-3 13.527e-3
(b) 599.712e-3 39.655e-6 3.000 600.191e-3 478.897e-6
(c) 599.803e-3 866.189e-6 5.000 600.191e-3 387.538e-6
(d) 604.457e-3 3.636e-3 5.000 600.191e-3 4.266e-3
lab.
45
◦
(r) 600.191e-3 82.942e-6 4.000 600.191e-3 0
(a) 582.446e-3 1.192e-3 5.000 600.191e-3 17.745e-3
(b) 584.189e-3 240.581e-6 4.000 600.191e-3 16.002e-3
(c) 598.194e-3 229.861e-6 3.000 600.191e-3 1.997e-3
(d) 598.545e-3 654.487e-6 5.000 600.191e-3 1.646e-3
indoor
90
◦
(r) 881.992e-3 362.719e-6 10.000 881.992e-3 0
(a) 893.240e-3 820.525e-6 8.000 881.992e-3 11.248e-3
(b) 886.912e-3 1.921e-3 10.000 881.992e-3 4.920e-3
(c) 887.088e-3 830.455e-6 10.000 881.992e-3 5.096e-3
(d) 885.561e-3 957.555e-6 9.000 881.992e-3 3.569e-3
indoor
45
◦
(r) 881.702e-3 221.990e-6 5.000 881.702e-3 0
(a) 897.636e-3 3.285e-3 5.000 881.702e-3 15.934e-3
(b) 894.017e-3 2.142e-3 5.000 881.702e-3 12.314e-3
(c) 882.071e-3 607.033e-6 5.000 881.702e-3 369.144e-6
(d) 882.079e-3 1.165e-3 5.000 881.702e-3 377.119e-6
outdoor
90
◦
(r) 566.360e-3 20.239e-6 4.000 566.360e-3 0
(a) 576.559e-3 351.065e-6 4.000 566.360e-3 10.199e-3
(b) 565.040e-3 1.615e-3 5.000 566.360e-3 1.320e-3
(c) 564.474e-3 32.128e-6 3.000 566.360e-3 1.886e-3
(d) 564.664e-3 200.672e-6 4.000 566.360e-3 1.696e-3
outdoor
45
◦
(r) 2.192 107.789e-6 10.000 2.192 0
(a) 2.196 1.182e-3 10.000 2.192 4.463e-3
(b) 2.193 1.248e-3 10.000 2.192 1.761e-3
(c) 2.189 819.832e-6 10.000 2.192 2.303e-3
(d) 2.190 1.212e-3 10.000 2.192 1.587e-3
pilot
study
(r) 2.192 107.789e-6 10.000 2.192 0
(a) 2.214 14.497e-3 53.000 2.192 22.456e-3
(b) 2.218 21.181e-3 53.000 2.192 26.853e-3
(c) 2.188 4.148e-3 54.000 2.192 3.529e-3
(d) 2.188 4.740e-3 54.000 2.192 3.406e-3
Table 2: Area measurements for different experiments and
methods: ground truth (r), direct targeting (a), support point
(b), support line (c), support plane (d).
Record Meth. d [m]
ˆ
σ
d
[m] N d
re f
[m] ∆d [m]
indoor
90
◦
(r) 881.992e-3 362.719e-6 10.000 881.992e-3 0
(a) 893.240e-3 820.525e-6 8.000 881.992e-3 11.248e-3
(b) 886.912e-3 1.921e-3 10.000 881.992e-3 4.920e-3
(c) 887.088e-3 830.455e-6 10.000 881.992e-3 5.096e-3
(d) 885.561e-3 957.555e-6 9.000 881.992e-3 3.569e-3
indoor
45
◦
(r) 838.086e-3 37.490e-6 4.000 838.086e-3 0
(a) 862.706e-3 1.079e-3 4.000 838.086e-3 24.620e-3
(b) 854.846e-3 2.750e-3 5.000 838.086e-3 16.760e-3
(c) 840.750e-3 20.712e-6 3.000 838.086e-3 2.663e-3
(d) 839.188e-3 53.872e-6 3.000 838.086e-3 1.102e-3
outdoor
90
◦
(r) 883.245e-3 25.067e-6 4.000 883.245e-3 0
(a) 888.800e-3 14.479e-6 3.000 883.245e-3 5.555e-3
(b) 882.519e-3 807.959e-6 4.000 883.245e-3 726.362e-6
(c) 881.964e-3 813.967e-6 5.000 883.245e-3 1.282e-3
(d) 882.181e-3 249.838e-6 4.000 883.245e-3 1.065e-3
outdoor
45
◦
(r) 1.733 82.370e-6 5.000 1.733 0
(a) 1.747 2.096e-3 5.000 1.733 13.809e-3
(b) 1.737 2.827e-3 5.000 1.733 4.119e-3
(c) 1.729 472.108e-6 4.000 1.733 4.515e-3
(d) 1.731 632.497e-6 4.000 1.733 1.632e-3
pilot
study
(r) 1.733 82.370e-6 5.000 1.733 0
(a) 1.790 33.749e-3 27.000 1.733 56.605e-3
(b) 1.751 13.249e-3 26.000 1.733 18.326e-3
(c) 1.726 5.354e-3 27.000 1.733 6.882e-3
(d) 1.727 5.486e-3 27.000 1.733 6.431e-3
huge gain in accuracy is due to the definition of the
reference method, as the requirement that the pro-
jected laser beam has to be fully on the visible surface
causes the big systematic error of the measurement
method.
As a result of our experimental evaluation, we
will further work on improving the individual meth-
ods to automatically detect outliers (e.g. by employ-
Measuring Human-made Corner Structures with a Robotic Total Station using Support Points, Lines and Planes
25
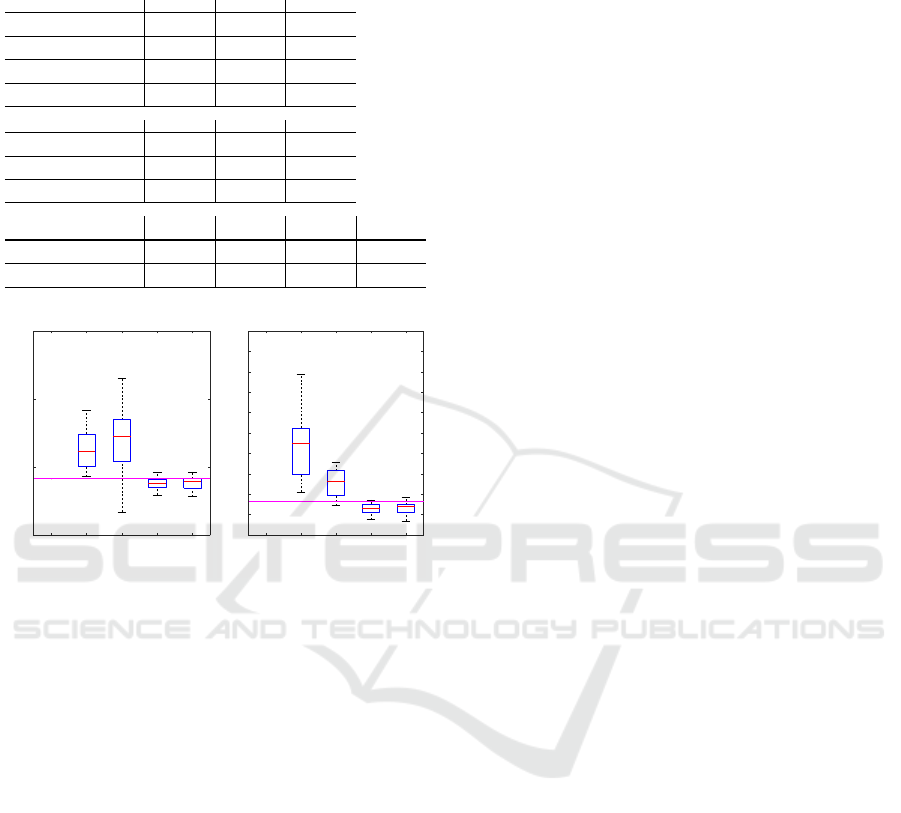
Table 3: Survey results for eight novice and one expert user
concerning the ease, usefulness, accuracy and rapidness of
the individual methods.
Question
Very easy [%] OK [%] Difficult [%]
How easy was it to use the
DIRECT method?
55.6 22.2 22.2
How easy was it to use the
POINT support method?
88.9 11.1 0
How easy was it to use the
LINE support method?
100 0 0
How easy was it to use the
PLANE support method?
100 0 0
Question
Yes [%] Not sure [%] No [%]
Do you think the POINT
support method is useful?
44.4 44.4 11.1
Do you think the LINE
support method is useful?
77.8 22.2 0
Do you think the PLANE
support method is useful?
88.9 11.1 0
Question
Direct [%] Point support
[%]
Line support
[%]
Plane support
[%]
Which method do you prefer for
ACCURATE measurements?
0 0 44.4 55.6
Which method do you prefer for
FAST measurements?
11.1 22.2 44.4 22.2
direct_ref
direct
point
line
plane
Method
2.15
2.2
2.25
2.3
Distance [m]
Box plot of measured distances
direct_ref
direct
point
line
plane
Method
1.7
1.72
1.74
1.76
1.78
1.8
1.82
1.84
1.86
1.88
1.9
Area [m
2
]
Box plot of measured areas
Figure 8: Pilot study results: distances between the two first
window corners (left) and areas of the window (right) (out-
liers removed before evaluation). The plots show the me-
dian of the distance and area measurements, the lower and
upper extremes, the 25
th
and the 75
th
percentile. The hori-
zontal lines are the reference distance and area.
ing a RANSAC scheme on multiple measurements),
and to further improve the GUI to more intuitively
and automatically guide users through the measure-
ment process.
We want to emphasize that, despite the basic al-
gorithmic concepts are known for years, practical ap-
plications are still largely missing due to the issues
arising in real measurement situations. As shown in
this work, it is therefore highly relevant to study these
concepts in practice to identify and overcome short-
comings of the underlying algorithms.
ACKNOWLEDGEMENTS
This work was funded by a grant from the Compe-
tence Centers for Excellent Technologies (COMET)
843272 with support from Hilti AG.
REFERENCES
Amann, M.-C., Bosch, T. M., Lescure, M., Myllylae, R. A.,
and Rioux, M. (2001). Laser ranging: a critical review
of usual techniques for distance measurement. Optical
Engineering, 40(1):10–19.
Braden, B. (1986). The Surveyor’s Area Formula. The Col-
lege Mathematics Journal, 17(4):326.
Coaker, L. H. (2009). Reflectorless Total Station Measure-
ments and their Accuracy, Precision and Reliability.
B.S. Thesis, University of Southern Queensland.
Criminisi, A., Reid, I., and Zisserman, A. (2000). Single
view metrology. International Journal of Computer
Vision, 40(2):123–148.
Ehrhart, M. and Lienhart, W. (2015). Image-Based Dy-
namic Deformation Monitoring of Civil Engineering
Structures from Long Ranges. Image Processing:
Machine Vision Applications VIII, 9405(1):94050J–
94050J–14.
Fathi, H. and Brilakis, I. (2013). A Videogrammetric As-
Built Data Collection Method for Digital Fabrication
of Sheet Metal Roof Panels. Advanced Engineering
Informatics, 27(4):466–476.
Fischler, M. A. and Bolles, R. C. (1981). Random Sample
Consensus: A Paradigm for Model Fitting with Ap-
plications to Image Analysis and Automated Cartog-
raphy. Commun. ACM, 24(6):381–395.
Hartley, R. and Zisserman, A. (2003). Multiple View Geom-
etry in Computer Vision. Cambridge University Press,
Cambridge, UK New York.
ISO 17123-3:2001 (2001). ISO 17123-3: Optics and opti-
cal instruments – Field procedures for testing geode-
tic and surveying instruments. Standard, International
Organization for Standardization, Geneva, CH.
Jadidi, H., Ravanshadnia, M., Hosseinalipour, M., and Rah-
mani, F. (2015). A Step-by-Step Construction Site
Photography Procedure to Enhance the Efficiency of
As-Built Data Visualization: A Case Study. Visual-
ization in Engineering, 3(1):1–12.
Juretzko, M. (2004). Reflektorlose Video-Tachymetrie ein
integrales Verfahren zur Erfassung geometrischer und
visueller Informationen. PhD thesis, Ruhr University
Bochum, Faculty of Civil Engineering.
Klasing, K., Althoff, D., Wollherr, D., and Buss, M. (2009).
Comparison of surface normal estimation methods for
range sensing applications. 2009 IEEE International
Conference on Robotics and Automation, pages 3206–
3211.
Leys, C., Ley, C., Klein, O., Bernard, P., and Licata, L.
(2013). Detecting outliers: Do not use standard devi-
ation around the mean, use absolute deviation around
the median. Journal of Experimental Social Psychol-
ogy, 49(4):764–766.
Martin, D. and Gatta, G. (2006). Calibration of total stations
instruments at the ESRF. Proceedings of XXIII FIG
Congress, pages 1–14.
Nichols, J. M. and Beavers, J. E. (2003). Development and
Calibration of an Earthquake Fatality Function. Earth-
quake Spectra, 19(3):605–633.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
26

Reda, A. and Bedada, B. (2012). Accuracy analysis and
Calibration of Total Station based on the Reflectorless
Distance Measurement. Master’s thesis, Royal Insti-
tute of Technology (KTH), Sweden.
Scherer, M. (2001). Advantages of the Integration of Im-
age Processing and Direct Coordinate Measurement
for Architectural Surveying - Development of the Sys-
tem TOTAL. FIG XXII International Congress.
Scherer, M. (2004). Intelligent Scanning with Robot-
Tacheometer and Image Processing: A Low Cost Al-
ternative to 3D Laser Scanning? FIG Working Week.
Scherer, M. and Lerma, J. L. (2009). From the Conven-
tional Total Station to the Prospective Image Assisted
Photogrammetric Scanning Total Station: Compre-
hensive Review. Journal of Surveying Engineering,
135(4):173–178.
Schneider, D. (2009). Calibration of a Riegl LMS-Z420i
based on a multi-station adjustment and a geomet-
ric model with additional parameters. The Interna-
tional Archives of the Photogrammetry, Remote Sens-
ing and Spatial Information Sciences 38 (Part 3/W8),
XXXVIII:177–182.
Schneider, P. and Eberly, D. (2003). Geometric Tools for
Computer Graphics. Boston Morgan Kaufmann Pub-
lishers, Amsterdam.
Schulz, T. (2007). Calibration of a Terrestrial Laser
Scanner for Engineering Geodesy. PhD thesis, ETH
Zurich, Switzerland.
Siu, M.-F., Lu, M., and AbouRizk, S. (2013). Combining
Photogrammetry and Robotic Total Stations to Obtain
Dimensional Measurements of Temporary Facilities
in Construction Field. Visualization in Engineering,
1(1):4.
Topcon Corporation (2011). Imaging Station IS Series, In-
struction Manual.
Uren, J. (2010). Surveying for Engineers. Palgrave Macmil-
lan, Basingstoke England New York.
Zeiske, K. (2004). Surveying made easy. https://www1.aps.
anl.gov/files/download/DET/Detector-Pool/
Beamline-Components/Lecia Optical Level/
Surveying en.pdf.
Measuring Human-made Corner Structures with a Robotic Total Station using Support Points, Lines and Planes
27
