Coherent Ray-Space Hierarchy Via Ray Hashing and Sorting

Nuno T. Reis, Vasco S. Costa and Jo

ao M. Pereira

INESC-ID / Instituto Superior T

ecnico, University of Lisbon, Rua Alves Redol 9, 1000-029 Lisboa, Portugal

Keywords:

Rasterization, Ray-Tracing, Ray-Hashing, Ray-Sorting, Bounding-Cone, Bounding-Sphere, Hierarchies,

GPU, GPGPU.

Abstract:

We present an algorithm for creating an n-level Ray-Space Hierarchy (RSH) of coherent rays that runs on a

GPU. Our algorithm uses a rasterization stage to process the primary rays, then inputs those results in the RSH

stage which processes the secondary rays. The RSH algorithm generates bundles of rays, hashes them and sorts

them. Thus we generate a ray list containing adjacent coherent rays to improve the rendering performance of

the RSH vs a classical approach. Moreover, scene geometry is partitioned into a set of bounding spheres and,

then, intersected with the RSH to further decrease the amount of false ray bundle-primitive intersection tests.

We show that our technique notably reduces the amount of ray-primitive intersection tests, required to render

an image. In particular it performs up to 50% better in this metric than other algorithms in this class.

1 INTRODUCTION

Naive Ray-Tracing (RT), algorithmic complexity is N

x M where N rays are tested against M polygons. Per-

formance is thus low, especially with complex scenes

due to the amount of intersection tests. To optimize

this naive approach, two common scene partition ap-

proaches, Object Hierarchies and Spatial Hierarchies,

are followed to reduce the intersection tests. Our work

instead focuses on Ray Hierarchy optimizations. This

is a less well explored area of the RT domain and one

that is complementary to the Object-Spatial Hierar-

chies. In particular, this paper presents the Coher-

ent Ray-Space Hierarchy (CRSH) algorithm. CRSH

builds upon the Ray-Space Hierarchy (RSH) (Roger

et al., 2007) and Ray-Sorting algorithms (Garanzha

and Loop, 2010). RSH uses a tree where each node

stores a bounding sphere-cone containing a set of

rays. The tree is built via a bottom-up procedure and

traversed in a top-down fashion. Our CRSH algorithm

adds Ray-Sorting to achieve higher efﬁciency in each

tree node and then expands on this basis with mesh

culling and improved hashing methods.

We hypothesize that improving the coherency of

the rays within each tree node shall lead to tighter

bounding sphere-cones, reducing the amount of inter-

sections. We use hashing, tuned to the type of the ray

(e.g. shadow, reﬂection and refraction), to improve hi-

erarchy efﬁciency. Finally we introduce whole mesh

bounding spheres to reduce intersection tests at the hi-

erarchy top level. This shallow spherical BVH allows

us to reduce ray-primitive intersections. We note that

our technique uses a rasterization stage to compute

primary rays, RT is reserved for secondaries.

Our main contributions are:

- a compact ray-space hierarchy (RSH) based on

ray-indexing and ray-sorting to reduce the amount

of ray-primitive intersections.

- improved hashing methods.

- culling meshes from the RSH prior to primitive

traversal.

2 BACKGROUND AND RELATED

WORK

Ray-tracing (Whitted, 1980) is a global illumination

technique for synthesis of realistic images through re-

cursive ray-casting. The ray tracing algorithm casts

primary rays from the eye. When the rays intersect

geometry they can generate extra secondary rays: e.g.

shadow, reﬂection and refraction rays.

These rays differentiate ray-tracing from the ras-

terization algorithm as they allow realistic reﬂec-

tions, refractions and shadows without additional

techniques. However at a cost making the ray-tracing

approach compute expensive. There is extensive and

ongoing research around its optimization. Much re-

search involves hierarchies, in the Object or Spatial

T. Reis N., S. Costa V. and M. Pereira J.

Coherent Ray-Space Hierarchy Via Ray Hashing and Sorting.

DOI: 10.5220/0006098001950202

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 195-202

ISBN: 978-989-758-224-0

195

domains, to decrease intersection tests in a divide and

conquer fashion.

Object and Spatial Hierarchies help accelerate in-

tersection calculations by culling polygons and ob-

jects far from the rays, hence by reducing the amount

geometry to test.

Ray-Space Hierarchies, use ray bundles or ray

caching to achieve the goal of reducing intersections.

Instead of creating hierarchies based on scene geom-

etry, they are based on the rays being cast in each

frame. Our work is based on this approach and em-

ploys ray bundling and ray hashing (Arvo and Kirk,

1987) (Aila and Karras, 2010).

Roger et al. (Roger et al., 2007)’s RSH algorithm

has ﬁve steps. The scene is ﬁrst rasterized, for the

primary ray trace output, unlike in a traditional ray-

tracer. The ﬁrst batch of secondary rays is generated

using this information and becomes the basis for the

RSH. The secondaries are bundled into nodes with a

sphere bounding ray origins and a cone bounding ray

directions: this is the bottom-level of the tree. Up-

per levels are created by merging nodes from lower

levels. Once the top-level is reached, the scene ge-

ometry is intersected with the RSH. Hits are stored as

triangle-id/node-id integer pairs. Only these hits will

be tested at the lower levels of the tree, reducing in-

tersection tests within each level. However, since rays

aren’t sorted, even at lower levels of the tree, nodes

will be quite wide requiring too much geometry inter-

sections and increasing the amount of intersections.

We attempt to solve this problem by sorting rays prior

to creating the RSH.

Garanzha and Loop (Garanzha and Loop, 2010)

introduced an algorithm using parallel primitives to

adapt the ray-tracing algorithm to the GPU. Their al-

gorithm sorts generated rays and creates tight-ﬁt frus-

tums on the GPU and then intersects them with the

scene’s Bounding Volume Hierarchy (BVH) tree built

on the CPU. One of the most interesting aspects is the

fast ray sorting step which is done with parallel GPU

primitives. This reduces the overall time of the op-

eration. This approach can be combined with Roger

et al’s (Roger et al., 2007) algorithm to create a more

efﬁcient RSH.

The DACRT (Mora, 2011) algorithm employs

a ray-stream approach that generates a kd-tree on

the ﬂy, while traversing scene geometry, in order to

achieve a low time to ﬁrst image. Similarly to Roger’s

RSH it also uses conic packets to bundle secondary

rays. However this procedure is limited by the fact

that it can only bundle rays with the exact same origin

within the same cone. In addition it ray-traces pri-

mary rays. This has additional computational over-

head, compared to a rasterization mechanism, hence

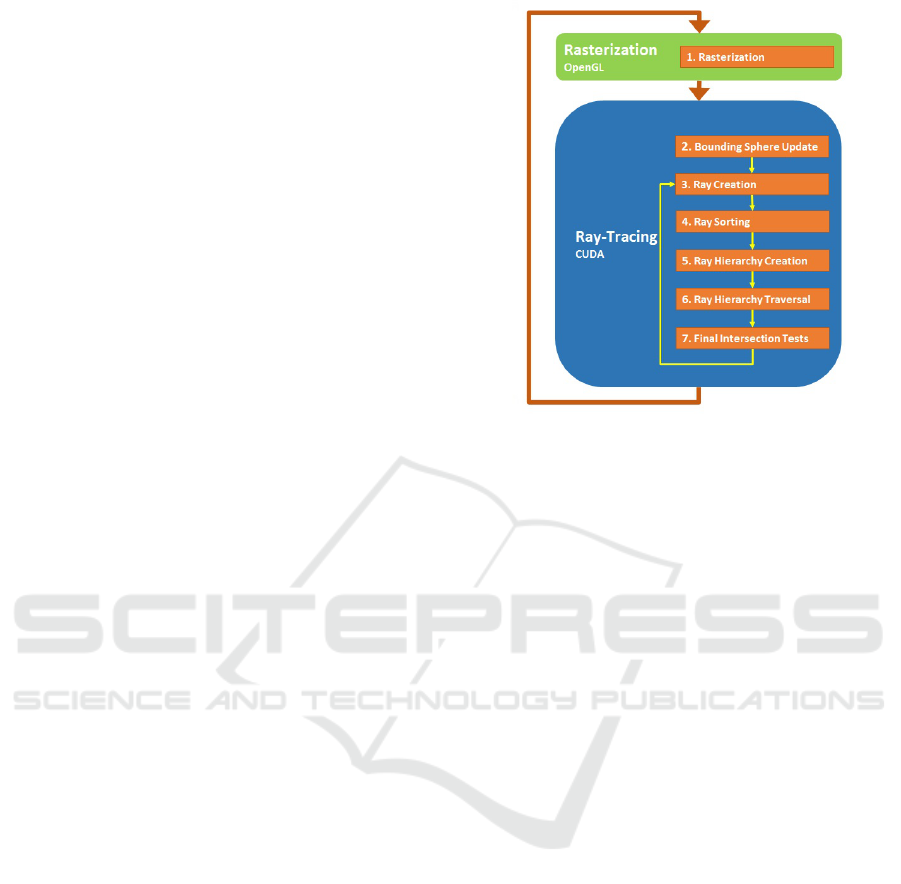
Figure 1: Coherent Ray-Space Hierarchy Overview.

it has worse rendering performance at primaries and

less opportunities for bundling secondaries.

CHC+RT (Mattausch et al., 2015) uses combined

hierarchies in ray space (RSH) and object space

(BVH). It does not use explicit ray bounding prim-

itives. It conservatively culls non-intersecting trian-

gle and screen-space batches. This approach is more

compute intensive on later stages due to the much

simpler RSH, but results in less branch divergence,

making it suitable for GPU implementation. The

BVH is built ofﬂine, on the CPU, then transferred

to the GPU. This high quality BVH has fast traver-

sal time, for rapid rendering of static or rigid-body

scenes, but the technique is poorly suited for dynamic

geometry with a high time to ﬁrst image.

3 OUR ALGORITHM

Our algorithm is performed in seven steps (see Fig-

ure 1). In each frame, steps 1 and 2 are executed just

once while steps 3 through 7 are executed once per ray

batch. Batches can have any combination of shadow,

reﬂection, or refraction rays.

3.1 Rasterization

Rasterization is the ﬁrst step to be performed. Al-

though Rasterization solves the rendering problem

conversely vs Ray-Tracing (i.e. projecting primi-

tives to the screen, vs projecting rays backwards to

the primitives), one can complement the other. The

ﬁrst set of rays, the primary rays, does not convey

the global illumination effects that Ray-Tracing can

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

196

achieve, e.g. Shadows, Reﬂections and Refractions.

Hence Rasterization can convey visual results similar

to tracing primary rays, while being much faster and

optimized in graphics hardware. Supplementing the

Rasterization of primary rays with the Ray-Tracing

of secondary rays get us the beneﬁts from both tech-

niques: the efﬁciency of Rasterization and the global

illumination effects from Ray-Tracing.

In order to combine both techniques, the output

from the fragment shaders used to rasterize the scene

must provide more than just the fragment colors. We

have to create different render targets according to the

information we want to store. In our case, we output

for each fragment its position and normal as well as

its diffuse and specular properties. In terms of imple-

mentation, the fragment shader outputs four different

textures, each containing four 32-bit ﬂoats per pixel.

These textures are generated with OpenGL/GLSL and

are then the ﬁrst level of secondary rays are computed

in CUDA.

3.2 Ray-Tracing

3.2.1 Bounding Sphere Update

Here we update object bounding spheres according

to the transformations (e.g. translate, scale) applied

to the object they contain. Since we only update

the center and radius, there is no need to recalcu-

late the bounding spheres in each frame (transforma-

tions do not invalidate bounding spheres). The min-

imum bounding sphere of the object meshes is pre-

computed with (G

artner, 1999)s algorithm so there is

no impact on render time performance.

3.2.2 Secondary Ray Creation

After the Rasterization step, we generate the sec-

ondary rays. We create an index, for each individual

ray, to speed up ray sorting later on. We use a different

hashing function for each type of ray (see Figures 2,

3). Since each ray has an origin and a direction it

would be straightforward to use these parameters to

create our hash. However for shadow rays it is suf-

ﬁcient to use the light-index, and the ray direction.

This is doable if we invert the origin of the shadow

ray so that it is located at the light source rather than

the originating fragment. To reduce the size of the

hash keys we convert the ray direction into spherical

coordinates (Glassner, 1990) and store both, the light

index and the spherical coordinates, into a 32-bit in-

teger, with the light index having the higher bit-value

such that the shadow rays are sorted a priori according

to the light source.

Figure 2: Shadow Ray Hash.

The Reﬂection and Refraction rays are also con-

verted to spherical coordinates. However, in this case,

the ray origin is used in the hash, given that these

rays are not coherent with regards to the origin, un-

like shadow rays.

Figure 3: Reﬂection and Refraction Ray Hash.

Once generation is complete, we have an array

with the generated secondary rays as well as two ar-

rays with the ray keys (ray hashes) and the ray val-

ues (ray position in the ray array) and a ﬁnal array

with head ﬂags which indicate if there is a ray in the

corresponding position within the key-value arrays,

where we store either a 0 or a 1, indicating if there is

a ray or not, respectively. Using the information from

the head ﬂags array we then run a trimming operator

on the key-value arrays (see Figure 4). This is done

by ﬁrst applying an inclusive scan operator (Merrill

and Grimshaw, 2009) on the head ﬂags array, which

gives us the number of positions each pair needs to be

shifted to the left. This is done in order to trim the

arrays (Pharr and Fernando, 2005).

Figure 4: Array Trimming.

3.2.3 Secondary Ray Sorting

Here we use a compression-sorting-decompression

scheme, expanding on prior work by Garanzha and

Loops (Garanzha and Loop, 2010). The compression

step exploits the local coherency of rays. Even for

secondary rays, the bounces generated by two adja-

cent rays have a good chance of being coherent. This

can result in the same hash value for both bounces.

Given this information, we compress the ray key-

value pairs into chunks, minimizing the number of

Coherent Ray-Space Hierarchy Via Ray Hashing and Sorting

197

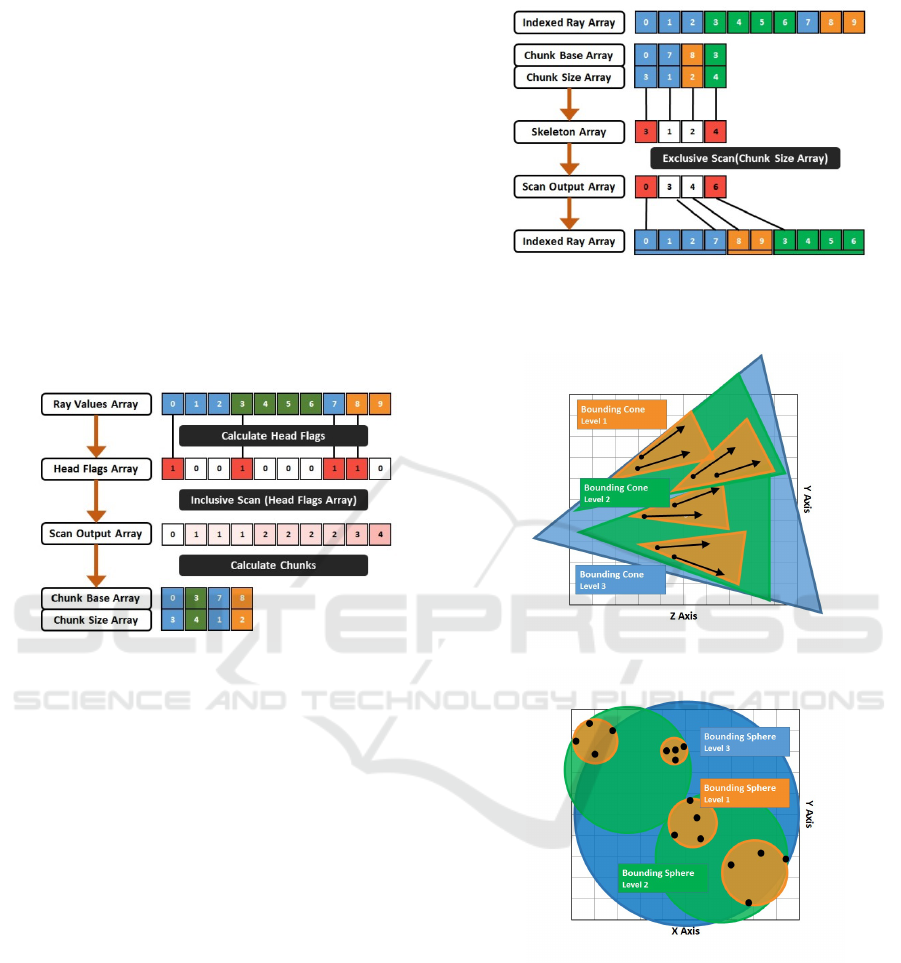
pairs that need to be sorted. To compress the pairs

we utilize a head ﬂags array with the same size as the

key-value pair array, initializing it with 0s in every

position and inserting 1s into positions in which the

key (hash) of the corresponding pair differs from the

previous pair. After populating the head ﬂags array

we apply an inclusive scan operator on it (Merrill and

Grimshaw, 2009). By combining the head ﬂags array

with the scan output array we create the chunk keys,

base and size arrays, which contain the hash, start-

ing index and size of the corresponding chunks (see

Figure 5). The chunk keys are represented in differ-

ent colors at the image below. The chunk base array

represents the original position of the ﬁrst ray in the

chunk while the chunk size array represents the size

of the chunk, needed for the ray array decompression.

Figure 5: Ray Compression into Chunks.

After ray compression we have an array of chunks

with the information required to reconstruct the initial

rays array. So we can begin the actual sorting. We

radix sort (Merrill and Grimshaw, 2010) the chunks

array according to the chunk keys.

Decompression works by creating a skeleton ar-

ray. This skeleton array is similar to the head ﬂag

arrays we created before except that it contains the

size of the sorted chunks. Next we apply an exclusive

scan operator on the skeleton array. This will give us

the positions of the chunks starting positions on the

sorted key and value arrays. After creating these two

arrays for each position in the scan array we ﬁll the

sorted ray array. We start in the position indicated in

the scan array and ﬁnish after ﬁlling the number of

rays contained within the corresponding chunk.

3.2.4 Ray Hierarchy Creation

With the sorted rays we can now create the actual hi-

erarchy. Since the rays are now sorted coherently the

hierarchy will be much tighter in its lower levels, giv-

ing us a smaller number of intersection candidates as

we traverse further down the hierarchy. Each node in

the hierarchy is represented by a sphere and a cone

Figure 6: Ray Decompression from Chunks.

(see Figures 7, 8).

Figure 7: Bounding Cone - 2D View.

Figure 8: Bounding Sphere - 2D View.

The sphere contains all the nodes ray origins while

the cone contain the rays themselves (see Figure 9).

This structure is stored with eight ﬂoats: the sphere

center and radius (four ﬂoats) and the cone direction

and spread angle (four ﬂoats). Construction of the

hierarchy is done in a bottom-up fashion. We start

with the leaves, with spheres of radius 0 and a cone

spread angle equal to 0. These leaves correspond to

sorted rays. Parent nodes are created by merging child

nodes. The number of children combined per node is

parametrized.

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

198

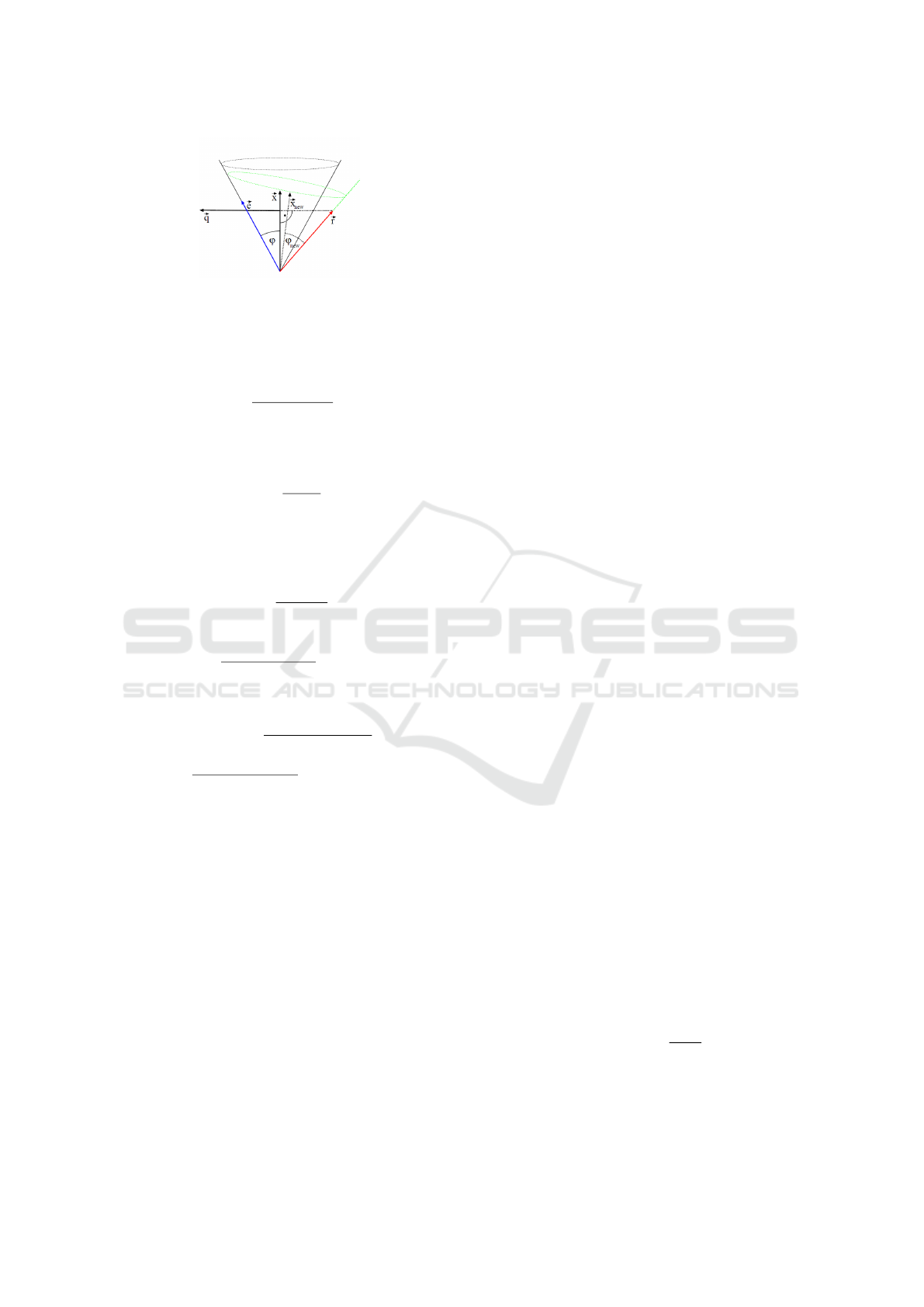
Figure 9: Cone-Ray Union - 2D View. courtesy of (Sz

ecsi,

2006).

We use the formulas below to create compact

cones (Sz

ecsi, 2006) for the ﬁrst level nodes.

~q =

(~x ·~r) ·~x −~r

|(~x ·~r) ·~x −~r|

(1)

~e =~x · cos(φ) +~q · sin φ (2)

new

~e +~r

|~e +~r|

(3)

cosφ

new

=~x

new

·~r (4)

Otherwise we use these formulas to merge cones:

new

+ ~x

|~x

+ ~x

(5)

cosφ

new

arccos(~x

+ ~x

)

+ max(φ

,φ

) (6)

Finally we merge spheres with this formula:

center

new

center

+ center

(7)

radius

new

|center

− center

+ max(radius

,radius

)

(8)

Each ray needs to know the corresponding pixel.

Rays are out of order due to sorting. We need a way

to map rays back to screen pixels. Since the hierarchy

is not tied to geometry in the scene it does not matter

for hierarchy creation whether the scene is dynamic

or static. What matters is the number of ray bounces,

so if there are more pixels occupied in the screen, the

hierarchy will have more nodes.

Roger et al. (Roger et al., 2007) also noted that

some nodes might become too large as we travel

higher up into the hierarchy. To mitigate this prob-

lem we decided to limit the number of levels gener-

ated and subsequently the number of levels traversed.

Since rays are sorted before this step, there is much

higher coherency between rays in the lower levels.

If we focus on these rays and ignore the higher lev-

els of the hierarchy we will have better results (as we

shall see in Section 5). There is a possibility that we

might end up having more local intersection tests but

since the nodes in the higher levels of the hierarchy

are quite large, we would most likely end up having

intersections with every single triangle. Thus having

no real gain from calculating intersections on these

higher level nodes to begin with.

3.2.5 Ray Hierarchy Traversal

Once we have an hierarchy tree we can traverse it.

Prior to traversal we compute the bounding spheres

for each object in the scene using Bernd Gartners al-

gorithm (G

artner, 1999).

For the top level of the ray tree we intersect tree

nodes with bounding spheres to further cull intersec-

tions. Finally we traverse the tree in a top-down order,

intersecting each node with geometry. Since parent

nodes fully contain child nodes, triangles rejected on

parent nodes will not be tested again on child nodes.

Let us say we start traversing the tree with the root

node. If a triangle does not intersect the root then this

means that speciﬁc triangle will not intersect any of

the children. Since it is the root node, no ray in the

scene will intersect it so we do not have to do any

further intersections with it. We store the intersection

information per level in an array so that child nodes

know the sets of triangles they have to compute inter-

sections against. The intersection tests being run at

this stage are coarse grained. They use the triangle

bounding spheres since we have to do the actual in-

tersection tests in the ﬁnal stage anyway. Intersection

tests are run in parallel so there is an issue regarding

empty spaces in the textures that contain intersection

information. These arrays need to be trimmed using

the same procedure that was used after ray generation.

These hits are stored as an int32 in which the ﬁrst 18

bits store the node id and the last 14 bits store the tri-

angle id. This is not a problem for larger scenes as

those are processed in triangle batches. Each hit only

needs to store the maximum number of triangles per

batch.

To calculate the intersection with the node, i.e. the

union of a sphere and a cone, we simplify the prob-

lem by enlarging the triangles bounding sphere (Er-

icson, 2004) and reducing the cones size (see Fig-

ure 10). Cone-sphere intersections were described by

Amanatides (Amanatides, 1984). We use the formula

in Roger et al. (Roger et al., 2007).

result = |C − H| × tan α +

d + r

cosα

> |P − H| (9)

Coherent Ray-Space Hierarchy Via Ray Hashing and Sorting

199

Table 1: OFFICE (251.55 K shadow rays), CORNELL (184.72 K shadow & 524.29 K reﬂection rays), SPONZA (256.71 K

shadow rays) global rendering performance.

100000000

200000000

300000000

400000000

500000000

600000000

700000000

RAH Office Our Office RAH Cornell Our Cornell RAH Sponza Our Sponza

Total Intersections

OFFICE CORNELL SPONZA

ALGORITHM TOTAL # ISECT RELATIVE % TOTAL # ISECT RELATIVE % TOTAL # ISECT RELATIVE %

Brute Force 9133.13 M 100% 606.91 M 100% 17058.58 M 100%

RAH Algorithm 469.68 M 5.14% 72.87 M 12.01% 632.41 M 3.71%

Our Algorithm 170.07 M 1.86% 53.58 M 8.83% 405.62 M 2.38%

Table 2: OFFICE, CORNELL, SPONZA rendering details.

OFFICE CORNELL SPONZA

LEVEL 2 LEVEL 1 LEVEL 2 LEVEL 1 LEVEL 2 LEVEL 1

RAH Algorithm

# SH INTERSECTIONS 142.73 M 202.03 M 3.00 M 5.17 M 266.60 M 261.49 M

# SH MISSES 117.47 M 186.41 M 2.35 M 3.61 M 233.91 M 248.46 M

# SH HITS 25.25 M 15.62 M 0.65 M 1.56 M 32.69 M 13.04 M

# RE INTERSECTIONS 6.49 M 17.80 M

# RE MISSES 4.26 M 14.31 M

# RE HITS 2.23 M 3.49 M

Our Algorithm

# SH INTERSECTIONS 11.56 M 85.57 M 0.75 M 2.38 M 266.60 M 62.67 M

# SH MISSES 0.86 M 76.46 M 0.45 M 0.98 M 258.76 M 53.12 M

# SH HITS 10.70 M 9.12 M 0.30 M 1.40 M 7.83 M 9.55 M

# RE INTERSECTIONS 2.74 M 10.27 M

# RE MISSES 1.45 M 6.98 M

# RE HITS 1.28 M 3.29 M

Figure 10: Cone-Ray Union - 2D View. courtesy of (Roger

et al., 2007).

3.2.6 Final Intersection Tests

After traversing the hierarchy we have an array of

node id and triangle id pairs which represent candi-

dates for the local intersection tests (M

oller, 1997). In

this ﬁnal step all that remains is to ﬁnd out which is

the closest intersected triangle for each ray and accu-

mulate shading. Depending on the depth that we want

for the algorithm we might need to output another set

of secondary rays. Since the algorithm is generic, all

that is necessary for this is to output these rays onto

the ray array that we used initially and continue from

the ray-sorting step.

4 TEST METHODOLOGY

We implemented our CRSH algorithm in

OpenGL/C++ and CUDA/C++ and then com-

pared it with our implementation of RAH (Roger

et al., 2007) over the same architecture. We map

our algorithm onto the GPU, fully parallelizing it

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

200

there. We achieve this mainly by the use of parallel

primitives, like preﬁx sums (Blelloch, 1990). We

used the CUB (Merrill and Grimshaw, 2009; Merrill

and Grimshaw, 2010) library to perform parallel

radix sorts and preﬁx sums.

We measure the amount of intersections, includ-

ing misses and hits, to evaluate ray hierarchy algo-

rithms proﬁciency at reducing the amount of ray-

primitive intersection tests required to render an im-

age. All scenes were rendered at 512 ×512 resolution

using an hierarchy depth of 2 and a node subdivision

of 8 (each upper level node in the hierarchy consists

of the combination of 8 nodes from the level directly

below).

The test information was collected using a

NVIDIA GeForce GTX 770M GPU with 3 GB of

RAM. Our algorithm is completely executed on the

GPU (including hierarchy construction and traversal)

so the CPU has no impact on the test results.

We used three different scenes, OFFICE, COR-

NELL and SPONZA.

The OFFICE scene (36K triangles) is representa-

tive of interior design applications. It is divided into

several sub-meshes; therefore it adapts very well to

our bounding volume scheme. For this scene the em-

phasis was on testing shadow rays.

We selected CORNELL (790 triangles). as it is rep-

resentative of highly reﬂective scenes. It consists an

object surrounded by six mirrors. On this scene we

focused on testing reﬂection rays although it also fea-

tures shadow rays in it.

SPONZA (66K triangles), much like OFFICE, is

representative of architectural scenes. For this scene

the emphasis was also on testing shadow rays but for

scenes that do not conform with our bounding volume

scheme. This scene does not adapt well to our scheme

as is not divided into submeshes.

5 RESULTS AND DISCUSSION

5.1 Intersection Results

We hypothesised that our more coherent RSH needs

to compute fewer intersections to render a scene.

We expect more expressive results for shadow rays.

As shadow rays have low divergence classiﬁcation

should be more coherent than for reﬂection rays. Ad-

ditionally our hierarchy should be more coherent with

reﬂection rays than one based on RAH due to the

hashing used. However the incoherence of reﬂection

rays, vs shadow rays, should lead to a lower quality

hierarchy.

Our initial expectations for Ofﬁce were to get a

much lower number of intersection tests with our al-

gorithm than with RAH. The scene is a good ﬁt to

our bounding volume scheme and our highly coherent

shadow ray hierarchy. Results (see Table 2) conﬁrm

our initial expectations: we compute 63.79% less in-

tersections than RAH on this scene. 98.14% less than

a brute force approach.

The Cornell scene has reﬂection rays, which are

more incoherent, so we expected worse results than

with Ofﬁce. Still we compute 26.47% less intersec-

tions (shadow and reﬂection rays combined) than the

RAH algorithm and 91.17% less than the brute force

approach.

The ﬁnal scene, Sponza, is a whole mesh. We did

not employ object subdivision in this scene. Hence

we expected worse results than with Ofﬁce since we

would only get the beneﬁt of the shadow ray hierarchy

and none from the bounding volume scheme.

We compute 35.86% less intersections than RAH

and 97.62% less than brute force. Since there is no

mesh culling for this scene the results are not as good

as with Ofﬁce but we still manage to outperform RAH

even without using an integral part of our algorithm.

5.2 Performance Results

These tests were run over the course of 58 frames and

the results for each phase are the average of these 58

frames.

The major time consuming steps are hierarchy

traversal and ﬁnal intersections. The biggest advan-

tage between our algorithm and the RAH algorithm

resides in the time spent traversing the hierarchy. Our

algorithm is 2.18x faster at traversal than RAH in Of-

ﬁce (see Table 3). This increased time spent travers-

ing the hierarchy means RAH takes about 100% more

time to render each frame than our algorithm.

Table 3: OFFICE, CORNELL, SPONZA render times.

OFFICE CORNELL SPONZA

RAH TIME (MS) TIME (MS) TIME (MS)

RAY CREATION 40.24 125.73 41.22

RAY COMPRESSION 0.00 0.00 0.00

RAY SORTING 0.00 0.00 0.00

RAY DECOMPRESSION 0.00 0.00 0.00

HIERARCHY CREATION 122.17 366.99 126.50

Ours TIME (MS) TIME (MS) TIME (MS)

RAY CREATION 40.43 128.13 41.50

RAY COMPRESSION 16.65 53.92 17.15

RAY SORTING 11.82 50.97 12.70

RAY DECOMPRESSION 99.72 251.95 98.62

HIERARCHY CREATION 130.63 407.09 137.84

Ours vs RAH SPEEDUP SPEEDUP SPEEDUP

HIERARCHY TRAVERSAL 2.18X 1.53X 1.06X

FINAL INTERSECTION TESTS 1.32X 1.02X 1.14X

Much like Ofﬁce, the Cornell scene takes most of

its time on traversal and calculating the ﬁnal intersec-

Coherent Ray-Space Hierarchy Via Ray Hashing and Sorting

201

tions. However due to the lower geometric complex-

ity the absolute values aren’t as high. Our algorithm

performs traversal 1.53x faster than RAH in Cornell,

a signiﬁcant reduction.

Finally for the Sponza scene we see a similar rel-

ative time spent in the traversal of the hierarchy vs

previous scenes. Even though the Sponza scene isn’t

subdivided into separate object meshes, we manage to

slightly outperform RAH at traversal.

6 CONCLUSIONS AND FUTURE

WORK

Our paper described an algorithm to create a Ray-

Space Hierarchy which markedly reduces the inter-

sections, required to ray-trace a scene, due to im-

proved coherency and a shallow BVH.

We achieved our goal of reducing intersections us-

ing a Ray-Space Hierarchy. This technique is orthog-

onal to the use of both Object and Space Hierarchies.

These can be used together to obtain even better re-

sults. Our results show a reduction in computed inter-

sections of 50% for shadow rays and 25% for reﬂec-

tion rays compared to previous state of the art RSHs.

There is room for improvements: Since the hash

determines how rays are sorted, an hierarchy will

improve if we enhance the ray spatial coherency.

We used spherical bounding volumes and a shallow

BVH. In the future we aim to combine our coher-

ent ray hierarchy with a deeper BVH to further de-

screase ray-primitive intersections e.g. (Bradshaw

and O’Sullivan, 2004).

ACKNOWLEDGEMENTS

This work was supported by national funds through

Fundac¸

ao para a Ci

encia e Tecnologia (FCT) with ref-

erence UID/CEC/50021/2013.

REFERENCES

Aila, T. and Karras, T. (2010). Architecture Considera-

tions for Tracing Incoherent Rays. In Proceedings of

the Conference on High Performance Graphics, pages

113–122. Eurographics Association.

Amanatides, J. (1984). Ray Tracing with Cones. SIG-

GRAPH Computer Graphics, 18(3):129–135.

Arvo, J. and Kirk, D. (1987). Fast Ray Tracing by Ray Clas-

siﬁcation. SIGGRAPH Computer Graphics, 21(4):55–

64.

Blelloch, G. E. (1990). Preﬁx Sums and their Applications.

Technical report, Carnegie Mellon University.

Bradshaw, G. and O’Sullivan, C. (2004). Adaptive Medial-

Axis Approximation for Sphere-tree Construction.

ACM Transactions on Graphics (TOG), 23(1):1–26.

Ericson, C. (2004). Real-Time Collision Detection. Series in

Interactive 3-D Technology. Morgan Kaufmann Pub-

lishers Inc.

Garanzha, K. and Loop, C. (2010). Fast Ray Sorting and

Breadth-First Packet Traversal for GPU Ray Tracing.

Computer Graphics Forum, 29(2):289–298.

artner, B. (1999). Fast and Robust Smallest Enclosing

Balls. In Proceedings of the 7th Annual European

Symposium on Algorithms, ESA ’99, pages 325–338.

Springer-Verlag.

Glassner, A. S., editor (1990). Graphics Gems. Academic

Press, Inc.

Mattausch, O., Bittner, J., Jaspe, A., Gobbetti, E., Wimmer,

M., and Pajarola, R. (2015). CHC+RT: Coherent Hier-

archical Culling for Ray Tracing. Computer Graphics

Forum, 34(2):537–548.

Merrill, D. and Grimshaw, A. (2009). Parallel Scan for

Stream Architectures. Technical report, University of

Virginia, Department of Computer Science.

Merrill, D. G. and Grimshaw, A. S. (2010). Revisiting Sort-

ing for GPGPU Stream Architectures. In Proceedings

of the 19th International Conference on Parallel Ar-

chitectures and Compilation Techniques, PACT ’10,

pages 545–546. ACM.

oller, T. (1997). A Fast Triangle-Triangle Intersection

Test. Journal of Graphic Tools, 2(2):25–30.

Mora, B. (2011). Naive Ray-Tracing: A Divide-And-

Conquer Approach. ACM Transactions on Graphics

(TOG), 30(5):117.

Pharr, M. and Fernando, R. (2005). GPU Gems 2: Pro-

gramming Techniques for High-Performance Graph-

ics and General-Purpose Computation. GPU Gems.

Addison-Wesley Professional.

Roger, D., Assarsson, U., and Holzschuch, N. (2007). Whit-

ted Ray-tracing for Dynamic Scenes Using a Ray-

space Hierarchy on the GPU. In Proceedings of the

18th Eurographics Conference on Rendering Tech-

niques, EGSR ’07, pages 99–110. Eurographics As-

sociation.

ecsi, L. (2006). The Hierarchical Ray Engine. In WSCG

Full Papers Proceedings, pages 249–256. V

aclav

Skala-UNION Agency.

Whitted, T. (1980). An Improved Illumination Model for

Shaded Display. Commun. ACM, 23(6):343–349.

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

202