Spontaneous Emission of a Dressed Atomic System
in a Strong Light Field
A. V. Bogatskaya and A. M. Popov
D. V. Skobeltsyn Institute of Nuclear Physics, Moscow State University, Moscow, 119991, Russia
Keywords: Quantum Description of Interaction of Light and Matter, Photoionization of Atoms, Rydberg States,
Interference Stabilization.
Abstract: New approach to the study of the spontaneous emission of an atomic system driven by a strong light field is
developed. This approach is based on the accurate consideration of quantum system interaction with
vacuum quantized field modes in the first order of perturbation theory, while the strong light field is
considered classically. The proposed approach is applied to study the dynamics of field-driven atomic
systems. Among them are Rabi oscillations in two-level system, resonant and nonresonant Raman and
Rayleigh scattering, interference stabilization of Rydberg atoms. It is demonstrated that analyzing the
spontaneous emission allows to study the specific features of quantum systems dressed by the field.
1 INTRODUCTION
Study of the nonperturbative atomic dynamics in
strong laser fields is the core problem of nonlinear
optics (Akhmanov and Nikitin, 1997). Typically this
dynamics is studied in the semiclassical approach
(Agostini and Di Mauro, 2004; Couairon and
Mysyrowicz, 2007; Krausz and Ivanov, 2009; Chin,
2010). It means that while the atomic system is
analyzed from quantum-mechanical point of view
the electromagnetic field is considered still classical-
ly. In (Bogatskaya et al, 2016) the possibility to use
semiclassical approach for analyzing radiative
processes in high intensity fields was questioned. It
was demonstrated that the application of the semi-
classical approach to study emission of the quantum
system driven by high intensity laser field is
generally in contradiction with quantum electro-
dynamical calculations. Also it means that
spontaneous emission from the quantum system is
neglected. If laser field is strong enough the
probability of spontaneous transitions is negligibly
small in comparison with stimulated transitions.
Nevertheless, any stimulated emission starts from a
spontaneous background radiation. It means that in
order to study initial stage of any nonlinear process
one need to take into account spontaneous processes
as well. On the other hand it is known atomic
spectrum can be dramatically reconstructed by the
strong external laser field (Delone and Krainov,
1994; Fedorov, 1997). New quantum object with
essentially different spectrum than the field-free
atomic spectrum, (so called the dressed atom),
appears to exist. The simplest example of such
reconstruction is the AC Stark shift of energy levels
in relatively weak laser field. Another example of
the dressed atom is the so called Kramers -
Henneberger atom that appears to exist in
superatomic fields (Fedorov, 1997). The sponta-
neous emission from
this dressed by the laser field
atomic system can provide the unique information
about its energy spectrum. To study the structure of
dressed atom one needs to take into account the
interaction with the electromagnetic vacuum. The
interaction with vacuum modes also should be taken
into account for analyzing a lot of nonlinear
processes. A lot of practical applications of theory
including interaction of the atomic system with both
classical and vacuum field modes can be found in
quantum optics (Scally and Zubairy, 1997).
The aim of this paper is to develop the approach
for studying first-order spontaneous radiative
processes in a quantum system driven by a strong
classical laser field. This approach is based on the
first order perturbation theory applied to the
interaction of the atomic system dressed by the
strong laser field with a lot of quantized field modes
in the assumption that initially all the modes are in a
vacuum state. The proposed approach is applied for
Bogatskaya A. and Popov A.
Spontaneous Emission of a Dressed Atomic System in a Strong Light Field.
DOI: 10.5220/0006099301290136
In Proceedings of the 5th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2017), pages 129-136
ISBN: 978-989-758-223-3
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
129

study of a number of quantum systems such as
quantum dots, quantum wires, clusters in the
presence of the intense laser field.
2 ATOM DYNAMICS IN A
STRONG LASER FIELD IN
THE PRESENCE OF
QUANTIZED
ELECTROMAGNETIC FIELD
We analyse the atomic system using the following
Hamiltonian
),()(),(
0
ε
ε
rVHtrHH
f

++= ,
(1)
where
),()(
0
trWrHH
at

+=
;
)(rH
at

is the atomic
Hamiltonian,
)(tEdW


⋅−=
represents the interaction
of atom with classical laser field in the dipole
approximation,
f
H - Hamiltonian of the set of field
modes excluding laser field mode,
),(
ε
rV

stands for
the interaction of the atom with the quantized
electromagnetic field,
red


= is the dipole moment,
r

is the electron radius-vector and
ε
is the set of
quantized field mode coordinates.
We are going to deal with the quantized field
using perturbation theory. In the case when there is
no interaction with quantized field modes one can
write the well-known equation
),()(
),(
0
trtH
t
tr
i


 ψ
ψ
=
∂
∂
,
(2)
which describes the atomic dynamics in a classical
laser field. Initial condition can be written as
)()0,( rtr


φ
ψ
==
,
(3)
where
)(r

φ
is some stationary or unstationary state
of the atomic discrete spectrum or continuum. We
will suppose also that at the initial instant of time all
field modes are in the vacuum state
{}
0
. Provided
that we know the solution of equation (2), the
solution of the general equation with the
Hamiltonian (1)
()
),,()(
),,(
0
trVHtH
t
tr
i
f
ε
ε


 Ψ++=
∂
Ψ∂
,
(4)
and initial condition
{}
0)()0,,( ×==Ψ rtr


φε
can be
found by means of the perturbation theory.
Wave function of zero-order approximation
excluding interaction with the quantum field modes
reads
}0{),(),,(
)0(
×=Ψ trtr


ψε ,
(5)
We are going to find the solution of (4) in the form:
),,(),,(),,(
)0(
trtrtr εδεε



Ψ+Ψ=Ψ
,
(6)
with
)0(
Ψ<<Ψ δ .
Substituting (6) in (4) in the first order of
smallness one obtains:
()
),,(),,()(
),,(
)0(
0
trVtrHtH
t
tr
i
f
εεδ
εδ



Ψ+Ψ+
=
∂
Ψ∂
(7)
with the initial condition
0)0,,( ==Ψ tr
ε
δ

.
In fact (7) can be formulated as Schroedinger
equation for the
Ψ
δ
with the source in the right
hand. For further analysis of eq. (7) let us remind
that initially we have vacuum in all field modes.
Therefore in the first order of perturbation theory
Ψ
δ
contains only one-photon excitations in a some
field mode:
{}

×=Ψ
λ
λλ
δψεδ
,
0,0,...0,1,....0,0),(),,(
k
kk
trtr


,
(8)
Here
),( tr
k

λ
δ
ψ
is the electron wave function
provided that one photon with wave vector
k

and
polarization
λ
has appeared.
As the interaction of the atom with quantized field
can be written in a form
λ
λ
λ
λ
λ
εε
k
k
k
k
k
edVrV


−== )(),(
,



,
(9)
(
λ
ε
k
is the field operator of mode
{}
λ
,k
and
λ k
e

is
the polarization vector) for a given mode with one-
photon excitation one can write:
()
()
.0),(,),()(
,23),(,
),(
)(
0
trVktrhtH
ktrk
t
tr
i
kk
f
k
kk
k





ψλδψ
λωδψλ
δ
ψ
λλ
λ
λλ
λ
++=
×+
∂
∂
(10)
Here
)( f
k
h
λ
is the Hamiltonian of the field mode
λ ,k
. Provided that λωλ
λ
λ
,23,
,
)(
kkh
k
f
k
⋅= , and
λ
ε
ε
λ
,
2
0 k
norm
k
= , (
3
4 L
knorm λ
ωπε =
is the
auxiliary normalizing constant,
3
L
is the
normalization volume), the final form of the eq. (10)
can be written as
PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology
130

)exp(),(
2
)(
),()(
),(
0
titred
trtH
t
tr
i
k
norm
k
k
k
λλ
λ
λ
ωψ
ε
δψ
δψ
×××−
=
∂
∂





(11)
with the initial condition
0)0,( ==tr
k

λ
δ
ψ
.
It is obvious that the expression

= rdtrtW
kk
3
2
),()(
λλ
δψ
(12)
represents the probability to find a photon in the
mode
λ ,k
as a function of time. Then the total
probability to emit the photon of any frequency and
polarization during the transition
if →
is

=
λ
λ
,
)()(
k
kfi
tWtW
(13)
As the spectrum of field modes is dense, we can
replace the sum in eq. 13 by the integral:

Ω= dd
c
Lkd
L
kk λλ
ωω
ππ
2
33
3
3
3
3
8
2
)2(
2
(14)
After the integration over angular distribution of
photons and summation over possible polarizations
the probability of the spontaneous decay in the
spectral interval
),(
ω
ω
ω
d+
can be expressed in the
form
λωω
ωω
π
ω
,/
2
32
3
3
ck
Wd
c
L
dW
=
×=
(15)
where
λ ,k
W is given by (12). One should note, that
the expression (14) does not depend on the
normalization volume, as
3
,
1~ LW
k λ
.
3 RABI OSCILLATIONS IN A
TWO-LEVEL SYSTEM AND
TRIPLET MOLLOW
Let us restrict ourselves to the consideration of two-
level system (energy levels and stationary state wave
functions
1
E
and
i
ϕ
,
2,1=i
respectively) inter-
acting with near resonant field of frequency
)(
1221
EE −=≈
ω
ω
and initially (
)0=t
being in
the state
1
.
Figure 1: Dressing of two-level system in a resonant
electromagnetic field.
In the case of exact resonance
0
21
≡−=Δ
ω
ω
ω
wave function of the system governed by the
classical field with electric field
t
ω
ε
ε
cos
0
=
can be
represented in a form
)exp()()(),(
2,1
tE
i
rtCtr
n
n
nn

=
−=



ϕψ
(16)
with
tC Ω= cos
1
and
tiC Ω−= sin
2
, where
2
021
ε
d=Ω
is the Rabi frequency. One can easily
see that in our case dressing means splitting of each
level into two quasienergy states with energies
Ω±→ 
ii
EE
. The structure of this splitting for the
case
21
ω
<<Ω
is performed at fig.1. It means that
the line of spontaneous emission corresponding to
the transition
)(
12
EE
k
−==
ω
ω
λ
should split up
into three lines
Ω±= 2,
ω
ω
ω
λ k
, so-called triplet
Mollow (Mollow, 1969). To confirm this statement
we will find the solution of general equation (11) in
a form
)exp()()(),(
2,1
)(
tE
i
rtCtr
n
n
n
k
nk

=
−=



ϕδψ
λ
λ
.
(17)
Then the equations for amplitudes
)( λ k
n
C
reads
()
,))(exp())(exp(
2121
*
)(
2
)(
1
titi
CCi
kk
kk
Ω+−+Ω−−
×Ω−Ω−=
ωωωω
λλ
λλ

()
.))(exp())(exp(
2121
*
)(
1
)(
2
titi
CCi
kk
kk
Ω+++Ω−+−
×Ω−Ω−=
ωωωω
λλ
λλ

(18)
Here
22
21
*

norm
d ε
=Ω is the coupling constant of the
quantum system with quantized field. First terms in
(18) mean the transitions between two atomic states
of the system under the resonant laser field while
second terms stand for the emission of photons
2
Spontaneous Emission of a Dressed Atomic System in a Strong Light Field
131

{}
λ
,k
. General analytical solution of eq. (18) with
initial conditions
0)0(
)(
2,1
==tC
k λ
we can write as
















Ω±−
Ω±−
+
Ω
−
−
×Ω=
















Ω±−
Ω±−
+
Ω
−
−
×Ω=
4/)2(
)2/)2(sin
sin4
4/)(
)2/)(sin
)()(
4/)2(
)2/)2(sin
cos4
4/)(
)2/)(sin
)
()(
2
21
21
2
2
2
21
21
2
2*
2
)(
2
2
21
21
2
2
2
21
21
2
2*
2
)(
1
ωω
ωω
ωω
ωω
ωω
ωω
ωω
ωω
λ
λ
λ
λ
λ
λ
λ
λ
λ
λ
k
k
k
k
k
k
k
k
k
k
t
t
t
tC
t
t
t
tC
(19)
It represents emission of photons near the
frequencies
Ω±= 2,
ω
ω
ω
λ k
and subsequent Rabi
oscillations of the atomic population probabilities.
The probability to emit photon
{}
λ
,k
is
2
)(
2
2
)(
1
)(
λλ
λ
kk
k
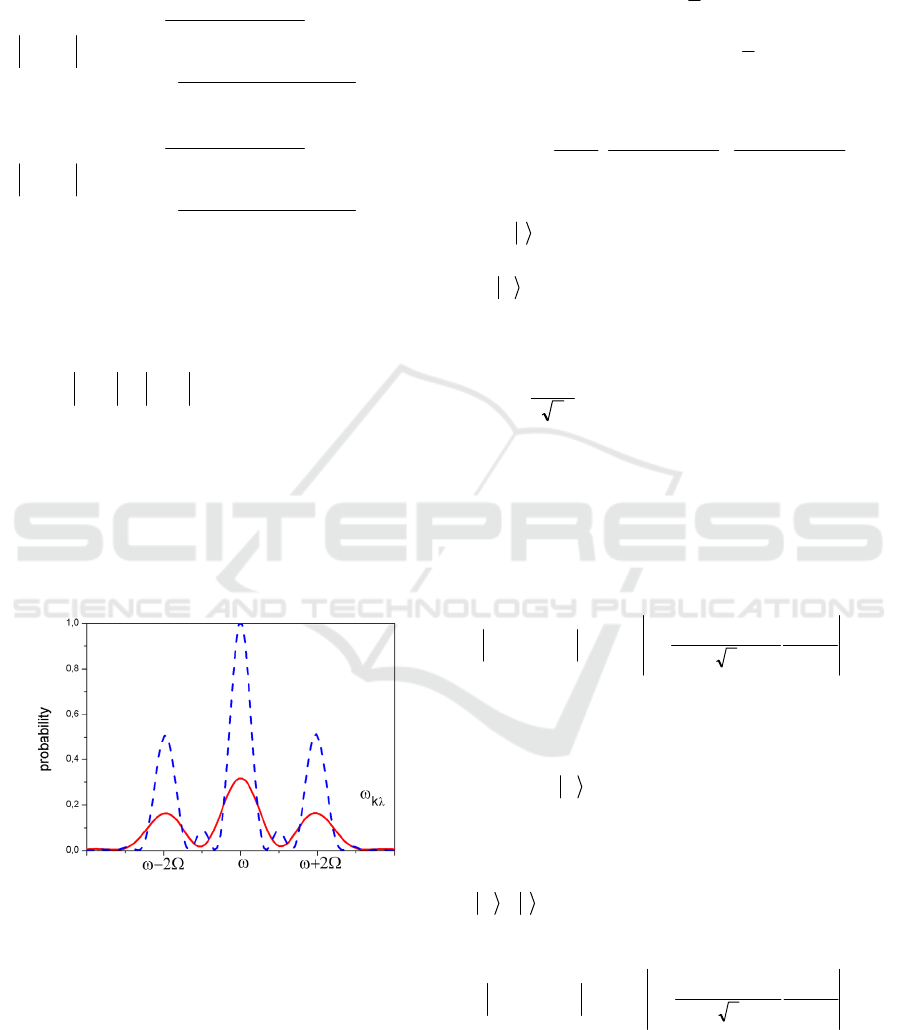
CCtW += and is given at fig.2 for
two different laser pulse durations. As we supposed
earlier, the initial line splits into three lines that are
known as triplet Mollow. The intensity of the central
line is twice larger in comparison with satellites at
frequencies
Ω±= 2
ω
ω
λ k
. As the duration of the
pulse increases the splitting of the initial line into the
triplet Mollow becomes more and more pronounced
(see solid and dashed curves at fig.2).
Figure 2: Triplet Mollow for short (solid) and long (dash)
laser pulses. Pulse durations are 10
4
and 2 10
4
at.un.
4 NONRESONANT
SPONTANEOUS RAMAN AND
RAYLEIGH SCATTERING
In this chapter we will study Raman and Raylegh
scattering of laser radiation by atomic system. To
obtain the general expression for probabilities of
Raman and Raylegh scattering let us consider the
atomic dynamics in classical laser field also in the
first order of perturbation theory. Then
,exp)()(
exp)(),(
)1(

≠






−+






−=
in
nnn
ii
tE
i
rtC
tE
i
rtr





ϕ
ϕψ
(20)
where








+
+
+
−
−
=
)(
))(exp(
)(
))(exp(
2
)(
0
)1(
ωω
ωω
ωω
ωω
ni
ni
ni
nini
n
titiEd
tC

(21)
Substituting (20) and (21) into (11) and assuming
that
i
is the initial atomic state one derives the
equation for probability amplitude to find the atom
in
f
and the photon in the mode {}
λ
,k
:
).)(exp()(
2
)exp())((
)1(
)(
)(
tideC
titEdCCi
kfnfnk
in
n
norm
n
fnfn
k
n
k
f
λλ
λ
λ
ωω
ε
ω
+−
−=


≠






(22)
Second term in the right part of (22) stands for the
emission of photon
{}
λ
,k
while the first one
describes the evolution of atomic wave function in
the classical field after the emission of photon and
here we will neglect such evolution. From (22) one
derives:
.)(2
1
22
))((
)(
2
0
2
2
)(
tEE
ded
tC
kif
in
ni
nikfn
norm
k
f
×+−−×
−
=∞→

≠
λ
λ
λ
ωωπδ
ωω
ε
ε






(23)
This is the probability of Stoks component of the
spontaneous Raman scattering corresponding to the
final state
f
and emission of a photon
)(
ifk
EE −−=
ω
ω
λ

(24)
If the final state coincides with the initial one
if =
we derive the expression for the Rayleigh
scattering
,)(2
1
22
))((
)(
2
0
2
2
)(
t
ded
tC
k
in
ni
nikin
norm
k
i
×−×
−
=∞→

≠
ωωπδ
ωω
ε
ε
λ
λ
λ






(25)
when the frequency of spontaneous photon is the
same as for laser radiation. Not far from resonanse
when laser frequency is
ni
ω
ω
≈
with definite value
PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology
132

of
n
, the transition takes place through the only
intermediate state and summation over all
intermediate states in expressions (23) and (25)
should be omitted:
.)(2
1
22
))((
)(
)(
2
0)(
2
2
)(
)(
tEE
ded
tC
kiif
ni
niknif
norm
k
if
×+−−×
−
=∞→
λ
λ
λ
ωωπδ
ωω
ε
ε






(26)
5 FOUR-LEVEL SYSTEM
DYNAMICS IN A PRESENCE
OF QUANTIZED
ELECTROMAGNETIC FIELD
To provide more insight into atomic dynamics in
discrete spectrum we will study the spontaneous
emission in four-level system
3,2,1,0
with
even parities for
2,0
and odd ones for
3,1
. The
wave function of the system

=
−=
3
0
)exp()()(),(
n
nnn
tE
i
rtCtr


ϕψ
(27)
is obtained from the set of equations
)exp(cos)(
0
titdCCi
fn
n
fnnf
ωωε

−=


(28)
with initial condition
0)0(,1)0(
3,2,10
====
=
tCtC
i
.
Then the equation (11) is also equivalent to a set of
equations for amplitudes
)(
)(
tC
k
f
λ
for different
{}
λ
,k
modes:
).exp()exp()()(
2
)(
)exp(cos)(
3
0
0
)(
)(
titE
i
rtCed
titdCCi
k
n
nnn
norm
k
fn
n
fn
k
n
k
f
λλ
λ
λ
ωϕ
ε
ωωε


=
−−
−−=





(29)
The positions of energy levels were chosen as
follows
1.0,2.0,25.0
322110
===
ω
ω
ω
and hence
55.0
30
=
ω
. Hereafter all values will be given in
atomic units. Nonzero values of the dipole matrix
elements were chosen equal to each other
1
21323010
==== dddd
. The duration of laser pulse
was
4
104 ×= τ , laser intensity was 10
-3
, that means
the Rabi frequency is
4
105
−
×=Ω . The spectrum of
spontaneous emission for various spectral intervals
and different detuning of the laser frequency from
the frequency of transition
30 →
(
)55.0
30
=
ω
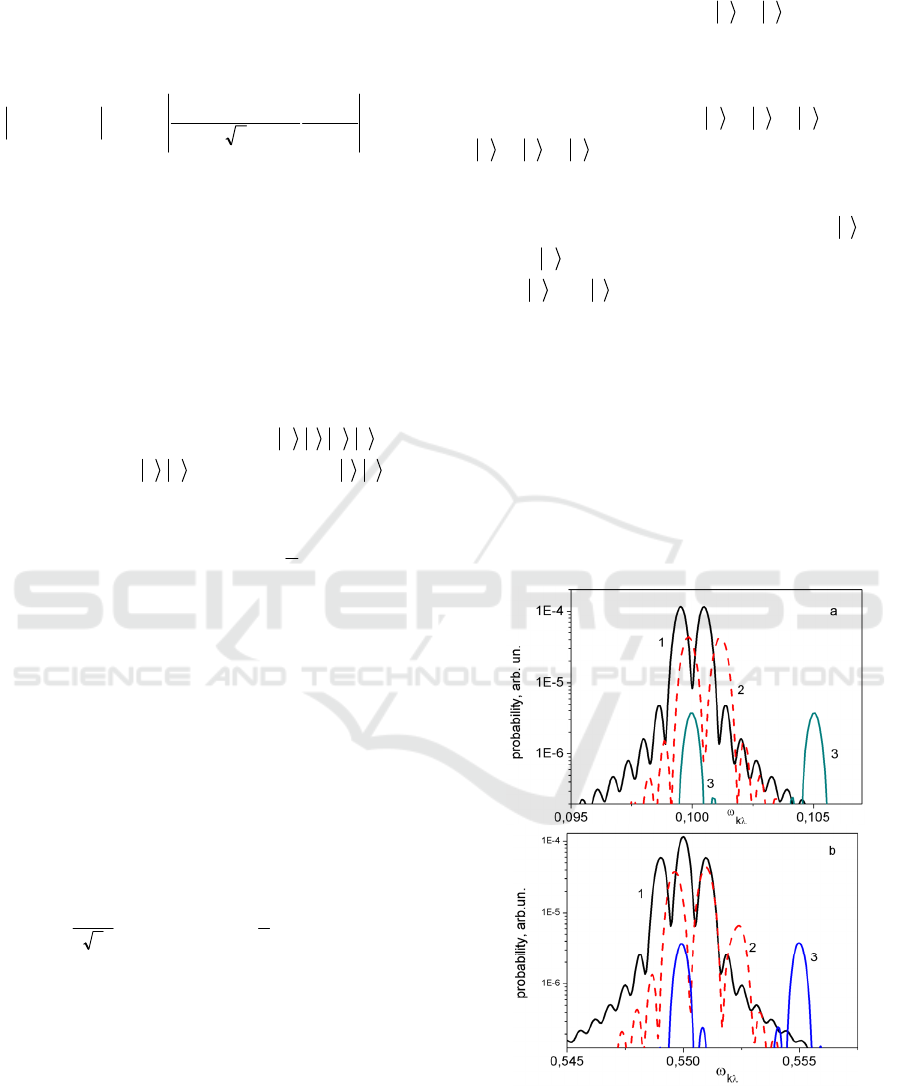
are presented at fig.3. First we should mention that
in the laser frequency range
005.0
30
>−
ω
ω
for
definite laser pulse parameters both Raman and
Raleigh processes
230 →→
and
030 →→
correspondingly have nonresonant
character and can be studied using the expression
(23). Near the resonance the situation is changing
dramatically due to dressing of the upper
3
and
ground
0
levels by external laser field. As far as
levels
0
and
3
split into two sublevels the lines of
Raman also splits into two lines (fig.3a) while the
Rayleigh scattering line is divided into three lines,
that corresponds to the Mollow triplet. In the case of
exact resonance the value of this splitting is equal to
Ω2
(сurves 1). For the near-resonance case
001.0
30
=−=
ω
ω
δ
the splitting of states becomes
asymmetrical and the position of doublet Raman and
triplet Rayleigh lines changes (curves 2). Further
increment of the detuning (curves 3) results in the
formation the ordinary Raman and Rayleigh lines
with frequencies
30
ω
ω
−
and
ω
respectively.
Figure 3: Spectral lines of Raman (a) and Rayleigh (b)
processes in dependence on laser frequency detuning
(
30
ω
ω
δ
−=
) from the atomic transition frequency (1 -
0=
δ
, 2 - 001.0=
δ
, 3 - 005.0=
δ
). Pulse duration is
40000, Rabi frequency
4
105
−
×=Ω .
Spontaneous Emission of a Dressed Atomic System in a Strong Light Field
133

Rest lines with frequency
32
ω
and
30
ω
can be
interpreted as spontaneous transitions
23 →
and
03 →
resulting from the nonresonant excitation
of level
3
by laser radiation.
6 STABILIZATION IN A
PRESENCE OF QUANTIZED
ELECTROMAGNETIC FIELD
The interference stabilization (IS) of Rydberg atoms
was first predicted in (Fedorov and Movsesian,
1988), analyzed in detail in subsequent works
(Fedorov et al, 1996; Fedorov and Tikhonova,
1998), as well as in (Fedorov, 1997). According to
(Fedorov, 1988), IS occurs due to destructive
interference of the amplitudes of transitions to a
continuum from excited Rydberg states coherently
repopulated by Raman Λ-type transitions during
laser excitation. It is known that the widths of these
transitions are determined by Fermi’s golden rule
2
0
22 επ


nE
d=Γ
(30)
Here,
nE
d

is the matrix element of the dipole
moment operator for the
ω +=→
nn
EEE
transition and
0
ε
is the electromagnetic field
strength amplitude of the wave. According to
(Fedorov, 1997), the IS threshold is determined by
the overlap of ionization widths of Rydberg states
and can be written in the atomic system of units in
the form:
1
35
0
> ωε
(31)
or by passing to intensities:
310*
ω ≈> II
. For
example, for the emission frequency of a Ti:Sa laser,
we obtain from (31) the threshold intensity I* ≈ 2.5
× 10
12
W/cm
2
.
The general expression for the quasi-energy
spectrum of a field-dressed atom in the simplest
model of two close nondegenerate levels and a
nondegenerate continuum (1D) was obtained in
(Fedorov, 1988):






Γ−−±Γ−+=
±
22
1221
)(
2
1
EEiEE γ
(32)
Here,
2,1
E are unperturbed energy levels and Γ is the
ionization width calculated from (30) and assumed
the same for both levels. The imaginary part of (32)
determines the ionization width of shifted levels. A
structure of broadened quasienergy levels is seen to
change drastically at
12
EEГ −=
, which confirms
the threshold character of the IS. In the region
12
EEГ −>
the shift results in a form of a narrowing
quasienergy level located approximately at
2/)(
21
EE +
embedded into a widening one. In terms
of the time evolution of populations this means that
the decay (ionization) has a two-exponential
character. I.e., there are short- and long-living parts
of populations. Existence of the latter is a clear
manifestation of stabilization.
It follows from (32) that in the strong-field limit
12
EEГ −>
the decay rate of the long living
stabilized part of population decrease with
increasing intensity as:
I
EE
strong
1~
2
)(
Im2
2
12
Γ
−
=−=Γ
+
γ
(33)
In this chapter we are going to embed spontaneous
radiation in the stabilization phenomenon. We
employ with three-level system where there is a
ground state
0
and levels
2,1
which are
supposed to be Rydberg levels of the opposite parity
with respect to the ground state. The energies of
levels are chosen
5.0
0
−=E
for
0
,
3
1
105
−
×−=E
and
3
2
104
−
×−=E
for levels
2,1
respectively (we
are working within the atomic system of units).
In frames of previous consideration we solve
numerically the following system of equations:

=
′
′′′
Γ−=
2
1
)exp(
2
n
nnnnnn
tiC
i
Ci ω


,
0
0
=Ci

,
),)(exp()(
2
)(
00
0
)(
titC
edCi
kn
norm
kn
k
n
λ
λ
λ
ωω
ε
+××
×−=




,))(exp()()(
2
2
1
00
)(
0

=
′
′′′
−
×−=
n
nknkn
norm
k
titCed
Ci
ωω
ε
λλ
λ




(34)
where
2
0
4
0
2
2
42
ε
π
επ
nE
n
nEnEnn
d
dd

==Γ

′
′′
.
The first equation is obtained using the method of
adiabatic elimination of the continuum (Fedorov,
1997), as well as the approximation of equal
PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology
134

Rydberg-continuum dipole matrix elements for all
Rydberg levels efficiently involved in the process of
ionization. In our simulations we assume matrix
elements to be calculated in quasiclassical
approximation
)(1
3/55.1
ω nd
nE
=
, where principal
quantum number n is supposed to be 10 and
ω
equals 0.057 that corresponds to the radiation of Ti-
Sa laser pulse. Fig. 4 shows the spectrum of
spontaneous emission to the ground state for
different values of laser intensity. The situation
described at fig. 6a corresponds to the initial
population amplitudes of Rydberg levels
21)0(,21)0(
21
−== СС
(antisymmetrized
combination). In the absence of laser pulse one can
see two independent emission profiles from Rydberg
levels, but with the increase of radiation intensity
due to the interference of amplitudes of Raman
Λ -
type transitions Rydberg levels reconstructed
significantly. As a result emission lines gradually
merge forming new transition with the energy
)2/)((
210
EEE +−−
(curve 3 fig. 4a). Such initial
condition provides pretty resistant atomic system
with respect to ionization process. The fraction of
Figure 4: Reconstruction of the spectrum of the
spontaneous emission of an atom in the regime of
interference stabilization. Amplitudes of initially
populated Rydberg states are opposite (a) and the same
(b). Intensities of Ti:Sa laser ( 057.0=
ω
) are (1 - 0 , 2 -
5
105.2
−
× , 3 -
4
105.2
−
× ). Pulse duration is 40000.
population trapped in Rydberg states in this case is
very close to unity (fig. 5). Another situation is
developing for the symmetrized combination of
population amplitudes
21)0(,21)0(
21
== СС
. In
this case for rather high intensity of laser field when
12
EEГ −>>
we can clearly observe a two-
exponential dynamics of population decay (fig. 5)
showing short- and long-living parts of populations.
Such type of temporal dynamics is pronounced
in spontaneous emission spectra. Indeed, blue curve
on fig 4b represents the wide line of emission from a
rapidly disintegrating background, while the narrow
depletion in the center of this line results from long-
time decay of the small stable fraction of population.
The life times of these long- and short-living
fractions can be estimated as
2
12
)(2 EE −Γ
and
Γ
/1
correspondingly.
Figure 5: Temporal dependensies of the trapped
population for the initially populated simmetrized (1) and
antisimmetrized (2) states (see the text). Laser intenisity is
4
2.5 10 .
−
×
7 CONCLUSIONS
To conclude, general approach to analyze the
spontaneous emission of an atomic system driven by
a strong laser field is developed. It based on the first
order of perturbation theory for the interaction with
quantized vacuum field modes while the interaction
with the intense classical laser field is considered
numerically or analytically beyond the perturbation
theory. Several problems (Rabi oscillations and
formation of the Mollow triplet, spontaneous Raman
and Rayleigh scattering, ionization suppression in
the regime of interference stabilization) were
studied. It was demonstrated that the spontaneous
emission can be effectively used to study the
reconstruction of the energy spectrum by the laser
field, and different types of dressing were analyzed.
Spontaneous Emission of a Dressed Atomic System in a Strong Light Field
135

We would like to mention that our approach can
be used to study the spectrum and dynamics under
external fluence of artificial atoms, such as quantum
dots or quantum wires, and the coupling of these
atoms with photons (Michler et al, 2000; Santori et
al 2002; Faraon et al, 2008) or with crystalline
lattice via phonons (Förstner et al, 2003;
Machnikowski and Jacak, 2004; Ahn, et al, 2005).
Developed approach can be of significant interest for
the study of relaxation processes in a lot of modern
nanoelectronic devices devoted for information
receiving and processing (
Hoang et al, 2012; Jöns et
al, 2015)
.
ACKNOWLEDGEMENTS
This work was supported by the Russian Foundation
for Basic Research (projects no. 15-02-00373, 16-
32-00123).
REFERENCES
Agostini, P. and Di Mauro, L. F., 2004. Rep. Prog. Phys.,
67, 813.
Ahn, K. J., Förstner, J., and Knorr, A., 2005. Phys. Rev.
B 71, 153309.
Akhmanov, S. A. and Nikitin, S. Yu., 1997. Physical
Optics, Oxford.
Bogatskaya, A. V., Volkova, E. A., Kharin, V. Yu. and
Popov, A. M., 2016. Laser Phys. Lett., 13, 0453014.
Chin, S. L., 2010. Femtosecond Laser Filamentation
(SpringerSeries on Atomic, Optical, and Plasma
Physics vol 55) (New York: Springer).
Couairon, A. and Mysyrowicz, A., 2007. Phys. Rep. 441
47.
Delone, N. B., Krainov, V. P., 1994. Multiphoton
Processes in Atoms (Berlin: Springer-Verlag).
Delone, N. B., Goreslavsky S. P., Krainov, V. P., 1983. J.
Phys. B: At. Mol. Phys. 16, 2369.
Delone, N. B., Goreslavsky S. P., Krainov, V.P., 1989. J.
Phys. B: At. Mol. Phys.
22, 2941.
Faraon, A. et al., 2008. Nature Phys. 4 859.
Fedorov, M. V. and Movsesian, A. M., 1988. J. Phys. B,
21, L155.
Fedorov, M. V., Tehranchi, M.-M., and Fedorov, S. M.,
1996. J. Phys. B, 29, 2907.
Fedorov, M. V. and Tikhonova, O. V., 1998. Phys. Rev. A
58, 1322.
Fedorov, M. V., 1997. Atomic and Free Electrons in a
Strong Light Field, World Scientific.
Förstner, C., Weber, C., Danckwerts J., and Knorr, A.,
2003. Phys. Rev. Lett. 91 127401.
Jöns K. D., Rengstl, U., Oster, M., et al, 2015. J. Phys.
D 48, 085101.
Hoang, T. B., Beetz, J., Lermer, et al, 2012. Opt. Express,
20, 21758.
Krausz, F. and Ivanov, M., 2009. Rev. Mod. Phys., 81,
163.
Machnikowski, P. and Jacak, L., 2004. Phys. Rev. B 69,
193302.
Michler, P. et al., 2000. Science, 290, 2282.
Mollow, B. R., 1969. Phys. Rev. 188, 1969.
Santori, C., Fattal, D., Vucković, J., Solomon, G. S. and
Yamamoto, Y. 2002., Nature, 419, 594.
Scally, M. and Zubairy, S. 1997. Quantum Optics,
Cambridge University Press.
PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology
136