Fast Scalable Coding

based on a 3D Low Bit Rate Fractal Video Encoder

Vitor de Lima

, Thierry Moreira

, Helio Pedrini

and William Robson Schwartz

Institute of Computing, University of Campinas,

Campinas, SP, 13083-852, Brazil

Department of Computer Science, Universidade Federal de Minas Gerais,

Belo Horizonte-MG, 31270-010, Brazil

Keywords:

Video Compression, Fractal Encoding, Adaptive Transcoding, Scalable Coding.

Abstract:

Video transmissions usually occur at a ﬁxed or at a small number of predeﬁned bit rates. This can lead to

several problems in communication channels whose bandwidth can vary along time (e.g. wireless devices).

This work proposes a video encoding method for solving such problems through a ﬁne rate control that can be

dynamically adjusted with low overhead. The encoder uses fractal compression and a simple rate distortion

heuristic to preprocess the content in order to speed up the process of switching between different bit rates.

Experimental results show that the proposed approach can accurately transcode a preprocessed video sequence

into a large range of bit rates with a small computational overhead.

1 INTRODUCTION

Most video streaming services use a reliable point-

to-point channel to transmit videos and usually the

bit rate is ﬁxed or can be changed only to a few

different possibilities, which might cause visual in-

terruptions during the transmissions if the available

bandwidth of the channel is variable (Quinlan et al.,

2015; Wien et al., 2007; Zhai et al., 2008). This be-

havior frequently occurs in wireless communication.

Therefore, if the video server could adapt itself to the

client’s bandwidth, the user would have both the best

possible quality given the available bandwidth and the

least amount of interruptions.

A proposed solution to this problem is called

transcoding (Garrido-Cantos et al., 2013; Joset and

Coulombe, 2013; Yeh et al., 2013), which converts

the video stream into another one satisfying a given

constraint. Most of the proposed methods (Ahmad

et al., 2005) are extensions to well-known DCT-based

video encoders and are capable of changing the frame

rate, bit rate, spatial resolution or the standard used in

the transmission. Another approach is scalable cod-

ing (Schwarz et al., 2007; Helle et al., 2013; Hinz

et al., 2013), based on transmitting a single stream

divided into layers that can be acquired separately ac-

cording to the available bandwidth.

This work proposes an approach that compresses

the video at the maximum desired transmission rate

and includes some extra data. This data is used to

transcode the compressed video to a large range of bit

rates.

The target bit rate of this process can be dynam-

ically adjusted with low overhead and the scalable

coding algorithm is near optimal in a sense that it

must only read the compressed ﬁle, execute a binary

search in a table to ﬁnd the correct operating parame-

ters and write the resulting transcoded ﬁle.

To the best of our knowledge, the proposed ap-

proach is the ﬁrst scalable coding method based on

fractal video encoding. It relies exclusively on chang-

ing the resulting bit rate, taking advantage of the

spatio-temporal independency of the fractal codes to

avoid any changes to the frame rate or the spatial res-

olution.

In order to reduce the complexity of the algorithm,

the encoding is extremely simpliﬁed when compared

to other fractal-based approaches while still maintain-

ing an acceptable rate-distortion performance. Per-

ceptual quality comparisons with the x264 encoder

are presented.

This paper is organized as follows. Section 2

brieﬂy reviews some concepts related to this work.

The proposed video encoder based on volumetric

and searchless fractal methods is presented in Sec-

tion 3. Experimental results with well-known video

sequences are described and discussed in Section 4

and, ﬁnally, the conclusions and future work pre-

sented in Section 5.

de Lima V., Moreira T., Pedrini H. and Schwartz W.

Fast Scalable Coding based on a 3D Low Bit Rate Fractal Video Encoder.

DOI: 10.5220/0006100400240033

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 24-33

ISBN: 978-989-758-225-7

2 BACKGROUND

This section presents a brief review of fractal image

encoding, the searchless method for constructing col-

lages, some related fractal video encoders available in

the literature, and a perceptual quality metric used in

image comparisons.

2.1 Fractal Image Encoding

Fractal image encoders (Schwartz and Pedrini, 2011)

transmit a fractal that approximates the original im-

age. The ﬁrst of such methods was proposed in the

seminal paper by Jacquin (Jacquin, 1992), where the

method creates and transmits an operator, called col-

lage, capable of reconstructing an approximation of

the original image given a subsampled version of it.

During the decoding process, the collage is applied to

an arbitrary initial image, the result is subsampled and

this process is repeated until the image converges to a

ﬁxed point.

The usual process used to construct the collage

partitions the image into blocks (called range blocks)

and each one of them is matched with a same-sized

block in the subsampled image (called domain block)

after being transformed by a prespeciﬁed function.

This match is done either by exhaustive search or

through the use of specialized heuristics. In general,

the matching process is very time consuming; there-

fore, most fractal methods have extremely slow and

complex encoding processes, but the decoding is usu-

ally signiﬁcantly faster. The collage can rotate, ﬂip or

mirror the domain blocks and apply a transform into

their gray level values, such as the one used by Tong

and Pi (Tong and Pi, 2001)

G(D) = α(D −

DJ) + ¯rJ (1)

where G is the gray level transform, D is the down-

sampled domain block,

D is the mean value for the

domain block, ¯r is the mean value for the block in

the original scale (the range block), J denotes the unit

matrix, and α is a scale parameter.

2.2 Searchless Fractal Encoding

The searchless fractal image coding was introduced

by Furao and Hasegawa (Furao and Hasegawa, 2004)

as a less complex alternative algorithm for construct-

ing collages. In this approach, each range block has

only one candidate domain block to be matched. If

this matching does not achieve the desired recon-

struction quality, the range block is divided into four

blocks (which can be seen as a tree-based decompo-

sition) and the process continues recursively until the

range blocks reach a certain minimum size.

This approach was reﬁned by Wu et al. (Wu et al.,

2005) by dividing each range block in half either in

the vertical or horizontal direction and without im-

posing any limits to the size of the range blocks. The

smaller blocks have their ¯r parameter more coarsely

quantized than the larger ones, and blocks with only

one or two pixels are forced to have their α equal to

zero.

A 3D fractal video encoder based on an adap-

tive spatial subdivision data structure was proposed

by Lima et al. (Lima et al., 2011a), which demon-

strated to be efﬁcient at very low bit rates.

2.3 Fractal Video Encoding

The ﬁrst fractal video encoder was proposed by Hurd

et al. (Hurd et al., 1992) by creating a collage that

transforms the previous frame into the next one. This

transform could use either blocks from the original

scale or from a subsampled version of the frame. This

approach was enhanced by Fisher et al. (Fisher et al.,

1994) by varying the size of each used range block

through a quadtree.

The fractal video encoding method proposed by

Lazar and Bruton (Lazar and Bruton, 1994) and Li

et al. (Li et al., 1993) used tridimensional collages

that transform a subsampled version of a volume

formed by consecutive frames into the original sig-

nal by matching volumetric range and domain blocks.

Due to the extra dimension, this causes the encoding

process to be even more time consuming when com-

pared to the image encoders.

A faster variation of this volumetric approach was

proposed by Chabarchine and Creutzburg (Chabar-

chine and Creutzburg, 2001) that uses a simpler gray

scale transform, an extremely restricted domain pool

for each range block and a simple spatial subdivi-

sion structure. This method was capable of encoding

videos in real time, however, its rate-distortion per-

formance was poor. Another reﬁned volumetric frac-

tal encoder was introduced by Yao and Wilson (Yao

and Wilson, 2004) by using both vector quantization

and domain blocks to approximate the signal. The

approach could achieve a fair visual quality at low bi-

trates while being relatively fast, but its decoder suf-

fered from convergence problems. A video encoder

based on the compression of consecutive frame dif-

ferences using sparse decomposition through match-

ing pursuits was described by Lima and Pedrini (Lima

and Pedrini, 2010).

Fast Scalable Coding based on a 3D Low Bit Rate Fractal Video Encoder

2.4 Structural Dissimilarity

Most comparisons between video and image encoders

are based on metrics derived from the sum of squared

differences (SSD) or the mean squared error (MSE).

The SSD and the MSE between two images A and B

with size W × H are given by

SSD(A,B) =

W −1

∑

x=0

H−1

∑

y=0

x,y

− B

x,y

)

(2)

where A

x,y

and B

x,y

are the intensity of a pixel located

at (x,y) in A and B, respectively.

MSE(A,B) =

SSD(A,B)

W × H

(3)

The structural similarity (SSIM) index (Wang

et al., 2004) was proposed as a metric for comparing

images which is more properly correlated with

human perception. It maps two images into an index

in the interval [−1,1], where higher values are given

to more similar pairs of images, expressed as

SSIM(A,B) =

(2µ

+ c

)(2σ

+ c

)

(µ

+ µ

+ c

)(σ

+ σ

+ c

)

(4)

where µ

, µ

, σ

and σ

are the averages and vari-

ances of A and B, σ

is the covariance between A

and B, and both c

and c

are predeﬁned constants.

The structural dissimilarity (DSSIM) index is de-

rived from the structural similarity that results in more

distinct values, since a small variation in the original

SSIM indicates a large difference in image quality. It

is expressed as

DSSIM(x,y) =

1 − SSIM(x, y)

(5)

3 PROPOSED METHOD

The video encoder described in this section can be

separated into two different modules. Section 3.1 de-

scribes a heuristic used to decide the number, the po-

sition and the volume of the range blocks and Sec-

tion 3.2 describes how to encode volumetric blocks

of pixels using fractal codes and how to split them.

3.1 Rate-Distortion Heuristic

Our method is based on the heuristic created by Saupe

et al. (Saupe et al., 1998) for image compression with

some adjustments to enable fast scalable coding of the

compressed data and replacing the mean squared er-

ror (MSE) by the sum of squared differences (SSD),

therefore, the total volume of each block contributes

to the distortion measure.

Initially, a group of consecutive frames is prepro-

cessed by encoding it at a relative high bit rate by us-

ing a predeﬁned i

upper

value. It is subdivided into a

uniform grid of range blocks with 16 × 16 × 16 pix-

els, which are encoded and inserted into the priority

queue.

The rate-distortion heuristic creates a new pair

of range blocks at each iteration which replaces the

one taken from the queue. Instead of destroying this

parent block, the algorithm then keeps all the range

blocks created during the entire process marking them

with the number of the iteration in which they were

created.

At every ∆i iterations, the group of frames is en-

coded by the arithmetic encoder several times to gen-

erate a table that associates how many iterations must

be considered to satisfy each desired maximum rate.

This reencoding process has a very low overhead

since the rate-distortion heuristic creates, at each step,

several versions of the same content with different bit

rates and distortions. The transcoder reads this en-

coded group of frames, uses the table to choose a

maximum number of iterations i

target

that achieves the

desired bit rate, and rewrites the ﬁle ignoring every

block that was created after i

target

and discarding both

the iteration number associated with each block and

the encoding parameters of the unused blocks.

Table 1: Uniform quantizers applied according to the vol-

ume of the range block.

Volume Quantization step Number of used bits

1 16 4

2 16 4

4 16 4

8 8 5

16 8 5

32 4 6

64 4 6

128 2 7

256 2 7

512 1 8

1024 1 8

2048 1 8

4096 1 8

The entire process is applied independently to

each group consecutive frames allowing the target

rate to be completely different for each part of the

video during the scalable coding. Therefore, then the

target rate can ﬂuctuate during the transmission of the

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

video. Some encoders use Rate-Distortion Optimiza-

tion (Ortega and Ramchandram, 1998) to adjust the

rate of each group of frames in order to minimize the

total distortion, but since it is impossible to preview

the bandwidth of the transmission channel, this ap-

proach cannot be used in such a case.

3.2 Fast Fractal Block Video Encoding

During every iteration of the rate distortion heuristic,

each range block of the group of frames is encoded

by a generalization to three dimensions of the fractal

image encoder described by Lima et al. (Lima et al.,

2011b). Each range block with dimensions a, b and c

at the coordinates (x,y,z) is matched against a domain

block with dimensions equal to 2a, 2b and 2c located

= x − a + p

× a/2

= y −b + p

× b/2

= z −c + p

× c/2

(6)

where parameters p

, p

and p

must be equal to 0,

1 or 2. Range blocks with volumes smaller than 512

pixels have all these parameters set to 1. This rela-

tionship between the range and the domain block is

illustrated in Figure 1. The domain block is trans-

formed by Equation 1, before the matching, with the

best α parameter chosen among the values in the set

{0.25,0.5,0.75,1.0}.

Each parent block is divided by choosing the di-

rection (along horizontal, vertical or temporal axis)

and the position of the cutting plane used to split it

into two range blocks. This position is chosen in or-

der to minimize the function σ

×V

+σ

×V

, where

, σ

are the variances of the resulting blocks and

, V

are their volumes. The variances and averages

of every block are calculated using integral volumes

as described by Glassner (Glassner, 1990).

The resulting range blocks are encoded by trans-

mitting their α and ¯r parameters. Range blocks with

any dimension smaller than four pixels have their α

parameters set to zero.

All the required symbols and parameters

are encoded using a context-adaptive arithmetic

coder (Said, 2003). Each range block is encoded by

its α parameter, which occupies 2 bits in the worst

case, along with ¯r, which is quantized according to

the range block volume as shown in Table 1. For

range blocks with one or more dimensions smaller

than 2 pixels, the only transmitted parameter is ¯r.

Along with these parameters, the spatial subdivi-

sion tree for each block in the initial uniform subdivi-

sion is encoded by a sequence of symbols pointing to

the decoder, in a depth-ﬁrst order, whether a certain

region was subdivided or not, which direction it was

split and the coordinate of the splitting plane. The α

parameter and the binary decision symbols in the spa-

tial subdivision tree have their own high order adap-

tive contexts, one for each possible value of blogV c,

where V is the total volume of the encoded block. The

direction in which each block is split is encoded by

another set of 3 high order adaptive contexts chosen

according to the direction used to split its parent.

The ¯r parameter is encoded as the difference be-

tween a quantized prediction and the real quantized

value. The prediction is calculated as the average of ¯r

of the neighboring blocks located at the top, to the left

and behind the encoded block weighted by their area

of contact. This difference is encoded by the Adap-

tive Goulomb-Rice code described by Weinberger et

al. (Weinberger et al., 1996), using one context for

each possible blogV c in the same manner as the other

parameters.

The intermediary representation created by the en-

coder and supplied to the scalable coding process en-

codes the iteration number in which each block was

created using the same Adaptive Goulomb-Rice code

as ¯r and it stores the ¯r and α for every block, including

the ones that were split by the rate-distortion heuristic

(which are not included in the ﬁnal stream sent to the

decoder).

The decoding process is accelerated by three

different and complementary methods. The initial

volumetric image that is used in the ﬁrst iteration

of the decoder is composed by ﬁlling each range

block with its mean (for more details, see the work

by Moon et al. (Moon et al., 2000)). The used

pixel intensity transform is the one proposed by

Øien and Lepsøy (Øien and Lepsøy, 1995) with

additional proofs and details given by Pi et al. (Pi

et al., 2003). Each iteration is applied according

to the Gauss-Seidel inspired method proposed by

Hamzaoui (Hamzaoui, 1999), which uses only one

image during the iterations to overwrite each range

block with its updated contents. The use of these

methods assures that the decoding process converges

in 4 iterations or less, instead of the usual 8 to 10

iterations used by other fractal decoders.

4 EXPERIMENTAL RESULTS

The video sequences were encoded on an Intel Core

2 Duo E6750 processor, 2.66 GHz with 8GB of

RAM running the Arch Linux operating system. The

method was implemented using the C++ program-

ming language without any SIMD optimizations.

Each group had at most 32 frames in it because of

Fast Scalable Coding based on a 3D Low Bit Rate Fractal Video Encoder

Figure 1: A few possible relationships between a range and a domain block in the proposed video encoder.

Table 2: The number of frames for the video sequences, the encoding time of the proposed method and the size of each

encoded ﬁle with and without the extra data used by the scalable coding process.

Sequence # Frames Time Size Size without

(s) (KB) additional data (KB)

Foreman 300 5.8 390.5 194.7

Car phone 457 6.1 392.6 200.6

Bus 150 5.4 382.6 188.0

Football 260 5.5 387.1 193.5

Akiyo 300 5.0 336.8 170.5

Hall monitor 300 5.2 366.7 187.7

Bowing 300 5.0 343.0 175.6

Miss America 179 5.8 315.9 149.1

precision limits in the construction of the integral

volumes and to ensure that every range block in the

initial partition had at least one element in its domain

pool.

The proposed approach is compared to the

H.264 encoder, called x264 (x264, 2016), using

the standard grayscale benchmark sequences ’Fore-

man’, ’Car phone’, ’Bus’, ’Football’, ’Akiyo’, ’Hall

monitor’, ’Bowing’, and ’Miss America’ in the

CIF format (CIPR, 2015). Table 2 presents, for

each sequence, the number of frames, the average

encoding time needed to generate the intermediate

ﬁle used by the transcoder

, the resulting ﬁle size

of this initial encoding, and the ﬁnal ﬁle size at the

maximum available bit rate in the preprocessed ﬁle

(i.e. without any extra data used by the scalable

coding process).

The video sequences in the following experiments

were encoded at low bit rates, which implies that the

results had high distortions when measured by Equa-

tion 2. As demonstrated by Wang et al. (Wang et al.,

2004), the ambiguity of the metrics derived from the

SSD from a perceptual point of view is high and be-

comes even larger as the distortion increases. It is

important to observe that both α and ¯r parameters are

It is important to mention that this process is executed

only once and each intermediate ﬁle is stored and used when

necessary.

quantized (i.e. they must assume one of a small set of

possible values instead of being continuous), which

causes a mean shift and a contrast change in every

range block, even though the effect of these quantiza-

tions is perceptually negligible.

In order to ensure a proper comparison between

both methods, the mean structural dissimilarity is

used in the experiments. This metric is widely ac-

cepted for its simplicity and reasonably accuracy, be-

ing employed in the design of several image encoders,

such as (Krause, 2010), and has a built-in implemen-

tation in the x264.

The bit rate was varied to closely match the same

values in both encoders. As observed in Figure 2, the

proposed encoder outperforms the x264 codec at very

low bit rates in high motion sequences. The motion

compensation algorithm of the H.264 encoder cannot

operate properly in these conditions given that an ac-

curate prediction of each frame would require a large

amount of bits.

The x264 was conﬁgured to closely match the be-

havior of the proposed encoder by forcing it to insert a

keyframe at every 32 frames and compiling it without

any CPU speciﬁc optimizations. The Rate-Distortion

heuristic, described in Section 3.1, was conﬁgured to

use 125000 iterations for each entire sequence and

∆i was set to 1000 iterations. The encoding process

shown in Table 2 is executed only once and gener-

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

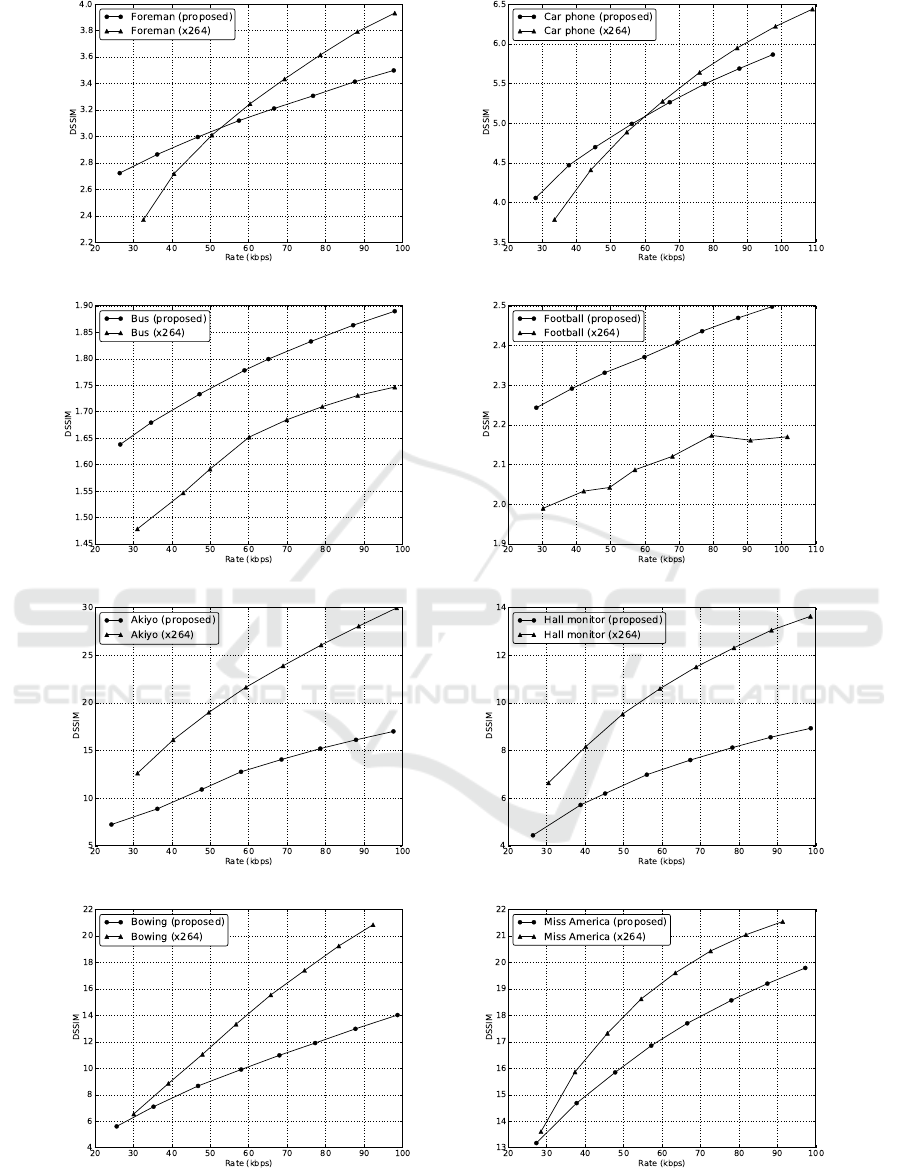
Figure 2: Mean structural dissimilarity at different rates for the proposed video encoder and the x264 encoder.

Fast Scalable Coding based on a 3D Low Bit Rate Fractal Video Encoder

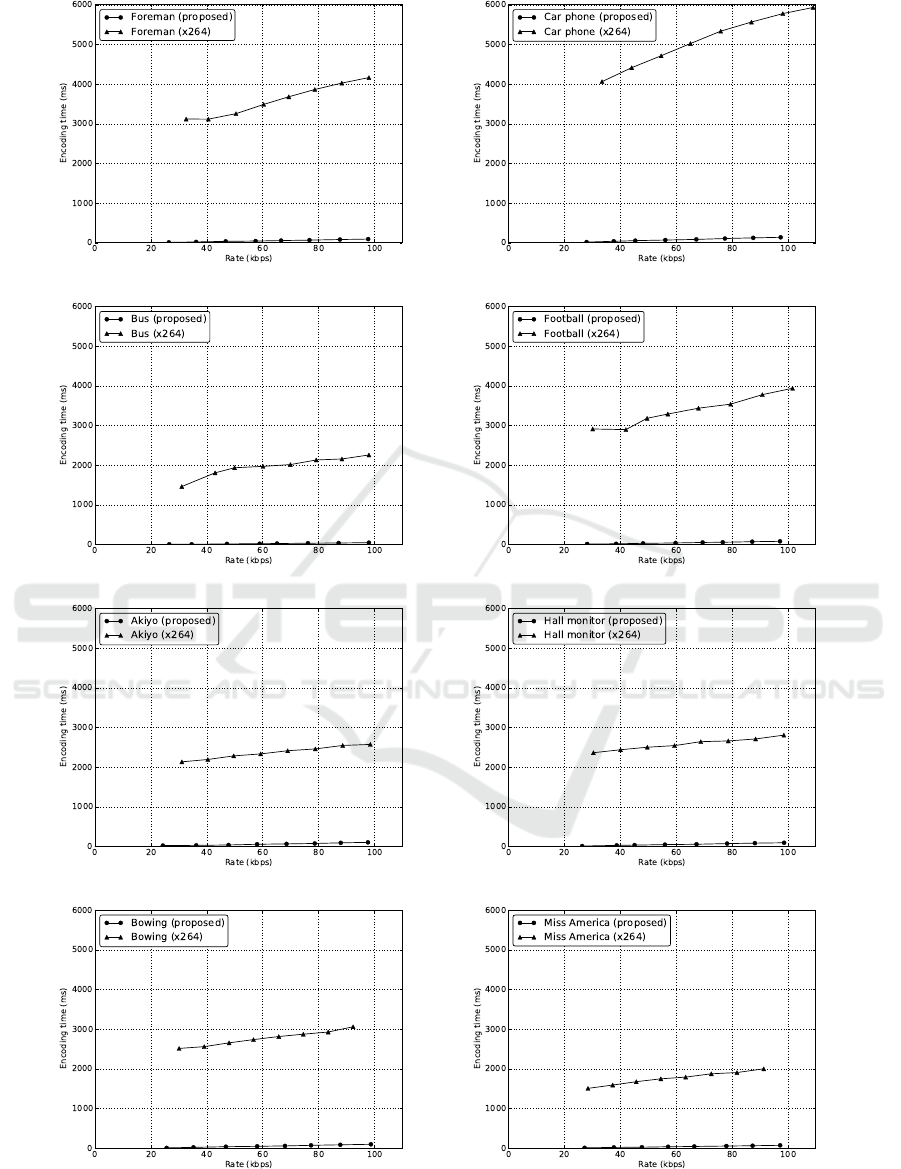
Figure 3: Encoding time at different rates for the video transcoder and the x264 encoder.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

0 20 40 60 80 100

100

Obt ained Rat e (kb ps)

Requested Rate (kbps)

Foreman

0 20 40 60 80 100

100

Obt ained Rat e (kb ps)

Requested Rate (kbps)

Car phone

0 20 40 60 80 100

100

Obt ained Rat e (kb ps)

Requested Rate (kbps)

Bus

0 20 40 60 80 100

100

Obt ained Rat e (kb ps)

Requested Rate (kbps)

Football

0 20 40 60 80 100

100

Obt ained Rat e (kb ps)

Requested Rate (kbps)

Akiyo

0 20 40 60 80 100

100

Obt ained Rat e (kb ps)

Requested Rate (kbps)

Hall monitor

0 20 40 60 80 100

100

Obt ained Rat e (kb ps)

Requested Rate (kbps)

Bowing

0 20 40 60 80 100

100

Obt ained Rat e (kb ps)

Requested Rate (kbps)

Miss America

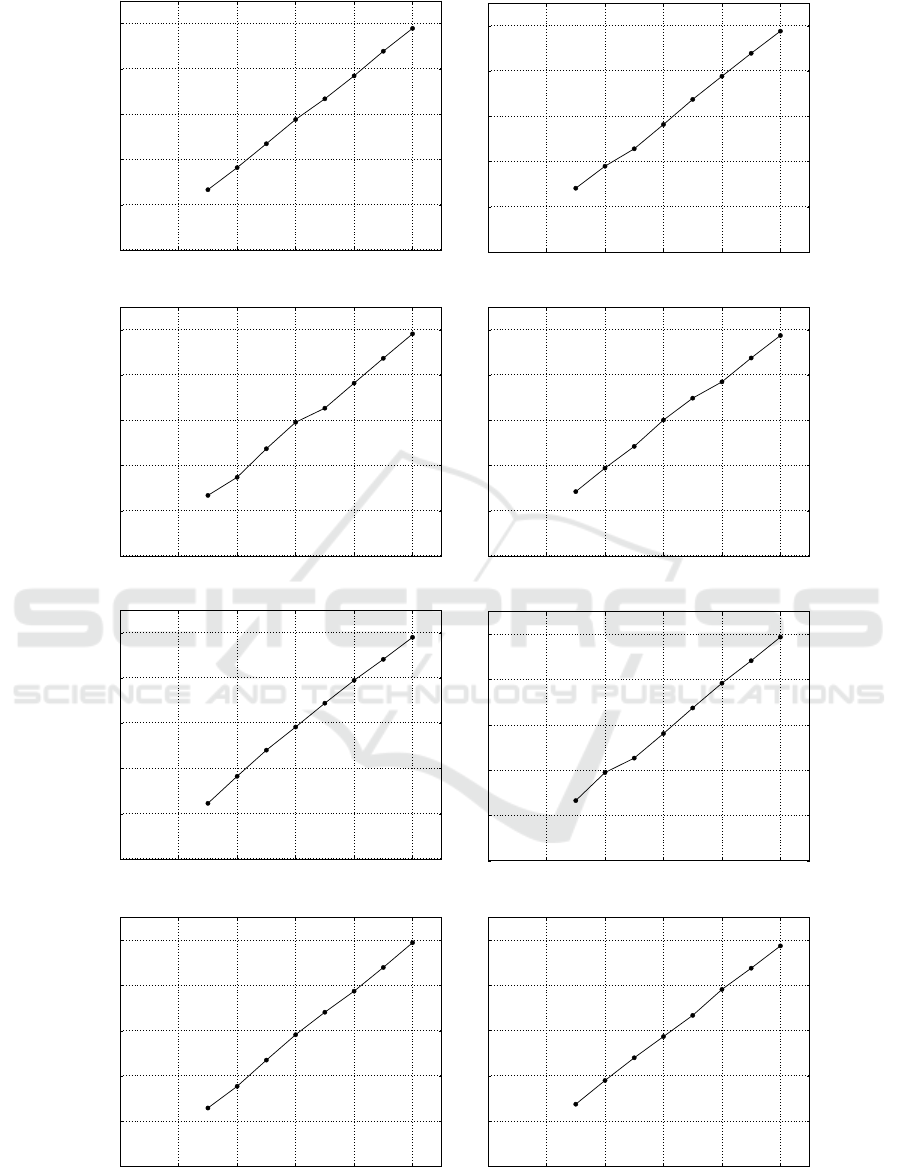
Figure 4: Requested and obtained rates for the proposed method.

Fast Scalable Coding based on a 3D Low Bit Rate Fractal Video Encoder

ates the compressed video combined with extra data

to allow the fast scalable coding of the sequence. As

shown in the last column of the table, the overhead of

the extra data is quite large, almost doubling the size

of the compressed video.

Figure 3 shows the speed of the scalable coding

process. The required time to encode the sequences

is at most 140 ms at the highest bit rates. Regardless

the preprocessing step, which is performed only once

and can be considered as an ofﬂine process, the pro-

posed method is much faster than directly encoding

the video with x264.

The scalable coding algorithm is limited only by

how fast the data can be read and written since the

total transcoding time is linearly correlated with the

target rate. Figure 4 shows that the rate control is pre-

cise, achieving the desired constraint with a negligible

error.

5 CONCLUSIONS

The proposed approach can rapidly transcode a pre-

processed video sequence into a large range of differ-

ent bit rates with extreme ﬁne control of the resulting

rate. It employs a fast fractal encoding method using

volumetric range and domain blocks matched against

each other using a generalization of a fast fractal en-

coder to three dimensions.

It is important to mention that the proposed rate

control and the transcoding heuristic could be applied

to other encoding methods that are not based on frac-

tals but are still adaptive. The near-optimal behavior

of the transcoding algorithm, combined with better

block encoding methods, could result in viable alter-

native to the current commonly used video encoders.

ACKNOWLEDGMENTS

The authors are thankful to the Minas Gerais Re-

search Foundation (FAPEMIG), S

ao Paulo Research

Foundation (FAPESP grants #2015/03156-7 and

#2015/12228-1) and Brazilian National Council for

Scientiﬁc and Technological Development (CNPq

grant #305169/2015-7) for their ﬁnancial support.

REFERENCES

Ahmad, I., Wei, X., Sun, Y., and Zhang, Y.-Q. (2005). Video

Transcoding: An Overview of Various Techniques and

Research Issues. IEEE Transactions on Multimedia,

7:793–804.

Chabarchine, A. and Creutzburg, R. (2001). 3D Fractal

Compression for Real-Time Video. In 2nd Interna-

tional Symposium on Image and Signal Processing

and Analysis, pages 570–573, Pula, Croatia.

CIPR (2015). Sequences. http://www.cipr.rpi.edu/resource/

sequences/.

Fisher, Y., Rogovin, D., and Shen, T. (1994). Fractal (Self-

VQ) Encoding of Video Sequences. Visual Communi-

cations and Image Processing, 2308(1):1359–1370.

Furao, S. and Hasegawa, O. (2004). A Fast No Search Frac-

tal Image Coding Method. Signal Processing: Image

Communication, 19(5):393–404.

Garrido-Cantos, R., De Cock, J., Martnez, J., Van Leuven,

S., and Garrido, A. (2013). Video Transcoding for

Mobile Digital Television. Telecommunication Sys-

tems, 52(4):2655–2666.

Glassner, A. S. (1990). Graphics Gems. In Multidimen-

sional Sum Tables, pages 376–381. Academic Press

Professional, Inc., San Diego, CA, USA.

Hamzaoui, R. (1999). Fast Iterative Methods for Fractal Im-

age Compression. Journal of Mathematical Imaging

and Vision, 11:147–159.

Helle, P., Lakshman, H., Siekmann, M., Stegemann, J.,

Hinz, T., Schwarz, H., Marpe, D., and Wiegand,

T. (2013). A Scalable Video Coding Extension of

HEVC. In Data Compression Conference, pages 201–

210, Snowbird, UT, USA.

Hinz, T., Helle, P., Lakshman, H., Siekmann, M., Stege-

mann, J., Schwarz, H., Marpe, D., and Wiegand, T.

(2013). An HEVC Extension for Spatial and Quality

Scalable Video Coding. In Proc. SPIE, volume 8666,

pages 866605–866605–16.

Hurd, L., Gustavus, M., and Barnsley, M. (1992). Frac-

tal Video Compression. In Thirty-Seventh IEEE Com-

puter Society International Conference, pages 41–42.

Jacquin, A. (1992). Image Coding Based on a Fractal The-

ory of Iterated Contractive Image Transformations.

IEEE Transactions on Image Processing, 1(1):18–30.

Joset, D. and Coulombe, S. (2013). Visual Quality and File

Size Prediction of H.264 Videos and Its Application

to Video Transcoding for the Multimedia Messaging

Service and Video on Demand. In IEEE International

Symposium on Multimedia, pages 321–328.

Krause, P. K. (2010). FTC - Floating Precision Texture

Compression. Computers and Graphics, 34(5):594–

601.

Lazar, M. and Bruton, L. (1994). Fractal Block Coding of

Digital Video. IEEE Transactions on Circuits and Sys-

tems for Video Technology, 4(3):297–308.

Li, H., Novak, M., and Forchheimer, R. (1993). Fractal-

Based Image Sequence Compression Scheme. Optical

Engineering, 32(7):1588–1595.

Lima, V. and Pedrini, H. (2010). A Very Low Bit-rate Min-

imalist Video Encoder based on Matching Pursuits.

In 15th Iberoamerican Congress on Pattern Recogni-

tion, pages 176–183, S

ao Paulo, SP, Brazil. Springer-

Verlag.

Lima, V., Schwartz, W. R., and Pedrini, H. (2011a). Fast

Low Bit-Rate 3D Searchless Fractal Video Encod-

ing. In 24th SIBGRAPI Conference on Graphics,

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

Patterns and Images, pages 189–196, Maceio, AL,

Brazil. IEEE.

Lima, V., Schwartz, W. R., and Pedrini, H. (2011b). Fractal

Image Encoding Using a Constant Size Domain Pool.

In VII Workshop of Computer Vision, pages 137–142,

Curitiba, PR, Brazil.

Moon, Y. H., Kim, H. S., and Kim, J. H. (2000). A Fast

Fractal Decoding Algorithm based on the Selection of

an Initial Image. IEEE Transactions on Image Pro-

cessing, 9(5):941–945.

Øien, G. and Lepsøy, S. (1995). A Class of Fractal Image

Coders with Fast Decoder Convergence, chapter Frac-

tal Image Compression, pages 153–175. Springer-

Verlag, London, UK.

Ortega, A. and Ramchandram, K. (1998). Rate-Distortion

Methods for Image and Video Compression. IEEE

Signal Processing Magazine, 15(6):23–50.

Pi, M., Basu, A., and Mandal, M. (2003). A New Decod-

ing Algorithm based on Range Block Mean and Con-

trast Scaling. In International Conference on Image

Processing, volume 3, pages II – 271–4, Barcelona,

Spain.

Quinlan, J. J., Zahran, A. H., Ramakrishnan, K. K., and

Sreenan, C. J. (2015). Delivery of Adaptive Bit

Rate Video: Balancing Fairness, Efﬁciency and Qual-

ity. In IEEE International Workshop on Local and

Metropolitan Area Networks, pages 1–6.

Said, A. (2003). Lossless Compression Handbook, chap-

ter Arithmetic Coding. Communications, Network-

ing, and Multimedia. Academic Press.

Saupe, D., Ruhl, M., Hamzaoui, R., Grandi, L., and Marini,

D. (1998). Optimal Hierarchical Partitions for Fractal

Image Compression. In IEEE International Confer-

ence on Image Processing, pages 737–741, Chicago,

IL, USA.

Schwartz, W. R. and Pedrini, H. (2011). Improved Fractal

Image Compression based on Robust Feature Descrip-

tors. International Journal of Image and Graphics,

11(04):571–587.

Schwarz, H., Marpe, D., and Wiegand, T. (2007). Overview

of the Scalable Video Coding Extension of the

H.264/AVC Standard. IEEE Transactions on Circuits

and Systems for Video Technology, 17(9):1103–1120.

Tong, C. and Pi, M. (2001). Fast Fractal Image Encoding

based on Adaptive Search. IEEE Transactions on Im-

age Processing, 10(9):1269–1277.

Wang, Z., Bovik, A., Sheikh, H., and Simoncelli, E. (2004).

Image Quality Assessment: From Error Visibility to

Structural Similarity. IEEE Transactions on Image

Processing, 13(4):600 –612.

Weinberger, M., Seroussi, G., and Sapiro, G. (1996).

LOCO-I: A Low Complexity, Context-based, Loss-

less Image Compression Algorithm. In Data Com-

pression Conference, pages 140–149, Snowbird, UT,

USA. IEEE Computer Society.

Wien, M., Cazoulat, R., Graffunder, A., Hutter, A., and

Amon, P. (2007). Real-Time System for Adaptive

Video Streaming Based on SVC. IEEE Transac-

tions on Circuits and Systems for Video Technology,

17(9):1227–1237.

Wu, X., Jackson, D., and Chen, H. (2005). Novel Fractal

Image-Encoding Algorithm Based on a Full-Binary-

Tree Searchless Iterated Function System. Optical En-

gineering, 44(10):107002–107014.

x264 (2016). Video Encoder. http://www.videolan.org/

developers/x264.html.

Yao, Z. and Wilson, R. (2004). Hybrid 3D Fractal Coding

with Neighbourhood Vector Quantisation. EURASIP

Journal on Applied Signal Processing, 2004:2571–

2579.

Yeh, C.-H., Jiang, S.-J. F., Lin, C.-Y., and Chen, M.-J.

(2013). Temporal Video Transcoding Based on Frame

Complexity Analysis for Mobile Video Communica-

tion. IEEE Transactions on Broadcasting, 59(1):38–

46.

Zhai, G., Cai, J., Lin, W., Yang, X., and Zhang, W.

(2008). Three Dimensional Scalable Video Adap-

tation via User-End Perceptual Quality Assessment.

IEEE Transactions on Broadcasting, 54(3):719–727.

Fast Scalable Coding based on a 3D Low Bit Rate Fractal Video Encoder