
Noise-resistant Unsupervised Object Segmentation in Multi-view Indoor
Point Clouds
Dmytro Bobkov
1
, Sili Chen
2
, Martin Kiechle
3
, Sebastian Hilsenbeck
4
and Eckehard Steinbach
1
1
Chair of Media Technology, Technical University of Munich, Arcisstr. 21, Munich, Germany
2
Institute of Deep Learning, Baidu Inc., Xibeiwang East Road, 10, Beijing, China
3
Chair of Data Processing, Technical University of Munich, Arcisstr. 21, Munich, Germany
4
NavVis GmbH, Blutenburgstr. 18, Munich, Germany
Keywords:
Object Segmentation, Concavity Criterion, Laser Scanner, Point Cloud, Segmentation Dataset.
Abstract:
3D object segmentation in indoor multi-view point clouds (MVPC) is challenged by a high noise level, varying
point density and registration artifacts. This severely deteriorates the segmentation performance of state-of-
the-art algorithms in concave and highly-curved point set neighborhoods, because concave regions normally
serve as evidence for object boundaries. To address this issue, we derive a novel robust criterion to detect
and remove such regions prior to segmentation so that noise modelling is not required anymore. Thus, a
significant number of inter-object connections can be removed and the graph partitioning problem becomes
simpler. After initial segmentation, such regions are labelled using a novel recovery procedure. Our approach
has been experimentally validated within a typical segmentation pipeline on multi-view and single-view point
cloud data. To foster further research, we make the labelled MVPC dataset public (Bobkov et al., 2017).
1 INTRODUCTION
Unsupervised segmentation of 3D indoor scenes into
objects remains a highly challenging topic in com-
puter vision despite many years of research. Seg-
mentation using data from handheld depth sensors,
e.g., Kinect, is a well-studied research topic due to
low price and flexibility (Soni et al., 2015), (Karpathy
et al., 2013) and (Jiang, 2014). Most existing datasets
include only single-view data and focus on small en-
vironments due to the high effort involved in record-
ing building-scale environments using handheld sen-
sors. When recording large indoor environments the
operational costs and time constraints become more
important as the environment has to be free of dy-
namic objects during the time of scanning. Compared
to Kinect-based solutions, laser scanners have a clear
advantage in this context as they provide a larger scan-
ning range (typically more than 30 meters) and wider
angle of view. With these systems, it is possible to
scan an area of ten thousand square meters within a
day, which is practically impossible using any Kinect-
like sensor. A number of mapping platforms equipped
with laser scanners have been developed using either a
wearable backpack (Liu et al., 2010) or a moving trol-
ley (Huitl et al., 2012). The sensors progressively take
measurements and integrate them into a 3D model
using a SLAM system, while the platform is moved
through the indoor space.
As a result of the specific scanning procedure
required for large indoor environments (e.g., floors
and buildings), multi-view point cloud (MVPC) data
acquired using a moving platform tend to have the
following drawbacks when compared to single-view
data:
1. Unreliable surface normal information caused by
registration artifacts. These are mostly due to in-
accuracies when registering multiple range scans
into a single 3D map. Such artifacts are most
pronounced in large datasets, because registration
noise tends to accumulate over time (Pomerleau
et al., 2013). This complicates the object segmen-
tation using solely normal information.
2. Varying point density. This is caused by large
scanner setup and strict time constraints, so that it
is, sometimes, simply impossible to scan the ob-
jects from various directions.
The available single-view depth indoor datasets
(N. Silberman and Fergus, 2012), (Lai et al., 2013),
(Xiao et al., 2013) are not representative for building-
scale indoor applications, because of the aforemen-
Bobkov D., Chen S., Kiechle M., Hilsenbeck S. and Steinbach E.
Noise-resistant Unsupervised Object Segmentation in Multi-view Indoor Point Clouds.
DOI: 10.5220/0006100801490156
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 149-156
ISBN: 978-989-758-226-4
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
149

tioned differences to MVPC data. The dataset of
(Song and Xiao, 2014) is not suitable for evalua-
tion of point cloud-based segmentation algorithms be-
cause severe misalignment artifacts are present in the
point cloud data. This is due to the fact that object
labelling has been done in depth images only. The
large dataset of (Armeni et al., 2016) has been cap-
tured using a static laser scanner, which experiences
lower noise level as compared to a moving scanning
platform. This setup is, however, significantly limited
for large environments due to small scanning range
and longer capture times. Other available multi-view
datasets are not applicable, because they are either
limited in size and contain only single objects (Mian
et al., 2006) or capture outdoor environments (Boyko
and Funkhouser, 2014), which have different geomet-
ric properties than indoor scenes. To fill this gap be-
tween single-view and multi-view indoor datasets, we
provide an annotated point cloud dataset that reflects
these real world constraints. Our dataset spans 6 room
scenes with various objects, such as tables, chairs,
lamps etc. and is made available to the scientific com-
munity (Bobkov et al., 2017) in order to foster further
research in this area.
Existing approaches for 3D point cloud segmen-
tation are usually tested on single-view datasets.
Hence, they do not consider the important peculiar-
ities of MVPC data and tend to perform poorly on
such datasets. Furthermore, these approaches have
been designed specifically for depth-based datasets
(Jiang, 2014), (Song and Xiao, 2014), (Deng et al.,
2015), (Fouhey et al., 2014), (Tateno et al., 2015).
Other methods make strong assumptions on scene
planarity (Mattausch et al., 2014). Supervised meth-
ods achieve good segmentation performance (Karpa-
thy et al., 2013), (Soni et al., 2015), but require mas-
sive amount of labelled training examples, which are
unavailable for MVPC datasets. Therefore, this paper
considers unsupervised methods. The performance
of state-of-the-art segmentation methods (Stein et al.,
2014), (van Kaick et al., 2014) on MVPC is not satis-
factory. This is due to the high noise level in highly-
curved concave regions, which normally serve as a
strong evidence for object boundaries (Fouhey et al.,
2014), (Stein et al., 2014). To overcome this limita-
tion, we propose a novel point set-based criterion to
detect such concave noisy regions and temporarily re-
move them prior to scene segmentation. We further
propose a procedure to restore such noisy regions af-
ter initial segmentation.
The contributions of this paper are the following:
• Method to robustly detect high-noise regions.
It helps to overcome limitations of state-of-the-
art object segmentation algorithms that perform
(a) Input data (b) Pre-processed
point cloud
(c) Non-convex
point removal
(d) Supervoxel
clustering
(e) Segmentation (f) Recovery
Figure 1: Processing steps of the analysed segmentation
pipeline. Steps shown in bold are novel contributions of
this paper. Note that curvature values are color coded in (b)
and (c): low value is green and high is red.
(a) RGB image (b) Point cloud (c) Surface graph
Figure 2: Illustration of noisy region influence (b) on sur-
face graph. In (c) erroneous connections resulting from
noise in a planar region are highlighted. After non-convex
region removal step these noisy points in the planar region
have been removed as well as the erroneous connections.
poorly on MVPC datasets due to the specific prop-
erties of such data.
• A new MVPC dataset with labelling for objects
and parts. It has been acquired using a laser scan-
ner and contains scenes of office environments.
2 METHODOLOGY
To illustrate the improvements achievable with the
proposed concave/convex region criterion, we first
consider a typical 3D object segmentation pipeline,
as described in (Stein et al., 2014). One normally
performs pre-processing on the input point cloud
(Fig. 1a) data to remove outliers and other artifacts.
This is typically done in combination with normal and
curvature calculation (Fig. 1b). Afterwards, the su-
pervoxel (surface-patch) adjacency graph is extracted
from the point cloud, e.g., using the approach of (Pa-
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
150

n
n
n
𝑁
+
= 45
𝑁
+
= 4
𝑁
+
= 16
𝑁
−
= 9
𝑁
−
= 24
𝑁
−
= 17
Figure 3: Illustration of high-curvature regions. Left: con-
cave region. Middle: convex region. Right: ambiguous
region. The numbers N
+
and N
−
indicate the number of
points in positive and negative half-space respectively.
pon et al., 2013), in order to reduce the complex-
ity of the input data (Fig. 1d). Finally, segmenta-
tion is performed on the given graph using a state-
of-the-art graph partitioning method (Fig. 1e). We
propose to augment the segmentation pipeline by the
additional steps of curved non-convex point removal
(Fig. 1c) and recovery according to the proposed cri-
terion (Fig. 1f). We present the details of each of these
steps and discuss the limitations of the state-of-the-art
approaches. We consider point clouds with viewpoint
that is the direction from which the range sensor has
detected this point. For preprocessing (smoothing and
curvature and normal estimation) we use the method
of (Rusu et al., 2008). We have not noticed any signif-
icant improvement when using the estimation method
of (Boulch and Marlet, 2012).
2.1 Classification into Convex and
Non-convex Points
Limitation of Supervoxels and Normals. In order
to reduce the computational complexity, we group
points according to the algorithm of (Papon et al.,
2013). It essentially over-segments 3D point cloud
data into patches called supervoxels (Fig. 1d). The
supervoxels are desired not to span boundaries across
objects. Unfortunately, this is not the case for noisy
highly-curved concave regions, which often coincide
with object boundaries. This effect is illustrated in
Fig. 2. Note the false connections (circled in red)
within the wall of the table in the middle of the scene
within a concave high-curvature region. If we would
just remove all high-curvature regions, this would
severely degrade the segmentation performance, be-
cause many of the removed points represent impor-
tant connections within objects that should not be par-
titioned. This effect is not specific to supervoxels
only, but occurs in any patch-based surface represen-
tation as surface estimation is negatively influenced
by noise.
Noise-resilient Convexity/Concavity Criterion. We
derive a novel convexity/concavity criterion operating
on point set statistics that is robust to noise in the nor-
mal estimation in order to cope with the aforemen-
tioned limitations. The criterion is defined for the
neighborhood with radius R of a given point ~p. In
particular, for a given point coordinate (p
x
, p
y
, p
z
) and
its normal (n
x
,n
y
,n
z
) (Fig. 3), one can define a plane
having the same normal as ~n and containing point ~p.
The plane equation is given in Hessian form:
n
x
· x + n
y
· y + n
z
· z + d = 0, (1)
where d is the distance to the origin and can be com-
puted from (1) by using p
x
, p
y
, p
z
instead of x, y,z.
This tangent plane divides the whole space into two
half-spaces. We compute in which half-space a par-
ticular point is located with (1). By analysing convex
and concave neighborhood regions, we find that the
points within R are typically located within the same
half-space as the normal direction ~n for the concave
regions, and for convex ones in the other half-space.
We compare the number of points within each half-
space to determine whether the given point neighbor-
hood R is non-convex and if yes, it will be removed:
m(~p,R) =
non-convex , if N
+
≥ α
t
· N
−
convex , if N
+
< α
t
· N
−
,
(2)
where N
+
is the number of points in the neighborhood
R lying within the same half-space as the normal vec-
tor of the local surface ~n(R), and N
−
is the number
of neighboring points lying within the opposite half-
space and α
t
is the threshold to detect noisy regions.
We illustrate the choice of the value of α
t
on the ex-
ample of the regions in Fig. 3. Concave and ambigu-
ous regions need to be removed for the best segmenta-
tion performance. In contrast, convex regions have to
be preserved. For α
t
= 0.1 the convex region in Fig. 3
is classified as non-convex and removed. Its removal
leads to over-segmentation of the object. For α
t
= 1.0
the ambiguous region (that mostly consists of mea-
surement noise) will be classified as convex and thus
preserved. Experiments on laser scanner data indicate
that with α
t
= 0.2 such regions will be correctly clas-
sified for the used datasets (see further results in Dis-
cussion). The point neighborhoods satisfying the non-
convex condition in (2) and with curvature θ > θ
t
will
be temporarily removed (Fig. 1c). From this point
on, we denote concave and ambiguous regions as non-
convex for the sake of simplicity.
2.2 Supervoxel Clustering and Graph
Partitioning
After noisy high-curvature non-convex regions have
been removed, edge weights between neighboring su-
pervoxels can be adequately computed. For this, we
consider supervoxel ~p
i
= (~x
i
, ~n
i
,N
i
), with centroid ~x
i
,
normal vector ~n
i
and edges to adjacent supervoxels.
Noise-resistant Unsupervised Object Segmentation in Multi-view Indoor Point Clouds
151

We do not want to strictly enforce the condition of
concave object boundaries. Instead, we argue that
concavity is just one indicator for the object bound-
ary and Euclidian distance and surface normals still
serve as evidence for object boundaries in case of non-
concave regions. Therefore, we calculate the graph
edge weight between neighboring supervoxels as fol-
lows:
w
e
=
a · D
2
, if convex edge
D , if concave edge,
(3)
where D is the definition for edge weight described in
(Papon et al., 2013), but implemented differently by
the authors in Point Cloud Library:
D =
|~x
1
−~x
2
|
R
seed
· w
s
+ (1 − | cos(~n
1
,~n
2
)|) · w
n
, (4)
where |~x
1
−~x
2
| is the Euclidean distance between two
nodes (centroids of supervoxel patches), R
seed
is the
seed radius,~n
1
and~n
2
are normals of two supervoxels
and w
s
and w
n
are spatial and normal weights, respec-
tively. Note that we omit the color difference term
compared to original formulation as it does not nec-
essarily improve segmentation results, also observed
in (Karpathy et al., 2013). The parameter a denotes
the weight for considering the importance of concav-
ity when partitioning objects. A lower value for a in-
creases the weight of the concavity criterion in the
segmentation process. Based on experimental results
and to be able to segment various objects, we strike a
trade-off by using a = 0.25 for all experiments. From
(3), it is clear that in case of similar weights con-
cave edges will be preferred as object boundaries in
most cases. Nonetheless, in case a convex edge con-
nects two remotely located regions with drastically
different surface, the spatial and normal distance can
serve as evidence for object partitioning. Similarly
to (Stein et al., 2014), we set R
seed
/R
voxel
= 4 for all
used datasets, where R
voxel
is the voxel radius. In our
experiments, we set w
s
= 0.2 and w
n
= 0.5 for all
datasets, as we have observed that normal information
is more characteristic when describing the surface ge-
ometry compared to the Euclidian distance.
When partitioning the extracted graph of scenes
with complex geometry, we observed that sim-
ple region-growing algorithms do not perform well.
Therefore, we instead use adaptive statistics-based
graph-based segmentation algorithm of (Felzen-
szwalb and Huttenlocher, 2004) (Fig. 1e). Other
graph partitioning algorithms, such as spectral clus-
tering and normalized mincut do not achieve such a
good trade-off between accuracy and speed.
2.3 Recovery of Previously Removed
Noisy Non-convex Points
It is necessary to recover the removed non-convex
high-curvature points and assign them to correct la-
bels. While recovering such points, the most similar
labelled points in the vicinity need to be determined.
The local surface geometry is important for this pur-
pose. For this reason, we use the graph edge weight
defined in (4) as our similarity metric. We have ob-
served that simple region growing algorithms based
on seeds (i.e. known labels) are sensitive to outliers,
which often occur at such highly-curved regions. To
overcome this problem, we constrain the number of
propagated labels per iteration. Furthermore, we start
with connections having lower weights as these ex-
hibit higher similarity and compute this metric in the
vicinity R
voxel
of the given point. Within one iter-
ation, we limit the number of points to recover to
a certain percentage P
r
of the number of currently
unlabelled points that have labelled neighbors (P
r
=
80%). We have experimentally found that K = 20
such iterations are sufficient to recover non-convex
points (observe an example of the restored labels in
Fig. 1f). The pseudocode for the algorithm is given
in Algorithm 1. Here LabelledRadiusPoints(P,R) re-
turns labelled neighboring points around P within the
search radius R. LabelO f (P) returns the point label.
Note that W denotes a triplet with point, distance and
weight.
Algorithm 1: Label Removed Non-convex Points.
Q ← labelled points
U ← unlabelled points
for k = 0 to K − 1 do
W ← {}
for all P
n
∈ U do
M ← LabelledRadiusPoints(P
n
,R
Voxel
)
if M 6=
/
0 then
jmin ← argmin
∀M
j
∈M
D(P
n
,M
j
)
D
min
← D(P
n
,M
jmin
) (4)
L
min
← LabelO f (M
jmin
)
W ← W ∪ {M
jmin
,D
min
,L
min
}
if k 6= K − 1 then
Sort W with ascending order of D
N
Preserve
← Rnd(Length(W ) · P
r
)
for i = 0 to N
Preserve
− 1 do
Q ← Q ∪W
i
3 EXPERIMENTAL EVALUATION
In this section, we present quantitative results on
manually labelled laser scanner-based indoor point
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
152

cloud data. We further provide experimental results
for Kinect data. We benchmark our results against
the state-of-the-art geometry-based unsupervised seg-
mentation algorithms of (Stein et al., 2014) (Locally
Convex Connected Patches - LCCP) and (van Kaick
et al., 2014). For this, we use the publicly accessible
algorithm implementations provided by the authors.
3.1 Laser Scanner Dataset and
Evaluation Metric
For rigorous evaluation of various segmentation ap-
proaches and due to the lack of publicly available
multi-view point cloud datasets, we manually label
6 indoor scenes by specifying object parts and their
relationship to each other. The point cloud data has
been acquired using a mobile mapping platform with
3 Hokuyo UTM-30LX laser scanners. While the anal-
ysis can be done on the data from any range sensor,
we chose laser scanners as they offer a fast acquisi-
tion procedure in large indoor environments. As the
platform is moved through the environment, its laser
scanners perform range measurements in one hori-
zontal and two intersecting vertical planes, thus in-
crementally building a 3D map. The average scan-
ning time per room constitutes several minutes. The
captured scenes represent typical office environments
with various objects. The total number of objects is
156, which contain 452 semantic object parts (e.g.
chair back, leg, arm etc., see Fig. 4).
When labelling, some may regard a chair as a
whole object, while others may regard it as a col-
lection of parts, such as chair back, chair leg etc. It
is unclear which of this labelling is correct. There-
fore, we derive labelling on several object levels, e.g.
fine and coarse ground truth (GT). Fine GT includes
object parts, while coarse GT capture objects them-
selves. Finally, the proper GT given the segmenta-
tion result will be generated based on the predicted
label as well as coarse and fine GT data. Prior to la-
belling, we employ plane segmentation to remove ar-
chitectural parts of buildings, such as walls and floor.
Furthermore, due to the rather coarse resolution of the
point clouds, we do not separately label small objects
that are not distinguishable from noise, e.g., the pen
lying on the table. As an evaluation metric, we pro-
pose an extension to under-segmentation (UE) ME
us
and over-segmentation error (OE) ME
os
that was first
mentioned in (Richtsfeld et al., 2012). Compared to
the original version, we evaluate with respect to an
object and its parts so that most appropriate GT is
considered (see (Bobkov et al., 2017) for details).
Table 1: Comparison of the segmentation methods on the
laser scanner data. Used error metric is multi-scale over-
and under-segmentation, where smaller is better. Top value
is ME
OS
and bottom value is ME
US
. Bold entries indicate
best performance per scene. Average processing time of our
approach is less than 10s per scene.
Scene Our LCCP Our+LCCP van Kaick
1
15.3% 35.8% 23.8% 37.1%
5.6% 12.2% 6.5% 16.3%
2
6.2% 30.4% 20.2% 25.6%
0.6% 9.0% 6.1% 23.6%
3
10.9% 20.5% 17.3% 17.7%
8.9% 9.7% 6.1% 78.7%
4
8.8% 18.8% 11.0% 32.9%
17.5% 143.7% 88.3% 647.8%
5
6.6% 29.6% 22.3% 27.8%
8.7% 23.2% 4.3% 80.8%
6
15.1% 21.2% 17.7% 37.6%
12.5% 36.9% 28.8% 104.4%
Mean
11.4% 26.0% 18.8% 29.8%
8.9% 39.1% 23.3% 158.6%
3.2 Experimental Results
Laser Scanner SLAM Dataset. We first present re-
sults scene-wise in Table 1. Here we include results
for the two aforementioned algorithms (LCCP and
van Kaick), as well as a combination of our criterion
(non-convex region removal and recovery) with the
LCCP segmentation algorithm (”Our+LCCP”). For
all laser scanner-based room datasets we used the
same parameters for our method, in particular R
seed
=
12cm, C = 3, θ
t
= 0.03, k = 3, thus no parameter tun-
ing for a particular scene has been performed. For
LCCP we used same R
voxel
and R
seed
, while other pa-
rameters are described in (Stein et al., 2014). From
the results in Table 1 one can observe that the pro-
posed algorithm significantly outperforms LCCP as
well as the approach of (van Kaick et al., 2014) for
both multi-scale UE and OE. The three scenes along
GT data and segmentation results of the analyzed al-
gorithms are provided in Fig. 4. Observe in the right
column of Fig. 4 the case when LCCP segmentation
deteriorates due to noisy normals. One can see that
the high UE of LCCP stems from the fact that it has
merged the chair in the top part of the scene with the
table. The method of (van Kaick et al., 2014) also
shows limited performance on partitioning the table
from the adjacent chairs. In contrast, the proposed
method has produced better results by separating the
chairs from the table. Limited LCCP performance
is mostly due to noisy normals and low-density re-
gions in the neighborhood of chairs. The method of
Van Kaick et al. is limited on such scenes as it can-
not handle sparsity in the data. On the other hand,
our method is more robust with respect to such re-
Noise-resistant Unsupervised Object Segmentation in Multi-view Indoor Point Clouds
153

Figure 4: Example results for manually labelled scenes 1, 3 and 4 (left, middle and right column respectively). Here row A
is given for illustration, but not used by any of the algorithms. B is the fine GT. C illustrates coarse GT. D represents LCCP
segmentation results. E shows segmentation results of the approach of (van Kaick et al., 2014). F corresponds to segmentation
results of the proposed method.
gions. Furthermore, observe that LCCP as well as our
method have over-segmented the left part of the scene
containing kitchen cupboards and objects on the table.
And finally, in the right part of the scene, both algo-
rithms are unable to correctly segment the corner ta-
ble, thus increasing OE. For scene 3 (middle column
of Fig. 4), LCCP over-segments the objects behind
the cupboard in the upper part of the scene, whereas
our method correctly segments such parts, and thus
has a lower OE. The method of (van Kaick et al.,
2014) shows high UE on this scene. Also note that our
convex/concave criterion combined with LCCP algo-
rithm (”Our+LCCP”) gives clear improvement.
NYU Dataset. We further evaluate the algorithms on
the NYUv2 Kinect dataset (N. Silberman and Fergus,
2012). It contains 1449 scenes with realistic cluttered
conditions, captured from a single viewpoint. Quanti-
tative evaluation on 654 test scenes is provided in Ta-
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
154
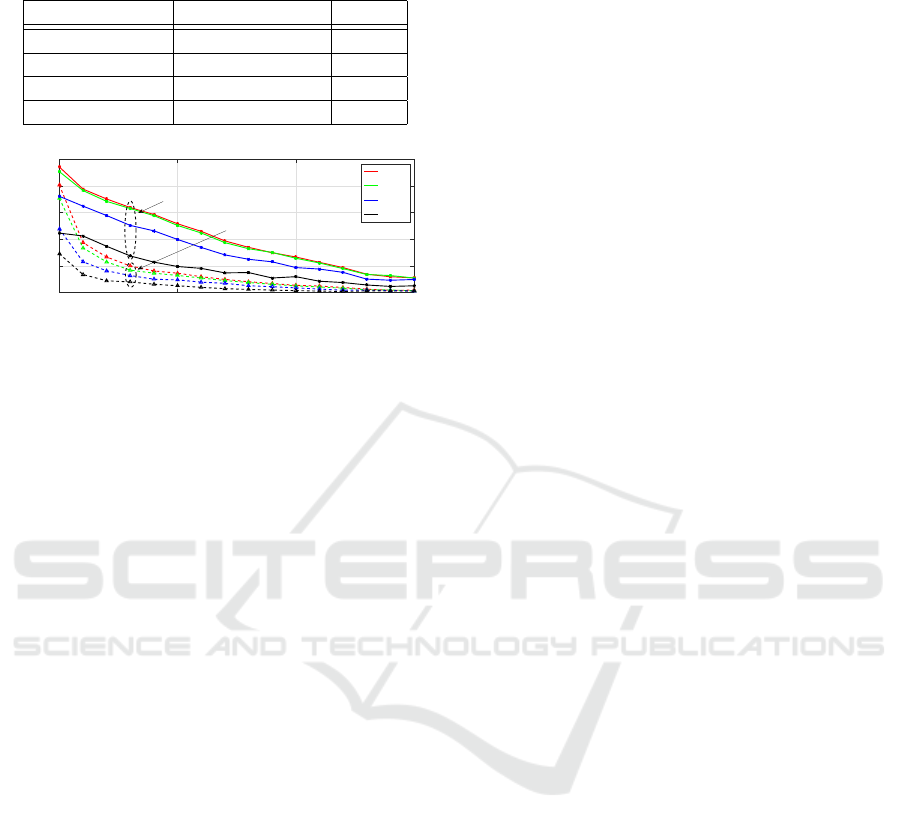
Table 2: Performance of segmentation methods on the NYU
dataset using weighted overlap (WO) (bigger is better).
Method Learned features WO
Proposed No learning 58.0%
LCCP No learning 57.6%
Silberman et al. Depth 53.7%
Gupta et al. Depth+RGB 62.0%
0 0.05 0.1 0.15
Curvature threshold θ
t
0
0.2
0.4
0.6
0.8
1
Relative number of
removed edges
α
t
=0.1
α
t
=0.2
α
t
=0.5
α
t
=1.0
Inter-object connections
Intra-object connections
Figure 5: Gain achieved by removing non-convex noisy
regions vs. curvature threshold θ
t
- significant number of
inter-object connections are removed (solid). Note the low
number of removed intra-object connections (dashed).
ble 2. We used θ
t
= 0.02, C = 3, k = 5, R
seed
= 16cm
for all scenes. For comparison we also provide the
performance of LCCP and training-based methods of
(N. Silberman and Fergus, 2012) and (Gupta et al.,
2013). Observe that our method achieves reasonable
performance in spite of being learning-free, as com-
pared to (Gupta et al., 2013).
Parameter Sensitivity. For illustration of the cur-
vature threshold θ
t
we show the number of inter-
object vs. intra-object edges that are removed in the
laser scanner dataset in Fig. 5. One can see that by
choosing its value in the range 0.02 to 0.03 a signifi-
cant number of inter-object connections are removed
(e.g. 68.31%), whereas most of the intra-object con-
nections are preserved (e.g. 77.21%). This allows
us to significantly simplify the segmentation problem
while achieving even better performance. Please note
that we also varied α
t
, which confirms the choice of
α
t
= 0.2 for this dataset. Due to marginal improve-
ment, we fix parameter k = 3 for all scenes in the laser
scanner dataset. We want to point that the parameter
k offers the trade-off between UE and OE, in particu-
lar higher k would result in lower OE and higher UE.
Should one thrive for low UE, the parameter k has
to be reduced. The parameter for graph partitioning
C should be chosen jointly with seed resolution R
seed
depending on the desired size of the smallest segment.
Finally, R
seed
should be greater than the average point
cloud resolution, as indicated in (Papon et al., 2013).
Limitations. Removing high-curvature non-convex
regions can sometimes result in the situation that
some regions become too sparse, therefore no connec-
tions within the object remain. This, apparently, will
lead to erroneous over-segmentation of the object. We
further acknowledge the simplicity of the used crite-
rion of a concave edge, which can fail in some cases
(TV set in scene 1 in Fig. 4).
4 CONCLUSION
This paper presents a novel approach for segmen-
tation of multi-view indoor point clouds. To ad-
dress particular properties of these datasets, such as
non-uniform density and high level of noise, we de-
rived a novel noise-resilient criterion for the detection
of noisy non-convex regions. This step makes the
graph partitioning (and thus segmentation) problem
simpler and reduces the number of erroneous con-
nections due to noise. By combining the proposed
point removal step with state-of-the-art segmentation
algorithms, one can significantly improve their per-
formance. In spite of being designed for MVPC data,
the algorithm achieves state-of-the-art performance
on single-view point cloud data. We further introduce
a new laser scanner dataset to illustrate experimen-
tally that there is a discrepancy between single-view
and multi-view point clouds in terms of noise level,
especially at high-curvature regions. The proposed
dataset spans 6 rooms within an office environment
and contains 452 object parts. It is especially valu-
able to the scientific community as the moving laser
scanner-based approaches are particularly suitable for
the mapping and 3D reconstruction of large indoor en-
vironments.
REFERENCES
Armeni, I., Sener, O., Zamir, A. R., Jiang, H., Brilakis,
I., Fischer, M., and Savarese, S. (2016). 3d seman-
tic parsing of large-scale indoor spaces. In Proceed-
ings of the IEEE International Conference on Com-
puter Vision and Pattern Recognition.
Bobkov, D., Chen, S., Kiechle, M., Hilsenbeck,
S., and Steinbach, E. (2017). Supplementary
material for paper: Noise-resistant unsupervised
object segmentation in multi-view indoor point
clouds. https://github.com/DBobkov/segmentation.
Accessed: 2016-11-29.
Boulch, A. and Marlet, R. (2012). Fast and robust normal
estimation for point clouds with sharp features. Com-
puter Graphics Forum, 31(5):1765–1774.
Boyko, A. and Funkhouser, T. (2014). Cheaper by the
dozen: Group annotation of 3D data. In UIST.
Deng, Z., Todorovic, S., and Jan Latecki, L. (2015). Se-
mantic segmentation of rgbd images with mutex con-
straints. In The IEEE International Conference on
Computer Vision (ICCV).
Noise-resistant Unsupervised Object Segmentation in Multi-view Indoor Point Clouds
155

Felzenszwalb, P. F. and Huttenlocher, D. P. (2004). Effi-
cient graph-based image segmentation. International
Journal on Computer Vision, 59(2):167–181.
Fouhey, D., Gupta, A., and Hebert, M. (2014). Unfold-
ing an indoor origami world. In Fleet, D., Pajdla, T.,
Schiele, B., and Tuytelaars, T., editors, Computer Vi-
sion ECCV 2014, volume 8694 of Lecture Notes in
Computer Science, pages 687–702. Springer Interna-
tional Publishing.
Gupta, S., Arbelez, P., and Malik, J. (2013). Perceptual or-
ganization and recognition of indoor scenes from rgb-
d images. In Computer Vision and Pattern Recogni-
tion (CVPR), 2013 IEEE Conference on, pages 564–
571.
Huitl, R., Schroth, G., Hilsenbeck, S., Schweiger, F., and
Steinbach, E. (2012). TUMindoor: an extensive image
and point cloud dataset for visual indoor localization
and mapping. In IEEE International Conference on
Image Processing (ICIP 2012), Orlando, FL, USA.
Jiang, H. (2014). Finding approximate convex shapes in
rgbd images. In Computer Vision ECCV 2014, vol-
ume 8691 of Lecture Notes in Computer Science,
pages 582–596. Springer International Publishing.
Karpathy, A., Miller, S., and Fei-Fei, L. (2013). Ob-
ject discovery in 3D scenes via shape analysis. In
Robotics and Automation (ICRA), 2013 IEEE Inter-
national Conference on, pages 2088–2095.
Lai, K., Bo, L., Ren, X., and Fox, D. (2013). Rgb-d object
recognition: Features, algorithms, and a large scale
benchmark. In Consumer Depth Cameras for Com-
puter Vision, pages 167–192. Springer.
Liu, T., Carlberg, M., Chen, G., Chen, J., Kua, J., and Za-
khor, A. (2010). Indoor localization and visualization
using a human-operated backpack system. In Indoor
Positioning and Indoor Navigation (IPIN), 2010 In-
ternational Conference on, pages 1–10.
Mattausch, O., Panozzo, D., Mura, C., Sorkine-Hornung,
O., and Pajarola, R. (2014). Object detection and
classification from large-scale cluttered indoor scans.
Computer Graphics Forum, 33(2):11–21.
Mian, A., Bennamoun, M., and Owens, R. (2006). Three-
dimensional model-based object recognition and seg-
mentation in cluttered scenes. Pattern Analysis
and Machine Intelligence, IEEE Transactions on,
28(10):1584–1601.
N. Silberman, D. Hoiem, P. K. and Fergus, R. (2012). In-
door segmentation and support inference from RGBD
images. In ECCV.
Papon, J., Abramov, A., Schoeler, M., and Worgotter, F.
(2013). Voxel cloud connectivity segmentation - su-
pervoxels for point clouds. In Computer Vision and
Pattern Recognition (CVPR), 2013 IEEE Conference
on, pages 2027–2034.
Pomerleau, F., Colas, F., Siegwart, R., and Magnenat, S.
(2013). Comparing icp variants on real-world data
sets. Autonomous Robots, 34(3):133–148.
Richtsfeld, A., Morwald, T., Prankl, J., Zillich, M., and
Vincze, M. (2012). Segmentation of unknown ob-
jects in indoor environments. In Intelligent Robots and
Systems (IROS), 2012 IEEE/RSJ International Con-
ference on, pages 4791–4796.
Rusu, R. B., Marton, Z. C., Blodow, N., Dolha, M., and
Beetz, M. (2008). Towards 3D point cloud based ob-
ject maps for household environments. robotics and
autonomous systems.
Song, S. and Xiao, J. (2014). Sliding shapes for 3d object
detection in depth images. In Computer Vision–ECCV
2014, pages 634–651. Springer International Publish-
ing.
Soni, N., Namboodiri, A. M., Jawahar, C., and Rama-
lingam, S. (2015). Semantic classification of bound-
aries of an RGBD image. In Proceedings of the
British Machine Vision Conference (BMVC 2015),
pages 114.1–114.12. BMVA Press.
Stein, S., Schoeler, M., Papon, J., and Worgotter, F. (2014).
Object partitioning using local convexity. In Com-
puter Vision and Pattern Recognition (CVPR), 2014
IEEE Conference on, pages 304–311.
Tateno, K., Tombari, F., and Navab, N. (2015). Real-
time and scalable incremental segmentation on dense
slam. In Intelligent Robots and Systems (IROS), 2015
IEEE/RSJ International Conference on, pages 4465–
4472. IEEE.
van Kaick, O., Fish, N., Kleiman, Y., Asafi, S., and Cohen-
Or, D. (2014). Shape segmentation by approximate
convexity analysis. ACM Transactions on Graphics.
Xiao, J., Owens, A., and Torralba, A. (2013). Sun3d: A
database of big spaces reconstructed using sfm and
object labels. In Computer Vision (ICCV), 2013 IEEE
International Conference on, pages 1625–1632.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
156
