
Deep Manifold Embedding for 3D Object Pose Estimation
Hiroshi Ninomiya
1
, Yasutomo Kawanishi
1
, Daisuke Deguchi
2
, Ichiro Ide
1
, Hiroshi Murase
1
,
Norimasa Kobori
3
and Yusuke Nakano
3
1
Graduate School of Information Science, Nagoya University, Furo-cho, Chikusa-ku, Nagoya-shi, Aichi, Japan
2
Information Strategy Office, Nagoya University, Furo-cho, Chikusa-ku, Nagoya-shi, Aichi, Japan
3
Toyota Motor Corporation, Toyota-cho, Toyota-shi, Aichi, Japan
Keywords:
3D Object, Pose Estimation, Manifold, Deep Learning.
Abstract:
Recently, 3D object pose estimation is being focused. The Parametric Eigenspace method is known as one
of the fundamental methods for this. It represents the appearance change of an object caused by pose change
with a manifold embedded in a low-dimensional subspace. It obtains features by Principal Component Anal-
ysis (PCA), which maximizes the appearance variation. However, there is a problem that it cannot handle a
pose change with slight appearance change since there is not always a correlation between pose change and
appearance change. In this paper, we propose a method that introduces “Deep Manifold Embedding” which
maximizes the pose variation directly. We construct a manifold from features extracted from Deep Convolu-
tional Neural Networks (DCNNs) trained with pose information. Pose estimation with the proposed method
achieved the best accuracy in experiments using a public dataset.
1 INTRODUCTION
The demand for automated robots for industrial and
life-related fields is increasing. In the industrial field,
picking up some industrial parts, such as automo-
tive parts and appliance parts, has been automated
by robots. Recently, a competition named Amazon
Picking Challenge (Correll et al., 2016) was held to
improve the technology for picking up 3D objects.
Meanwhile, in the life-related field, Human Support
Robot, which helps daily life, has been developed for
the aging society (Broekens et al., 2009). It will be
used for housework, nursing care, and so on. In such
situations, the task of picking up 3D objects and hand-
ing them over to humans occur frequently. In either
cases, it is a common issue for robots to grab an ob-
ject, so such technology is required. To grab an ob-
ject, 3D object pose estimation is necessary.
A conventional object pose estimation
method (Chin and Dyer, 1986) is based on tem-
plate matching. This method estimates an object
pose by many templates taken from various view
points of the target object beforehand. The estimation
result is obtained from the best matched template.
Thus, many templates are required for accurate pose
estimation.
0 deg. 90 deg.
225 deg. 315 deg.
Appearance change: Large
Pose change: 90 deg.
Appearance change:
Small
Pose change: 90 deg.
Figure 1: Appearance change and pose change.
To solve this problem, Murase and Nayar pro-
posed the Parametric Eigenspace method (Murase
and Nayar, 1995). It represents the pose change
of an object with a manifold embedded in a low-
dimensional subspace obtained by Principal Compo-
nent Analysis (PCA). This method can reduce the
number of templates since it interpolates unknown
poses by cubic spline.
Since PCA focuses only on the appearance of an
object, some poses may be mapped to similar points
in a low-dimensional subspace in case their appear-
ances differ only slightly, as shown in Figure 1. This
deteriorates the pose estimation accuracy. As shown
in Figure 2, it is difficult to distinguish between points
Ninomiya H., Kawanishi Y., Deguchi D., Ide I., Murase H., Kobori N. and Nakano Y.
Deep Manifold Embedding for 3D Object Pose Estimation.
DOI: 10.5220/0006101201730178
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 173-178
ISBN: 978-989-758-226-4
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
173

L䠖Maximize appearance
variation
Feature
extraction by
PCA
Manifold
construction
Conventional
method
L
Figure 2: Manifold construction by PCA.
mapped to similar points on the manifold in the low-
dimensional subspace in case each point corresponds
to a very different pose, because PCA is an unsuper-
vised learning method which maximizes the appear-
ance variation; the pose variation is not considered.
This means that it may be difficult to estimate the
exact pose of the target object by its overall appear-
ance. Therefore, PCA will not be effective when par-
tial appearance is very important for distinguishing
object poses. This gives us the idea of pose estima-
tion by learning the relationship between partial ap-
pearance and its exact pose.
In this paper, we propose a supervised feature ex-
traction method for pose manifold considering pose
variation. To extract features considering pose vari-
ation, we use a supervised learning method instead
of an unsupervised learning method such as PCA.
We focused on Deep Convolutional Neural Networks
(DCNNs) (Krizhevsky et al., 2012), which is one of
the deep learning models, as a supervised learning
method.
Figure 3 shows the overview of the proposed
method. DCNNs demonstrate very high performance
on various benchmarks, such as generic object recog-
nition and scene recognition (Razavian et al., 2014),
since they can automatically obtain appropriate fea-
tures for various tasks. For this reason, we considered
that pose discriminative features can be obtained by
DCNNs trained with pose information as supervisory
signals. Therefore we introduce the concept of “Deep
Manifold Embedding” that is a supervised feature ex-
traction method for a pose manifold using deep learn-
ing technique.
The rest of this paper describes the manifold-
based pose estimation method in Section 2, explains
the detailed process flow of the proposed method in
Section 3, reports evaluation results in Section 4, and
concludes the paper in Section 5.
2 MANIFOLD-BASED POSE
ESTIMATION
Figure 4 shows the process flow of the proposed
manifold-based pose estimation method. First, a man-
ifold which represents object pose changes from fea-
J: Maximize pose variation
Feature
extraction by
Deep Learning
Manifold
construction
Proposed
method
J
Figure 3: Manifold construction by deep learning.
Obj. ݊
Image
Feature extraction
Manifold
Test
Image
Calculate
distance
Output
(Pose)
Pose
estimation
Interpolation
Manifold
construction
Figure 4: Process flow of manifold-based pose estimation.
tures obtained by a feature extraction method is con-
structed. In the pose estimation phase, an input image
is projected onto the obtained feature space. Finally,
the pose estimation result is obtained from the nearest
manifold point.
In order to construct a feature that could distin-
guish poses, we focused on deep learning as a super-
vised learning method. Deep learning is a machine
learning method, which can learn feature extraction
and classification simultaneously. The feature ob-
tained by this method is known to have a higher dis-
criminative power than hand-crafted features (Don-
ahue et al., 2013). For this reason, we should be able
to obtain a very effective feature for pose estimation
by deep learning trained with pose information. Ac-
cordingly, the manifold constructed from the feature
obtained by deep learning should be able to handle
pose changes even with a slight appearance change,
which is difficult to be handled by features obtained
by PCA.
We call this supervised feature extraction method
for pose manifold using deep learning technique as
“Deep Manifold Embedding”.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
174
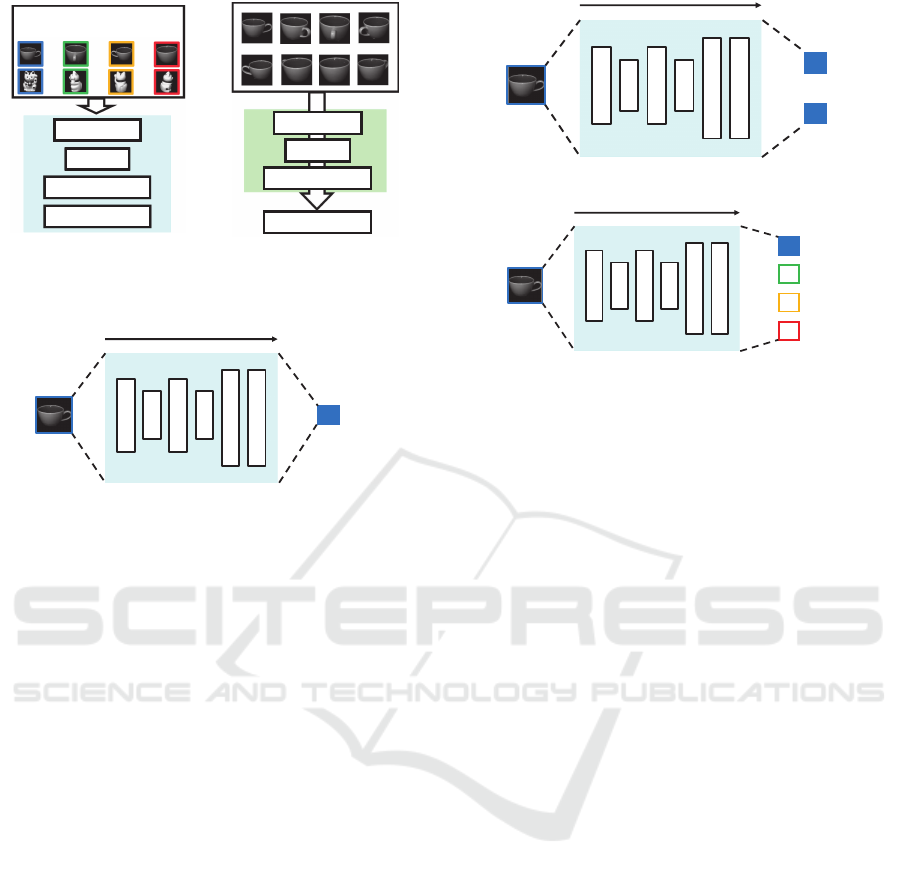
270
deg.
180
deg.
90
deg.
0
deg.
Convolution
Pooling
Fully-connected
Fully-connected
Figure 5: Training DC-
NNs with pose informa-
tion.
Convolution
Pooling
Fully-connected
Feature vector
Figure 6: Extracting fea-
tures from trained DC-
NNs.
Convolution
Pooling
Convolution
Pooling
Fully-connected
Fully-connected
ߠ
[deg.]
ߠ [deg.]
Figure 7: Pose-R-Net.
3 DEEP MANIFOLD
EMBEDDING
To obtain the features for manifold construction by
deep learning, we first train a DCNN with pose in-
formation. Training samples are images with objects
taken at arbitrary pose angles around an axis. Figure 5
shows the overview of the training of the DCNN with
pose information. In this way, we can train a DCNN
which maximizes the pose variation, and thus can ob-
tain very effective features for pose estimation. Then,
we extract features from the trained DCNN. Mean-
while, Figure 6 shows the overview of extracting fea-
tures from the trained DCNN. We input training sam-
ples for extracting features to the trained DCNN, and
the activations of the middle layer are used as fea-
tures. Manifolds are constructed from those features
with interpolation as same as the conventional Para-
metric Eigenspace method.
There are various ways of representing pose infor-
mation. Here, we propose three models with different
ways of pose representation;
• Pose-R-Net: Regression model trained with pose
information represented by angle (deg.) directly.
• Pose-CyclicR-Net: Regression model trained
with pose information represented by trigonomet-
ric functions to consider pose cyclicity.
• Pose-C-Net: Classification model trained with
Convolution
Pooling
Convolution
Pooling
Fully-connected
Fully-connected
sin
ߠ
cos
ߠ
ߠ [deg.]
Figure 8: Pose-CyclicR-Net.
Convolution
Pooling
Convolution
Pooling
Fully-connected
Fully-connected
0 deg.䠖 1
270 deg.䠖 0
90 deg.䠖 0
180 deg.䠖 0
ߠ [deg.]
Figure 9: Pose-C-Net.
pose informationrepresented as a categorical vari-
able, which means that pose is discretized.
Details of each model are described in the following
sections.
3.1 Pose-R-Net
Figure 7 shows the overview of the Pose-R-Net. We
trained DCNNs with pose information θ represented
by degree directly. The number of output layer unit is
one. We used squared error as the loss function.
There is a risk that the training loss becomes un-
fairly big because this model does not consider the
cyclictiy of poses. For example, if a 0 deg. sample is
estimated as 355 deg., the DCNN trains 355 deg. loss
in spite of the fact that the actual loss is only 5 deg.
3.2 Pose-CyclicR-Net
Figure 8 shows the overview of the Pose-CyclicR-
Net. As same as the Pose-R-Net, this model is a
regression model that uses squared error as the loss
function. However, here we represent pose informa-
tion θ as sinθ and cosθ to consider the cyclicty of
poses. Therefore, the number of output layer units is
two.
This model is trained with pose information con-
sidering pose cyclicity, so it can solve the problem of
Pose-R-Net.
3.3 Pose-C-Net
Unlike the previous two models, this model solves the
pose estimation problem as a pose classification prob-
lem.
Deep Manifold Embedding for 3D Object Pose Estimation
175

Figure 10: Object examples in COIL-20 (Nene et al., 1996).
؞؞؞
0 deg. 5 deg. 10 deg.
345 deg. 350 deg. 355 deg.
Figure 11: Examples of pose changes.
Figure 9 shows the overview of the Pose-C-Net.
We trained a DCNN with pose information θ as a cat-
egorical variable. Therefore, the number of output
layer units is the same as the number of pose classes.
We used cross entropy as the loss function.
4 EVALUATION EXPERIMENTS
To confirm the effectiveness of the proposed method,
we conducted pose estimation experiments using a
public dataset. We introduce below the dataset and
the experimental conditions, and then report and dis-
cuss the results from the experiment.
4.1 Datasets
We used the public dataset named Columbia Object
Image Library (COIL-20) (Nene et al., 1996). It is
composed of gray-scale images of 20 objects. Im-
ages of the objects were taken at pose intervals of 5
deg. around a vertical axis, and each image size was
normalized to 128 × 128 pixels. In total, it contains
1,440 images. Figure 10 shows examples of objects
in the dataset, and Figure 11 shows the pose change
of an object.
Table 1: DCNN architecture.
Input Units: 128 × 128
Kernel: 5 × 5
Convolution 1 Channel: 16
Maxpooling: 5 × 5
Kernel: 5 × 5
Convolution 2 Channel: 32
Maxpooling: 5 × 5
Fully-connect 3 Units: 512
Fully-connect 4 Units: 512
Fully-connect 5 Units: 512
Units: 1 (Pose-R-Net)
Output Units: 2 (Pose-CyclicR-Net)
Units: 36 (Pose-C-Net)
4.2 Experimental Condition
4.2.1 DCNN Training
Table 1 shows the network architecture of each
DCNN model. The number of output layer units dif-
fer for each model because of difference of pose rep-
resentation, but the other structure is the same. Ker-
nels, weights, and biases were initialized with ran-
dom values. We used Rectified Linear Units (ReLU)
(Nair and Hinton, 2010) as an activation function.
Squared loss function was used to train the Pose-
R-Net and the Pose-CyclicR-Net models, and cross
entropy loss function was used to train the Pose-C-
Net. Kernels, weights, and biases were updated by
using back-propagation. We used the dropout tech-
nique (Hinton et al., 2012) for enhancing the general-
ization capability. The evaluation was performed in a
two-fold cross validation setting. Validation sets were
as follows:
• Set 1: 0, 10, 20, ···, 350 deg.
• Set 2: 5, 15, 25, ···, 355 deg.
4.2.2 Manifold Construction
We evaluated two conventional features and five deep
learning based features. The conventional features
were (1) a pixel feature, and (2) a PCA feature. Here,
the pixel feature is composed of raw pixel values, and
the PCA feature is the coefficients obtained from the
pixel feature calculated by PCA. Deep learning based
features are features extracted from the Pose-R-Net,
the Pose-CyclicR-Net, and the Pose-C-Net. In addi-
tion, two features extracted from DCNNs trained for
object category classification were prepared for com-
parison. One model trained with object category in-
formation including COIL-20 was named Obj-C-Net.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
176

Table 2: Experimental results (Manifold based).
Manifold MAE [deg.]
Pixel 1.16
PCA 1.39
Obj-C-Net 1.70
OverFeat 1.89
Pose-R-Net (Proposed) 1.59
Pose-CyclicR-Net (Proposed) 1.72
Pose-C-Net (Proposed) 1.09
Table 3: Experimental results (DCNN only).
DCNN model MAE [deg.]
Pose-R-Net 28.32
Pose-CyclicR-Net 9.29
Pose-C-Net 7.92
Its structure is the same as the Pose-R-Net, the Pose-
CyclicR-Net, and the Pose-C-Net except for the num-
ber of output layer units. Obj-C-Net has 20 units in
the output layer since COIL-20 is composed of 20
objects. The other model is a pre-trained model with
the ImageNet 2012 training set (Deng et al., 2009),
named OverFeat (Sermanet et al., 2013). We ex-
tracted features from the first fully-connected layer
following convolution layers in each DCNN. In other
words, the Pose-R-Net, the Pose-CyclicR-Net, the
Pose-C-Net, and the Obj-C-Net models extract fea-
tures from Fully-connect 3 layer, and OverFeat model
extracts features from Fully-connect 8 layer. Their
feature dimensions are 512 and 4,096 respectively,
and these features were used to construct manifolds.
In the manifold construction by PCA, the
eigenspace dimension of each object was decided
based on cumulative contribution over 80%. The
average dimension of each eigenspace was around
10 for all objects. The pixel feature dimension was
16,384.
All the features used are summarized as follows:
• Pixel: Raw pixel values
• PCA: Coefficients obtained from the pixel feature
calculated by PCA
• Obj-C-Net: Deep learning-based feature trained
with object category information including COIL-
20
• OverFeat: Deep learning-based feature trained
with object category information including Ima-
geNet 2012 training set
• Pose-R-Net (Proposed): Deep learning-based
feature trained with pose information represented
directly by angle (deg.)
• Pose-CyclicR-Net (Proposed): Deep learning-
based feature trained with pose information rep-
0
1
2
3
4
5
6
7
0
30
60
90
120
150
180
210
240
270
300
330
Estimation error [deg.]
Pose [deg.]
PCA Pose-C-Net
240 deg.
250 deg.
0 deg.
Figure 12: Experimental results (an object which has very
similar appearance poses).
resented by trigonometric functions
• Pose-C-Net (Proposed): Deep learning-based
feature trained with pose information represented
as a categorical variable
4.3 Results and Discussion
Table 2 shows the experimental results. As for
the evaluation criteria, we used Mean Absolute Er-
ror (MAE). The manifold constructed from features
obtained from Pose-C-Net performed the best out
of the eight manifolds. Features extracted from
DCNNs trained with object category information;
Obj-C-Net and OverFeat, showed low performance.
We consider the reason for this is that they were
trained without considering pose information. Fea-
tures extracted from Pose-R-Net and Pose-CyclicR-
Net showed lower performances than features ex-
tracted from Pose-C-Net. We consider the reason for
this is that it is difficultfor regression models to get rid
of the effect of pose cyclicity. In contrast, Pose-C-Net
manifold showed high accuracy because the classifi-
cation model was not affected by pose cyclicity.
Next, we compared with the output of DCNNs
shown in Table 3. All of the manifold-based pose esti-
mation methods showed higher performances than all
of the DCNN only methods. We considered the rea-
son for this is that manifold-based pose estimation can
estimate an unknown pose thanks to the interpolation.
Lastly, we investigate the effectiveness of the pro-
posed method for an object which has very similar
appearance poses. Figure 12 shows the experimental
results. The object appearances are very similar be-
tween 240 deg. to 260 deg. since the handle of the
cup is almost missing. It is difficult to estimate such
poses exactly by features obtained by PCA because
Deep Manifold Embedding for 3D Object Pose Estimation
177

of the small appearance change. In contrast, features
extracted from Pose-C-Net shows better results than
features obtained by PCA in such poses. We consider
the reason for this is that Pose-C-Net was trained con-
sidering pose information, so features extracted from
it can handle a pose change with slight appearance
change without deteriorating the pose estimation ac-
curacy of the other pose changes.
From the above results, we confirmed the effec-
tiveness of the proposed method.
5 CONCLUSION
In this paper, we proposed an accurate pose esti-
mation method named “Deep Manifold Embedding”
which is a supervised feature extraction method for
pose manifold using deep learning technique. We ob-
tained pose discriminative features from deep learn-
ing trained with pose information. Manifolds con-
structed from the features were effective for pose
estimation, especially in case of a pose change
with a slight appearance change. Experimental re-
sults showed that the proposed method is effective
compared with the conventional method which con-
structs manifolds from the features obtained by PCA.
Here we conducted pose estimation experiments only
around a specific rotation axis, but this method can
estimate poses around an arbitrary rotation axises if
there are corresponding training data.
As future work, we will consider a more suit-
able DCNN architecture, investigate the robustness to
complex background and various illumination condi-
tions, and compare with other state-of-the-art meth-
ods.
ACKNOWLEDGEMENTS
Parts of this research were supported by MEXT,
Grant-in-Aid for Scientific Research.
REFERENCES
Broekens, J., Heerink, M., and Rosendal, H. (2009). As-
sistive social robots in elderly care: A review. Geron-
technology, 8(2):94–103.
Chin, R. T. and Dyer, C. R. (1986). Model-based recog-
nition in robot vision. ACM Computing Surveys,
18(1):67–108.
Correll, N., Bekris, K. E., Berenson, D., Brock, O.,
Causo, A., Hauser, K., Okada, K., Rodriguez, A., Ro-
mano, J. M., and Wurman, P. R. (2016). Lessons
from the Amazon picking challenge. arXiv preprint
arXiv:1601.05484.
Deng, J., Dong, W., Socher, R., Li, L.-J., Li, K., and Fei-Fei,
L. (2009). Imagenet: A large-scale hierarchical image
database. In Proc. 22nd IEEE Computer Society Conf.
on Computer Vision and Pattern Recognition, pages
248–255.
Donahue, J., Jia, Y., Vinyals, O., Hoffman, J., Zhang,
N., Tzeng, E., and Darrell, T. (2013). DeCAF: A
deep convolutional activation feature for generic vi-
sual recognition. arXiv preprint arXiv:1310.1531.
Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I.,
and Salakhutdinov, R. R. (2012). Improving neural
networks by preventing co-adaptation of feature de-
tectors. arXiv preprint arXiv:1207.0580.
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012).
Imagenet classification with deep convolutional neu-
ral networks. In Pereira, F., Burges, C. J. C., Bottou,
L., and Weinberger, K. Q., editors, Advances in Neu-
ral Information Processing Systems 25, pages 1097–
1105. Curran Associates, Inc.
Murase, H. and Nayar, S. K. (1995). Visual learning and
recognition of 3-D objects from appearance. Int. J.
Comput. Vision, 14(1):5–24.
Nair, V. and Hinton, G. E. (2010). Rectified linear units im-
prove restricted Boltzmann machines. In Furnkranz,
J. and Joachims, T., editors, Proc. 27th Int. Conf. on
Machine Learning, pages 807–814. Omnipress.
Nene, S. A., Nayar, S. K., and Murase, H. (1996). Columbia
object image library (COIL-20). Technical report,
CUCS-005-96, Department of Computer Science,
Columbia University.
Razavian, A. S., Azizpour, H., Sullivan, J., and Carlsson,
S. (2014). CNN features off-the-shelf: An astounding
baseline for recognition. In Proc. 27th IEEE Conf. on
Computer Vision and Pattern Recognition Workshops,
pages 512–519.
Sermanet, P., Eigen, D., Zhang, X., Mathieu, M., Fergus,
R., and LeCun, Y. (2013). OverFeat: Integrated recog-
nition, localization and detection using convolutional
networks. arXiv preprint arXiv:1312.6229.
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
178
