Quality Enhancement Techniques for Building Models

Derived from Sparse Point Clouds

Steffen Goebbels and Regina Pohle-Fr¨ohlich

Institute for Pattern Recognition, Faculty of Electrical Engineering and Computer Science,

Niederrhein University of Applied Sciences, Reinarzstr. 49, 47805 Krefeld, Germany

Keywords:

Point Clouds, Building Reconstruction, CityGML, Linear Optimization, True Orthophotos.

Abstract:

This paper describes processing steps that improve both geometric consistency and appearance of CityGML

models. In addition to footprints from cadastral data and sparse point clouds obtained from airborne laser

scanning, we use true orthophotos to better detect and model edges. Also, procedures to heal self-intersection

of polygons and non-planarity of roof facets are presented. Additionally, the paper describes an algorithm

to cut off invisible parts of walls. We incorporate these processing steps into our data based framework for

building model generation from sparse point clouds. Results are presented for German cities of Krefeld and

Leverkusen.

1 INTRODUCTION

During recent years, 3D city models have become

increasingly important for planning, simulation, and

marketing, see (Biljecki et al., 2015). CityGML is

the XML based standard for exchanging and storing

such models, see (Gr¨oger et al., 2012). A common

approach to automate the generation of city models

is to use cadastral data in combination with point

clouds from airborne laser scanning. However, pub-

licly available point clouds of our home country of-

ten are sparse and currently consist of less than ten

points per square meter. This makes it very difﬁcult

to recognize small roof structures which are typical

for dormers and tower roofs.

There are two main approaches to roof reconstruc-

tion (see (Tarsha-Kurdi et al., 2007), cf. (Haala and

Kada, 2010; He, 2015; Henn et al., 2013; Perera and

Maas, 2012)): Model driven approaches select stan-

dard roofs from a catalogue so that they optimally ﬁt

with the points from the cloud. In general, only larger

roof structures ﬁnd their way into these building mod-

els. To the contrast, data driven methods detect planes

and combine even small roof facets to complete roofs

(see e. g. (Elbrink and Vosselman, 2009; Kada and

Wichmann, 2013)). Our experiments in (Goebbels

and Pohle-Fr¨ohlich, 2016) show that a data driven ap-

proach even is able to deal with dormers, but their

outline might be distorted due to sparse coverage by

laser scanning points. Therefore, one needs additional

information to correctly model such small structures.

For example, in (Wichmann and Kada, 2016) simi-

lar dormers are detected to merge their point clouds.

Thus, a prototype dormer model can be generated

based on a much higher point density. Also, Demir et.

al. describe in (Demir et al., 2015) a procedure to de-

tect repeating structures in point clouds. In this paper

Figure 1: Orthophoto (left) vs. true orthophoto (right).

we use true orthophotos as additional information. An

orthophoto is a geometrically corrected areal photo

that ﬁts with the coordinate system at ground level.

In a true orthophoto, not only the ground level ﬁts

with the coordinate system but also all levels above

the ground including the roof, see Figure 1. We de-

tect edges of such photos and adjust models according

to these edges.

The given paper is not only concerned with better

modeling structures but also with improving geomet-

Goebbels S. and Pohle-FrÃ˝uhlich R.

Quality Enhancement Techniques for Building Models Derived from Sparse Point Clouds.

DOI: 10.5220/0006103300930104

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 93-104

ISBN: 978-989-758-224-0

ric consistency, cf. (Gr¨oger and Pl¨umer, 2009; Zhao

et al., 2013). One can apply general methods for re-

pairing arbitrary 3D polygon models. But most build-

ing models have vertical walls, so that one only has

to deal with roof structures that can be projected to

2D. Zhao et al. propose an approach that corrects all

types of geometric error using shrink-wrapping that

works on a watertight approximationof the tessellated

building. Alam et al. (Alam et al., 2013) describe

methods to correct single geometric problems of ex-

isting CityGML models. We present complementary

and different processing steps to improve such single

aspects of geometric quality during model generation.

The algorithms deal with self-intersecting polygons,

planarity of polygons, and correctness of wall bound-

aries. Violation of planarity is a common problem of

city models. It is regarded as difﬁcult to correct. We

ﬁx missing planarity with a surprisingly simple but

powerful linear program. The ideas are applied but

not limited to CityGML.

2 PREVIOUS WORK

We apply the algorithms of this paper in connection

with our model generation workﬂow in (Goebbels and

Pohle-Fr¨ohlich, 2016), cf. Figure 2. In this section,

we shortly summarize our previous work and explain

how the subsequent sections contribute to this au-

tomated model generation workﬂow. However, our

workﬂow only serves as an example and might be re-

placed by other methods.

Figure 2: City model of our hometown.

We detect roof facets on a height map that is inter-

polated from the sparse point cloud. The height map

consists of a raster with 10 ×10 cm

cell size which

ﬁts with the accuracy of data. It is partially initialized

with the cloud points. To complete the map, we use

an interpolation method that maintains step edges.

Before we detect roof planes using a RANSAC

algorithm, we ﬁrst classify regions according to gra-

dient directions. To this end, we handle all regions

with gradients shorter than a threshold value as ﬂat

roofs. These areas might have arbitrary and noisy

gradient angles. For remaining areas we determine

minima of a gradient angle histogram. Each inter-

val between two subsequent minima classiﬁes the an-

gles that belong to roof facets with approximately the

same gradient direction. On regions of such homo-

geneous gradient angles we estimate planes and ﬁnd

roof facets using RANSAC. Filtering by gradient an-

gles excludes outliers. It also avoids difﬁculties with

RANSAC. For example, we do not ﬁnd planes that in-

tersect with many roof facets without themselves be-

ing a roof plane. The intermediate result is a 2D raster

map in which cells are colored according to the roof

facet they belong to.

We complete gaps in the raster map of roof facets

using region growing. To maintain the characteris-

tic appearance of the roof, we consider intersection

lines between estimated planes (ridge lines) and step

edges according to the height map as boundaries for

growing. However, small structures like dormers do

not show straight and parallel edges after this proce-

dure. To improve model quality, we now addition-

ally consider cadastral building part information and

edges that are visible in true orthophotos, see Section

From the raster map we can directly determine in-

ner roof facets that completely lie within a surround-

ing facet. Such inner facets become openings in the

surrounding facet polygon. That is also true for open-

ings of a building’s footprint from cadastral data. Bor-

der polygons of other openings are outer polygons of

inner roof facets (with inverse orientation) so that we

only have to detect outer polygons.

We determine each roof facet’s outer 2D boundary

polygon using Pavlidis algorithm that moves along

the facet’s contour. Leading to a watertight roof,

we determine and merge polygon segments that are

shared between adjacent facets. A topologically rele-

vant vertex is a vertex at which more than two roof

facets meet. Such vertices are detected. Then 2D

roof polygons are simpliﬁed using a modiﬁed Ramer-

Douglas-Peucker algorithm. This algorithm does not

allow topologically relevant vertices to be removed

from the polygons. Therefore, the roof remains wa-

tertight.

To overcome the precision that is limited by the

10×10 cm

cell size, we project vertices to edges of

the cadastral footprint and to intersection lines (ridge

edges) as well as to intersection points of ridge lines.

This might lead to self-intersecting polygons. A so-

lution to resolve this problem is described in Section

To generate a 3D model, height values have to be

added to the 2D polygons. These heights are com-

puted using estimated plane equations. To avoid small

artiﬁcial step edges, mean values are used for vertices

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

with same x- and y-coordinates but only slightly dif-

ferent z-coordinates that lie within a threshold dis-

tance. This deliberately violates planarity of roof

facets. To heal this problem, we use linear opti-

mization in a post-processing step, see Section 6.

CityGML requires planarity, see (Gr¨oger et al., 2012,

p.25). To some extend, many city models violate this

requirement, cf. (Wagner et al., 2013), and can be cor-

rected using our linear program. However, our work-

ﬂow can alternatively generate planar roof facets by

not using mean values and allowing small step edges.

Then linear optimization can be used to eliminate step

edges instead of establishing planarity, see Section 8.

Another CityGML requirement is that, together

with the ground plane, roof and wall polygons com-

pletely belong to a building’s outer hull. Therefore,

we have to cut away invisible segments of walls. The

linear program for planarization might change slopes

of roof facets which in turn inﬂuences visibility of

walls. In Section 7 we ﬁnally describe a wall pro-

cessing step that has to run after planarization.

The complete workﬂow consists of following

steps:

• Computation of a height map that is interpolated

from the point cloud

• Estimation of roof facets in 2D raster domain

• Adjusting boundaries, see Section 4

• Contour detection gives 2D boundary polygons

• Simpliﬁcation of boundary polygonsand mapping

to ridge lines, step edges, etc. (might lead to addi-

tional self-intersections)

• Resolving self-intersections (see Section 5)

• Adding z-coordinate values

• Planarization of roof facets (see Section 6)

• Cutting and merging walls to visible segments

(see Section 7)

3 REFERENCE DATA SET

We apply the presented techniques to a square kilo-

meter of the city center of the German city of Krefeld

with 3987 buildings that we process from a sparse

point cloud with ﬁve to ten points per square meter,

see Figure 3. The area corresponds to the UTM inter-

val [32330000,32331000]×[5689000, 5690000]. Ad-

ditionally, we use data of the city of Leverkusen.

Figure 3: City center as reference data set.

4 ADJUSTING BOUNDARIES OF

ROOF FACETS

In our workﬂow, we generate a 2D raster map in

which pixel colors refer to corresponding roof facets,

see Figures 4–6. However, due to the sparse point dis-

tribution of the reference laser scanning data, bound-

ary contours of small structures like dormers are not

straight and are only approximately correct. There

are also gaps in the raster map. We complete the

map and optimize boundary contours by applying re-

gion growing. The idea is to ﬁnd candidates of true

boundaries that become limits for the growing pro-

cess. We obtain such candidate lines from the point

cloud as well as from additional data sources. For

example, we compute intersection lines of estimated

plane equations that correspond with ridge lines, see

Figure 4. Cadastral footprints of building parts (see

Figure 4: Intersection lines between estimated planes.

Figure 5) and edges of true orthophotos are additional

information. It is important that additional data are

optional and not required. Only a minority of build-

ings possess building part deﬁnitions and such cadas-

tral data often do not cover dormers. If available,

one can generate a true orthophoto from overlapping

areal images - for example using the Structure from

Motion algorithm. Our pictures were computed from

such overlapping photos. An alternative method is to

improve orthophotos with the help of terrain and 3D

building models. Vice versa, there also exist various

approaches to combine LIDAR point clouds with in-

Quality Enhancement Techniques for Building Models Derived from Sparse Point Clouds

Figure 5: Raster maps of roof facets (left): Red cadastre

polygons are borders of building parts, black areas could

not be associated with roof facets. The picture on the right

hand side shows the derived model.

formation from areal images to improve 3D building

modeling. For example, Tong et. al. (Tong et al.,

2012) use edges of (true) orthophotos to adjust step

edges of ﬂat roofs in a city model that is based on a

Delauny triangulation. Areﬁ and Reinartz (Areﬁ and

Reinartz, 2013) decompose buildings and ﬁt paramet-

ric roof models according to ridge lines detected from

true orthophotos. In our experiments, we try to uti-

lize all types of edges to adjust roof boundaries that

already have been obtained from the point cloud.

We use true othophotos with pixels that represent

areas of 10 ×10 cm

. Although the photos originate

from areal images with only 60% horizontal and 50%

vertical overlap,edges of the images ﬁt well with laser

scanning data within our computing tolerance of 10

, cf. Figure 6. However, edges tend to be not ex-

actly straight. Also, a minor problem is that roofs may

have textures showing tiles or tar paper with many

edges. Unfortunately, shadows lead to more signif-

icant additional edges. A lot of research deals with

Figure 6: Red pixels belong to edges of a true orthophoto.

Colored areas belong to planes that we detect in the laser

scanning point cloud. Both data sources match quite well.

Small dormers are not sufﬁciently covered by laser scanning

points. Boundaries of larger dormers can be adjusted to the

edges.

removal of shadows, cf. (Guo et al., 2011) and the

literature cited there. However, our experiments with

the algorithm of (Finlayson et al., 2002) did not gave

sufﬁcient results. A reason might be the variety of col-

ors of our arial photos. But in our processing pipeline,

edges only act as limits for region growingand are not

used to detect roof facets. Therefore, wrongly placed

edges do not heavily disturb results: If an edge crosses

an interior region of a roof facet, then the facet’s area

grows on both sides of the edge. Thus, the edge be-

comes no boundary of the facet. However, shadows

may hide useful edges.

To ﬁnd relevant edges with Canny edge detector,

one has to individually ﬁnd a threshold that excludes

irrelevant edges from textures. Instead, we gener-

ate a kind of principal curvature image without need-

ing to select a threshold value, see Figure 7. After

anisotropic ﬁltering, we convert the orthophoto to a

grey image and compute second partial derivatives for

each pixel position in terms of a Hessian matrix, a

symmetric matrix with real eigenvalues. Then we ﬁl-

ter for pixel positions for which the matrix has a lo-

cally largest absolute eigenvalue, i.e., in terms of ab-

solute values, the eigenvalue has to be larger than the

eigenvalues of Hessian matrices of the two horizontal,

vertical or diagonal neighbors. At such positions, an

eigenvector

of the eigenvalue λ with largest abso-

lute value |λ| points into the direction of largest ab-

solute curvature. It is orthogonal to an eigenvector

of the eigenvalue µ, |µ| ≤ |λ|. If additionally |λ| > 0

and |µ| ≈ 0, then curvature is large in one direction

only and

is orthogonal to that direction. Thus,

is parallel to an edge. We mark the corresponding po-

sition in a picture E of edges. Typically, the Hessian

matrix is used to ﬁnd positions like corners, where

local geometry changes in two directions. We use it

differently to detect changes that only occur in one di-

rection. As a side effect, this direction can be used to

ﬁlter for edges that are parallel or orthogonal to seg-

ments of the building’s footprint.

Edges might be not connected in E. We connect

them by computing the principal curvature image in a

higher resolution. A reduction of the resolution (su-

persampling) then closes most gaps.

Figure 7: Results of Canny edge detector (middle) vs. our

curvature based method (right).

Once we have derivedboundariesfor region grow-

ing, we eliminate noise near computed and detected

edges, especially near pixels of E. Noise consists of

pixels at the wrong side of a line. To this end, we re-

move pixels that represent points closer than 30 cm

to these lines, depending on the type of line. Then,

in a ﬁrst pass of region growing, we expand each col-

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

ored area into the free space that has been created by

removing pixels of the area’s color. In doing so, we

do not cross the lines under consideration. The out-

come is that pixels on wrong sides of lines are deleted.

This gives straight boundaries at ridge lines, at edges

of building parts and at edges of the true orthophoto.

However, by deleting pixels, facets might become un-

connected. Such facets have to be split up into sepa-

rate connected components.

In a second pass of region growing, we let the col-

ored regions grow until they collide or reach one of

the previously discussed lines or pixels of E. Addi-

tionally, large height jumps (step edges) in the height

map limit region growing. Step edges with small

height differences can not be detected from the inter-

polated height map dependably. Here the edges from

orthophotos come into play.

A third pass of region growing is needed to take

care of areas that are still not colored. In this pass,

only other regions and the footprint from cadastral

data act as boundaries.

Figure 8 shows excerpts from a city model before

planarization is performed (see Section 6). Region

growing based on edges of the true orthophoto sig-

niﬁcantly improves the original model. However, due

to the resolution of data and quality of true orthopho-

tos, the outcome is far from being perfect. But it is a

good basis to apply heuristics that lead to parallel or

orthogonal edges.

5 CORRECTING

SELF-INTERSECTING ROOF

POLYGONS

Each roof facet consists of exactly one outer polygon

and zero or more inner polygons that deﬁne open-

ings within the roof. The outer polygon is oriented

counter-clockwise, the inner polygons are oriented

clockwise. CityGML does not allow polygons to have

self-intersections. However, such intersections often

do occur either because of the roof’s topology or be-

cause of over-simpliﬁcation. Therefore, we recur-

sively have to split up polygons until all intersections

are eliminated. We do this in the x-y-plane and add

height values (z-coordinates) later. To begin with, we

compute all points of self-intersection. If an intersec-

tion point is no known vertex, then we add it as a new

vertex to the polygon, cf. (Bogdahn and Coors, 2010).

But we also add it to all other polygons that cross that

point. This is necessary to easily decide about wall

visibility, see Section 7. Now, we haveto split up each

polygon at vertices that occur more than once within

Figure 8: Boundaries of the upper model are adjusted to

edges of a true orthophoto. This results in the second pic-

ture. Due to the region growing algorithm, some small roof

segments vanish, other small facets appear.

the polygon.

To simplify the outer polygon, we have to distin-

guish between two general cases of self-intersection

at a vertex: The polygon might really cross itself (case

a)) or it is tangent to itself (case b) ). We resolve inter-

sections using two passes. The ﬁst pass handles case

a), the second one deals with b):

a) This is an error situation that might occur if one

snaps vertices to other places like ridge lines. For

example, vertex A in Figure 9a) might have been

moved upwards. After dividing the polygon into

non-self-intersecting segments, all segments with

clockwise orientation (like the dark green triangle

in the ﬁgure) have to be removed. The space cov-

ered by this segment might also be shared with

Quality Enhancement Techniques for Building Models Derived from Sparse Point Clouds

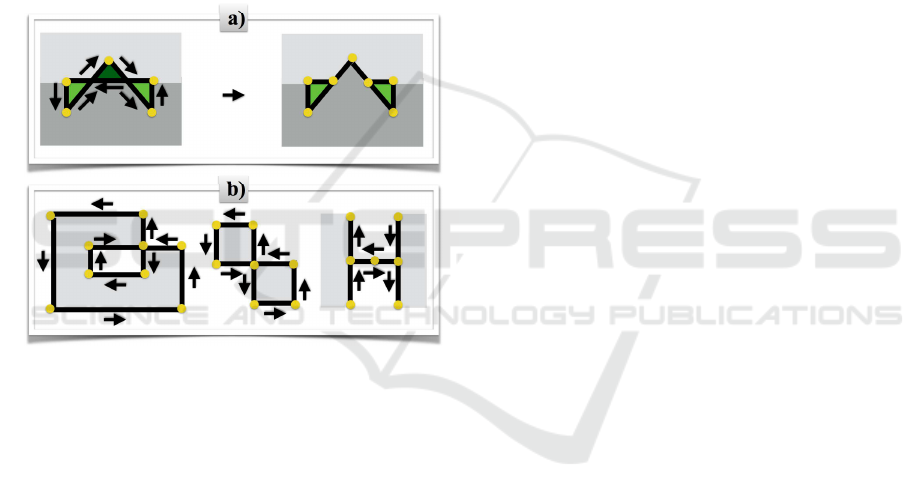
multiple adjacent roof facets. To heal this error

in practice, it is often sufﬁcient to snap the wrong

segment’s vertices to the nearest vertex of the seg-

ment’s longest edge.

b) This is a regular situation. As in a), we split up

into non-self-intersecting polygons. We discard

polygons with zero area that occur if there are

edges that are used twice (different directions of

traverse, see edges between vertices A and B in the

second example of Figure 9b)). All segments with

counter-clockwise orientation become new outer

polygons. The second example of Figure 9b) is re-

solved to two outer polygons. All segments with

clockwise orientation become additional new in-

ner polygons. This happens in the ﬁrst example

of Figure 9b).

A B

Figure 9: Resolving self-intersections.

To simplify previously existing inner polygons,

we ﬁrst merge them if possible: We compute a list

of all edges of all inner polygons. Then we remove

edges that occur twice but with different direction of

traverse. We put together remaining edges to new in-

ner polygons. Then we split them up in the same man-

ner as the outer polygon with one exception: Under

the preliminary that openings like the one in the ﬁrst

example of 9b) are not part of the outer surrounding

facet, openings of inner polygons are not relevant, we

do not have to recursively generate inner polygons of

inner polygons. Thus, such polygons are discarded.

Now, the roof facet is decomposed into a list of

one or more non-self-intersecting outer polygons and

a list of zero or more non-self-intersecting inner poly-

gons. For each inner polygon, we have to ﬁnd the

unique outer polygon that surrounds it. Then we can

write a separate roof facet for each outer polygon with

its corresponding openings, i.e., inner polygons.

For the square kilometer of the city center, the al-

gorithm has to resolve 174 points of self-intersection

with crossing. These points result from merging ver-

tices and snapping vertices to ridge lines. Also, poly-

gons are separated at 450 tangent points.

6 PLANARIZATION OF ROOF

FACETS

CityGML only offers primitives to describe planar

surfaces. Therefore, e.g., dome roofs or curved roofs

have to be approximated by plane fragments. How-

ever, often CityGML models violate planarity to some

extend. The easiest way to heal non-planar surfaces

is to triangulate them. This actually is done in prac-

tice, see (Boeters et al., 2015). More sophisticated

algorithms optimize roof structures. By locally ad-

justing a single roof facet to become planar, adjacent

facets might loose this property. Therefore, in con-

trast to the algorithm in (Alam et al., 2013), we solve

a global optimization problem to establish planarity

of all roof facet’s at the same time. Due to the lin-

ear nature of roof planes, linear programming appears

to be an appropriate means. This approach differs

from more general shape preserving algorithms based

on non-linear optimization, cf. (Bouaziz et al., 2012;

Deng et al., 2015; Tang et al., 2014) and the literature

cited there. Non-linear optimization of energy func-

tions in fact is standard in architecture reconstruction.

Another example ist the work of Arikan et al. (Arikan

et al., 2013). They use a Gauss-Seidel algorithm to

snap together polygons.

We execute the linear program with the simplex

algorithm that is implemented in the GNU Linear

Programming Kit library GLPK (Makhorin, 2009). In

brief, the basic idea behind such a linear program is

presented in (Goebbels et al., 2017). Here we give an

extended description that also covers additional rules

and reﬁnements that are necessary to make the solu-

tion work in practice.

, k ∈ {1, 2, ...,n}, denotes a roof polygon with

vertices p

k,1

,. . ., p

k,m

∈V,

k, j

= (p

k, j

.x, p

k, j

.y, p

k, j

.z),

where V ⊂ R

is the roof’s ﬁnite vertex set.

The task is to replace z-coordinates p

k, j

.z with

new height values

k, j

.h = p

k, j

.z+ p

k, j

− p

k, j

−

k, j

, p

k, j

−

≥ 0, such that the polygons become

planar. We do not change x- and y-coordinates dur-

ing this processing step. This is important to keep

the footprint from cadastral data and to obtain a linear

optimization problem. A related approach for quad-

rangular meshes is presented in (Mesnil et al., 2016).

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

It propagates z-coordinated changes by solving linear

equations to keep surface elements planar.

For each polygon P

, we determine three non-

collinear vertices p

k,u

, p

k,v

, and p

k,w

such that, if pro-

jected to the x-y-plane, p

k,u

and p

k,v

have a largest

distance. Then p

k,w

is selected such that the sum

of x-y-distances to p

k,u

and p

k,v

becomes maximal

and vectors~a

:= (p

k,u

.x− p

k,v

.x, p

k,u

.y− p

k,v

.y) and

:= (p

k,w

.x − p

k,v

.x, p

k,w

.y − p

k,v

.y) become linear

independent.

We compare all vertices of P

with the

reference plane deﬁned by the three points

k,u

.x, p

k,u

.y, p

k,u

.h), (p

k,v

.x, p

k,v

.y, p

k,v

.h), and

k,w

.x, p

k,w

.y, p

k,w

.h).

According to CityGML guidelines, one has to

consider all combinations of three non-collinear ver-

tices and compare against the corresponding planes

(see (SIG3D, 2014, p.5)). But for numerical stability

we restrict ourselves to the previously selected ver-

tices with large distances.

We can uniquely write each point (p

k, j

.x, p

k, j

.y),

j ∈ {1,...,m

}, as linear combination

k, j

.x, p

k, j

.y) = (p

k,v

.x, p

k,v

.y) + r

k, j

+ s

k, j

with scalars r

k, j

, s

k, j

. Using constants

k, j

:= −p

k, j

.z+ (1−r

k, j

−s

k, j

k,v

k, j

k,u

.z+ s

k, j

k,w

.z,

we introduce auxiliary variables α

k, j

deﬁned by

k, j

:= −p

k, j

+ p

k, j

−

+(1−r

k, j

−s

k, j

)(p

k,v

− p

k,v

−

)

k, j

k,u

− p

k,u

−

)

k, j

k,w

− p

k,w

−

) + c

k, j

. (1)

If the facet P

is planar then α

k, j

= 0 for all j. But be-

cause coordinates typically are rounded to three dec-

imals in CityGML model ﬁles, we have to allow α

k, j

to be within certain bounds:

−δ

≤ α

k, j

≤ δ

To deﬁne bound δ

, let ν

be the reference plane’s

normal vector. Since the plane belongs to a roof facet,

we can assume ν

.z > 0. Let µ be an error threshold

(for example µ := 0.001 m if coordinates are given in

millimeters), then

:= µ+

1−ν

√

2·µ. (2)

This means that each vertex p

k, j

has to be closer to

the reference plane than

.z·δ

= µ



.z+

√

1−ν



The right side reaches a maximum for ν

.z = 1/

√

so that the maximum distance to the plane is less or

equal

√

3µ.

In bound (2), the ﬁrst summand µ allows z-

coordinates to vary up to µ. The second expression

is constructed to take care of deviations into x- and y-

directions up to µ. Depending on the normal ν

, such

deviations result in height changes on the reference

plane that are up to a magnitude of

√

1−ν

√

2·µ. If

the roof facet has large slope and appears to be nearly

vertical, then ν

is close to zero and we allow large

deviations of z coordinates. When processing the ref-

erence data, such larger bounds in fact are required to

maintain the shape of some tower roofs, see Figure

10.

Figure 10: If one chooses µ as a bound for height

changes and does not consider rounding errors of x- and y-

coordinates, then linear optimization changes the shape of

the tower (from left to right).

Depending on the model’s application, it might

be necessary to make changes to certain roof vertices

more expensive. For example this is the case if ver-

tices belong to facades that should be textured with

photos (cf. Figure 11). Such vertices often have x- and

y-coordinates that also occur within the terrain inter-

section curve of a building. We introduce costs to the

objective function in terms of the weights ω(p). Such

weights do not inﬂuence the existence of solutions.

Summing up, we use a linear program with struc-

tural variables p

k, j

and p

k, j

−

for p

k, j

∈V, aux-

iliary variables α

k, j

, k ∈ {1,. . .,n}, j ∈ {1, ...,m

and weights ω(p), p ∈V, see formulas (1, 2):

Minimize

∑

p∈V

ω(p)[p.h

+ p.h

−

]

s.t. p.h

, p.h

−

≥ 0, −δ

≤ α

k, j

≤ δ

for all p ∈V, k ∈ {1,.. . ,n}, j ∈ {1,. ..,m

We are looking for a global minimum that always

exists because each ﬂat roof is a feasible solution.

But the global minimum might require large height

changes for single vertices. To this end, we also intro-

duce a bound ε > 0 for height changes at each vertex:

p.h

≤ ε, p.h

−

≤ ε for all p ∈V.

Quality Enhancement Techniques for Building Models Derived from Sparse Point Clouds

Figure 11: Texturing of facades requires higher precision

of z-coordinates. Black areas between textures and roofs

indicate that walls are too high whereas slopes of roof facets

are too small.

If one chooses ε too small, then there might be no

feasible solution. Therefore, we start planarization of

a building with a small value (ε = 0.1 m) and then

iteratively double it until a solution is found.

Figure 12: Shed roofs or dormers have walls (step edges)

within a roof.

If there are vertices with same x- and y-

coordinates but different z-values (see Figure 12),

then in an optimal solution the order of their z-

coordinates might be different. Then the set of vis-

ible walls and the appearance of the roof might also

change. To avoid this, we sort the vertices by increas-

ing z-coordinates. Let v

,··· , v

∈V be vertices with

.x = v

.x, v

.y = v

.y, 1 ≤i, j ≤ l and

.z ≤v

.z ≤··· ≤ v

.z.

For 1 ≤ i < l we add constraints

i+1

.z+ v

i+1

−v

i+1

−

−v

.z−v

+ v

−

≥0.

(3)

Although we use weights to make changes to fa-

cades more expensive, experiments show that vertices

of upper wall edges might change their heights in-

dependently. Vertices with the same original height

then might get different z-coordinates so that corre-

sponding facade edges get a wrong slope. Therefore,

we collect all pairs of vertices of upper facade edges

for which the vertices have approximately the same

z-coordinates. Then we add rules that ensure that for

each pair the new height values do not differ to much

from each other.

Also, one has to add lower bounds v.z + v.h

−

v.h

−

≥ b to ensure that changed height values are not

below the ground plane z-coordinate b of each build-

ing.

If two roof polygons share three or more non-

collinear vertices then optimization can’t ﬁnd differ-

ent planes for these polygons. Therefore, prior to

running the linear program, we analyze sequences

of three consecutive non-collinear vertices that are

shared with same z-coordinates between each two

roof facets. If one roof facet is an inner polygon of the

other facet then we merge both roof segments. This

reduces the number of roof facets and simpliﬁes the

model. Otherwise, if the z-coordinate of the middle

vertex was replaced by a mean value to avoid step

edges, we undo that modiﬁcation.

Nevertheless, the optimization changes normal

vectors of roof segments. We allow that. But if one

wants to exclude such solutions that involve larger

changes of normal vectors, one can add further re-

strictions to the linear program that bound x- and y-

coordinates of normal vectors only to vary in a cer-

tain range deﬁned by κ ≥ 0. In order to keep con-

straints linear in p.h = p.h

− p.h

−

, we do not nor-

malize cross products of vectors that contain struc-

tural variables. Let

ν := (p

k,v

− p

k,u

) ×(p

k,w

− p

k,u

)

then conditions read (1 ≤k ≤ n):

−κ|

ν|≤[(p

k,v

.y− p

k,u

.y)(p

k,w

.h− p

k,u

.h)

−(p

k,v

.h− p

k,u

.h)(p

k,w

.y− p

k,u

.y)] −

ν.x ≤ κ|

ν|.

−κ|

ν|≤[(p

k,v

.h− p

k,u

.h)(p

k,w

.x− p

k,u

.x)

−(p

k,v

.x− p

k,u

.x)(p

k,w

.h− p

k,u

.h)] −

ν.y ≤ κ|

ν|.

Under these restrictions, optimization of some build-

ings may fail so that roofs keep unevennesses. There

is a trade-off between planarity and authenticity of

roof slopes.

In our reference data set, 59% of buildings be-

come 0.001-approximate planar if we set threshold

value ε to 0.1. We do not use GLPK’s exact ratio-

nal arithmetic because of performance issues. The

standard ﬂoat arithmetic causes some rounding errors.

If we apply the algorithm to its own output, then we

see that still not all buildings have approximate pla-

nar roof facets. But then all buildings become ap-

proximate planar with ε = 0.1. Thus, the true share

of buildings that are already given with approximate

planar roof facets is up to 59%.

If we successively double ε to 0.2, 0.4, 0.8, 1.6,

and 3.2, an additional number of 11%, 10%, 10%,

6%, and 3% of buildings become approximate planar

through optimization. All buildings become approx-

imate planar by choosing ε = 6.4. Figure 13 shows

what happens to the complex roof of a church. Run-

ning time for a single-threaded implementation is less

than ﬁve seconds on an i5 processor.

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

100

Figure 13: Two 3D prints of a church: The silver version

shows the situation before linear optimization. Non-planar

roof facets are triangulated, and some triangles show differ-

ent slopes than others. The red model is the result of pla-

narization. It is free of such artifacts. The ﬁgure also shows

visualizations of the two models with different colors for

each roof facet.

7 POST-PROCESSING OF WALLS

After ﬁnding planar roof polygons, we generate ver-

tical walls that reach from roof edges down to the

ground plane. The height of the ground plane is taken

from a digital elevation model. At this point in time,

each wall polygon has four different vertices. To gen-

erate a well-formed CityGML model, we now have

to cut off invisible parts of the walls, see Figure 14.

To this end, we use the precondition that no vertex of

a roof or wall polygon lies on the inner part of any

roof or wall edge. Thus, any vertex also is a vertex of

all adjacent polygons. Therefore, we can determine

visibility by comparing the pair of upper vertices of

each wall with all roof edges between pairs of ver-

tices that have the same x- and y-coordinates as the

two wall vertices. With one exception, there can be at

Figure 14: Walls of a conference center and theatre are dis-

played as wire frames, if their normal vector points away

from the view point. Otherwise they are painted grey. The

ﬁrst ﬁgure shows the model with uncut walls. The second

picture only shows parts of walls that are visible from the

outside of each single building (without considering neigh-

bor buildings). The view points through the ground surface

to the sky.

most two roof edges that fulﬁll this condition. The ex-

ception is the existence of openings that are modeled

using inner polygons. Other roof facets can be posi-

tioned within openings. If two inner polygons share

a common edge, then there might be up to four roof

edges that have to be considered. Thus we exclude

walls that belong to edges shared between inner poly-

gons from further considerations since they do not be-

long to the building. The procedure in Section 5 takes

care of this.

Obviously, there has to be at least one (ﬁrst) roof

edge with the same coordinates as the upper wall ver-

tices. If there is a second roof edge with exactly these

coordinates (including z-coordinates), then the edge is

a ridge line and no wall is needed. If there is no sec-

ond other roof edge with same x- and y-coordinates

Quality Enhancement Techniques for Building Models Derived from Sparse Point Clouds

101

(and arbitrary z-coordinates), then we deal with an

outer wall belonging to the building’s footprint. This

wall is completely visible. There are three remaining

cases, see Figure 15:

a) z-coordinates of the upper wall vertices are both

greater than the corresponding z-coordinates of

the second roof edge: In this case, the lower edge

of the wall has to be replaced by the roof edge.

b) z-coordinates of the upper wall vertices are both

less or equal to the corresponding z-coordinates

of the second roof edge: The wall completely is

invisible because it is adjacent to a higher segment

of the building.

c) One z-coordinate of the upper wall vertices is

greater or equal and one z-coordinate is less or

equal to the corresponding z-coordinate of the sec-

ond roof edge: Only a triangle part of the wall

is visible. A new vertex has to be introduced at

the intersection point between the two edges. The

wall polygon is replaced by a triangle, and the new

vertexalso has to be inserted to affected roof poly-

gons.

Case c) is the reason why we cut off invisible parts

of walls only after the linear optimization step. Op-

timization leads to different slopes of roof edges,

so that intersection points might change x- and y-

coordinates. If we would add these intersection points

before optimization takes place, then we would pin

together both roof facets and do not allow x- and y-

coordinate changes. This reduces the number of fea-

sible solutions and might change the appearance of

the roof.

Figure 15: Visibility analysis of walls: Red polygons repre-

sent walls and black edges are parts of roof facets.

For the tested square kilometer, 11,015 z-

coordinates of wall polygons are modiﬁed according

to case a), 36,619 wall polygons are removed along

case b), and 8,394 walls are replaced by a triangle as

described in case c).

Finally, adjacent walls with equal orientation can

be merged to larger polygons. This happens 15,416

times.

8 CONCLUSIONS AND FURTHER

WORK

Presented techniques have been successfully applied

to improve city models of the cities of Krefeld and

Leverkusen. However, for about 1% of buildings, en-

forcing planarity leads to visible changes of roofs’

appearances (z-coordinate errors of more than 2 m).

Section 6 describes a general approach to planariza-

tion that can be applied to arbitrary CityGML mod-

els. But within our workﬂow we can directly generate

planar roof facets if we do not snap together vertices

to avoid step edges. Then instead of establishing pla-

narity, linear optimization can be used to eliminate

step edges while at the same time planarity is main-

tained. To this end, height differences

v.z+ v.h

−v.h

−

−u.z−u.h

+ u.h

−

have to be minimized for each pair of vertices u,v ∈

V with u.x = v.x, u.y = v.y, and u.z ≤ v.z, where

v.z −u.z is less than a threshold bound β for un-

wished step heights like β = 0.5 m. Please note that

constraints (3) ensure that such differences are non-

negative. For such vertices u und v, we add sum-

mands w·(v.h

−v.h

−

−u.h

+ u.h

−

) to the original

objective function

∑

p∈V

ω(p)[p.h

+ p.h

−

], where w

is a large weight that forces height differences to be

smaller than a given precision (if compatible with

constraints) whereas the original objective function

avoids unnecessary height changes. For example

we set w to the overall number of variables times

εmax{ω(p) : p ∈V}/(µ/2) (see Section 6 for mean-

ing of symbols). By allowing local height changes

up to ε := β, the linear program of Section 6 then

minimizes step edges with height differences below

ε. If compliant with auxiliary conditions, height dif-

ferences become smaller than precision so that step

edges vanish. Unfortunately, it turns out that in prac-

tice the optimization of step edges leads to visible roof

changes similar to the changes caused by planariza-

tion.

Starting from scratch, overall processing time for

all of Leverkusen’s 66,400 buildings on 79 square

kilometers is about four hours on two cores of an i5

processor with 4 GB of RAM. The Simplex algorithm

theoretically has an exponential worst-case running

time but turns out to be extremely fast for our small

optimization problems. With respect to worst-case

situations, it could be replaced by an interior point

method so that all processing steps run in polynomial

time.

So far, our processing workﬂow is data based. We

plan to extend it to a hybrid data and model driven

approach. For special structures with small footprints

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

102

Figure 16: Preserving rectangular shapes: raster represen-

tation of roof facets without and with shape estimation.

like tower spires, we are experimenting to ﬁt objects

from a catalogue. To recognize such structures, we

will both use edges from orthophotos as well as the

interpolated height map. Since many roof facets have

rectangular or triangular shapes, we will detect and

maintain such shapes, see Figure 16 for ﬁrst results.

In contrast to (Nan et al., 2010), we will not directly

ﬁt geometric objects to the 3D point cloud but use the

2D raster representation.

ACKNOWLEDGEMENTS

We would like to thank cadastre ofﬁces of the cities

of Krefeld and Leverkusen as well as the state cadas-

tre ofﬁce of North Rhine-Westphalia for support-

ing us with buildings’ footprints, laser scanning data

and true orthophotos. Especially, Johannes Schar-

mann and Marco Oestereich gave us valuable sup-

port. Cadastral data are protected by copyright

(Geobasisdaten der Kommunen und des Landes NRW

Geobasis NRW 2016).

REFERENCES

Alam, N., Wagner, D., Wewetzer, M., von Falkenhausen,

J., Coors, V., and Pries, M. (2013). Towards au-

tomatic validation and healing of CityGML models

for geometric and semantic consistency. ISPRS Ann.

Photogramm. Remote Sens. and Spatial Inf. Sci., II-

2/W1:1–6.

Areﬁ, H. and Reinartz, P. (2013). Building reconstruction

using dsm and orthorectiﬁed images. Remote Sens.,

5(4):1681–1703.

Arikan, M., Schw¨arzler, M., Fl¨ory, S., Wimmer, M., and

Maierhofer, S. (2013). O-snap: Optimization-based

snapping for modeling architecture. ACM Trans.

Graph., 32(1):6:1–6:15.

Biljecki, F., Stoter, J., Ledoux, H., Zlatanova, S., and

C¸ ¨oltekin, A. (2015). Applications of 3d city models:

State of the art review. ISPRS Int. J. Geo-Inf., 4:2842–

2889.

Boeters, R., Ohori, K. A., Biljecki, F., and Zlatanova,

S. (2015). Automatically enhancing CityGML lod2

models with a corresponding indoor geometry. In-

ternational Journal of Geographical Information Sci-

ence, 29(12):2248–2268.

Bogdahn, J. and Coors, V. (2010). Towards an automated

healing of 3d urban models. In H., K. T., G., K., and

C., N., editors, Proceedings of international confer-

ence on 3D geoinformation, International Archives of

Photogrammetry, Remote Sensing and Spatial Infor-

mation Sciences, pages 13–17.

Bouaziz, S., Deuss, M., Schwartzburg, Y., Weise, T., and

Pauly, M. (2012). Shape-up: Shaping discrete ge-

ometry with projections. Computer Graphics Forum,

31(5):1657–1667.

Demir, I., Aliaga, D. G., and Benes, B. (2015). Procedural

editing of 3d building point clouds. In 2015 IEEE In-

ternational Conference on Computer Vision (ICCV),

pages 2147–2155, Washington, DC. IEEE Computer

Society.

Deng, B., Bouaziz, S., Deuss, M., Kaspar, A.,

Schwartzburg, Y., and Pauly, M. (2015). Interactive

design exploration for constrained meshes. Comput.

Aided Des., 61(C):13–23.

Elbrink, S. O. and Vosselman, G. (2009). Building recon-

struction by target based graph matching on incom-

plete laser data: analysis and limitations. Sensors,

9(8):6101–6118.

Finlayson, G. D., Hordley, S. D., and Drew, M. S. (2002).

Removing shadows from images. In Proceedings of

the 7th European Conference on Computer Vision-

Part IV, ECCV ’02, pages 823–836, Berlin. Springer.

Goebbels, S., Pohle-Fr¨ohlich, R., and Rethmann, J. (2017).

Planarization of CityGML models using a linear pro-

gram. In Operations Research Proceedings (OR 2016

Hamburg), pages 1–6, Berlin. Springer, to appear.

Goebbels, S. and Pohle-Fr¨ohlich, R. (2016). Roof recon-

struction from airborne laser scanning data based on

image processing methods. ISPRS Ann. Photogramm.

Remote Sens. and Spatial Inf. Sci., III-3:407–414.

Gr¨oger, G. and Pl¨umer, L. (2009). How to achieve con-

sistency for 3d city models. ISPRS Int. J. Geo-Inf.,

15(1):137–165.

Gr¨oger, G., Kolbe, T. H., Nagel, C., and H¨afele, K. H.

(2012). OpenGIS City Geography Markup Language

(CityGML) Encoding Standard. Version 2.0.0. Open

Geospatial Consortium.

Guo, R., Dai, Q., and Hoiem, D. (2011). Single-image

shadow detection and removal using paired regions.

In Proceedings of the 2011 IEEE Conference on Com-

puter Vision and Pattern Recognition, CVPR ’11,

pages 2033–2040, Washington, DC. IEEE Computer

Society.

Haala, N. and Kada, M. (2010). An update on automatic

3d building reconstruction. ISPRS Journal of Pho-

togrammetry and Remote Sensing, 65:570–580.

He, Y. (2015). Automated 3D Building Modeling from Air-

Quality Enhancement Techniques for Building Models Derived from Sparse Point Clouds

103

borne LiDAR Data (PhD thesis). University of Mel-

bourne, Melbourne.

Henn, A., Gr¨oger, G., Stroh, V., and Pl¨umer, L. (2013).

Model driven reconstruction of roofs from sparse LI-

DAR point clouds. ISPRS Journal of Photogrammetry

and Remote Sensing, 76:17–29.

Kada, M. and Wichmann, A. (2013). Feature-driven 3d

building modeling using planar halfspaces. ISPRS

Ann. Photogramm. Remote Sens. and Spatial Inf. Sci.,

II-3/W3:37–42.

Makhorin, A. (2009). The GNU Linear Programming Kit

(GLPK). Free Software Foundation, Boston, MA.

Mesnil, R., Douthe, C., Baverel, O., and L´eger, B. (2016).

From descriptive geometry to fabrication-aware de-

sign. In Adriaenssens, S., abd M. Kohler, F. G.,

Menges, A., and Pauly, M., editors, Advances in

Architectural Geometry, pages 62–81, Z¨urich. vdf

Hochschulverlag.

Nan, L., Sharf, A., Zhang, H., Cohen-Or, D., and Chen, B.

(2010). Smartboxes for interactive urban reconstruc-

tion. ACM Trans. Graph., 29(4):93:1–93:10.

Perera, S. N. and Maas, N. G. (2012). A topology based

approach for the generation and regularization of roof

outlines in airborne laser scanning data. In Seyfert, E.,

editor, DGPF Tagungsband 21, pages 400–409, Pots-

dam. DGPF.

SIG3D (2014). Handbuch f¨ur die Modelierung von 3D

Objekten, Teil 1: Grundlagen. Geodateninfrastruktur

Deutschland, 0.7.1 edition.

Tang, C., Sun, X., Gomes, A., Wallner, J., and Pottmann, H.

(2014). Form-ﬁnding with polyhedral meshes made

simple. ACM Trans. Graph., 33(4):70:1–70:9.

Tarsha-Kurdi, F., Landes, T., Grussenmeyer, P., and

Koehl, M. (2007). Model-driven and data-driven

approaches using LIDAR data: Analysis and com-

parison. International Archives of Photogrammetry,

Remote Sensing and Spatial Information Sciences,

36(3/W49A):87–92.

Tong, L., Li, M., Chen, Y., Wang, Y., Zhang, W., and Cheng,

L. (2012). A research on 3d reconstruction of building

rooftop models from LiDAR data and orthophoto. In

Proceedings of the 20th International Conference on

Geoinformatics (GEOINFORMATICS), Hong Kong,

pages 1–5, Washington, DC. IEEE Computer Society.

Wagner, D., Wewetzer, M., Bogdahn, J., Alam, N., Pries,

M., and Coors, V. (2013). Geometric-semantical con-

sistency validation of CityGML models. In Pouliot,

J. and et. al., editors, Progress and New Trends in

3D Geoinformation Sciences, Lecture notes in geoin-

formation and cartography, pages 171–192, Berlin.

Springer.

Wichmann, A. and Kada, M. (2016). Joint simultaneous

reconstruction of regularized building superstructures

from low-density LIDAR data using icp. ISPRS Ann.

Photogramm. Remote Sens. and Spatial Inf. Sci., III-

3:371–378.

Zhao, J., Stoter, J., and Ledoux, H. (2013). A framework for

the automatic geometric repair of CityGML models.

In Buchroithner, M., Prechtel, N., and Burghardt, D.,

editors, Cartography from Pole to Pole, Lecture Notes

in Geoinformation and Cartography, pages 187–202,

Berlin. Springer.

GRAPP 2017 - International Conference on Computer Graphics Theory and Applications

104