High Order Diffraction Suppression of the Membrane with Hexagonal

Hole Array

Ziwei Liu

1,2,3

, Lina Shi

1,2

, Tanchao Pu

1,2,3

, Changqing Xie

1,2

, Hailiang Li

1,2

and Jiebin Niu

1,2

Key Laboratory of Microelectronic Devices & Integrated Technology,

Institute of Microelectronics of Chinese Academy of Sciences, Beijing 100029, China

Jiangsu National Synergetic Innovation Center for Advanced Materials, Nanjing 210009, China

University of Chinese Academy of Sciences, Beijing 101408, China

Keywords:

Diffraction Gratings, Binary Optics, Optical Design Fabrication, Spectroscopy, High-Resolution.

Abstract:

We propose the array of hexagonal holes with the completely suppression of the 2nd, 3rd, and 4th order diffrac-

tions. The membrane with holes can be free-standing and scalable from X-rays to far infrared wavelengths.

We numerically and experimentally demonstrate that the 2nd, 3rd and 4th order diffractions near the 1st or-

der diffraction are completely suppressed. The hexagonal hole with some size results in a desired diffraction

pattern. Our results should be of great interest in a wide spectrum unscrambling for any wavelength range.

1 INTRODUCTION

Diffraction gratings are optical components with a pe-

riodic structure, which disperse different wavelengths

of light into its constituent spectrum. They play a

crucial role in modern optical science, especially in

extreme-ultraviolet and soft x-ray regions. Over a pe-

riod of several decades, the applications of diffraction

gratings are extensively used in astrophysical plasma

diagnosis and synchrotron radiation light monochro-

mator (K. P. Beuermann, 1998; Y. Saitoh, 2000).

Normally, conventional diffraction gratings are used

as dispersion elements in spectral measurement, the

diffracted beams corresponding to consecutive orders

may overlap, depending on the spectral content of

the incident beam and the grating density (V. Da-

neu, 2000; I. Shoshan, 1977). The higher the spec-

tral order, the greater the overlap into the next order

(V. Daneu, 2000; I. Shoshan, 1977; K. Yamane, 2003;

Y. W. Huang, 2004). However, in many applications,

only the ﬁrst order is meaningful and necessary. The

data obtained with this grating due to the high-order

diffraction contamination will decrease the accuracy

of spectral data. The single-order diffractions with

accurate spectroscopic data have been the major con-

cern.

Sinusoidal amplitude transmission grat-

ings(STGs) can suppress the high-order diffraction

efﬁciently which have only 0th- and ±1

order

diffractions in a visible light region, but it’s hard

to extend to x-ray region. Due to the all known

materials in the extreme ultraviolet and x-ray regions

have complex refractive index and are very close to

unity. The fabrication with high line density grating is

difﬁcult to achieve according today’s nanofabrication

technology. In recent years, many new gratings

which have quasi-sinusoidal transmission functions

have been designed to solve this problem, but still

limited to the modern photolithography technology,

especially for applications in the extreme-ultraviolet

and x-ray regions. The pattern structure of the

gratings is recognized by many as the key to suppress

high-order diffraction effectively and decrease the

difﬁculty of fabrication.

In this Letter, we introduce a novel design of

single-order diffraction which can suppress high-

order diffraction signiﬁcantly as sinusoidal amplitude

gratings do. The key idea is to make the hexago-

nal holes follow the rectangle array, leading to dom-

inant ±1

diffraction orders on the observation line

(M. Born, 1997; L. Cao, 2007; L. Kuang, 2010;

M. E. Warren, 1995; G. Vincent, 2008). Compared

with the previous schemes, the single-order diffrac-

tion grating with binary transmittance value of 0

and 1 based on this kind of transmission function

(F. J. Torcal-Milla, 2008; C. Xie, 2010; C. Xie, 2012),

which is larger than the value of 6.25% for ideal si-

nusoidal amplitude grating. This new type of single

optical element with the capabilities of quasi-single

order diffraction named hexagonal aperture gratings

Liu Z., Shi L., Pu T., Xie C., Li H. and Niu J.

High Order Diffraction Suppression of the Membrane with Hexagonal Hole Array.

DOI: 10.5220/0006103400590064

In Proceedings of the 5th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS 2017), pages 59-64

ISBN: 978-989-758-223-3

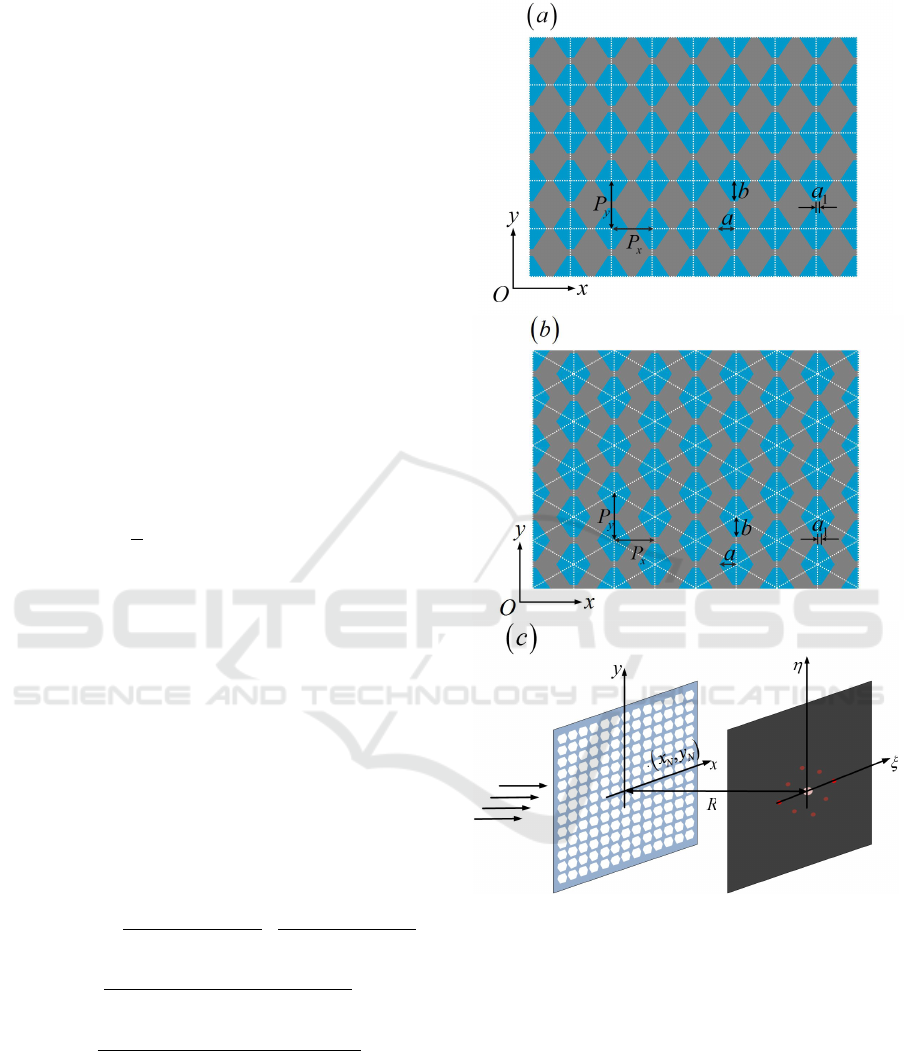
(HAGs) as shown in Figure 1, consists of a series

of periodically arranged hexagonal apertures. Such

structure has great advantages in extreme-ultraviolet

and x-ray regions. In addition, HAGs on the glass

substrate are easy to fabricate. Both numerical solu-

tion and experimental results demonstrate the diffrac-

tion efﬁciency of the HAGs. It offers a new idea of

single-order diffraction and beneﬁt in fabrication.

2 DESIGN AND SIMULATIONS

We start the design from the array of hexagonal holes

as shown in Figure 1. The (x,y) and (η,ξ) are the

coordinate systems in the hole plane and diffraction

plane respectively. For a membrane that contains a

large number of identical and similarly oriented holes,

the light distribution in the Fraunhofer diffraction pat-

tern is given by (W. Goodman, 1996),

U(p,q) = C

∑

−ik(px

+qy

)

−ik(px

+qy

)

(1)

Here C =

√

P/(λR), P is the power density inci-

dent on the hole array, λ is the incident light wave-

length, R is the distance between the hole array plane

and the diffraction plane. The coordinates of the hole

center are (x

),(x

),.. . (x

), and k is the

wave vector. The integration extends over the hole

area and the integral expresses the effect of a single

hole. The sum represents the superposition of the co-

herent diffraction patterns.

For the square array of N

hexagonal holes of

the side 2a

along the x axis, the diagonal 2a along

the y axis, and the height along axis as shown in Fig.

1(a), the diffraction intensity pattern is

I(p,q) = U (p, q) ∗U

∗

(p,q)

= I

sin

kpP

/2)

·sin

(kpP

/2)

sin

kqP

/2)

·sin

(kqP

/2)



cos(kpa

−kqb) −cos kpa

kp(a + a

) ·(kp(a −a

) + kqb)

coskpa −cos(kpa

+ kqb)

kp(a + a

) ·(−kp(a −a

) + kqb)



(2)

Here I

= C

· (N

· 2(a + a

)b)

is the peak

irradiance of the diffraction pattern. For simplicity,

here we set I

= 1,P

and P

(shown in Fig. 1) are

respectively the periods along the x and y axes.

Figure 1: The array of hexagonal holes. The side along

the x axis is 2a

, the diagonal along the x axis is 2a and

the height along the y axis is 2b. (a) The square array with

periods P

and P

. (b) The triangle array with periods 2P

and P

. (c) The coordinate systems in the aperture plane and

observation planes.

Similarly, for the triangle array as shown in Fig.

1(b), the diffraction intensity pattern is

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

I(p,q) = U(p,q) ∗U

∗

(p,q)

= I

sin

/2 ·kp2P

/2)

·sin

(kp2P

/2)

sin

kqP

/2)

·sin

(kqP

/2)

· cos

(kp2P

/4 + kqP

/4)



cos(kpa

−kpb) −coskpa

kp(a + a

) ·(kp(a −a

) + kqb)

coskpa −cos(kpa

+ kqb)

kp(a + a

) ·(−kp(a −a

) + kqb)



(3)

The parameters are same as the square array except

the period 2P

along the x axis.

Here, we focus on the diffraction intensity along

the x axis since spectral measurement is usually at

one direction. For the square and triangle arrays, the

diffraction intensity according to Eq.(2) and (3) along

the x axis are both given by

I(p) = I

sin

kpP

/2)

·sin

(kpP

/2)



sin(kp(a + a

)/2 ·sin(kp(a −a

)/2)

kp(a + a

)/2 ·kp(a −a

)/2



(4)

And thus the m-th order diffraction along the x

axis is

I(m)=I



sin(m(a + a

)π/P

)·sin(m(a −a

)π/P

)

m(a + a

)/2·m(a −a

)π/P



(5)

In real spectral measurement, only the near diffrac-

tions (such as the 2

, 3

and 4

order diffractions)

will overlap the 1st order diffraction. The far diffrac-

tions are usually very small and have little effects on

the 1

order diffraction. Thus we will consider the

structure parameters which lead to the zeros of the

, 3

and 4

order diffractions. Equation (4) shows

that the diffractions along the x axis have nothing to

do with the parameters of b and P

. The diffractions

along the x axis depend on the parameters of a, a

and

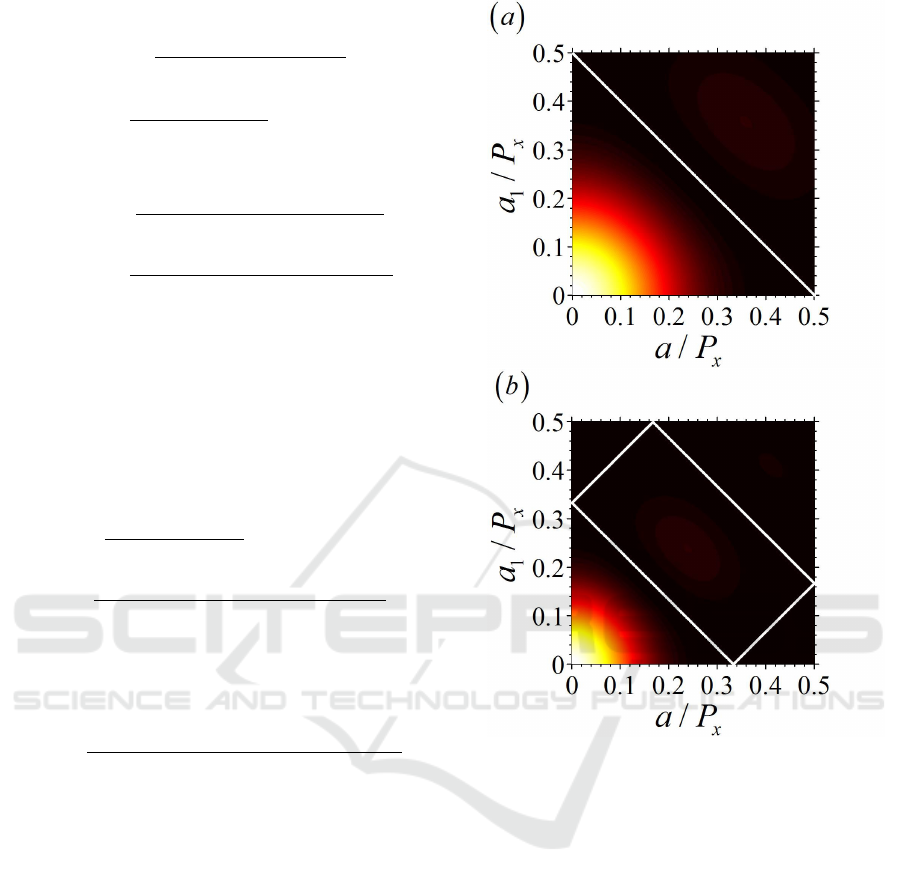
as shown in Fig.2.

According to Equation (5) and Fig.2,the 2

, 3

and 4

order diffractions I(2) = I(3) = I(4) = 0 as

= P

/12 and a = 5P

/12. At the same time, the 5

order diffraction I(5) = 0.0004435I

= 0.0016I(1),

the 0

order diffraction I(0) = I

, the 1

order

diffraction I(1) = 0.2772I

Figure 3 presents the diffraction intensity pat-

tern the array of hexagonal holes with a

= P

/12,

Figure 2: (a) The dependent relation of the 2

order

diffraction on a,a

and P

. The white line denotes the 2

order diffraction is zero. (b) The dependent relation of the

order diffraction on a,a

and P

. The white line denotes

the 3

order diffraction is zero.

a = 5P

/12 and b = P

/12 according to Eq.(2) and

(3). Comparing with the diffraction pattern of con-

ventional 1:1 traditional gratings(TGs), higher-order

diffraction components of HAGs are suppressed by

about three orders, which is weak enough for appli-

cation and very similar to the ideal sinusoidal trans-

mission gratings. As expected, the 0

and 1

order

diffractions are kept along x axis, and the 2

, 3

and

diffractions disappear. The logarithm of diffrac-

tion intensity along x axis in Fig.3(c) and (d) presents

clearly the complete suppression of the 2

, 3

and

order diffractions. The 5

order diffraction is

smaller than the noise between the 0

and 1

order

diffractions. Insets in Fig. 3 shows clearly intensity

distributions of the 0

and 1

order diffractions. Fig-

ure 3 shows that the high order diffractions along axis

High Order Diffraction Suppression of the Membrane with Hexagonal Hole Array

Figure 3: The far-ﬁeld diffraction intensity pattern of the

hexagonal hole array. The diffraction intensity along the x

axis. Insets: the 0

and 1

order diffractions. (a)(b) For the

square array. (c)(d) For the triangle array. (e)(f) The typical

diffraction patterns by 1:1 TGs.

are effectively suppressed by the array of hexagonal

holes.

Figure 3 also presents important ﬁgures of merit

of the HAGs, the relative diffraction efﬁciency of the

±1

orders (the +1

or −1

order diffracted light

intensity divided by the 0

order diffracted light in-

tensity) is 27.16%. For the triangle array, the relative

diffraction efﬁciency of the ±1

orders are 27.13%.

For the HAGs, the smallest feature size in both of

the arrays is 4µm, making it much easier to fabri-

cate, compared with sinusoidal amplitude transmis-

sion gratings designed previously. In addition, the gap

between the apertures is ﬂexible for the practical ap-

plications, which have not effect on the result.

3 EXPERIMENTAL RESULTS

AND DISCUSSION

A proof-of-principle experiment is performed to con-

ﬁrm our theoretical and numerical results. The

square array of hexagonal holes with 4cm × 4cm

area is fabricated on a glass substrate by DESIGN

WRITE LAZER 2000 from Heidelberg Instruments

Mikrotechnik GmbH. The microphotograph of fabri-

cated structure is illustrated in Fig.4(a) and (b). Pe-

riods P

and P

of the quasi-rectangle array along the

x and y axes are respectively 24µm and 28µm. The

structure consists of 1500 ×1500 holes. The entirety

experimental setup for optical demonstration is shown

in Fig.4(c). A collimated laser beam from Sprout

(Lighthouse Photonics) with wavelength of 632nm

was used to illuminate the fabricated the hexagonal

hole array, and the far-ﬁeld diffraction pattern from

the gratings was focused by a lens and then recorded

on a charge coupled device (CCD) camera (ANDOR

DU920P-BU2) with 1612 ×1214 pixels and 4.4µm

pixel size was placed in the far ﬁeld to record the

diffraction patterns.

The measurement results are shown in Fig.5. As

expected, the higher-order contributions of the fabri-

cated HAGs are signiﬁcantly suppressed. The inte-

grated diffraction intensity of the diffraction orders

along the ξ axis is shown in Fig.5(b). The relative

diffraction efﬁciency is an important parameter for

describing the characteristics of the HAGs. For per-

fect HAGs, it agrees well with the theoretical value,

the higher-order diffraction components are signiﬁ-

cantly suppressed, which is only about 0.6% of the

±1

order in amplitude. It is obvious that only 0

and ±1

orders exist along the ξ axis, which is agrees

well with the numerical simulation and the optimal

case to suppress higher order diffraction is achieved.

The relative diffraction efﬁciencies of the square ar-

ray of the 1

order is 30.27%. For the triangle array,

the +1

order is 25.82%, respectively. The experi-

mental result differs slightly from the ideal intensity

distribution shown in Fig.3. This may be attributed

to the limited dynamic range and signal-to-noise ra-

tio of the CCD, ﬁlter inhomogeneity, slightly tilted

installation of the measured HAGs and the inevitable

imperfection of the fabrication. Nevertheless, the ex-

perimental results clearly verify that the HAGs with

quasi suppression of higher-order diffractions are su-

perior to a conventional transmission grating.

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology

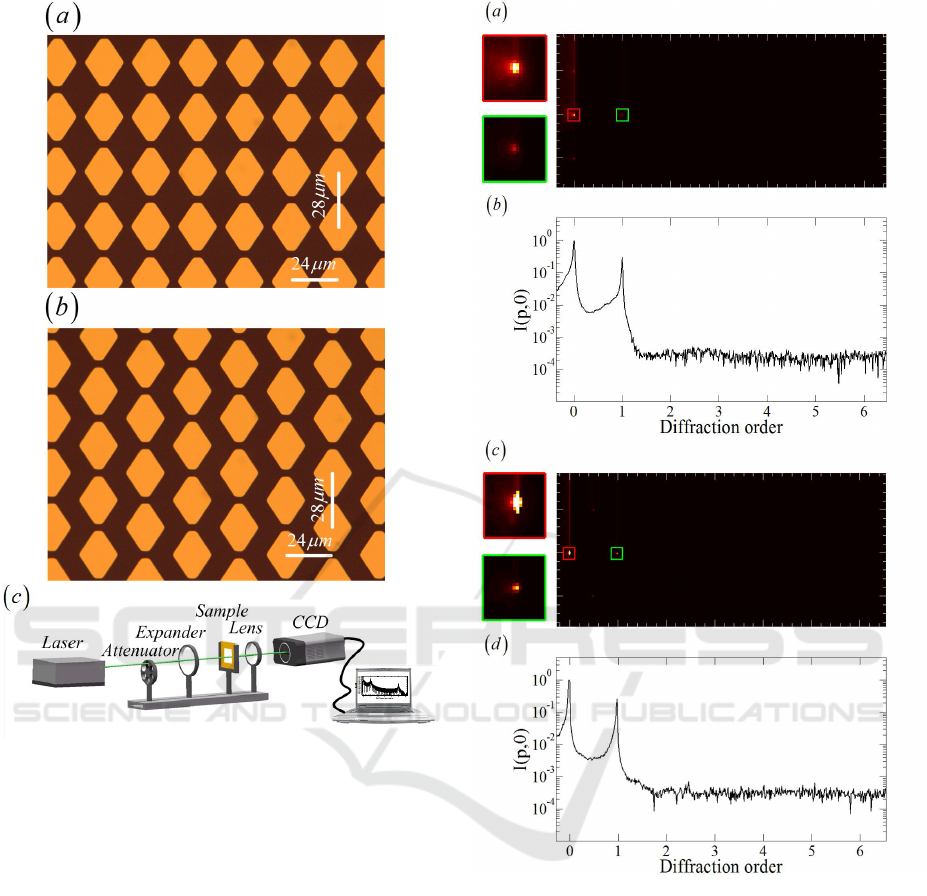
Figure 4: (a) The schematic illustration of HAGs. (b) Mi-

crophotograph of the fabricated quasi-rectangle array with

4cm×4cm area. (c) Experimental setup for the optical mea-

surement.

4 CONCLUSIONS

In conclusion, the binary structure with hexagonal

hole array has been proposed to suppress the high-

order diffractions which may lead to wavelength over-

lapping in spectral measurement. We obtian the rel-

ative diffraction efﬁciency 27.72% of the ﬁrst order

diffraction, which is higher than 25% of the ﬁrst or-

der diffraction for ideal sine grating. The membrane

with holes can be free-standing and scalable from

X-rays to far infrared wavelengths. Both numeri-

cal and experimental results have demonstrated the

, 3

and 4

order diffractions are completely sup-

pressed. The binary hole array offers an opportunity

for high-accuracy spectral measurement and will pos-

sess broad potential applications in optical science

and engineering ﬁelds.

Figure 5: (a) (c)The far-ﬁeld diffraction intensity pattern

of the quasi-triangle array of rectangular holes. (b) (d)The

diffraction intensity along the x axis.

ACKNOWLEDGEMENTS

We thank Yongliang Zhang for the valuable discus-

sion. We thank the Optics Laboratory for the use of

their equipment.

REFERENCES

C. Xie, X. Zhu, H. (2012). Toward two-dimensional

nanometer resolution hard X-ray differential-

High Order Diffraction Suppression of the Membrane with Hexagonal Hole Array

interference-contrast imaging using modiﬁed photon

sieves. Opt. Lett. 37, 749-751.

C. Xie, X. Zhu, L. S. (2010). Spiral photon sieves apodized

by digital prolate spheroidal window for the genera-

tion of hard-x-ray vortex. Opt. Lett. 35, 1765-1767.

F.J. Torcal-Milla, L. M. Sanchez-Brea, E. B. (2008).

Diffraction of gratings with rough edges. Opt. Express

16, 19757.

G.Vincent, R. Haidar, S. C. (2008). Realization of si-

nusoidal transmittance with subwavelength metallic

structures. J. Opt. Soc. Am. B 25, 834.

I. Shoshan, N. N. Danon, U. P. O. (1977). Performance

of a very high resolution soft x-ray beamline BL25SU

with a twin-helical undulator at SPring-8. Rev.

Sci.Instrum. 71, 3254.

K. P. Beuermann, R. Lenzen, H. B. (1998). Properties of a

transmission grating behind a grazing incidence tele-

scope for cosmic x-ray spectroscopy. Appl. Opt.16,

1425.

K. Yamane, Z. Zhang, K. O. (2003). Optical pulse com-

pression to 3.4fs in the monocycle region by feedback

phase compensation. Opt. Lett. 28, 2258.

L. Cao, E. Frster, A. F. (2007). Single order x-ray diffraction

with binary sinusoidal transmission grating. Appl.

Phys. Lett. 90 053501.

L. Kuang, C. Wang, Z. W. (2010). Quantum-dot-array

diffraction grating with single order diffraction prop-

erty for soft x-ray region. Rev. Sci. Instrum. 81,

073508.

M. Born, E. W. (1997). Principles of Optics. Cambridge U.

Press, 7th ed.(expanded) edition.

M. E.Warren, R. E. Smith, G. A. V. (1995). High-efﬁciency

subwavelength diffractive optical element in GaAs for

975 nm. Opt. Lett. 20, 1441.

V. Daneu, A. Sanchez, T. Y. F. (2000). Narrowband oper-

ation of a pulsed dye laser without intracavity beam

expansion. J. Appl.Phys. 48, 4495.

W. Goodman, J. (1996). Introduction to Fourier Optics.

McGraw-Hill, 2nd edition.

Y. Saitoh, H. Kimura, Y. S. (2000). Performance of a very

high resolution soft x-ray beamline BL25SU with a

twin-helical undulator at SPring-8. Rev. Sci.Instrum.

71, 3254.

Y. W. Huang, S. T. Hu, S. Y. Y. (2004). Tunable diffrac-

tion of magnetic ﬂuid ﬁlms and its potential applica-

tion in coarse wavelength-division multiplexing. Opt.

Lett.29, 1867.

PHOTOPTICS 2017 - 5th International Conference on Photonics, Optics and Laser Technology