3D Plane Labeling Stereo Matching with Content Aware Adaptive

Windows

Luis Horna and Robert B. Fisher

IPAB, The University of Edinburgh, Edinburgh, U.K.

Keywords:

Stereo Matching, 3D Labeling, Adaptive Windows.

Abstract:

In this paper, we present an algorithm that exploits both the underlying 3D structure and image entropy to

generate an adaptive matching window. The presented algorithm estimates real valued disparity maps by

smartly exploring a 3D search space using a novel hypothesis generation approach that acts like a propagation

scheduler. The proposed approach is among the top performing results when evaluated in the Middlebury,

KITTI 2015 benchmarks.

1 INTRODUCTION

The problem of 3D plane labeling to estimate depth

from two or more images has become the focus area

of modern stereo matching algorithms. The core is-

sue in 3D plane labeling using two images (left I

and

right I

views of a scene) is ﬁnding the correspon-

dences for each pixel from image I

to I

by assigning

a 3D plane that produces a real valued disparity

. This

process is better modeled as an optimization problem

where the objective is to compute the disparity assign-

ment that minimizes eq.1.

E(D) = argmin

NumP

∑

) +

∑

q∈N(p)

)}

(1)

E(D) is the cost of the disparity assignment (en-

ergy), D is a set of planes and D

encodes a plane

at pixel p, that gives the disparity of the pixel at p

with respect to another image. D

(q) is the disparity

estimated using plane D

evaluated at pixel q. The

plane D

has two parameters: a 3D unit normal vec-

tor ˆn

= (n

) and disparity d

. The disparity

of pixel q = (x

) using D

is given by:

(q) = a ∗ x

+ b ∗ y

+ c (2)

where a = − ˆn

/ ˆn

, b = −ˆn

/ ˆn

and c = ( ˆn

∗x

ˆn

∗ y

+ ˆn

∗ d

)/ ˆn

as in (Bleyer et al., 2011). C

is a function that measures the similarity/dissimilarity

The displacement along a search area is known as dis-

parity.

of two pixels (e.g. I

(p) and I

(p + D

(p))), and

NumP is the number of pixels in the image. N(p)

is a neighborhood around p, and q is a neighbor of

p. V

(smoothness term) is a function that evalu-

ates how well the disparity at position p ﬁts its neigh-

bors. Eq.1 is typically represented as Markov Ran-

dom Field (MRF) and minimized using either Graph

Cuts (GC), Loopy Belief Propagation (LBP) or Tree

Re-weighted with Sequential (T RW-S) update. In this

paper inference/minimization is done using T RW -

S(Kolmogorov, 2007).

In this paper, we present an algorithm that exploits

the underlying 3D structure, image texture to gener-

ate an adaptive matching window, and a 3D search

using a novel hypothesis generation approach to esti-

mate real valued disparity maps.

2 RELATED WORK

The idea of assigning planes per pixel to estimate

sub-pixel disparity has been previously used in (Klaus

et al., 2006; Woodford et al., 2007; Bleyer et al., 2011;

Besse et al., 2012; Olsson et al., 2013; Heise et al.,

2013; Taniai et al., 2014; Sinha et al., 2014; Yam-

aguchi et al., 2014). These algorithms can be clas-

siﬁed in two categories: ﬁxed plane inference (FPI)

and dynamic plane inference (DPI). FPI algorithms

make an initial disparity estimation and then extract

the planes, which are then used during the inference

process to estimate disparity. By contrast DPI algo-

rithms assign one or more planes to each pixel, and

then propagate “good” planes (i.e. low/high scores

162

Horna L. and B. Fisher R.

3D Plane Labeling Stereo Matching with Content Aware Adaptive Windows.

DOI: 10.5220/0006105401620171

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 162-171

ISBN: 978-989-758-227-1

depending on the cost function) to neighbors/regions

under the assumption that neighbors/regions are likely

to have the same plane. Then in a reﬁnement stage the

planes are improved, thus the planes are dynamically

updated. DPI algorithms in particular have become

the state of the art (e.g. (Bleyer et al., 2011; Besse

et al., 2012; Heise et al., 2013; Taniai et al., 2014)).

Common issues in DPI algorithms include the use

of large adaptive windows (commonly using (Yoon

and Kweon, 2006)) or segment (Li et al., 2015) based

similarity cost to compute the similarity/dissimilarity

cost, which can result in a strong bias towards large

planes. A possible solution to this issue is to change

the window size, which requires either some assump-

tion about the 3D structure or image content. How-

ever, changing the window size can result in poor per-

formance in textureless areas and thus requires addi-

tional assumptions such as the uniqueness constraint

or occlusion penalties. Another issue in DPI algo-

rithms such as (Bleyer et al., 2011; Besse et al., 2012)

is that the hypothesis generation and propagation is

done sequentially.

2.1 Contributions

To address some of the issues described the proposed

approach makes the following contributions:

• Content aware adaptive window aggregation: Re-

duces error and loss of details.

• Use of a cost function that imposes a local hy-

pothesis uniqueness, unlike (Klaus et al., 2006;

Woodford et al., 2007; Olsson et al., 2013; Ya-

maguchi et al., 2014; Sinha et al., 2014; Bleyer

et al., 2011; Besse et al., 2012; Taniai et al., 2014):

Helps to handle textureless surfaces, and does not

required higher order interactions (unlike (Vogel

et al., 2015)) in a MRF.

• Use of a cost function that penalizes disparity val-

ues outside a deﬁned search range: Prevents in-

valid disparity values assignment.

• Use of a single global hypothesis per disparity

plane: Eliminates the need to update multiple hy-

potheses.

• Use of a hypothesis generator that acts as a prop-

agation scheduler: Helps to do a search in a 3D

space.

3 PROPOSED ALGORITHM

The proposed approach to estimate a 3D plane label-

ing per pixel has the following components:

• Content aware slanted windows to compute the

data term (pixel similarity measure).

• Uniqueness and out of range terms.

• Adaptive search range.

• Smoothness term that adapts to image content.

• Hypothesis generation/update that acts as a prop-

agation scheduler.

The novel content aware windows exploit both in-

tensity and 3D structure (if available) to adapt the

window size and similarity function. It’s important to

note that the proposed hypothesis generation provides

an alternative to sequential algorithms (e.g. (Bleyer

et al., 2011; Besse et al., 2012)) and does not impose

restrictions to the pairwise interactions like (Taniai

et al., 2014).

3.1 Content Aware Adaptive Similarity

Function

DPI algorithms commonly use the adaptive window

(eq.4) from (Yoon and Kweon, 2006), which has the

following issues: bias towards large planes (good

quality in textureless areas), center pixel bias for

large windows (results in loss of detail, e.g. ﬁg.1),

and noisy results for small windows. The center

pixel bias can be reduced by using the windows from

(Zhang et al., 2009), which adapts better to local im-

age changes, but can give poor results if the windows

are poorly estimated or window size is not large (par-

ticularly in textureless areas). To compensate for the

center pixel bias while keeping good performance in

textureless areas, a texture measure L

(eq.3) is used

to balance the inﬂuence of eq.4 and eq.5 (ﬁxed size

modiﬁed version of (Zhang et al., 2009)) in eq.7.

(

−



∑

q∈N(p)

−

−I

h(p)

)

(3)

) =

∑

q∈N(p)

−

−I

) (4)

) =

∑

q∈N

(p)

−

−I

) (5)

) =

∑

s∈N

(q)

−

−I

) (6)

) = L

· AW

) + (1 − L

) ·CW

) (7)

where Z, Z

, Z

are normalization constants such that

the weights in the neighbourhood add up to one, h(p)

is a 5 × 5 entropy ﬁlter, |I

− I

| is the L1 distance in

RGB space, N(p) is the neighborhood around p (n×n

window), N

(p) and N

(q) are the horizontal (1 × n)

and vertical (n × 1) neighborhoods around p and q.

Eq.3 is the adaptively ﬁltered version of h(p), which

is done to clean the noisy measure, and better balance

and CW

close to edges.

3D Plane Labeling Stereo Matching with Content Aware Adaptive Windows

163

(a)

(b)

Figure 1: Raw result of Pipes image with AW (a) and AW +

CW (b) functions. Parameters used as in sec.6.

The adaptive window from (Zhang et al., 2009)

was modiﬁed as follows: Use of range terms for ver-

tical and horizontal directions. Only horizontal arms

are computed, while the vertical arm remains of a

ﬁxed size. The pixel similarity function is given by:

) = αc

(p)) + c

(p)) (8)

) = min(|∇I

− ∇I

p+D

|,τ

grad

) (9)

) = min(χ(I

, p,D

),τ

cen

) (10)

where, I

is the reference image, and I

is the

target image, c

) is the truncated absolute differ-

ences of gradients, c

) is the Truncated Hamming

distance of census transform(Zabih and Li, 1994)), χ

computes the census transform at p and displacement

and Hamming distance, α balances the pixel-wise

cost inﬂuence. Note that D

(p) is the disparity result-

ing from the evaluation of plane D

at pixel p.

The adaptive window described so far works un-

der the assumption that the window size remains con-

stant all over the image, which can lead to either loss

of detail

(large windows), noisy results (small win-

dows), and bias towards large planes. To reduce these

effects the window size is selected based on a local

In particular adaptive windows have a tendency to lose

thin vertical details.

measure W

, which describes the behavior of an ini-

tial disparity map gradient around a region. A region

is a superpixel segment obtained using SLIC(Achanta

et al., 2012). The behavior of the initial disparity

map gradient is ﬁrst measured along the pixels in the

segment perimeter (eq.11), then a segment difference

measure is computed using the median disparity of

neighbouring segments (eq.12), and later propagated

per pixel (eq.13) to reduce the effect of noise from the

initial disparity map. Thus window size at each pixel

p is computed using n = Ω(p) in eq.14.

ˆw

N(p)|

∑

q∈

N(p)



−

| ≥



(11)

(

N(p)|

∑

q∈

N(p)

min(|

−

|,K

) : ˆw

> τ

0 : otherwise

(12)

(

∑

q∈N(p)

−

−I



Z =

∑

q∈N(p)

−

−I

)

(13)

Ω(p) =

(

: W

> τ

and T

> τ

: otherwise

(14)

where,

and

are the median disparities (to

compensate for noise in the initial estimate) of the

segments where pixels p and q come from.

N(p) is

the perimeter of the segment where p comes from.

Notice that eq.12 computes a value per segment,

while eq.13 does it per pixel by aggregating neighbor-

ing values based on intensity similarity. τ

is dynam-

ically computed from W

using Otsu threshold. Eq.11

measures the number of pixels that can be considered

and edge for being above a threshold.

3.2 Uniqueness and Out of Range

Terms

The Similarity function described above only takes

into consideration intensity to compute a matching

score. However, this has the implicit assumption that

each pixel has a unique match, which in general is not

necessarily true (e.g.2), especially in occluded areas

and textureless regions that are prone to have multi-

ple matches (see red boxes in ﬁg.3). Eq.15 penalizes

each pixel that has multiple matches (similar to (Kol-

mogorov and Zabih, 2001)).

U(D

) =

(

unique

: L(Dp)

0 : otherwise

(15)

where L(Dp) is true when a pixel p is mapped to

d + D

which has more than one match. This is done

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

164

per hypotheses, which means it’s a local uniqueness

terms, unlike (Kolmogorov and Zabih, 2001) and (Vo-

gel et al., 2015) where it’s represented as part of the

MRF.

Figure 2: Example of uniqueness constraint violation; two

pixels (red arrows) in left image scanline map to a single

pixel in right image (red pixel).

A plane D

evaluated at a different pixel q in

the image could have disparity values that lie outside

a deﬁned search range of disparities. Eq.16 penal-

izes disparity values that lie outside a deﬁned search

range.

O(D

) =











1 − exp(−|D

− minD|/σ

) : D

< minD

1 − exp(−|D

− maxD|/σ

) : D

> maxD

0 : otherwise

(16)

where minD and maxD are the minimum and max-

imum of the disparity search range, while σ

is the

maximum deviation allowed for values outside the

search range. Eq.7 is updated to include eq.15 and

eq.16, which then becomes:

) = C

) +U (D

) + O(D

) (17)

Note that the proposed uniqueness term requires

to keep track of its current value after inference to up-

date the current cost (eq.17) and prevent energy from

oscillating in later iterations.

3.3 Search Range Detection

To detect spurious disparities the probability distri-

bution (from the normalized disparity histogram) of

each disparity present in both the left and right dis-

parity maps is computed using an initial search range

[minD,maxD], and an n-point (n is 18% of the initial

disparity search range) Parzen window is applied to

smooth the probability distribution.

Finally, a search ﬁnds the lowest (min

D) and

largest disparities (max

D) that are above a threshold

maxD

and τ

minD

maxD

. It’s possible that min

is over estimated and max

D under estimated, which

is addressed by min

D = max(minD, min

D − ∆minD),

and max

D = min(maxD, max

D + ∆maxD). The esti-

mated bounds on the disparities are used to eliminate

or penalize unrealistic disparities. max

D is used dur-

ing the inference process, and min

D during the post-

processing stage.

3.4 Smoothness Term

The assumption made by the proposed edge model is

that possible depth discontinuities are allowed small

variations, while areas with a similar intensity are al-

lowed to have larger changes, by contrast in (Besse

et al., 2012; Taniai et al., 2014) the maximum varia-

tion is constant.

) =

(

λω(D

,K2) : |F

− F

| < τ

di f f

λω(D

,K1) : otherwise

(18)

(

−|I

(p)−I

(q)|



∑

q∈N(p)

−|I

(p)−I

(q)|

)

(19)

where K1 < K2, I

is a gray level image after

applying the quick shift segmentation

(Vedaldi and

Soatto, 2008; Vedaldi and Fulkerson, 2008), w

and

λ are weights, F

and F

come from a local cue map

F, and τ

di f f

is a threshold, which means the growth

limit of the smoothness term adapts based on the local

cue map F (eq.22), while ω(D

,K) is given by:

ω(D

,K) = min(|D

(p)−D

(p)|+|D

(q)−D

(q)|,K)

(20)

is computed using the intensity gradient of the

reference image, and is used to locate possible depth

discontinuities. Using the image gradient can lead to

problems in areas where the gradient is noisy (e.g. im-

age or texture is noisy). This issue can be partially

addressed by ﬁltering both the image and gradient,

which can provide a two-fold advantage. First, the

gray level of the reference image is ﬁltered (eq.21) to

remove potential sources of noise (e.g. noisy edges or

sensor noise). Second, a ﬁlter is applied to the gra-

dient magnitude (eq.22) to remove false edges (e.g.

small letters on a wall).

(p) =

(

∑

q∈N(p)

−

−I

|∇I

(p)|



Z =

∑

q∈N(p)

−

−I

)

(21)

(

∑

q∈N(p)

−

−I

|∇

(p)|



Z =

∑

q∈N(p)

−

−I

)

(22)

where I is the color image, |∇

(q)| = |∇

(q)| +

|∇

(q)|, and ∇

(q) and ∇

(q) are obtained us-

ing the Sobel gradient operator.

To handle noise in the image.

3D Plane Labeling Stereo Matching with Content Aware Adaptive Windows

165

(a) (b) (c)

Figure 3: Raw result of Teddy image (τ

grad

= 5/255, τ

cen

= 5/25, random initialization, and no multi-scale). (a) Groundtruth

Teddy image; (b) Uniqueness term is disabled; (c) Uniqueness term is enabled.

4 HYPOTHESIS GENERATION

AND PROPAGATION

The model described so far makes the assumption that

each pixel has associated a set of planes from which

a single optimal plane assignment (D) is found us-

ing T RW -S. The proposed hypothesis generation al-

gorithm will give each pixel p a set GH

= D

∪H

∪

∪ V

. D

is the current solution, H

is gener-

ated from pixel coordinates using (r-sampling), DS

is generated from the pixels that belong to the same

segment

(P-sampling), V

is generated from pixels

coming from another view (V -sampling). Using these

disparity planes at each pixel allows the following:

1. Pixels can keep their current plane assignment D

2. Pixels propagate their planes to close and distant

pixels via r-sampling.

3. Segments help to propagate large disparity planes

to distant pixels via P-sampling.

4. Views propagate their planes via V -sampling.

Note that hypothesis generation is done from a

single disparity plane assignment D for both left and

right views, and the hypothesis generation is effec-

tively acting as a propagation scheduler once infer-

ence is done.

4.1 r-sampling

Algorithms that use plane propagation commonly as-

sume that neighboring pixels are likely to have the

same plane (Bleyer et al., 2011; Besse et al., 2012)

or that planes are shared within a certain area (Taniai

et al., 2014). The proposed r-sampling tries to gen-

erate hypotheses that are shared in a region (similar

to (Taniai et al., 2014)), but also include a few planes

from a distant region. The pixel coordinates used for

A segment will be a set of pixels that are grouped using

some logical criteria e.g. spatial distance and color similar-

ity.

sampling are (X,Y ) =



(divs ∗ b(x + i)/divsc + r + i,

divs∗b(y+ j)/divsc+r + j) | ( j,i) ∈ [−r,r]×[−r,r]



which come from a window of width 2r + 1. (x , y) are

the coordinates of pixel p, and divs = 2r + 1. The r-

sampled plane at pixel p sampled with (i, j) is given

by:

i j

= D

(23)

This sampling is repeated for each (i, j) ∈ [−r,r]×

[−r,r] generated by a window centered at p, which

means each pixel has a set of hypotheses:

[

i=−r

[

j=−r

i j

(24)

The purpose of this sampling strategy is to in-

clude the planes from all neighbors in the divs ×divs

window centered at p and also neighbors that come

from distant divs × divs windows. Fig.4 shows how a

3 × 3 window (i.e r = 1) would generate several hy-

potheses, where each colored box is a different plane.

For illustration purposes we will center our atten-

tion around the “red plane” and its eight neighbors.

...H

represent the hypothesis generated by using i

and j according to eq.24. In particular ﬁg.4 demon-

strates how each of the non-purple planes are trans-

formed into a hypothesis. Also note that the planes

from the purple pixels are used as well (although they

are not necessarily the same!). This is meant to allow

the propagation of distant neighbors. This hypothesis

generation strategy is similar to that of (Taniai et al.,

2014), but ours does not impose a sub-modular re-

quirement to the pairwise interaction in the generated

hypothesis.

4.2 P-sampling

One assumption commonly used in stereo matching

is that pixels with similar intensity have a similar

disparity value or disparity plane. An easy way to

group pixels is to use super-pixels or segments (e.g.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

166

(a) (b) (c)

Figure 4: Hypothesis generation: (a) Teddy image; (b) r-sampling; (c) Ds

= Dφ(p).

SLIC(Achanta et al., 2012) in this paper), which are

then initialized with a plane. The disparity plane Ds

is assigned to a segment s

by randomly selecting a

plane from the planes associated with the pixels that

belong to the segment:

= Dφ(p) (25)

denotes a plane at pixel p that was assigned

by function Dφ(p) which randomly selects a plane

such that it belongs to the same segment as pixel p.

This criteria will only generate one hypothesis per

pixel, although there may be other planes in the same

segment. This is done under the assumption that one

of planes selected may be correct without the need

of ﬁtting one plane to the entire segment. Although

each Ds

is assigned to several pixels (depending on

the super-pixel algorithm used), it may be desirable to

create additional hypotheses from the segments that

surround s

. To sample the neighboring segments the

centroid of each s

is computed, all neighboring s

centroid segments are sorted by their polar angle with

respect to s

, and ﬁnally only the ﬁrst P elements are

selected.

(

∪ (

[

i=1

)



Θ(s

) < ... < Θ(s

)

(26)

where s

∈ N(s

) and Θ(s

) is the function

that evaluates the polar angle with respect to the cen-

troid of s

4.3 V -sampling

The hypotheses H

and DS

so far are generated from

only one view. Since left and right sets of disparity

planes are computed it’s possible that one them con-

tains planes which could be used to generate a better

set of hypothesis. The additional set of hypotheses

is computed by mapping the planes H

∪ DS

from

the other view to the current image. This process will

be referred to as V -sampling and can be expressed by

= Dw

∪ Hw

∪ DSw

, where Dw

is the current

solution of the other view, Hw

and DSw

are the

mapped versions of r-sampling and P-sampling hy-

potheses from the other view. Note that this doubles

the number of hypotheses. For instance: assume two

views are used, then for r = 2 and P = 6 the number

of hypotheses generated would be 32 for one view,

but after doing V -sampling the number of hypotheses

would be 64. Note that (Bleyer et al., 2011) follows

a similar approach (i.e. mapping the planes from one

view to the other), but only generates one hypothesis.

5 REFINEMENT

Using the algorithms from the previous section, hy-

potheses are generated and a unique disparity plane

is assigned to each pixel (i.e D

). The solution is

then reﬁned by generating a new set of hypothe-

ses Gre f

= D

∪ Hre f

∪ DSre f

with perturba-

tions(Bleyer et al., 2011) added to the plane param-

eters (normal vector ˆn

and disparity d

), and the do-

ing inference once again. The hypothesis reﬁnement

process is:

1. Given the current disparity map D

curr

, ∆n

= κ,

∆d

= Sr ×κ as input.

2. For t = 1 to s steps do:

(a) compute pixel hypothesis re-sampling (Hre f

see sec.5.1.

(b) compute segment hypothesis re-sampling

(DSre f

), see sec.5.2.

= D

∪Hre f

∪DSre f

and ob-

tain a new solution

curr

(d) set D

curr

, ∆n

= ∆n

t−1

/2 and ∆d

∆d

t−1

/2.

This means that for each pixel in the disparity map

three situations can happen: a plane is propagated

from a neighbor, a plane is reﬁned and propagated

3D Plane Labeling Stereo Matching with Content Aware Adaptive Windows

167

from a neighbor, or a plane stays the same. Prop-

agation is done simultaneously during the hypothesis

reﬁnement process, which happens due to the way hy-

potheses are generated. Also note that V-sampling is

not used. To the best of our knowledge no other al-

gorithm performs simultaneous propagation and re-

ﬁnement, which could have the potential to reduce

the space needed to store hypotheses. The reﬁnement

process doubles the number of hypotheses. For in-

stance: if r-sampling (r = 2) and P-sampling(P = 6)

generate 32 hypotheses, then reﬁnement would add

32 additional hypotheses (with perturbations added).

5.1 Pixel Hypothesis Re-sampling

To overcome local minima of the current dispar-

ity plane assignment, and obtain a reﬁned version

of r-sampling, each pixel is updated by randomly

adding a perturbation selected from [−∆n

,∆n

] (uni-

form distribution) and [−∆d

,∆d

] (uniform distribu-

tion) which are initially set to ∆n

= κ (the new nor-

mal vector has to be normalized) and ∆d

= Sr × κ,

(Sr search range in disparity units), with κ = 0.2 as

recommended in (Besse et al., 2012). This process

is repeated several times. After each step ∆n

and

∆d

are updated by setting them to ∆n

= ∆n

t−1

and ∆d

= ∆d

t−1

/2. This process generates a new set

of hypotheses Hre f

= H

∪ Hn

where Hn

is gen-

erated using r-sampling from D

after perturbations

have been added.

5.2 Segment Hypothesis Re-sampling

Reﬁned versions of the disparity planes image seg-

ment are obtained by creating variants of the current

set of disparity planes per image segment. First, for

each segment in the current image random disparity

planes (DSr

) are generated using P-sampling and

then noise is added. This generates a new set of hy-

potheses DSu

= Ψ(DSr

∪ DSrn

), where DSr

was

generated via P-sampling, DSrn

is the perturbed ver-

sion of DSr

, and Ψ is a function that takes each

pair of planes DSr

and DSrn

and returns the one

whose cost locally minimizes eq.1, with respect to

the current solution. This leaves P plane hypotheses

per segment. Another set of hypotheses DSU

is then

generated, in which each segment SU

has a number

from [1...n]. These numbers are used as multipliers

to control the random interval [−∆d

,∆d

], such that

∆

= i ×∆d

. Thus each element of DSU

is the ∆

perturbed version of a plane generated by Dφ(p) to al-

low large jumps of disparity that can change an entire

segment. This re-sampling produces a set of hypothe-

ses DSre f

= DSu

∪ DSU

6 OVERALL DISPARITY

ESTIMATION PROCESS

The disparity estimation process can now be summa-

rized as follows:

1. Initialize solution Dle f t and Dright to either a

random plane per pixel or initialize from a pre-

computed disparity map.

2. For t = 1 to s steps do:

(a) Generate hypotheses GHle ft

and GHright

see sec.4.

(b) Do inference and compute new solutions

Dle f t

and

Dright.

Dle f t and

Dright, see

sec.5.

(d) set Dle f t =

Dle f t and Dright =

Dright.

Random initialization is done by selecting a ran-

dom uniform disparity. The normal ˆn is selected from

the uniform distribution of a unit sphere. ∆d and ∆ ˆn

are selected in the same way. Fig.5 shows interme-

diate stages for the teddy image, using the proposed

algorithm with random initialization. It can be ob-

served that our approach is effectively propagating the

planes and also minimizing eq.1. Notice that in the

ﬁrst propagation the outline of the underlying 3D sur-

face can already be seen. When using a pre-computed

disparity map

to initialize the current solution, the

normal vectors are computed at ﬁve scales, averag-

ing, and creating a plane per pixel by estimating the

parameters of eq.2 using the normal vectors and cur-

rent disparity.

Finally, the proposed algorithm is extended to

multi-scale:

1. Precompute disparity maps Dle f t

pre

and

Dright

pre

(e.g. using SGM or random ini-

tialization).

2. Estimate window size from Dle f t

pre

and

Dright

pre

(if disparity map was precomputed).

3. Compute initial solution Dle f t and Dright by

downscaling Dle ft

pre

and Dright

pre

to one quar-

ter size and solving.

4. Compute updated solution at half-size by initial-

izing with current Dle f t and Dright.

5. Compute updated solution at full-size by combin-

ing Dle f t

pre

and Dright

pre

with current Dle f t and

Dright. i.e compute GH pre

∪ GH

for left and

right, then do inference to update current solu-

tions, and update maxD (sec.3.3).

6. Compute updated solution at full-size by initializ-

ing with current Dle f t and Dright.

The pre-computed disparity map is obtained using

SGM, see support material.

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

168

(a) (b) (c) (d)

Figure 5: Proposed algorithm with random initialization (τ

grad

= 5/255, τ

cen

= 5/25, and no multi-scale), intermediate and

ﬁnal results: (a) Initial random conﬁguration; (b) First propagation, E = 123,257.02; (c) First Reﬁnement, E = 87,134.61;

(d) Final Result, E = 82,334.98.

7. Compute occlusion detection and post-

processing.

The post-processing is done by computing oc-

cluded, and mismatched areas as in (

Zbontar and Le-

Cun, 2015). Then masks containing non-occluded

areas, and depth edges

are eroded and marked as

occluded to reduce the fattening effect. Then minD

is updated (sec.3.3), and disparities lower than minD

are marked as occluded. The occluded areas are then

ﬁlled in using simple background interpolation and

ﬁltered by applying a weighted median ﬁlter. The

non-occluded areas are NOT post-processed.

All experimental results were carried out using

the multi-scale approach with pre-computed initial-

ization. The proposed algorithm uses the following

parameters for all scales: aggregation window sizes

of ω

= 41 × 41, ω

= 25 × 25, τ

grad

= 3/255, τ

cen

9/25, σ

= 10/255, σ

= 0.5, τ

= 2.5, τ

di f f

= 0.07,

α = 30, K

= 1, K

= 6, r = 2, P = 6, τ

= 2, τ

= 0.5,

= 8, τ

unique

= 0.01. For quarter and half size

λ = 0.06, and λ = 0.12 for full size. The disparity

estimation is iterated 4 times at quarter size, 1 time

at half-size and 4 times at full size. The reﬁnement

iterations are set to 5 times each scale. These param-

eters were obtained by using the Middlebury train-

ing data, and every ﬁfth image from KITTI 2015 and

2012 training data.

7 PROPOSED APPROACH VS.

STATE OF THE ART

The approach presented in this paper was validated

in three stages. First, the proposed content aware

adaptive windows are compared to the traditional ap-

proach, as well as the tolerance to noise and evalua-

tion of r−sampling performance. Then the proposed

algorithm is extensively validated on three data sets:

detected using Canny edge detector.

The new Middlebury (15 images) data set (Scharstein

et al., 2014), KITTI 2015(Menze and Geiger, 2015)

and 2012(Geiger et al., 2012) (up to 200 images).

The only parameters that are set differently are ∆minD

(10 for Middlebury and 5 for KITTI), ∆maxD (60 for

Middlebury and 20 for KITTI) and τ

maxD

(0.0028 for

Middlebury and 0.0003 for KITTI).

Table 1: Comparative table of the proposed content aware

function vs adaptive windows. Evaluation done with the

Middlebury training data set at half size in non occluded

areas before post-processing.

Function %bad noc avg. error rms

AW 13.62 2.00 7.62

AW +CW 13.58 1.98 7.67

AW +CW +U 12.95 1.82 7.28

To test the performance of the proposed similar-

ity function three competing functions are compared

(tab.1): AW is the traditional approach (eq.4) with

the enabled out of range term , but no uniqueness

term. AW + CW is the proposed adaptive window

(eq.7) with the enabled out of range term, but no

uniqueness term. AW +CW +U is the proposed adap-

tive window with the out of range and local unique-

ness terms (eq.17). Our innovations (eq.17) clearly

improve on the popular adaptive windows(Yoon and

Kweon, 2006) commonly used in DPI algorithms.

Table 2: Evaluation of r-sampling and proposed approach

(all stages enabled) tolerance to noise in initial disparity

map, using every ﬁfth image from KITTI 2015 training

data. ns0 no noise, and added disparity noise [−1, 1] (ns1),

[−2,2] (ns2), [−3, 3] (ns3).

Algorithm

%bad

D1-bg

%bad

D1-fg

%bad

D1-all

ns0

2.96 9.26 3.86

LSL

2.90 9.55 3.86

ns1

2.94 9.49 3.89

ns2

2.96 9.39 3.88

ns3

2.94 9.85 3.94

3D Plane Labeling Stereo Matching with Content Aware Adaptive Windows

169

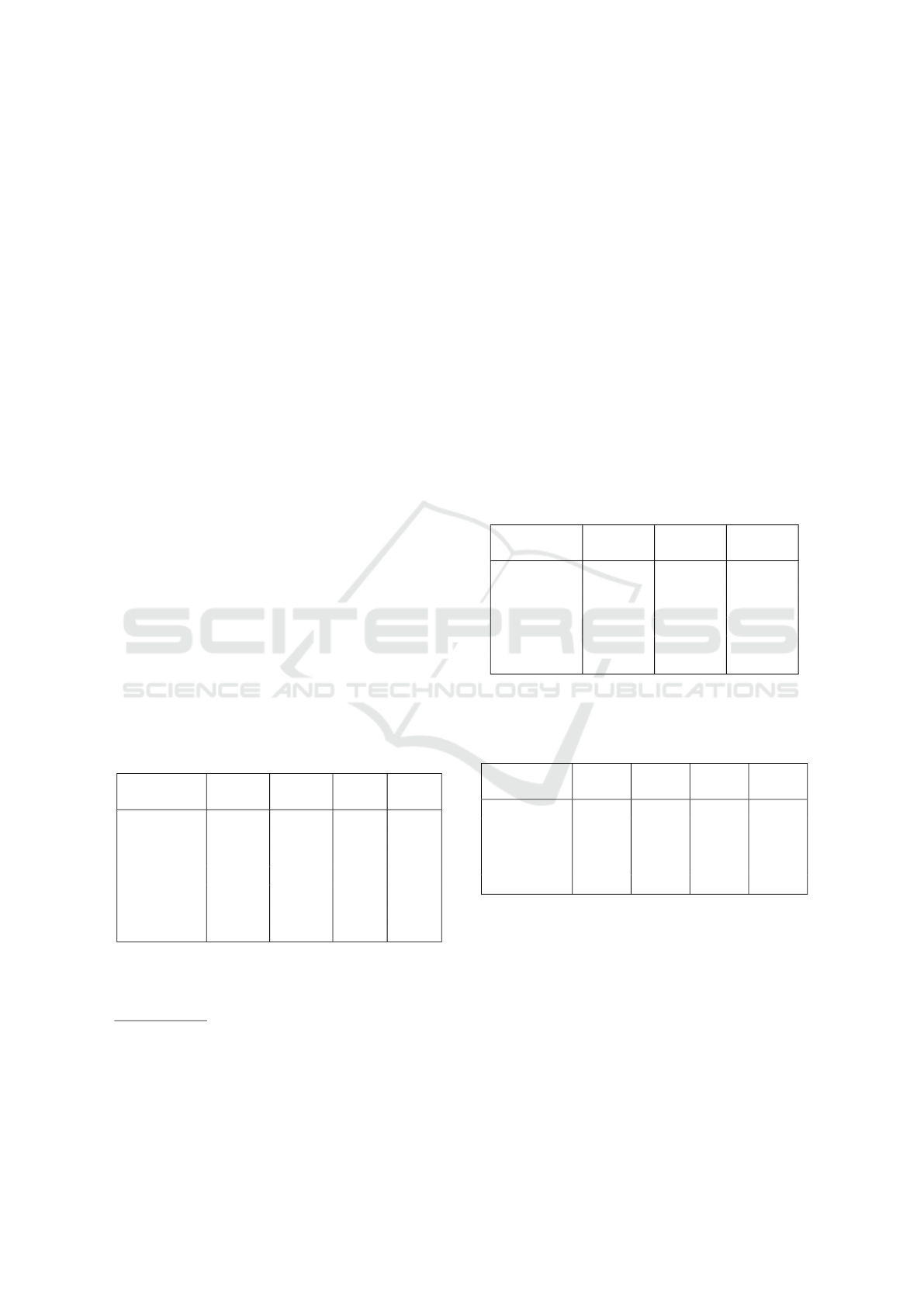
To evaluate the effectiveness of r-sampling we re-

place it with the pixel shared hypotheses LSL from

(Taniai et al., 2014). In tab.2 our sampling strategy

(ns0) in general matches the performance of LSL, and

even gives improved performance for foreground ob-

jects D1 − f g, which is caused by the larger number

of hypotheses 25 for r-sampling vs. 16 for L SL due

to different hypothesis generation strategies. The per-

formance of our approach in tab.2 shows that the pro-

posed approach ns0 is robust to several levels of uni-

form real valued noise added to the initial disparity

map.

The main competitors to our algorithm are

MCNCC(

Zbontar and LeCun, 2015) and MDP(Li

et al., 2016a), since they were evaluated using the

same data sets (see tab.3 and tab.4). To compare to the

state of the art, from all data sets competitors were se-

lected by choosing the best performing convolutional

neural network algorithms and the best performing al-

gorithm not using convolutional neural networks. For

the KITTI 2015 and 2012 results, algorithms must ap-

pear in both data sets evaluation tables. The proposed

algorithm is among top performers in the Middle-

bury (tab.3) and KITTI 2015/2012 (tab.4 and tab.5).

In tab.3 the disparity map is evaluated only in non-

occluded areas, integer and sub-pixel scores are com-

puted using an error pixel threshold of 2.0 (rank 9

out of 44) and 0.5 (rank 8

out of 44) respectively.

Table 3: Comparative table of results (on non-occluded pix-

els) on the new Middlebury data set. Only non-anonymous

entries are used for comparison: PMSC(Li et al., 2016b),

Mesh and MeshE(Zhang et al., 2015), APAP(Park and

Yoon, 2016), MCNCC(

Zbontar and LeCun, 2015), MDP(Li

et al., 2016a).

Algorithm

%bad >

2.0

%bad >

0.5

avg.

error

rms

Our

10.50

9th

43.2

8th

3.17 15.6

PMSC

6.87

1st

39.1

1st

2.27 12.9

MeshE

7.29

2nd

40.1

2nd

2.50 15.4

APAP

7.46

3rd

50.9

12th

3.89 21.1

MCNCC

8.29

5th

40.7

4th

3.82 21.3

MDP

12.6

10th

61.8

27th

5.28 23.1

Mesh

13.4

11th

51.2

13th

4.63 20.1

In the KITTI benchmark, our algorithm ranks 8

(out of 38), and 14

(out of 83) for KITTI 2015 and

Submitted to both KITTI and Middlebury benchmarks

as LPU.

Unpublished work at the time of submission.

Mesh(Zhang et al., 2015) using the cost from (

Zbontar

and LeCun, 2015), but not published.

Unpublished work at the time of submission.

2012 respectively. The evaluation on KITTI 2012

proved more challenging (tab.5) mostly in the pres-

ence of reﬂective regions, and color image misalign-

ment (the gray images are colored, and not properly

aligned to the ground truth shape image). The top per-

forming algorithms (for KITTI 2015 and 2012) cur-

rently achieve high performance by: exploiting scene

speciﬁc content to solve ambiguities (e.g. cars in

Disp.v2), training speciﬁcally for the data set (e.g.

MCNCC), or using multiple image pairs to estimate

disparity (e.g. PRSM, OSF). By contrast the proposed

algorithm achieves top performing results in multiple

data set by: using only one image pair, solving at dif-

ferent scales, not using scene speciﬁc features (e.g.

cars), and generating a set of hypothesis from a single

initial hypothesis.

Table 4: Comparative table of results (all pixels evaluated)

on the KITTI 2015 data set. Only non-anonymous entries

are used for comparison: Disp.v2(Guney and Geiger, 2015),

PRSM(Vogel et al., 2015), OSF(Menze and Geiger, 2015).

Algorithm

%bad

D1-bg

%bad

D1-fg

%bad

D1-all

Our

8th

3.55 12.30 5.01

Disp.v2

1st

3.00 5.56 3.43

MCNCC

3rd

2.89 8.88 3.89

PRSM

5th

3.02 10.52 4.27

MDP

12th

4.19 11.25 5.36

OSF

15th

4.54 12.03 5.79

Table 5: Comparative table of results (all pixels evaluated)

on the KITTI 2012(Geiger et al., 2012) data set. Only non-

anonymous entries are used for comparison.

Algorithm

%bad

noc

%bad

occ

avg.

noc

avg.

occ

Our

14th

3.22 4.27 0.80 1.00

Disp. v2

2nd

2.37 3.09 0.70 0.80

MCNCC

4th

2.43 3.63 0.70 0.90

PRSM

8th

2.78 3.00 0.70 0.70

OSF

15th

3.28 4.07 0.80 0.90

8 CONCLUSIONS

The proposed algorithm delivers top performing re-

sults even though only one global hypothesis is used

(eliminating the need to update multiple hypotheses),

and no convolutional neural network (e.g. (Zhang

et al., 2015;

Zbontar and LeCun, 2015; Guney and

Geiger, 2015)) or prior 3D models (e.g. cars) are used.

The use of r-sampling and P-sampling are novel, sim-

ple and effective ways of simulating a propagation

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

170

scheduler, which can be executed in parallel, unlike

those from (Bleyer et al., 2011; Besse et al., 2012;

Zhang et al., 2015). The proposed similarity function

is also capable of reducing some of the loss of detail

and error caused by the popular adaptive window ap-

proach.

ACKNOWLEDGEMENTS

This research was done with the support of the Mex-

ican CONACYT programme and the European Com-

mission.

REFERENCES

Achanta, R., Shaji, A., Smith, K., Lucchi, A., Fua, P.,

and S

usstrunk, S. (2012). Slic superpixels com-

pared to state-of-the-art superpixel methods. PAMI,

34(11):2274–2282.

Besse, F., Rother, C., Fitzgibbon, A., and Kautz, J. (2012).

Pmbp: Patchmatch belief propagation for correspon-

dence ﬁeld estimation. International Journal of Com-

puter Vision, 110(1):2–13.

Bleyer, M., Rhemann, C., and Rother, C. (2011). Patch-

match stereo - stereo matching with slanted support

windows. In Proceedings of the British Machine Vi-

sion Conference, 11:1–11.

Geiger, A., Lenz, P., and R.Urtasun (2012). Are we ready

for autonomous driving? the kitti vision benchmark

suite. CVPR, pages 3354–336.

Guney, F. and Geiger, A. (2015). Displets: Resolving stereo

ambiguities using object knowledge. CVPR.

Heise, P., Klose, S., Jensen, B., and Knoll, A. (2013). Patch-

match with huber regularization for stereo matching.

ICCV, pages 2360–2367.

Klaus, A., Sormann, M., and Karner, K. (2006). Segment-

based stereo matching using belief propagation and a

self-adapting dissimilarity measure. ICPR, 3:15–18.

Kolmogorov, V. (2007). Convergent tree-reweighted mes-

sage passing for energy minimization. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

28(10):1568–1583.

Kolmogorov, V. and Zabih, R. (2001). Computing vi-

sual correspondence with occlusions using graph cuts.

ICCV, 2:508–515.

Li, A., Chen, D., Liu, Y., and Yuan, Z. (2016a). Coordi-

nating multiple disparity proposals for stereo compu-

tation. CVPR.

Li, L., Zhang, S., Yu, X., and Zhang, L. (2016b). Pmsc:

Patchmatch-based superpixel cut for accurate stereo

matching. IEEE Transactions on Circuits and Systems

for Video Technology.

Li, Y., Min, D., Brown, M. S., Do, M. N., and Lu, J. (2015).

Sped-up patchmatch belief propagation. ICCV.

Menze, M. and Geiger, A. (2015). Object scene ﬂow for

autonomous vehicles. CVPR.

Olsson, C., Ul

en, J., and Boykov, Y. (2013). In defense of

3d-label stereo. CVPR, pages 1730–1737.

Park, M.-G. and Yoon, K.-J. (2016). As-planar-as-possible

depth map estimation. Submitted to IEEE TPAMI.

Scharstein, D., Hirschm

uller, H., Kitajima, Y., Krathwohl,

G., Nesic, N., Wang, X., and Westling, P. (2014).

High-resolution stereo datasets with subpixel-accurate

ground truth. In German Conference on Pattern

Recognition (GCPR), pages 31–42.

Sinha, S., Scharstein, D., and Szeliski, R. (2014). Ef-

ﬁcient high-resolution stereo matching using local

plane sweeps. CVPR, pages 1582–1589.

Taniai, T., Matsushita, Y., and Naemura, T. (2014). Graph

cut based continuous stereo matching using locally

shared labels. CVPR, pages 1613–1620.

Vedaldi, A. and Fulkerson, B. (2008). VLFeat: An open

and portable library of computer vision algorithms.

http://www.vlfeat.org/.

Vedaldi, A. and Soatto, S. (2008). Quick shift and kernel

methods for mode seeking. ECCV, 5305:705–718.

Vogel, C., Schindler, K., Konrad, and Roth, S. (2015). 3d

scene ﬂow estimation with a piecewise rigid scene

model. IJCV, pages 1–28.

Zbontar, J. and LeCun, Y. (2015). Stereo matching by train-

ing a convolutional neural network to compare image

patches. Submitted to JMLR.

Woodford, O. J., Reid, I. D., Torr, P. H. S., and Fitzgibbon,

A. W. (2007). On new view synthesis using multiview

stereo. In Proceedings of the British Machine Vision

Conference, pages 1–10.

Yamaguchi, K., McAllester, D., and Urtasun, R. (2014). Ef-

ﬁcient joint segmentation, occlusion labeling, stereo

and ﬂow estimation. ECCV, pages 756–771.

Yoon, K. and Kweon, I. (2006). Adaptive support-weight

approach for correspondence search. IEEE Transac-

tions on Pattern Analysis and Machine Intelligence,

28(4):650–656.

Zabih, R. and Li, J. (1994). Non-parametric local trans-

forms for computing visual correspondence. ECCV,

12:151–158.

Zhang, C., Li, Z., Cheng, Y., Cai, R., Chao, H., and Rui,

Y. (2015). Meshstereo: A global stereo model with

mesh alignment regularization for view interpolation.

ICCV.

Zhang, K., Lu, J., and Lafruit, G. (2009). Cross-based lo-

cal stereo matching using orthogonal integral images.

IEEE Transactions on Circuits and Systems for Video

Technology, 19(7):1073–1079.

3D Plane Labeling Stereo Matching with Content Aware Adaptive Windows

171