
Parallelized Flight Path Prediction using a Graphics Processing Unit
Maximilian G
¨
otzinger
1
, Martin Pongratz
2
, Amir M. Rahmani
2,3
and Axel Jantsch
2
1
Department of Information Technology, University of Turku, Turku, Finland
2
Institute of Computer Technology, TU Wien, Vienna, Austria
3
Department of Computer Science, University of California, Irvine, U.S.A.
Keywords:
CUDA, GPU, Canny, RANSAC, Image Processing, Parallel Algorithm, Flight Path Prediction, Based on
Memorized Trajectories.
Abstract:
Summarized under the term Transport-by-Throwing, robotic arms throwing objects to each other are a vision-
ary system intended to complement the conventional, static conveyor belt. Despite much research and many
novel approaches, no fully satisfactory solution to catch a ball with a robotic arm has been developed so far. A
new approach based on memorized trajectories is currently being researched. This paper presents an algorithm
for real-time image processing and flight prediction. Object detection and flight path prediction can be done
fast enough for visual input data with a frame rate of 130 FPS (frames per second). Our experiments show
that the average execution time for all necessary calculations on an NVidia GTX 560 TI platform is less than
7.7ms. The maximum times of up to 11.7ms require a small buffer for frame rates over 85 FPS. The results
demonstrate that the use of a GPU (Graphics Processing Unit) considerably accelerates the entire procedure
and can lead to execution rates of 3.5× to 7.2× faster than on a CPU. Prediction, which was the main focus of
this research, is accelerated by a factor of 9.5 by executing the devised parallel algorithm on a GPU. Based on
these results, further research could be carried out to examine the prediction system’s reliability and limitations
(compare (Pongratz, 2016)).
1 INTRODUCTION
Customer needs and requirements are becoming in-
creasingly personalized in almost all product fields.
Manufacturers have to produce a large number of
products that are similar, but not completely identical.
As not every personalized product has to pass through
the same production stages, the currently used static
conveyor belt no longer matches the application pro-
file; more flexible types of product lines are needed.
Transport-by-Throwing (Pongratz et al., 2012) de-
scribes an alternative solution whereby robot arms
pass on their payload: one throws it, and another
one catches it. Just as with communication networks
with hop-by-hop routing, passing is repeated until the
transport good reaches its final destination in the pro-
duction process. Despite many novel approaches, a
fully satisfactory solution to catch an object has not
yet been developed. In the last 25 years, many other
studies (B
¨
auml et al., 2011; Hong et al., 1995) have
been concerned with the topic of catching a thrown
ball, but the best results achieved a success rate of
about 80% or less. All of these studies has one fact
in common; the predictions are based on a model of
the involved physical laws. Pongratz et al. propose
a strategy based on memorized trajectories (Pongratz
et al., 2010; Pongratz, 2016).
The hypothesis is that humans learn object-
catching based on experience, for example, the way
a child learns to catch a ball. It does not contem-
plate about physics when trying to catch. A child only
learns from its experiences: after numerous failed at-
tempts, it is able to catch an object in the right way
based on memorized previous experience. By anal-
ogy, in the approach proposed by Pongratz et al. the
ball’s flight is captured and compared with a set of
stored reference (Figure 1) throws to enable predic-
tion of the trajectory and the location where the ob-
ject can be caught (Pongratz et al., 2012). Although
the execution time of the prediction is as important
as its accuracy, its real-time constraints have not been
examined until now (Pongratz et al., 2010). If the esti-
mation algorithm takes up too much of the processor’s
capacity, the computation time will interfere with the
camera’s sample rates (Hong et al., 1995). Image pro-
cessing, as well as the comparison of the determined
386
GÃ˝utzinger M., Pongratz M., Rahmani A. and Jantsch A.
Parallelized Flight Path Prediction using a Graphics Processing Unit.
DOI: 10.5220/0006105903860393
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 386-393
ISBN: 978-989-758-227-1
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

pos
1
pos
2
pos
3
pos
4
pos
5
traj
1
traj
2
traj
3
traj
4
traj
5
traj
6
traj
7
traj
8
pos
1
pos
2
pos
3
pos
4
pos
5
pos
6
pos
7
pos
8
...
pos
1
pos
2
pos
3
pos
4
pos
5
pos
6
pos
7
pos
8
...
pos
1
pos
2
pos
3
pos
4
pos
5
pos
6
pos
7
pos
8
...
pos
1
pos
2
pos
3
pos
4
pos
5
pos
6
pos
7
pos
8
...
pos
1
pos
2
pos
3
pos
4
pos
5
pos
6
pos
7
pos
8
...
pos
1
pos
2
pos
3
pos
4
pos
5
pos
6
pos
7
pos
8
...
pos
1
pos
2
pos
3
pos
4
pos
5
pos
6
pos
7
pos
8
...
pos
1
pos
2
pos
3
pos
4
pos
5
pos
6
pos
7
pos
8
...
pos
14
pos
13
pos
12
pos
11
pos
10
pos
9
pos
8
pos
7
pos
6
Figure 1: The Transport-by-Throwing approach deals with a robot arm that catches thrown objects with the help of a prediction
based on stored trajectories.
data with all the numerous database entries, require a
huge number of calculation steps. Managing the mas-
sive amount of computation in a short period leads
to the necessity of employing high-performance hard-
ware/accelerators. An FPGA (Field Programmable
Gate Array) based implementation can accelerate the
procedure (Pongratz, 2009), but this would result in
higher development costs. A GPU (Graphics Pro-
cessing Unit) can speed up the software wholly or
partially by parallelizing the operations (Fung et al.,
2005).
In this paper, we deal with such real-time con-
straints and deploy GPUs for performing both object
detection as well as flight path prediction. The here
stated results shall enable examination of the system’s
accuracy in future works.
The rest of the paper is organized as follows. The
concepts and the setup are described in Section 2.
Section 3 shows our implementation of the RANSAC
algorithm and the flight path prediction. In Section 4,
we present and discuss the results from our experi-
ments. Finally, Section 5 concludes the paper.
2 SETUP AND CONCEPT
The ability to catch a thrown object requires knowl-
edge about the trajectory and other attributes of the
motion of the object (Barteit et al., 2009), which we
gather with cameras. The thrown object is a tennis
ball with a velocity from 4.6
m
s
to 5.4
m
s
. The light sys-
tem consists of multiple floodlights and results in a
sufficient illumination of the whole scene. Changing
light intensity is compensated by a light profile for
the algorithm which influences the thresholds of the
detection algorithms. The distance of the ball to each
camera is in the range of 0.6m to 3.2m. Figures 2
and 3 show the experimental setup that is briefly ex-
plained here in this section.
Figure 2: The Throwing-and-Catching test environment
consists in a robot arm, multiple LED floodlights, two par-
allel aligned cameras, and a throwing device that accelerates
a tennis ball to overcome the distance of about 2.5m.
2.1 Capturing the Scene
Obtaining a 3D view of a scene using only one cam-
era potentially results in low-level accuracy and ro-
bustness (B
¨
auml et al., 2011). Therefore, we opted
to use two cameras (IDS uEye UI-3370CP) working
synchronously and manually aligned in parallel with
a baseline distance of approximately 0.92m. These
two cameras support a resolution of 2048-by-2048
pixels at a frame rate of 75FPS (frames per second)
and 2048-by-800 pixels at 110FPS. To predict the
flight path in time while still having the advantages of
this high resolution, a cropping system based on Bi-
nary Large Objects (BLOBs) detection was used that
provides output images with only 300-by-300 pixels
where the ball is roughly in the center.
The following hardware was used for image pro-
cessing and flight path prediction: a computer with
an i7-4770S CPU clocked at 3.10GHz, 8GB main
memory clocked at 667MHz and an NVidia GeForce
GTX 560 Ti graphics card (NVidia, 2015) with 384
cores (with compute capability 2.1). This GPU fam-
Parallelized Flight Path Prediction using a Graphics Processing Unit
387

Figure 3: This coil-based throwing device accelerates a ten-
nis ball to overcome the distance of about 2.5m.
ily was used as it is a rather standard representative
of GPUs in general. Other - more up to date - GPUs
would change the specific figures but not the general
trend and conclusion. Besides, Intel claims that its
integrated GPUs are starting to get equal with dis-
crete graphics cards
1
. To have also some results for
Catching-and-Throwing devices based on embedded
system, we chose this - weak - graphics processor.
2.2 Detecting the Flying Object
After a coil-based throwing device (Figure 3) ac-
celerated the tennis ball, it appears on both camera
images. Various methods for detecting circles ex-
ist (D’Orazio et al., 2002) but two of them are well-
known, distinguished by their accuracy, and often
used for object detection: the Hough Transformation
and the RANSAC algorithm. Both procedures per-
form efficiently when images are not noisy, but the
Hough Transformation was highlighted as being more
accurate when detecting objects in the presence of
noise (Jacobs et al., 2013). On the other hand, the
duration of this algorithm depends on the number of
pixels in the edge image (Wu et al., 2012). One cir-
cle is drawn in the Hough Space for each possible
radius around each edge pixel. Therefore, the more
pixels present, the more time is needed. In compar-
ison, the time required by the RANSAC algorithm
only depends on the number of iterations. The algo-
rithm chooses randomly three points to span a pos-
sible circle. In other words, only one circle is drawn
per iteration; not for every possible radius as it was for
the Hough Transformation. Since the number of iter-
ations needed is much less than the number of edge
pixel multiplied by possible radii, the RANSAC algo-
rithm performs typically faster.
Both algorithms require an edge image for detect-
ing objects in an accurate way. We use the Canny
1
http://www.extremetech.com/extreme/221322-intel-
claims-its-integrated-gpus-now-equal-to-discrete-cards
Edge Detector algorithm since it achieves good re-
sults and is commonly used (Luo et al., 2008). Its
implementation is carried out in four steps: Gaus-
sian filtering, Sobel filtering, non-maximum suppres-
sion, and hysteresis thresholding (Ogawa et al., 2010).
The first three procedures are linearly separated in x-
and y-direction so that they run efficiently on parallel
hardware (Luo et al., 2008). In contrast to these steps,
the hysteresis thresholding is an iterative algorithm.
Therefore, this step is not parallelizable and limits the
performance of edge detection.
To improve the quality of the edge images, the im-
ages’ backgrounds can be subtracted as an additional
step. Changing lighting conditions may lead to a non-
perfect background subtraction, but the edge images
and consequently the detection is still more accurate.
2.3 Flight Path Prediction
After the ball’s center point has been detected in both
images, the triangulation step converts these two po-
sitions to one 3D position. Due to the imperfect align-
ment of the stereo vision system, the distortion of the
cameras, and other effects, the vision system has been
calibrated with the help of a Matlab toolbox
2
. The
result of the calibration process are the intrinsic pa-
rameters of the individual cameras (e.g., focal length,
distortion coefficients) and the extrinsic parameters of
the stereo system (baseline and orientation).
Since every pair of frames offer a new position
of the thrown ball, its movement in space and time is
known. From that moment, we can start the prediction
of the ball’s further flight path. Figure 4 shows two
different approaches for estimating a flight path based
on this technique: either comparing the ball’s posi-
tions with their counterparts in the database directly
or comparing the rates of change from one position to
the next. Because of the high similarity of both ver-
sions, we introduce only the former. To find the most
similar trajectory, the Euclidean distances between
each position of the actual flight and its counterpart
in the database are calculated. Afterwards all these
distances are added up to a total distance, which gives
information on how well the actual flight matches a
database trajectory. The database trajectory that leads
to the smallest sum of distances is the most simi-
lar trajectory and is, therefore, selected to predict the
flight path of the thrown tennis ball. One challenge of
this algorithm lies in the enormous number of possi-
bilities to fit the actual flight in a reference trajectory.
Four examples of possible flight paths compared with
one and the same trajectory of the database are shown
2
Available at: http://www.vision.caltech.edu/bouguetj/
calib doc/
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
388

Figure 4: The two prediction approaches: comparing di-
rectly the balls positions, or comparing its rates of change
from one position to the next.
in Figure 5. While the first example represents a fairly
good match, the second example shows a lack of con-
gruence between the two flight paths. However, the
reason might be that the actual flight’s positions are
not present in the database trajectory which still fits
best (examples 3 and 4 of Figure 5).
2.4 Software Development Environment
Two options for programming a GPU exist: CUDA
(Compute Unified Device Architecture) (NVidia,
2014), which was developed by NVidia in 2006 and
OpenCL (Open Computer Language) by the Khronos
Group (Khronos, 2015). We selected CUDA as de-
velopment environment because of its better perfor-
mance (Karimi et al., 2010), and a more comprehen-
sive documentation.
3 IMPLEMENTING
PARALLELIZED FLIGHT PATH
PREDICTION
Based on the edge image object detection is per-
formed. Because the background subtraction is sim-
ple to implement and parallelized algorithms for the
Canny Edge Detector (Luo et al., 2008), the Hough
Circle Transformation (Askari et al., 2013; Chen
et al., 2011), and the RANSAC algorithm (Wang
et al., 2011) have been reported before, we do not de-
scribe their implementation in detail. Instead, we fo-
cus on the flight path prediction. We show the perfor-
mance differences of all algorithms in Section 4; also
the comparison of the straight-forward and inverse-
checking version of the Hough Circle Transforma-
tion (Askari et al., 2013; Chen et al., 2011).
To enable database access as fast as possible, an
initializing function loads all reference trajectories
and stores the data in the GPU’s memory in a 3D array
as a first step (similar to (Gowanlock et al., 2015)).
These three dimensions are needed for the different
trajectories, the trajectories’ various positions, and the
positions’ various coordinates. The size of the GPU’s
memory limits the number of reference throws, but
as has been shown (Pongratz, 2016), small databases
also lead to acceptable catching results.
example 1 example 2
example 3 example 4
positions of the actual flightpaths
positions of a database trajectory
Figure 5: Four examples comparing actual flight paths with
the same database trajectory.
The challenge of the flight path prediction algo-
rithm lies in the enormous number of possibilities to
fit the actual flight in all reference trajectories. On the
one hand, many reference trajectories exist that have
to be compared with the actual flight, and on the con-
trary, many different possibilities exist on how to fit
the actual flight in a reference trajectory (Figure 5).
Next we describe our algorithm which makes use of
the parallel architecture of a GPU.
To examine every possibility, the actual flight’s
positions are shifted over the various trajectories of
the database. Additionally, the possibility must be
included that not all the actual positions are aligned
with their counterpart in the database trajectory. Fig-
ure 6 shows such a shift of one actual flight over one
database trajectory. However, since the focus is on
a parallelized algorithm, the term “shift” is not com-
pletely correct. Each database trajectory is examined
in a separate block, and each possible alignment of
the actual flight with a database trajectory is exam-
ined in a separate thread. Therefore, for each of the
database’s trajectories one block exists, and for each
possibility to fit the actual flight, a thread is needed
and created. Since all blocks have to have the same
number of threads, the number of required threads de-
pends on the longest database trajectory. Separating
the examinations of the various alignments in differ-
ent threads is equal to parallelizing the act of shifting
the actual flight over a database trajectory.
To speed up the whole procedure, all positions of
the actual flight and database trajectories are moved
from the global- to the shared memory before the dis-
tance calculation begins. This step accelerates the
procedure because accessing GPU’s global memory
consumes much more time than accessing its shared
memory (NVidia, 2014). However, it should be noted
that this extra step may lead to a demand for more
threads than alignments of the actual flight that are
possible in the database trajectories. This requirement
Parallelized Flight Path Prediction using a Graphics Processing Unit
389
<>
<>
<>
<>
P
db,
0
P
db,
1
P
db,
2
P
db,
3
P
db,
5
P
db,
6
P
db,
7
P
db,
8
P
db,
9
P
db,
4
P
af,
0
P
af,
1
P
af,
2
P
af,
3
P
af,
5
P
af,
4
<>
<>
<>
<>
<>
P
db,
0
P
db,
1
P
db,
2
P
db,
3
P
db,
5
P
db,
6
P
db,
7
P
db,
8
P
db,
9
P
db,
4
P
af,
0
P
af,
1
P
af,
2
P
af,
3
P
af,
5
P
af,
4
<>
<>
<>
<>
<>
<>
P
db,
0
P
db,
1
P
db,
2
P
db,
3
P
db,
5
P
db,
6
P
db,
7
P
db,
8
P
db,
9
P
db,
4
P
af,
0
P
af,
1
P
af,
2
P
af,
3
P
af,
5
P
af,
4
<>
<>
<>
<>
<>
<>
P
db,
0
P
db,
1
P
db,
2
P
db,
3
P
db,
5
P
db,
6
P
db,
7
P
db,
8
P
db,
9
P
db,
4
P
af,
0
P
af,
1
P
af,
2
P
af,
3
P
af,
5
P
af,
4
<>
<>
<>
<>
<>
P
db,
0
P
db,
1
P
db,
2
P
db,
3
P
db,
5
P
db,
6
P
db,
7
P
db,
8
P
db,
9
P
db,
4
P
af,
0
P
af,
1
P
af,
2
P
af,
3
P
af,
5
P
af,
4
<>
<>
<>
<>
P
db, 0
P
db, 1
P
db, 2
P
db, 3
P
db, 4
P
db, 5
P
db, 6
P
db, 7
P
db, 8
P
db, 9
P
db, 0
P
db, 1
P
db, 2
P
db, 3
P
db, 4
P
db, 5
P
db, 6
P
db, 7
P
db, 8
P
db, 9
P
db,
0
P
db,
1
P
db,
2
P
db,
3
P
db,
5
P
db,
6
P
db,
7
P
db,
8
P
db,
9
P
db,
4
P
db, 0
P
db, 1
P
db, 2
P
db, 3
P
db, 4
P
db, 5
P
db, 6
P
db, 7
P
db, 8
P
db, 9
P
db, 0
P
db, 1
P
db, 2
P
db, 3
P
db, 4
P
db, 5
P
db, 6
P
db, 7
P
db, 8
P
db, 9
P
db,
0
P
db,
1
P
db,
2
P
db,
3
P
db,
5
P
db,
6
P
db,
7
P
db,
8
P
db,
9
P
db,
4
P
db, 0
P
db, 1
P
db, 2
P
db, 3
P
db, 4
P
db, 5
P
db, 6
P
db, 7
P
db, 8
P
db, 9
P
db, 0
P
db, 1
P
db, 2
P
db, 3
P
db, 4
P
db, 5
P
db, 6
P
db, 7
P
db, 8
P
db, 9
P
af, 0
P
af, 1
P
af, 2
P
af, 3
P
af, 4
P
af, 5
P
af, 0
P
af, 1
P
af, 2
P
af, 3
P
af, 4
P
af, 5
P
af,
0
P
af,
1
P
af,
2
P
af,
3
P
af,
5
P
af,
4
P
af, 0
P
af, 1
P
af, 2
P
af, 3
P
af, 4
P
af, 5
P
af, 0
P
af, 1
P
af, 2
P
af, 3
P
af, 4
P
af, 5
P
af,
0
P
af,
1
P
af,
2
P
af,
3
P
af,
5
P
af,
4
P
af, 0
P
af, 1
P
af, 2
P
af, 3
P
af, 4
P
af, 5
P
af, 0
P
af, 1
P
af, 2
P
af, 3
P
af, 4
P
af, 5
Figure 6: An actual flight path is shifted over a database trajectory to find the place where the sum of all Euclidian distances
is the smallest. A predefined parameter decides how many of the actual flight positions (paf) are allowed to be outside of the
database trajectory.
is caused by the fact that all points of all trajectories
and the actual flight have to be moved to the shared
memory to guarantee correct calculations of all Eu-
clidean Distances. So, if there are trajectories with
more points than possible alignments, more threads
are needed.
Additionally, there is a fact that has to be noted
when allowing some positions of the actual flight to
be outside of the database trajectory’s boundaries.
Distances of an actual flight’s positions that are not in
alignment with a database position are not included in
further calculations. The fact that the sum consists of
fewer addends leads to a smaller total distance. As a
result, it might occur that a trial that examines fewer
positions, results in a smaller distance, although it fits
less well than the one that examines more positions.
Therefore, all results have to be normalized meaning
that the sum of total distances d
total
has to be divided
by the number of positions that have been considered
in the calculation.
4 RESULTS AND DISCUSSION
This chapter provides information about execution
times, the detection’s accuracy, and the real-time be-
havior of the entire program. All presented figures of
execution time include the time for processing both
images of the stereo-camera-system.
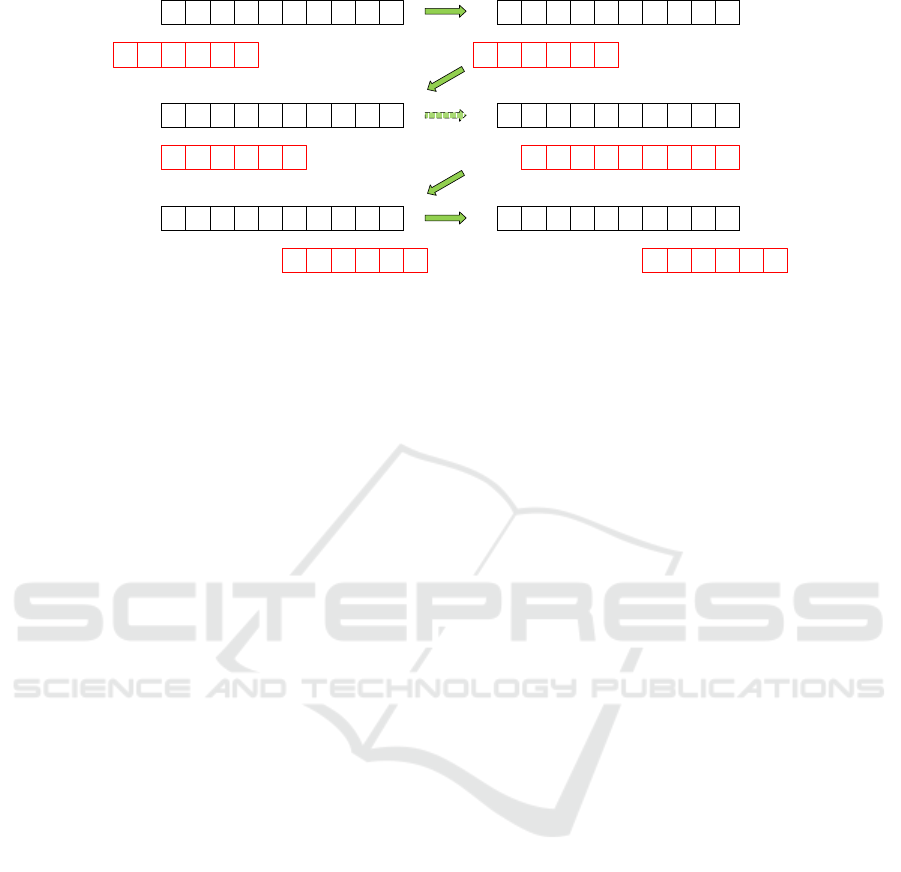
4.1 Canny Edge Detector
We have studied and compared the edge detection
with and without background subtraction and found
that it significantly improves the quality of an edge
image (Figure 7).
The background subtraction does affect not only
the accuracy of the edge images but also the the ex-
ecution times of the Canny Edge Detector. Figure 8
shows the execution times of background subtraction
plus Canny Edge Detector and the Canny Edge Detec-
tor without a background subtraction. Performing the
background subtraction and the Canny Edge Detec-
tor takes slightly more time than creating edge images
without subtracting the background when there are no
other objects present in the images. In the case of
other objects displayed in the image, the Canny Edge
Detector without a background subtraction takes up
to 1.6× more time than performing both steps com-
bined. This situation is caused by the hysteresis step
of the Canny Edge detector which leads to a higher
processing time when more pixels are in the image.
The slight slope of the graphs is caused by the ball
approaching the cameras from frame to frame. The
more the flight advances, the larger the ball is dis-
played in the images. The more edge pixels in the
frames, the more time is taken by the hysteresis pro-
cedure. One flight was processed 1000 times in a row
to obtain reliable measurements and to capture infor-
mation about variances in the computation time. Fig-
ure 8 shows the minimum, maximum, and average ex-
ecution times of the 92 frames of a flight.
4.2 Object Detection
Two different approaches of the Hough Circle Trans-
formation have been implemented and compared with
each other: the straightforward strategy and the
inverse-checking strategy. While threads of the for-
mer strategy that are assigned to an edge point have
to start a loop to draw a circle, each thread of the lat-
ter strategy must start a loop to draw a circle. There-
fore, performing the inverse-checking strategy results
in an execution time 9.4 to 17 times longer compared
with straightforward strategy. The data obtained do
not confirm the statements made in the studies (Askari
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
390
Canny
Canny
background
subtraction
Figure 7: The additional step of background subtraction im-
proves an edge image’s quality.
0
0,5
1
1,5
2
2,5
3
3,5
4
4,5
1 11 21 31 41 51 61 71 81 91
execution time (ms)
frame number
avg exec time (without bg subtraction)
avg exec time (after bg subtraction)
min exec time (without bg subtraction)
min exec time (after bg subtraction)
max exec time (without bg subtraction)
max exec time (after bg subtraction)
Figure 8: Execution times of background subtraction plus
Canny Edge Detector and of the Canny Edge Detector with-
out a background subtraction.
et al., 2013; Chen et al., 2011). Possibly, they in-
cluded images with a huge amount of edge points, in
which case it might be better to perform the inverse-
checking strategy. The background subtraction af-
fected the Hough Circle Transformation’s execution
times as well: detecting the ball with an untouched
background took up to 2.7× more time than doing this
after the background subtraction step.
Besides, Figure 9 shows that the execution times
of both the Hough Circle Transformation and the
RANSAC algorithm are almost the same at the be-
ginning of the flight when the ball’s image consists in
only a few pixels. Afterward, the RANSAC algorithm
is executing up to 3.4 times faster than the Hough Cir-
cle Transformation.
To obtain reliable statements about the average
tracking error of the determined center point to the
real one, the results of the Hough Circle Transfor-
mation and the RANSAC algorithm were addition-
ally analyzed with the help of the Rauch-TungStriebel
0
2
4
6
8
10
12
14
1 11 21 31 41 51 61 71 81 91
execution time (ms)
frame number
avg exec time (RANSAC algorithm)
min exec time (RANSAC algorithm)
max exec time (RANSAC algorithm)
avg exec time (Hough Circle Transformation)
min exec time (Hough Circle Transformation)
max exec time (Hough Circle Transformation)
Figure 9: Execution times of the Hough Circle Transforma-
tion and the RANSAC algorithm for each frame of an entire
flight.
Table 1: Tracking error of ball positioning.
Detection algorithm Background avg. track-
ing error
Hough Circle subtracted 2.73 mm
Hough Circle untouched 25.81 mm
RANSAC subtracted 2.78 mm
RANSAC untouched 25.96 mm
smoother
3
. This filter examines the recorded flight
path from front to back and reverse, to create a
smoothed flight path. This smoothing process cor-
rects physically impossible trajectories. Table 1
shows what Figure 7 had already suggested: Subtract-
ing the background considerably improves the detec-
tion’s accuracy as well. In this case, the localized po-
sition is only about 2 to 3mm away from the Rauch-
Tung-Striebel smoother estimated one.
4.3 Prediction
While the accuracy of both prediction algorithms has
been examined earlier (Pongratz, 2016), their execu-
tion times are presented here. Figure 10 shows the
temporal behavior of both methods as functions of
the number of reference trajectories. The average and
minimum time rise fairly linearly as the number of
reference trajectories in the database increases. While
the minimum execution time increases very slowly,
the average time’s graph definitively illustrates the
impact of including a higher number of reference
throws. This behavior is caused by a larger number
of blocks when more trajectories are in the database.
The temporal behavior of the two approaches is al-
most even, but the time required is slightly different.
While a database with up to 120 trajectories leads to
3
Available at: http://becs.aalto.fi/en/research/bayes/
ekfukf/
Parallelized Flight Path Prediction using a Graphics Processing Unit
391
0
0,5
1
1,5
2
2,5
1 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200
execution time (ms)
number of reference trajectories
avg exec time (compare rates of change)
min exec time (compare rates of change)
max exec time (compare rates of change)
avg exec time (compare positions)
min exec time (compare positions)
max exec time (compare positions)
Figure 10: The predictions execution time as a function of
the number of reference trajectories for the comparison of
positions and rates of change.
nearly identical execution times, a small difference
is observed when the number of reference throws in-
creases. For this purpose, the database was filled with
200 dummy trajectories, all with a length of 92, which
is equivalent to the longest trajectories of an already
existing database. A comparison of the various trials
with different database sizes would not be fair.
4.4 Entire Procedure
The best solution for each step was selected to exam-
ine the execution time of the entire procedure. Each
pair of frames had to run through the following tasks:
clearing the GPU storage, background subtraction,
Canny Edge Detector, RANSAC algorithm, triangu-
lation, coordinate translation, and prediction.
Figure 11 shows the combined execution times of
five different flights that have been processed 1000
times in a row. The shorter time, as well as the rapid
increase of the time at the beginning of the flight, is
caused by the throwing device, which partially cov-
ered the ball. The slight slope of the graphs is due by
the ball approaching the cameras from frame to frame.
Without our good light profile
4
, which changes the
Canny Edge Detector’s thresholds in the course of
the ball’s flight, the execution times would signifi-
cantly increase, and the detection would not work that
well. The average maximum time of the different
flights was about 7.69ms and enables a frame rate of
130FPS. Because of maximum execution times that
were, in rare cases, over 10ms, a small buffer is re-
quired for compensation. Without such a buffer, there
would not be sufficient computational power for the
frame rate of 110FPS of the camera system used.
4
To counteract the heterogeneity of the room’s illumina-
tion (to improve the detection of the ball), we created a light
profile by trial and error.
0
2
4
6
8
10
12
14
1 11 21 31 41 51 61 71 81 91
execution time (ms)
frame number
average execution time
minimum execution time
maximum execution time
Figure 11: The execution times of five flights were pro-
cessed, examined, and combined for this chart.
0
5
10
15
20
25
30
35
40
execution time (ms)
GPU's maximum execution time
GPU's average execution time
CPU's maximum execution time
CPU's average execution time
Figure 12: Average and maximum times of the various tasks
when performing it on a GPU and on a CPU.
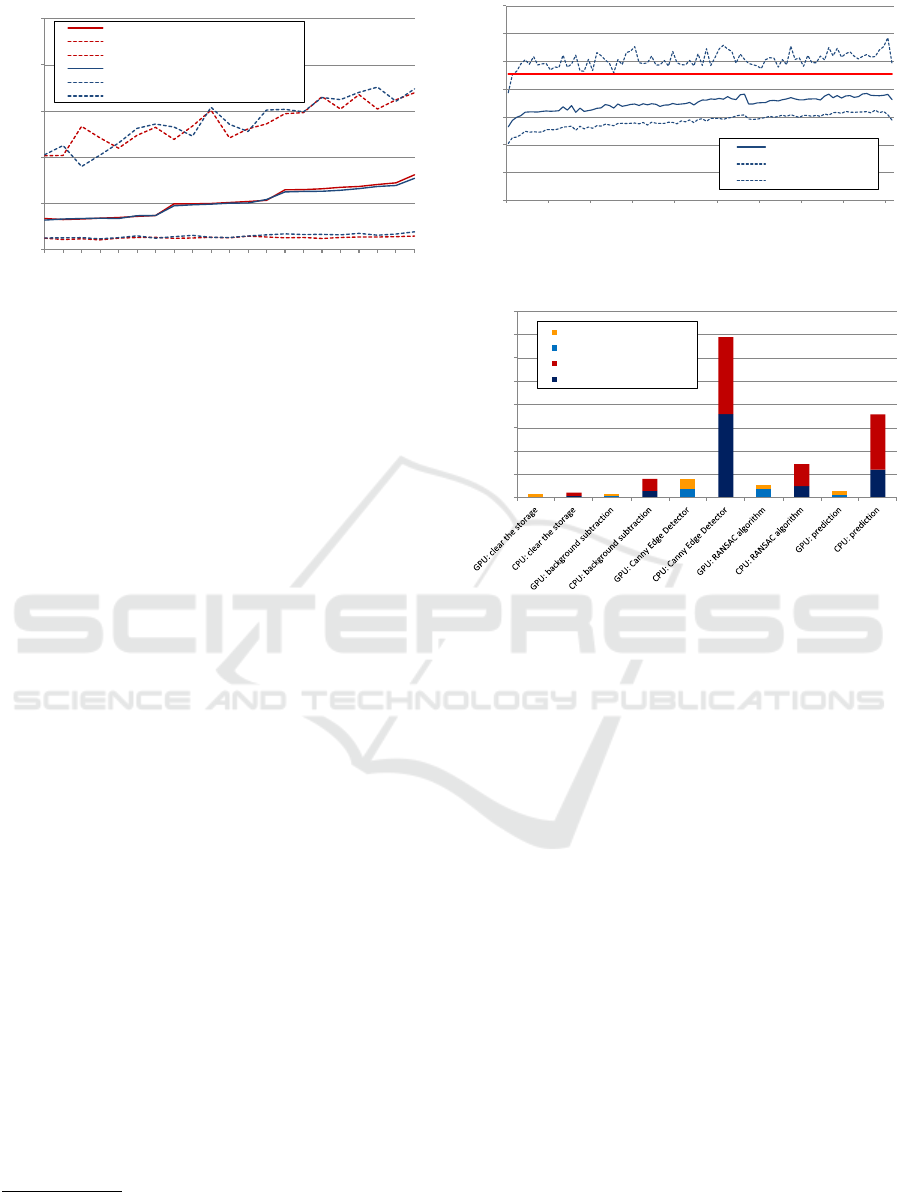
For examining the speed-up achieved by using a
GPU instead of a CPU, the entire program was rewrit-
ten to a purely sequential approach on a CPU to be
executable on a CPU. To compare execution times,
one flight was processed 1000 times in a row and the
required times for the various steps were measured.
Figure 12 shows that the largest increase in speed was
measured for the Canny Edge Detector (9.74×) and
the prediction (9.55×), followed by background sub-
traction (5.35×), storage clearing (2.04×), and the
RANSAC algorithm (1.26×). In short, a single frame
was processed 3.46 to 7.17 faster on a GPU than on a
CPU. Hence, this demonstrates that the selected GPU
is a viable platform for this application as it gives a
significant performance improvement compared with
the CPU based reference implementation.
Besides the real-time requirement also the track-
ing accuracy of the algorithms is a major concern for
the application. The achieved tracking error, com-
pared to the Rauch-Tung-Striebel smoothened trajec-
tory, was well below 4 cm for 99 % of the tracked
balls over a distance from 0.7 to 3m (Pongratz, 2016).
VISAPP 2017 - International Conference on Computer Vision Theory and Applications
392

5 CONCLUSION
One of the main questions here was whether a GPU
can perform the ball detection and flight path predic-
tion fast enough to achieve a high frame rate. The
results of the NVidia GTX 560 Ti GPU show exe-
cution times that enable data processing at 130FPS.
Moreover, using a GPU for the required calculations
proved to be a beneficial idea. The implemented pro-
gram was 3.46 to 7.17 faster when running on a GPU
than on a CPU; Intel i7-4770S. Using a newer GPU
would - most probably - accelerate the whole pro-
cedure. However, using this five years old GPU is
representative of GPUs in general. Additionally, as
earlier mentioned, integrated GPUs also offer compu-
tation possibilities. The performance we reached by
using the GPU shows that processing this flight path
prediction will most probably be possible also on an
embedded system with an onboard GPU.
We performed numerous optimizations to enable
such high-speed computation on the GPU used. Well-
thought-out algorithms and letting some data make a
detour over the fast shared memory were the keys to
success. However, some constraints still have to be
considered to achieve an execution time short enough
for this frame rate. Firstly, a small buffer is needed to
compensate for the maximum execution times, which
can be slightly too high for 110FPS (the two cam-
eras captured the scene with 110FPS). Secondly, the
Hough Circle Transformation turned out to be compu-
tationally too costly and time-consuming. Therefore,
the RANSAC algorithm had to be used to achieve the
desired execution time.
Additionally, the background subtraction step and
the adapting threshold profile used for the Canny
Edge Detector were necessary for achieving these ex-
ecution times. Otherwise, a considerably higher num-
ber of edge points would be in the images, which
would lead to an execution time that is too high for
110FPS. These additional computational steps also
enable a more precise detection. For the future, we
plan to consider an approach similar to (Tang et al.,
2015) to use more than one trajectory for the predic-
tion and examine the influences on the prediction ac-
curacy.
Detecting other - more complex - objects than a
ball will require both more computational power and
more convoluted algorithms. The detection will be
more complicated, and the prediction would have to
take also into account the object’s orientation with its
three degrees of freedom.
REFERENCES
Askari, M. et al. (2013). Parallel gpu implementation of
hough transform for circles. In IJCSI.
Barteit, D. et al. (2009). Measuring the intersection of a
thrown object with a vertical plane. In INDIN.
B
¨
auml, B. et al. (2011). Catching flying balls and preparing
coffee: Humanoid rollin’justin performs dynamic and
sensitive tasks. In ICRA.
Chen, S. et al. (2011). Accelerating the hough transform
with cuda on graphics processing units. Department
of Computer Science, Arkansas State University.
D’Orazio, T. et al. (2002). A ball detection algorithm for
real soccer image sequences. In ICPR.
Fung, J. et al. (2005). Openvidia: Parallel gpu computer
vision. In ACM Multimedia.
Gowanlock, M. et al. (2015). Indexing of spatiotemporal
trajectories for efficient distance threshold similarity
searches on the gpu. In IPDPS.
Hong, W. et al. (1995). Experiments in hand-eye coordina-
tion using active vision. In Lecture Notes in Control
and Information Sciences.
Jacobs, L. et al. (2013). Object tracking in noisy radar data:
Comparison of hough transform and ransac. In EIT.
Karimi, K. et al. (2010). A performance comparison of
CUDA and opencl. CoRR, abs/1005.2581.
Khronos, G. (2015). Opencl.
Luo, Y. et al. (2008). Canny edge detection on nvidia cuda.
In CVPRW.
NVidia, C. (2014). Cuda architecture.
NVidia, C. (2015). Geforce gtx 560 ti.
Ogawa, K. et al. (2010). Efficient canny edge detection us-
ing a gpu. In ICNC.
Pongratz, M. (2009). Object touchdown position prediction.
Master’s thesis, Vienna University of Technology.
Pongratz, M. (2016). Bio-inspired transport by throwing
system; an analysis of analytical and bio-inspired ap-
proaches. PhD thesis, TU Wien 2016.
Pongratz, M. et al. (2010). Transport by throwing - a bio-
inspired approach. In INDIN.
Pongratz, M. et al. (2012). Koros initiative: Automatized
throwing and catching for material transportation. In
Leveraging Applications of Formal Methods, Verifica-
tion, and Validation, pages 136–143.
Tang, X. et al. (2015). Efficient selection algorithm for fast
k-nn search on gpus. In IPDPS.
Wang, W. et al. (2011). Robust spatial matching for object
retrieval and its parallel implementation on gpu. IEEE
Transactions on Multimedia, 13(6).
Wu, S. et al. (2012). Parallelization research of circle detec-
tion based on hough transform. In IJCSI.
Parallelized Flight Path Prediction using a Graphics Processing Unit
393
