A Heuristic for Optimization of Metaheuristics by Means of
Statistical Methods
Eduardo B. M. Barbosa
1
and Edson L. F. Senne
2
1
Brazilian National Institute for Space Research, Rod. Presidente Dutra,
Km. 40 - Cachoeira Paulista, SP - 12630-000, São Paulo, Brazil
2
School of Engineering at Guaratinguetá, Univ. Estadual Paulista, Av. Dr. Ariberto Pereira da Cunha,
333 - Guaratinguetá, SP - 12516-410, São Paulo, Brazil
Keywords: Metaheuristics, Fine-tuning, Combinatorial Optimization, Nonparametric Statistics.
Abstract: The fine-tuning of the algorithms parameters, specially, in metaheuristics, is not always trivial and often is
performed by ad hoc methods according to the problem under analysis. Usually, incorrect settings influence
both in the algorithms performance, as in the quality of solutions. The tuning of metaheuristics requires the
use of innovative methodologies, usually interesting to different research communities. In this context, this
paper aims to contribute to the literature by presenting a methodology combining Statistical and Artificial
Intelligence methods in the fine-tuning of metaheuristics. The key idea is a heuristic method, called
Heuristic Oriented Racing Algorithm (HORA), which explores a search space of parameters, looking for
candidate configurations near of a promising alternative, and consistently finds good settings for different
metaheuristics. To confirm the validity of this approach, we present a case study for fine-tuning two
distinct metaheuristics: Simulated Annealing (SA) and Genetic Algorithm (GA), in order to solve a classical
task scheduling problem. The results of the proposed approach are compared with results yielded by the
same metaheuristics tuned through different strategies, such as the brute-force and racing. Broadly, the
proposed method proved to be effective in terms of the overall time of the tuning process. Our results from
experimental studies reveal that metaheuristics tuned by means of HORA reach the same good results than
when tuned by the other time-consuming fine-tuning approaches. Therefore, from the results presented in
this study it is concluded that HORA is a promising and powerful tool for the fine-tuning of different
metaheuristics, mainly when the overall time of tuning process is considered.
1 INTRODUCTION
The tuning of the algorithms parameters, especially,
in metaheuristics, is not always trivial and often is
performed by ad hoc methods according to the
problem under analysis. Usually, the choice of
incorrect settings can result in an unexpected
behaviour of the algorithm, as to converge to a local
optimum, or even to present a random behaviour,
which does not converges to a good solution within
a certain time limit.
In general, there are many challenges related to
the tuning of metaheuristics (e.g.: parameters
domain, approach strategy, etc.) which require the
use of innovative methodologies. These challenges
usually interest to different research communities.
Therefore, in the contemporary literature there are
many researches (e.g.: Dobslaw, 2010; Lessman et
al., 2011; Neumüller et al., 2011; Ries et al., 2012;
Akbaripour and Masehian, 2013; Amoozegar and
Rashedi, 2014; Calvet et al., 2016; and many others)
addressed to them. Amongst them, it stands out the
using of statistical techniques supported by efficient
methods, in order to aid the process understanding
and also to reach effective settings.
This paper aims to contribute to the literature by
presenting a methodology combining Statistical and
Artificial Intelligence methods in the fine-tuning of
metaheuristics, such as Design of Experiments
(DOE) (Montgomery, 2012) and the concept of
Racing (Maron and Moore, 1994; Birattari et al.,
2002). The key idea is consider the parameter
configurations as a search space and explore it
looking for alternatives near of the promising
candidate configurations, in order to consistently
find the good ones. Broadly, our approach focuses
its searches on dynamically created alternatives in an
B. M. Barbosa E. and L. F. Senne E.
A Heuristic for Optimization of Metaheuristics by Means of Statistical Methods.
DOI: 10.5220/0006106402030210
In Proceedings of the 6th International Conference on Operations Research and Enterprise Systems (ICORES 2017), pages 203-210
ISBN: 978-989-758-218-9
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
203

iterative process, and employs a racing method to
efficiently evaluate and discard some alternatives, as
soon as gather enough statistical evidences against
them.
Since the last decades, a variety of strategies for
fine-tuning of metaheuristics have emerged in the
literature, where it highlight CALIBRA (Adeson-
Díaz and Laguna, 2006), which uses DOE to define
a parameters search space; F-Race (Birattari et al.,
2002) and its iterated version I/F-Race (Balaprakash
et al., 2007), with an efficient evaluation of
candidate configurations; and ParamILS (Hutter et
al., 2009), whose the alternatives are created from
the modifications of a single parameter value.
Inspired by them, our strategy brings these
characteristics all together in a single heuristic
method, where the exploration of the search space is
performed through the candidate configurations in
the neighborhood of a promising alternative. The
advantage to combine different strategies can be
summarized as the hability to define the search
space, and the efficiency to focus the search on the
candidate configurations inside this search space.
Our results confirm the validity of this approach
through a case study to fine-tune metaheuristics
from distinct natures, such as Simulated Annealing
(SA) and Genetic Algorithm (GA), and its
effectivity when compared with other tuning
approaches, such as brute-force and racing. The
quality of the proposed settings for each of them will
be evaluated by applying the metaheuristics in a
classical optimization problem, such as the task
scheduling problem to minimize the total weighted
tardiness (TWTP) in a single machine.
The rest of the paper is structured as follows:
Section 2 presents the problem of tuning
metaheuristics and our approach combining Statistic
and Artificial Inteligence methods to address this
problem. In Section 3 there is an overview about the
scheduling problem, as well as the metaheuristics
that will be used in the case study. The proposed
approach is applied in a case study (Section 4) to
fine-tune the metaheuristics SA and GA. Section 4
also presents the case study results and its analyzes.
Our final considerations are in Section 5.
2 THE PROBLEM OF TUNING
METAHEURISTICS
Informally, this problem consists of determining the
parameter values, such that the algorithms can
achieve the best performance to solve a problem
within a time limit. This problem is itself an
optimization problem, where the goal is to optimize
an algorithm (e.g.: better performance, rise the
quality of solutions, etc.) to solve different problems
(Blum and Roli, 2003; Talbi, 2009).
In general, let M be a metaheuristic with a set of
parameters applied on problems P = {p
1
, p
2
, ..., p
n
}.
The parameters (e.g.: , , ..., ) of M can assume a
finite set of values and its cardinality can also vary
extensively according to M and P studied. If  is a
set of candidate configurations, such that  is any
setting of M, then the problem of tuning
metaheuristics can be formalized as a state-space:
W = (

, P).
(1)
This problem consists of knowing which is the
best setting    present in W to solve problems P.
The expected number of experiments for fine-
tuning of M on P is the product of (||  ||  ... 
||)  |P|. For example, M is a metaheuristic with the
following parameters A, B, C, D, where A = {a
1
, a
2
,
a
3
}, B = {b
1
, b
2
, b
3
, b
4
}, C = {c
1
, c
2
, c
3
}, and D =
{d
1
, d
2
, d
3
, d
4
, d
5
}. Let |P| = 50. So, the expected
number of experiments for fine-tuning of M on
problems P is (3  4  3  5)  50 = 9000. In short,
the best setting of M to solve P is an alternative in
(1), such that its determination, in the worst
hypothesis, will be given by means of a full search
in the state-space W.
2.1 Heuristic Oriented Racing
Algorithm
This research proposes an automatic approach to
avoid a full search in the state-space (1) and still find
a good setting of M to solve P. To do that we
combine Statistical and Artificial Intelligence
methods (e.g.: DOE and Racing, respectively) to
consistently find the good settings based on
statistical evaluations of a wide range of problems.
The tuning process begins with an arbitrary
selection of n instances (n > 1) from a class of
optimization problems, and follows by the
definitions of ranges for the parameters of
metaheuristic. The previously selected instances are
treated as a training set, on which are performed
experimental studies with the Response Surface
Methodology (RSM) to define the best parameters
settings for each instance. Therefore, at the end of
the experimental phase there will exist n different
settings for each parameter, being each one related
to an instance.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
204

The settings identified in the training set ensure
diversity for the parameters, and they are used to
define the bounds of each parameter, that is, a search
space of parameters limited by the maximum and
minimum values of each parameter in the training
set. From there, the goal is to pursue alternatives
dynamically created in the neighborhood of some
best known candidate configuration, regarding the
previously defined bounds of the search space. For
each of the alternatives, the target algorithm is ran in
an expanded set of instances, bigger than the
previous one.
This process (Figure 1) is called Heuristic
Oriented Racing Algorithm (HORA), due the way of
exploring the alternatives in the search space, that is,
using a heuristic method, and by its evaluation
process through a racing method.
Figure 1: Schema of the proposed approach.
The heuristic method used in the fine-tuning
process is illustrated as a pseudo-code in Figure 2.
The algorithm receives a promising candidate
configuration (S
0
), the search space bounds (B) and
the number of neighbors (M). The alternatives (n)
are created in a main loop and its costs (C) are
achieved by running the target metaheuristic (Mh)
once on different instances (i). The solutions are
evaluated by the nonparametric Friedman statistic
(T), and the worst ones are discarded according to
the statistical evidences. At each iteration new
alternatives are created in the neighborhood of some
best known candidate configuration (S). The process
continues with the surviving ones and the best
parameter setting (S
*
) is selected as one that has the
lowest expected rank.
Just as a racing method, in HORA some
candidate configurations, that is, those considered to
be good according to the statistical evaluations, are
evaluated on more instances. However, it should be
highlight that the HORA employs a racing method
to evaluate the set of candidate configurations.
Besides that, both methods (HORA and racing)
differ among them in the way of creation the set of
candidate configurations, such that in HORA the
alternatives are created on demand in an iterative
process, while in racing they are predefined before
the fine-tuning process.
Input: S
0
, B, M
Output: S
*
S  S
0
;
S'  {};
n  {};
C  {};
do while
i  newInstance();
n  newNeighbors(S, B, M);
S'  S'  n;
for each s  S' do
C  C  Mh(s, i);
end
T  statisticalTests(C);
S'  collectElite(S', T);
S  identifyBest(S');
until termination criteria is met
S
*
 S;
return S
*
;
Figure 2: Pseudo-code of the heuristic method for fine-
tuning metaheuristics.
2.2 The Dynamic of the Search Space
The most intuitive way for solving the problem of
tuning metaheuristics is the brute-force approach.
Broadly, this strategy runs the same number of
experiments for all alternatives in the set of
candidate configurations. Nevertheless, any
alternative with inferior quality in this set must be
tested as the good ones.
To avoid this kind of problem, a traditional
racing method employs efficient statistics to
evaluate the candidate configurations and discard
A Heuristic for Optimization of Metaheuristics by Means of Statistical Methods
205

those considered statistically inferior as soon as
gather enough statistics against them.
Even considering the efficiency of a racing
method to evaluate the alternatives, both approaches
(brute-force and racing) start the tuning process with
a large set of candidate configurations. Thus,
according to the size of this set, its evaluation must
be initially slow.
Different to the traditional approaches, the set of
candidate configurations in HORA is dynamically
built during the tuning process. The candidate
configurations are created on demand in the
neighborhood of some best known alternative, as a
sequence of sets of candidate configurations:

0
 
1
 
2
 ...
From the step k to k+1 the set of candidate
configurations is built possibly discarding some
alternatives considered statistically inferior. Given
that some candidate configurations persist in this set,
they are evaluated on more instances. Nevertheless,
it is important to note that all the created alternatives
must be evaluated on the same instances previously
used on evaluating of the persistent alternatives.
k = 1 k = 2 k = 3
|| = 3 || = 5 || = 6
k = 4 k = 5 k = 6
|| = 5 || = 7 || = 3
Figure 3: Illustrative process to create (black) and exclude
(gray) alternatives from the search space.
To illustrate this process (Figure 3), let us
consider any search space, where at each iteration k,
m = 3 candidate configurations are created. At the
end of an iteration, all alternatives in the set  of
candidate configurations are evaluated and those
with inferior quality are discarded. Therefore, the set
 is dynamic, that is, its size can increase or
decrease. The process continues pursuing the
alternatives in the search space until meet a stop
criteria (e.g.: number of alternatives in , runtime
limit, among others).
The evaluation of the created candidate
configurations is done in blocks by instance
according to its cost (e.g.: the objective function
value). So, the best performance is ranked as 1, the
second as 2, and so on. In case of ties between the
alternatives, it gives the average ranking to each one.
For a detailed description of the evaluation process
by means of the racing method using the
nonparametric Friedman statistic, we refer to
Birattari et al. (2002 and 2009).
3 CONSIDERED PROBLEM AND
METAHEURISTICS
Scheduling problems are related with the limited
resources distribution aiming the achievement of
efficient work. It is classical optimization problem
involving tasks that must be arranged in m machines
(m ≥ 1) subject to some constraints, in order to
optimize an objective function. The key idea is to
find the tasks processing order and decide when and
on which machine each task should be processed.
A typical scheduling problem is one on which
the objective is minimize the total weighted
tardiness in a single machine (TWTP). These
problems formally expressed as 1|1,d
j
|w
j
T
j
(Schmidt,
2000), involve a set of tasks J = {1, 2, ..., n} to be
processed in a single machine continuously available
to process at most one task at a time. Each task (j 
J) spends a positive and continuous processing time
p
j
(time units), has a weight w
j
of one task over the
others, a start time r
j
, and a due date d
j
. In general,
tardiness may be understood as the difference
between the effective completion time and the due
date of the tasks, such that the tardiness (T
j
) can be
computed as max(0, C
j
 d
j
), where C
j
is the
effective completion time of task j.
Metaheuristics are one of the best-known
approaches to solving problems for which there is no
specific efficient algorithm. Usually, these
algorithms differ from each other in terms of
searching pattern, but offer accurate and balanced
methods for diversification (search space
exploration) and intensification (exploitation of a
promising region) and share features, such as the use
of stochastic components (involving randomness of
variables) and have a variety of parameters that must
be set according to the problem under study.
The Simulated Annealing (SA) is a probabilistic
method proposed in Kirkpatrick et al. (1983) and
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
206

Cerny (1985) in order to find the global minimum of
an objective function with numerous local minima.
Widely applied to solve optimization problems, SA
simulates a physical process from which a solid is
cooled slowly, so that the final product becomes a
homogeneous mass to achieve a minimum energy
configuration (Bertsimas and Tsitsiklis, 1993).
The SA performance is strongly influenced by a
number of parameters. For example, the high
temperature in the early stages increases the
likelihood of acceptance a low quality solution.
Beyond the initial temperature, it is important to set
the number of iterations performed on a same
temperature, and their cooling rate. Usually, the
cooling temperature occurs steadily at a predefined
rate , so that slower, greater the holding of the
search space (Roli e Blum, 2003; Talbi, 2009).
By the other hand, the Genetic Algorithm (GA)
is a population-based method invented by Holland
(1975) inspired in the principles of survival from
Darwin’s evolution theory. GA simulates an
evolution process in which the fitness of individuals
(parents) is crucial to generate new individuals
(children). The basic operating principle of a GA is
to apply the operators (selection, crossover and
mutation) on individuals of the population at every
generation. Its performance is strongly influenced by
a set of parameters, such as the number of
generations, crossover and mutation rates.
In a typical GA, the individuals are crossed at a
rate between 0.4 and 0.9. For example, if the rate is
fixed at 0.5, then half of the population will be
formed from the selection and crossover operations.
However, if there is no crossover, the population
mean fitness must increases to match the best
individual fitness rate. From that point, it can only
be improved through the mutation. In general, the
mutation rate is about 0.001, but may vary according
to the problem under analysis.
4 EXPERIMENTAL STUDIES
In our study were selected a set of parameters of
each metaheuristic. Those parameters are the most
frequently used in the literature and seems to
influence the performance of the SA and GA,
regardless the studied problem. The considered
parameters for SA are: value of the initial
temperature (T
0
), number of iterations on one
temperature stage (SA
max
) and temperature cooling
rate (); while the chosen parameters for GA are:
mutation rate (p
m
), crossover rate (p
c
), population
size () and number of generations (n). The
parameters levels (Table 1) were chosen within the
real limits of parameters, in order to promote
diversity in the search space, as well as differences
between each particular parameter setting.
For this study, we define a training set with n = 4
instances arbitrarily selected from the benchmark
wt40, a TWTP with 40 tasks from the OR-Library
(Beasley, 1990). The experimental studies were
conducted with a circumscribed Central Composite
Design (CCD), whose the axial points establish new
limits for an interest region (e.g.: the search space of
parameters). A circumscribed design can be used to
enlarge the search space exploration if its bounds
are in the region of operability, that is, within the
real limits of parameters. On the other hand, if the
region of interest matches with the parameter limits,
another kind of CCD must be chosen (e.g.: face-
centred or inscribed) to avoid the parameters
infeasibility.
Table 1: Metaheuristics parameters and its levels for the
experimental studies.
SA Low High GA Low High
T
0
1.00e4 1.50e6 p
m
0.001 0.025
SA
max
500 1500 p
c
0.400 0.900

0.900 0.980

10 100
n 100 1000
After the experimental studies we have four
different results for each parameter, being each one
related to an instance. Through those results, we
defined the search space of parameters, whose the
bounds are the maximum and minimum values of
the parameters in the training set. Accordingly, the
SA search space is:
 T
0
: [1.16e5, 1.65e5];
 SA
max
: [1316, 1596]; and
 : [0.945, 0.948].
Whereas, we have the following search space for
GA:
 p
m
: [0.014, 0.057];
 p
c
: [0.684, 0.725];
 : [69, 101]; and
 n: [775, 1267].
It is noteworthy in the results, that some
parameter values are outside of the limits initially
defined (Table 1). However, as pointed before, this
occurs due the experimental studies, where the axial
points of the CCD overcome the previously set
limits in order to ensure an appropriate estimation of
parameters.
A Heuristic for Optimization of Metaheuristics by Means of Statistical Methods
207

From there, the exploration of the search space
of parameters is done by creating the alternatives in
the neighborhood of some best known candidate
configuration. For each of the alternatives we ran the
target metaheuristics (e.g.: SA and GA) during 15s
on an expanded set of instances (e.g.: for this study,
the expanded set matches all 125 instances from the
benchmark wt40). This process was repeated 10
times and the results of fine-tuning of the
metaheuristics by means of HORA are presented in
terms of mean and standard deviation (  ) in
Table 2. This table also presents the total time (in
seconds) of the tuning process.
Table 2: Fine-tuning of metaheuristics (HORA).
SA Settings GA Settings
T
0
1.29e5  4.22e4
p
m
0.040  0.012
SA
max
1391  87
p
c
0.699  0.211

0.946  0.001

80  11
--
-- n
983  115
t
698s
t
875s
For comparisons, we considered the previously
defined search space of parameters, and two fine-
tuning approaches, as the Deceive, a brute-force
approach, and a racing algorithm based in the F-
Race method, called Racing. The settings used for
both approaches are the same, such that, for SA we
define: T
0
= {1.16e5, 1.26e5, 1.35e5, 1.45e5, 1.55e5,
1.65e5}, SA
max
= {1316, 1409, 1502, 1596}, and  =
{0.945, 0.946, 0.948}; and for GA we consider: p
m
=
{0.014, 0.028, 0.043, 0.057}, p
c
= {0.684, 0.698,
0.711, 0.725},  = {69, 85, 101}, and n = {775, 939,
1103, 1267}.
Each possible combination leads to one different
metaheuristic setting, such that, the search spaces
have 72 and 192 different candidate configurations
for the SA and GA, respectively. The idea is use
Deceive and Racing to select the good as possible
candidate configuration out a lot of options. To do
that, for the considered approaches, we run the target
algorithms during 15s on the same extended set of
instances previously used (e.g.: 125 instances from
the benchmark wt40). This process was repeated 10
times and the results of fine-tuning of the studied
metaheuristics by means of brute force and racing
method are presented in terms of mean and standard
deviation (  ) in Tables 3 and 4. These tables
also present the total time (in seconds) of the tuning
process.
It is noted on results that HORA method is the
most effective in the fine-tuning of the
metaheuristics, in terms of the overall time process.
Since it demands a little portion of the time required
by the brute-force and racing algorithm,
respectively. The pointed divergence can be justified
by the size of the set of alternatives, fairly large for
Deceive and Racing, as well as the way of creating
the set of candidate configurations in the search
space. Given that in HORA it is dynamically done
during the tuning process, whereas the others
(Deceive and Racing) use predefined sets of
alternatives.
Table 3: Fine-tuning of metaheuristics (Brute-force).
SA Settings GA Settings
T
0
1.34e5

4.39e4
p
m
0.053  0.007
SA
max
1419

112
p
c
0.710  0.214

0.946

0.001

90  11
--
-- n
988  190
t
5460s
t
15274s
Table 4: Fine-tuning of metaheuristics (Racing).
SA Settings GA Settings
T
0
1.20e5

3.67e4
p
m
0.051  0.010
SA
max
1316

0
p
c
0.695  0.210

0.946

0.001

90  13
--
-- n
1087  144
t
3213s
t
11700s
The results also show the similarity between the
settings, by means of HORA and Racing. It is
emphasised that both approaches employ the same
evaluation method for the candidate configurations.
4.1 Experimental Results
In general, the metaheuristics employ some degree
of randomness to diversify its searches and avoid
confinement in the search space. Thus, a single run
of these algorithms can result in different solutions
from the next run. So, to test the quality of our
settings, our experimental results were collected
after 5 run of the metaheuristics SA and GA on the
TWTP.
To generalize our results and compare them
among themselves, we use:
100
)(
)()(
*
*



sf
sfsf
gap
,
(2)
where f(s) is our computed solution and f(s
*
) is the
best known solution of the problem. Thus, the lower
the value of gap for the metaheuristics, the better the
performance of the algorithms.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
208

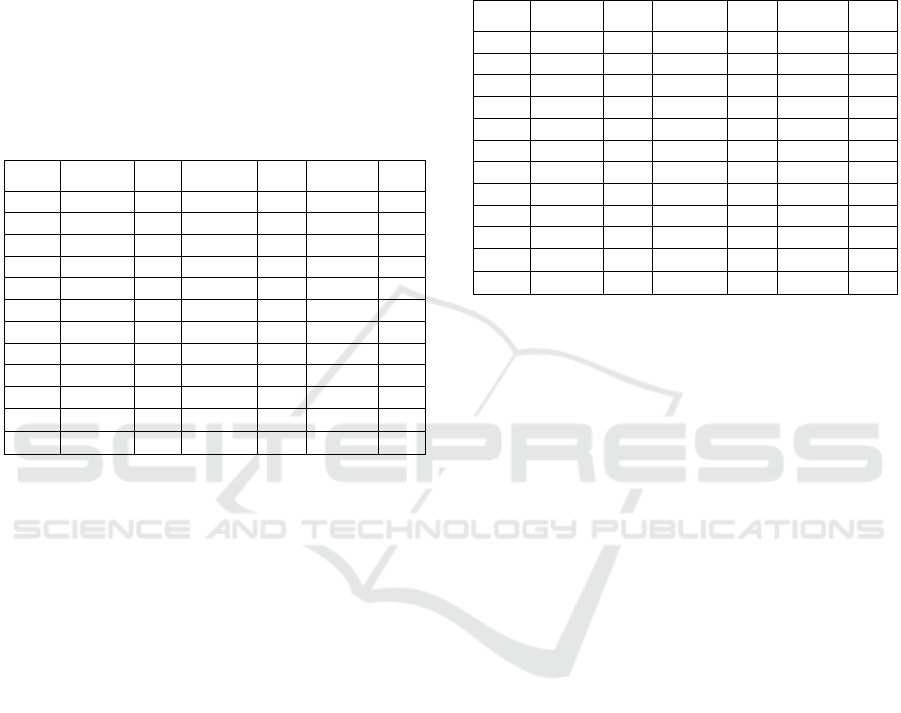
We compare the HORA results with Deceive and
Racing. The settings of the metaheuristics through of
each approach were presented in Tables 2, 3 and 4,
for HORA, Deceive and Racing, respectively.
The set of results in Tables 5 and 6 are best
found value of (2) and its corresponding runtime (t),
in 5 run of the studied metaheuristics, in the first 10
instances of the benchmark wt40, from the OR-
Library (Beasley, 1990). In these tables, the results
of the approaches are underlined by the capital
letters D, H and R for Deceive, HORA and Racing,
respectively.
Table 5: SA statistics for the first 10 instances of wt40.
Inst.
D
gap
D
t
H
gap
H
t
R
gap
R
t
1
0.00 56 0.00 36 0.00 42
2
4.65 96 0.00 35 0.00 29
3
6.70 89 0.00 54 0.00 28
4
0.00 45 0.00 33 0.00 29
5
0.00 44 0.00 27 0.00 21
6
0.00 51 0.00 41 0.00 30
7
0.00 87 3.91 81 3.91 68
8
0.00 53 0.00 47 0.00 39
9
0.00 58 0.52 85 1.36 82
10
0.00 62 0.00 56 0.00 38

1.14 64 0.44 50 0.53 41

2.32 18 1.17 19 1.20 18
The SA statistics (Table 5) reveal an increasing
of the quality of solutions, when the tuning approach
HORA is chosen. It is also noted the similarity
between results of HORA and Racing in the most
instances. According to the statistics, when
considering the gap, the metaheuristics tuned with
HORA is better (closely followed by Racing). When
considering the execution time, the metaheuristics
tuned by Racing is faster (closely followed by
HORA).
The GA statistics (Table 6) reveal a decreasing
of the quality of solutions (e.g.: arithmetic mean) for
HORA and Racing approaches, when comparing its
results with SA. In both cases the results are about
the double of the results above (Table 5). Over
again, it is noted the similarity between the results of
HORA and Racing in almost all the selected
instances, but for GA, HORA is little faster than
Racing. However, as observed the runtime is also
increased.
In summary, the tuning of metaheuristics by
means of the HORA method are competitive and
showed the better results for both algorithms. The
presented results were statistically analyzed by
means of t-test at the significance level of 5%, and
the comparisons between HORA  Deceive, as well
as HORA  Racing, were not significant. Therefore,
considering the time required to the tuning process,
HORA is more effective, since it demand less time
than the brute-force and racing approaches for
achieving the statistically same results.
Table 6: GA statistics for the first 10 instances of wt40.
Inst.
D
gap
D
t
H
gap
H
t
R
gap
R
t
1
0.00 57 0.00 36 0.00 62
2
0.00 100 0.00 65 3.10 51
3
6.70 53 6.70 55 6.70 57
4
0.00 38 1.29 43 1.29 56
5
0.00 30 0.00 5 0.00 7
6
1.34 85 0.00 105 0.00 112
7
0.00 83 0.00 54 0.00 32
8
0.00 50 0.00 89 0.00 94
9
0.34 68 0.00 79 0.00 50
10
0.00 127 0.04 95 0.04 121

0.84 69 0.80 63 1.11 64

1.99 28 2.00 29 2.09 33
5 CONCLUSIONS
This paper presented a method addressed to the
problem of tuning metaheuristics. The problem was
formalized as a state-space, whose the exploration is
done effectively by a heuristic method combining
Statistical and Artificial Intelligence methods (e.g.:
DOE and racing, respectively).
The proposed method, called HORA, applies
robust statistics on a limited number of instances
from a class of problems, in order to define a search
space of parameters. Thus, from the alternatives
dynamically created in the neighborhood of some
best known candidate configuration, it employs a
racing method to consistently find the good settings.
However, it should be highlight that HORA differs
from the racing method in the way how the
alternatives are created, that is, while racing uses a
predefined set of candidate configurations, in HORA
the alternatives are created on demand in an iterative
process. This feature ensures the dynamic of the
search space, such that in some situations it
increases and others, it decreases, as well as it makes
the evaluation process more efficient.
From a case study, HORA was applied for fine-
tuning two distinct metaheuristics. Its results were
compared with the same metaheuristics tuned by
means of different approaches, such as the brute-
force and racing. The HORA method proved to be
effective in terms of overall time of the tuning
process, since it demands a little portion of the time
A Heuristic for Optimization of Metaheuristics by Means of Statistical Methods
209

required by the other studied approaches. Through
the experimental studies it is noted that the
metaheuristics SA and GA tuned by means of
HORA can reach the same results (eventually better)
than the other studied fine-tuning approaches, but
the tuning process is much more faster with HORA.
This better performance can be explained by the way
of exploring the alternatives in the search space, that
is, pursuing the good ones in the neighborhood of
some best known candidate configuration, and by
the efficiency of its evaluation process with a racing
method.
In the scope of this study, the metaheuristics SA
and GA, as well as the problem TWTP, were used
only to demonstrate the HORA approach addressed
to the problem of tuning metaheuristics. The results
achieved show that the proposed approach may be a
promising and powerful tool mainly when it is
considered the overall time of tuning process.
Additional studies must be conducted in order to
verify the effectiveness of the proposed
methodology considering other metaheuristics and
problems.
REFERENCES
Adeson-Diaz, B., Laguna, M., 2006. Fine-tuning of
algorithms using fractional experimental designs and
local search. Operations Research, Baltimore, v. 54, n.
1, p. 99-114.
Amoozegar, M.; Rashedi, E., 2014. Parameter tuning of
GSA using DOE. In: 4th International Conference on
Computer and Knowledge Engineering (ICCKE), 4.,
2014, p. 431-436.
Akbaripour, H.; Masehian, E., 2013. Efficient and Robust
Parameter Tuning for Heuristic Algorithms.
International Journal of Industrial Engineering &
Production Research, Tehran, v. 24, n. 2, p. 143-150.
Balaprakash, P., Birattari, M., Stützle, T., Dorigo, M.,
2007. Improvement strategies for the F-Race
algorithm: sampling design and iterative refinement.
In: 4th International Workshop On Hybrid
Metaheuristics, 4., 2007, p. 108-122.
Beasley, J. E., 1990. OR-Library: Distributing test
problems by electronic mail. Journal of the
Operational Research Society, Oxford, v. 41, n. 11, p.
1069-1072.
Bertsimas, D., Tsitsiklis, J., 1993. Simulated annealing.
Statistical Science, Hayward, v. 8, n. 1, p. 10-15.
Birattari, M., Stützle, T., Paquete, L., Varrentrapp, K.,
2002. A racing algorithm for configuring
metaheuristics. In: Genetic apnd Evolutionary
Computation Conference, 2002, New York. p. 11-18.
Birattari, M., Yuan, Z., Balaprakash, P., Stützle, T., 2009.
F-Race and iterated F-Race: an overview. Bruxelles:
Iridia Technical Report Series. 21 p.
Blum, C., Roli, A., 2003. Metaheuristics in combinatorial
optimization: overview and conceptual comparison.
ACM Computing Surveys, v. 35, n. 3, p. 268-308.
Calvet, L.; Juan, A. A.; Serrat, C.; Ries, J. 2016. A
statistical learning based approach for parameter fine-
tuning of metaheuristics. SORT (Statistics and
Operations Research Transactions), v. 40, n. 1, p. 201-
224.
Cerny, V., 1985. Thermodynamical approach to the
traveling salesman problem: an efficient simulation
algorithm. Journal of Optimization Theory and
Applications, v. 45, p. 41-51.
Dobslaw, F., 2010. A parameter tuning framework for
metaheuristics based on design of experiments and
artificial neural networks. In: Sixth International
Conference On Natural Computation, 6., 2010, Cairo,
p. 1-4.
Holland, J. H., 1975. Adaptation in natural and artificial
systems. Boston: University of Michigan Press, 211 p.
Hutter, F., Hoos, H., Leyton-Brown, K., Stützle, T., 2009.
ParamILS: an automatic algorithm configuration
framework. Journal of Artificial Intelligence Research,
v. 36, p. 267-306.
Kirkpatrick, S., Gelatt, C. D., Vecchi, M. P., 1983.
Optimization by simulated annealing. Science,
London, v. 220, n. 4598, p. 671-680.
Lessmann, S.; Caserta, M.; Arango, I. M., 2011. Tuning
metaheuristics: A data mining based approach for
particle swarm optimization. Expert Systems with
Applications, v. 38, n. 10, New York: Pergamon Press,
p. 12826-12838.
Maron, O., Moore, A. W., 1994. Hoeffding races:
accelerating model selection search for classification
and function approximation. Advances in Neural
Information Processing Systems, San Mateo, p. 59-66.
Montgomery, D. C., 2012. Design and analysis of
experiments. 8th ed. New Jersey: John Wiley & Sons
Inc.. 699 p.
Neumüller, C.; Wagner, S.; Kronberger, G.; Affenzeller,
M., 2011. Parameter Meta-optimization of
Metaheuristic Optimization Algorithms. In: 13th
International Conference on Computer Aided Systems
Theory (EUROCAST 2011), 13., 2011, Las Palmas de
Gran Canaria, p. 367-374.
Ries, J.; Beullens, P.; Salt, D., 2012. Instance-specific
multi-objective parameter tuning based on fuzzy logic.
European Journal of Operational Research, v. 218, p.
305-315.
Schmidt, G., 2000. Scheduling with limited machine
availability. European Journal of Operational
Research, Amsterdam, v. 121, p. 1-15.
Talbi, E.G., 2003. Metaheuristics: from design to
implementation. New Jersey: John Wiley & Sons Inc.,
593 p.
ICORES 2017 - 6th International Conference on Operations Research and Enterprise Systems
210