Decomposition of the Cardiac and Respiratory Components from

Impedance Pneumography Signals

Marcel Mły

nczak

and Gerard Cybulski

1,2

Institute of Metrology and Biomedical Engineering, Faculty of Mechatronics, Warsaw University of Technology,

Boboli 8, 02-525, Warsaw, Poland

Department of Applied Physiology, Mossakowski Medical Research Centre, Polish Academy of Sciences, Pawinskiego 5,

02-106 Warsaw, Poland

Keywords:

Ambulatory Monitoring, Impedance Pneumography, Cardiorespiratory Activity, Decomposition.

Abstract:

Impedance pneumography (IP) measures changes of thoracic electrical impedance connected with change of

the air volume in the lungs. The electrode conﬁguration used in IP applications causes that electrical heart

activity is visible in the IP signals. The aim of this paper is to assess the opportunity to decompose both respi-

ratory and cardiac components and its quality using various methods. Ten students performed static breathing

sequences, intended both for calibration and testing. Our prototype, Pneumonitor 2, and the reference pneu-

motachometer, were used. The accuracy of calculating tidal volume and heart rate, the calibration procedure

and the time of analysis, were considered. Mean 86.5% accuracy of tidal volume calculating and only 2.7%

error of heart rate estimation were obtained using moving average smoothing ﬁlters, for simple short record-

ing of free breathing calibration procedure, in three body positions. More sophisticated adaptive ﬁltering also

provided good accuracy, however the processing time was 100-times higher, compared to simple methods.

It seems impedance pneumography, without ECG, could be enough for measuring basic cardiorespiratory

activity, particularly during ambulatory recordings, in which the least disturbing equipment is desirable.

1 INTRODUCTION

1.1 Problem

In nowadays there is increasing number of conditions,

when measuring respiration activity (e.g., tidal vol-

ume, TV ) could be necessary to improve the inference

about training, diagnostics or even treatment. There is

a strong need to perform such studies during natural

functioning of the subjects, due to reliability of data

gathered outside medical environment (Poupard et al.,

2008; Koivumaki et al., 2012).

However, direct method, pneumotachometry

(PNT ), could not be reliably carried out outside the

laboratory, due to its limitations (unportability and

use of face mask). From that perspective a devel-

opment of alternative methods, which could provide

the possibility to measure ventilation can be visi-

ble (Houtveen et al., 2006; Mły

nczak and Cybulski,

2012). One of those methods is impedance pneumog-

raphy (IP), which measures changes of transthoracic

electrical impedance, based on changes of amount of

air in the lungs. It could be used both in laboratory

and ambulatory settings (Seppa et al., 2010; Seppa

et al., 2013b).

The most common way of performing impedance

measurements is tetrapolar method, in which two

electrodes apply current signal and two remaining

measure voltage, which is related to the electrical

impedance. Various electrode conﬁguration were

studied and utilized, however usually voltage elec-

trodes are positioned in the same place, on the midax-

illary line at about 5th-rib level (Seppa et al., 2013a).

This setting is similar to the one used in ambu-

latory ECG recordings, where single ﬁrst ECG lead

conﬁguration is applied. Shifting the placement from

the chest to the midaxillary line might change the

shape of the ECG signals, however it does not change

the timing relationships between particular waves and

cycles. Based on that, cardiac components were ob-

served in the IP signals, because of the electrical, not

mechanical, activity of the heart (Seppa et al., 2011).

The sample raw IP signal, obtained during the pre-

liminary measurements, is presented in the Figure 1.

In order to provide accurate respiratory param-

eters (particularly peak-related values, like TV , or

MÅ

CyÅ

Dczak M. and Cybulski G.

Decomposition of the Cardiac and Respiratory Components from Impedance Pneumography Signals.

DOI: 10.5220/0006107200260033

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 26-33

ISBN: 978-989-758-212-7

Figure 1: Sample of the raw IP signal consisting of both

respiratory and cardiac components.

maximum ﬂow during inspiration and expiration)

these cardiac components should be removed and

somehow ignored from the I P signal.

However, preprocessing methods could impact on

the recorded signal. Firstly, by degrading the cor-

respondence between respiratory IP component and

reference signal in the areas of minimums and max-

imums of the signals. Secondly, due to the non-zero

mean value of the cardiac component of the IP signal

between the beginning of P wave and the ending of T

wave, particularly caused by QRS cycle and T wave.

1.2 Related Work

The problem has already been observed in the past

and some algorithms were used or introduced in the

literature, as in the author’s previous paper (Mły

nczak

et al., 2015).

Apart from simple ﬁltration or moving average,

Savitzky-Golay-related smoothing method was car-

ried out, due to its well performance at minimums

and maximums (Savitzky and Golay, 1964). For the

graphical comparison the basic methods were applied

on the sample raw IP signal and the outputs were

showed in the Figure 2.

There are also more sophisticated approaches pre-

sented in the literature. Seppa et al. proposed

the method to remove cardiac components adaptively

based on simultaneous recording of ECG, which was

inspired from Schuessler’s work on removing cardio-

genic oscillations from esophageal pressure signals

(Seppa et al., 2011; Schuessler et al., 1998). Reinsh

et al. and Schoenberg et al. suggested smoothing

splines (Reinsch, 1967; Schoenberg, 1964; Poupard

et al., 2008). Yasuda and Barros offered the method

of ﬁltering non-correlated noise in impedance cardio-

graphy, which could be applied for impedance pneu-

mography too (Barros et al., 1995).

Figure 2: The comparison of basic ﬁltration methods out-

puts applied on the sample raw IP signal.

Empirical Modes Decomposition (EMD) and En-

semble Empirical Modes Decomposition (EEMD)

were also evaluated, however the choice of modes,

which are strictly related to respiratory activity, was

not clear and trivial (Wang et al., 2016). From the

other hand, wavelet denoising, based on different

wavelets families, seems to be reliable tool to remove

cardiac component in the IP signal as well (Math-

works, 2016).

Adaptive ﬁltering and Scaled Fourier Linear Com-

biner (SFLC) was used by Yasuda et al. to assess

obstructive sleep apnea and central hypopnea based

on changes of thoracic impedance and HRV (Yasuda

et al., 2005). Cardiac-related artefacts could be also

attenuated during motion artefact removing process,

presented in Ansari et al. work (Ansari et al., 2016).

However, it is worth noted, that cardiac-related

component in the IP signal was usually treated as

noise (Seppa et al., 2010), and still all mentioned al-

gorithms intended to remove cardiac component from

the IP signal, in order respiratory one to be as shape-

connected to reference as it possible.

1.3 Objectives

Consequently, it seems important to evaluate whether

there is the possibility to separate both components

in IP signal and use both of them as valuable sig-

nals; respiratory component to calculate quantitative

volume-, ﬂow- and time-related parameters, and car-

diac one to measure heart rate (HR), tachogram and

heart rate variability (HRV ) parameters.

Therefore, the aim of this paper is to assess

the quality of various preprocessing methods, which

could be applied on raw IP signal in order to separate

respiratory and cardiac components, concerning ﬁve

Decomposition of the Cardiac and Respiratory Components from Impedance Pneumography Signals

aspects:

• What calibration procedure could provide the best

data for further measurements?

• What are determination coefﬁcients (R

) of the

calibration model between respiratory component

of IP to the reference for calibration data?

• What are inspiratory and expiratory tidal volumes

(TV

& TV

) between respiratory component of

IP to the reference for testing data?

• Is cardiac component subtracted from raw signal

is comparable to the single-lead E CG signal in

terms of HR and HRV calculation possibilities?

• What is the analysis duration and complexity?

The goal of the work is to indicate the most ro-

bust algorithm from both respiratory, and cardiac per-

spective. Different compromise approaches were dis-

cussed.

2 METHODS

2.1 Subjects & Devices

The participants of the study were 10 generally

healthy students (all males, without any respiratory

disease reported), who were informed about the aim

of the study and wrote the consents.

The Table 1 presents the basic information about

the study group.

Table 1: Information about the study participants.

Minimum Mean Maximum

Weight [kg] 65.0 77.4 100.0

Height [cm] 171.0 179.3 187.0

BMI 20.75 24.14 33.41

Age 19 23 27

The Flow Measurement System with a Spirometer

Unit M909 and a Fleisch-type Heatable Flow Trans-

ducer 5530, with a Conical Mouthpiece M9114 con-

nected to the PNT sensor, was used without any re-

sistance as a reference device, made by Medikro Oy

(Kuopio, Finland). The system was calibrated with

the 3L syringe to provide accurate ﬂow values every-

day.

IP signals were gained from our impedance pneu-

mography prototype, Pneumonitor 2, which also en-

ables to measure ECG signal and motion (from 3-axis

accelerometer module). Single-lead ECG signal from

our prototype was treated as reference to analyze car-

diac components extracted from IP.

Originally, sampling frequency of the reference

device was 200Hz, however due to the Pneumonitor

2 setting ( f

= 250Hz), all signals were transformed

(interpolated) to that sampling frequency.

2.2 Protocol & Analysis

The scheme of analysis is presented in the Figure 3.

PNT

Filtering

Detrending

Integration

Breathing phases

establishing

Applying calibration coefﬁcients

Preprocessed IP

Integrated PNT

Calibration

Filtering

Detrending

Preprocessed IP

Decomposition

PNT

Integration

Integrated PNT

ECG

HRV curve

estimating & analysis

Cardiac IP Respiratory IP

Inspiration & Expiration

TV calculating & analysis

Calibration

Main measurements

Figure 3: The scheme of analysis, distinguishing signals,

operations and ﬁnal analyses; the whole is performed for

each body position separately.

In order to deal with ﬁrst question marked in ob-

jective subsection, we proposed three types of cali-

bration protocols, regarding time of registration and

breathing regularity:

1. free breathing registered for 30 seconds, consid-

ered as the simplest and the quickest procedure,

hereafter called ’Calibration Procedure 1’,

2. free breathing recorded for 2 minutes, to evalu-

ate the impact of longer measurement, hereafter

called ’Calibration Procedure 2’,

3. ﬁxed breathing, shallow and deep alternately, 4

times each, for three frequencies, 6, 10 and 15

breaths per minute (BPM), to check, whether

adding various rates and depths of breathing may

improve the calibration quality meaningly, here-

after called ’Calibration Procedure 3’.

As we observed, body position has signiﬁcant im-

pact on the values of calibration coefﬁcients provided

for each subjects, therefore all 3 calibration procedure

were performed in three body positions (supine, sit-

ting and standing).

Finally, we asked to perform the test procedure

consisting of 6 normal breaths and then 6 deep breaths

(the difference was subjective), for three breathing

rates (6, 10 and 15 BPM) and for three body posi-

tions (listed above). That data were also used to per-

form calibration (hereafter called ’Calibration Pro-

cedure 4’), in order to evaluate the largest possible

BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing

accuracy, due to use of the same measurement both

for calibration and for testing.

The reference breathing phases for each recording

were calculated using simple amplitude thresholding

of the ﬂow-related raw PNT signal. Three states, in-

spiration, expiration and breathing pause, were auto-

matically marked. Some heuristics were also added

in order to remove the artefacts and very short phases

and errors. Then, the volume-related reference sig-

nals were obtained by linearly detrended integration,

using Simpson’s rule, of pneumotachometry signal.

All IP signals (intended both for calibration and

for testing purposes) were next processed by various

techniques, listed below:

1. Moving average smoothing with 0.5 second win-

dow, considered as mild one.

2. Moving average smoothing with 1 second win-

dow, as proposed by Koivumaki et al. (Koivumaki

et al., 2012).

3. Moving average smoothing with 1.5 second win-

dow, intended to be strong one.

4. Savitzky-Golay 2nd-order ﬁlter with 25 probes

window (Savitzky and Golay, 1964).

5. Savitzky-Golay 7th-order ﬁlter with 25 probes

window.

6. Subtraction of raw IP signal and the noise com-

ponent from least mean square adaptive ﬁltration,

then smoothed by 200 ms window.

7. The same subtraction as in algorithm 6, however

smoothed stronger, by 400 ms window.

8. The process of 25-fold decimation (performed

twice using 5-fold coefﬁcient), then applying 10th

order least-square FIR ﬁlter with 1 Hz pass and

2.5 Hz stop frequencies, at the end the spline inter-

polation to return to original sampling frequency.

9. The same process as in algorithm 8, but use of

10th order stable Chebyshev IIR 1 Hz pass fre-

quency ﬁlter.

10. Wavelet denoising using soft heuristic SURE

thresholding and scaled noise option, on detail

coefﬁcients obtained from the decomposition at

level 5 by ’sym8’ wavelet.

11. Wavelet denoising using minimax thresholding at

level 5 by ’db5’ wavelet.

12. Smoothing Splines, presented by Reinsh (Rein-

sch, 1967).

The output of each algorithm was treated as a res-

piratory component in IP signal.

The calibration was performed by calculating the

single coefﬁcient from linear modeling of the volume-

related reference and processed respiratory IP com-

ponent, after detrending and mean removal (the post-

processing removes the need to take into account the

intercept coefﬁcient of linear modeling). The cali-

bration was performed for signals gained during each

breathing protocols and for all three body positions.

The calibration coefﬁcients and determination coefﬁ-

cients of the linear model were stored.

In order to compare TV values, separate inspira-

tory and expiratory TV were estimated as the differ-

ence between the extremums before and after each

breathing phase, e.g., for inspiration, TV

was calcu-

lated as the difference between the maximum found

during short breathing pause after inspiration and

before expiration, and the minimum found during

breathing pause before that inspiration, as suggested

by Poupard et al. (Poupard et al., 2008).

ECG signals were also compared for signals mea-

sured for all three body positions. However, due to

the fact, that for 4 participants reference ECG signals

were weak during sitting and standing, only those,

which were recorded during supine position, were

taken into account. The R points were automatically

marked using simple thresholding technique.

The cardiac IP component was estimated as a dif-

ference between raw signal and respiratory compo-

nent. We evaluated whether the possibility to extract

the R points from cardiac IP component was linked

with the equivalent of signal-to-noise ratio (SN, as-

sumed as the ratio between mean absolute value of the

cardiac IP component after mean removal, and mean

absolute value of the respiratory IP component after

mean removal as well).

All analyses were performed using MATLAB

software. The processing time of the algorithms

were measured with the computer processor Intel i5

(1200MHz), without any accelerations. It is worth

noted, that the speciﬁc numbers are of secondary im-

portance, the most essential is their mutual relation-

ship.

3 RESULTS

Breathing phases were ﬁrstly estimated from refer-

ence signal. The sample output of the algorithm for

the ﬁrst participant, from 1st calibration procedure,

for supine body position, is presented in the Fig. 4.

Next, we performed the calibration for all signals

gained from all participants. In the Fig. 5 sample rela-

tionship between respiratory IP component and refer-

ence with linear model between them, are presented.

Decomposition of the Cardiac and Respiratory Components from Impedance Pneumography Signals

Figure 4: Sample output of the algorithm to detect breathing

phases from reference PNT signal.

Figure 5: Sample relationship between respiratory compo-

nent of impedance pneumography signal and reference, and

linear calibration model.

In the Tables 2 and 3 we gathered mean determina-

tion coefﬁcients of linear models, and mean process-

ing times of the algorithms, respectively, depending

on the calibration procedures.

Further, we used calculated calibration coefﬁ-

cients to evaluate the accuracy of tidal volumes, mea-

sured both for inspiration and expiration. We gathered

all accuracies for both breathing phases in the Table 4,

distinguishing algorithm type and calibration proce-

dure. The accuracy is shown as absolute and relative

errors. We also presented the compatibility and the

Bland-Altman plots for the calculated tidal volumes,

for 1st calibration procedure and for 7th algorithm.

They are presented in the Fig. 6 and 7, respectively.

Table 2: The mean determination coefﬁcient of the linear

model, depending on the algorithm and calibration proce-

dure.

Algorithm Procedure [%]

1 2 3 4

1 94.2 91.1 92.2 92.1

2 95.3 91.2 92.3 92.2

3 94.4 89.6 92.0 92.0

4 82.8 82.7 90.8 90.2

5 79.5 79.9 90.1 89.5

6 90.9 88.9 91.8 91.5

7 93.3 90.6 92.1 91.9

8 93.1 90.6 92.0 91.8

9 3.7 11.4 46.8 50.2

10 91.2 89.1 91.6 91.2

11 88.7 87.2 91.6 91.1

12 92.9 87.2 91.6 91.6

Table 3: The mean processing times of the algorithm, de-

pending on the calibration procedure.

Algorithm Procedure

1 2 3 4

1 [ms] 3.4 7.1 11.4 18.3

2 [ms] 4.4 9.9 11.6 15.9

3 [ms] 5.9 11.7 13.1 19.3

4 [ms] 5.6 12.3 13.5 18.3

5 [ms] 5.5 11.6 12.5 17.3

6 [s] 0.17 1.06 1.77 3.52

7 [s] 0.16 1.06 1.70 3.73

8 [ms] 24.4 26.0 36.3 42.3

9 [s] 0.15 0.14 0.17 0.19

10 [ms] 29.9 37.6 43.5 56.1

11 [ms] 24.8 29.8 27.9 38.8

12 [s] 1.63 25.53 45.16 106.09

Then, we compared the tachograms estimated

from reference ECG and cardiac component of IP

signal for all subjects, for supine body position. The

sample signals obtained for ﬁrst subject are presented

in the Fig. 8.

The comparison of the accuracy of the heart rate

estimation for cardiac components derived from IP

signal using different algorithms is presented in the

Table 5.

The minimal overall error of cardiac calculations

from IP was obtained for third algorithm.

We observed no statistically signiﬁcant correspon-

dence between the accuracy of cardiac calculations

from IP signals, and the SN ratio.

BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing

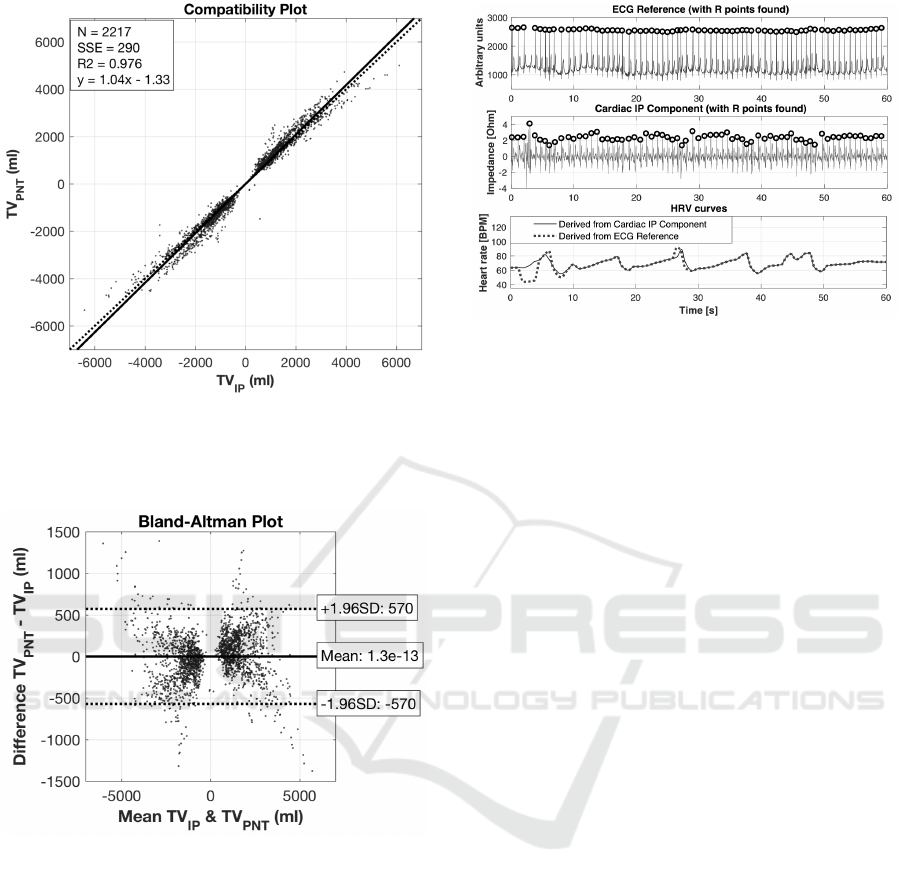
Figure 6: Compatibility plot for tidal volumes, calculated

both for inspirations’ and expirations’ values, for all partic-

ipants, for each body positions, for 1st calibration procedure

and for 7th algorithm.

Figure 7: Bland-Altman plot for tidal volumes, calculated

both for inspirations’ and expirations’ values, for all partici-

pants, for each body positions, for 1st calibration procedure

and for 7th algorithm.

4 DISCUSSION

In this work various algorithms were evaluated for

decomposition of the respiratory and cardiac com-

ponents in IP signal accuracy. Among them no one

seemed to be the best in every assessed aspect. Still

important thing remains, what will be the best criteria

for decomposition optimization.

The results showed, that from respiratory perspec-

tive moving average smoothing with short window

or 7th algorithm provided the best results, however

the time of operation was quite long for the second

Figure 8: Sample comparison of the cardiac IP component

with reference ECG signal, and the HRV curves derived

from those signals.

one. In cardiac analysis, moving average smoothing

with longer window appears to have the best compat-

ibility to ECG reference. It seems that mixing the

approaches, depending on the analyzed signal, could

give the most reliable results.

The results also demonstrated, that because of the

linear relationship between respiratory IP component

and reference volume signal, there is no need to dis-

tinguish the depth and rate of breathing during cali-

bration procedure. On the other hand, the shorter time

of calibration registration allows to get higher deter-

mination coefﬁcient of linear model, and increase the

mean accuracy of tidal volume calculation.

The purpose of the testing was not to evaluate

the accuracy of using calibration coefﬁcient indepen-

dently on body position; all results assumed different

coefﬁcients calculated for different positions.

There are some limitations of this study. There

were only 10 participants, only males - this proba-

bly had no direct impact on the results, but it seems

worth to apply the analysis in women’s signals, which

are quite different, e.g., due to the geometry of the

chest. Further, the measurements were carried out

only in static conditions, without considering motion

artifacts; and there was no multi-lead ECG reference

device. At the end, in ambulatory situations, the reg-

istrations are longer and would be more diversiﬁed,

which may affect the overall accuracy.

Therefore, future plans include performing mea-

surements during dynamic conditions, which imitate

natural functioning of subjects, and then changing the

way of pre-processing (particularly detrending part)

from ”global” approach, to the ”local” one, in order

to deal with non-linear and non-stationary drift of the

baseline impedance.

From the analytics perspective, there is a need for

Decomposition of the Cardiac and Respiratory Components from Impedance Pneumography Signals

Table 4: The comparison of tidal volume estimating accu-

racy, regarding algorithm type and calibration procedure;

all absolute errors are in milliliters, except 9th algorithm

(marked in italics), in which are in liters, and all relative

errors are in percent; statistical signiﬁcance is presented by

∗

abbreviations: A - absolute error, R - relative error, p -

p-value of paired T test.

Alg. Procedure

1 2 3 4

1 A 214.7 240.5 251.0 165.3

R 13.8 16.0 17.1 11.8

p 0.91 0.90 0.83 0.76

2 A 206.0 245.7 284.2 205.7

R 13.5 16.7 19.3 14.4

p 0.74 0.77 0.77 0.71

3 A 238.1 278.5 338.7 273.9

R 15.6 19.1 23.2 19.2

p 0.57 0.61 0.71 0.68

4 A 317.9 298.9 251.9 181.2

R 19.8 18.6 18.1 14.0

p 0.91 0.94 0.88 0.84

5 A 343.5 311.8 264.1 200.6

R 21.6 19.5 19.8 16.1

p 0.91 0.93 0.87 0.84

6 A 246.8 255.5 246.4 160.7

R 16.1 17.0 17.2 12.1

p 0.96 0.94 0.83 0.75

7 A 223.8 243.0 247.9 161.8

R 14.7 16.4 17.2 11.9

p 0.90 0.88 0.81 0.71

8 A 234.3 251.2 240.1 153.0

R 14.9 16.5 16.5 11.2

p 0.99 0.99 0.88 0.80

9 A 1.60 1.49 1.19 1.13

R 97.1 92.0 85.5 82.2

p 0.94 0.72 0.01

∗

0.00

∗

10 A 246.6 258.4 248.0 162.3

R 15.7 16.9 17.0 11.8

p 0.94 0.96 0.92 0.90

11 A 267.9 273.1 249.3 165.5

R 17.1 17.7 17.3 12.3

p 0.92 0.94 0.92 0.89

12 A 309.9 320.9 379.2 317.4

R 19.3 21.6 26.2 22.5

p 0.56 0.59 0.72 0.74

further improvement and assessment of the compo-

nents’ decomposition, e.g., using time series algo-

rithms utilized in econometrics ﬁeld.

The possibility to remove the classical ECG reg-

istration from ambulatory cardiorespiratory measure-

ments in the situations, in which direct sophisticated

analysis of multi-lead ECG signal is not necessary,

has to be evaluated in the broader manner.

Table 5: The comparison of heart rate derived from car-

diac IP components and compatibility of the shape of HRV

curve; only the best algorithms are presented; ﬁfth subject

did not have any recognizable cardiac component, there-

fore was removed from presenting; abbreviations: A - abso-

lute error [BPM], R - relative error in percent, CC - cross-

correlation coefﬁcient between HRV curves derived from

ECG reference and cardiac IP component, SN - the equiva-

lent of signal-to-noise ratio.

Subject Algorithm

2 3 7 12

1 A −0.05 −0.18 0.47 −0.16

R −0.1 −0.3 0.7 −0.2

CC 0.44 0.45 0.83 0.40

SN 0.09 0.10 0.06 0.09

2 A 3.91 1.26 1.68 3.70

R 5.8 1.9 2.5 5.5

CC 0.46 0.40 0.38 0.50

SN 0.40 0.46 0.32 0.51

3 A 2.17 −1.04 −3.99 −2.53

R 3.2 −1.5 −6.0 −3.8

CC 0.40 0.54 0.51 0.48

SN 0.15 0.17 0.13 0.19

4 A 0.66 1.38 −0.12 0.66

R 1.1 2.3 −0.2 1.1

CC 0.43 0.60 0.28 0.43

SN 0.56 0.57 0.53 0.56

6 A 17.25 8.38 28.86 12.26

R 32.7 15.9 54.6 23.2

CC −0.03 −0.09 0.09 0.01

SN 0.34 0.42 0.26 0.43

7 A 0.01 0.01 0.02 0.01

R 0.01 0.02 0.02 0.02

CC 1.0 1.0 1.0 1.0

SN 0.25 0.26 0.22 0.25

8 A 0.05 0.05 0 0.05

R 0.1 0.1 0 0.1

CC 0.98 0.98 1.0 0.98

SN 0.20 0.22 0.20 0.21

9 A 0.02 0.03 0.02 0.02

R 0.02 0.04 0.02 0.02

CC 1.0 0.91 1.0 1.0

SN 0.32 0.37 0.31 0.39

10 A 5.62 1.44 0.87 1.61

R 8.6 2.2 1.3 2.5

CC −0.02 0.28 0.34 0.33

SN 0.13 0.15 0.11 0.15

5 CONCLUSIONS

Impedance pneumography could be used to measure

respiratory activity, intended primarily for ambulatory

conditions. In order to get volume values, the calibra-

BIOSIGNALS 2017 - 10th International Conference on Bio-inspired Systems and Signal Processing

tion for each participant is needed. However, short

recording of free breathing, for various body posi-

tions, seemed to be enough to get the highest accuracy

of tidal volume estimation.

Raw impedance signal obtained from the chest

consists of both respiratory and cardiac components,

the second most commonly regarded as an element

to be removed. The study showed, that there is the

possibility to measure and extract each component

from impedance pneumography separately, with re-

liable accuracy, 86.5% and 97.3%, respectively for

tidal volume and heart rate estimation.

Simple moving average smoothing (with 1s win-

dow for respiratory analysis, and with 1.5s window

for cardiac one) were the best algorithm regarding

compromise between tidal volume and heart rate ac-

curacy, and time of processing. More sophisticated

adaptive ﬁltering also provided good accuracy, how-

ever the processing time was 100-times higher, com-

paring to simple methods.

Cardiac component is not equally visible in ev-

ery participant, however obtained compatibility be-

tween ECG reference seems promising, particularly

concerning ambulatory long-term measurements.

ACKNOWLEDGEMENTS

This study was supported by the research programs of

institutions the authors are afﬁliated with.

REFERENCES

Ansari, S., Ward, K., and Najarian, K. (2016). Motion Ar-

tifact Suppression in Impedance Pneumography Sig-

nal for Portable Monitoring of Respiration: an Adap-

tive Approach. IEEE J. Biomed. Heal. Informatics,

11(4):1–1.

Barros, A. K., Yoshizawa, M., and Yasuda, Y. (1995). Fil-

tering noncorrelated noise in impedance cardiogra-

phy. IEEE Transactions on Biomedical Engineering,

42(3):324–327.

Houtveen, J. H., Groot, P. F. C., and De Geus, E. J. C.

(2006). Validation of the thoracic impedance derived

respiratory signal using multilevel analysis. Int. J.

Psychophysiol., 59(2):97–106.

Koivumaki, T., Vauhkonen, M., Kuikka, J. T., and Haku-

linen, M. a. (2012). Bioimpedance-based measure-

ment method for simultaneous acquisition of respi-

ratory and cardiac gating signals. Physiol. Meas.,

33(8):1323–1334.

Mathworks (2016). Wavelet Denoising.

http://www.mathworks.com/help/wavelet/ug/wavelet-

denoising.html. [Online; accessed 07-August-2016].

Mły

nczak, M. and Cybulski, G. (2012). Impedance pneu-

mography: Is it possible? In XXX Symp. Photonics

Appl. Astron. Commun. Ind. High-Energy Phys. Exp.

(Wilga 2012), volume 8454, pages 84541T–19.

Mły

nczak, M., Niewiadomski, W.,

Zyli

nski, M., and Cybul-

ski, G. (2015). Veriﬁcation of the Respiratory Param-

eters Derived from Impedance Pnumography during

Normal and Deep Breathing in Three Body Postures.

In IFMBE Proc., volume 45, pages 162–165.

Poupard, L., Mathieu, M., Sart

ene, R., and Goldman, M.

(2008). Use of thoracic impedance sensors to screen

for sleep-disordered breathing in patients with cardio-

vascular disease. Physiol. Meas., 29(2):255–267.

Reinsch, C. H. (1967). Smoothing by spline functions. Nu-

merische Mathematik, 10(3):177–183.

Savitzky, A. and Golay, M. J. E. (1964). Smoothing and

Differentiation of Data by Simpliﬁed Least Squares

Procedures. Anal. Chem., 36(8):1627–1639.

Schoenberg, I. J. (1964). Spline functions and the problem

of graduation. Proceedings of the National Academy

of Sciences, 52(4):947–950.

Schuessler, T. F., Gottfried, S. B., Goldberg, P., Kearney,

R. E., and Bates, J. H. T. (1998). An adaptive ﬁlter

to reduce cardiogenic oscillations on esophageal pres-

sure signals. Ann. Biomed. Eng., 26(2):260–267.

Seppa, V. P., Hyttinen, J., Uitto, M., Chrapek, W., and

Viik, J. (2013a). Novel electrode conﬁguration for

highly linear impedance pneumography. Biomed. Eng.

/ Biomed. Tech., 58(1):35–38.

Seppa, V.-P., Hyttinen, J., and Viik, J. (2011). A method

for suppressing cardiogenic oscillations in impedance

pneumography. Physiol. Meas., 32(3):337–345.

Seppa, V. P., Uitto, M., and Viik, J. (2013b). Tidal breath-

ing ﬂow-volume curves with impedance pneumogra-

phy during expiratory loading. In Proc. Annu. Int.

Conf. IEEE Eng. Med. Biol. Soc. EMBS, volume 2013,

pages 2437–2440.

Seppa, V.-P., Viik, J., and Hyttinen, J. (2010). Assessment

of pulmonary ﬂow using impedance pneumography.

IEEE Trans. Biomed. Eng., 57(9):2277–2285.

Wang, Z., Wu, D., Chen, J., Ghoneim, A., and Hossain,

M. A. (2016). A Triaxial Accelerometer-Based Hu-

man Activity Recognition via EEMD-Based Features

and Game-Theory-Based Feature Selection. IEEE

Sens. J., 16(9):3198–3207.

Yasuda, Y., Umezu, A., Horihata, S., Yamamoto, K.,

Miki, R., and Koike, S. (2005). Modiﬁed thoracic

impedance plethysmography to monitor sleep apnea

syndromes. Sleep Med., 6(3):215–224.

Decomposition of the Cardiac and Respiratory Components from Impedance Pneumography Signals