Color-based and Rotation Invariant Self-similarities

Xiaohu Song, Damien Muselet and Alain Tremeau

Univ. Lyon, UJM-Saint-Etienne, CNRS, LaHC UMR 5516, F-42023, Saint-Etienne, France

Keywords:

Color Descriptor, Self-similarity, Classiﬁcation, Invariance.

Abstract:

One big challenge in computer vision is to extract robust and discriminative local descriptors. For many

applications such as object tracking, image classiﬁcation or image matching, there exist appearance-based

descriptors such as SIFT or learned CNN-features that provide very good results. But for some other applica-

tions such as multimodal image comparison (infra-red versus color, color versus depth, ...) these descriptors

failed and people resort to using the spatial distribution of self-similarities. The idea is to inform about the

similarities between local regions in an image rather than the appearances of these regions at the pixel level.

Nevertheless, the classical self-similarities are not invariant to rotation in the image space, so that two rotated

versions of a local patch are not considered as similar and we think that many discriminative information is

lost because of this weakness. In this paper, we present a method to extract rotation-invariant self similarities.

In this aim, we propose to compare color descriptors of the local regions rather than the local regions them-

selves. Furthermore, since this comparison informs us about the relative orientations of the two local regions,

we incorporate this information in the ﬁnal image descriptor in order to increase the discriminative power of

the system. We show that the self similarities extracted by this way are very discriminative.

1 INTRODUCTION

Evaluating self-similarities within an image consists

in comparing local patches from this image in or-

der to determine, for example, the patch pairs that

look similar. This information is used for super-

resolution (Glasner et al., 2009; Chih-Yuan et al.,

2011), denoising (Zontak and Irani, 2011), inpaint-

ing (Wang et al., 2014), ... The spatial distribution of

the self-similarities within each image is also a ro-

bust and discriminative descriptor that is very use-

ful in some applications. Indeed, in order to com-

pare images that look very different because of light

variations, multi-modality (infrared versus color sen-

sors) or, for example, the images of ﬁgure 1, the

appearance-based descriptors such as SIFT (Lowe,

1999) or Hue histograms (van de Weijer and Schmid,

2006) completely fail whereas the self-similarities

provide accurate information (Kim et al., 2015). We

can note that CNN features (Krizhevsky et al., 2012)

do not cope with this problem because they are based

on learned convolutional ﬁlters that can not adapt

themselves alone to a new modality. Consequently,

these deep-features have been recently mixed with

self-similarities in order to improve the results (Wang

et al., 2015).

The idea of self-similarity consists in describing

the content of the images by informing how similar

are some local regions from each other (Shechtman

and Irani, 2007; Chatﬁeld et al., 2009; Deselaers and

Ferrari, 2010). By this way, when two red and tex-

tured regions are similar in an image, their contribu-

tion to the ﬁnal descriptor will be the same as this

of two green and homogeneous regions. This repre-

sentation is also invariant to any illumination condi-

tion variations, to changes in the colors of the objects

(a red bike will have the same description as a blue

one) and to modiﬁcations of the textures. For exam-

ple, the ﬁgures {1(c), 1(e), 1(g)}, {1(j), 1(l), 1(n)}

and {1(q), 1(s), 1(u)} show some self-similarities

we have evaluated from the 3 images 1(a), 1(h) and

1(o) respectively. For this aim, we have extracted

3 patches {1(b), 1(d), 1(f)}, {1(i), 1(k), 1(m)} and

{1(p), 1(r), 1(t)} at corresponding positions in each

image 1(a), 1(h) and 1(o) repectively and we have

evaluated the similarities between each of this patch

with all the patches in the corresponding images. We

can see that the similarities remain stable across varia-

tions in colors and textures and consequently their lo-

cal (Shechtman and Irani, 2007; Chatﬁeld et al., 2009)

or global (Deselaers and Ferrari, 2010) spatial distri-

bution can be used to efﬁciently describe the contents

of the images.

344

Song X., Muselet D. and Tremeau A.

Color-based and Rotation Invariant Self-similarities.

DOI: 10.5220/0006107503440351

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 344-351

ISBN: 978-989-758-225-7

(a)

(b) (c)

(d) (e)

(f) (g)

(h)

(i) (j)

(k) (l)

(m) (n)

(o)

(p) (q)

(r) (s)

(t) (u)

Figure 1: The images 1(a), 1(h) and 1(o) represent the same symbol but do not share any shape or color information at the

pixel level. The local patches numbered 1 (1(b), 1(i), 1(p)), 2 (1(d), 1(k), 1(r)) and 3 (1(f), 1(m) and 1(t)) are extracted

from similar relative positions in these 3 images. The ﬁgures 1(c), 1(j), 1(q), 1(e), 1(l), 1(s), 1(g), 1(n) and 1(u) represent the

similarities (evaluated with our method) between these respective patches and the image from where they have been extracted.

They represent self-similarities.

In this context, the classical approaches propose

to extract the similarity between two local patches

by evaluating their correlation (Shechtman and Irani,

2007; Chatﬁeld et al., 2009). The drawback of the

correlation is that it is based on a pixelwise multipli-

cation and hence is not invariant to rotation. Indeed,

the similarity between two patches can be very low if

the ﬁrst one of these patches is a rotated version of

the second one. The image 2(c) represents the simi-

larities between the patch 2(b) extracted from the im-

age 2(a) and all the patches in the image 2(a) with the

correlation-based method. We can see that only a part

of the bike frame is detected by this way because the

orientations of the other parts of the frame are differ-

ent.

In this paper, we propose to associate each patch

in an image with one particular spatio-colorimetric

descriptor and to evaluate the similarity between two

patches by comparing their descriptors. The proposed

descriptor represent both the colors of the pixels in the

patch and their relative spatial positions while being

invariant to rotation. In order to design this descrip-

tor we exploit the work from Song et al. (Song et al.,

2009). The similarities evaluated by this way are dis-

played in the image 2(d). In this case, we can see that

almost the whole frame of the bike can be detected

whatever the orientation of each part. Furthermore,

we will show that our descriptor-based self-similarity

evaluation provides us the information of the angle

difference between the orientations of the two com-

pared patches and that this information can be intro-

duced in the representation of the spatial distribution

of the self-similarities in an image.

In the second part of this paper, we present how

the classical approaches extract the self-similarities

from the images and how they represent their spa-

tial distribution. Then, in the third part, we intro-

duce our new local spatio-colorimetric descriptor on

which is based our self-similarity evaluation. We pro-

pose to represent the spatial distribution of the self-

similarities by a 3D structure presented in the fourth

part. The ﬁfth part is devoted to the experimental re-

sults obtained in object classiﬁcation task and we con-

clude in the sixth part.

2 RELATED WORKS

Shechtman et al. have designed a local descriptor

based on self-similarity (Shechtman and Irani, 2007;

Kim et al., 2015). Considering one patch, the idea

consists in measuring the similarity between it and its

Color-based and Rotation Invariant Self-similarities

345

(a) (b)

Figure 2: The images 2(c) and 2(d) represent the similarities between the patch 2(b) extracted from the image 2(a) and all the

patches in the image 2(a) with the correlation-based method (2(c)) and with our descriptor-based method (2(d)).

surrounding patches. To determine the similarity be-

tween two patches, they propose ﬁrst to evaluate the

pixelwise sum of square differences (SSD) and second

they transform this distance to a similarity measure

SM = exp(−

SSD

) where σ is related to the variance

of all the SSD locally evaluated. Then, the neigh-

borhood of the considered patch is discretized on a

log-polar grid and the maximal value of SM is stored

within each bin grid. Chatﬁeld et al. have also shown

that the use of this local description provide better re-

sults than appearance-based descriptors such as SIFT

for matching non-rigid shape classes (Chatﬁeld et al.,

2009).

Deselaers et al. argue that in the context of ob-

ject classiﬁcation and detection, the self-similarities

should be evaluated globally rather than locally (De-

selaers and Ferrari, 2010). Thus, they proposeto com-

pare each patch with all the patches in the image.

Since this approach is highly time consuming, they

propose an alternative to the classical pixelwise simi-

larity evaluation that is based on the bag-of-words ap-

proach. Indeed, they associate each patch with a vec-

tor which can be its discrete cosine transform (DCT)

or the patch itself (reshaped into a vector) and apply

a k-means clustering in this vector space in order to

get the most frequent vectors. Then, giving a patch,

they evaluate its distance with all the cluster represen-

tatives and associate it with the nearest neighbor. By

this way the similarity measure between two patches

is a binary value, 1 if the patches are associated with

the same cluster representatives and 0 if not. In order

to design their global descriptor, called SSH for Self-

Similarity Hypercube, Deselaers et al. ﬁrst propose

to project a regular D

grid onto the image. Then,

they evaluate the similarity between all the patches

in one grid cell GC

and all the patches in the im-

age. This returns a correlation surface whose size is

the same as the image size. Then, they sub-sample

this correlation surface to the size D

and put it in

the grid cell GC

. By doing that for all the grid cells

, i = 1,...,D

, they obtain their 4D SSH of

size D

which represent the global repar-

tition of the self-similarities in the image.

In these main works, the self-similarities are eval-

uated either by using pixelwise correlation between

patches or by comparing the indexes of the associ-

ated cluster representatives of the two patches. In the

ﬁrst case, the extraction of the self-similarities can be

highly time consuming and in the second case, the

similarity between two patches is a binary value, 0

or 1. Furthermore, the results provided by the sec-

ond approach are highly dependent on the quality of

the clustering step. Consequently, we propose another

approach that speed up the self-similarity evaluation

while giving a real value as similarity measure be-

tween two patches. Therefore, we propose to evaluate

a color descriptor of each patch and then to evaluate

a similarity measure between these descriptors. Since

these descriptorsare not dependent on the orientations

of the patches, our self similarities are rotation invari-

ant. This is illustrated in Fig.2, where we can see

that the classical correlation-based approaches (image

2(c)) can not detect all the self-similarities in the im-

age whereas the self-similarities detected by our ap-

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

346

proach in image 2(d) clearly underline the discrimi-

native power of the proposed color descriptor as well

as its rotation invariance. Our local descriptor is in-

troduced in the next section.

3 ROTATION INVARIANT

DESCRIPTOR

In this section, we present our spatio-colorimetric de-

scriptor used to evaluate the self-similarities. There-

fore, we propose to exploit the paper from Song et

al. (Song et al., 2009). The main idea of this paper,

presented in the next paragraph, consists in applying

an afﬁne transform from image space to color space in

order to design a local descriptor. Nevertheless, this

descriptor requires a rotation invariant local region

detection in order to be invariant to rotation. In the

context of self similarity extraction, the image (or a

part of the image) is dense sampled in order to extract

patches at regular positions and to evaluate the simi-

larity between each pair of patches. If the descriptor

of each patch is not stable across rotation in the image,

the extracted self-similarities will not be invariant to

rotation. Consequently, in the second paragraph we

propose to extend the approach of Song et al. in order

to design a new rotation invariant descriptor.

3.1 The Spatio-colorimetric Descriptor

from Song et al. (Song et al., 2009)

Song et al. have proposed a way to extract a de-

scriptor from each detected local region (patch) in

an image. The main idea consists in applying an

afﬁne transform to the pixels of the considered patch,

from the image space to a color space. Thus, con-

sidering a pixel P

characterized by the 3D-position

} = {c

} in the color space Co

and the 2D-position {x

} in the patch-relative

space Pa so that the center of the patch has {0, 0} for

coordinates. Song et al. propose to deﬁne an afﬁne

transform from the patch space to the color space as:

























(1)

where t

, t

and t

are the translation parameters and

the m

are the rotation, scale and stretch parameters.

This equation can be re-written as follows:

[Af] × [Pa] = [Co].

It is based on the coordinates of one pixel but all

the pixels of the patch can be accounted by adding

columns in the matrices [Pa] and [Co]. Since there

exists no such afﬁne transform from the image space

to a color space, Song et al. propose to estimate the

best one as the least-squares solution:

Af = Co[Pa

Pa]

−1

. (2)

Once the transform parameters have been de-

termined, they apply the transform to the 4 pix-

els corresponding to the corners of the patch

and whose coordinates in the patch space are

{−sx/2, −sy/2}, {sx/2,−sy/ 2}, {−sx/2,sy/2} and

{sx/2,sy/2}, where sx and sy are the width and height

of the patch, respectively. The positions of these cor-

ners in the color space after applying the afﬁne trans-

form constitute the descriptor:

Descriptor = A f ×





−sx/2 sx/2 −sx/2 sx/2

−sy/2 −sy/2 sy/2 sy/2

1 1 1 1





(3)

The use of the least-squares solution method pro-

vides the discriminating power of the descriptor. In-

deed, the resulted destination position of a pixel de-

pends not only on its color but also on the colors and

the relative positions of the other pixels of the local

region. Thus, considering two patches characterized

by the same colors but by different spatial color ar-

rangements, the resulted descriptors will be different.

This characteristic is very interesting in the context of

object recognition.

Nevertheless, in the context of self-similarity eval-

uation, the patches are dense sampled without any in-

formation about their orientation. So, the x and y axis

of the patches are all oriented along the horizontal and

vertical directions respectively. In this case, this de-

scriptor is not stable across rotation in the image space

and we show in the next paragraph the way to reach

this invariance.

3.2 The Proposed Rotation Invariant

Descriptor

We consider two patches Pa

and Pa

so that the sec-

ond one is a rotated version of the ﬁrst one:





= Rot ×





. (4)

By applying the approach of Song et al. on these

two patches, we can determine one afﬁne transform

for the ﬁrst patch Af

= Co[Pa

]

−1

and one

for the second patch Af

= Co[Pa

]

−1

. From

equation (4), we have Pa

= Rot.Pa

and then:

Color-based and Rotation Invariant Self-similarities

347

= Co[Pa

]

−1

= Co[(Rot.Pa

)

(Rot.Pa

)]

−1

(Rot.Pa

)

= Co[Pa

.Rot

.Rot.Pa

]

−1

.Rot

= Co[Pa

.Pa

]

−1

.Rot

= Af

.Rot

(5)

because for any rotation matrix Rot, Rot

.Rot =

Identity.

By using these two transforms Af

and Af

in the

equation (3), we can see that the descriptors of the two

patches Pa

and Pa

are different. So these descrip-

tors can not be used directly in order to ﬁnd rotation

invariant self similarities in images.

However, the equation (5) shows that the trans-

forms obtained for two patches, the second patch be-

ing a rotated version of the ﬁrst, are related to each

other by the rotation applied in the patch space. Our

intuition is to use this transform itself as a descriptor

after removing the rotation from it. Since this rota-

tion is applied in the patch space, it is a 2D rotation

and can be represented by a 2x2 matrix Rot

2x2

. Thus,

we propose to rewrite the transform A f

of the patch

, k = 1 or 2, as follows:









































= Mk

3x2

+ Tk

3x1

(6)

Since each transform Af

is evaluated in the

corresponding patch Pa

relative coordinates system

(where the center of the patch has {0,0} for co-

ordinates), the translation parameters in T1

3x1

and

3x1

are the same and the only variation between

and Af

holds in the Mk

3x2

matrices. Further-

more, from equation (5), we can deduce that M2

3x2

Rot

2x2

. Our aim is to remove the rotation term

from the Mk

3x2

matrices so that they become iden-

tical. Therefore, we propose to use the QR factor-

ization tool. This factorization decomposes a matrix

3x2

into a product of a rotation matrix Qk

3x3

and

a triangular upper right matrix Rk

3x2

so that Mk

3x2

3x3

3x2

. Since the rotation matrix is applied in

the 2D patch space, it is a 2D rotation and so can

be represented by a 2x2 matrix. So we rather pro-

pose to apply the QR factorization on the transpose

of the Mk

3x2

matrix. By this way, we will obtain

3x2

= Qk

2x2

2x3

and hence Mk

3x2

= Rk

2x3

2x2

where the matrix Qk

2x2

contains the rotation part of

the matrix Mk

3x2

. Since the matrix Rk

2x3

is not sensi-

tive to rotation variation we have R1

2x3

= R2

2x3

To summarize, considering two patches, we pro-

pose to:

• evaluate the afﬁne transforms (from image space

to color space) Af

and Af

of the patches by us-

ing the Song et al. method (Song et al., 2009)

(equation (2)),

• decompose each transform Af

into two trans-

forms Mk

3x2

(rotation, scale, stretch) and Tk

3x1

(translation) (equation (6)),

• apply the QR factorization on the transposes of

the Mk

3x2

matrices giving two matrices Rk

2x3

and

2x2

Previously, we have shown that if the second patch

is a rotated version of the ﬁrst one Pa

, we have

3x1

= T2

3x1

and R1

2x3

= R2

2x3

. Consequently, we

propose to take these two matrices Tk

3x1

and Rk

2x3

as the rotation invariant descriptor for the patch Pa

Since the matrix Rk

2x3

is a triangular upper right ma-

trix, we consider only the 5 non-zero values among

its 6 values. Thus, the descriptor we propose in this

paper is constituted by only 3+ 5 = 8 values.

Thus, the advantages of our descriptor is three-

fold. First since it represents both the colors and

their relative spatial distribution in the patch space,

it is highly discriminative and so can determine if two

patches are similar or not. Second, the time process-

ing required to evaluate the similarity between two

patches is very low since each descriptor is consti-

tuted by only 8 values. Third, this descriptor is fully

invariant to rotation in the patch space. The discrim-

inative power and the rotation invariance property of

our descriptor can be checked in the ﬁgures 1 and 2.

4 REPRESENTATION OF THE

SPATIAL DISTRIBUTION OF

THE ROTATION INVARIANT

SELF-SIMILARITIES

We consider one patch Pa

in an image and we

want to represent the spatial distribution of the self-

similarities around this particular patch. If in its sur-

rounding, one other patch Pa

has similar colors spa-

tially arranged in a similar way as Pa

, the similarity

between their descriptors will be high, even if there

exists a rotation between them in the image space.

In this case, 3 values can be used to represent the

relative position and orientation of these patches: 2

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

348

values ∆x and ∆y represent the translation along the

x and the y axis respectively, and 1 value ∆θ repre-

sents the rotation angle between these two patches.

The translation values are easily obtained by evaluat-

ing the differences between the x and y coordinates of

the centers of the patches. The ∆θ can be obtained

from their respective Qk

2x2

matrix introduced in the

previous section. Indeed, these matrices represent the

rotation in the image space applied to each patch so

that they match the same position in the color space.

Consequently if the patch Pa

is rotated by an angle

and the patch Pa

by an angle θ

in order to match

the same position, the ∆θ is just the difference be-

tween these two angles. Consequently, we propose to

create a 3D structure around the patch Pa

whose axis

are ∆x, ∆y and ∆θ and to put the value of the similar-

ity between Pa

and Pa

in the cell whose coordinates

are {x

− x

− y

,θ

− θ

}, where x

and y

are the

position in the image space of the center of the patch

, k = 0 or 1. Likewise, we can do the same for

all the patches Pa

, i > 0, around Pa

in order to rep-

resent the spatial distribution of the self-similarities

around Pa

. For this, the neighborhood of the patch

is discretized into a grid of size 5x5 and the angle

axis is discretized into 4 values. The maximal sim-

ilarity is stored within one cell if several similarities

are falling in the same position. This representation is

similar to this proposed by Shechtman et al. (Shecht-

man and Irani, 2007) but since we can ﬁnd similarities

between patches with different orientations, we have

added a third dimension for the angle. The dimension

of the feature of Shechtman et al. was 4 radial inter-

vals x 20 angles = 80 while our is 100 (5 ∆x intervals

x 5 ∆y intervals x 4 angles).

5 EXPERIMENTS

5.1 Experimental Approach

The rotation invariance of our self-similarity having

been theoretically demonstrated, we propose to assess

the discriminative power of the ﬁnal descriptor and

to compare it with the other self-similarities that are

classically used in many applications, as mentioned

in the introduction. For this purpose, we consider

the context of object classiﬁcation by using the PAS-

CAL VOC 2007 dataset (Everingham et al., ). This

dataset contains 9963 images representing 20 classes.

The aim of this experiment is not to get state-of-the-

art classiﬁcation score on the considered dataset, but

rather to fairly compare the discriminative powers of

the different self-similarity descriptors. In order to

test our self-similarity, we propose to use the Bag-

of-words approach which is based on the following

successive steps:

• keypoint detection (dense sampling is used for all

tested methods),

• local descriptor extraction around each keypoint

(we use the 3D structures presented in the previ-

ous section for our method),

• clustering in the descriptor space, the cluster rep-

resentatives are called visual words (k-means is

used with 400 words for all tested methods),

• in each image, each local descriptor is associated

with the nearest visual word,

• each image is characterized by the histogram of

visual word,

• learning on the train images and classiﬁcation of

the test images (linear SVM is used for all tested

methods).

Furthermore, we propose to compare our results

with the local self-similarity descriptor (Shechtman

and Irani, 2007) and with the global self-similarity

descriptor (Deselaers and Ferrari, 2010). For both,

we use the codes provided by the authors. For the

global self-similarity descriptor, we have constructed

the SSH (with D

= D

= 10) from the image and

consider each grid cell as a feature. So, this feature is

also of dimension 100. For all the approaches, we re-

duce the dimension of the features to 32 by applying

PCA.

5.2 Results

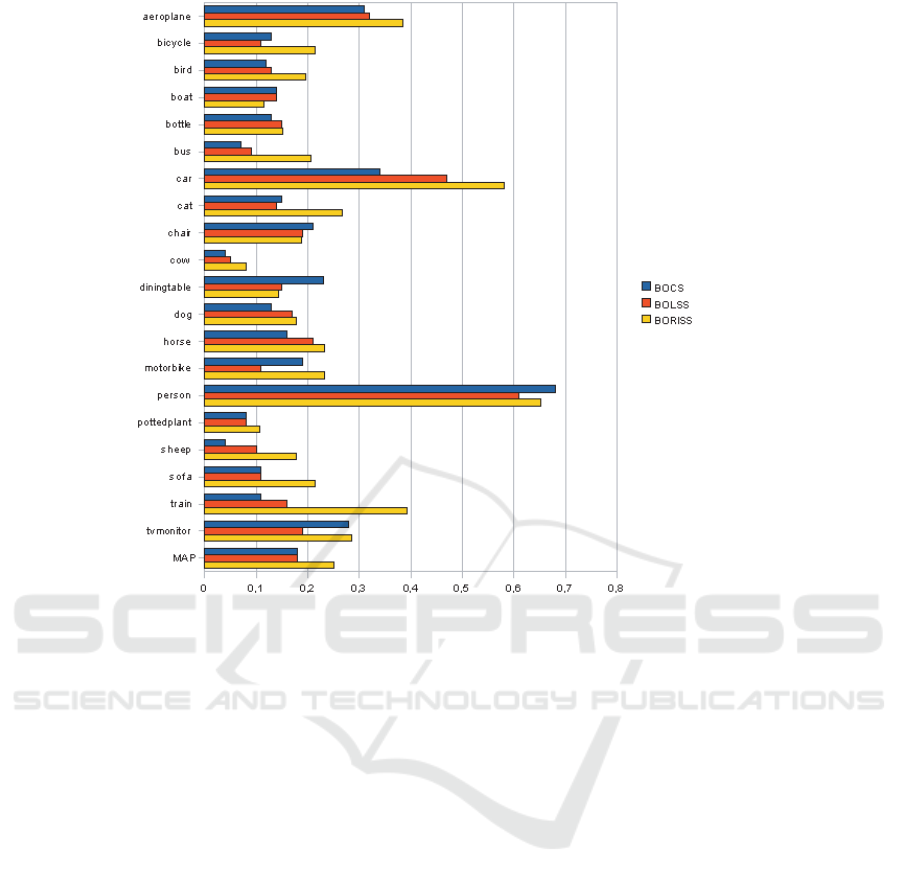
The results are shownin ﬁgure 3. In this ﬁgure, BOCS

stands for Bag Of Correlation Surfaces (Deselaers and

Ferrari, 2010), BOLSS stands for Bag Of Local Self

Similarities and BORISS is our proposed approach

and means Bag Of Rotation Invariant Self Similari-

ties.

In this ﬁgure, we can see that our approach outper-

forms the two other ones for most of the 20 classes.

Furthermore, the Mean Average Precision (MAP)

provided by our BORISS is 25% while it is around

18% for the two other approaches. This experiment

shows that the self similarities are more efﬁcient to

characterize the content of an image if they are in-

variant to the rotation. Of course, these results are

not competitive with the ones provided by SIFT or

CNN features, but the aim of these experiments was to

showthat adding color and rotation invarianceinto the

self-similarity descriptors improves the discriminat-

ing power of the ﬁnal features. These results clearly

show that our self-similarity representation is a good

candidate to be used as complementary information

with the appearance-based features.

Color-based and Rotation Invariant Self-similarities

349

(Deselaers)

(Shechtman)

(This paper)

Figure 3: Mean average precision obtained by the three tested approaches on the VOC 2007 database.

6 CONCLUSION

In this paper, we have presented a new method to rep-

resent the spatial distribution of the self-similarities in

an image. First, we have proposed to extract rotation

invariant self-similarities. This extraction is based

on a comparison of new spatio-colorimetric descrip-

tors. We have shown that these descriptors extract dis-

criminative information from local regions while be-

ing very compact and invariant to rotation. Then, we

have proposed a 3D structure to represent the spatial

distribution of these self-similarities. This structure

informs about the translation and rotation there exist

between two similar local regions. The experimental

results provided by this method outperform those of

the classical self-similarity based approaches. In this

work, we found a way to represent translation and ro-

tation that occur between self-similar regions and as

future works we are trying to add the other possible

transformation such as scale variation or stretch. Fi-

nally, the discriminative color descriptors introduced

in this paper could be used as a color texture descrip-

tor since it is representing both the colors and their

spatial distributions within the local neighborhood.

REFERENCES

Chatﬁeld, K., Philbin, J., and Zisserman, A. (2009). Efﬁ-

cient retrieval of deformable shape classes using local

self-similarities. In NORDIA workshop in conjunction

with ICCV.

Chih-Yuan, Y., Jia-Bin, H., and Ming-Hsuan, Y. (2011).

Exploiting self-similarities for single frame super-

resolution. In Proceedings of the 10th Asian Con-

ference on Computer Vision - Volume Part III, pages

497–510, Berlin, Heidelberg. Springer-Verlag.

Deselaers, T. and Ferrari, V. (2010). Global and efﬁcient

self-similarity for object classiﬁcation and detection.

In Proceedings of the IEEE Conference on Computer

Vision and Pattern Recognition (CVPR), San Fran-

cisco, DC, USA. IEEE Computer Society.

Everingham, M., Van Gool, L., Williams, C.

K. I., Winn, J., and Zisserman, A. The

PASCAL Visual Object Classes Challenge

2007 (VOC2007) Results. http://www.pascal-

network.org/challenges/VOC/voc2007/workshop/

index.html.

Glasner, D., Bagon, S., and Irani, M. (2009). Super-

resolution from a single image. In ICCV.

Kim, S., Min, D., Ham, B., Ryu, S., Do, M. N., and Sohn,

K. (2015). Dasc: Dense adaptive self-correlation de-

scriptor for multi-modal and multi-spectral correspon-

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

350

dence. In IEEE Conference on Computer Vision and

Pattern Recognition (CVPR), pages 2103–2112.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Im-

agenet classiﬁcation with deep convolutional neural

networks. In Pereira, F., Burges, C., Bottou, L., and

Weinberger, K., editors, Advances in Neural Informa-

tion Processing Systems 25, pages 1097–1105. Curran

Associates, Inc.

Lowe, D. G. (1999). Object recognition from local scale-

invariant features. In Proceedings of the IEEE Inter-

national Conference on Computer Vision (ICCV), vol-

ume 2, pages 1150–1157 vol.2. IEEE Computer Soci-

ety.

Shechtman, E. and Irani, M. (2007). Matching local self-

similarities across images and videos. In Proceedings

of the IEEE Conference on Computer Vision and Pat-

tern Recognition (CVPR).

Song, X., Muselet, D., and Tremeau, A. (2009). Local

color descriptor for object recognition across illumi-

nation changes. In ACIVS09, pages 598–605, Bor-

deaux (France).

van de Weijer, J. and Schmid, C. (2006). Coloring local fea-

ture extraction. In Proceedings of the European Con-

ference on Computer Vision (ECCV), volume 3952 of

Lecture Notes in Computer Science, pages 334–348.

Wang, J., Lu, K., Pan, D., He, N., and kun Bao, B. (2014).

Robust object removal with an exemplar-based image

inpainting approach. Neurocomputing, 123:150 – 155.

Wang, Z., Yang, Y., Wang, Z., Chang, S., Han, W., Yang,

J., and Huang, T. S. (2015). Self-tuned deep super

resolution. In IEEE Conference on Computer Vision

and Pattern Recognition Workshops (CVPRW).

Zontak, M. and Irani, M. (2011). Internal statistics of a sin-

gle natural image. In Proceedings of the IEEE Con-

ference on Computer Vision and Pattern Recognition

(CVPR).

Color-based and Rotation Invariant Self-similarities

351