Motion Error Classification for Assisted Physical Therapy
A Novel Approach using Incremental Dynamic Time Warping and
Normalised Hierarchical Skeleton Joint Data
Julia Richter, Christian Wiede, Bharat Shinde and Gangolf Hirtz
Department of Electrical Engineering and Information Technology,
Technische Universit
¨
at Chemnitz, Reichenhainer Str. 70, 09126 Chemnitz, Germany
Keywords:
Health Care, Medical Training Therapy, Support Vector Machines, Motion Sequence Matching, Incremental
Dynamic Time Warping.
Abstract:
Preventive and therapeutic measures can contribute to maintain or to regain physical abilities. In Germany,
the growing number of elderly people is posing serious challenges for the therapeutic sector. Therefore,
the objective that has been pursued in recent research is to assist patients during their medical training by
reproducing therapists’ feedback. Extant systems have been limited to feedback that is based on the evaluation
of only the similarity between a pre-recorded reference and the currently performed motion. To date, very
little is known about feedback generation that exceeds such similarity evaluations. Moreover, current systems
require a personalised, pre-recorded reference for each patient in order to compare the reference against the
motion performed during the exercise and to generate feedback. The aim of this study is to develop and
evaluate an error classification algorithm for therapy exercises using Incremental Dynamic Time Warping
and 3-D skeleton joint information. Furthermore, a normalisation method that allows the utilisation of non-
personalised references has been investigated. In our experiments, we were able to successfully identify errors,
even for non-personalised reference data, by using normalised hierarchical coordinates.
1 INTRODUCTION
With regard to our steadily ageing population, the
maintenance of each individual’s health should be a
priority for our society. Beside preventive measures,
rehabilitation with the aim of recovering physical ca-
pabilities especially after a surgery is an important as-
pect. Thus, elderly with a total hip endoprothesis, for
example, require an appropriate rehabilitation in or-
der to recover from the surgery and to restore their
mobility.
In contrast to this aim, rehabilitation facilities are
facing challenges in maintaining a high quality dur-
ing the medical training therapy because of a lack of
therapists. Recent evidence suggest that the number
of therapists is insufficient to give adequate feedback
to patients (Richter et al., 2016). Detailed feedback,
however, is necessary to ensure a correct exercise exe-
cution. Consequently, there remains an urgent need to
solve this problem. Recent research has been carried
out to support the rehabilitation process with technical
assistance systems. To date, little is known about the
recognition of typical errors that occur during certain
exercises. This study therefore seeks to investigate the
recognition of errors that are characteristic for the ex-
ercise hip abduction. Moreover, we investigated the
effect of using non-personalised reference and train-
ing data on the error recognition accuracy and present
a solution to avoid a deterioration of accuracy. This
solution encompasses the utilisation of normalised hi-
erarchical joint coordinates.
The paper is organised as follows: Section 2 gives
an overview about related work and evinces the re-
search gap. Section 3 describes the methods that were
developed to identify patients’ motions errors. More-
over, in Section 4, the evaluation methodology is in-
troduced. The results are presented and discussed in
Section 5, whereas the paper is concluded in Sec-
tion 6. Moreover, we give an outlook to future work.
2 RELATED WORK
Capturing and assessing motions in real-time is an
emergent field of research. Yurtman et al. distributed
wearable motion sensors, i. e. accelerometers, gyro-
Richter, J., Wiede, C., Shinde, B. and Hirtz, G.
Motion Error Classification for Assisted Physical Therapy - A Novel Approach using Incremental Dynamic Time Warping and Normalised Hierarchical Skeleton Joint Data.
DOI: 10.5220/0006108002810288
In Proceedings of the 6th International Conference on Pattern Recognition Applications and Methods (ICPRAM 2017), pages 281-288
ISBN: 978-989-758-222-6
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
281

scopes and magnetometers, over the human body in
order to evaluate a therapy exercise as correct or
incorrect (Yurtman and Barshan, 2013). They de-
tected occurrences of template signals in the sequence
acquired during the therapy session using Dynamic
Time Warping (DTW). Tormene et al. matched data
with the help of DTW for post-stroke rehabilitation
(Tormene et al., 2009). The data was obtained from
strain sensors worn into a long-sleeve shirt. Tak et al.
presented an approach for human abnormality detec-
tion in video sequences (Tak et al., 2011). They cal-
culated distance curves from the detected foreground
regions in each image and performed a Fourier trans-
form on every distance curve. After that, they de-
duced motion similarities by comparing a predefined
human motion sequence with the motion that was per-
formed by the user in real-time. For this step, they
applied DTW and Dynamic Group Warping.
Especially since the launch of the Kinect ver-
sion 1.0 in 2010, researchers investigated assessment
methods using the skeleton that is detected in depth
images using the algorithm of Shotton et al. (Shot-
ton et al., 2013). Recent work focused on the evalu-
ation of motions during sports, such as dancing, bal-
let training and Tai Chi exercises, using the Kinect
skeleton. Since our application is similar to this type
of training, relevant principles are briefly described
in the following. Huang et al. applied DTW to com-
pare a pre-recorded reference sequence from a teacher
against the dancing motion performed by a student
(Huang et al., 2013). Instead of using the Euclidean
distance as a distance metric for the DTW cost ma-
trix calculation, they determined angles derived from
body motion vectors. A warping path aligned the two
sequences, so that the accumulated distance was min-
imal. A final score was calculated from the accumu-
lated distances along the warping path. In order to as-
sess the rhythm, the magnitudes of body motion vec-
tors were transformed to the frequency domain. Thus,
the feedback given by this system provided the grade
of similarity in comparison with the reference motion.
However, this feedback did not contain information
about specific motion errors. Another approach that
aimed at generating feedback for ballet training analy-
ses motion trajectories with spherical self-organizing
maps (Muneesawang et al., 2015). The system pro-
vided feedback in a virtual environment, i. e. by dis-
playing information on the screens in a 3-D Cave Au-
tomatic Virtual Environment (CAVE). The work of
Lin et al. focused on assessing Tai Chi exercises (Lin
et al., 2013). They calculated the mean Euclidean dis-
tance and the mean angle difference between joints
of a reference and the current exercise. The compari-
son with thresholds yielded a final score indicating the
grade of similarity. In the field of physical rehabilita-
tion, similar approaches can be found. Several studies
aimed at comparing a reference recording of a ther-
apy exercise with an exercise currently performed by
a patient. Su et al. captured personalised trajectories
from joints of interest and calculated the minimal ac-
cumulated Euclidean distance using DTW (Su et al.,
2014). By means of fuzzy logic, they generated a tex-
tural output from the DTW joint values that informed
the patient after the exercise whether the performance
was bad, good or excellent. Moreover, they stated that
future work should investigate normalisation methods
that allow a patient to use the system without person-
alised pre-recordings. Since it is often helpful for the
patient to receive the feedback directly during the ex-
ercise, Khan et al. introduced a method for continu-
ous evaluation, which is called Incremental Dynamic
Time Warping (IDTW), (Khan et al., 2014). This ex-
tension of DTW enables the comparison between the
complete reference exercise and an incomplete exer-
cise that the patient currently performs. After every
new frame, the IDTW algorithm determines the ref-
erence segment that matches best with the currently
performed part of the exercise. The DTW value cal-
culated from both partial sequences then represented
the similarity between the reference and the current
execution. This method, however, is not able do de-
termine specific errors that occur during the exercise
performance.
Overall, these studies presented principles and so-
lutions to assess the similarity between a pre-recorded
reference and a currently performed motion. Al-
though these studies showed that such kind of feed-
back is highly beneficial for the user, no study exists
so far that recognises and communicates specific er-
rors. The purpose of this investigation is to explore
approaches that allow the recognition of errors that
typically occur during the performance of hip abduc-
tion exercises. In this context, we intent to investigate
a normalisation method in order to avoid taking pre-
recordings and examples of incorrect motions for new
patients. Therefore, the performances of two types of
coordinate representation, i. e. local and normalised
hierarchical coordinates, were compared against each
other by using three different scenarios. Since we in-
tend to give continuous feedback to the patient, we
employed the IDTW algorithm described by Khan et
al. (Khan et al., 2014).
3 METHODS
This section describes the applied and implemented
methods for motion error identification. First of all,
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
282

Kinect Skeleton
Local and Hierarchical Coordinates
IDTW
Feature Vector Generation
Classification
Correct
Incorrect
E1 E2 E3 E4
Figure 1: Procedure overview.
the input skeletons were pre-processed, which in-
cludes local and hierarchical coordinate transforma-
tion. Secondly, IDTW was used to determine the cor-
responding reference frame for every new incoming
frame for certain joints. The coordinates from this de-
termined reference frame and the current frame were
thereupon used for feature vector generation and fi-
nally for error identification. At this point, a hierar-
chical SVM was used to classify the motion in the
current frame as correct or incorrect in a first level.
In a second hierarchical level, the classifier identified
which errors the incorrect motion encompassed. Fig-
ure 1 gives an overview about this procedure.
3.1 Kinect Skeleton
The input data for the following algorithms were
Kinect skeletons. Therefore, we briefly present the
Kinect skeleton data structure in this section.
A coordinate of a joint in camera coordinates is
given by a 1×3 vector of the form
joint
i
=

x
cam,i
y
cam,i
z
cam,i

,
i ∈ {1, ..., 20}
(1)
whereas x
cam,i
, y
cam,i
and z
cam,i
are the x, y and z com-
ponents of the joints in the 3-D camera coordinate
system S
cam
. Figure 2 illustrates the twenty obtained
joints. The joint indices i are defined in this figure.
For the exercise hip abduction, we defined joints
of interest, which are relevant for the error identifi-
cation. These relevant joints are those with indices
i = {3, 4, 17, 18, 19, 20}. In the following, all pro-
cessing steps were performed only for these relevant
joints.
1 hip
centre
2 spine
3 shoulder
centre
4 head
13 hip
left
14 knee
left
16 foot
left
19 ankle
right
20 foot
right
15 ankle
left
17 hip
right
18 knee
right
5 shoulder
left
6 elbow
left
7 wrist
left
8 hand
left
9 shoulder
right
10 elbow
right
11 wrist
right
12 hand
right
Figure 2: Twenty skeleton joints provided by Kinect version
1.0 with the corresponding indices i (frontal view).
3.2 Local and Normalised Hierarchical
Coordinates
The pre-processing step firstly comprised the calcu-
lation of a rotation matrix R, so that the coordinates
became invariant with respect to the rotation of the
Kinect, and secondly the transformation of all joints
to local or normalised hierarchical coordinates re-
spectively.
Rotation Matrix. A coordinate transformation was
applied to make the data translation and rotation in-
variant in case of different sensor orientations while
capturing the data. The rotation matrix R is calcu-
lated using the first frame of a repetition. We thereby
assumed that the person is standing straight at the start
of an exercise.
The x-axis x of the new coordinate system is de-
fined as the unit vector between the right and the left
hip joint, see Equation 2. Then, h is defined as the
vector between the shoulder center and the left hip,
see Equation 3. The new z-axis z is the cross product
of h and the new x-axis x, as formulated in Equation 4.
Finally, according to Equation 5, the new y-axis y is
the cross product of the obtained z-axis and the x-axis.
x =
joint
17
− joint
13
k
joint
17
− joint
13
k
(2)
h = joint
13
− joint
3
(3)
Motion Error Classification for Assisted Physical Therapy - A Novel Approach using Incremental Dynamic Time Warping and Normalised
Hierarchical Skeleton Joint Data
283

S
cam
S
loc
y
loc
z
cam
y
cam
x
cam
R,t
i
x
loc
z
loc
y
h,3
x
h,3
z
h,3
S
h,i
Figure 3: Coordinate transformation from camera coordi-
nate system S
cam
to local coordinate system S
loc
(black) and
hierarchical coordinate systems S
h,i
(blue) with correspond-
ing parent joints. Only S
h,3
is illustrated as an example for
the hierarchical representation.
z =
x × h
k
x × h
k
(4)
y =
z × x
k
z × x
k
(5)
The resulting rotation matrix is denoted as
R =

x
|
y
|
z
|

. (6)
This rotation matrix was used for the calculation of
both local and normalised hierarchical coordinates,
which is described in the following.
Local Coordinates. Joints joint
loc,i
in local coor-
dinate representation were obtained from the joints
joint
i
in camera coordinate representation according
to
joint
loc,i
= R ·

joint
|
i
− joint
|
1

. (7)
Consequently, the coordinates of each local joint are
given with respect to the hip centre joint
1
. The lo-
cal camera system is denoted as S
loc
and illustrated in
Figure 3. Compared to hierarchical coordinates, the
disadvantage of local coordinates is that every joint’s
position is a sum of all the joints vectors it is con-
nected to. This results in a summation of deviations
from the reference. In contrast to that, hierarchical co-
ordinates allow to observe the deviation of every sin-
gle joint from the reference independent from other
joint vectors.
Normalised Hierarchical Coordinates. In the
same way as in the study from Khan et al. (Khan et al.,
2014), we transformed the joints, which are originally
represented in the camera coordinate system S
cam
, to a
hierarchical representation in coordinate systems S
h,i
.
Moreover, we normalised the limbs to make the al-
gorithm invariant to different body sizes and propor-
tions.
The hip centre is on the highest hierarchical level.
The joints that are connected to the hip centre, specif-
ically both hip joints and the spine, are on the second
level and are called child joints of the hip. Vice versa,
every child joint has a parent joint on the next higher
hierarchical level to which it is connected to. The par-
ent joint of the hip centre is defined as the hip centre
itself. This hierarchy is constructed until the hands,
the head and the feet are reached. Every child joint
is finally represented in the coordinate system of its
parent joint.
The single hierarchical coordinate systems S
h,i
have the orientation R as calculated in Equation 6.
In contrast to the local coordinate system, they have
their origin in the corresponding parent joints. In
other words, the camera coordinate system is trans-
lated by the coordinate of every parent joint, which
results in the translation vectors described in Equa-
tion 8. Thereby, parent( joint
i
) denotes the parent
joint of every joint. Every joint is then represented
in its corresponding single coordinate systems S
h,i
.
t
i
= parent( joint
i
) (8)
The hierarchical coordinate of each joint joint
h,i
is
calculated according to Equation 9: Firstly, the child
joint joint
i
is translated by t
i
. Secondly, this translated
joint is multiplied by the rotation matrix R.
joint
h,i
= R ·

joint
|
i
−t
|
i

(9)
Finally, the lengths of the limbs are normalised, see
Equation 10. Consequently, the obtained normalised
hierarchical joints joint
hn,i
have now a length equal to
one.
joint
hn,i
=
joint
h,i
k
joint
h,i
k
(10)
Figure 3 illustrates the transformation from cam-
era coordinates to local and hierarchical coordinates
respectively.
3.3 Incremental Dynamic Time
Warping
In order to identify possible incorrect motions during
a patient’s exercise execution, we compared a pre-
recorded reference of one repetition with the patient’s
current motion execution. This reference defines the
correct motion execution. In this study, the reference
was captured from the patient, which we call person-
alised reference, as well as from a therapist, which we
denote as non-personalised reference.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
284

Since we aim at giving continuous feedback, the
IDTW algorithm by Khan et al. (Khan et al., 2014)
was employed to compare the reference against the
patient’s motion. In the following, the principle of the
IDTW algorithm is described. For more details, we
refer to the publication by Khan et al.
The IDTW algorithm aligns an incomplete pa-
tient’s sequence with the complete reference sequence
and thereby allows a frame-wise feedback generation.
In our study, both the reference and the partial cur-
rent recordings consisted of a sequence of local or
normalised hierarchical 3-D coordinates of a specific
joint. In principal, both reference and current se-
quence can contain any data format.
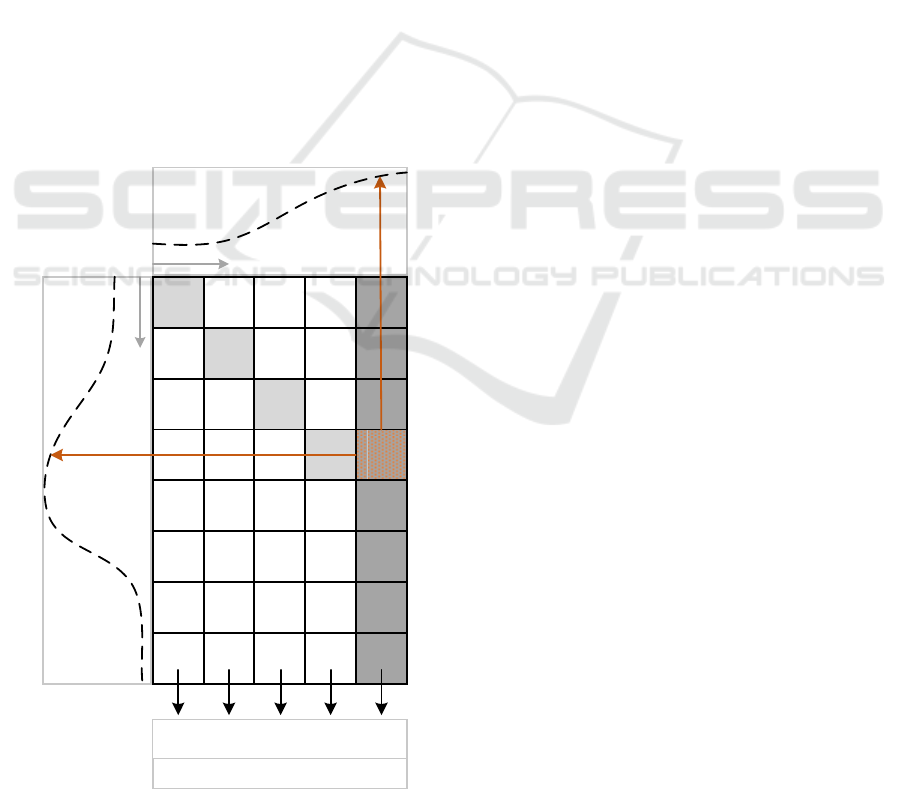
Khan et al. calculated the IDTW distances joint-
wise. For every single joint, a cumulative cost ma-
trix G is calculated, whereas the DTW values in G
are the accumulated Euclidean differences between a
reference and a current coordinate. The calculation of
this matrix is illustrated in Figure 4. Every time a new
frame is acquired and new joint coordinates are calcu-
lated, a new column is appended to G. The reference
frame that fits best to the latest acquired current frame
is determined by finding the minimal DTW value in
min
DTW
DTW
DTW
DTW
min
DTW
DTW
DTW
DTW
DTW
reference
current
part
min
DTW
min
DTW
min
DTW
min
DTW
frame
frame
min
DTW
min
DTW
min
DTW
min
DTW
dd d d d
cur
ref
Figure 4: Cumulative cost matrix G for one single joint,
which is updated frame-wise.
this column. In this way, the algorithm selects the part
of the reference that matches best with the current par-
tial sequence.
Khan et al. used the IDTW algorithm to give feed-
back by colour-coding the single joints according to
their minimal DTW values for every incoming frame.
In our approach, we extended the IDTW algorithm
to determine the reference frame joint
i,ref
that corre-
sponds to the currently acquired frame joint
i,cur
. In
this way, we were able to calculate a distance vec-
tor d
i,frame
that describes the difference between the
joint position in the current frame and the correspond-
ing reference joint position. Consequently, instead of
minimal DTW values, we obtained a feature vector
for every new frame as an output of the IDTW algo-
rithm, as illustrated in Figure 4.
In order to reset the cost matrix after each repeti-
tion, we implemented an algorithm to detect the end
of a performed repetition. This algorithm is based
on the distance between the left and the right ankle.
The cost matrix was reset when the end of a repetition
was detected, which means that all the elements were
deleted. The feature vector calculation is described in
the following section.
3.4 Feature Vector Generation
For the error classification, we calculated a feature
for every interesting joint, which characterises the
difference d
i,frame
between the current joint position
joint
i,cur
and the corresponding reference joint posi-
tion joint
i,ref
, see Equation 11.
d
i,frame
= joint
i,cur
− joint
i,ref
,
i ∈ {3, 4, 17, 18, 19, 20}
(11)
The concatenation of the relevant joints d
i,frame
repre-
sents the feature vector FV
frame
for one frame:
FV
frame
=

d
3,frame
d
4,frame
... d
20,frame

(12)
3.5 Classification
In this study, we distinguished between the classes
listed in Table 1. According to therapists, the de-
scribed errors are frequently occurring when patients
train without a therapist’s feedback. A linear multi-
class one-versus-all Support Vector Machine (SVM)
was trained with feature vectors that were calculated
from recordings of different persons. These persons
performed several repetitions of the exercise hip ab-
duction according to the descriptions in Table 1. De-
pending on the scenario, the training and testing con-
figurations changed. This methodology will be ex-
plained in detail in Section 4.
Motion Error Classification for Assisted Physical Therapy - A Novel Approach using Incremental Dynamic Time Warping and Normalised
Hierarchical Skeleton Joint Data
285

Table 1: Classes with labels L and description for exercise
hip abduction.
L Class Description
C Correct The exercise is performed in a
correct way.
BK Bent
Knee
The abducted leg is not straight,
but bent while performing the
motion. The joints of the leg do
not form a straight line.
FO Foot
Outside
The leg is rotated outwards,
which results in a rotated posi-
tion of the toe joint.
UB Upper
Body
The joints of the torso and head
are moving although their posi-
tion should not change.
WP Wrong
Plane
The joints of the abducted leg are
not moving in the plane that is
spanned by the joints of the sup-
porting leg and the straight torso.
As a result, the whole classifier consists of five
single one-versus-all SVMs, whereas the first SVM
classifies whether the motion in the current frame is
correct or incorrect (first hierarchy). The other SVMs
(second hierarchy) decide whether the specific errors
were detected if the first SVM predicts the motion as
incorrect. If none of the five classifiers responds, we
assumed the motion in the tested frame to be correct.
In this way, we have designed a hierarchical SVM.
4 EVALUATION
METHODOLOGY
In order to evaluate the capability of the system to
work with non-personalised data, we distinguished
three scenarios, which are summarised in Table 2.
The scenarios correspond to the grade of personal-
isation: Scenario 1 is using only personalised data,
while scenario 3 works only with non-personalised
data. Consequently, scenario 3 is the most challeng-
ing one where we expected the lowest accuracy. The
scenarios are presented and explained in detail in the
following:
Scenario 1. For every patient, an individual machine
was trained and tested with the individual patient’s
data and his or her own reference ref
i
. For this pur-
pose, every person’s recordings were split in training
P
i,train
and testing set P
i,test
. Consequently, in practi-
cal applications, training data as well as the patient’s
reference have to be recorded for every new patient,
which is rather impractical. For this scenario, the data
Table 2: Scenarios S1-S3 for evaluation.
Scenario Train Test
S1 P
i,train
, ref
i
P
i,test
, ref
i
S2 P
train
, ref
train
P
i,test
, ref
i
S3 P
train
, ref P
i,test
, ref
of ten probands was used.
Scenario 2. In contrast to scenario 1, one single ma-
chine was trained with the motion data of three per-
sons P
train
and their individual reference data ref
train
.
These were other persons than the probands in sce-
nario 1. Just as in scenario 1, the test was performed
with each test person’s individual reference ref
i
while
the data from the ten probands P
i,test
mentioned in sce-
nario 1 was used. In practice, only the new patient’s
reference, but not his or her training data, has to be
recorded. Obviously, this would be more practicable
than scenario 1.
Scenario 3. The machine was trained with the mo-
tion data of the three persons P
train
mentioned in sce-
nario 2. In contrast to scenario 1 and scenario 2, the
reference ref has not been changed according to the
person. For testing, the very same reference ref was
used for all test samples of the ten persons P
i,test
. This
means that, in practice, neither training data nor a ref-
erence has to be recorded for a new patient. This
would considerably reduce the effort for both patients
and therapists.
When we consider these scenarios, we can con-
clude that practicability increases from scenario 1 to
scenario 3, because the need of taking recordings be-
fore the training decreases: scenario 1 needs record-
ings from the patient’s correct motions as well as from
the incorrect motions and the patient’s reference be-
fore a training session can start. In contrast to that,
scenario 3 requires neither of these recordings, be-
cause it works with pre-recorded data from other per-
sons. The question we want to answer is whether the
results of scenario 3, which is the desired implemen-
tation, are still equivalent to those of scenario 1 and
scenario 2. We moreover investigated whether the re-
sults improve for these scenarios if we use normalised
hierarchical coordinates instead of non-normalised lo-
cal coordinates.
To compare the performance when using local or
hierarchical coordinates, we determine the overall ac-
curacy η
all
for all classes N for every scenario accord-
ing to Equation 13:
η
all
=
1
N
·
N
∑
n=1
η
n
, (13)
whereas η
n
is the accuracy for every single one-
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
286

versus-all classifier, see Equation 14.
η
n
= (TPR
n
+ TNR
n
) · 0.5 (14)
These accuracies η
n
are calculated for every single
one-versus-all classifier to evaluate the detection of
single error types. TPR
n
and TNR
n
are the true posi-
tive and the true negative rates for each class.
5 RESULTS AND DISCUSSION
The overall accuracies η
all
for the three scenarios us-
ing the two different coordinate representations are
presented in Table 3. It becomes obvious that, when
using local, i. e. non-normalised coordinates, the
overall accuracy considerably deteriorates from sce-
nario 1 to scenario 3. This complies with our ex-
pectations: the less personalised data is used, the
higher is the negative influence of factors, such as
body size and proportions, on the accuracy. In con-
trast to local coordinates, the accuracy only slightly
decreases when using normalised hierarchical coor-
dinates. These results suggest that normalised hier-
archical coordinates should be used instead of local
coordinates in order to avoid the recording of person-
alised data for each new patient without loosing clas-
sification performance.
Based on this finding, we elaborated the accura-
cies η
n
of the single classes for scenario 3 using nor-
malised hierarchical coordinates, which is the most
challenging scenario but the one with highest practi-
cal relevance as well. The results are summarised in
Table 4. It is apparent from this table that 84 % of the
samples that have been labelled as correct were also
classified as correct. In 16 % of the tested frames,
an error was detected although the test persons per-
formed the exercise correctly. This is mainly because
of the relatively high false positive rate (FPR) of the
FO classifier, which results in a detected error in the
second stage of the hierarchical SVM. The table also
reveals that in 75 % of the frames that have been la-
belled as incorrect, an error could be identified. Tak-
ing the true positive rates (TPRs) of the error classes
Table 3: Overall accuracies η
all
for the three scenarios S1,
S2 and S3 with local and normalised hierarchical coordi-
nates.
Scenario η
all
,
local
η
all
,
hierarchical
S1 0.83 0.86
S2 0.75 0.81
S3 0.67 0.82
Table 4: Confusion matrices and corresponding accuracies
η
n
for scenario 3 using normalised hierarchical coordinates.
L: samples that were classified to be C, BK, FO, UB or WP.
L: samples that were classified to be C, BK, FO, UB or WP.
L L η
n
C 0.84 0.16
0.82
C 0.25 0.75
BK 0.81 0.19
0.90
BK 0.02 0.98
FO 0.52 0.48
0.68
FO 0.17 0.83
UB 0.87 0.13
0.91
UB 0.04 0.96
WP 0.65 0.35
0.81
WP 0.03 0.97
BK, UB and WP into consideration, we see that in at
least 65 % of the frames where the specific error was
present this very error could be identified. When we
consider the error classes BK, UB and WP, the FPRs
are low. This is of high importance in order not to
confuse the patient by giving him feedback about er-
rors that he or she actually has not performed. Only
the error FO could not be successfully detected. The
low TPR in FO is one reason for the low FPR in C,
whereas the high FPR in FO is responsible for the
high false negative rate (FNR) in C. For this reason,
we performed a second test excluding the class FO.
The improved results are presented in Table 5. The
TPR of C increased to 90 % and the true negative rate
(TNR) to 81 % when using normalised hierarchical
coordinates in scenario 3.
At this point we would like to stress that the pre-
sented results in Table 4 represent a low-level classifi-
cation, which is based on the single frames in an exer-
cise sequence. Given the low FPRs (below 5 %) and
the relatively high TPR (at least 65 %) we achieved
for the classes BK, UB and WP, the error can be reli-
ably detected. It is remarkable that the errors could be
detected by just using the distance vector between an-
other person’s reference and the current patient’s ex-
Table 5: Overall accuracies η
all
for the three scenarios S1,
S2 and S3 with local and normalised hierarchical coordi-
nates without class FO.
Scenario η
all
,
local
η
all
,
hierarchical
S1 0.90 0.90
S2 0.78 0.85
S3 0.72 0.87
Motion Error Classification for Assisted Physical Therapy - A Novel Approach using Incremental Dynamic Time Warping and Normalised
Hierarchical Skeleton Joint Data
287

ercise sequence. A potential error source is the match-
ing of the sequences using IDTW. In case of inaccu-
rate matching, both sequences could possibly not be
correctly aligned. This results in an incorrect distance
vector and hence in an insignificant feature. A general
challenge we encountered is the noise in the obtained
3-D Kinect skeleton. This noise causes misclassifi-
cations, because the joints are inaccurately localised.
Some of the persons, for example, wore short, wide
trousers. The ends of the trousers were frequently
recognised as the knee joints because of the working
principle of the Kinect. Incorrect localisations espe-
cially affect the error FO since the foot joints are often
error-prone.
6 CONCLUSIONS AND FUTURE
WORK
In this study, we presented a method to detect incor-
rect motions during therapy exercises. In our exper-
iments, we achieved results of high quality even if
we used non-personalised data, i. e. neither the cur-
rent person’s reference nor the person’s training data.
The most obvious finding to emerge from this study
is that by using hierarchical normalised joint repre-
sentation, a unified model that was trained with other
persons’ data can be used for new patients. As this
method allows the usage of pre-recorded data from
other persons, a direct start for new patients without
the need of recording their individual error motions
and their reference is possible. Moreover, the study
has confirmed that simple distance vectors are suit-
able feature vectors for error classification.
Nevertheless, future research should concentrate
on the investigation of more distinctive features to fur-
ther increase the accuracy and on a subsequent high-
level processing using filtering techniques. For prac-
tical applications, the generation of synthetic training
data would be sensible. In this way, the pre-recording
of motion data could be avoided completely, which
would simplify the extension with further exercises,
such as hip extension and hip flexion. Another inves-
tigation will focus on the input for the IDTW. Cur-
rently, the trajectories of single joints were evaluated,
but we did not contextualise them. Therefore, we plan
to fuse all joint information into one single cost ma-
trix. Another aspect for future work will be automatic
joint filtering to find joints that are relevant for differ-
ent exercises.
Taken together, this study created a base for fur-
ther research that shows high potential for the re-
quired assistance in the therapy sector.
ACKNOWLEDGEMENTS
This project is funded by the European Social Fund
(ESF). Moreover, we would like to thank all the per-
sons who participated during the exercise recordings.
REFERENCES
Huang, T.-C., Cheng, Y.-C., and Chiang, C.-C. (2013).
Automatic Dancing Assessment Using Kinect. In
Advances in Intelligent Systems and Applications-
Volume 2, pages 511–520. Springer.
Khan, N. M., Lin, S., Guan, L., and Guo, B. (2014). A
visual evaluation framework for in-home physical re-
habilitation. In Multimedia (ISM), 2014 IEEE Inter-
national Symposium on Multimedia, pages 237–240.
IEEE.
Lin, T.-Y., Hsieh, C.-H., and Lee, J.-D. (2013). A kinect-
based system for physical rehabilitation: Utilizing tai
chi exercises to improve movement disorders in pa-
tients with balance ability. In 2013 7th Asia Modelling
Symposium, pages 149–153. IEEE.
Muneesawang, P., Khan, N. M., Kyan, M., Elder, R. B.,
Dong, N., Sun, G., Li, H., Zhong, L., and Guan, L.
(2015). A machine intelligence approach to virtual
ballet training. IEEE MultiMedia, 22(4):80–92.
Richter, J., Wiede, C., Apitzsch, A., Nitzsche, N., L
¨
osch,
Christiane amd Weigert, M., Kronfeld, T., Weisleder,
S., and Hirtz, G. (2016). Assisted Motion Control in
Therapy Environments Using Smart Sensor Technol-
ogy: Challenges and Opportunities. In Proceedings of
Zukunft Lebensr
¨
aume Kongress 2016, pages 90–102.
Shotton, J., Girshick, R., Fitzgibbon, A., Sharp, T., Cook,
M., Finocchio, M., Moore, R., Kohli, P., Criminisi,
A., Kipman, A., et al. (2013). Efficient human pose
estimation from single depth images. Pattern Analy-
sis and Machine Intelligence, IEEE Transactions on,
35(12):2821–2840.
Su, C.-J., Chiang, C.-Y., and Huang, J.-Y. (2014). Kinect-
enabled home-based rehabilitation system using Dy-
namic Time Warping and fuzzy logic. Applied Soft
Computing, 22:652–666.
Tak, Y.-S., Rho, S., and Hwang, E. (2011). Mo-
tion Sequence-Based Human Abnormality Detection
Scheme for Smart Spaces. Wireless Personal Commu-
nications, 60(3):507–519.
Tormene, P., Giorgino, T., Quaglini, S., and Stefanelli, M.
(2009). Matching incomplete time series with dy-
namic time warping: an algorithm and an application
to post-stroke rehabilitation. Artificial intelligence in
medicine, 45(1):11–34.
Yurtman, A. and Barshan, B. (2013). Detection and eval-
uation of physical therapy exercises by dynamic time
warping using wearable motion sensor units. In Infor-
mation Sciences and Systems 2013, pages 305–314.
Springer.
ICPRAM 2017 - 6th International Conference on Pattern Recognition Applications and Methods
288