
Rate-Distortion Optimized Wavelet-based Irregular Mesh Coding
Jonas El Sayeh Khalil
1
, Adrian Munteanu
2
and Peter Lambert
1
1
ELIS Department, IDLab, Ghent University-iMinds, Sint-Pietersnieuwstraat 41, B-9000, Ghent, Belgium
2
Dept. of Electronics and Informatics, Vrije Universiteit Brussel, Pleinlaan 2, B-1050, Brussels, Belgium
Keywords:
Quality-scalable Mesh Representation, Wavelet-based Mesh Coding, Rate-Distortion Optimization.
Abstract:
This work investigates the optimization of mesh quality at lossy rates for a lossless scalable wavelet-based
irregular mesh codec. Whereas previously proposed wavelet-based irregular mesh codecs offer coarse-grain
resolution scalability, in this paper we propose a coding scheme which enables fine-grain quality scalability.
This is done by avoiding the use of geometric data in the encoding process, which reduces dependencies within
the data stream and allows for an unrestricted storage and transmission order of wavelet subband bitplanes
and connectivity information. This in turn allows us to perform rate-distortion optimization, whereby the
subband bitplanes to be encoded are determined by minimizing distortion subject to an overall target bitrate.
Experimental results show that the proposed coding approach offers fine-grain quality scalability, achieves
optimality in rate-distortion sense and improves compression performance over the state of the art.
1 INTRODUCTION
As the amount and the quality of obtained media in-
creases, so does the need for efficient compression in
multimedia domains. This need ignited advancements
in subsequently audio, image, and video compression
systems. Today, advanced compression solutions are
also required for three-dimensional data. While the
gaming industry tries to cope with increasing quality
requirements by making use of shader tricks, and the
movie industry makes use of huge rendering farms for
their rendering needs, we observe that, in general, a
scalable coding solution is required. With the rise of
virtual and augmented reality applications, the advent
of 3D printing and the increasing detail of 3D scan-
ners comes the need for lossless storage and transmis-
sion, while offering interactivity in a scalable way.
Wavelet-based techniques have been successful
in multimedia compression, including several 3D
codecs. A wavelet-based solution uses a set of high-
pass and low-pass filters to obtain a low-resolution
base mesh where all high-frequency data have been
removed, and a set of wavelet subbands containing
increasingly higher frequency information. By ex-
ploiting fine-grain quality scalability, which allows
for scaling the quality of reconstructed data by decod-
ing per wavelet subband bitplane, data can be trans-
mitted such that the distortion in the reconstructed
mesh decreases optimally.
Contributions. In this work, we investigate our pre-
vious wavelet-based irregular mesh codec offering
resolution scalability and propose a coding scheme
based on it which offers quality scalability. This im-
proves over the state of the art in two ways: (1) the
coding performance at low bitrates is improved by our
proposed algorithm by performing rate-distortion op-
timization, and (2) functionally, an additional form of
scalability is offered without negatively impacting the
lossless coding rate.
The remainder of this work is structured as fol-
lows: related work is given in Section 2, our
resolution-scalable codec we improve upon is de-
scribed in Section 3, our contributions are detailed in
Sections 4 and 5 and we evaluate the proposed codec
in Section 6. Section 7 concludes this work.
2 RELATED WORK
Until today, triangle meshes have been the main rep-
resentation of 3D models for real-time rendering. A
mesh is often seen as the combination of both geome-
try information, i.e., the positions of the vertices, and
connectivity or topology, i.e., the edges (and conse-
quently the triangles) between these vertices. Mesh
coding has been an active topic of research for over
two decades. State-of-the-art single-rate coders, e.g.,
(Touma and Gotsman, 1998), proved to be insufficient
212
El Sayeh Khalil J., Munteanu A. and Lambert P.
Rate-Distortion Optimized Wavelet-based Irregular Mesh Coding.
DOI: 10.5220/0006108602120219
In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 212-219
ISBN: 978-989-758-224-0
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

despite good performance, as single-rate codecs only
allow for decoding an entire mesh. An ad-hoc solu-
tion is the use of Levels of Detail (LODs), obtained by
simplifying a mesh several times using a decreasing
amounts of vertices to approximate the mesh. This al-
lows for improved interactivity but increases the stor-
ing cost as each LOD is stored separately.
Pioneering work in progressive mesh representa-
tions was done by Hoppe (Hoppe, 1996). In this work,
Hoppe describes how a mesh can be simplified ver-
tex per vertex, minimizing an energy function at ev-
ery step. This results in a so-called continuous LOD
chain: this progressive mesh representation generates
a nearly continuous spectrum of LODs where each
new level is obtained by splitting one vertex of the
previous level. Each obtained level is optimal given
a specific number of vertices. Further improvements
in compression performance was obtained by group-
ing the individual increments in batches, each batch
splitting half of the decoded vertices (Pajarola and
Rossignac, 2000). (Peng and Kuo, 2005) and (Valette
et al., 2009) present state-of-the-art codecs which al-
low for fine-grain vertex-by-vertex resolution control.
The idea of constructing scalable representations
and compression systems is well-known in signal
processing. In this context, wavelets play a major
role, being used to generate multiresolution repre-
sentations of an input signal and to build scalable
codecs based on them. Wavelet-based scalable codecs
include well-known examples for images (Said and
Pearlman, 1996; Munteanu et al., 1999; Taubman
and Marcellin, 2001), for video (Taubman and Za-
khor, 1994; Ohm, 1994; Andreopoulos et al., 2004),
and were introduced for surfaces by Lounsbery et
al. (Lounsbery et al., 1997). Essentially, Lounsbery et
al. established the link between subdivision schemes
and multiresolution analysis for meshes. Subdivi-
sion schemes result in semi-regular meshes, however,
whereas models are most efficiently represented using
irregular meshes, allowing for adaptive sampling of a
surface. This avoids oversampling near areas lack-
ing high frequencies, and undersampling where high
frequencies are present. One solution is to convert ir-
regular meshes to semi-regular ones in a preprocess-
ing step (Payan et al., 2015). Semi-regular mesh cod-
ing allows for superior compression performance due
to the implicit connectivity knowledge (Khodakovsky
et al., 2000; Denis et al., 2010). However, not ev-
ery application allows for a lossy remeshing step,
and the inherent oversampling associated with semi-
regularity results in a larger number of vertices and,
consequently, a higher rendering cost.
Few wavelet transforms for irregular meshes have
been proposed in the literature. Bonneau describes a
generalization of Haar-wavelets in (Bonneau, 1998).
Valette et al. (Valette et al., 1999; Valette and Prost,
2004a) propose an extension of the work of Louns-
bery et al., describing a new subdivision approach
which is not restricted to 1-to-4 subdivision, but al-
lows creating one, two, three or four triangles from a
single triangle. In (Valette and Prost, 2004b), Valette
et al. describe how this wavelet transform can be
efficiently encoded, resulting in the state-of-the-art
Wavemesh codec. Recently we proposed a wavelet-
based irregular mesh codec (El Sayeh Khalil et al.,
2016) which we will refer to as EMD+16 in the
remainder of this paper. This codec produced im-
proved coding performance over Wavemesh in low
and midrange bitrates, and additionally tackled a
new untouched issue: whereas scalable mesh cod-
ing mainly focuses on minimizing the distortion for a
given amount of bits, efficient rendering requires min-
imizing the distortion for a given triangle limit, which
is directly related to a given memory limit.
In this paper we build upon EMD+16. Observ-
ing that the decoding of higher-range bits only yields
marginal improvements in visual quality, we focus on
the low and midrange rates and examine the possibil-
ity and the effect of performing a rate-distortion op-
timized storage and transmission of wavelet subband
bitplanes. Rate-distortion performance is optimized
by identifying at every encoding step the wavelet sub-
band bitplane which maximally reduces distortion in
the reconstructed mesh at minimum cost in bits.
3 FEATURE-PRESERVING
IRREGULAR MESH CODING
In (El Sayeh Khalil et al., 2016), we describe
EMD+16, a wavelet-based irregular mesh coding sys-
tem with implicit preservation of important visual fea-
tures. We reiterate the most important aspects of this
codec, of which an overview is given in Figure 1.
3.1 Wavelet Transform
The wavelet transform is based on the lifting scheme
proposed by Sweldens (Sweldens, 1998). This
scheme is composed of three steps to perform the for-
ward wavelet transform.
Downsampling and Retriangulation. A low-pass
filtering step splits vertices into even and odd ver-
tices. Each odd vertex is surrounded by even neigh-
bouring vertices, forming a patch. After downsam-
pling, the remaining polygonal patches are retriangu-
lated while implicitly preserving geometric features,
Rate-Distortion Optimized Wavelet-based Irregular Mesh Coding
213
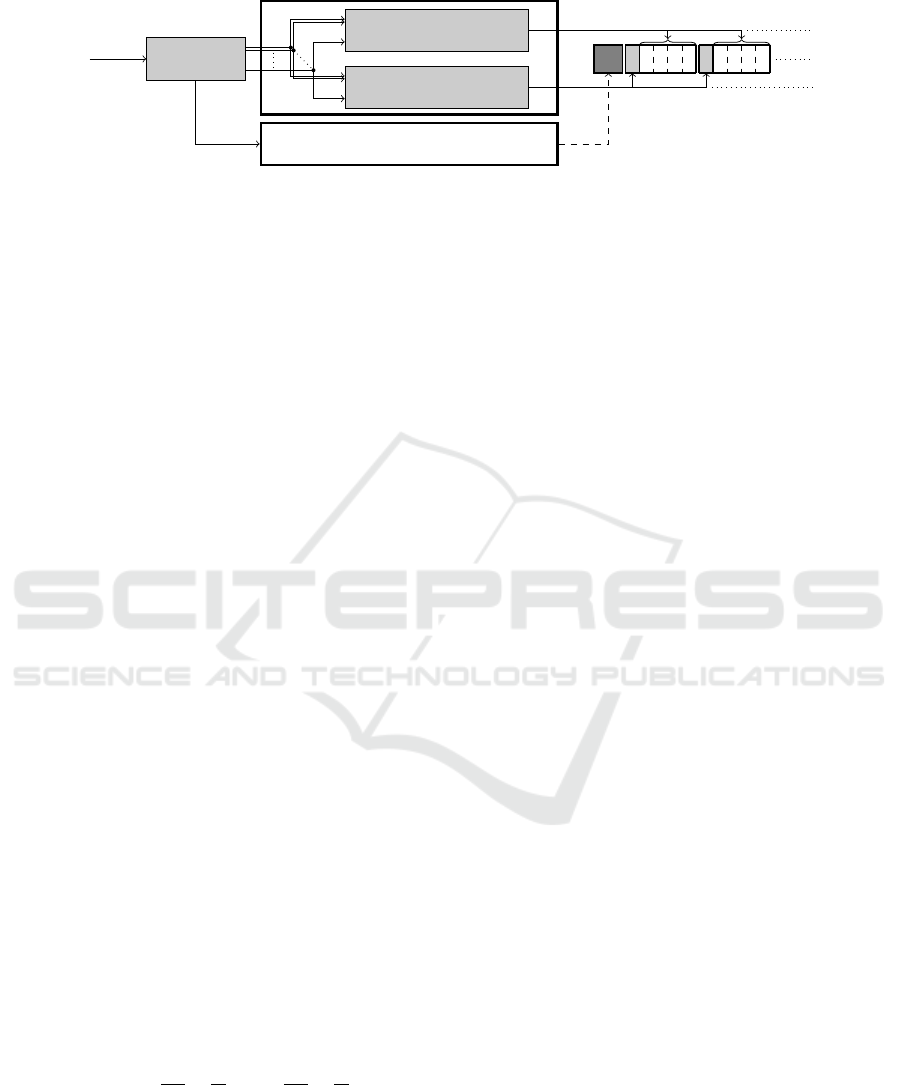
Wavelet
Transform
Geometry Coder
Connectivity Coder
Base Mesh Coder
Wavelet Subband Coder
M
M
0
W
j
C
j
Figure 1: Overview of the original mesh coder. The transform step generates a base mesh and a sequence of wavelet subbands.
In this work, we modify the coding components to allow for an unrestricted storage and transmission order.
resulting in a lower-resolution approximation of the
higher-resolution mesh. Inversely, the upsampling
step adds a vertex per patch, and trivially retriangu-
lates each patch by connecting each border vertex
with the newly added odd vertex.
Prediction Step. The high-frequency data is pre-
dicted using the local patch information, determining
a prediction error per patch. To allow the same pre-
dictions during reconstruction, additional information
is required to determine the low-resolution patches.
Additional connectivity data is common to all irreg-
ular mesh codecs, but the higher cost per triangle is
compensated by requiring fewer triangles overall.
Update Step. The low-frequency data can finally
be post-processed to avoid aliasing artefacts. In the
given codec however, this step is chosen to be a null-
operation to avoid smoothing artefacts around geo-
metric features which should remain sharp.
3.2 Wavelet Subband Coder
The incremental data consists of two key components.
Firstly, the connectivity information has to be en-
coded to allow for locating the patches. For every
edge of the intermediate mesh, a single bit describes
if the edge was a new edge which was constructed
by retriangulation, or if the edge was present in the
higher-resolution mesh. Secondly, the wavelet coef-
ficients are represented as vectors in global orthonor-
mal space and indicate the prediction errors of the odd
vertices. Due to Successive Approximation Quanti-
zation (SAQ), the wavelet coefficients can be coded
bitplane by bitplane. The quantizers are defined as:
Q
p
(w) =
(
s(w)
j
|w|
2
p
∆
+
ξ
2
p
k
, if
|w|
2
p
∆
+
ξ
2
p
> 0
0, otherwise
(1)
with 2
p
∆ the quantization cell width, ξ the width of
the deadzone, and s() the sign function.
The connectivity information and wavelet coef-
ficients are both encoded using an octree structure.
This octree structure decouples the encoding process
from any mesh traversal order and allows for exploit-
ing spatial locality. Within the octrees, the connectiv-
ity samples are encoded at the edge middles, while the
geometry samples are encoded at the predicted posi-
tions. For the encoder and decoder to operate in a
synchronized fashion, a template mesh is used to map
the samples. (El Sayeh Khalil et al., 2016) does not
give requirements for this, but indicates that the pre-
vious resolution is used for the template mesh.
4 GEOMETRY-INDEPENDENT
TEMPLATE MESHES
The original design of EMD+16 allows for resolution
scalability and only for a limited form of quality scal-
ability: at each resolution, the decoder can determine
the amount of quality bits for the newly added ver-
tices; however, a new resolution can only be decoded
after fully decoding the previous resolution. This is
a disadvantage of using this previous resolution as a
template mesh for coding the connectivity informa-
tion and wavelet coefficients of the next resolution.
Dependencies between data blocks are shown in Fig-
ure 2(a), clearly showing that this approach allows
only one order in which data can be transmitted, de-
picted in Figure 2(b).
Instead, we explore quality-scalable encoding of
irregular meshes where the wavelet subbands are en-
coded at possibly different quality levels. Moreover,
the subband bitplanes are encoded in a rate-distortion
optimal manner, ensuring minimal distortion in the re-
constructed mesh for any target bitrate.
We propose to use the base mesh as a first template
mesh again. However, instead of reconstructing each
resolution using its previous resolution, effectively
doing an identical inverse transform on the template
mesh as performed on the actual mesh, we propose to
perform a modified inverse transform which only uses
connectivity information. This results in a template
mesh which increases in resolution by only predict-
ing the added vertices without requiring the decoded
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
214

increasing resolution
increasing quality
C
(0)
G
(0)
3
G
(0)
2
G
(0)
1
G
(0)
0
C
(1)
G
(1)
3
G
(1)
2
G
(1)
1
G
(1)
0
C
(2)
G
(2)
3
G
(2)
2
G
(2)
1
G
(2)
0
(a) (b)
increasing resolution
increasing quality
C
(0)
G
(0)
3
G
(0)
2
G
(0)
1
G
(0)
0
C
(1)
G
(1)
3
G
(1)
2
G
(1)
1
G
(1)
0
C
(2)
G
(2)
3
G
(2)
2
G
(2)
1
G
(2)
0
(c) (d) (e) (f)
Figure 2: Data dependencies and coding orders. Fig. 2(a)
shows dependencies in EMD+16, and Fig. 2(b) the only
possible coding order; Fig. 2(c) shows dependencies in the
proposed framework, Figs. 2(d), 2(e) and 2(f) possible cod-
ing orders. For resolution j, C
( j)
represents the connectivity
data and G
( j)
i
the geometry data at bitplane i.
wavelet coefficients to reposition these vertices. The
result is that the connectivity and geometry of a reso-
lution can be decoded as soon as the connectivity of
the previous resolution is known. The resulting de-
pendencies are depicted in Figure 2(c): the encoder
is able to store the data blocks in an unrestricted or-
der as long as (a) the order of connectivity informa-
tion blocks is maintained, (b) geometry information
within each resolution is stored in the correct order,
and (c) connectivity information for a specific reso-
lution is encoded before geometry information. This
allows for storing and transmitting the blocks in any
order: resolution per resolution as before (Fig. 2(d)),
bitplane by bitplane or purely quality-scalable (Fig.
2(e)), or in any arbitrary order that preserves the de-
pendencies as indicated above (e.g., Fig. 2(f)).
5 RATE-DISTORTION
OPTIMIZATION
Rate-distortion optimization requires encoding data
blocks such that the distortion is minimal at all bit-
rates. Such distortion optimization depends on the
distortion measure used and as such does not yet have
an unambiguous solution. Our aim is to show that
such optimizations are indeed possible by proposing
a rate-distortion optimization algorithm, proving that
an optimized subband bitplane storage and transmis-
sion order is enabled by our codec architecture.
We construct our optimization algorithm by con-
sidering the distortions introduced by the wavelet
transform. With N
( j)
the number of wavelet coeffi-
cients for resolution j, the remaining distortion D
( j)
p
related to this j
th
resolution decoded up to bitplane p
is given by:
D
( j)
p
=
N
( j)
∑
i=1
α
( j)
i
d
( j)
i,p
, (2)
with d
( j)
i,p
the distortion on the odd vertex o
( j)
i
when
the most significant bits of wavelet coefficient i of res-
olution j are decoded up to the p
th
bitplane, i.e.,
d
( j)
i,p
= |x
( j)
i
−
˜
x
( j)
i,p
|
= |x
( j)
i
− (
˜
x
( j)
i
+ w
( j)
i,p
)|
(3)
In Equation 3,
˜
x
( j)
i
is the predicted position of odd
vertex o
( j)
i
and
˜
x
( j)
i,p
is its reconstructed position when
decoding the most significant bitplanes of the accom-
panying wavelet coefficient w
( j)
i
up to bitplane p. To
simplify notations, we drop the superscript j and sub-
script i as the following paragraphs always handle a
specific odd sample i of a specific resolution j.
If we denote the total number of bitplanes by p
max
,
then w
p
max
= 0, i.e., when no bitplanes are encoded,
the wavelet coefficient is zero and the prediction is not
corrected: d
p
max
= |x −
˜
x|. The distortion becomes
exactly 0 as soon as the least-significant bitplane is
decoded: w
0
= w = x −
˜
x and d
0
= |x − (
˜
x + w
0
)| =
|x − (
˜
x + x −
˜
x)| = 0.
The wavelet coefficients are encoded using SAQ,
so let q
p
= Q
p
(w); the wavelet coefficient up to bit-
plane p can be dequantized as w
p
= Q
−1
p
(q
p
), with:
Q
−1
p
(q
p
) =
(
0, q
p
= 0
s(q
p
)
|q
p
| −
ξ
2
p
+ δ
2
p
∆, q
p
6= 0
(4)
where 0 ≤ δ < 1 determines the placement of w
p
within the quantization cell. In the current implemen-
tation, it is chosen to be δ = 0.5.
To find weights α for the wavelet coefficients,
we first assign weights β
k
to all vertices. These
weights indicate an estimation of the effect on the
full-resolution mesh of repositioning vertices. After
downsampling, the position of each removed odd ver-
tex o
( j)
i
is influenced by the positions of its neigh-
bours. Hence, the weights of these neighbour ver-
tices of o each increase by β
o
/d with d the amount
of neighbours. The weight of a wavelet coefficient is
given by its accompanying odd vertex: α = β
o
.
At the highest resolution, each vertex (and conse-
quently each wavelet coefficient) has a weight of 1/N.
If the downsampling terminates at a tetrahedral base
mesh counting four vertices, each vertex (and con-
sequently each wavelet coefficient on average) has a
weight of 1/4. This indicates that a single wavelet
Rate-Distortion Optimized Wavelet-based Irregular Mesh Coding
215

R
D
( j)
D
( j)
p+1
D
( j)
p
R
( j)
p+1
R
( j)
p
Figure 3: Generic rate-distortion curve. With decreasing
bitplane p the rate increases and the distortion decreases.
coefficient at a lower resolution is equally valuable as
a multitude of wavelet coefficients at a higher reso-
lution. Note that the use of such weights is similar
to the scaling of wavelet coefficients prior to encod-
ing – see e.g. (Said and Pearlman, 1996), rendering
biorthogonal transforms approximately unitary.
The complete algorithm for assigning weights is
presented in Algorithm 1.
Algorithm 1: Assigning weights to vertices.
1: for all v ∈ M do
2: v.β ← 1/N
3: end for
4: while downsampling do
5: for all v
o
∈ M
i,o
do
6: d ← valence(v
o
)
7: for all v ∈ neighbourhood(v
o
) do
8: v.β ← v.β + v
o
.β/d
9: end for
10: end for
11: end while
At each resolution, a rate-distortion curve such as
shown in Figure 3 can be found. Optimization comes
down to considering the rate-distortion curves for ev-
ery resolution, and coding at every step the informa-
tion which introduces the largest distortion decrease
at the lowest rate. With P
j
the last encoded bitplane
of resolution j, we would encode the next bitplane of
resolution j
0
with
j
0
= argmax
j:P
j
6=0
D
( j)
P
j
− D
( j)
P
j
−1
R
( j)
P
j
−1
− R
( j)
P
j
(5)
Up to this point, we did not handle connectiv-
ity blocks. To start decoding a specific resolution,
the connectivity information of all previous resolu-
tions has to be decoded. This decoding comes at
a rate but does not introduce a distortion decrease
in mean-squared-error sense. Furthermore, as the
most-significant bitplanes are mostly zero, decoding
these highest bitplanes also requires rate often with-
out decreasing distortion either. Hence, Equation 5 is
adapted to consider multiple bitplanes together to find
the most optimal slope. We generalize the definition
of P
j
to encompass any data block required to encode
resolution j. Consequently, P
j
will start at p
max
+1 as
it counts for all p
max
wavelet subband bitplanes and
an additional data block for the connectivity informa-
tion. With L the first unencoded resolution, we will
encode k
0
bitplanes of resolution j
0
using:
( j
0
,k
0
) = argmax
j∈[0,L],k∈[1,P
j
]
D
( j)
P
j
− D
( j)
P
j
−k
R
( j)
P
j
−k
− R
( j)
P
j
(6)
For this, we make two conventions:
• R
( j)
p
max
+1
= 0;R
( j)
p
max
= R
( j)
conn
6= 0
• D
( j)
p
max
+1
= D
( j)
p
max
This states that encoding the connectivity informa-
tion, i.e., the first data block of a resolution, intro-
duces a rate of R
( j)
conn
while not decreasing the dis-
tortion; this corresponds to adding vertices to the de-
coded mesh without refining their locations. The dis-
tortions D
( j)
p
,∀p ∈ [0, p
max
] are defined in Equation 2.
6 EXPERIMENTAL EVALUATION
To evaluate our codec, we assume a raw storage of the
base mesh. In practice, the wavelet transform stops
at a resolution which is small enough to benefit from
scalability, while remaining qualitative enough to be
used as a base resolution. To evaluate, however, the
transform is applied until no more downsampling can
be performed. The base mesh is included in the re-
sults by counting B = 3Qn
v
+3dlog
2
(n
v
)en
t
bits, with
Q the amount of quantization bits per vertex, n
v
the
number of vertices in this base mesh and n
t
the num-
ber of triangles. The base meshes were clearly neg-
ligible, hence the produced coding numbers can be
entirely ascribed to the wavelet subband codec itself.
We have used the METRO tool (Cignoni et al.,
1998) to obtain the distortion values, reported as
root-mean-squared (RMS) errors, while rates are ex-
pressed in amount of bits per vertex (bpv). The result-
ing rate-distortion curves have been made convex by
removing non-convex ratepoints.
6.1 Accuracy of the Template Mesh
Using a template mesh which does not take into ac-
count geometry information, i.e., a template which
develops using only connectivity information, had an
effect on the implementation: possibly overlapping
vertices in the template mesh have to be handled prop-
erly, by repositioning these vertices equally by both
the encoder and decoder without relying on the en-
counter order. Note that these geometric modifica-
tions do not alter the geometry of the decoded meshes
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
216

Table 1: Additional cost when using an accurate template.
All models have been encoded using 12 bit precision.
Model (#verts) Rate increase
teapot (1,292) +0.068bpv (+0.21%)
beethoven (2,521) +0.187bpv (+0.55%)
triceratops (2,832) −0.017bpv (-0.052%)
elk (5,194) +0.015bpv (+0.049%)
fandisk (6,475) −0.015bpv (-0.057%)
maxplanck (7,399) −0.013bpv (-0.044%)
venushead (8,268) +0.022bpv (+0.074%)
bimba (8,857) +0.094bpv (+0.31%)
horse (19,851) +0.022bpv (+0.087%)
screwdriver (65,538) +0.182bpv (+0.89%)
rabbit (67,039) +0.073bpv (+0.32%)
dino (129,026) +0.074bpv (+0.37%)
Average +0.23%
after inverse wavelet transformation; they can only al-
ter where samples are encoded in the octrees.
Both the use of this updated template mesh as well
as the occasional repositioning of overlapping sample
positions can have an influence on the exploitability
of the spatial correlations within the data. However,
the effects of using the new geometry-agnostic tem-
plate proved to be negligible.
This can also be seen in the final bitrates. Table 1
lists the changes in lossless bitrates for several mod-
els. We observe that the bitrate increases on aver-
age by 0.23%, while in some cases the bitrate even
goes down. These results show that lowering the ac-
curacy of the template mesh does not hinder the ex-
ploitation of spatial correlations, on the contrary it
is clear that topological locality information is pre-
served. Vertices that are located closely together will
have mapped vertices in the template mesh which
are also located closely together due to topological
proximity, albeit possibly at another global position
(hence, falling within a different octree cell) due to
geometry information not being taken into account.
6.2 Rate-distortion Optimization
Rate-distortion optimization orders the data such that
the quality gains come at the lowest rates. The results
for the three models considered in (El Sayeh Khalil
et al., 2016) are given in Figure 4. For fandisk and
horse the improvements compared with a resolution-
scalable transmission order are clear at low bitrates,
obtaining similar qualities at a lower cost. At higher
bitrates the improvements are minimal. This indi-
cates that the resolution-scalable transmission at high
bitrates is in general already nearly optimal in rate-
distortion sense.
Visual results of our proposed codec are given in
Figure 5. As it was also observed in (El Sayeh Khalil
et al., 2016), the information in the lower resolution
wavelet subbands contributes the most to the shape
of such densely sampled models, while higher resolu-
tions only serve to increase the quality when render-
ing from very nearby: Figure 5(c) already resembles
very closely the original mesh depicted in Figure 5(d).
In theory, a rate-distortion optimization should al-
ways be on par or better; in practice this is the case
if the optimization algorithm calculates distortions in
the spatial domain. Our results show that an opti-
mization based on the proposed weighted wavelet co-
efficients while ignoring topological information also
proves to give superior results. The coding overhead
is minimal: the storage increases only a fraction of a
bit per vertex, due to the need to identify the resolu-
tion of each subsequent data block.
6.3 State of the Art Comparison
For comparison, we mainly investigated the
overall improvement over EMD+16. As in
(El Sayeh Khalil et al., 2016), we also compare
with Wavemesh (Valette and Prost, 2004b) and
IPR (Valette et al., 2009). EMD+16 was imple-
mented using ratepoints at every resolution; this is
more coarse-grain than our proposed codec which
gives a ratepoint after every bitplane. For Wavemesh
we made use of the publicly available software with
wavelet geometrical criterion enabled. We also made
a comparison with IPR for the models for which we
received their decoded results.
Figure 6 shows a comparison with the state of the
art. It shows even more competitive results brought
by the proposed codec compared with EMD+16. In
the case of the feature-rich model fandisk, our results
after rate-distortion optimization improve over both
Wavemesh and IPR. In the case of horse, the results
are entirely on-par with or better than previous work,
even at the lowest rates. Finally, for the feature-poor
model rabbit, results remain nearly unchanged com-
pared with EMD+16; IPR remains the better solution.
Results over a small set of models are summa-
rized in Table 2. This table makes use of a measure
similar to the Bjøntegaard delta rate (Bjøntegaard,
2001), as was also described in (El Sayeh Khalil et al.,
2016). It interpolates the ratepoints within a limited
rate range, samples the distortion values and measures
the differences in rate at these samples. This way we
can find a maximal, minimal and average value of
these differences, with a positive difference indicating
that a state-of-the-art codec requires more bits for the
same quality, and a negative difference indicating that
the state-of-the-art codec outperforms our proposed
codec. In this case, the limited rate range over which
Rate-Distortion Optimized Wavelet-based Irregular Mesh Coding
217

0
0.01
0.02
0.03
0.04
0.05
0 1 2 3 4 5 6
distortion (RMS forward+backward)
bitrate (bpv)
with RDO
without RDO
(a) Fandisk
0
0.01
0.02
0.03
0.04
0.05
0 1 2 3 4 5 6
distortion (RMS forward+backward)
bitrate (bpv)
with RDO
without RDO
(b) Horse
0
0.002
0.004
0.006
0.008
0.01
0 1 2 3 4 5 6
distortion (RMS forward+backward)
bitrate (bpv)
with RDO
without RDO
(c) Rabbit
Figure 4: Rate-distortion optimization.
(a) 0.25bpv (0.16% tris) (b) 0.5bpv (0.73% tris) (c) 3bpv (6.8% tris) (d) 33.3bpv (241 607 tris)
Figure 5: Visual results at specific rates. Figures 5(a), 5(b) and 5(c) show the model at increasing rates. Observe that 3bpv is
still in the low bitrate range considering a lossless rate of 33.3bpv for this 18 bit quantized fertility model shown in 5(d).
Table 2: Rate savings w.r.t. the state of the art. To obtain
the same quality at rates up to 3bpv, the numbers indicate in
bpv (∆
avg
) the average rate savings, (∆
max
) the largest rate
savings, and (∆
min
) the smallest rate savings. A positive
value means more rate is required than the proposed codec,
a negative value means the proposed codec performs worse.
Model Coder ∆
avg
∆
max
∆
min
teapot
EMD+16 +0.22 +1.00 0.0
(1,292)
beethoven
EMD+16 +0.32 +0.81 0.0
(2,521)
triceratops EMD+16 +0.07 +0.59 0.0
(2,832) Wavemesh −0.72 +0.43 −1.30
elk EMD+16 +0.16 +0.60 0.0
(5,194) Wavemesh +0.10 +1.20 −0.28
fandisk EMD+16 +0.08 +0.73 0.0
(6,475) Wavemesh +0.25 +0.93 +0.04
IPR +0.43 +2.90 −0.03
maxplanck EMD+16 +0.09 +0.39 0.0
(7,399) Wavemesh −0.25 +0.04 −0.37
venushead
EMD+16 +0.06 +0.73 −0.04
(8,268)
bimba EMD+16 +0.10 +0.39 0.0
(8,857) Wavemesh +0.28 +1.1 +0.14
horse EMD+16 +0.10 +0.39 0.0
(19,851) Wavemesh +0.15 +0.84 −0.17
IPR +2.40 +7.60 +0.55
screwdriver EMD+16 +0.01 +0.78 0.0
(65,538) Wavemesh −0.04 +0.01 −2.1
rabbit EMD+16 +0.011 +0.29 0.0
(67,039) Wavemesh +0.06 +1.3 0.0
IPR −0.15 +0.40 −0.80
dino EMD+16 +0.02 +0.94 0.0
(129,026) Wavemesh −0.08 0.0 −2.50
we measure is taken up to 3bpv for the proposed
codec. Furthermore, our rate-distortion optimization
and quality-scalable decoding improves all results of
EMD+16. At such low bitrates, relatively high gains
of up to 1bpv are obtained. Observe that the minimal
rate difference is zero as both the proposed codec and
EMD+16 start at the same base mesh, resulting in the
same distortion at the same rate. This confirms that
our rate-distortion optimized codec never performs
worse than EMD+16, as the minimal differences are
never negative. The comparison with Wavemesh and
IPR shows that in most cases the proposed codec is
also more favourable at these low bitrates, except for
dino where we are on par at best.
7 CONCLUSIONS
We have shown how to achieve quality scalabil-
ity and optimized rate-distortion performance for the
wavelet-based irregular mesh codec EMD+16 which
employs octree-based encoding of both connectivity
and geometry information. Gains up to 1bpv are ob-
tained at low bitrates, while at higher bitrates the orig-
inal codec design is nearly optimal in rate-distortion
sense. Furthermore, the results and working imple-
mentation serve as a proof-of-concept that an unre-
stricted storage and transmission of subband bitplanes
can be provided using the proposed framework.
ACKNOWLEDGEMENTS
The research activities as described in this paper were
funded by Ghent University, iMinds, Flanders Inno-
GRAPP 2017 - International Conference on Computer Graphics Theory and Applications
218

0
0.01
0.02
0.03
0.04
0.05
0 1 2 3 4 5 6
distortion (RMS forward+backward)
bitrate (bpv)
Proposed
EMD+16
Wavemesh
IPR
(a) Fandisk
0
0.01
0.02
0.03
0.04
0.05
0 1 2 3 4 5 6
distortion (RMS forward+backward)
bitrate (bpv)
Proposed
EMD+16
Wavemesh
IPR
(b) Horse
0
0.002
0.004
0.006
0.008
0.01
0 1 2 3 4 5 6
distortion (RMS forward+backward)
bitrate (bpv)
Proposed
EMD+16
Wavemesh
IPR
(c) Rabbit
Figure 6: Comparison with the state of the art.
vation & Entrepreneurship (VLAIO), the Fund for
Scientific Research-Flanders (FWO-Flanders), and
the European Union.
REFERENCES
Andreopoulos, Y., Munteanu, A., Barbarien, J., van der
Schaar, M., Cornelis, J., and Schelkens, P. (2004). In-
band motion compensated temporal filtering. Signal
Process. Image, 19(7):653–673. Special Issue on Sub-
band/Wavelet Interframe Video Coding.
Bjøntegaard, G. (2001). Calculation of average PSNR
differences between RD-curves. Technical Report
VCEG-M33, ITU-T SG16/Q6, Austin, TX, USA.
Bonneau, G.-P. (1998). Multiresolution analysis on irregu-
lar surface meshes. IEEE Trans. Vis. Comput. Graph-
ics, 4(4):365–378.
Cignoni, P., Rocchini, C., and Scopigno, R. (1998).
METRO: measuring error on simplified surfaces.
Comput. Graph. Forum, 17(2):167–174.
Denis, L., Satti, S. M., Munteanu, A., Cornelis, J., and
Schelkens, P. (2010). Scalable intraband and compos-
ite wavelet-based coding of semiregular meshes. IEEE
Trans. Multimedia, 12(8):773–789.
El Sayeh Khalil, J., Munteanu, A., Denis, L., Lambert,
P., and Van de Walle, R. (2016). Scalable feature-
preserving irregular mesh coding. Comput. Graph.
Forum.
Hoppe, H. (1996). Progressive meshes. In Proc. 23rd SIG-
GRAPH Conf. Computer Graphics, pages 99–108.
Khodakovsky, A., Schr
¨
oder, P., and Sweldens, W. (2000).
Progressive geometry compression. In Proc. 27th
SIGGRAPH Conf. Computer Graphics and Interactive
Techniques, pages 271–278.
Lounsbery, M., DeRose, T. D., and Warren, J. D. (1997).
Multiresolution analysis for surfaces of arbitrary topo-
logical type. ACM Trans. Graph., 16(1):34–73.
Munteanu, A., Cornelis, J., Van der Auwera, G., and
Cristea, P. (1999). Wavelet-based lossless compres-
sion scheme with progressive transmission capability.
Int. J. Imag. Syst. Tech., 10(1):76–85.
Ohm, J. R. (1994). Three-dimensional subband coding with
motion compensation. IEEE Trans. Image Process.,
3(5):559–571.
Pajarola, R. and Rossignac, J. R. (2000). Compressed pro-
gressive meshes. IEEE Trans. Vis. Comput. Graphics,
6(1):79–93.
Payan, F., Roudet, C., and Sauvage, B. (2015). Semi-regular
triangle remeshing: A comprehensive study. Comput.
Graph. Forum, 34(1):86–102.
Peng, J. and Kuo, C.-C. J. (2005). Geometry-guided pro-
gressive lossless 3D mesh coding with octree (OT)
decomposition. In Proc. 32nd SIGGRAPH Internat.
Conf. Computer Graphics and Interactive Techniques,
pages 609–616.
Said, A. and Pearlman, W. A. (1996). A new, fast, and
efficient image codec based on set partitioning in hier-
archical trees. IEEE Trans. Circuits Syst. Video Tech-
nol., 6(3):243–250.
Sweldens, W. (1998). The lifting scheme: A construction
of second generation wavelets. SIAM J. Math. Anal.,
29(2):511–546.
Taubman, D. and Zakhor, A. (1994). Multirate 3-D sub-
band coding of video. IEEE Trans. Image Process.,
3(5):572–588.
Taubman, D. S. and Marcellin, M. W. (2001). JPEG
2000: Image Compression Fundamentals, Standards
and Practice. Kluwer Academic Publishers, Norwell,
MA, USA.
Touma, C. and Gotsman, C. (1998). Triangle mesh com-
pression. In Proc. Graphics Interface Conf., pages
26–34.
Valette, S., Chaine, R., and Prost, R. (2009). Progressive
lossless mesh compression via incremental paramet-
ric refinement. Comput. Graph. Forum, 28(5):1301–
1310.
Valette, S., Kim, Y.-S., Jung, H.-Y., Magnin, I., and Prost,
R. (1999). A multiresolution wavelet scheme for ir-
regularly subdivided 3d triangular mesh. In Proc. In-
ternat. Conf. Image Processing, pages 171–174.
Valette, S. and Prost, R. (2004a). Wavelet-based multires-
olution analysis of irregular surface meshes. IEEE
Trans. Vis. Comput. Graphics, 10(2):113–122.
Valette, S. and Prost, R. (2004b). Wavelet-based progressive
compression scheme for triangle meshes: Wavemesh.
IEEE Trans. Vis. Comput. Graphics, 10(2):123–129.
Rate-Distortion Optimized Wavelet-based Irregular Mesh Coding
219
