ATL Transformation of Queueing Networks to Queueing Petri Nets

Issam Al-Azzoni

Department of Software Engineering, College of Computer and Information Sciences,

King Saud University, Riyadh, Saudi Arabia

Keywords:

Model Transformation, MDE, ATL, Queueing Networks, Queueing Petri Nets, QPME.

Abstract:

This paper presents an approach for model transformation from Queueing Network Models (QNMs) into

Queueing Petri Nets (QPNs). This would open up the beneﬁts of QPNs in analyzing the performance of

QNMs. We present metamodels for QNMs and QPNs, and then present the transformation rules in the ATL

model transformation language. To validate our approach, we apply it to analyze the performance of a QNM

and compare the results with those obtained using analytic methods. Although the approach is presented using

ATL and Ecore meta modeling language in the context of the Eclipse Modeling Project, it can be realized

using other modeling frameworks and languages.

1 INTRODUCTION

Models have become the de facto standard approach

to deal with complexity present in today’s software

systems. Model-Driven Engineering (MDE) encom-

passes approaches that consider models not just as

documentation artifacts, but as central artifacts in

the software engineering process (da Silva, 2015).

Model transformation is a fundamental part of MDE.

In model transformation, a model can be automati-

cally transformed into another model that can be at a

different level of abstraction or in a different formal-

ism altogether. In doing so, the generated models can

be analyzed in possibly more efﬁcient ways than the

original source models.

There exist several model transformation lan-

guages. In particular, the ATLAS Transformation

Language (ATL)

is a well-known model transforma-

tion language with an Integrated Development Envi-

ronment (IDE) developed on top of the Eclipse plat-

form. ATL language and toolkit are parts of the

Eclipse Modeling Project (EMP)

set of tools and lan-

guages which provide MDE capabilities to the Eclipse

community.

Queueing Network Models (QNMs) provide

a powerful notation for modeling and analyzing

the performance of many different kinds of sys-

tems (Harchol-Balter, 2013). QNMs help in predict-

ing system performance during the design phase. This

http://www.eclipse.org/atl/

https://eclipse.org/modeling/

is useful to detect potential problems before the re-

sources are actually committed. In addition, these

performance models help in managing design trade-

offs and alternatives. QNMs can be analyzed using

analytic techniques or simulation. The analytic tech-

niques allow for quick performance analysis, however

these can only be applied on speciﬁc kinds of QNMs

under several assumptions and conditions. Many

QNMs can only be analyzed using simulation. The

main drawback of simulation is the incurred compu-

tational cost.

An approach to reduce the simulation cost

is to transform QNMs into Queueing Petri Nets

(QPNs) (Kounev, 2006; Kounev et al., 2012) that

have equivalent performance characteristics. QPNs

provide a powerful general-purpose modeling formal-

ism that can be exploited for modeling systems and

analyzing their performance. One tool for analyz-

ing QPNs is QPME (Queueing Petri net Modeling

Environment)

which includes a simulation engine

(SimQPN (Kounev and Buchmann, 2006)) especially

optimized to simulate QPNs. SimQPN has been de-

signed to exploit the knowledge of the structure and

behavior of QPNs to improve the efﬁciency of sim-

ulation. The main challenge of this approach is that

QPMs and QPNs are two different formalisms with

different notations and constructs. In order to over-

come this challenge, developing an automated trans-

formation from QNMs into QPNs is desired.

This paper attempts to ﬁll this gap by presenting

http://qpme.sourceforge.net/

Al-Azzoni I.

ATL Transformation of Queueing Networks to Queueing Petri Nets.

DOI: 10.5220/0006110002610268

In Proceedings of the 5th International Conference on Model-Driven Engineering and Software Development (MODELSWARD 2017), pages 261-268

ISBN: 978-989-758-210-3

261

out

Route 1:

Poisson (λ=3)

Route 2:

Poisson (λ=4)

Route 3:

Poisson (λ=5)

Route 4:

Poisson (λ=6)

Service Rates:

= 10, µ

= 20, µ

= 10

Figure 1: Routes for connection-oriented network (based on Figure 18.5 in (Harchol-Balter, 2013)).

an approach for model transformation from QNMs

into QPNs. The transformations rules are presented

using ATL in the context of the EMP. To the best of

our knowledge, this paper is the ﬁrst to present model

transformation from QNMs into QPNs. One needs

to note that although the model transformation is pre-

sented using ATL in the context of EMP, the same

concepts can be realized using other model transfor-

mation languages and tools such as QVT

The organization of the paper is as follows. Sec-

tion 2 covers the Ecore metamodels for QNMs and

QPNs. We present in Section 3 the ATL rules for

transforming QNs into QPNs. Section 4 discusses a

case study that validates our model transformation ap-

proach. The conclusion and future work are discussed

in Section 5.

2 METAMODEL DEFINITIONS

2.1 Queueing Network Models

Queueing network models provide powerful nota-

tions for modeling and analyzing the performance

of many different kinds of systems (Harchol-Balter,

2013). A designer of a software system, for instance,

can develop a queueing network model that captures

performance-relevant details of the system and then

use it to analyze its performance. The model is useful

for the designer to verify whether or not performance-

related requirements are met. In addition, the model

can help the designer in making design decisions that

improve the system performance and to manage de-

sign tradeoffs that are typically faced in the design of

software systems.

A queueing network is made up of servers. Each

server is associated with a queue. Jobs that arrive

to a busy server (already executing another job) are

queued in the server’s queue. There can be several

http://www.omg.org/spec/QVT/

classes of jobs. Each job class represents a workload

in the queueing network. There are two main types of

workloads: open and closed. For an open workload,

the jobs arrive from outside the network. For a closed

workload, the number of jobs inside the network is

constant and there is no job arriving from outside the

network. The open workload intensity is character-

ized by the job arrival rates to the servers. On the

other hand, the closed workload intensity is character-

ized by the number of jobs circulating in the network.

A server uses a ﬁxed scheduling policy to choose

the next job to serve. First-Come-First-Served

(FCFS) and Last-Come-Fist-Served (LCFS) are ex-

ample scheduling policies. When a server serves a

job of a given class, the service time refers to the

time it takes the job to run on this server. The ser-

vice time distribution depends on the server and the

job class. The exponential distribution is a common

service time distribution. The distribution parameters

are those parameters that are needed to characterize

the distribution. For example, the exponential distri-

bution requires a single parameter: the rate µ. For

the exponential distribution, the mean is 1/µ. For a

server, the service time distributions and their param-

eters need to be speciﬁed for all job classes that can

be served by the server.

For an open class workload, jobs arrive from out-

side the network. Jobs of a given class can arrive to

one or more servers. The arrival time distributions

and their parameters need to be speciﬁed for each job

class at each server to which its jobs arrive. The Pois-

son distribution is a common arrival time distribution

and it requires a single parameter λ. For a closed class

workload, the workload intensity is characterized by

the number of jobs circulating in the network. Thus,

the number of jobs needs to be speciﬁed. In order to

model interactive systems, a think device is used for

closed class workloads. A think device can be thought

of as an inﬁnite server farm that can serve any incom-

ing job immediately. The think device requires a think

MODELSWARD 2017 - 5th International Conference on Model-Driven Engineering and Software Development

262

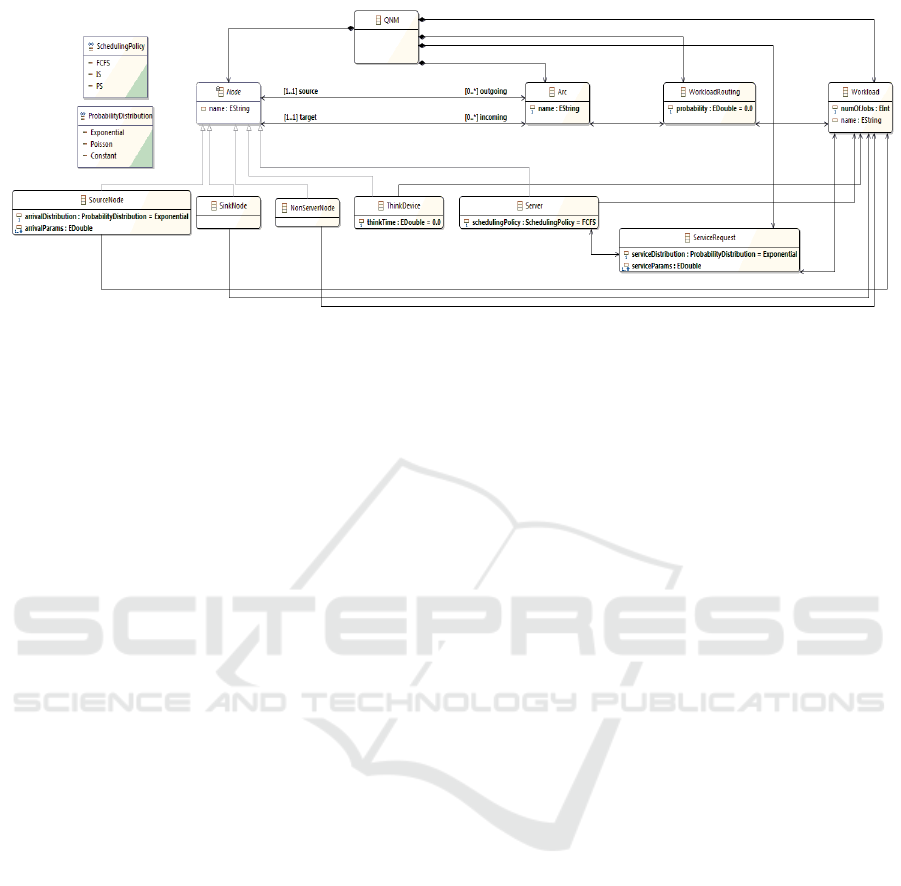
Figure 2: Ecore metamodel for queueing networks.

time distribution and its parameters.

When a job is served by a server, it can be routed

to another server or outside the network. We consider

networks of queues with probabilistic routing. For a

job of class c, P

i, j

denotes the probability that job at

server i of class c next moves to server j. P

i,out

denotes

the probability that job at server i of class c is routed

outside the network after it is served by the server i.

The routing probabilities need to be completely spec-

iﬁed for all workloads in a given queueing network.

There are several performance metrics that can be

computed for a given queueing network model. These

include the average job response time T , the average

number of jobs in the system N, and the utilization

and throughput for a given server. The job response

time is the time difference between the time when the

job leaves the system and the time when the job ar-

rived to the system. The number of jobs in the sys-

tem includes those jobs in the queues plus the ones

being served. For multi-classed networks, T and N

can be computed at a class level basis. The utilization

of a server is the fraction of time the sever is busy.

The throughput of a server is the rate of job com-

pletions at the server. In this paper, we use several

performance metrics to validate the model-to-model

transformation.

We discuss a queueing network model example

borrowed from (Harchol-Balter, 2013). It models a

network where each packet follows a particular route

based on its type. The routes are shown in Figure 1.

There are four servers and four job classes (work-

loads). All of the four workloads are open. The ser-

vice rates depend only on the servers, thus jobs of all

classes are served at the rate of µ

(packets per second)

at server i. The service times are exponentially dis-

tributed and the job arrivals follow Poisson processes.

The rates are given in the ﬁgure. An example for a

performance metric to be computed is the average re-

sponse time for packets on route 2.

Figure 2 shows the Ecore metamodel for queueing

networks. A queueing network model is composed of

one or more Nodes, zero or more Arcs, one or more

Workloads, zero or more WorkloadRoutings, and zero

or more ServiceRequests. The Arc class connects

nodes. For any given arc, there is one source node and

one target node. Node is an abstract class and there

are ﬁve types of nodes: SourceNode, SinkNode, Non-

ServerNode, ThinkDevice and Server. SourceNodes

and SinkNodes are used for open workloads to repre-

sent the entry and exit points. ThinkDevice node is

used to represent the think device. A NonServerNode

is optionally used in batch processing closed work-

loads in which there is no think device. In such

workloads, we can use a NonServerNode to re-route

a job after it ﬁnishes service to a server so that the

job starts a new service cycle with a think time of

zero. A Server node provides a processing service.

A Server has a scheduling policy represented by the

attribute schedulingPolicy whose type is the enumer-

ated type SchedulingPolicy. In Figure 2, we include

representative scheduling policies that are used in the

case study presented in the paper. Note that the at-

tributes arrivalDistribution and arrivalParams are used

in SourceNode class to characterize the arrival time

process in open workloads.

A Workload has an optional name and a nu-

mOfJobs attribute used in closed workloads to rep-

resent the number of jobs. A Server is associated

with zero to many Workloads. For the other types

of nodes, a node is associated with one Workload.

This is because a server may serve jobs of differ-

ent workloads. A ServiceRequest associates Work-

loads with Servers. ServiceRequests represent the ser-

vice times. Since the service time of a job depends

on its class (workload) and the server, the relations

from ServiceRequest to Server and ServiceRequest

to Workload are one to one in both cases. The Ser-

viceRequest class has two attributes used to charac-

ATL Transformation of Queueing Networks to Queueing Petri Nets

263

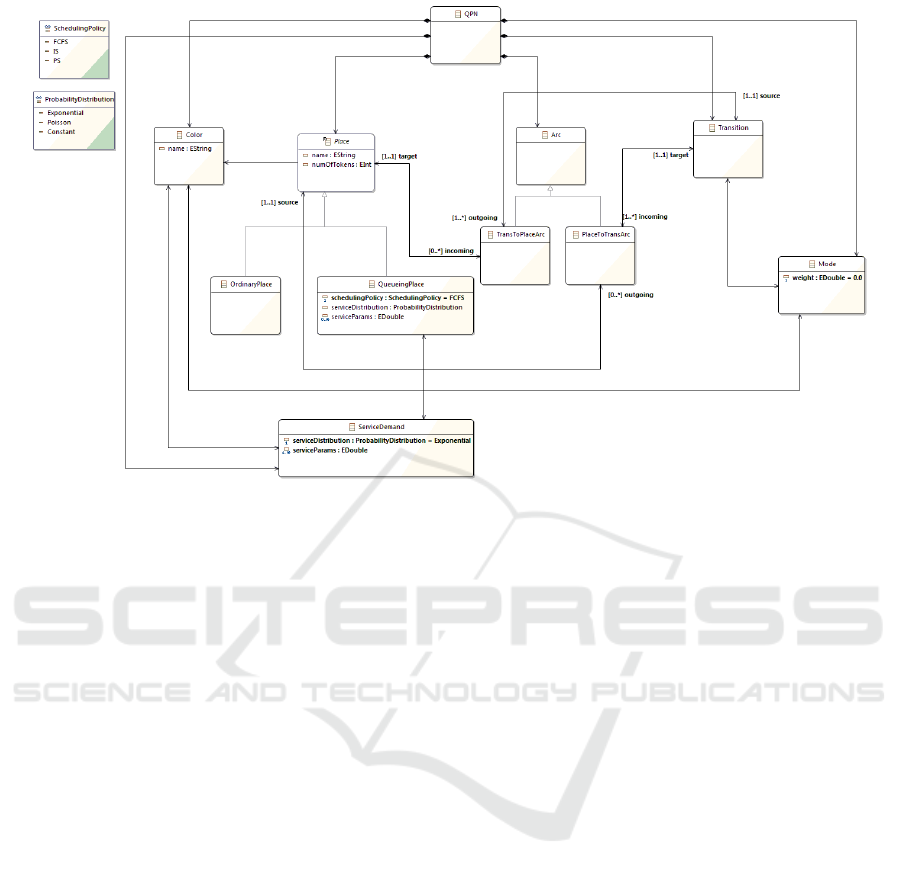
Figure 3: Ecore metamodel for queueing Petri nets.

terize the service time: serviceDistribution and ser-

viceParams. The value of the ﬁrst attribute sets the

service time distribution. An enumerated type, Proba-

bilityDistribution, is used to enumerate the supported

probability distributions. We only include the three

distributions used in the case study, however the tool

QPME supports several others as well. The distribu-

tion parameters are represented by the sequence ser-

viceParams. The job routing probabilities are rep-

resented using WorkloadRoutings. Each Workload-

Routing is a associated with one Arc and one Work-

load and it has a probability property. For example,

to represent the routing probability P

i, j

, the modeler

creases a WorkloadRouting whose probability is set

to P

i, j

. The WorkloadRouting is associated with the

Arc from Server i to Server j and with the Workload

representing job class c.

The metamodel shown in Figure 2 can be used to

deﬁne a wide variety of queueing network models in-

cluding networks which have no product-form solu-

tions. However, the metamodel cannot capture net-

works having one or more of the following features:

1. Jobs can change classes after being served.

2. Some servers have load-dependent service times.

3. Some servers have ﬁnite queue capacities.

4. Job routing is not probabilistic.

2.2 Queueing Petri Nets

Queueing Petri nets extend Colored Generalized

Stochastic Petri Nets (CGSPNs) by allowing queues

to be integrated into places of CGSPNs. In QPNs,

there are two types of places: ordinary places and

queueing places. The ordinary places are deﬁned the

same way as in CGSPNs. Queueing places, on the

other hand, add queueing and timing aspects to the

places of CGSPNs. A queueing place consists of two

components: a queue and a depository. When an in-

put transition of a queueing place ﬁres, tokens are in-

serted into the queue of the queueing place accord-

ing to the queue’s scheduling policy. After comple-

tion of its service, a token is moved to the depository

where it becomes available for the output transitions

of the place. The queue has an associated service

station for which service time distribution needs to

be deﬁned. QPNs strengthen the power of CGSPNs

modeling by the direct inclusion of queueing aspects

into their models. The reader is referred to (Kounev,

2006; Kounev et al., 2012) for more comprehensive

overview of QPNs.

Figure 3 shows the Ecore metamodel for QPNs.

A QPN model is composed of one or more Places,

zero or more Transitions, zero or more Arcs, zero

or more Modes, zero or more ServiceDemands, and

one or more Colors. The Arc class connects places

to transitions and vice-versa: TransToPlaceArc con-

nects a Transition to a Place and PlaceToTransArc

connects a Place to a Transition. There are two types

MODELSWARD 2017 - 5th International Conference on Model-Driven Engineering and Software Development

264

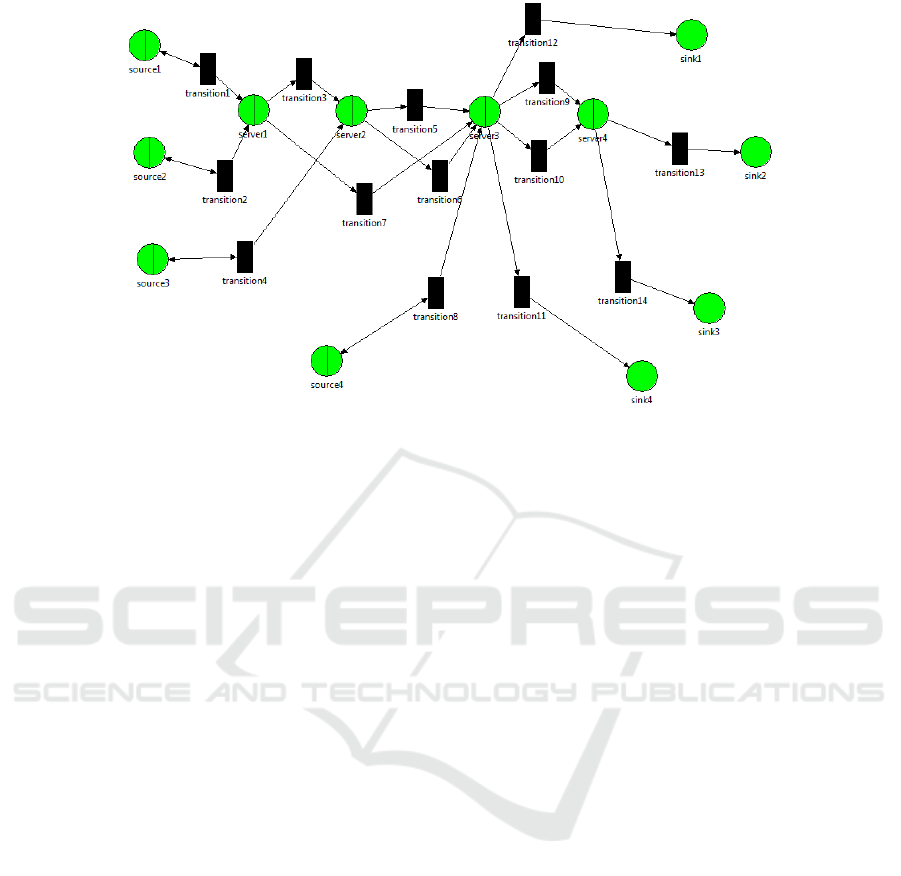
Figure 4: The QPN corresponding to the connection-oriented network of Figure 1.

of places: QueueingPlaces and OrdinaryPlaces. A

QueueingPlace has the necessary attributes to deﬁne

the scheduling policy of its queue. A Place is associ-

ated with one or more Colors. A Place has a name and

numOfTokens attribute which sets the initial marking.

When a place has more than one color, it is neces-

sary to deﬁne the token service time distribution and

the distribution parameters for each color. This is

achieved by using a ServiceDemand that associates

one QueueingPlace with a single Color. If a queueing

place has a single color, it sufﬁces to deﬁne the token

service time distribution and its parameters by using

the attributes of the QueueingPlace, serviceDistribu-

tion and serviceParams, without the need to use any

ServiceDemand. A Transition is associated with one

or more Modes. The Mode class has a single attribute

deﬁning the ﬁring weight of the mode.

We use QPME to create the QPNs and to ana-

lyze their models. QPME is an open-source tool for

stochastic modeling and analysis of QPNs. QPME

has a discrete-event simulation engine specialized for

QPNs. It exploits the knowledge of the structure and

behavior of QPNs to improve the efﬁciency of simula-

tion. Using simulation in QPME, many performance

metrics can be computed including metrics deﬁned on

the token response times, queue utilization, and token

population and occupancy.

3 MODEL TRANSFORMATION

OF QNMs INTO QPNs

The ATL code for the QN to QPN transformation

is presented in the Appendix. It consists of two

helpers and ten rules. The allArcs helper calculates

a set that contains all the Arc model elements of

the input MultiClassQN model. Similarly, the all-

SourceNodes helper calculates a set that contains all

the SourceNode model elements of the input Multi-

ClassQN model. All the rules are matched rules that

follow the declarative style of specifying transforma-

tions. The target elements are created and initialized

following the ATL execution semantics of matched

rules.

4 CASE STUDY

In this section, we validate our model transforma-

tion approach using the the queueing network exam-

ple presented in Section 2.1. For the queueing net-

work, we create a source model that conforms to the

Ecore metamodel for queueing networks. Then, we

use the ATL toolkit to run the ATL module (presented

in the Appendix) which generates a target model that

conforms to the Ecore metamodel for queueing Petri

nets. We then use QPME to analyze the queueing

Petri net and compute the required performance met-

rics. We compare the computed performance met-

rics using QPME simulation with the analytic results

using queueing theory. The resulting QPN model is

ATL Transformation of Queueing Networks to Queueing Petri Nets

265

shown in Figure 4.

In the QN model of the connection-oriented net-

work of Figure 1, there are 12 nodes: four servers,

four source nodes, and four sink nodes. There are

four open workloads and each workload has its own

source and sink nodes. There are 14 arcs connect-

ing the nodes. Each arc is associated with a single

WorkloadRouting element having probability that is

equal to one. Thus, there are 14 WorkloadRouting el-

ements. Each WorkloadRouting element is associated

with one workload. There are 10 ServiceRequest ele-

ments that are used to deﬁne the service rates: server1

serves workloads 1 and 2, server2 serves workloads 1

and 3, server3 serves workloads 1, 2, 3, and 4, and

server4 serves workloads 2 and 3.

The resulting QPN model is shown in Figure 4.

It consists of 12 places: eight queueing places and

four ordinary places. For each server or source node

in the source QN model, there is one corresponding

queueing place in the target QPN model. For each

sink node in the source QN model, there is one cor-

responding ordinary place in the target QPN model.

There are four colors: one color corresponding to

each workload in the source QN model. There are 14

transitions: one transition for each arc in the source

QN model. Each transition is associated with a sin-

gle mode whose ﬁring weight is equal to the corre-

sponding arc’s WorkloadRouting probability. There

are 10 ServiceDemands: one ServiceDemand for each

ServiceRequest in the source QN model. There are

32 arcs in the target QPN model: 28 arcs are gener-

ated by rule Arc while four arcs are generated by rule

SourceNode.

Table 1 compares several performance metrics

computed analytically using queueing theory with

the results of QPME simulation. The details of

how the analytic results are determined can be found

in (Harchol-Balter, 2013). The table includes server

utilization, the average number of packets at each

server, the average packet response time at each

server, and the average response time for packets on

Route 2. The table demonstrates the high accuracy of

QPME simulation.

5 CONCLUSION AND FUTURE

WORK

In this paper, we have presented a new approach for

transforming QNMs into QPNs using ATL. The ap-

proach was validated using a case study in which sev-

eral performance metrics were predicted with high ac-

curacy. Our approach can be applied on QNMs with

several workloads (job classes) that can be of differ-

Table 1: A comparison between the analytic and QPME

simulation results for the network of Figure 1.

Performance Metric Analytic Result QPME Simulation Result

Utilization - Server 1 0.7 0.7

Utilization - Server 2 0.8 0.8

Utilization - Server 3 0.9 0.9

Utilization - Server 4 0.9 0.9

Average Number of Packets - Server 1 2.333 2.335

Average Number of Packets - Server 2 4 3.994

Average Number of Packets - Server 3 9 9.001

Average Number of Packets - Server 4 9 9.007

Average Packet’s Response Time - Server 1 0.333 0.334

Average Packet’s Response Time - Server 2 0.5 0.499

Average Packet’s Response Time - Server 3 0.5 0.5

Average Packet’s Response Time - Server 4 1 1.001

Average Response Time for Packets on Route 2 1.833 1.835

ent types (open and closed). The QNMs supported by

our approach need not be of product form.

The following points outline the main ideas in our

future work. First, it is of interest to implement the

transformation using other transformation languages

such as QVT on models conforming to MOF. Sec-

ond, a new plug-in on Eclipse can be developed to

help a user in creating QNMs and to apply the model

transformation and performance prediction in an au-

tomated fashion. Third, we can apply our approach

on larger case studies. Finally, it is of interest to ex-

pand the queueing network metamodel to support new

features such as those mentioned at the end of Sec-

tion 2.1.

REFERENCES

da Silva, A. R. (2015). Model-driven engineering: A survey

supported by the uniﬁed conceptual mode. Computer

Languages, Systems & Structures, 43:139–155.

Harchol-Balter, M. (2013). Performance Modeling and De-

sign of Computer Systems: Queueing Theory in Ac-

tion. Cambridge University Press, 1st edition.

Kounev, S. (2006). Performance modeling and evaluation of

distributed component-based systems using queueing

Petri nets. IEEE Transactions on Software Engineer-

ing, 32(7):486–502.

Kounev, S. and Buchmann, A. (2006). SimQPN: a tool and

methodology for analyzing queueing Petri net mod-

els by means of simulation. Performance Evaluation,

63(4):364–394.

Kounev, S., Spinner, S., and Meier, P. (2012). Introduc-

tion to queueing Petri nets: Modeling formalism, tool

support and case studies. In Proceedings of the In-

ternational Conference on Performance Engineering,

pages 9–18.

MODELSWARD 2017 - 5th International Conference on Model-Driven Engineering and Software Development

266

APPENDIX: ATL TRANSFORMATION CODE

-- @path MultiClassQN=/MultiClassQN2QPN/Metamodels/MultiClassQN.ecore1

-- @path MultiClassQPN=/MultiClassQN2QPN/Metamodels/MultiClassQPN.ecore2

module MultiClassQN2QPN;3

create OUT : MultiClassQPN from IN : MultiClassQN;4

helper def: allArcs : Set(MultiClassQN!Arc) =5

MultiClassQN!Arc.allInstances()->asSet();6

helper def: allSourceNodes : Set(MultiClassQN!SourceNode) =7

MultiClassQN!SourceNode.allInstances()->asSet();8

rule Main {9

from qn : MultiClassQN!QNM10

to qpn : MultiClassQPN!QPN (11

places <- qn.nodes,12

transitions <- qn.arcs,13

modes <- qn.workloadRoutings,14

colors <- qn.workloads,15

serviceDemands <- qn.serviceRequests,16

arcs <- thisModule.allArcs->collect(e | thisModule.resolveTemp(e, ’qpn_ia’))17

->union(18

thisModule.allArcs->collect(e | thisModule.resolveTemp(e, ’qpn_oa’))19

)->union(20

thisModule.allSourceNodes->collect(e | thisModule.resolveTemp(e, ’qpn_oas’))21

)22

)23

}24

rule Server {25

from qn_s : MultiClassQN!Server26

to qpn_qp : MultiClassQPN!QueueingPlace (27

name <- qn_s.name,28

schedulingPolicy <- qn_s.schedulingPolicy,29

color <- qn_s.workload,30

incoming <-qn_s.incoming->collect(e | thisModule.resolveTemp(e, ’qpn_oa’)),31

outgoing <- qn_s.outgoing->collect(e | thisModule.resolveTemp(e, ’qpn_ia’))32

)33

}34

rule SourceNode {35

from qn_s : MultiClassQN!SourceNode36

to qpn_qp : MultiClassQPN!QueueingPlace (37

name <- qn_s.name,38

schedulingPolicy <- #IS,39

serviceDistribution <- qn_s.arrivalDistribution,40

serviceParams <- qn_s.arrivalParams,41

numOfTokens <- 1,42

color <- qn_s.workload,43

incoming <-thisModule.resolveTemp(qn_s, ’qpn_oas’),44

outgoing <- qn_s.outgoing->collect(e | thisModule.resolveTemp(e, ’qpn_ia’))45

),46

qpn_oas : MultiClassQPN!TransToPlaceArc (47

source <- qn_s.outgoing->collect(e | thisModule.resolveTemp(e, ’qpn_t’))->first(),48

target <- thisModule.resolveTemp(qn_s, ’qpn_qp’)49

)50

}51

rule SinkNode {52

from qn_s : MultiClassQN!SinkNode53

to qpn_op :MultiClassQPN!OrdinaryPlace (54

name <- qn_s.name,55

color <- qn_s.workload,56

incoming <-qn_s.incoming->collect(e | thisModule.resolveTemp(e, ’qpn_oa’)),57

outgoing <- qn_s.outgoing->collect(e | thisModule.resolveTemp(e, ’qpn_ia’))58

)59

}60

ATL Transformation of Queueing Networks to Queueing Petri Nets

267

rule NonServerNode {61

from qn_s : MultiClassQN!NonServerNode62

to qpn_op : MultiClassQPN!OrdinaryPlace (63

name <- qn_s.name,64

numOfTokens <- qn_s.workload.numOfJobs,65

color <- qn_s.workload,66

incoming <-qn_s.incoming->collect(e | thisModule.resolveTemp(e, ’qpn_oa’)),67

outgoing <- qn_s.outgoing->collect(e | thisModule.resolveTemp(e, ’qpn_ia’))68

)69

}70

rule ThinkDevice {71

from qn_s : MultiClassQN!ThinkDevice72

to qpn_op : MultiClassQPN!QueueingPlace (73

name <- qn_s.name,74

schedulingPolicy <- #IS,75

serviceDistribution <- #Exponential,76

serviceParams <- Sequenceqn_s.thinkTime,77

numOfTokens <- qn_s.workload.numOfJobs,78

color <- qn_s.workload,79

incoming <-qn_s.incoming->collect(e | thisModule.resolveTemp(e, ’qpn_oa’)),80

outgoing <- qn_s.outgoing->collect(e | thisModule.resolveTemp(e, ’qpn_ia’))81

)82

}83

rule Arc {84

from qnm_a : MultiClassQN!Arc85

to qpn_t : MultiClassQPN!Transition (86

incoming <- qpn_ia,87

outgoing <- qpn_oa88

),89

qpn_ia : MultiClassQPN!PlaceToTransArc (90

source <- qnm_a.source,91

target <- qpn_t92

),93

qpn_oa : MultiClassQPN!TransToPlaceArc (94

source <- qpn_t,95

target <- qnm_a.target96

)97

}98

rule ServiceRequest {99

from qn_sr : MultiClassQN!ServiceRequest100

to qpn_sd : MultiClassQPN!ServiceDemand (101

serviceDistribution <- qn_sr.serviceDistribution,102

serviceParams <- qn_sr.serviceParams,103

queueingPlace <- qn_sr.server,104

color <- qn_sr.workload105

)106

}107

rule WorkloadRouting {108

from qn_wr : MultiClassQN!WorkloadRouting109

to qpn_m : MultiClassQPN!Mode (110

weight <- qn_wr.probability,111

transition <- qn_wr.arc,112

color <- qn_wr.workload113

)114

}115

rule Workload {116

from qn_w : MultiClassQN!Workload117

to qpn_c : MultiClassQPN!Color (118

name <- qn_w.name119

)120

}121

MODELSWARD 2017 - 5th International Conference on Model-Driven Engineering and Software Development

268