Operationalization of the Blending and the Levels of Abstraction
Theories with the Timed Observations Theory
Marc Le Goc
1
and Fabien Vilar
1,2
1
Aix-Marseille University, Laboratory for Sciences of Information and Systems (LSIS), UMR CNRS 7296, Marseille, France
2
TOM4, Salon de Provence, France (www.tom4web.com)
Keywords:
Conceptual Integration Networks, Conceptual Blending, Abstraction, Level of Abstraction, Gradient of
Abstraction, Knowledge Engineering.
Abstract:
Providing a meaning to observations coming from humans (interviews) or machines (data sets) is a necessity to
build adequate analysis and efficient models that can be used to take a decision in a given domain. Fauconnier
and Turner demonstrates in 1998 the cognitive power of their Blending Theory where the blending of multiple
conceptual networks is presented as a general-purpose, fundamental, indispensable cognitive operation to this
aim. On the other hand, Floridi proposed in 2008 a theory of levels of abstraction as a fundamental epistemo-
logical method of conceptual analysis that can also be used to this aim. Both theories complete together but
both lack of mathematical foundations to build an operational data and knowledge modeling method that helps
and guides the Analysts and the Modeling Engineers. In this theoretical paper, we introduce the mathemati-
cal framework, based on the Timed Observations Theory, designed to build a method of abstraction merging
together the Blending Theory and the Levels of Abstraction Theory. Up to our knowledge, this is the first
mathematical theory allowing the operationalization of the Blending Theory and the Levels of Abstraction
Theory. All over the paper, the mathematical framework is illustrated on an oral exchange between three per-
sons observing a vehicle. We show that this framework allows to build a rational meaning of this exchange
under the form of a superposition of three abstraction levels.
1 INTRODUCTION
With the always increasing amount of data collected
over things connected on information networks, the
need for data and knowledge analysis became a cru-
cial stake for most of the industrial and service activi-
ties, including the research activity itself. The main
difficulty with data and knowledge analysis resides
in the introduction, in a controlled way, of semantics
in the syntactic patterns provided by human analysts
with the eventual help of Statistic Learning or Data
Mining algorithms. There is then a crucial need for
models able to guide a rationale interpretation of data
providing from humans or machines.
(Fauconnier and Turner, 1998) proposed the the-
ory of Conceptual Integration Networks, also called
the Blending Theory, that defines a common concep-
tual operation, the blending of conceptual spaces, to
provide a meaning and a way to compress the repre-
sentations that are useful for knowledge memoriza-
tion and manipulation. Blending of different concep-
tual spaces plays a fundamental role in the construc-
tion of meaning in everyday life, in the arts and sci-
ences, and especially in the social and behavioral sci-
ences (Fauconnier and Turner, 2003). The essence
of the conceptual blending operation is to establish a
new conceptual space through the matching between
the contain of different conceptual spaces. Faucon-
nier and Turner suggest that the capacity for complex
conceptual blending is the crucial capacity needed for
thought and language (Fauconnier and Turner, 2003).
Another but complementary point of view is pro-
posed in (Floridi, 2008; ?) to address the problem
of defining the nature of natural, human or artificial
agents with the notion of Level of Abstraction. The
Levels of Abstraction Theory aims to clarify implicit
assumptions and to allow the resolution of possible
conceptual confusions with the comparison between
different point of view about the same phenomenon
(concrete or abstract). Similarly to the Blending The-
ory, it provides a detailed and controlled way of com-
paring analyses and models (Floridi, 2008) with the
introduction of multiple levels of abstraction in con-
ceptual analysis. It constitutes then a crucial and pow-
364
Le Goc M. and Vilar F.
Operationalization of the Blending and the Levels of Abstraction Theories with the Timed Observations Theory.
DOI: 10.5220/0006111103640373
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 364-373
ISBN: 978-989-758-220-2
Copyright
c
 2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

erful tool to address the analysis and the modeling of
the phenomenon under consideration. Floridi argued
that for discrete systems, whose observables take on
only finitely-many values, the method is indispensable
(Floridi, 2008).
These two theories share common goals but de-
velop different ways to achieve them, and both lack
of mathematical foundations. The aim of this paper
is to propose an adequate mathematical framework
that provides for the first time, up to our knowledge,
a strong formal foundation to these theories. The pro-
posed mathematical framework, called Tom4A Timed
Observation Method for Abstraction, is build on the
Timed Observations Theory (TOT, (Le Goc, 2006))
and constitutes the basis of a new abstraction ap-
proach . Clearly, our long term goal is to develop
software tools able to discover and to model knowl-
edge representations from sets of timed data so that
the human interpretation is intuitive, immediate and
independent of the learning and the modeling tools.
To make the mathematical framework as sim-
ple and intuitive as possible, the main concepts
are illustrated with a running example of three
speakers discussing about a vehicle (cf. Section
2), the original text coming from the web site
of the Society for the Philosophy of Information
(http://www.socphilinfo.org/node/150). Section 3
provides the principles and the formal modeling tools
of the TOT that will be used all along this paper. Sec-
tion 4 describes the building of the conceptual spaces
of the three speakers. Section 5 introduces the blend-
ing process to build the common model used by the
speakers to understand together. Section 6 define the
notion of generic conceptual space. This section ends
the introduction of the basic modeling elements of the
Blenbing Theory. Section 7 introduces the basis of the
Levels of Abstraction Theory that will be used to add
an inference structure to the blended and the generic
conceptual spaces and to organize them with both a
disjoint and a nested gradients of abstraction. This
section shows also that the formalized notion of gra-
dient of abstraction constitute a powerful tool to cap-
ture and to represent the meaning in a coherent and
formal way. Finally, section 8 proposes a short syn-
thesis of Tom4A, and provide some insights about our
future works.
2 RUNNING EXAMPLE
In this section, only the factual elements of the run-
ning example are given in verbatim, its analysis ac-
cording to the Levels of Abstraction Theory being
available in http://www.socphilinfo.org/node/150:
Suppose we join Alice, Bob, and Carol earlier on
at the party. They are in the middle of a conversation.
We do not know the subject of their conversation, but
we are able to hear this much:
• Alice observes that its (whatever it is) old engine
consumed too much, that it has a stable market
value but that its spare parts are expensive;
• Bob observes that its engine is not the original
one, that its body has been recently re-painted but
that all leather parts are very worn;
• Carol observes that it has an anti-theft device in-
stalled, is kept garaged when not in use, and has
had only a single owner.
The point to notice in these elements is the fact the
three speakers observe properties about an unknown,
for us, system. The three speakers exchange then
observations about the system. Since Aristotle, we
know that this type of discourse can be resumed with
a set of apophantic formulas of the form Subject1-
Copula-Subject2. Each observation is then a propo-
sition, that is to says a relation between two subjects,
the nature of the relation being defined with a verb
(the copula) linking the two subjects. For example,
Alice’s observation it has a stable market value is a
proposition that can be represented with the binary
predicate is linking the subject MarketValue and the
other subject stable: is(MarketValue, stable). So, the
exchange can be re-written to make clear the different
observations of each speakers:
1. Alice: its engine is old.
2. Alice: its engine consumed too much.
3. Alice: it has a stable market value.
4. Alice: its spare parts are expensive.
5. Bob: its engine is not the original one.
6. Bob: its body has been recently re-painted.
7. Bob: all leather parts are very worn.
8. Carol: its anti-theft device is installed.
9. Carol: it is kept garaged when not in use.
10. Carol: it has had only a single owner.
Each but the 9
th
proposition can be easily formal-
ized with a binary predicate. Because of the use of the
when connector, the observation 9 links two proposi-
tions: is(it, not
in use) and is kept(it, garaged). Yet,
numerous of these observations use verbs conjugated
to the past, meaning that the observations have a time
reference. Temporal versions of the first order Predi-
cate Logic would then be used to formalize such ob-
servations but the interpretation of the resulting for-
mulas is accessible for only specialists of these logics.
Operationalization of the Blending and the Levels of Abstraction Theories with the Timed Observations Theory
365

To keep an intuitive interpretation of the formu-
las, Tom4A uses the modeling principles of the Timed
Observations Theory that are introduced in the next
section. These principles will be applied (i) to build
the conceptual space of the three speakers, (ii) to de-
fine the corresponding blended and generic spaces
and (iii) to model the blended space with a Gradient
of Abstraction (GoA) according to (Floridi, 2008).
3 MODELING WITH THE TOT
The Timed Observations Theory (TOT) provides a
mathematical framework to model dynamic processes
from timed data. The TOT is currently the math-
ematical basis of the TOM4L (Timed Observation
Mining for Learning) Knowledge Discovering from
Databases process (Le Goc et al., 2015; ?), and
the TOM4D (Timed Observation Modeling for Diag-
nosis) Knowledge Engineering methodology (Pom-
ponio and Le Goc, 2014). Tom4A aims at introducing
levels of abstraction and generic spaces (Le Goc and
Gaeta, 2004) in TOM4L and Tom4D according to the
notion of conceptual equivalence (Zanni et al., 2006).
The aim of the TOT is to model an observed pro-
cess defined as a couple (X(t), Θ(X, ∆)) where X (t) is
an arbitrarily constituted set X(t) = {x
1
(t), ..., x
n
X
(t)}
of n
X
timed functions x
i
(t) of continuous time t (the
dynamic process), X = {x
1
, x
2
, ..., x
n
X
} is the set of the
n
X
variable names x
i
corresponding to each time func-
tions x
i
(t) and Θ(X, ∆) is an observation program im-
plemented in a human or a computer, the set ∆ = {δ
j
}
being a set of constant values. A dynamic process
X(t) is said to be observed by a program Θ(X, ∆)
when this latter aims at writing timed observations de-
scribing the modifications over time of the functions
x
i
(t) of X(t):
Definition 1. Timed Observation
Let Γ = {t
k
}
t
k
∈ℜ
be a set of arbitrary timestamps t
k
at
which Θ(X, ∆) observes a time function x
i
(t) ∈ X(t)
and θ(x
θ
, δ
θ
, t
θ
) be a predicate implicitly implemented
in Θ(X, ∆);
A timed observation (δ
j
, t
k
) ∈ ∆ × Γ made on x
i
(t)
is the assignation of the values x
i
, δ
j
and t
k
to the
predicate θ(x
θ
, δ
θ
, t
θ
) such that θ(x
i
, δ
j
, t
k
).
For example, Alice’s observation it has a stable
market value is represented with the timed observa-
tion (stable, t
k
), t
k
being the (unknown) timestamps
of the instant where Alice pronounces this sentence
during the conversation. So, Alice play the role of the
observation program Θ(X, ∆) and the assigned ternary
predicate is(MarketValue, Stable, t
k
), corresponding
to θ(x
i
, δ
j
, t
k
), provides a meaning to the timed obser-
vation (stable, t
k
). The explicit link between a vari-
able x
i
(MarketValue) and a constant δ
j
(stable) is
made with the notion of observation class:
Definition 2. Observation Class
Let X = {x
i
}
i=1...n
n
X
be the set of variable names cor-
responding to X(t) and ∆ = {δ
j
} a set of constant
values an observation program Θ(X, ∆) can use.
An observation class O
k
= {..., (x
i
, δ
j
), ...} for
Θ(X, ∆) is a subset of X × ∆.
Any association establishing a mapping ∆ 7→ X for
each δ
j
of ∆ can be made. The simplest way, and the
most used, to define observation classes is the use of
singletons O
j
= {(x
i
, δ
j
)} where the pair (x
i
, δ
j
) is the
unique element the set O
j
. For example, the obser-
vation class O
A
s
= {(MarketValue, stable)} has been
implicitly used by Alice to reason about the system
(i.e. it). It is then obvious that doing so, all but the
observation 9 (it is kept garaged when not in use) are
occurrences of a particular observation class, the ob-
servations 9 linking together two occurrences of two
different observation classes:
1. Alice, its engine is old:
O
A
4
(t
1
) ≡ (old, t
1
), O
A
4
= {x
A
4
, old}.
2. Alice, its engine consumed too much:
O
A
6
(t
2
) ≡ (too
much, t
2
), O
A
6
= {x
A
6
, too much}.
3. Alice, it has a stable market value:
O
A
2
(t
3
) ≡ (stable, t
3
), O
A
2
= {x
A
2
, stable}.
4. Alice, its spare parts are expensive:
O
A
8
(t
4
) ≡ (expensive, t
4
), O
A
8
= {x
A
8
, expensive}.
5. Bob, its engine is not the original one:
O
B
1
(t
5
) ≡ (original, t
5
), O
B
1
= {x
B
1
, original}.
6. Bob, its body has been recently re-painted:
O
B
3
(t
6
) ≡ (recently, t
6
), O
B
3
= {x
B
3
, recently}.
7. Bob, all leather parts are very worn:
O
B
5
(t
7
) ≡ (very worn, t
7
), O
B
5
= {x
B
5
, very worn}.
8. Carol, its anti-theft device is installed:
O
C
1
(t
8
) ≡ (installed, t
8
), O
C
1
= {x
C
1
, installed}.
9. Carol, it is kept garaged when not in use:
O
C
3
(t
10
) ≡ (garaged, t
10
), O
C
3
= {x
C
3
, garaged},
O
C
2
(t
11
) ≡ (not
in use, t
11
), O
C
2
=
{x
C
2
, not in use}.
10. Carol, it has had only a single owner:
O
C
5
(t
12
) ≡ (single, t
12
), O
C
5
= {x
C
5
, single}.
Carol’s observation number 9 defines two
timed observations, O
C
2
(t
11
) ≡ (not in use, t
11
) and
O
C
3
(t
10
) ≡ (garaged, t
12
), corresponding to two
observation classes O
C
2
= {x
C
2
, not in use} and
O
C
3
= {x
C
3
, garaged}. The role of the timestamps t
k
of
a timed observation is to provide a temporal reference
in a flow of observations. Carol’s meaning of the term
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
366

when being unclear, the timestamps allows to provide
a meaning to it: the when can be interpreted as a
reference to the past. In other words, the observation
9 can be interpreted as: when it is not in use, it is
kept garaged. Such an interpretation entails that the
status of the usage of it must be defined before the
assertion of the location. The TOT defines the notion
of timed binary relation to represent a sequential
relation between two observations classes O
i
and O
j
:
Definition 3. Temporal Binary Relation
A temporal binary relation r
i j
(O
i
, O
j
, [τ
−
i j
, τ
+
i j
]), τ
−
i j
∈
ℜ, τ
+
i j
∈ ℜ, is an oriented relation between two ob-
servation classes O
i
and O
j
that is timed constrained
with the [τ
−
i j
, τ
+
i j
] interval.
This definition leads to define Carol’s obser-
vation number 9 with the timed binary relation
r
C
23
(O
C
2
, O
C
3
, [0, τ
+
23
]), τ
−
23
= 0 meaning that the end of
the usage of it can coincide with the beginning of the
put in the garage (i.e. may be t
10
= t
11
). This ex-
ample suffices to provide an intuitive comprehension
of Tom4D’s operational definition of knowledge (cf.
(Pomponio and Le Goc, 2014) for a justification of
this definition):
Definition 4. Any relation logically consistent
with a binary temporal relation of the form
r
i j
(C
i
, C
j
, [τ
−
i j
, τ
+
i j
]) is a piece of knowledge.
Figure 1: Basic Concepts of TOM4D models.
A model being an organized set of knowledge rep-
resentations, the knowledge under consideration is a
set of binary relations between time functions x
i
(t),
constants δ
i
and stochastic clocks Γ
i
(cf. Figure 1).
Figure 2: Tom4D’s Representation of a Dynamic Function.
The notion of dynamic function plays a pivot role
in the Tom4D modeling methodology. Figure 2 shows
a graphical representation of the dynamic function
x
i2
(t) = f (x
i1
(t)). The timed function x
i1
(t) is linked
to a particular component c
i
, itself being a part of the
container of all the components, i.e. the system S. The
dynamic function x
i2
(t) = f (x
i1
(t)) is defined over the
Cartesian product ∆
x
i1
× ∆
x
i2
of the definition domain
of the timed functions x
i1
(t) and x
i2
(t) respectively
and implements a set of decision rule of the form:
∀t ≥ t
1
, ∀δ
1 j
∈ ∆
x
i1
, ∃δ
2 j
∈ ∆
x
i2
,
x
i1
(t
1
) = δ
1 j
f
=⇒ x
i2
(t) = δ
2 j
. (1)
Figure 3: Finite State Machine Model of a Tom4D Func-
tion.
Such a set of decision rule specifies the Finite
State Machine (FSM) of figure 3 constituting the
behavioral model of the f dynamic function with
∆
x
i1
= {δ
11
, δ
12
} and ∆
x
i2
= {δ
21
, δ
22
}. According to
Tom4D, a rectangle represents a discernible state s
i j
labeled with a proposition about the value of one or
more functions at a particular timestamps, x
i2
(t
1
) =
δ
21
for s
21
for example. An arrow represents a transi-
tion between two discernible states. Such a transition
is conditioned with an occurrence of a particular ob-
servation class, O
x
i1
(t
1
) ≡ (δ
11
, t
1
) for example. This
means that the dynamic function f implements the
ternary predicate equals = (x
i
, δ
j
, t
k
) of definition 1.
In other words, the semantics of the ternary predicate
θ(x
θ
, δ
θ
, t
θ
) of definition 1 is given by the following
two simple decision rules:
r
1
: ∀t ≥ t
1
, x
i1
(t
1
) = δ
11
=⇒ x
i2
(t) = δ
21
r
2
: ∀t ≥ t
2
, x
i1
(t
2
) = δ
12
=⇒ x
i2
(t) = δ
22
(2)
Clearly, with boolean sets, such a FSM is not nec-
essary, these two basic decision rules are sufficient.
But generally speaking, as figure 2 shows, a Tom4D
dynamic function x
2
(t
k
) = f (x
1
(t
k
)) implements a de-
cision model M
f
specifying a set of decision rules
linking the evaluation of a criterion c(M
f
, x
i1
(t
1
))
about the value of a variable x
i1
at time t
1
to a decision
d(M
f
, x
i2
(t)) about the value of another variable x
i2
at
a posterior timestamps (or the same but not before):
r
j
: ∀t ≥ t
1
, c(M
f
, x
i1
(t
1
)) = δ
1 j
=⇒ d(M
f
, x
i2
(t)) =
δ
2 j
. This formalism is necessary and sufficient to pro-
vide a formal meaning to the 11 observations of the
speakers, and to build a semantic model of this ex-
change.
Operationalization of the Blending and the Levels of Abstraction Theories with the Timed Observations Theory
367

4 SPEAKERS’ CONCEPTUAL
SPACE
According to (Fauconnier and Turner, 1998), mental
spaces are small conceptual packets constructed as
we think and talk, for purposes of local understanding
and action. They are very partial assemblies contain-
ing elements, and structured by frames and cognitive
models. They are interconnected, and can be modified
as thought and discourse unfold.
Figure 4: Observation Number 3 (Alice).
To apply this notion, let us consider again Alice’s
observation it has a stable market value. According to
the Tom4D methodology, this observation can be for-
malized with a dynamic function x
A
2
(t) = f
A
2
(x
A
1
(t))
(cf. figure 4) where x
A
1
(t) is the time function rep-
resenting the Market Value evolution over time, and
x
A
2
(t) is the time function representing Alice’s assess-
ments about the Market Value. The variable x
A
1
de-
notes then Alice’s Market Value concept. At the par-
ticular instant she is speaking, Alice’s evaluation of
the evolution of x
A
1
(t) is stable: she assigns then the
value stable to the variable x
A
2
. By construction, the
definition domain of the variable x
A
2
is then at least a
boolean set ∆
x
A
2
= { stable, not stable }, the constant
not stable meaning anything but stable. This justifies
the two states FSM implemented in the f
A
2
assessment
function.
The definition domain of the variable x
A
1
is un-
known. Nevertheless, if we interpret the concept of
the Market Value with a usual dictionary, we can de-
duce that the dimension of x
A
1
is an amount of money
in a particular currency. This means that the defini-
tion domain of x
A
1
is the set N of the natural num-
bers representing a number of cents in the implicit
currency: x
A
1
∈ N. In other words, Alice’s assess-
ment function f
A
2
is defined over the Cartesian product
N × ∆
x
A
2
. Now, clearly, the values of the variable x
A
1
must be provided by a dynamic measurement function
x
A
1
(t) = f
A
1
(x
A
it
(t)). Such a function is either imple-
mented in Alice’s mind or, more surely, Alice make
an implicit reference to an external function aiming
at providing the Market Value of Alice’s system it
A
.
This explains the relation, denoted with a dotted line,
between the component labeled c
A
1
and the variable x
A
it
of figure 4. This component representing the term it
in Alice’s observation it has a stable market value, it
formalizes Alice’s notion of the system about which
she talks. The component c
A
1
is then the container of
all the components of the system.
Figure 5: Alice’s Conceptual Space.
Doing so for its four observations, it is simple to
build a formal model of Alice’s conceptual space as
given in figure 5. This figure shows that Alice’s ob-
servations concerned a system c
A
1
made of two com-
ponents c
A
2
and c
A
3
representing respectively Alice’s
notion of engine and spare parts. Two time functions
are linked with the component c
A
2
: x
A
engine1
(t) which
is the input of the dynamic function f
A
3
that counts
the age of c
A
2
, and x
A
engine2
(t), the input of f
A
5
that
measure the consumption of c
A
2
. The time function
x
A
7
(t) = f
A
7
(x
A
spare
parts Set
(t)) is a measurement func-
tion similar to f
A
1
, the dynamic functions f
A
4
, f
A
6
and
f
A
8
being assessment functions similar to f
A
2
. Obvi-
ously, these assessment functions use different deci-
sion models (the decision rules haven’t been repre-
sented to simplify the figure 5).
Figure 6: Bob’s Conceptual Space.
Figure 6 shows Bob’s conceptual space that has
been made with the same method. To understand
Bob’s observations, a conceptual space made with
two assessment functions, x
B
3
(t) = f
B
3
(x
B
2
(t)) and
x
B
5
(t) = f
B
5
(x
B
4
(t)), must be built where x
B
2
(t) repre-
sents the current painting timestamps of the system’s
body and x
B
4
(t) the status of the leather parts. The
function x
B
1
(t) = f
B
1
(x
B
engine
(t)) is an assertion func-
tion allowing Bob to assert the original status of what
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
368

Bob names the engine c
B
2
. An assertion function can
directly provide a fact (or a property) from a time
function, at the opposite of an assessment function
which must operate on the values computed with a
measurement function as f
B
4
for f
B
5
. The dynamic
function x
B
2
(t) = f
B
2
(x
B
painting
(t)) is a dating function
that provides the timestamps of the most recent paint-
ing of the system body. Finally, Bob’s notion of the
system is the following set of components: C
B
=
{c
B
1
, c
B
2
, c
B
3
, c
B
4
, c
B
5
}, c
B
5
being linked with c
B
3
.
Figure 7: Carol’s Conceptual Space.
Similarly, the same method leads to Carol’s con-
ceptual space of figure 7. The interpretation of Carol’s
observation number 9 (when it is not in use, it is
kept garaged) leading to the timed binary relation
r
C
23
(O
C
2
, O
C
3
, [0, τ
+
23
]), it is represented with two succes-
sive assertion functions: the first, x
C
2
(t) = f
C
2
(x
C
it
(t))
asserts the status of the usage of the system c
C
1
, the
second, x
C
3
(t) = f
C
3
(x
C
2
(t)), asserts the location of c
C
1
according to the values of x
C
2
(t). The two others
observations 8 and 10 of Carol (its anti-theft device
is installed and it has had only a single owner re-
spectively) are modeled with the assertion functions
x
C
1
(t) = f
C
1
(x
C
anti-theft devise
(t)) and x
C
5
(t) = f
C
5
(x
C
4
(t)).
The particularity of the observation 10 is that to as-
sert that c
C
1
has had only one owner, the function
x
C
5
(t) = f
C
5
(x
C
4
(t)) needs the computing of the owner
number. This is then the role of the counting function
x
C
4
(t) = f
C
4
(x
C
owners
(t)).
The conceptual space of Alice, Bob and Carol are
those built by each of these speakers to produce their
observations. The building of a blended space is now
required to understand together the 10 observations.
5 BLENDED CONCEPTUAL
SPACE
Blending is the usual name of the conceptual integra-
tion operation aiming to project at least two differ-
ent conceptual spaces into a third one, the blended
conceptual space: conceptual integration-like fram-
ing or categorization-is a basic cognitive operation
that operates uniformly at different levels of abstrac-
Figure 8: Blended Conceptual Space.
tion and under superficially divergent contextual cir-
cumstances (Fauconnier and Turner, 1998). To cite
again Fauconnier and Turner, Projection is the back-
bone of analogy, categorization, and grammar and
they consider that it is an established and fundamen-
tal finding of cognitive science that structure mapping
and metaphorical projection play a central role in the
construction of reasoning and meaning.
Since nothing is said in the example, we must
make the following hypothesis to build a blended and
a generic conceptual space: Alice, Bob and Carol
speak about the same system. With this hypothesis,
Tom4A’s formalization principles make very simple
the conceptual integration operation because the 10
observations are independent. Figure 8 shows the
structure of the blended conceptual space. The expo-
nents have been kept to clarify the links between the
individual conceptual space and the resulting blended
space after the projections of Alice’s space firstly,
next Bob’s one and Carol’s space lastly:
• The system is now represented with a unique com-
ponent : c
1
≡ c
A
1
≡ c
B
1
≡ c
C
1
.
• The components of c
1
is the fusion of the Alice,
Bob and Carol component sets:
C = {c
1
, c
A
2
, c
C
2
, c
A
3
, c
B
3
, c
C
3
, c
B
4
, c
B
5
}.
• The time function’s set is the fusion of the time
function’s sets: X(t) = {x
A
its
(t), x
A
1
(t), ..., x
C
1
(t)}.
• The dynamic function’s set is also the fusion of
the corresponding sets: F = { f
A
1
, ..., f
B
5
, f
C
1
}.
In figure 8, the 10 observations of the conversa-
tion have been organized in three abstraction levels.
The lowest contains the more concrete observations
of Alice, Bob and Carol: those concerning the status
of the system c
1
. The abstraction’s level of the middle
Operationalization of the Blending and the Levels of Abstraction Theories with the Timed Observations Theory
369

concerns its usage and contains Carol’s observations
number 9 and 10 only. The highest abstraction level
concerns the cost usage of the system c
1
. Only Alice
made observations at this level of abstraction.
6 GENERIC CONCEPTUAL
SPACE
One of the interesting features of Fauconnier and
Turner’s theory is the notion of generic conceptual
space. This usual notion in the domain of Knowl-
edge Engineering is of the main importance to model
a knowledge corpus (cf. the CommonKads method-
ology (Schreiber et al., 2000) or (Pomponio and
Le Goc, 2014) for a detailed illustration). Tom4D’s
Knowledge Engineering methodology allows to build
generic conceptual spaces according to a notion of
conceptual equivalence (Zanni et al., 2006) between
different knowledge roles. A knowledge role is an ab-
stract label that indicates the role that the domain
knowledge to which the label is attached plays in
an inference process (Bredeweg, 1994). So, the ba-
sic idea of the conceptual equivalence is that when
two different concepts play the same role in a reason-
ing process, they can be considered as conceptually
equivalent.
Let us consider together Alice’s observation num-
ber 3 (it has a stable market value) and Bob’s observa-
tion number 7 (all leather parts are very worn). Fig-
ures 5 and 6 show that these two observations uses
two assessment functions, f
A
2
and f
B
5
, and two mea-
surement functions, f
A
1
and f
B
4
. It is obvious that, in
Alice’s and Bob’s reasoning, the functions f
A
2
and f
B
5
plays the same role: to assess something about the
system. Similarly, the role of f
A
1
and f
B
4
is to measure
the level of some time function. It is then clear that
the time functions x
A
2
(t) and x
B
3
(t), although basically
different, play the same role in Alice’s and Bob’s rea-
soning. The same analysis holds for the others time
functions. As a consequence, these two observations
can be represented with the same pattern made of type
of function linking type of variable (cf. figure 9). A
set of such patterns is called the functional network. It
is build from the projection from a concrete concep-
tual space, typically a blended space, to the space of
the function’s types. To build the figure 9, let us de-
fine the type of functions used by our three speakers.
The type of an assessment function is called Dis-
cretization: this is the function’s type of the dynamic
functions f
A
2
, f
A
4
, f
A
6
, f
A
8
, f
B
3
, f
B
5
and f
C
5
. The Dis-
cretization function’s type corresponds to the Quanti-
zation operation in the Discrete Event Systems com-
munity. It is represented with a function of the
form x
D
2
= f
D
(Ψ, x
D
1
) where Ψ is a set Ψ = {ψ
i
} of
thresholds values ψ
i
. The definition domain of f
D
is
∆
x
D
1
× ∆
x
D
2
where ∆
x
D
1
is a cardinal set and ∆
x
D
2
is an
ordinal set or a set without any topology. The con-
stants δ
x
D
2
i
of ∆
x
D
2
denote ranges of values (i.e. inter-
vals) in ∆
x
D
1
so that the number of elements in ∆
x
D
2
is
the numbers of thresholds values ψ
i
in Ψ plus one. As
a consequence, any function mapping a cardinal set to
an ordinal set or an a-topology set can be represented
with a f
D
function type. In the running example, the
time functions x
A
2
(t), x
A
8
(t), x
A
6
(t), x
C
5
(t), x
A
4
(t), x
B
3
(t)
and x
B
5
(t) are linked with the variable’s type x
D
2
.
The type of an assertion function, the dynamic
functions f
B
1
, f
C
1
, f
C
2
and f
C
3
, is a called Classifica-
tion. A classification function implements a reasoning
that uses a set R
f
of classification rules of the form (N
denotes the set of natural numbers):
∀x
C
1
∈ ∆
x
C
1
, ∃n ∈ N, x
C
1
= δ
x
C
1
i
=⇒ x
C
2
= n (3)
In this equation, n denotes a particular class so that
x
C
2
= n means that the class corresponding to the
value of x
C
1
is the n
th
class. A classification func-
tion is then represented with a function of the form
x
C
2
= f
C
(R
f
, x
C
1
), its definition domain being ∆
x
C
1
× N
where ∆
x
C
1
is any type of set. Any function mapping
a set to N can be represented with a f
C
function type.
The time functions x
C
2
(t), x
C
3
(t), x
B
1
(t) and x
C
1
(t) are
then linked with the variable’s type x
C
2
.
The type of a measurement function is a Model-
ing function. It concerns the dynamic functions f
A
1
,
f
A
5
, f
A
7
and f
B
4
. It is represented with a function of the
form x
M
2
= f
M
(M
f
, x
M
1
) where M
f
is a model provid-
ing the value of x
M
2
given those of x
M
1
. The definition
domain of f
M
is ∆
x
M
1
× ∆
x
M
2
where ∆
x
M
1
and ∆
x
M
2
are
cardinal sets. Any function mapping two ordinal sets
can be represented with a f
M
function type. The time
functions x
A
1
(t), x
A
7
(t), x
A
5
(t) and x
B
4
(t) are then linked
with the variable’s type x
M
2
.
The type of a counting function is a Numbering
function ( f
A
3
and f
C
4
). A numbering function is a
function of the form x
N
2
= f
N
(P
f
, x
N
1
) where P
f
is a
counting process (i.e. a Poisson process or a discrete
Markov counting model for examples). The defini-
tion domain of f
N
is ∆
x
N
1
×∆
x
N
2
where ∆
x
N
1
and ∆
x
N
2
are
two ordinal sets: any function mapping two ordinal
sets can be represented with a f
N
function type. The
time functions x
C
4
(t) and x
A
3
(t) are then linked with the
variable’s type x
N
2
.
The last type of function of the running example
corresponds to the dating function f
B
2
: it is called the
Time-Stamping function type and is represented with
a function of the form x
T
2
= f
T
(T
f
, x
T
1
) where T
f
is a
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
370

time stamping process providing the timestamps t
k
of
the current value of x
T
1
. The definition domain of f
T
is ∆
x
T
1
× ∆
x
T
2
where ∆
x
T
1
can be any kind of set, ∆
x
T
2
being an ordinal set. So, any function mapping a set
to an ordinal set can be represented with a f
T
function
type. Only the time function x
B
2
(t) is linked with the
variable’s type x
N
2
.
Figure 9: Generic Conceptual Space.
Mapping the dynamic and the time functions of
the blended space of figure 8 with the corresponding
types leads to the functional network of figure 9. The
components have also been associated with abstract
components so that C
1
is linked with the S compo-
nent, C
A
3
is linked with C
3
D
, C
C
3
is linked with C
2
N
, C
A
2
is
linked with C
3
C
, C
1
C
and C
1
D
, the pair (C
B
3
, C
B
5
) is linked
with C
N
1
, C
B
4
with C
1
D
and finally, C
C
2
with C
1
C
. An ab-
stract component specifies the properties or the con-
straints that a concrete component must satisfy to be
considered as an instance of this abstract component.
The reference to any concrete element in the blend
being contained in the projection from the blended to
the generic conceptual space, the functional network
is more compact than the blend.
An important remark is that, when forgetting the
projection, there is no way to come back from the
generic to the blended space. In other words, it is
impossible to build Alice, Bob and Carol observa-
tions with the only functional network of figure 9: the
blended space of figure 8 is a particular instantiation
of the functional network of figure 9.
7 LEVELS OF ABSTRACTION
Fauconnier and Turner’s theory aims at studying the
creation of specific structures that emerge out of the
blending operation. The level of abstraction of the
emerging structures is then an inherent property of the
structures themselves (cf. the three levels of abstrac-
tion in figures 8 and 9).
Nevertheless, Newell builds an ontological notion
of level of abstraction where a level of abstraction de-
scribes a system that transforms a medium through its
components, providing primitive treatments, and de-
fines (Newell, 1981):
1. laws of compositions of the components to spec-
ify the contraints that any structure must satisfy at
this level of abstraction, and
2. laws of behavior to establish how the system be-
havior emerges from a particular composition of
its components.
Newell uses this notion to describe an information
system with four levels of abstraction, the physic level
(electromagnetic waves), the circuits level (transis-
tors), the logic level (boolean algebra) and the symbol
level (program), from the most concrete (continuous
space) to the most abstract (purely discrete space),
and proposes the existence of the Knowledge Level
that it places above these ones. The Knowledge Level
is characterized by the fact that there is no law of com-
position because the system behavior is governed by a
Principle of Rationality: described at the Knowledge
Level, a system is an agent whose components are
goals, actions and a body (i.e. a knowledge corpus);
and which processes its input informations to deter-
mine the (output) actions to take in order to reach its
goals.
On an another hand, Floridi’s uses an epistemo-
logical point of view to develop its Method of Lev-
els of Abstraction (Floridi, 2008; ?). A level of ab-
straction (LoA) is a finite but non-empty set of ob-
servables (Floridi, 2008, p. 10), and the word system
refers to the object of study, a process in science or
engineering or a domain of discourse. The behaviour
of a system, at a given LoA, is defined to consist of
a predicate whose free variables are observables at
that LoA. The substitutions of values for observables
that make the predicate true are called the system be-
haviours. A Level of Abstraction is then a particular
organization of variables, observables, behaviors and
transition rules between values. A moderated LoA is
defined to consist of a LoA together with a behaviour
at that LoA, (Floridi, 2008, p. 11).
The Method of Levels of Abstraction organizes
LoA’s in Gradient of Abstraction (GoA). A GoA al-
lows to vary the LoA to make observations at different
Operationalization of the Blending and the Levels of Abstraction Theories with the Timed Observations Theory
371

granularity levels: the higher the level of abstraction,
the fewer but richer the information. The quantity of
information in a model varies with the LoA: a lower
LoA, of greater resolution of finer granularity, pro-
duces a model that contains more information than a
model produced at a higher, or more abstract, LoA,
(Floridi, 2008, p. 18). Foridi’s theory distinguishes
two kinds of GoA: disjoint GoAs, where the LoA are
independent together, and nested GoAs where each
LoA incrementally describes the same phenomena.
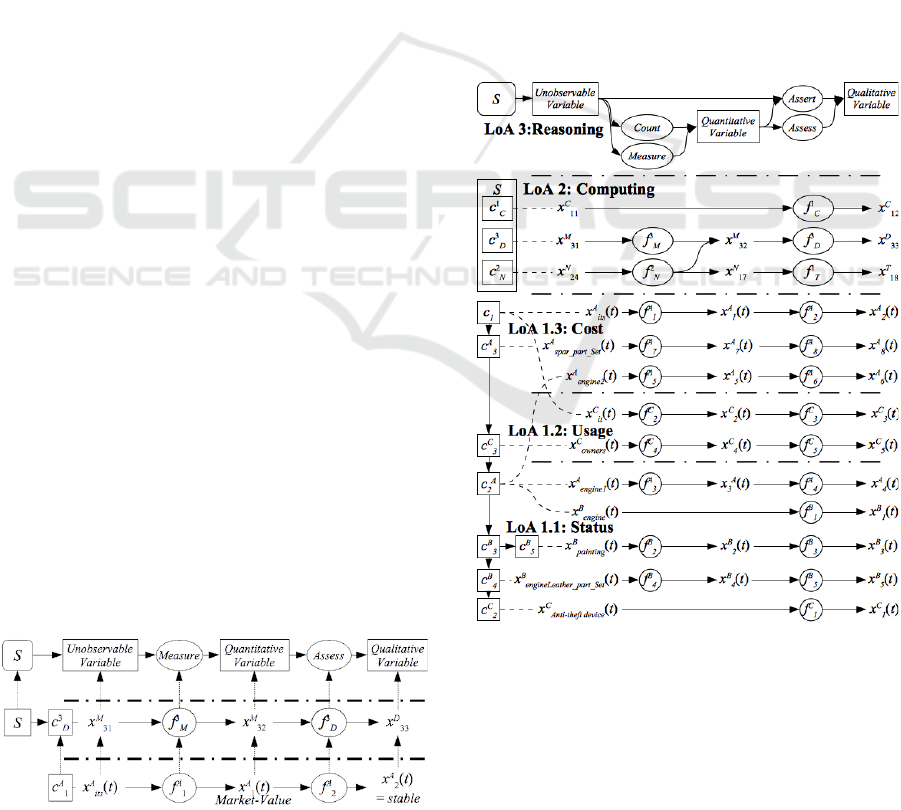
Tom4A defines three moderated LoA’s. The most
concrete is called the Observation LoA: the blended
space of figure 8 constitutes the moderated LoA for
the running example at the Observation Level of Ab-
straction. It formally describes the observations of the
speakers according to the TOT mathematical frame-
work. It is made with a set of binary relations
linking concrete components, time functions and dy-
namic functions constituting respectively the Struc-
tural Model, the Behavioral Model and the Functional
Model of the observed process (X(t), Θ(X , ∆)) (cf.
section 3 and (Pomponio and Le Goc, 2014) for a de-
tailed example).
The intermediate LoA is called the Computing
LoA: the functional network of figure 9 is the moder-
ated LoA for the example at the Computing Level of
Abstraction. It formally describes the types of com-
puting that are required to create timed observations
from an observed process. The Computing LoA con-
tains the necessary and sufficient corpus of knowledge
to specify the programs that could generate the timed
observations of the Observation LoA. It is made of
binary relations linking types of components, vari-
ables and functions, describing the logical approach
to build the timed observations at the Observation
LoA.
The highest LoA according to Tom4A is the Rea-
soning LoA: it is made with at least one inference
structure describing the way of using the type of func-
tions of the Computing LoA to achieve a particular
goal. It is made of binary relations linking knowl-
edge roles and type of inferences, describing the ele-
mentary reasoning steps that are required to achieve a
goal.
To build a model at this level of abstraction, let
Figure 10: Alice’s Observation 3 at three LoA.
us consider again Alice’s observation it has a stable
market value. The first point to notice is that Alice
uses the term market value to build its observation.
This term has been represented with the time function
x
A
2
(t) (cf. figure 10), which is a Discretization func-
tion represented with the variable’s type x
D
33
. At the
Knowledge Level, the role of a discretization function
is to transform a Quantitative Variable in a Qualita-
tive Variable. Such a transformation aims at defining
the level of a quantitative variable regard to thresh-
olds (cf. section 6). In the same spirit, the role of a
modeling function f
3
M
is to provide a quantitative eval-
uation of the Unobservable Variable x
M
31
which char-
acterizes, at the Knowledge Level, the phenomena of
the evolution of the time function x
A
its
(t). The role of
System is then those of a transfer function graphically
represented a rectangle with round corners (Schreiber
et al., 2000): to provide values for each of its vari-
ables. Finally, according to Tom4A, the complete
meaning of Alice’s observation number 3 is given in
figure 10.
Figure 11: Gradients of Abstraction of the Conversation.
In figure 11, the blended, the generic and the in-
ference conceptual spaces have been organized in two
Gradient of Abstraction (GoA): a disjoint GoA which
constitutes the lowest abstraction level, the Observa-
tion LoA, and contains the Blended Conceptual Space
of figure 8, and a nested GoA made of the Obser-
vation LoA, the Computing LoA and the Reasoning
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
372

LoA. The Generic Conceptual Space of figure 9 is rep-
resented with the intermediate abstraction level, the
Computing LoA. The effect of the conceptual equiva-
lence appears clearly: even if they aim at representing
the same thing, the functional network of figure 11
is much more compact than the Generic Conceptual
Space of figure 9. Up to our knowledge, the Rea-
soning LoA has no counter part in the Blending The-
ory. The fundamental interest of this LoA appears in
figure 11: it allows to identify the common aim of
the speakers to explicit some properties of a (still un-
known) system in order to state its qualities and de-
fects. A concrete illustration of such a disjoint and
nested GoA can be found in (Le Goc, 2004).
8 CONCLUSION
This paper proposes a formal framework, called
Tom4A (Timed Observations Method for Abstrac-
tion), that provides for the first time, up to our
knowledge, a strong mathematical foundation to
both the Blending Theory (Fauconnier and Turner,
1998) and the Method of Abstraction Theory (Floridi,
2008). Constructed on the Timed Observations The-
ory (TOT), Tom4A completes the Tom4D Knowl-
edge Engineering methodology (Timed Observations
Methodology for Diagnosis, (Pomponio and Le Goc,
2014)) and the Tom4L Knowledge Discovery in
Databases process (Timed Observations Mining for
Learning, (Le Goc et al., 2015; ?)), also based on the
TOT. The basic concepts of Tom4A are progressively
introduced with a running example, an exchange be-
tween three speakers, whose original text comes from
the web site of the Society for the Philosophy of Infor-
mation (http://www.socphilinfo.org/node/150). This
example provides for the first time, still up to our
knowledge, the first conceptual model of such an ex-
change under the formal form of two gradients of ab-
straction, defining the meaning of this exchange.
Our long term goal is to develop software tools
able to discover and to model knowledge representa-
tions from sets of timed data so that the human inter-
pretation is intuitive, immediate and independent of
the learning and the modeling tools. The next step of
this work is then to propose a new formalization of
the analogical reasoning based on the combination of
the TOT and the Category Theory (Mac Lane, 1978).
REFERENCES
Bredeweg, B. (1994). The CommonKads Library for Exper-
tise Modelling, chapter Model-based diagnosis and
prediction, p.121-153. IOPress.
Fauconnier, G. and Turner, M. (1998). Conceptual integra-
tion networks. Cognitive Science, (22):133–187.
Fauconnier, G. and Turner, M. (2003). Conceptual blend-
ing, form and meaning. Recherches en communica-
tion, n
◦
19 (2003)., (19):57–86.
Floridi, L. (2008). The method of levels of abstraction.
Minds and Machines, 18:303–329.
Floridi, L. (2010). Levels of abstraction and the turing test.
Keybenetes, 39(3):423–440.
Le Goc, M. (2004). Sachem. a real time intelligent diagno-
sis system based on the discrete event paradigm. Sim-
ulation, The Society for Modeling and Simulation In-
ternational Ed., 80(11):591–617.
Le Goc, M. (2006). Notion d’observation pour le di-
agnostic des processus dynamiques: Application
`
a
Sachem et
`
a la d
´
ecouverte de connaissances tem-
porelles. Hdr, Aix-Marseille University, Facult
´
e des
Sciences et Techniques de Saint J
´
er
ˆ
ome.
Le Goc, M. and Ahdab, A. (2012). Learning Bayesian Net-
works From Timed Observations. LAP LAMBERT
Academic Publishing GmbH & Co. KG.
Le Goc, M., Barthelot, F., and Pascual, E. (2015). Emer-
gence of regularities in the stochastic behavior of hu-
man. In IEEE International Conference on Data Min-
ing Workshop, ICDMW 2015, Atlantic City, NJ, USA,
November 14-17, 2015, pages 381–388. IEEE Com-
puter Society.
Le Goc, M. and Gaeta, M. (2004). Modeling Strutures in
Generic Space, a Condition for Adaptiveness of Mon-
itoring Cognitive Agent. Journal of Intelligent and
Robotics Systems, 41(2-3):113–140.
Mac Lane, S. (1978). Categories for the Working Mathe-
matician, volume 5. Springer-Verlag New York.
Newell, A. (1981). The knowledge level. AI Magazine,
2(2):1–20.
Pomponio, L. and Le Goc, M. (2014). Reducing the gap
between experts’ knowledge and data: The tom4d
methodology. Data & Knowledge Engineering, DOI
10.1016/j.datak.2014.07.006.
Schreiber, G., Akkermans, H., Anjewierden, A., de Hoog,
R., Shadbolt, N., de Velde, W. V., and Wielinga, B.
(2000). Knowledge Engineering and Management:
The CommonKADS Methodology. MIT Press.
Zanni, C., Le Goc, M., and Frydman, C. (2006). Con-
ceptual equivalence at knowledge level for diag-
nosis applications. KES, International Journal of
Knowledge-Based and Intelligent Engineering Sys-
tems, 10(3):225–246.
Operationalization of the Blending and the Levels of Abstraction Theories with the Timed Observations Theory
373