Hierarchical Techniques to Improve Hybrid Point Cloud Registration

Ferran Roure

, Xavier Llad

, Joaquim Salvi

, Tomislav Privani

and Yago Diez

ViCOROB Research Institute, University of Girona, Girona, Spain

Faculty of Electrical Engineering and Computing, University of Zagreb, Zagreb, Croatia

GSIS Tokuyama Lab., Tohoku University, Sendai, Japan

Keywords:

Point Cloud Matching, Algorithms and Data Structures, Regular Grid, Hierarchical Approach.

Abstract:

Reconstructing 3D objects by gathering information from multiple spatial viewpoints is a fundamental prob-

lem in a variety of applications ranging from heritage reconstruction to industrial image processing. A central

issue is known as the ”point set registration or matching” problem. where the two sets being considered are

to be rigidly aligned. This is a complex problem with a huge search space that suffers from high computa-

tional costs or requires expensive and bulky hardware to be added to the scanning system. To address these

issues, a hybrid hardware-software approach was presented in (Pribani

c et al., 2016) allowing for fast soft-

ware registration by using commonly available (smartphone) sensors. In this paper we present hierarchical

techniques to improve the performance of this algorithm. Additionally, we compare the performance of our

algorithm against other approaches. Experimental results using real data show how the algorithm presented

greatly improves the time of the previous algorithm and perform best over all studied algorithms.

1 INTRODUCTION AND

PREVIOUS WORK

The registration or matching of objects is a funda-

mental problem in areas such as computer vision

(da Silva Tavares, 2010) and computational geome-

try (Agarwal et al., 2003; Diez and Sellar

es, 2011)

with applications areas as diverse as medical imaging

(Oliveira and Tavares, 2014), road network match-

ing (Diez et al., 2008) or mobile phone apps (Pro-

jectTango, 2016; StructureSensor, 2016). A typical

instance of the problem in 3D is that of object recon-

struction. This requires gathering 3D object informa-

tion from multiple viewpoints. Acquisition devices

are used to capture discrete points in the surfaces of

objects which are then represented as point clouds.

Since every view usually contains 3D data corre-

sponding to a different spatial coordinate system it is

necessary to transform the information from all the

views into a common coordinate system (see Figure

1 for a graphical example). From a formal stand-

point, two such systems are related through three an-

gles of rotation and a three-dimensional translation

vector. In order to register two objects represented

as point clouds, a minimum of three point correspon-

dences are needed to determine a 3D rigid motion.

Thus, the number of possible correspondences is in

O(n

), making the design of algorithms that can nav-

igate this search space efﬁciently an important issue.

For the purpose of the current discussion, al-

gorithms can be divided into two main categories:

coarse and ﬁne matching algorithms (D

ıez et al.,

2015). Coarse registration algorithms do not require

an initial pose and aim at ”producing an estimate that

is good enough for some ﬁne registration methods

to start from” (Besl and McKay, 1992; Aiger et al.,

2008). Fine registration methods provide the ﬁnal

registration (Besl and McKay, 1992; Rusinkiewicz

and Levoy, 2001).

Concerning coarse registration, most approaches

aim at pure software solutions. Different strategies

exist to improve efﬁciency. For instance, approaches

based on shape descriptors determine point corre-

spondences based on local shapes measures (Mian

et al., 2010; Roure et al., 2015b). Other strategies

include data ﬁltering (Rusinkiewicz and Levoy, 2001;

ıez et al., 2012) or devising novel searching strate-

gies to speed up the search for correspondences be-

tween points (Aiger et al., 2008). There are meth-

ods which expect as the input of the 3D reconstruc-

tion system not only 3D point position data, but also

the normal vectors of every 3D point (Makadia et al.,

2006). Another generic way to increase the efﬁciency

of any parallelized method is to use GPU implementa-

Roure F., LladÃ¸s X., Salvi J., PribaniÄ

G T. and Diez Y.

Hierarchical Techniques to Improve Hybrid Point Cloud Registration.

DOI: 10.5220/0006112600440051

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 44-51

ISBN: 978-989-758-225-7

Figure 1: Registration example, two views from the bust model are brought to the same coordinate system by rigid motion µ.

tions (Choi et al., 2011). Perhaps the most signiﬁcant

contributions in terms of computational gain made re-

cently correspond to searching strategies (Aiger et al.,

2008) (Mellado et al., 2014).

Coarse matching can also be tackled with the as-

sistance of hardware. At its most basic level, the

acquisition system can be upgraded with dedicated

parts to gain information on some of the parameters

(Matabosch et al., 2008; Martins et al., 2015). This

type of solutions (usually involving the installation of

robot arms and/or turntables) demands complex in-

stallations and are often expensive.

A recent trend (ProjectTango, 2016; StructureSen-

sor, 2016) seeks to use sensors from mobile devices

in order to help registration. These sensors are com-

monly available and less expensive, circumventing

many of the previous problems. The goal in this case

is to propose hybrid 3D registration methods which

combine the best features of software and mechanical

approaches. Signiﬁcantly, (Pribani

c et al., 2016) pre-

sented a hybrid algorithm with a hardware part based

on smartphone technology that managed to gain ac-

cess to rotation data that could then be used to search

for the remaining translation part of the rigid motion

by software means.

The idea of disaggregating the rotation and trans-

lation part was not new and can be found, for example

in (Larkins et al., 2012). Once the rotation part of the

problem is solved (either by using hardware data as

in the former reference or by software means as in

the later), what remains is determining the translation

vectors that brings the two sets being registered closer

together. To solve this problem it is enough to ﬁnd one

single correspondence between one point in each set

so that the resulting translation brings the sets close

enough for a ﬁne registration to succeed. This yields

an immediate O(n) asymptotic cost for this version of

the problem.

In this paper we present an algorithm that extends

the work in (Pribani

c et al., 2016). By using the hard-

ware part developed in the mentioned reference, we

are able to focus on the software solution of the trans-

lation problem. We propose a hierarchical approach

that ﬁnds a coarse matching solution by selecting one

point in one set and determining a correspondence in

the other in the following way. First, the search is ini-

tialised by using the center of masses of the set. Then,

the search proceeds using a regular sample grid. Ini-

tially only the overlap between bounding boxes of the

sets is considered. Next, the sets are divided in regular

cells and the number of points in each cell is consid-

ered. Finally, the result of the coarse step of the algo-

rithm is determined by computing the residues con-

sidering the points in the sets.

The rest of the paper is organised as follows. Sec-

tion 2 introduces the paper that motivates this research

and provides details on the approach used in the cur-

rent work. The experiments in Section 3 illustrate the

validity of our approach and compare it with other

registration methods. This comparison includes not

only the original algorithm (Pribani

c et al., 2016) but

also two widely used registration methods: a) The

4PCS method, which is one of the most widely used

(Aiger et al., 2008), and b) its improved version, the

super4PCS method (Mellado et al., 2014) which is, to

the best of our knowledge, the fastest general-purpose

coarse matching algorithm to date. The paper ends

with a summary of the ﬁndings of the paper with spe-

cial attention to the most salient results reported in the

experiments in Section 4.

Hierarchical Techniques to Improve Hybrid Point Cloud Registration

2 MATERIALS AND METHODS

In this section we start by providing some details on

the algorithm that motivates this research. On the sec-

ond part we provide details on the new approach to the

problem.

2.1 Previous Algorithm

A pipeline for the registration problem where exist-

ing methods can be classiﬁed is presented in ﬁgure 2.

The algorithm presented in (Pribani

c et al., 2016) can

be described as a hybrid hardware-software coarse

matching algorithm.

More speciﬁcally, no ﬁltering or detection steps

where used (although the algorithm does allow for

them) and the searching strategies part was divided

in two steps.

• In the ﬁrst step, the authors roughly determine the

rotation between the two sets by using a smart-

phone capable of providing 3D orientation data

(from the accelerometer and magnetometer sen-

sors). The sensors provide orientation angle data

that can be used to produce an orientation matrix

for the scanning system respect to a certain world

reference axis. These orientation matrices can be

composed from view to view to obtain the afore-

mentioned rough rotation correspondence.

• In the second step, the rotationally aligned sets

are matched also for translation. As the rotational

alignment is expected to be noisy, so a robust

translation matching algorithm is required in or-

der for the subsequent ﬁne registration algorithm

to succeed.

It is important to note that the data used for the

experiments in the reference where made available by

the same authors in (Roure et al., 2015a). This will al-

low us to produce reliable comparison results in sec-

tion 3 as well as focus on the improvement of the

translation part of the problem in the current work.

Consequently, what is left is to solve the translation

problem:

• Once the two sets A and B have been regis-

tered up to rotation, the goal is to ﬁnd a trans-

lation τ such that τ(B) is close enough to A in

terms of the mean Euclidean distance of the Near-

est Neighbouring (NN) point pairs between sets.

Close enough in this case stands for a pose that

allows the subsequent ﬁne matching algorithm

(Rusinkiewicz and Levoy, 2001) to converge to

the best possible alignment without stalling at any

local minimum.

• The search is initialised by determining a point in

set A for which a correspondence will be searched

for. In this case, the authors choose this point x

randomly among the 100 closest points to the cen-

tre of masses of set A.

• The algorithm then searches for the best corre-

spondence for x

among all the points in set B.

To do this a grid-based greedy search is performed

that tries several possible translations. At every

iteration, the best translation is chosen by com-

puting the distance between A and each of the

proposed τ(B) and choosing the best. This step

is commonly referred to as residue computation.

The grid is then subsequently expanded around

the current best point and a new iteration starts.

Notice that with this strategy, the number of points

explored in the grid and, thus, the number of

residues computed, is constant for all executions.

However, for every residue computation, the time

needed will vary depending on how close the two

sets are.

• After ﬁnishing the grid-based search, a translation

vector is outputted. This data is joined with the

rotation estimation obtained from the sensors and

the combination becomes the result of the match-

ing algorithm. Then the algorithm proceeds as de-

scribed in Figure 2 by running a ﬁne matching al-

gorithm (Rusinkiewicz and Levoy, 2001).

2.2 Our Approach

In this section we provide details on the algorithm

being introduced. Mainly we propose a hierarchical

look at the sets being matched in order to avoid un-

necessary residue computations and, thus save com-

putation time. A graphical summary of our algorithm

can be found in Figure 3.

After obtaining the rotation data, the problem we

are left with is ﬁnding the translation τ that brings the

two sets being matched (A and B) as close together

as possible. A naive approach would be to choose a

point in set A and try all the possible correspondences

with all the poins in set B. This would have O(n) cost

(with n=|B|) which is already feasible in most cases.

The authors in (Pribani

c et al., 2016) realised how it is

not necessary to explore the whole search space and

that, by taking samples using a grid it was possible to

”zoom in” a good enough coarse solution so the sub-

sequent ﬁne matching algorithm would produce the

best possible solution.

However, the algorithm used to explore the grid

treated all possible translation equally. The exact

same process was undergone by the ﬁrst translation

tested than to the ﬁnal one (which was much closer to

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

FINE

MATCHING

COARSE MATCHING

DESCRIPTORS

SEARCHING

STRATEGIES

FILTERING

DETECTION

REFINEMENT

Figure 2: Scheme of the Registration Pipeline.

Figure 3: Hierarchical approach. In successive approximations of the software part of the coarse matching algorithm more

and more detailed information is considered. First, the algorithm is initialised by using centers of masses. Second, the overlap

volumes of the bounding boxes of the sets being matched are considered. Third, the number of points contained in a Regular

Grid is taken into account. Finally, full sets are used.

the ﬁnal solution after having undergone several algo-

rithmic iterations). This resulted in a large number of

operations where the distance between two sets had

to be computed (residue computations). In our case,

we take this into account and look at the sets being

matched using varying levels of detail. For the sake

of simplicity from now on we will consider that each

new iteration increases the level of detail being con-

sidered.

The resulting algorithm follows:

• Consider A and B to be registered up to rota-

tion. Find the translation τ such that τ(B ) is close

enough to A for the subsequent ﬁne matching al-

gorithm to succeed.

• In our case, our algorithm is stable enough so it

can be initialized directly by using the centres of

masses of the two sets (Figure 3, left). As the fol-

lowing steps optimize high level (bounding box)

overlap between the two sets, we can perform a

faster initialization. Consequently, x

is chosen

to be the centre of mass of set A and the search

grid of set B is built around the centre of mass of

set B .

• In the ﬁrst iteration of the grid-based search ((Fig-

ure 3, middle left), our algorithm only considers a

bounding box computed for each set: B(A ) and

B(B). For each grid point b the translation τ

vector b − x

is computed and the volume overlap

between τ

(B(B)) and B(A ) is considered. All

the points in this ﬁrst level of the grids are con-

sidered until the optimal volume overlap is com-

puted.

• In the second iteration of this new grid-based

search (Figure 3, middle right), the two sets be-

ing matched are stored inside a 3D regular grid.

The bounding box of each set is divided in regu-

larly distributed cells and each point in the set is

simply assigned to the cell it belongs to. For each

cell, we annotate only the number of points stored

in it and we consider it to be the ”weight” of the

cell. With this we obtain a type of mid level repre-

sentation of each of the two sets that groups points

in terms of spatial proximity and summarises the

set as a number of weighted cubic regions. In this

case for each translation τ

considered we check

whether or not there are enough points in the cells

intersected by every translated cell. Finding the

best score in terms of possibly matched points

is the goal in this step. However, the bounding

box overlap values are required to remain within

a threshold of the value obtained in the previous

step.

• In the third and ﬁnal step of the grid-based search,

Hierarchical Techniques to Improve Hybrid Point Cloud Registration

(Figure 3, right), all the points in the sets are con-

sidered and the residues between the sets are com-

puted. As is usual in this type of computations, a

monte-carlo approach is used in order to speed up

these computations (D

ıez et al., 2012).

• After ﬁnishing the grid-based search the algo-

rithm proceeds as is usual by running a ﬁne

matching algorithm (Rusinkiewicz and Levoy,

2001) with the rotation data obtained from the

sensors and the translation data obtained from the

grid-based search.

3 EXPERIMENTS

In this section we present experiments with real data

that show how the algorithm presented in this paper

improves the behaviour of the algorithm used in (Prib-

ani

c et al., 2016). At the same time, we also compare

the algorithm presented in this paper to state of the

art point set matching algorithms in order to illustrate

the efﬁciency of our approach. The code for all the

algorithms considered was implemented in C++. All

experiments where run using a 33MHz processor un-

der a linux Ubuntu operating system.

Some signiﬁcant improvement in the run-times re-

ported here for the algorithm by (Pribani

c et al., 2016)

and in the original paper can be observed. This is

mostly due to code optimization and parameter tun-

ing. Due to the fact that the algorithm presented

in this paper extends and improves that in (Pribani

et al., 2016) we were able to use some of the proﬁl-

ing information studied to improve our code to also

improve that of (Pribani

c et al., 2016).

Consequently, and in order to keep the compari-

son fair, we present these improved results in this pa-

per. Additionally, this allows us to show clearly what

part of the improvement in running times respect to

the results previously reported correspond to general

code optimization and what part correspond to the use

of the hierarchical approach presented in this paper.

From now on, an for the sake of brevity, we will re-

fer to the previous algorithm as the regular grid algo-

rithm.

3.1 Data Used

The data used in this section corresponds to the

”bust” or ”mannequin” dataset used in (Pribani

c et al.,

2016) and made available in (Roure et al., 2015a).

This data can be downloaded from http://eia.udg.edu/

3dbenchmark. Using this data makes the compari-

son with the improved paper more meaningful while

the fact that it is publicly available ensures the repro-

ducibility of the experiments presented here.

The data consist of a set of 5 views from the ”bust”

model (see Figure 4). This corresponds to a real-

sized mannequin of a human body scanned with a 3D

structured-light system. See (Pribani

c et al., 2010;

Pribani

c et al., 2013) for more details on the model

and acquisition procedure. Each of the 5 views of the

model contain ≈ 450000 points. No post-processing

whatsoever was performed.

Consequently, this dataset presents quite a lot of

noise and the overlap between some of the views is

very low (ranging from 60-70% in consecutive views

to around 10% for the most distant views). This

represent a challenging scenario for any registration

method.

Figure 4: Left: bust0 view of Bust model. Right: Detail of

bust0 view.

The experiments consisted in registering the 5

available views each against all different views. This

provided us with 20 different registration scenarios.

Amongst these, 4 registration instances presented low

(around 10%) overlap, 6 presented medium (between

30 and 50%) overlap and the remaining 10 presented

high (approximately between 60 and 85% ) overlap.

All the results produced in this section were required

to meet these overlap percentages and later checked

manually to ensure correctness.

3.2 Runtime Improvement due to the

Hierarchical Approach

In order to evaluate whether or not the hierarchical

approach described in section 2 helps improve the

run-time performance of the algorithm, we run the

code-optimised version of the regular grid algorithm

against the algorithm that we are presenting. Table

1 presents results corresponding to ﬁve representative

registration examples. The ﬁrst half of the table cor-

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

responds to the regular grid method, the second half

of the table depicts the results of our new proposal.

Within each half of the table, the two initial rows and

the ﬁnal row correspond to sets with high overlap, the

third row to sets with low overlap and the fourth to

medium overlap.

All registration instances where also checked for

correctness manually. The ﬁrst column lists the views

involved in the registration, the second and third col-

umn contains information on the overlap obtained for

set A after coarse and ﬁne alignment respectively.

The fourth and ﬁfth column present times for the

coarse matching algorithms as well as the total time

(which includes the former as well as the time for ﬁne

matching). All times are presented in seconds.

Table 1 shows how the proposed approach per-

forms faster than the regular grid algorithm. On aver-

age (over all views) the time needed by the new algo-

rithm was less than half that of the regular grid algo-

rithm. Notice how the overlap after coarse matching

is sometimes higher for the regular grid algorithm.

This happens due to this degree of overlap being

the only criteria that is considered while our approach

relies on other criteria to speed up the search (such

as bounding box overlap or coincidence of points in

grid cells). In any case, the small reduction in coarse

matching overlap does not affect the success of the

subsequent ﬁne matching algorithm as can be seen in

the third column of the table.

3.3 Comparison With SOA Methods

In this section we study the performance of our al-

gorithm against state of the art point cloud match-

ing algorithms. Speciﬁcally, we consider, additionally

to the algorithm that motivated the current research,

(Pribani

c et al., 2016) two widely used registration

methods. The 4PCS method (Aiger et al., 2008) is

a widely used general-purpose point cloud matching

method that also counts with an improved version

called super4PCS (Mellado et al., 2014) which is, to

the best of our knowledge, the fastest general-purpose

coarse matching algorithm to date.

The ﬁrst issue that needs to be addressed is that

of the nature of the methods being considered. The

two grid based methods are hardware-software hybrid

methods, so they rely on the fact that they can obtain

information on the rotation part of the problem and

take advantage of this to make the software part of the

algorithm much simpler (they only look for a transla-

tion). Conversely the two 4PCS-based methods are

actually looking for rotation as well as translation, so

they are exploring a larger search space. While we ac-

knowledge this, the point of hybrid methods is actu-

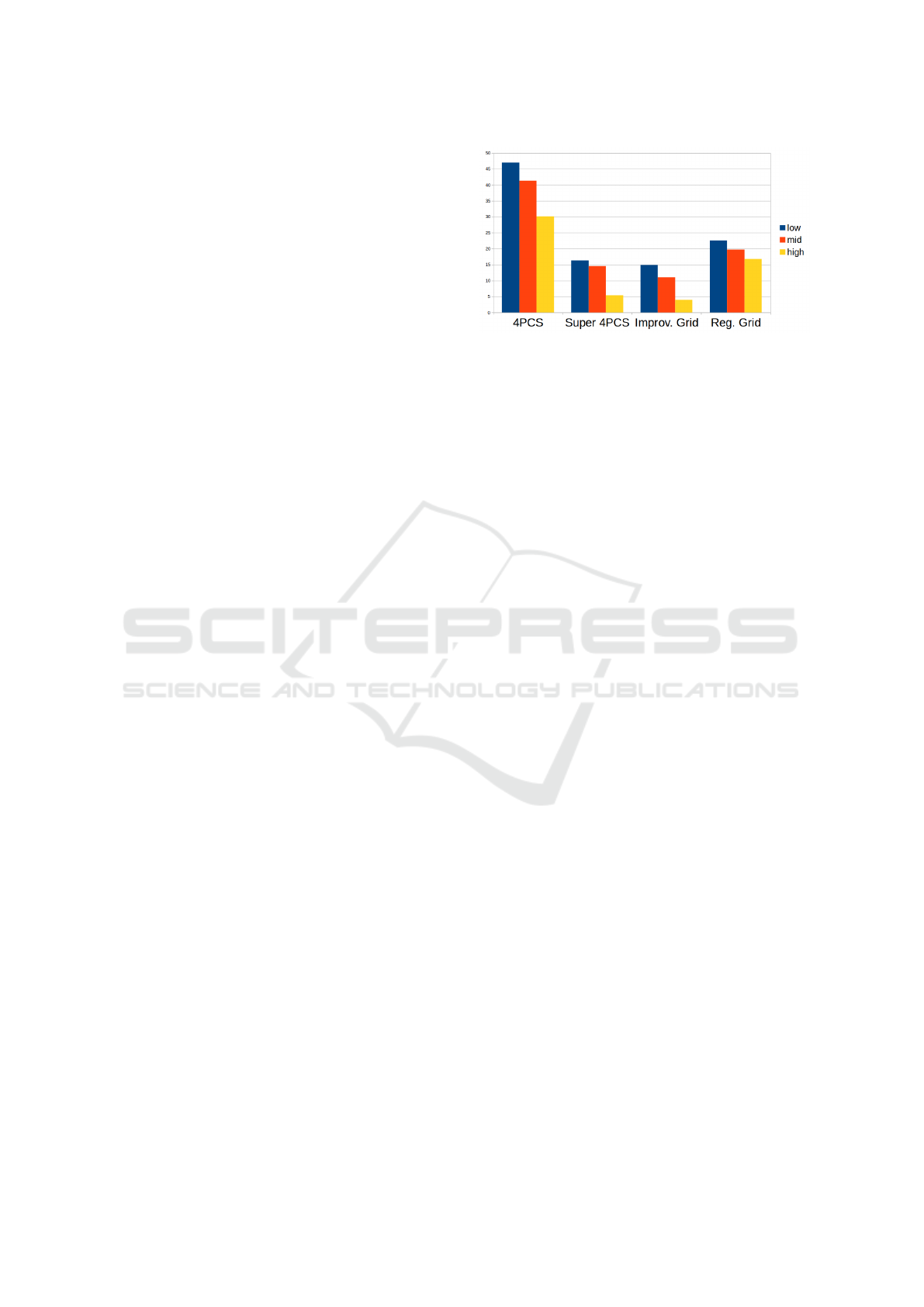
Figure 5: Run-times for: 4PCS algorithm (Aiger et al.,

2008), Super4PCS (Mellado et al., 2014), Improved Grid

(current paper) and Regular Grid (Pribani

c et al., 2016).

ally that the information that they get from hardware

provides an advantage over pure software methods.

In order to limit this as much as possible, we run the

4PCS-based methods both with the original sets and

also with the same rotation-aligned methods used by

the hybrid methods. We found out that the algorithms

were faster with the rotation aligned sets, so these are

the numbers that we report here.

Regarding parameter tuning and precision: Grid

based algorithms mainly needed to determine the size

of the grid. After trying 10 different grid sizes, we

found out that grids with very few points (six grid

points per iteration) did miss the correct result in some

cases. Consequently, we include results correspond-

ing to the fastest results among those grids that pro-

duced correct results (this corresponds to grids with 6

points per coordinate for a total of 18 points per grid

iteration). Conversely, 4PCS algorithm required quite

a lot of parameter tuning and were prone to missing

the correct result if the parameters were not set prop-

erly. The numbers presented here correspond to the

best running time that we could achieve after trying

several parameter conﬁgurations (so they correspond

to different parameter settings). Figure 5 presents run-

times for the four algorithms studied. For each of

them, data is separated in registration scenarios with

low overlap (ﬁrst bar, in blue), medium overlap (sec-

ond bar, in red) and high overlap (third bar, in yellow).

All times are presented in seconds. Results show how

the rotation information obtained from hardware sen-

sors allows to make the software part of these algo-

rithms quite fast. Speciﬁcally, the previously existing

regular grid method outperforms the well-established

4PCS method and is the most robust method over-

all in the sense that it presents less relative differ-

ence in execution times between sets with high and

low overlap. The times of the 4PCS algorithm are

somewhat skewed by some registrations that are way

slower than the others. If we ignore these cases, the

running times of this algorithm become slightly in-

Hierarchical Techniques to Improve Hybrid Point Cloud Registration

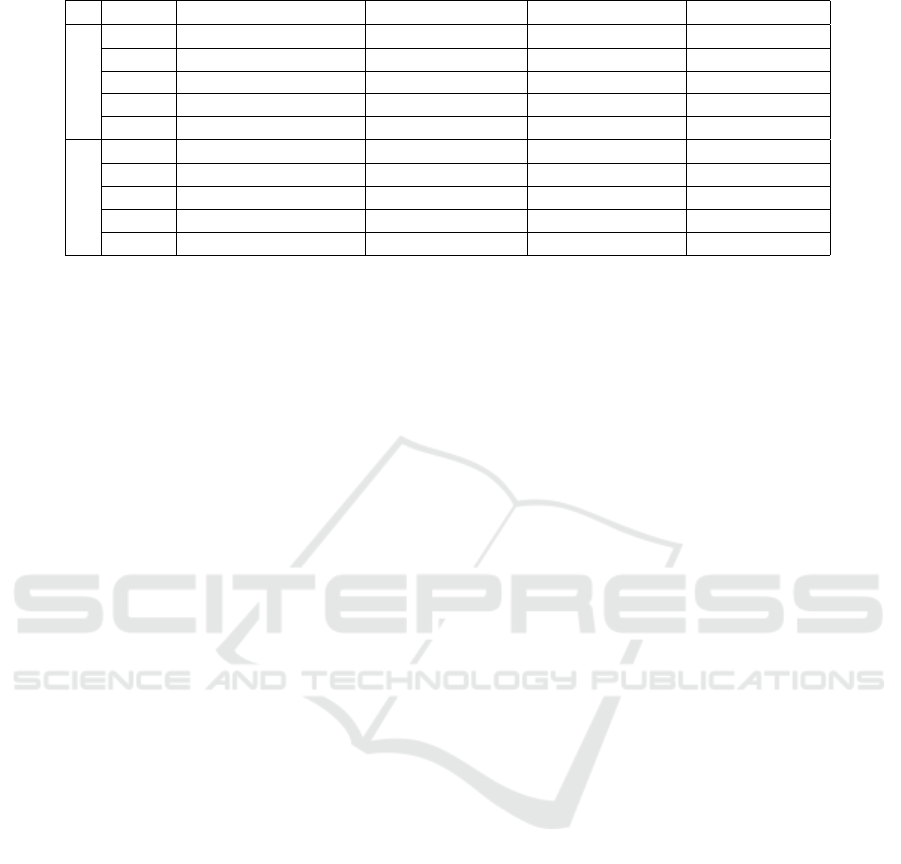
Table 1: Details on the runt-time improvement obtained by the hierarchical approach introduced in the current paper.

Views Overlap % Coarse Overlap % Fine Coarse Time (s) Total Time (s)

Regular Grid

0 - 1 15.03% 86.36% 14.23 17.39

1 - 2 17.70% 72.24% 18.52 21.26

1 - 4 8.15% 9.87% 19.14 22.17

2 - 4 11.03% 43.38% 15.13 17.84

3 - 4 19.71% 76.53% 12.55 15.10

Our Approach

0 - 1 11.89% 86.34% 0.0087 3.40

1 - 2 17.44% 72.28% 0.010 3.87

1 - 4 3.81% 9.84% 9.014 12.24

2 - 4 11.03% 43.30% 7.63 10.11

3 - 4 15.28% 76.58% 3.63 7.13

ferior to those of the regular grid algorithm although

quite far from those of the super4PCS algorithm.

The algorithm presented in this paper is the fastest

of the four algorithms studied and outperforms (for

this particular type of problem) even the super4PCS

algorithm. In further detail, while the super4PCS is

the fastest algorithm in 5 of the 10 high overlap cases

(with an average total time of 3.97s for all the match-

ing process against the 4.01s average for our algo-

rithm), it also struggled to ﬁnd a solution in 10 of the

20 cases. In these cases it failed to ﬁnd the best solu-

tion and stalled under 5% overlap after ﬁne matching.

After careful parameter tuning, it was possible to ob-

tain the best solution but the resulting executions took

longer. The resulting aggregate of the times of the

fastest parameter conﬁgurations leading to a correct

solution is what has ﬁnally been reported. All things

considered, the current paper obtained a 19.67% im-

provement over the super4PCS algorithm.

4 CONCLUSIONS

In this paper we have shown how the hierarchical ap-

proach (Figure 3) used to improve the translation de-

termination part of the hybrid algorithm presented in

(Pribani

c et al., 2016) results in reducing the aver-

age computation time to less than half. Results run

with real data show (Table 1, second column) how

this reduction is achieved at the price of some of

the overlap obtained after the coarse matching step.

This does not, however, reduce the algorithm accu-

racy after the reﬁnement step. Additionally, we have

shown how hybrid algorithms can outperform two

well established coarse registration methods includ-

ing a 19% improvement over the super4PCS (Mellado

et al., 2014) algorithm which is, to the best of our

knowledge, the best pure-software, general-purpose

point cloud registration algorithm to date.

ACKNOWLEDGEMENTS

We want to thank the authors of the state of the art

algorithms considered for making their code publicly

available. Yago Diez is supported by the IMPACT

Tough Robotics Challenge Project of Japan Science

and Technology Agency.

REFERENCES

Agarwal, P. K., Har-Peled, S., Sharir, M., and Wang,

Y. (2003). Hausdorff distance under translation for

points and balls. In Proceedings of the Nineteenth An-

nual Symposium on Computational Geometry, SCG

’03, pages 282–291, New York, NY, USA. ACM.

Aiger, D., Mitra, N. J., and Cohen-Or, D. (2008). 4-points

congruent sets for robust pairwise surface registration.

In SIGGRAPH, volume 27(3), page 85.

Besl, P. J. and McKay, N. D. (1992). A method for regis-

tration of 3-d shapes. IEEE Transactions on Pattern

Analysis and Machine Intelligence, 14(2):239–256.

Choi, S., Kim, S., and Chae, J. (2011). Real-time 3d regis-

tration using gpu. Machine Vision and Applications,

pages 837–850.

da Silva Tavares, J. M. R. (2010). Image processing and

analysis: applications and trends. In AES-ATEMA#

8217; 2010 Fifth International Conference.

Diez, Y., Lopez, M. A., and Sellares, J. A. (2008). Noisy

road network matching. In International Conference

on Geographic Information Science, pages 38–54.

Springer Berlin Heidelberg.

ıez, Y., Mart

ı, J., and Salvi, J. (2012). Hierarchical normal

space sampling to speed up point cloud coarse match-

ing. Pattern Recognition Letters, 33:2127 – 2133.

ıez, Y., Roure, F., Llad

o, X., and Salvi, J. (2015). A quali-

tative review on 3d coarse registration methods. ACM

Computing Surveys (CSUR), 47(3):45.

Diez, Y. and Sellar

es, J. A. (2011). Noisy colored

point set matching. Discrete Applied Mathematics,

159(6):433–449.

Larkins, R. L., Cree, M. J., and Dorrington, A. A. (2012).

Veriﬁcation of multi-view point-cloud registration for

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

spherical harmonic cross-correl. In 27th Conf. Image

Vision Comp. New Zealand, pages 358–363. ACM.

Makadia, A., Patterson, A., and Daniilidis, K. (2006). Fully

automatic registration of 3d point clouds. In Computer

Vision and Pattern Recognition, 2006 IEEE Computer

Society Conference on, volume 1, pages 1297–1304.

Martins, A., Bessant, M., Manukyan, L., and Milinkovitch,

M. (2015). R2obbie-3d, a fast robotic high-res. sys-

tem for quant. phenotyping of surf. geom. and colour-

texture. PLoS ONE, 10(6):1–18.

Matabosch, C., Foﬁ, D., Salvi, J., and Batlle, E. (2008).

Registration of surfaces minimizing error propagation

for a one-shot multi-slit hand-held scanner. Pattern

Recognition, 41(6):2055 – 2067.

Mellado, N., Aiger, D., and Mitra, N. J. (2014). Super 4pcs

fast global pointcloud registration via smart indexing.

In Computer Graphics Forum, volume 33(5), pages

205–215. Wiley Online Library.

Mian, A., Bennamoun, M., and Owens, R. (2010). On the

repeatability and quality of keypoints for local feature-

based 3d object retrieval from cluttered scenes. Inter-

national Journal of Computer Vision, 89(2):348–361.

Oliveira, F. P. and Tavares, J. M. R. (2014). Medical image

registration: a review. Computer Methods in Biome-

chanics and Biomedical Engineering, 17(2):73–93.

PMID: 22435355.

Pribani

c, T., Diez, Y., Fernandez, S., and Salvi, J. (2013).

An efﬁcient method for surface registration. In VIS-

APP (1), pages 500–503.

Pribani

c, T., Diez, Y., Roure, F., and Salvi, J. (2016). An

efﬁcient surface registration using smartphone. Ma-

chine Vision and Applications, 27(4):559–576.

Pribani

c, T., Mrvo

s, S., and Salvi, J. (2010). Efﬁcient mul-

tiple phase shift patterns for dense 3d acquisition in

structured light scanning. Image and Vision Comput-

ing, 28(8):1255–1266.

ProjectTango (2016). Project tango. https://www.google.

com/atap/projecttango/#project. Accessed: 2016-09-

20.

Roure, F., D

ıez, Y., Llad

o, X., Forest, J., Pribanic, T., and

Salvi, J. (2015a). An experimental benchmark for

point set coarse registration. In Int. Conf. on Com-

puter Vision Theory and Applications.

Roure, F., Diez, Y., Llad

o, X., Forest, J., Pribanic, T., and

Salvi, J. (2015b). A study on the robustness of shape

descriptors to common scanning artifacts. In 14th Int.

Conf. Mach. Vis. App., MVA., pages 522–525. IEEE.

Rusinkiewicz, S. and Levoy, M. (2001). Efﬁcient variants of

the icp algorithm. In IEEE International Conference

on 3D Digital Imaging and Modeling, pages 145–152.

StructureSensor (2016). Structure sensor. http://structure.

io/. Accessed: 2016-09-20.

Hierarchical Techniques to Improve Hybrid Point Cloud Registration