Medical Imaging: Exams Planning and Resource Assignment

Hybridization of a Metaheuristic and a List Algorithm

Nathalie Klement

, Nathalie Grangeon

and Michel Gourgand

Ecole Nationale Sup´erieure d’Arts et M´etiers, LSIS CNRS UMR 7296,

8 boulevard Louis XIV, 59046 Lille Cedex, France

LIMOS CNRS UMR 6158, Universit´e Blaise Pascal,

Complexe Universitaire des C´ezeaux, 63178 Aubi`ere Cedex, France

Keywords:

Hybridization, Metaheuristic, List Algorithm, Medical Imaging.

Abstract:

The presented work is about optimization of the hospital system. An existing solution is the pooling of

resources within the same territory. This may involve different forms of cooperation between several hospitals.

Problems of sizing, planning and scheduling may be considered. We deﬁne the problem of activities planning

with resource assignment. To solve this problem, we propose a hybridization between a metaheuristic and a

list algorithm. Single based metaheuristics are used. This proposition requires a new encoding inspired by

permutation problems. This method is easy to apply: it combines already known methods. With the proposed

hybridization, the constraints to be considered only need to be integrated into the list algorithm. For big

instances, the solver used as a reference returns only lower and upper bounds. The results of our method

are very promising. It is possible to adapt our method on more complex issues through integration into the

list algorithm of the constraints. It would be particularly interesting to test these methods on real hospital

authorities to assess their signiﬁcance.

1 INTRODUCTION

Given the current economic situation, everything is

done to move towards a better use of goods and ser-

vices production systems. The hospital system also

follows this trend as much or less resources are allo-

cated to it but it should work more efﬁciently to meet

a demand that is increasing. To do so, in 2015, the

french government deﬁned the HGT: Hospital Group

of Territory, an evolution of the HCT previously pre-

sented (Gourgand et al., 2014a). It is a coopera-

tion between public institutions, which are at different

places, that implement a common strategy and jointly

manage some functions and activities through delega-

tions or skills transfer between them. Some decision

support tools are needed to manage this new kind of

organization.

The aim of our work is the development of a de-

cision support tool to help to manage HGTs or any

hospital cooperations. This tool should be used at dif-

ferent levels: strategic, tactical or operational, to deal

with problems of sizing, planning, resources assign-

ment or scheduling. It should be used to anticipate

the creation of a new cooperation, to manage this or-

ganization day to day, or to react in case of hazard

or crisis situation. In this paper, we take the prob-

lematic of medical imaging over a HGT as an exam-

ple. Some material resources, such as X-ray, scan-

ner, MRI, are located at different places belonging to

the HGT. Human resources work there and have spe-

ciﬁc competences on these material resources. Some

patients need to pass an exam on such a material re-

source. The planning horizon can be some days or

weeks, divided in periods of half-days. Some incom-

patibilities and time constraints are deﬁned. The tac-

tical level will be discussed in this paper: the objec-

tive is to assign the exams to human and material re-

sources during a period. The other levels can easily

be solved by our method which uses some operational

research purposes.

2 STATE OF THE ART

Since the last ten years, many methods of opera-

tional research have been used to solve hospital sys-

tem problems. (Rais and Viana, 2011) referenced

around two hundred and ﬁfty articles about opera-

tional research for hospital system in general. (Car-

260

Klement N., Grangeon N. and Gourgand M.

Medical Imaging: Exams Planning and Resource Assignment - Hybridization of a Metaheuristic and a List Algorithm.

DOI: 10.5220/0006113002600267

In Proceedings of the 10th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2017), pages 260-267

ISBN: 978-989-758-213-4

doen et al., 2010) referenced more than one hundred

and twenty articles about planning and scheduling of

operating theater. (Van den Bergh et al., 2013) made

a literature review about scheduling human resources

and referenced around three hundred articles.

But articles dealing with multi-place system in

hospital network are scarce, or their case study are

quite limited. Planning surgical vacations by specialty

is dealt by (Santib´a˜nez et al., 2007). Availability of

operating theater, beds capacity, surgeons preferences

and waiting list are considered. The proposed model

allocates specialties to operating theater, and is ap-

plied to a Canadian study case, composed by eight

hospitals, over four weeks. (Everett, 2002) developed

a support aid tool to manage the waiting list of pa-

tients who need a surgical act. The system is made

up by several hospitals, working in cooperation. The

waiting list is common for all the hospitals. Each day,

each patient is assigned to one place according to the

availability of the hospitals. If no hospital is available

on one day, patients are assigned the next day. As-

signment of resources is not considered. (VanBerkel

and Blake, 2007) developed a tool to reduce the wait-

ing time and to plan beds capacity in a surgery ser-

vice, over several places. It is a problem of allocation

of the ﬁxed resources, in an other Canadian example.

This tool aims at studying a redistribution of postoper-

ative beds between the places, using simulation tools.

Problem of capacity in intensive care unit can result

in the cancellation of programmed acts, an overload

of medical team or a reject of urgent patients. Thus,

urgent patients could be transferred to further places.

A cooperative solution is studied by (Litvak et al.,

2008), taking into example a case in the Netherlands.

Some hospitals belonging to the same territory share

some beds to urgent patients.

Researchs are done about the pooling of resources.

(Trilling et al., 2006) dealt with the problem of

scheduling human resources over different services

in one hospital. The objective is to share resources

within larger surgical suite, in order to reduce the

costs. At another level, it can be seen as a sharing

of resources from different places within larger orga-

nization such as HGT. In this paper, concerned re-

sources are stretchers and nurses, who are common

resources used for any hospital services and locations.

A lot of researches about hospital system are dedi-

cated. Articles consider three problems: sizing, plan-

ning and scheduling. Most of the papers focuses on

one particular problem. Their models and resolution

methods are not easily reusable. Our proposed model

and tool are generic, so they could be reused as often

as possible.

3 ANALYSIS

To analyze our system, we split the system into three

subsystems: the physical subsystem (physical enti-

ties used to perform all the activities, their geographi-

cal distribution and their interconnections),the logical

subsystem (ﬂows that the system should treat, all ac-

tivities concerning the treatment of these ﬂows and all

entities in the system relating to them) and the deci-

sion subsystem (center of decision which contains all

the decision rules).

3.1 Physical Subsystem

The HGT is composed by several places. There is a

known distance between each place.

On each place, there are one or several material

resources. A material resource belongs to a type (for

instance X-ray, scanner or MRI). Each material re-

source has an opening schedule which deﬁnes the

times when the material resource is available over

each period. For example, a given material resource

may only be available ﬁve hours on Monday because

it needs a maintenance operation or because an exter-

nal doctor reserved it. Overtime may be allowed but

is limited in time.

Human resources compose a medical team. The

composition of this team depends on the considered

exam. This team should have a speciﬁc number of

stretchers, specialist doctors, nurses, etc. Human re-

sources belong to a given place but can work on other

places belonging to the same HGT, allowing a pool-

ing of human resources over the HGT. Moves are not

allowed within the same period, but between two pe-

riods. A time is given to human resources to go from

a place to another. A human resource can use one

or several types of material resource according to its

skills. A skillful human resource, who can work on

several types of material resources, is potentially less

efﬁcient than a human resource who can only work on

one type of material resource, or one particular mate-

rial resource. This efﬁciency should be translated in

the processing time of the concerned exams. Each

human resource has a planning which deﬁnes its reg-

ular work time, taking into account break times and

holidays. Time to move from one place to another is

included in the work time of human resources. Over-

time may be allowed but is limited in time.

3.2 Logical Subsystem

The logical subsystem deﬁnes the ﬂow: the set of ex-

ams to plan and assign, and the relationship between

these exams and the resources previously deﬁned.

Medical Imaging: Exams Planning and Resource Assignment - Hybridization of a Metaheuristic and a List Algorithm

261

An exam should be done before a period at the

latest, called a due date. Each exam has a known pro-

cessing time which depends on the assigned human

and material resources. Each exam starts at one pe-

riod and ends at the same one. Each exam has a refer-

ence place, where it should be done, if possible.

An exam needs a given number of human re-

sources and one material resource. All required re-

sources must be compatible with each other. By deﬁ-

nition, an exam is compatible with some material re-

sources, so the assigned material resource must be

compatible with the exam. This material resource be-

longs to a type, so the assigned human resources must

have the needed skill to use this type of material re-

source. The place where the exam is done is deduced

from the one where is located the assigned material

resource.

3.3 Decision Subsystem

The objective is to develop a model which, from a

set of exams, builds a planning associating the triplet

{exam, human resources, material resource} to a pe-

riod. The study is made in a predictive approach, all

the exams can be treated since the beginning of the

planning horizon. The objective of this model is not

to schedule exactly the exams but to assign one pe-

riod to each exam. This planning must optimize some

criteria and respect some constraints.

3.3.1 Criteria

Three categories of criteria can be deﬁned: econom-

ical, about the comfort of the patient, and about the

proper functioning of the HGT.

Concerning the economical aspects, criteria are

about the costs. Occupation rates of each place, each

material resource and each human resource help to

ensure the proper use of these entities. To be the most

economic, these occupation rates have to be maxi-

mized. However, it can be preferable to deﬁne a se-

curity margin, so the HGT can be reactive in case

of hazard. All exams are planned during the con-

sidered planning horizon. The makespan is the pe-

riod assigned to the last exam. It ensures that all ex-

ams are assigned as soon as possible. The smaller

the makespan is, more time remains free at the end

of the planning horizon to potentially treat the next

exams. The number of moves of human resources in

the HGT should be considered, as well as overtime of

human and material resources. Overtime and moves

have a cost for the HGT. It is better to minimize them.

But it can be interesting to allow some overtime or

some moves to increase the number of exams during

the considered period.

About the comfort of the patient, the criterion is

the number of exams done at their reference place. If

some exams cannot be done at their reference place,

the distances between the reference places and the ef-

fective ones may be minimized.

About the medical criterion, the number of ex-

ams done before their due dates has to be maximized.

Thus, if a patient needs other exams, the next ones

could be done on time. If an exam is planned after its

due date, the tardiness may be minimized.

3.3.2 Constraints

Constraints that Must Be Respected

• Each exam must be assigned to human resources,

one material resource and one period. The consid-

ered human resources must be assigned during the

period at the place where the considered material

resource is located.

• Compatibility between the material resource and

the exam: the assignment must satisfy the given

list of incompatibilities between exams and mate-

rial resources.

• Compatibility between skill of the human re-

source and the type of the material resource: for

each exam, the human resource must be able to

work on the considered material resource.

• If a human resource can move during the plan-

ning horizon, its moves are constrained: a human

resource can only work at one place during one

period.

Constraints that May Be Respected

• Exams should be done before their due dates and

at their reference place.

• Material resources and human resources may be

used or work during their opening schedule. Oth-

erwise, additional time is considered as overtime.

Overtime is limited in time.

4 CONSIDERED PROBLEMS

The considered problem is deﬁned as follow: exams

planning and assignment of needed material and hu-

man resources. The previous analysis was about the

complete problem. Some hypothesis are made to di-

vide this complete problem into three problems.

4.1 Hypothesis

The following hypothesis are made:

HEALTHINF 2017 - 10th International Conference on Health Informatics

262

• Only one human resource and one material re-

source are needed to perform exams. Human re-

sources are compatible with one or several types

of material resources.

• Processing time of the exams are given and ﬁxed.

• Opening schedules of material resources are equal

in every periods.

• To each exam, the release date is equal to the date

of appointment decision. These dates are equal to

zero: all exams are known at the beginning of the

planning.

• Distances between places are taken into account

in the time allocated to the human resources to

move from one place to another. This time is as-

sumed to be constant, all places are equidistant to

the others.

• Overtime is not allowed.

4.2 Deﬁnition of the Considered

Problems

The complete problem is divided into three problems

of increasing difﬁculty:

• Problem 1 is the more basic: human resources are

not considered. Only the material resources are

considered.

• Human resources are considered in Problem 2.

They can work on one or several types of mate-

rial resources. They cannot move, they work all

the time at the same place. The assignment of the

human resources at the places is given.

• Human resources are mobile in Problem 3. They

can work on several places, they can move from

one place to another. The assignment of the hu-

man resources at the places has to be built by the

model.

Two criteria are used in the following study:

• Sum of assigned periods to all exams, which en-

sure that all exams are planned as soon as possi-

ble.

• Number of exams assigned before their due date.

4.3 Analogy with the Bin Packing

Problem

Our problem can be seen as a bin packing problem

(Gourgand et al., 2014a). The bin packing problem

considers N items, with a given size, and some bins

with the same capacity. The aim is to pack all the

items in a minimum number of bins. The size of the

packed items has to respect the capacity of the bins.

Each item has to be assigned once and only once.

4.3.1 Without Human Resources

Considering Problem 1, the aim is to assign exams

to a material resource during a period. The planning

horizon is made by couples (resource, period). The

objective is to assign exams to couples (resource, pe-

riod). Exams have to be done as soon as possible: the

aim is to minimize the number of couples, (= the num-

ber of bins). An example is given by Figure 1, where

the assignment of exams to material resources MR

and MR

is considered. Table 1 summarizes

analogies between bin packing problem and Problem

1: exams planning with resources assignment.

Time

Bin

Resource

Period

Monday AM

Monday PM

Opening

schedule

of resources

Caption:

Exam

number X

Figure 1: Representation of Problem 1.

Table 1: Analogies between both problems.

Bin packing Problem of exams planning

problem with resources assignment

Data

Item Exam

Bin Couple (resource, period)

Size of an item Processing time of an exam

Capacity of a bin Opening schedule of resources

- Due date

- Reference place

Problem

Assign items Assign exams to one couple

to one bin (resource, period)

Constraints

Capacity of bins Opening schedule of resources

- Constraint of compatibility

Criteria

Minimize the number

of used bins

Minimize the sum of

assigned periods

4.3.2 With Human Resources

Exams have to be assigned to material and human re-

sources during one period. Analogy is made between

this problem and interdependentbin packingproblem.

Let’s take p

and p

two bin packing problems,

with a given number of bins. Groups of bins are de-

ﬁned in both problems. A group should be made by

one or several bins. Number of bins can be different

Medical Imaging: Exams Planning and Resource Assignment - Hybridization of a Metaheuristic and a List Algorithm

263

for both problems, but number of groups is the same.

Each item is assigned to one and only one bin in each

problem. Interdependence between both problems is

deﬁned as follow: if an item is assigned to a bin from

group g in problem p

, it must be assigned to a bin

from the same group g in problem p

. The aim is

to assign items in bins of both problem, by minimiz-

ing the number of used bins, satisfying capacity con-

straints and interdependence between both problems.

In our case, both problems p

and p

can be de-

ﬁned like this:

• p

: assignment of each exam to a material re-

source during a period, respecting the opening

schedule of the material resource during the pe-

riod and the compatibility between the exam and

the material resource.

• p

: assignment of each exam to a human resource

during a period, respecting the work time of the

human resource during the period and the compat-

ibility between the exam and the human resource.

Compatibility between exam and human resource

is not directly deﬁned but can be deduced: an exam

is compatible with a human resource if and only if

this exam is treated by a material resource from one

type and this human resource can work on this type of

material resource.

Thus, group g is the couple (period, type). In

both problems p

and p

, exam has to be assigned

during the same period to the same type of material

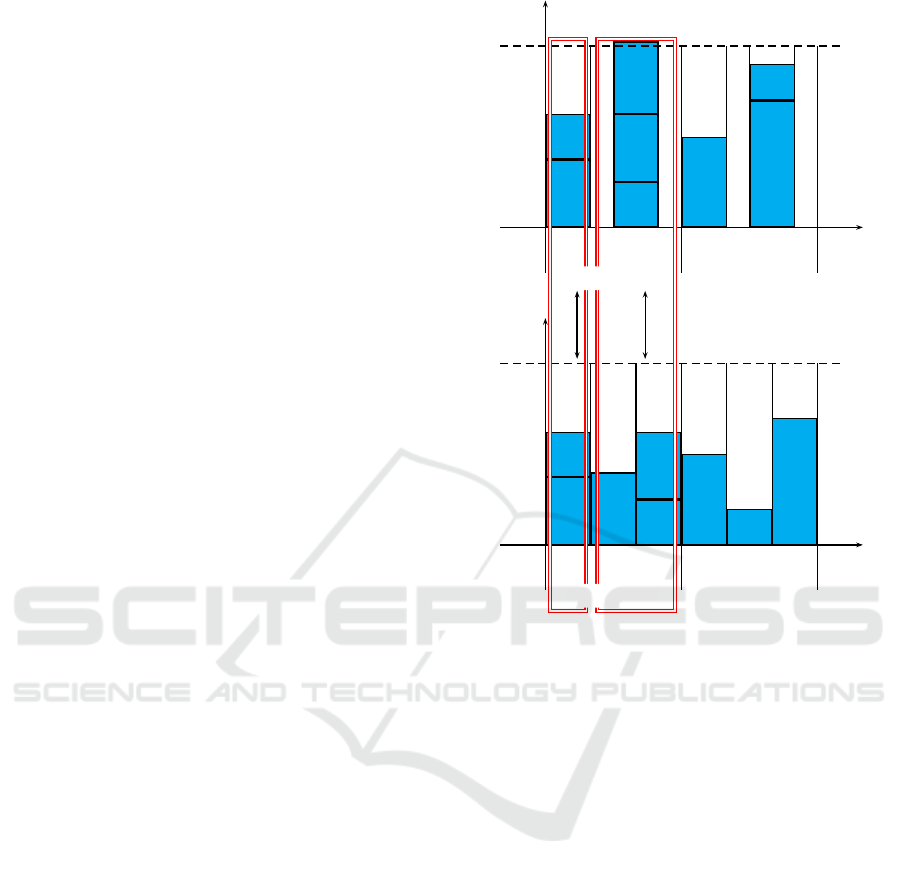
resource. Figure 2 illustrates the interdependent bin

packing problem in the HGT case. The lower portion

of the ﬁgure is the assignment of exams to material re-

sources and periods, in the same way as Figure 1. The

upper portion is the assignment of exams to human re-

sources and periods. In both portions, each exam has

to be assigned to the same period and the same type

(according to the type of the material resource and the

competencies of the human resource to use this type).

5 RESOLUTION METHOD

The bin packing problem is NP-Hard (Garey and

Johnson, 1979). Our problems are an extension of the

bin packing problem, so our problems of exams plan-

ning with resources assignment are also NP-Hard. In

the following, approximate methods are used to solve

them.

Our proposed method is a hybridization of a meta-

heuristic and a list algorithm. Our tool is convenient

because one part is generic: it can be used for any

of the considered problems. Only the list algorithm

needs to be speciﬁc to the considered problem.

Time

Bin

Type

Material

Resource

X-ray

Scanner

Period

X-ray

Scanner

Monday PM

Opening

schedule

of material

resources

Time

Bin

Type

Human

Resource

X-ray

Scanner

Period

X-ray

Scanner

Monday PM

Planning

of human

resources

Group 1

Group 2

Monday AM

Monday PM

Figure 2: Interdependent bin packing problem.

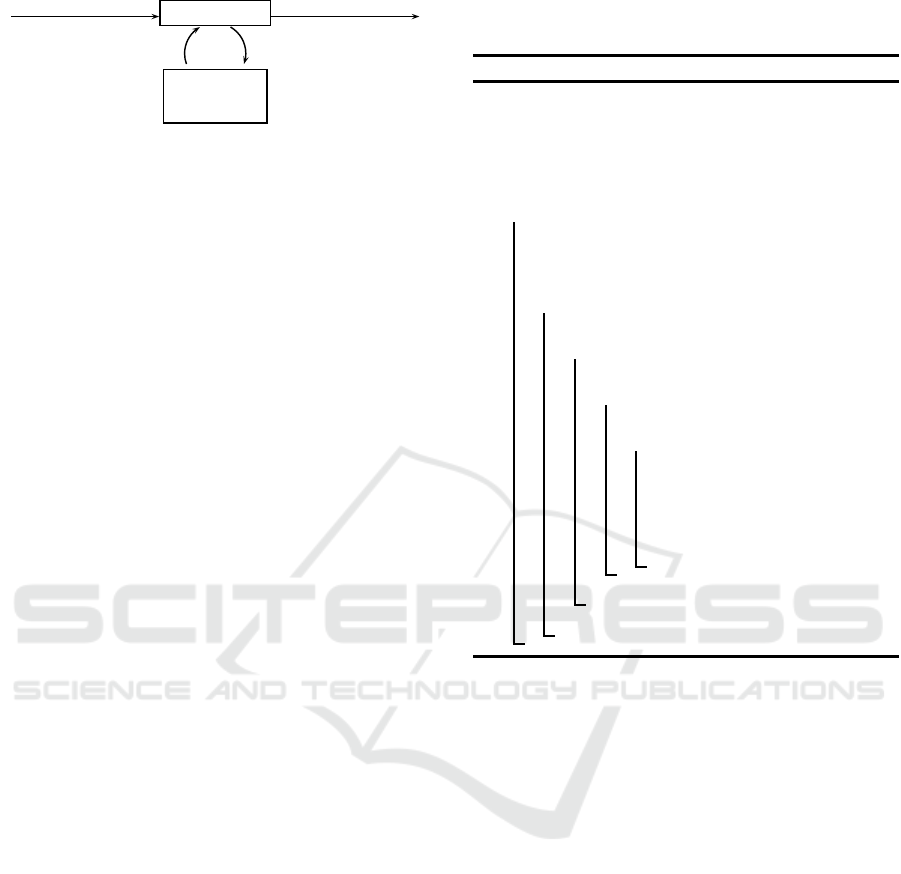
5.1 Genericity

The proposed tool, illustrated by Figure 3, uses a hy-

bridization of a metaheuristic and a heuristic, more

precisely a list algorithm. A single solution based

metaheuristic or a population based metaheuristic can

be used. The encoding used by the metaheuristic is

a list Y of exams. The list algorithm L considers

the exams according to their order in list Y to plan

and assign them to the required resources, consider-

ing the problem constraints. This builds a solution

X. The objective function H evaluates the solution

X. According to this evaluation, the solution is cho-

sen or not by the metaheuristic. At the end of the

running, the given solution by the hybridization is the

best listY

∗

of exams: the one which optimizes the ob-

jective function by applying the list algorithm. This

hybridization can be used to solve many problems:

the speciﬁcity of a given problem is only considered

in the list algorithm.

5.2 A List Y of Exams

The general scheme of the encoding is given by Equa-

tion (1), with Ω the set of all the lists Y and S the set

HEALTHINF 2017 - 10th International Conference on Health Informatics

264

A list Y of exams

Metaheuristic

List

algorithm

The best list Y

∗

Cost H of

this solution

Solution X?

(assignment

and planning)

Figure 3: Hybridization metaheuristic - List algorithm.

of all the admissible solutions X built by the list algo-

rithm L.

Y ∈ Ω −→

Heuristic L

L(Y) = X ∈ S −→

Criterion H

H(X) (1)

The set Ω is the set of all permutations of exams.

Cardinal of Ω is N! with N the number of exams. One

solution Y ∈ Ω is a list of exams. More details about

the encoding are given in (Gourgand et al., 2014b).

5.3 Metaheuristic

The metaheuristic performs in the set of solutions Ω.

An initial solution is randomly computed: a list of ex-

ams randomly sorted between one and the number of

exams. Several metaheuristics have been used: some

single solution based metaheuristics such as iterated

local search or simulated annealing. A neighborhood

system is used to visit the set of solutions, it allows

to go from one solution to another one. Neighbor-

hood system V is a permutation of two exams in the

list Y: the exam at position i permutes with the one

which is at position j. V satisﬁes the accessibility and

reversibility properties.

5.4 List Algorithm

A list algorithm is used to build the solution X from

the list Y: it assigns the exams to resources and to

periods.

List scheduling algorithms are one-pass heuristics

that are widely used to make schedules. A standard

list scheduling algorithm constructs a schedule by as-

signing each job in listed order to the ﬁrst machine

that becomes idle (Zhu and Wilhelm, 2006). It is

important to work with a list algorithm, because the

metaheuristic browses the set of solutions. So the

used algorithm needs to consider the order of the list

to assign exams to resources and periods.

Our problem has be analyzed as a bin packing

problem and some list algorithms have been proposed

since the deﬁnition of this problem (Johnson, 1973).

So our developed list algorithm is inspired by them.

For instance, considering Problem 1, in which human

resources are not considered, Algorithm 1 is an ex-

tension of the First Fit algorithm for the bin packing

problem. Other list algorithms can be adapted from

Algorithm 1 to solve the cases of Problems 2 and 3,

considering human resources.

Algorithm 1: List Algorithm First Fit HGT.

Data: List of exams (Y

)

i∈{1,N}

; opening

schedule of all resources during all

periods; processing time of all exam

1 Occupied time := 0 for all resources and all

periods

2 forall the i do

3 First resource, ﬁrst period,

assigned := false

4 while (assigned = false) AND current

period ≤ max of periods do

5 while (assigned = false) AND current

resource ≤ max of resources do

6 if exam Y

is compatible with

current resource then

7 if exam Y

ﬁts in couple

(resource, period) then

8 Assign exam Y

to couple

(resource, period)

9 Update occupied time of

couple (resource, period)

10 assigned := true

11 Next resource

12 Next period

5.5 Objective Function

Solutions are compared according to an objective

function which characterizes the quality of the solu-

tion. In our case, the objective function represents the

timing aspect of our problem. Exams have to be done

as soon as possible, thus the makespan, the period as-

signed to the last exam, should be considered. Be-

cause many solutions may have the same makespan,

we choose instead the sum of assigned periods to all

exams, so the solutions can be dissociated. This cri-

terion is written H

. Another criterion is considered

to ensure that most of the exams are assigned before

their due date. This criterion, written H

, is computed

as the number of exams assigned after their due date.

The weighed criteria method is used (Coello, 2000).

The objectivefunction is a weighed sum between both

criteria, deﬁned by Equation (2). ω

is chosen equal

to 5 because H

is always smaller than 10

so both

criteria are easily readable. This function has to be

minimized.

H(X) = 10

× H

(X) + H

(X) (2)

Medical Imaging: Exams Planning and Resource Assignment - Hybridization of a Metaheuristic and a List Algorithm

265

5.6 The Best List Y

∗

Algorithm 2 describes the whole method with the ex-

ample of stochastic descent as the used metaheuristic.

Stochastic descent may be used in an iterated local

search. The set Ω of the lists of exams is browsed

thanks to the metaheuristic using neighborhood sys-

tem V. Lists are compared thanks to the list algorithm

L and the objective function H. According to an ac-

ceptance criterion, some lists are selected. At the end,

the metaheuristic gives the best found list Y

∗

Algorithm 2: Hybridization between stochastic de-

scent and a list algorithm.

Data: Initial solution Y

1 X := L(Y)

2 while necessary do

3 Choose uniformly and randomly Y

′

∈ V(Y)

4 X

′

= L(Y

′

)

5 if H(X

′

) ≤ H(X) then

6 X := X

′

7 Y := Y

′

Result: Y

∗

= Y

6 EXPERIMENTS

The data are randomly generated but the characteris-

tics and the size of the data represent real instances.

The HGT is composed by 3 places. The planning

horizon is made by 8 to 40 periods. As a remind,

one period represents one half-day, thus the planning

horizon is between 4 and 20 days. 4 to 8 resources

are available. 50 to 500 exams need to be planned

and assigned. Incompatibilities between exams and

resources are randomly generated. Each processing

time is between 5 and 100. Each material resource

has an opening schedule equal to 300 minutes.

The results are detailed in Table 2. The host ma-

chine is powered by an Intel Xeon X5687 quad-core

CPU running at 3.6 GHz. The computation has been

stopped after thirty minutes. Each reported result is

the value of the objective function for the best solu-

tion found in less than thirty minutes, but most of the

time, the best solution is found in a few minutes. The

results are presented as a couple of values (H

)

with H

the number of exams assigned after their due

dates, and H

the sum of assigned periods to all the

exams. The results compare three methods:

• The resolution of the mathematical model with an

exact method by using the solver CPLEX. If no

optimal solution has been found in less than thirty

minutes by the solver, no result is written.

• Our results from the method previously published

in (Gourgand et al., 2014a), using two single so-

lution based metaheuristics (iterated local search

and simulated annealing) in a classical way: the

best value found by all these methods is reported.

• Our results from our proposed method detailed in

the current paper. The used metaheuristics are dis-

tinguished: iterated local search and simulated an-

nealing, written ILS* and SA*.

The results are promising. Firstly, this problem

has been solved by CPLEX thanks to our mathemat-

ical model previously proposed. The solver ﬁnds an

optimal solution only for small size of problems (less

than two hundred exams over four days). The solver

does not ﬁnd any solutions when the size of the prob-

lem increases. Then, it has been solved with two ap-

proximate methods: in a classical way, and with a

hybridization. Both methods ﬁnd an optimal solu-

tion for the small instances. For biggest instances,

the hybridization between a metaheuristic and a list

algorithm outperforms our previous method. Simu-

lated annealing seems to work better than iterated lo-

cal search.

7 CONCLUSION AND

PERSPECTIVES

The current hospital context needs to ﬁnd solutions

to improve efﬁciency of hospital systems. Hospital

cooperation has emerged, as Hospital Group of Terri-

tory. A pooling of resources may cause a better use

of the different places in a same territory. But this

cooperation needs some decision support tools to im-

prove or optimize their running. In this paper, we de-

ﬁned the general problem of activities planning with

resources assignment in a multi-place hospital con-

text.

Because this problem is NP-Hard, we propose an

approximate method to solve it: a hybridization be-

tween a metaheuristic and a list algorithm. The re-

sults are promising: our method ﬁnds good results in a

few minutes. An improvement of the results is in pro-

cess, using a population based metaheuristic: Particle

Swarm Optimization. Using PSO, the results are very

good for small instances: an optimal solution is found

in a few seconds, but the method still needs some tun-

ing for the biggest instances.

Thanks to the hybridization, our method can be

easily reusable. Indeed, to solve other problems, only

the list algorithm needs to be modiﬁed. The meta-

heuristic part will still be the same. Any kinds of

planning, assignment or scheduling problem can be

HEALTHINF 2017 - 10th International Conference on Health Informatics

266

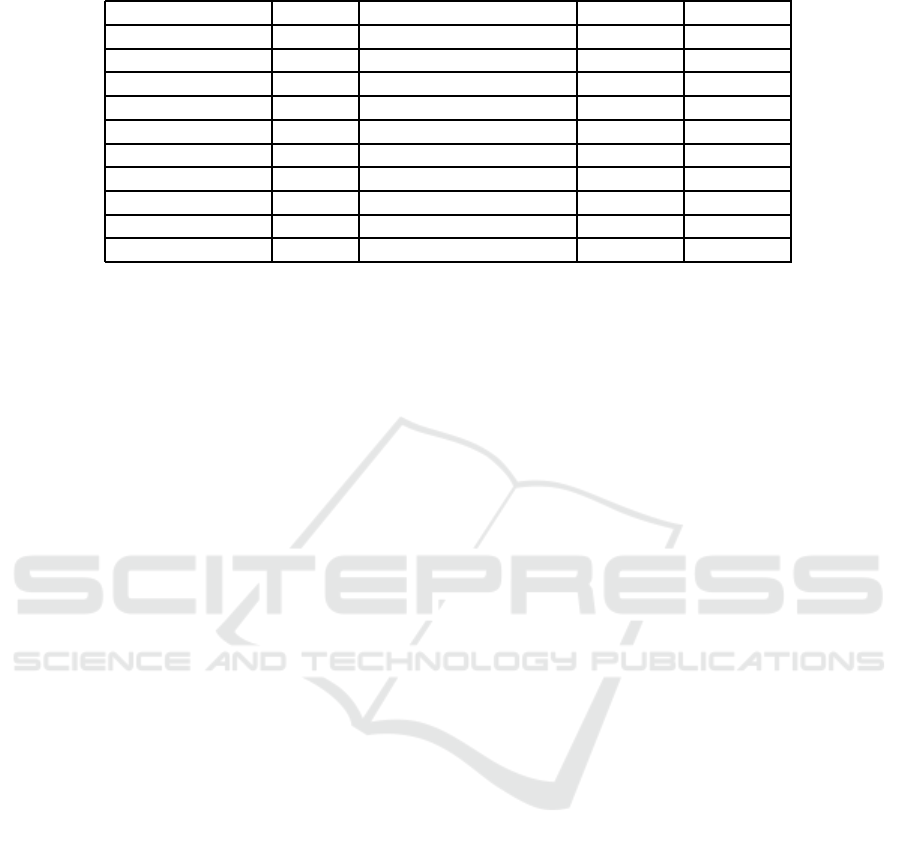
Table 2: Results: (number of exams assigned after their due dates; sum of assigned periods to all the exams).

Number of exams CPLEX (Gourgand et al., 2014a) ILS* SA*

50 (0;51) (0;51) (0;51) (0;51)

50 (1;150) (10;147) (1;151) (1;150)

100 (0;131) (0;131) (0;131) (0;131)

100 (0;517) (2;535) (1;516) (0;518)

200 (0;266) (0;266) (0;266) (0;266)

200 - (3;1197) (0;1154) (0;1135)

300 - (0;548) (0;537) (0;534)

400 (0;830) (0;890) (0;841) (0;835)

500 - (0;1350) (0;1241) (0;1234)

500 - (194;8218) (19;6382) (18;6659)

solved thanks to this tool by changing the list algo-

rithm: for instance, it has been used to solve an in-

dustrial problem (Silva et al., 2016). Problems with

human resources can easily be solved by developing

some new list algorithms dedicated to them. Then, a

direct application to a hospital system could be envis-

aged. Other applications in the hospital ﬁeld could be

done, in other hospital services, with other resources,

etc. We could extend our current work about med-

ical imaging to medical surgeries. More constraints

about medical team should be considered. The next

problematic is to consider patients with several ex-

ams or surgeries, by taking into account precedence

constraints between them.

REFERENCES

Cardoen, B., Demeulemeester, E., and Beli¨en, J. (2010).

Operating room planning and scheduling: A literature

review. European Journal of Operational Research,

201(3):921–932.

Coello, C. A. (2000). An updated survey of ga-based mul-

tiobjective optimization techniques. ACM Computing

Surveys (CSUR), 32(2):109–143.

Everett, J. (2002). A decision support simulation model for

the management of an elective surgery waiting sys-

tem. Health Care Management Science, 5(2):89–95.

Garey, M. R. and Johnson, D. S. (1979). Computers

and Intractability: A Guide to the Theory of NP-

completeness. WH Freeman and Company, New

York.

Gourgand, M., Grangeon, N., and Klement, N. (2014a). Ac-

tivities planning and resource assignment on multi-

place hospital system: Exact and approach methods

adapted from the bin packing problem. In 7th Inter-

national Conference on Health Informatics, Angers,

France, pages 117–124.

Gourgand, M., Grangeon, N., and Klement, N. (2014b).

An analogy between bin packing problem and per-

mutation problem: A new encoding scheme. In Ad-

vances in Production Management Systems. Innova-

tive and Knowledge-Based Production Management

in a Global-Local World, volume 438, pages 572–579.

Springer Berlin Heidelberg.

Johnson, D. S. (1973). Near-optimal bin packing algo-

rithms. PhD thesis, Massachusetts Institute of Tech-

nology.

Litvak, N., van Rijsbergen, M., Boucherie, R. J., and van

Houdenhoven, M. (2008). Managing the overﬂow of

intensive care patients. European journal of opera-

tional research, 185(3):998–1010.

Rais, A. and Viana, A. (2011). Operations research in

healthcare: a survey. International Transactions in

Operational Research, 18(1):1–31.

Santib´a˜nez, P., Begen, M., and Atkins, D. (2007). Surgical

block scheduling in a system of hospitals: an applica-

tion to resource and wait list management in a british

columbia health authority. Health care management

science, 10(3):269–282.

Silva, C., Klement, N., and Gibaru, O. (2016). A generic de-

cision support tool for lot-sizing and scheduling prob-

lems with setup and due dates. In International Joint

Conference - CIO-ICIEOM-IIE-AIM (IJC 2016), San

Sebastian, Spain. ICIEOM.

Trilling, L., Guinet, A., and Le Magny, D. (2006). Nurse

scheduling using integer linear programming and con-

straint programming. IFAC Proceedings Volumes,

39(3):671–676.

Van den Bergh, J., Beli¨en, J., De Bruecker, P., Demeule-

meester, E., and De Boeck, L. (2013). Personnel

scheduling: A literature review. European Journal of

Operational Research, 226(3):367–385.

VanBerkel, P. T. and Blake, J. T. (2007). A comprehen-

sive simulation for wait time reduction and capacity

planning applied in general surgery. Health care man-

agement Science, 10(4):373–385.

Zhu, X. and Wilhelm, W. E. (2006). Scheduling and lot

sizing with sequence-dependent setup: A literature re-

view. IIE transactions, 38(11):987–1007.

Medical Imaging: Exams Planning and Resource Assignment - Hybridization of a Metaheuristic and a List Algorithm

267