Bimodal Model-based 3D Vision and Defect Detection for Free-form

Surface Inspection

Christophe Simler, Dirk Berndt and Christian Teutsch

Fraunhofer Institute for Factory Operation and Automation IFF, Sandtorstrasse 22, 39106 Magdeburg, Germany

Keywords: Detection, Inspection, Free-form Surface, Photogrammetry, Photometric Stereo, Shape Analysis,

Model-based, Data Simulation, Merging, Supervised Classification, Image Segmentation.

Abstract: This paper presents a 3D vision sensor and its algorithms aiming at automatically detect a large variety of

defects in the context of industrial surface inspection of free-form metallic pieces of cars. Photometric

stereo (surface normal vectors) and stereo vision (dense 3D point cloud) are combined in order to

respectively detect small and large defects. Free-form surfaces introduce natural edges which cannot be

discriminated from our defects. In order to handle this problem, a background subtraction via measurement

simulation (point cloud and normal vectors) from the CAD model of the object is suggested. This model-

based pre-processing consists in subtracting real and simulated data in order to build two complementary

“difference” images, one from photometric stereo and one from stereo vision, highlighting respectively

small and large defects. These images are processed in parallel by two algorithms, respectively optimized to

detect small and large defects and whose results are merged. These algorithms use geometrical information

via image segmentation and geometrical filtering in a supervised classification scheme of regions.

1 INTRODUCTION

The context of this article is the industrial surface

inspection (defect detection) of free-form metallic

car parts. Such a part is shown at the top left of

figure 1. Inspection is performed just after the

production and is generally done by human experts.

This has the drawbacks to be tiring, costly and above

all subjective. Many efforts are currently done to

automate this process. Comparing to most of the

existing automated inspection procedures, the new

challenge is to handle free-form surfaces.

Standard industrial cameras and controlled

lighting are used in this work. Three examples of

defects visualized by a sensor composed of a camera

(resolution: 33um/pixel) and one punctual light

source are shown on figure 1. Traditionally in

industry, feature extraction and classification are

applied on images of relatively planar surfaces. Such

procedures applied on images of free-form surfaces

will lack of reliability because:

1- Visibility (shading) problem: because of

the free-form of the surface, the visibility of

a defect in the image depends too much on

the positions of light source and camera.

2- Background problem: the free-form of the

surface introduces natural edges which

cannot be easily discriminated from our

“unfeatured” defects.

Figure 1: Top-left: free-form mechanical parts of cars.

Others: examples of defects of different shape and size.

The first problem discards the direct use of such

images as input of the detection algorithm. Because

our defects are 3D, a solution is to use 3D vision

sensors. We use photometric stereo (building an

Simler C., Berndt D. and Teutsch C.

Bimodal Model-based 3D Vision and Defect Detection for Free-form Surface Inspection.

DOI: 10.5220/0006113304510458

In Proceedings of the 12th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2017), pages 451-458

ISBN: 978-989-758-225-7

451

image of surface normal vectors), avoiding the

shading problem and enabling the detection of our

“small” defects. However, it is only sensitive to the

defect depth gradient and its integration lacks of

reliability (Ne, 05). This limits the ability to detect

some of our flat “large” defects, such as the one at

the top right of figure 1. To overcome this problem,

an active stereo vision system (building a dense 3D

point cloud) is also used.

The second problem occurs whatever the data

used, and thus a pre-processing has to be done.

Some methods currently applied on images could be

applied on 3D data. Thus they are presented below

although only 3D data are used in our work. There

are two approaches suggested in the literature to

solve the second problem: restoration and

background subtraction.

Restoration: it filters the undesired elements. It is

used in inspection of textile, wood and metallic

surfaces to remove structural/statistical textures (Ts,

01) (Ts, 03), or repetitive patterns (He, 05) in which

the defect is embedded. Morphological filters are

also used to highlight defects of specific shapes (Zh,

02). However, natural edges have no specific

features and cannot be discriminated from our

defects, thus they cannot be filtered.

Background subtraction (applied on images and

3D data): it consists of building a (monochrome)

“difference” image (input of the classification

algorithm) by subtracting a reference data set (our

“background” is the data without defect) from the

real data set. In the difference image, the defect

generally contrasts in radiometry with the

background. In the context of change or motion

detection in images, the reference data set is often an

image of the same scene taken previously. In our

context it has to be built. In (Ch, 16), the theory of

sparse representation and dictionary learning is used

in the case of images. This approach generates a

“flexible” reference image, adjusted to the

uncertainties (localization, illumination, texture and

geometric tolerances of the part) of its corresponding

real image. The success of the method depends on

the reliability of the decomposition models and on

the quality of the dictionary, which is generally

learned (Lu, 13). However, the method has not been

yet extended to 3D data, and this is why we do not

use it in this work.

Another technic to obtain a reference data set is to

simulate the data from the CAD object model. To

perform that, we have developed a simulator

enabling to work in a 3D virtual space containing the

CAD and the sensor model. The sensor model can

be moved with respect to the CAD, and sensor data

can be simulated from a chosen viewpoint. In our

application, once the real sensor is localized with

respect to the object, the sensor model is positioned

accordingly in the virtual space in order to obtain

simulated data registered with the real data. This

model-based approach generates a “perfect”

reference data set, but not a “flexible” one like with

a dictionary. However, it has the great advantage to

be easily used with 3D data, and this is why we use

it in this work. In our context of image-based defect

detection, the CAD model is currently not very used

in industry, and when it is used it is generally

without data simulation.

In this work two 3D vision sensors are used (for

large and small defects). For each one, a model-

based background subtraction generates a difference

image. The independent and complementary

“photogrammetric” and “photometric” difference

images are the input of the classification algorithm

(see figure 2). Figure 3 shows the hardware of the

system. (Ne, 05) suggests a rendering technic

building an “improved” 3D point cloud by

combining a measured 3D point cloud and a surface

normal vector image. Data merging presenting a risk

of loss of information, it is not retained in this work.

Figure 2: Flow diagram of the defect detection system: 3D

vision sensor combination (solid boxes), background

subtraction via simulation from the CAD model (dotted

boxes), and finally feature extraction, classification,

merging and decision algorithm.

Photogrammetric

difference image

Photometric

difference image

Defect detection algorithm and decision

Simulated

data (ref.)

via sensor

models

(

localize

Real data:

surface normal

vector image

from photome-

tric stereo

CAD model

Real data:

dense 3D

point cloud

from active

stereo vision

ect

Background

subtraction

Background

subtraction

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

452

Figure 3: Hardware of the vision system (fully-calibrated).

The sensors and their ability to visualize defects in

their difference images are explicated in part 2. The

classification algorithm (and related works) is

detailed in part 3. The classification results are in

part 4 and part 5 is the conclusion.

2 SENSORS & VISUALIZATION

This section presents our two 3D vision sensors and

shows their complementarity and ability to visualize

defects in their difference images. The first sensor

uses photometry to visualize small defects (their

gradients are visualized), while the second uses

photogrammetry for visualizing large defects.

2.1 Photometry

The resolution of our camera is 33um/pixel,

enabling to visualize our small defects, which can be

as small as 0.3mm². Photometric stereo (building an

image of surface normal vectors) provides a

difference image of this resolution while avoiding

shading effect. The difference image visualizes the

defect depth gradient.

Photometric stereo consists in reconstructing the

surface normal vectors from N images N  3

having different illuminations. Let us consider the

case of a perfectly diffuse surface (Lambertian

reflectance model). For each pixel we have N

brightness equations: I



I



ρv



.n with 1  i 

N. I



 are the measured pixel intensities. v



 and

I



 are the (generally known) light source

directions (vectors) and intensities. n is the

(normalized) surface normal vector and ρ is the

surface albedo (generally unknown). Thus we have

N non-linear equations and three unknowns. This

system has a closed-form solution. See (He, 11) for

generalization.

Photometric stereo in our work and contributions:

our sensor contains eight distant and punctual light

sources (figure 3). We assume that our surface

reflectance has diffuse and specular components.

Also, our free-form surface and the 3D defects

produce shadows in the images. Thus, the i



intensity of a pixel in our sequence is not

systematically close to I



ρv



.n (Lambertian model),

but can be clearer due to specularity or darker due to

shadow. We discard these outliers using the method

of (Br, 12) and then estimate the normalized surface

normal vector and the albedo from (at least three)

inliers via least squares. Our contribution is that we

overcome the problem of the limited dynamic range

in intensity of the camera. For each illumination, a

robust high dynamic range (HDR) image is

computed from five acquisitions with different

exposure times (He, 14).

Our photometric stereo sensor provides a “color”

image containing the normalized surface normal

vectors (see figure 4.1, figure 6.1 is the raw image).

The difference image is formed with the Euclidian

distances between these real vectors and their

corresponding simulated ones (simulation in figure

4.2; difference image in figure 4.3). The intensity of

this image is related to the absolute value of the

defect depth gradient. Figure 5.1 shows a zoom of a

small defect (kind of dome). Without surprise, its

depth gradient is visible in the difference image

(figure 5.2). Photometric stereo is a gradient

measurement, and it is difficult to reconstruct the

defect depth by integration. Thus this approach has

difficulties to visualize properly large defects having

flat surfaces (missing material). An example is

shown on figure 4.3 (raw image on figure 6.1). To

overcome this problem, stereo vision is combined

with photometric stereo (part 2.2).

Figure 4: 1: Real (normalized) surface normal vector

image. 2: Simulated data. 3: “Photometric” difference

image (defect depth gradient are visible).

Background subtraction (pixel color vector distance)

fringe

projector

and camera

for active

stereo vision

Light

sources for

photometric

stereo

Central camera for

photometric stereo

Bimodal Model-based 3D Vision and Defect Detection for Free-form Surface Inspection

453

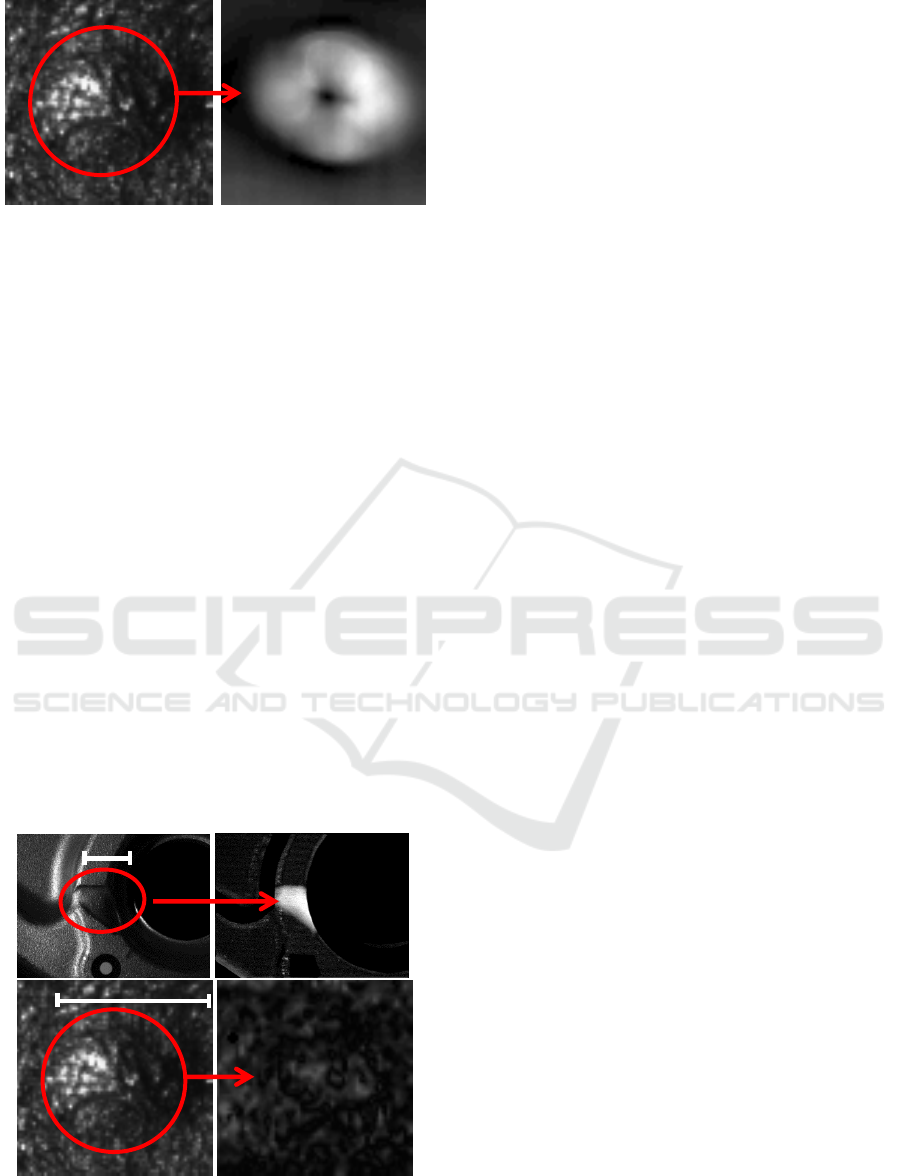
Figure 5: 1: Zoom of a small defect such as the one at the

bottom right of figure 1 (dome of area 0.8mm²). 2:

“Photometric” difference image.

2.2 Photogrammetry

Because photometric stereo is limited to visualize

large defects, this part introduces an active stereo

vision system (producing a dense 3D point cloud)

enabling their suitable visualization. The difference

image is formed with the Euclidian distances

between the real 3D points and their closest

simulated ones. The intensity of this image is related

to the absolute value of the defect depth. Without

surprise, large and deep defects are very visible with

photogrammetry (see figure 6.2; figure 6.1 is the raw

image), and the visibility is much better than with

photometry (compare figure 6.2 with figure 4.3).

The resolution of the “photogrammetric” difference

image is only of 0.9mm² (triangulation-based

methods generally provide a resolution loss (He,

11)). In fact, our stereo vision system cannot

visualize our smallest defects (figures 6.4). This is

not important because the photometric stereo system

handles the small defects (figure 5.2), but shows the

complementarity of the two systems.

Figure 6: 1: a large defect, 3: same as figure 5.1. 2 and 4:

“photogrammetric” difference images.

3 DETECTION ALGORITHMS

Automated and reliable defect detection algorithms

for the inspection of mechanical parts are more and

more needed in industry. Section 3.1 briefly presents

the main classification technics in image processing,

and positions our work with respect to them. Section

3.2 describes our defect detection algorithm.

3.1 Brief Background and Position of

our Method

Some detection algorithms are directly applied to 3D

measured data (Th, 15). However in the following

only image classification is considered, because our

detection algorithm has images in input (the

monochrome difference images). A classification

approach is characterized by the entities it considers

(pixels or objects), the feature extraction and the

classifier itself.

Whatever the context, the most used approach is

by far the classification of pixel features (intensity,

RGB vector …) (Lu, 14) (Ts, 03) (Zh, 02) and (Ch,

16). This approach is used in the article (Li, 07)

using the Torrance and Sparrow surface reflectance

model parameters (computed from photometric

stereo) as pixel features. However, with this technic

each pixel is processed individually without

considering its spatial context in the image (no

overall regularization). Pixel-wise classification is

not used in our work because it can provide a

relative instability (our defects are objects, not

pixels) and does not use any spatial information.

Approaches based on hidden Markov random fields

exploit spatial information (Sc, 09). The problem is

that they require initialization and are time

consuming when large images are processed.

Image segmentation avoids the previous

drawbacks and uses contextual information in order

to group pixels into objects (regions) (Ta, 10) (De,

09). In our work, a segmentation algorithm is

applied on the input image (a defect region should

contain at least one segmented object). Once image

segmentation is performed, two strategies can be

used for the classification.

The first is a pixel spectral classification and to

assign to a segmented object the predominant pixel

class within it (majority vote) (Li, 07). This method

does not use geometry, thus it is adequate when the

defects have few specific geometry or e.g. to detect

forests in aerial rural images.

The second is to design and classify a pattern for

the segmented object. When the defects have few

specific geometry (or in natural environment), the

Not visible

1 mm

10 mm

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

454

components of the pattern are generally only spectral

(Li, 07). In man-made environment, classes of

interest often have specific geometry (size, shape)

and in that case the pattern can possibly have

spectral and spatial components. For example, in

order to detect road and building in color (RGB)

aerial urban images, the article (Si, 11) forms a

pattern whose components are the mean RGB vector

over the segmented object (spectral), the area and

the eccentricity (spatial). The use of geometrical

features has improved the class separability and thus

the classification accuracy.

In our work the above second strategy is retained.

However, our defect class has not enough geometric

features to integrate spatial components into the

pattern. In contrast, the defects (or their gradients)

are generally clearer than the background in the

difference images (figure 2). Thus, spectral

components such as the mean intensity value can be

retained. Although (in our work) geometry cannot be

used to form pattern components, it can be exploited

in a soft manner just after the segmentation

(especially for our small defects) in order to

decrease the risk of false positives. If our defect

class has a geometric feature inside a range,

segmented objects outside this range are eliminated.

We call this operation the geometrical filter.

Supervised classification methods (Bi, 07) and

combination of different approaches are intensively

used to detect defects. For example, the article (Su,

08) combines neural network (NN) and fuzzy logic

in order to train a 6-class classifier. In this article,

object-based feature extraction is implicit because

the input image contains only the inspected part on a

perfectly dark background. In the context of road

and building extraction in color aerial urban images,

(Si, 10) combines a “3 class” support vector machine

(SVM) classifier with a single class SVM in order to

improve the classification accuracy.

In our work, the classification is supervised (via a

training set). However, sophisticated supervised

classification schemes such as NN or SVM are not

needed because our pattern has only one (spectral)

component and we have only two classes (defect or

not). Instead, during the learning the threshold is

manually fixed using a training set.

3.2 Our Detection Approach

Figure 7 shows that the two difference images are

processed in parallel by the algorithms algo3D and

algoN, optimized to detect large and small defects

and the results merged with a logical “or”.

Figure: 7: Defect detection algorithm and decision.

Algorithms algo3D and algoN have the same

structure as discussed in the previous section. The

input image is first segmented (object approach),

then a geometrical filter is applied to discard

improbable regions (against false positives).

Afterwards, a one dimensional radiometric pattern is

computed for each (remaining) segmented object.

Pattern classification is performed via a threshold

which was manually fixed using a training set

(supervised classification). It has been noticed that

when a defect area is larger than 5mm²

photogrammetry should be used, else photometry is

more reliable. Thus 5mm² is the border between

large and small defects.

3.2.1 algo3D

This algorithm, described on figure 8, is designed to

detect large defects (from 5 to 200mm²). These

defects have no shape feature, thus the geometrical

filter only discards segmented regions smaller than

0.9mm² (system resolution). The lower limit is

largely smaller than 5mm² because a segmented

region on the defect can be smaller than the defect.

A large defect has generally a depth upper than

0.3mm. A threshold of this value is applied on the

difference image, enabling to form a pattern

invariant with respect to the defect depth: the

number of white pixels in a segmented region

divided by the region area. It also generally discards

almost all the small aggregates produced by the

imperfections of the fringe projector (see figure 10,

left column). The morphological dilatation makes

more compact the large defect regions (suppression

of the holes), while the erosion limits the risk of

false positives by eliminating the possible remaining

bright (above the threshold) small aggregates.

Photogrammetric

difference image

Photometric

difference image

Defect or not

algo3D algoN

Merging

Bimodal Model-based 3D Vision and Defect Detection for Free-form Surface Inspection

455

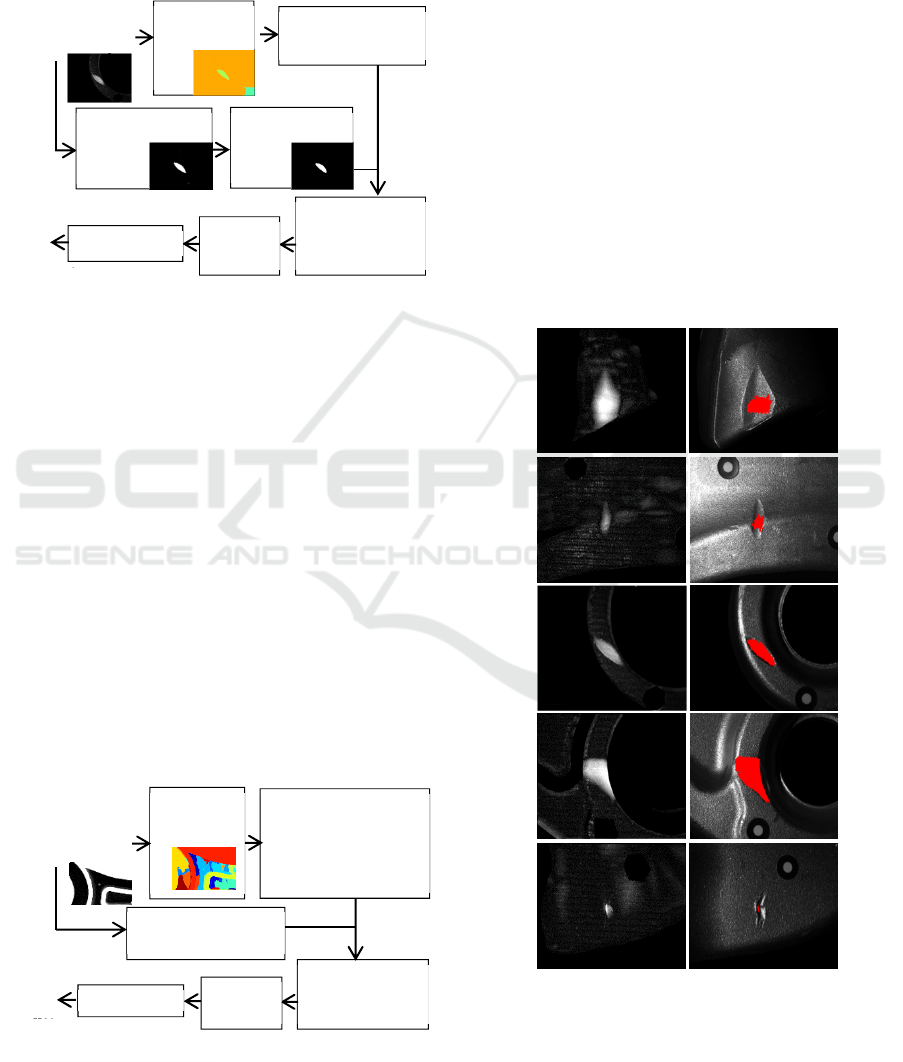
The lower limit of the geometrical filter enables

the detection of small defects which are larger than

0.9 mm²; however the morphological erosion

reduces this ability. In fact, Algo3D can detect some

small defects but is not optimized for that. In this

case algoN is more performant to detect them.

Figure 8: algo3D: large defect detection from the

photogrammetric difference image.

3.2.2 algoN

This algorithm, described on figure 9, is designed to

detect small defects (from 0.3 to 5mm²). It is the

defect’s gradients which are visible in the

photometric difference image, thus it is these regions

(or part of them) which can be detected instead of

the defect directly. Our small defects have rough

shape features, and thus also the segmented regions

lying on their gradients. They are never extremely

elongated and have no chaotic border. More

precisely, their areas, eccentricities, compactness

and concavities are inside some ranges (see the

geometrical filter in figure 9).

A Canny edge detector is applied to the

difference image to form a pattern invariant to the

defect depth: the percentage of edges in a segmented

region (notably defect’s gradient regions).

Figure 9: algoN: small defect detection from the

photometric difference image.

4 RESULTS

4.1 Qualitative Results

Figures 10, 11 and 12 show large and small defects

respectively detected by algo3D and algoN. The

difference image is at the left, the defect is shown at

the right and the segmented region of the highest

pattern (classified here as defect) is marked in red.

Sometimes the segmented region is spread over

the entire defect (or defect’s gradient), and

sometimes only on a part of it. This mainly happens

when the defect has strong depth only on a part of it

(and also only the segmented region of the highest

pattern is visualized, while possibly some others are

on the defect region and are classified as defect).

The two cases are equivalent because our aim is the

detection, not the accurate extraction. Among these

examples, no defect has been detected by both

algo3D and algoN (complementarity).

Figure 10: Large defects detected by algo3D. Left:

photogrammetric difference image. Right: the segmented

region of the highest pattern (classified as defect) is in red

on the raw image.

Threshold: 0.35

(learned via training set)

Photogrammetric

difference image

Defect

or not

Segmentation

(regions)

Region patterns

(number of white

pixels / area)

Highest

pattern

Classification

Threshold: 0.3mm

Morphological

filter

Geometrical filter

0.9<area<200mm²

Defect

or not

Geometrical filter

0.1 < area < 5mm²

eccentricity > 0.98

12.5<compactness<37

0.9 < concavity

Canny edge detector

(binary image)

Threshold: 0.082

(learned via training set)

Region patterns

(number of edge

pixels / area)

Highest

pattern

Classification

Photometric

difference image

Segmentation

(regions)

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

456

Figure 11: Small defects detected by algoN. Left:

photometric difference image. Right: like in figure 10.

Figure 12: Large and small defects respectively detected

by algo3D and algoN. Left: the photogrammetric (top) and

the photometric (bottom) difference images. Right: like in

figure 10.

4.2 Quantitative Results

Three hundred and sixty five acquisitions are used

for the test. This set includes one hundred and sixty

positives (containing at least one defect), with the

same overall quantity of large and small defects.

Consider algo3D (or equivalently algoN), the

highest pattern and its segmented region:

If the real class is positive: if the segmented

region is on the defect region and the pattern is

classified as positive, we have a true positive (TP). If

the pattern is classified as negative, we have a false

negative (FN). If the segmented region is outside the

defect region and the pattern is classified as positive,

we have a false positive (called FP2).

If the real class is negative: if the pattern is

classified as positive, we have a false positive

(called FP1). If the pattern is classified as negative,

we have a true negative (TN).

The overall accuracy (% of correct

classification) is: 100  /   

1  2  . The results of each method are

reported in table 1.

Table 1: Results of the algorithms.

algo3D algoN Merging

TP 112 48 133

TN 205 200 200

FP1 0 5 5

FP2 6 7 6

FN 42 105 21

Overall

accuracy (%)

86.8 67.9 91.2

algo3D provides good results (table 1). As expected,

it detects almost systematically the large defects

(>5mm²), and also sometimes smaller defects. Its

forty two FN are mainly small defects. The results of

algoN are less good. This was expected because it is

designed to detect only small defects. Sometimes

large defects are detected via the detection of parts

of them. More than 80% of the small defects are

detected, this is better than with algo3D. The

combination of these complementary algorithms

significantly improves the overall accuracy with

respect to algo3D. algoN is very useful because it

detects twenty one (generally small) defects that

algo3D not detects. Only twenty seven TP are

detected by both algo3D and algoN. This confirms

their high complementarity.

FP1 and FP2 are due to higher measurement

error at natural edges. These errors are often visible

in the difference images and sometimes detected,

particularly with algoN due to its higher sensitivity.

FN are the main problem because more numerous.

They occur mainly with small defects (algoN).

Generally, the segmentation extracts them suitably

(more exactly parts of their gradients are extracted),

thus the problem is a too low pattern. It happens

when the edges of the defect’s gradient are mainly

outside the segmented regions or when the defect is

not visible enough due to low depth gradient (too

few edges extracted).

5 CONCLUSION

A model based vision sensor and defect detection

algorithm combining stereo vision and photometric

stereo were presented. Measurement simulations via

the CAD model enabled to build two complementary

difference images. One visualizes well large defect

depths, making possible the detection of large

defects. The other makes visible small defect depth

gradients, enabling the detection of small defects.

The combination of the results of the two

complementary detectors enables to obtain an

overall accuracy of 91.2%. A future challenge is to

Bimodal Model-based 3D Vision and Defect Detection for Free-form Surface Inspection

457

reduce measurement error at natural edges (FPs).

FNs occur mainly with small defects and are

generally due to a low pattern. A second version of

algoN configured to detect defects having low depth

gradient could be tested. With this third class of

defects, the geometrical filter range for the area

could be from 0.1 to 2mm². The segmented regions

of the defects (or more exactly of parts of the defect

gradients) are relatively elliptic, thus an additional

shape feature “fit with an ellipse” could be included

in the geometrical filter or maybe even integrated as

spatial component into the pattern. The spectral

component of the pattern should be maintained

because other segmented regions are elliptic. To

have a higher spectral component, the Canny edge

detector should be much more sensitive.

The prototype will be completed to perform an

automatic inspection of the entire object via model-

based sensor planning (Ch, 11) and motion planning

(La, 06) technics. A robot arm will move the object

between two successive acquisitions. In the virtual

space, measurements will be simulated from each

computed viewpoint. Then during the plan execution

in the real world, real measurements will be done

from these viewpoints. Once the entire object is

captured, the defect detection processing can be

applied in parallel to the data of each viewpoint.

REFERENCES

Chen, S., Li., Y., and Kwok., NM., 2011. Active vision in

robotic systems: A survey of recent developments. Int.

Journal of Robotics Research, 30(11), 1343–1377.

LaValle, S., 2006. Planning Algorithms, Cambridge

University Press, ISBN 0-521-86205-1.

Bishop, C., 2007. Pattern recognition and machine

learning, Springer. ISBN: 978-0-387-31073-2.

Simler, C., 2011. An Improved Road and Building

Detector on VHR images. IEEE International

Geoscience and Remote Sensing Symposium.

Simler, C., Beumier, C., 2010. Building and Road

Extraction on Urban VHR Images using SVM

Combinations and Mean Shift Segmentation.

International Conference on Computer Vision Theory

and Applications (VISAPP).

Lu, D., 2004. Change detection techniques. International

Journal of remote sensing, 25(12), 2365-2407.

Scarpa, G. and all, 2009. Hierarchical multiple markov

chain model for unsupervised texture segmentation.

IEEE Trans.on Image Processing 18(8):1830-1843.

Tarabalka and all, 2010. Segmentation and classification

of hyperspectral images using watershed

transformation. Pattern Recognition, 43(7), 2367-

2379.

Debeir, O., Atoui H., Simler, C., 2009. Weakened

Watershed Assembly for Remote Sensing Image

Segmentation and Change Detection. International

Conference on Computer Vision Theory and

Applications (VISAPP).

Herbort, S., Wöhler, C., 2011. An Introduction to Image-

based 3D Surface Reconstruction and a Survey of

Photometric Stereo Methods. 3D Research, 2:4,

03(2011)4.

Nehab, D., Rusinkiewicz, S., Davis, J., Ramamoorthi, R.,

2005. Efficiently combining positions and normals for

precise 3d geometry. SIGGRAPH'05, 24(3), 536-543.

Bringier, B., Bony, A., Khoudeir, M., 2012. Specularity

and shadow detection for the multisource photometric

reconstruction of a textured surface. Journal of the

Optical Society of America A, 29(1), 11-21.

Herbort, S. 2014. 3D Shape Measurement and Reflectance

Analysis for Highly Specular and Interreflection-

Affected Surfaces. Thesis. TUD.

Linden, S., Janz, A., Waske, B., and all., 2007. Classifying

segmented hyperspectral data from a heterogeneous

urban environment using support vector machines. J.

Appl. Remote Sens., 1(1).

Tsai, D., Hsiao, B., 2001. Automatic surface inspection

using wavelet reconstruction. Pattern Recognition, 34,

1285-1305.

Tsai, D., Huang, T., 2003. Automated surface inspection

for statistical textures. IVC, 21(4), 307-323.

Henry, Y., Grantham, K., Pang. S., Michael K., 2005.

Wavelet based methods on patterned fabric defect

detection. Pattern Recognition, 38, 559-576.

Chai, W., Ho, S., Goh, C., 2016. Exploiting sparsity for

image-based object surface anomaly detection.

IEEE

ICASSP.

Lu, C., Shi, J., Jia, J., 2013. Online robust dictionary

learning. IEEE Conference CVPR.

Than, D. and all, 2015. Automatic defect detection and the

estimation of nominal profiles based on spline for free-

form surface parts. IEEE ICAIM.

Su, J., Tarng, Y., 2008. Automated visual inspection for

surface appearance defects of varistors using an

adaptive neuro-fuzzy inference system. The

International Journal of AMT, 25(7), 789-802.

Zheng, H., Kong L., Nahavandi, S., 2002. Automatic

inspection of metallic surface defects using genetic

algorithms. Journal of MPT, 125-126, 427-433.

Lindner, C., Leon, F., 2007. Model-based segmentation of

surfaces using illumination series. IEEE Transactions

on Instrumentation and Measurement, 56(4).

VISAPP 2017 - International Conference on Computer Vision Theory and Applications

458