
A Formal Semantics for Concept Understanding Relying on
Description Logics
Farshad Badie
Department of Communication, Aalborg University, Aalborg, Denmark
Keywords: Concept Understanding, Conceptualisation, Terminology, Interpretation, Formal Semantics, Description
Logics, Ontologies.
Abstract: In this research, Description Logics (DLs) will be employed for logical description, logical characterisation,
logical modelling and ontological description of concept understanding in terminological systems. It’s
strongly believed that using a formal descriptive logic could support us in revealing logical assumptions
whose discovery may lead us to a better understanding of ‘concept understanding’. The Structure of
Observed Learning Outcomes (SOLO) model as an appropriate model of increasing complexity of humans’
understanding has supported the formal analysis.
1 INTRODUCTION
The central focus of this research is on concepts. My
point of departure is the special focus on the fact that
there is a general problem concerning the notion of
‘concept’, in linguistics, psychology, philosophy and
computer science. This research aims at providing a
logical description (and analysis) of the use of
‘concepts’ in terminological knowledge
representation systems, and, thus, I need to assume
concepts’ applications in order to be comprehensible
in the context and in my logical formalism. Taking
into consideration (Baader et al., 2010) and
(Rudolph, 2011), a concept might be correlated with
a distinct ‘entity’ or to/with its essential features,
characteristics and properties. Note that an entity’s
properties express its relationships with itself and
with other entities. Through the lens of Predicate
Logic, a concept might be considered to be
equivalent to a [unary] predicate. It shall be
emphasised that this remark is not about language,
but this is how concepts are perceived by logicians.
Accordingly, it could be claimed that predicates
could—logically—express the characteristics of
concepts in terminological systems. More
specifically, predicates assign characteristics,
features and properties of concepts into some
subjects. It’s believed that predicates may determine
the applications of logical descriptions. As all
logicians know, predicates play fundamental roles in
reasoning processes and in giving satisfying
conditions for definitions of [logical] truth. By
taking into consideration that ‘a predicate expresses
a condition that the entities referred to may satisfy,
in which case the resulting sentence will be true (see
(Blackburn, 2016))’, predicates can be applied in
expressing meanings within formal semantics.
Subsequently, the formal semantics could focus on
multiple conditions through definitions of truth (and
falsity). The central objective of formal semantics
can be said to be formalising and manipulating the
relationships between the signifiers of a description
and what the signifiers do [or have been designed to
do], see (Jackendoff, 1990; Gray et al., 1992;
Barsalou, 1999; Resnik, 1999).
As mentioned, the central focus of this research
is on concepts (and through the lens of Predicate
Logic). Concepts and their interrelationships will be
used to establish the basic terminology adopted in
the modelled domain regarding the hierarchical
structures. My logical descriptions will have a
special focus on my methodological assumption that
expresses that ‘human beings can find out that an
individual thing/phenomenon is an instance of a
formed concept, and, thus, their individual grasp of
that concept (in the form of their conceptions)
provide foundations for producing their own
conceptualisations’. This article will focus on
describing and characterising humans’ concept
understandings and will deal with a formal-semantic
model for figuring out the underlying logical
42
Badie F.
A Formal Semantics for Concept Understanding Relying on Description Logics.
DOI: 10.5220/0006113800420052
In Proceedings of the 9th International Conference on Agents and Artificial Intelligence (ICAART 2017), pages 42-52
ISBN: 978-989-758-220-2
Copyright
c
2017 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

assumptions of ‘concept understanding’. The term
‘understanding’ will be observed from multiple
perspectives, and, subsequently, the expressiveness
of the semantic model’s descriptions will be
improved. The Structure of Observed Learning
Outcomes (SOLO) taxonomy is an appropriate
model of increasing complexity of humans’
understanding. SOLO as a descriptive model of
knowing and understanding can support my
formalism. Additionally, its taxonomical structure
could be expressed in the form of some logical
inclusions. In this research, the formal semantic
analysis of [concept] understanding is based on
Description Logics (DLs). I believe that DLs can
support me in proposing an understandable logical
description for clarifying concept understanding.
DLs as the profound formalism are used for
representing predicates and for formal reasoning
over them. They mainly focus on terminological
knowledge. It is of a terminological system’s
particular importance in providing a logical
formalism for knowledge representation systems,
and, also, for semantic representations and
ontologies (as formal and explicit specification of a
shared conceptualisation on the domains of interest),
see (Davies et al., 2003; Staab and Studer, 2009).
The main contributions of this research are: (i)
providing a formal semantics (relying on DLs) for
conceptual analysis of concept understanding, and
analysing a knowledge representation formalism for
expressing concept understanding, and (ii) designing
and formalising an ontology that provides a
structural representation of concept understanding
within the analysed semantic model.
2 DESCRIPTION LOGICS
First, I shall mention that (Baader et al., 2010) is my
main reference to Description Logics. Description
Logics (DLs) represent knowledge in terms of
individuals (objects, things), concepts (classes of
things), and roles (relationships between things).
Individuals correspond to constant symbols,
concepts to unary predicates, and roles to binary (or
any other n-ary) predicates and relations in Predicate
Logic. Reconsidering the predicate P in Predicate
Logic, we have [possibly specified] concept C in
DLs. There are two kinds of atomic symbols, which
are called atomic concepts and atomic roles. These
symbols are the elementary descriptions from which
we can inductively (by employing concept
constructors and role constructors) build the
specified descriptions. Considering N
C
, N
R
and N
O
as
the sets of atomic concepts, atomic roles and
individuals respectively, the ordered triple N
C
, N
R
,
N
O
represents a signature. The set of main logical
symbols in ALC (Attributive Language with
Complements: the Prototypical DL, see (Schmidt-
Schauss and Smolka, 1991)) is: { Conjunction (⊓:
And), Disjunction (⊔: Or), Negation
(¬: Not),
Existential Restriction (∃: There exists ... ),
Universal Restriction (∀: For all ... ) }. We also
have Atomic Concepts (A), Top Concept (
⊤:
Everything) and Bottom Concept (
⊥: Nothing) in
ALC.
In order to define a formal semantics, we need to
apply terminological interpretations over our
signatures. More particularly, any [terminological]
interpretation consists of (i) a non-empty set ∆ (that
is the interpretation domain and consists of any
variable that occurs in any of the concept
descriptions), and (ii) an interpretation function .
I
(let me call it ‘interpreter’). The interpreter assigns
to every individual (like a) a ‘a
I
∈ ∆
I
’. Also, it
assigns to every atomic concept A (or every atomic
unary predicate) a set A
I
⊆ ∆
I
, and to every atomic
role P (or every atomic binary predicate) a binary
relation
P
I
⊆ ∆
I
× ∆
I
. Table 1 reports the syntax
and the semantics of ALC.
Table 1: The Prototypical Description Logic.
Syntax Semantics
A A
I
⊆ ∆
I
P P
I
⊆ ∆
I
× ∆
I
⊤ ∆
I
⊥ ∅
C ⊓ D (C ⊓ D)
I
= C
I
∩ D
I
C ⊔ D (C ⊔ D)
I
= C
I
∪ D
I
¬C (¬C)
I
= ∆
I
\ C
I
∃R. C { a | ∃b.(a,b) ∈ R
I
∧ b ∈ C
I
}
∀R. C { a | ∀b.(a,b) ∈ R
I
⊃ b ∈ C
I
}
A knowledge base in DLs usually consists of a
number of terminological axioms and world
descriptions (so-called: ‘assertions’), see Table 2.
The terminological interpretation I is called a model
of an axiom [or a model of a basic world
description], if, and only if, it can semantically
satisfy it, see Tables 2 and 3. In the following Tables
P is an atomic role, R and S are role descriptions, A
is an atomic concept, and C and D are concept
descriptions.
A Formal Semantics for Concept Understanding Relying on Description Logics
43

Table 2: Axioms and World Descriptions in DLs.
Name Syntax
Semantics
Concept Inclusion Axiom C ⊑ D
C
I
⊆ D
I
Role Inclusion Axiom
R ⊑ S R
I
⊆ S
I
Concept Equality Axiom
C ≡ D C
I
= D
I
Role Equality Axiom
R ≡ S R
I
= S
I
Concept Assertion
C(a) a
I
∈ C
I
Role Assertion
R(a, b) (a
I
, b
I
) ∈ R
I
Table 3: Inductive Concept Descriptions.
Over Concept Over Role
A
I
⊆ ∆
I
P
I
⊆ ∆
I
× ∆
I
⊥
I
= ∅ ⊥
I
= ∅
(¬C)
I
= ∆
I
\ C
I
(¬R)
I
= (∆
I
× ∆
I
) \ R
I
(C ⊓ D)
I
= C
I
∩ D
I
(R ⊓ S)
I
= R
I
∩ S
I
Let me start the logical analysis with two examples:
Example 1. Mary has verified that ‘there is a young
student’ and ‘there is a non-old student’ are
expressing the same matter. Her verification
between these two propositions is expressible in DLs
by:
∃hasStudent.Young ≡ ∃hasStudent.¬Old. It’s
realisable that Mary has assumed the axiom stating
that
Young and Old are two disjoint concepts, and, in
fact, the logical term ‘
Young ⊓ Old ⊑ ⊥’ has formed
a terminological axiom for Mary. It’s obvious that
Mary’s interpretation over (i)
Young ⊓ Old ⊑ ⊥
(meaning that
Young and Old are disjoint concepts)
and (ii)
Person ⊑ Young ⊔ Old (meaning that every
person is either young or old) has played crucial
roles here. In fact, Mary has interpreted, and,
respectively, understood that these two sentences
(‘there is a young student’ and ‘there is a non-old
student’) have the same meanings. More
specifically, Mary’s terminological interpretation
(over i and ii) has produced her understanding of an
equivalence between the concept descriptions
∃hasStudent.Young and ∃hasStudent.¬Old. We
can see that Mary’s interpretation has been restricted
(limited) to her understanding of disjointness of the
concept descriptions
∃hasStudent.Young and
∃hasStudent.¬Old. At this point I shall claim that
the concepts (concept descriptions) C and D are
logically and semantically equivalent, when ‘for all’
possible terminological interpretations like I, we
have:
C
I
= D
I
. In this example, if one person, say
John, does not assume the axioms stating that
‘
Young and Old are two disjoint concepts’ and
‘every person is either young or old’, then there will
not be an equivalence relation between
∃hasStudent.Young and ∃hasStudent.¬Old. Let me
conclude that Mary’s and John’s understandings are
dissimilar, because they have had different
terminological interpretations in their minds (and it
is because of their different conceptions and concept
formations). For example, regarding John’s
terminological interpretation, the proposition ‘there
is a middle-aged student’ could be added beside
‘there is a young student’ and ‘there is a non-old
student’. In fact, John could have the axiom
‘Person
⊑ Young ⊔ MiddleAged ⊔ Old (meaning that every
person is young or middle aged or old)’ in his mind.
Consequently, John by taking this axiom (based on
his own conception) into consideration doesn’t
understand ‘
∃hasStudent.Young’ and
‘∃hasStudent.¬Old’ as equivalent concept
descriptions.
Example 2. Mary has verified that ‘Anna has a child
who is a philosopher’ and ‘Anna has a child who is a
painter’ could be jointly expressed by ‘Anna has a
child who is a philosopher and painter’. Translated
into DLs we have her expression as followings
:
∃hasChild.Philosopher ⊓ ∃hasChild.Painter ≡
∃hasChild.(Philosopher ⊓ Painter). Suppose that
Anna has two children and one is a philosopher and
the other one is a painter. Then,
∃hasChild.(Philosopher ⊓ Painter) is not equivalent
to
∃hasChild.Philosopher ⊓ ∃hasChild.Painter.
Actually, Mary has not proposed a correct
description, and this is because of her inappropriate
terminological interpretation. Accordingly, her
understanding has followed her inappropriate
interpretation. In fact, she incorrectly (semantically:
False) has understood that the proposition ‘Anna has
a child who is a philosopher and painter’ expresses
the same matter. Reconsidering the proposed
formalism,
∃hasChild.Philosopher ⊓
∃hasChild.Painter
and ∃hasChild.(Philosopher ⊓
Painter) are not—semantically—the same and there
should not be an equivalence symbol between them.
Thus, Mary’s interpretation has not been
satisfactory. Subsequently, her understanding is not
satisfactory and appropriate.
3 A SEMANTIC MODEL FOR
CONCEPT UNDERSTANDING
In this section I clarify my logical conceptions of
‘concept understanding’. The term ‘understanding’
is very complicated and sensitive in psychology,
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
44

neuroscience, cognitive science, philosophy and
epistemology. There has not been any complete
model for describing this term, but there are some
proper models of (i) understanding of understanding
(see (Foerster, 2003)), (ii) understanding
representation (see (Peschl and Riegler, 1999;
Webb, 2009)), and (iii) specification of the
components of understanding (i.e., from the
cognition’s and from the affects’ perspectives), see
(Chaitin, 1987; Kintsch et al., 1990; di Pellegrino et
al., 1992; MacKay, 2003; Zwaan and Taylor, 2006;
Uithol et al., 2011; Uithol and Paulus, 2014). This
research—by analysing a formal semantics—focuses
on the junctions of ‘understanding of concept
understanding’ and ‘concept understanding
representation’ in terminological systems, and, more
specifically, it focuses on logical analysis of concept
understanding and its terminological representation.
3.1 Concept Understanding as a
Relation (and Function)
I shall claim that concept understanding—as a
relation—could relate ‘the characteristics and
attributes of a concept’ with ‘a description’. More
specifically, understanding is a function (mapping)
from a concept into some propositions (and
statements) which could be interpreted as ‘concept
descriptions’. In fact, the characteristics and
properties of a concept by means of the
understanding function become mapped into
concept descriptions. Let me be more specific:
A. A human being—by concept understanding—
attempts to map the significant characteristics of
concepts into some concept descriptions. For
example, ‘breathing’—as a biological and
psychological process—is a characteristic and trait
of all animals, and, thus,
breathing (that is a role) is
the characteristic of the concept
Animal. Then, (i)
knowing the fact that the individual
horse is an
instance of the concept
Animal (Formally:
Animal(horse)), and (ii) drawing the [concept
subsumption] inference
‘Horse ⊑ Animal’,
collectively lead us to knowing and to understanding
that ‘horses breathe’ (or equivalently: ‘horses do
breathing’). The role
breathing could be manifested
in the concept Breath. Therefore, (i) and (ii)
collectively lead us to expressing the concept
description ‘
Animal(horse) ⊓ ∃hasTrait.Breath’ for
the individual
horse (as an instance of the concept
Animal), and, respectively, for the concept Horse (as
a sub-concept of Animal).
B. A human being—by concept understanding—
attempts to map the concepts’ properties and their
interrelationships with themselves into some concept
descriptions. For example, the one who knows that
‘male horses breathe’, by taking the terminological
and assertional axioms {
Animal(horse), Horse ⊑
Animal, MaleHorse ⊑ Horse, FemaleHorse ⊑ Horse}
into consideration can know and understand that
‘female horses breathe’ as well.
C. A human being—by concept understanding—
attempts to map the concepts’ properties and their
relationships with other concepts into some concept
descriptions. For example, the one who knows that
‘horses breathe’ (and as described:
Animal(horse) ⊓
∃hasTrait.Breath
), could—respectively—know and
understand that the individual
rabbit (that is an
animal) breathes as well. So, she/he could express
that ‘rabbits breathe’, and, in fact,
Animal(rabbit) ⊓
∃hasTrait.Breath.
Conclusion. Relying on Predicate Logic [and on
DLs], the phenomenon of ‘concept understanding’
could be interpreted as a ‘binary predicate’ [and as a
‘role’] of human beings on expressing some concept
descriptions. Let me represent this role by
‘
understanding’.
3.2 Concept Understanding as a
Conceptualisation
The concept understanding could be interpreted to
be the limit/type of conceptualisation. Accordingly,
humans need to conceptualise concepts in order to
understand them. In (Badie, 2016a) and (Badie,
2016b), I have defined a ‘conceptualisation’ as “a
uniform specification of the separated
understandings”. In fact, any concept understanding
could be interpreted as a local manifestation of a
global conceptualisation. Additionally, human
beings’ grasps of concepts could provide proper
foundations for generating their own
conceptualisations. I shall claim that ‘concept
understanding’ could be acknowledged as a limited
type of humans’ concept constructions, when the
concept constructions are supported by their own
conceptualisations. Therefore,
conceptualising is a
role of human beings. This conclusion—relying on
DLs—could be represented by the ‘role inclusion (or
role subsumption)’
understanding ⊑ conceptualising.
In other words, ‘understanding a concept’ has been
acknowledged as the sub-role of ‘conceptualising
that concept’. On the other hand, it is not the case
that all conceptualisations are understandings.
In
A Formal Semantics for Concept Understanding Relying on Description Logics
45

fact, all the conceptualised concepts could not be
understood.
3.3 Concept Understanding as an
Interpretation-based Model
Generally, an interpretation is the act of elucidation,
explication and explanation, see (Simpson and
Weiner, 1989). According to (Honderich, 2005) and
through the lens of philosophy, “…in existential and
hermeneutic philosophy, ‘interpretation’ becomes
the most essential moment of human life: The
human being is characterized by having an
‘understanding’ of itself, the world, and others. This
understanding, to be sure, does not consist—as in
classical ontology or epistemology—in universal
features of universe or mind, but in subjective–
relative and historically situated interpretations of
the social. …”. Regarding (Blackburn, 2016) and
through the lens of logic, an ‘interpretation’ of a
logical system assigns meanings (or semantic
values) to the formulae and their elements. At this
point I shall take into consideration that the
phenomenon of ‘interpretation’ could have a
conjunction with the phenomenon of ‘terminological
interpretation’ in formal languages. More
specifically, the one who has engaged her/his
interpretations to explicate [and justify] what [and
why] she/he means by classifying a
thing/phenomenon as an instance of a concept, needs
to interpret the non-logical signifiers of different
concept descriptions within her/his linguistic
expressions.
Considering any set of non-logical symbols (that
have no logical consequences) in a terminology, a
terminological interpretation over humans’
languages could be described to be constructed
based on the tuple Interpretation Domain,
Interpretation Function. The interpretation domain
(or the universe of interpretation) might be called
‘universe of discourse’. As mentioned in previous
section, the interpretation domain must be non-
empty. This non-empty set forms the range of any
variable that occur in any of the concept descriptions
within linguistic expressions. It’s a fact that the
collection of the rules and the processes that manage
different terms and descriptions in linguistic
expressions, cannot have any meaning until the non-
logical signifiers and constructors are given
terminological interpretations. The interpretations
prepare humans for producing their personal
meaningful [and understandable] concept
descriptions. Hence, I have recognised all ‘concept
understandings’ as ‘concept interpretations’. This
conclusion—relying on DLs—could be represented
by the ‘role inclusion’
understanding ⊑ interpreting.
Therefore, ‘concept understanding’ has been
expressed as the sub-role of ‘concept interpreting’.
But, on the other hand, not all interpretations (of
concepts) imply understandings (of concepts).
Equivalently, it is not the case that all
interpretations are understandings. In other words,
all the interpreted concepts may not be understood.
Accordingly, considering any interpretation as a
function, ‘concept understanding’ is recognised as
an ‘interpretation function’.
From this point I apply the function UND (as a
limit of the interpretation function I)
in my
formalism. Then, C
UND
represents ‘Concept
Understanding’, where C stands for Concept.
Consequently, considering UND as a kind of
interpretation, there exists a tuple like D
U
,
C
understood
, where (i) D
U
represents the understanding
domain (that consists of the variables that occur in
any of the concept descriptions which are going to
be understood), and (ii) C
understood
is the understood
concept. C
understood
is achievable based on the
understanding function –
UND
. Relying on the
function –
UND
,
C
UND
⊆ C
I
⊆ ∆
I
&
D
U
UND
⊆ ∆
I
.
It shall be stressed that D
U
UND
expresses
‘understanding all concepts belonging to the
understanding domain’. Note that –
UND
(that is a
function) can provide a model for a terminological
[and assertional] axiom. Therefore, the desired
model (i) is a restricted form of a terminological-
interpretation-based model, and (ii) can satisfy the
semantics of the terminological and assertional
axioms (read ‘UND ⊨ Axiom’: UND satisfies the
axiom), see Table 4. Consequently:
C
UND
⊆ C
I
⊆ ∆
I
& -
UND
: C → C
UND
Where: C
UND
⊆ D
U
UND
⊆ ∆
I
.
I shall emphasise that we are not able to conclude
that C
I
⊆ D
U
UND
. On the other hand, we certainly
know that , C
UND
⊆ ∆
I
(because C
UND
⊆ C
I
and C
I
⊆ ∆
I
). According to the analysed characteristics, the
UND understanding model in my terminology is
constructed based upon the tuple Understanding
Domain, Understanding Function as:
UND = D
U
UND
, -
UND
.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
46

Table 4: Understanding Model: Terminologies, World
Descriptions and their Semantics.
Name Description, Semantics
Understanding a
Concept Inclusion
UND ⊨ (C ⊑D) ⇒
C
UND
⊆ D
UND
Understanding a
Role Inclusion
UND ⊨ (R ⊑S) ⇒
R
UND
⊆ S
UND
Understanding a
Concept Equality
UND ⊨ (C ≡D) ⇒
C
UND
= D
UND
Understanding a
Role Equality
UND ⊨ (R ≡S) ⇒
R
UND
= S
UND
Understanding a
Concept Assertion
UND ⊨ C(a) ⇒
a
UND
∈ C
UND
Understanding a
Role Assertion
UND ⊨ R(a, b) ⇒
(a
UND
, b
UND
) ∈ R
UND
Table 5 is based on Table 4 and itemises inductive
concept descriptions and their semantics as the
products of the understanding model.
Table 5: Understanding Inductive Concept Descriptions.
Model Satisfies the
Vocabulary
Semantics
UND ⊨ ⊤
⊤
UND
= ⊤
UND ⊨ ⊥ ⊥
UND
= ∅
UND ⊨ ¬R (¬R)
UND
= ⊤ \ R
UND
UND ⊨ ¬C (¬C )
UND
= D
U
UND
\ C
UND
UND ⊨ (R ⊓ S) (R ⊓ S)
UND
=
R
UND
∩ S
UND
UND ⊨ (C ⊓ D) (C ⊓ D)
UND
= C
UND
∩ D
UND
3.4 Concept Understanding as a
Product of Functional Roles
How could we employ DLs in order to describe an
understanding function as a [functional] role of a
human being? Let me interpret functional roles
(features) as the roles that are existentially functions,
and, thus, they can express functional actions,
movements, procedures and manners of human
beings. Let N
F
be a set of functional roles and N
R
be
the set of role [descriptions]. Obviously: N
F
⊆ N
R
,
and informally, functional roles are some kinds of
roles.
Lemma. The UND understanding model is–
semantically—structured over:
a. the understanding domain (or D
U
),
b. the understanding function (or -
UND
), and
c. the set D
U
UND
(or equivalently, the effect of the
understanding function -
UND
on the Top
concept)
that represents understanding all
atomic concepts (everything) in the
understanding domain.
Analysis. The UND understanding model associates
with each atomic concept a subset of D
U
UND
, and
with each ordinary atomic role a binary relation over
D
U
UND
× D
U
UND
. Note that any functional role can be
recognised as a partial function. More specifically,
considering F = f
1
○ ··· ○ f
n
(F is a chain of
functional roles), the chain f
1
UND
○ ··· ○ f
n
UND
represents the composition of n partial
understanding functions. In fact, by employing
UND, any f
i
UND
—semantically—supports the
[overall] functional role F
UND
. Note that for all i in
(1,n), f
i+1
produces the input of f
i
. Therefore, the
understanding of f
i+1
(the output of f
i+1
) provides the
input of the understanding of f
i
. In particular, any
concept description could be understood over the
subsets of D
U
UND
. This characteristic is very useful
in making a strong linkage between the terms
‘understanding’ and ‘chain of functional roles’. It
supports my semantic model in scheming and
describing "the understanding as the product of a
chain of functional roles, where the functional roles
are the partial understanding functions". You will
see how it works.
3.5 Humans’ Functional Roles through
SOLO’s Levels
According to (Biggs and Collis, 2014), the Structure
of Observed Learning Outcomes (SOLO) taxonomy
is a proper model that can provide an organised
framework for representing different levels of
humans’ understandings. This model is concerned
with various complexities of understanding on its
different layers. According to SOLO and focusing
on humans’ levels of knowledge with regard to a
concept, we have:
Pre-structured knowledge. Here humans’
knowledge of a concept is pre-structured (and is
the product of their pre-conceptions).
Uni-structured knowledge. Humans have a
limited knowledge about a concept. They may
know one or few isolated fact(s) about a
concept.
Multi-structured knowledge. They are getting to
know a few facts relevant for a concept, but
they are still unable to link and relate them
together.
Related Knowledge. They have started to move
towards deeper levels of understanding of a
concept. Here they are able to link different
facts and to explain several conceptions of a
concept.
A Formal Semantics for Concept Understanding Relying on Description Logics
47

Extended Abstracts. This is the most
complicated level. Humans are not only able to
link lots of related conceptions [of a concept]
together, but they can also link them to other
specified and complicated conceptions. Now
they are able to link multiple facts and
explanations in order to produce more
complicated extensions relevant for a concept.
Obviously, the extended abstracts are the products of
deeper comprehensions of related structures. Related
structures are the products of deeper
comprehensions of multi-structures. The multi-
structures are the products of deeper
comprehensions of uni-structures, and the uni-
structures are the products of deeper
comprehensions of pre-structures. Let me select a
process (as a sample of humans’ functional roles)
from any of the SOLO’s levels and formalise it.
According to SOLO, creation (with regard to an
understood concept) is an instance of ‘extended
abstracts’, justification (with regard to an understood
concept) is an instance of ‘related structures’,
description (with regard to an understood concept) is
an instance of ‘multi-structures’ and identification
(with regard to an understood concept) is an instance
of ‘uni-structures’. Therefore, Creation,
Justification, Description and Identification are four
processes which could be analysed as functions in
the model. Any of these functions can support a
functional role as a ‘partial understanding function’:
i. Creation has interrelatedness with
creatingOf
that is a functional role and extends the humans’
mental abstracts.
ii. Justification has interrelatedness with the
functional role
justifyingOf that relates the lower
structures.
iii. Description has correlation with the
functional role
describingOf that produces the multi-
structures.
iv. Identification has correlation with the
functional role
identifyingOf that generates the uni-
structures.
It shall be emphasised that
identifyingOf,
describingOf, justifyingOf and creatingOf are only
four examples of functional roles within SOLO’s
categories, and, in fact, the SOLO’s levels are not
limited to these functions. For example,
followingOf
and
namingOf are two other instances of uni-
structures,
combiningOf and enumeratingOf are two
other instances of multi-structures,
analysingOf and
arguingOf are two other instances of related
structures, and formulatingOf and theorisingOf are
two other instances of extended abstracts.
As mentioned, the functional roles
creatingOf,
justifyingOf, describingOf and identifyingOf represent
the equivalent roles of the creation, justification,
description and identification functions respectively.
Furthermore, these functions are the partial functions
of the understanding function. Obviously, the
understanding function (that is a process) could also
be considered to be equivalent to a functional role
like
understandingOf. Employing the ‘role inclusion’
axiom we have: (1)
creatingOf ⊑ understandingOf,
(2)
justifyingOf ⊑ understandingOf, (3) describingOf ⊑
understandingOf
, and (4) identifyingOf ⊑
understandingOf. Equivalently: (1) creation ⊆
understanding, (2) justification ⊆ understanding,
(3) description ⊆ understanding, and (4)
identification ⊆ understanding.
It shall be claimed that understandingOf—
conceptually and logically—supports ‘the
understanding function based on the analysed
understanding model (or UND)’. Similarly, we can
define CRN, JSN, DSN and IDN as sub-models of
UND for representing creation, justification,
description and identification respectively. Any of
these models can—semantically—satisfy the
terminologies and world descriptions in Table 4.
Accordingly—relying on inductive rules—they can
satisfy concept descriptions in Table 5.
Note that CRN (as a model) fulfils the desires of
UND better (and more satisfying) than JSN, DSN
and IDN. Considering D
U
as the understanding
domain, we have:
D
U
UND
⊆
D
U
CRN
⊆
D
U
JSN
⊆
D
U
DSN
⊆
D
U
IDN
.
More specifically:
D
U
CRN
represents the model of creation over the
understanding domain. It consists of concepts
which are (or could be) ‘created’ by human
beings. Formally: C
CRN
∈ D
U
CRN
.
D
U
JSN
represents the model of justification over
the understanding domain. It consists of
concepts which are (or could be) ‘justified’ by
human beings. Formally: C
JSN
∈ D
U
JSN
.
D
U
DSN
represents the model of description over
the understanding domain. It consists of
concepts which are (or could be) ‘described’ by
human beings. Formally: C
DSN
∈ D
U
DSN
.
D
U
IDN
represents the model of Identification
over the understanding domain. It consists of
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
48

concepts which are (or could be) ‘identified’ by
human beings. Formally: C
IDN
∈ D
U
IDN
.
Proposition. The terminological axioms and the
world descriptions (in Table 4) and inductive
concept descriptions (in Table 5) are all valid and
meaningful for CRN, JSN, DSN and IDN. Therefore,
inductive concept descriptions are also valid and
meaningful over the concatenation of the creation,
justification, description and identification functions
that have supported these terminological models.
Proposition. All satisfactions based on IDN are
already satisfied by DSN, JSN and CRN over
D
U
DSN
,
D
U
JSN
and D
U
CRN
respectively. Informally, if a human
being is able to describe, justify and create with
regard to her/his conception of a concept, so, she/he
is already capable of identifying that concept.
Furthermore, she/he might be able to identify
something else with regard to her/his conception of
that concept.
Formal Analysis. The semantics of the composite
function ‘creation (justification (description
(identification (C))))’—that is the product of the
chain of functional roles—supports the proposed
semantic model on D
U
UND
, which is the central
domain of the understanding (central part of the
understanding domain). Considering all the roles
relevant for the concept C, we have:
1. (∀R
1
.C)
CRN
=
{ a ∈ D
U
CRN
| ∀b.(a,b) ∈ R
1
CRN
→ b ∈ C
CRN
}.
Therefore:
2. (∀R
2
.C)
JSN
=
{ a ∈ D
JSN
| ∀b.(a,b) ∈ R
2
JSN
→ b ∈ C
JSN
}.
Therefore:
3. (∀R
3
.C)
DSN
=
{ a ∈ D
U
DSN
| ∀b.(a,b) ∈ R
3
DSN
→ b ∈ C
DSN
}.
Therefore:
4. (∀R
4
.C)
IDN
=
{ a ∈ D
U
IDN
| ∀b.(a,b) ∈ R
4
IDN
→ b ∈ C
IDN
}.
In the afore-itemised formalism R
1
, R
2
, R
3
and R
4
stand for creatingOf, justifyingOf, describingOf and
identifyingOf respectively. Consequently, CRN, JSN,
DSN and IDN have been observed as roles of human
beings. Accordingly, it’s possible to represent the
chain of functional roles in the form of a collection
of implications as following:
(∀R
1
.C)
CRN
⇒ (∀R
2
.C)
JSN
⇒ (∀R
3
.C)
DSN
⇒
(∀R
4
.C)
IDN
.
It must be concluded that ‘any role based on a
conception of C’ to the left of any of arrows makes a
logical premise for ‘other roles based on conceptions
of C’ to the right of that arrow. It shall be stressed
that this is a very important terminological fact. The
concluded logical relationship represents a flow of
concept understanding from deeper layers to
shallower layers.
4 AN ONTOLOGY FOR
CONCEPT UNDERSTANDING
According to (Grimm et al., 2007; Staab and Studer,
2009), an ontology—from the philosophical point of
view—is described as studying the science of being
and existence. Ontologies must be capable of
demonstrating the structure of the reality of a
thing/phenomenon. They check multiple attributes,
particularities and properties that belong to a
thing/phenomenon because of its natural and
structural existence. An ontology—from another
perspective and through the lenses of information
and computer sciences—is described as an explicit
and formal specification of a shared
conceptualisation in a domain of interest. However,
in my opinion, there could be very strong
relationship between these two descriptions of
ontologies. In fact, ontologies in information
sciences attempt to mirror the things’/phenomena’s
structures in virtual and artificial systems. The
ontological descriptions in information sciences
tackle to provide appropriate logical and formal
descriptions of a phenomenon [and of its structure]
considering various concepts relevant for that
phenomenon. From this perspective, an ontology can
be schemed and demonstrated by semantic networks
and semantic representations. A semantic network is
a graph whose nodes represent concepts (e.g., unary
predicates) and whose arcs represent relations (e.g.,
binary/n-ary predicates) between the concepts.
Accordingly, semantic networks provide structural
representations of a thing/phenomenon. In Figure 1 I
have designed a semantic network as an ontology for
‘concept understanding’. This hierarchical semantic
representation, (1) specifies the conceptual
A Formal Semantics for Concept Understanding Relying on Description Logics
49
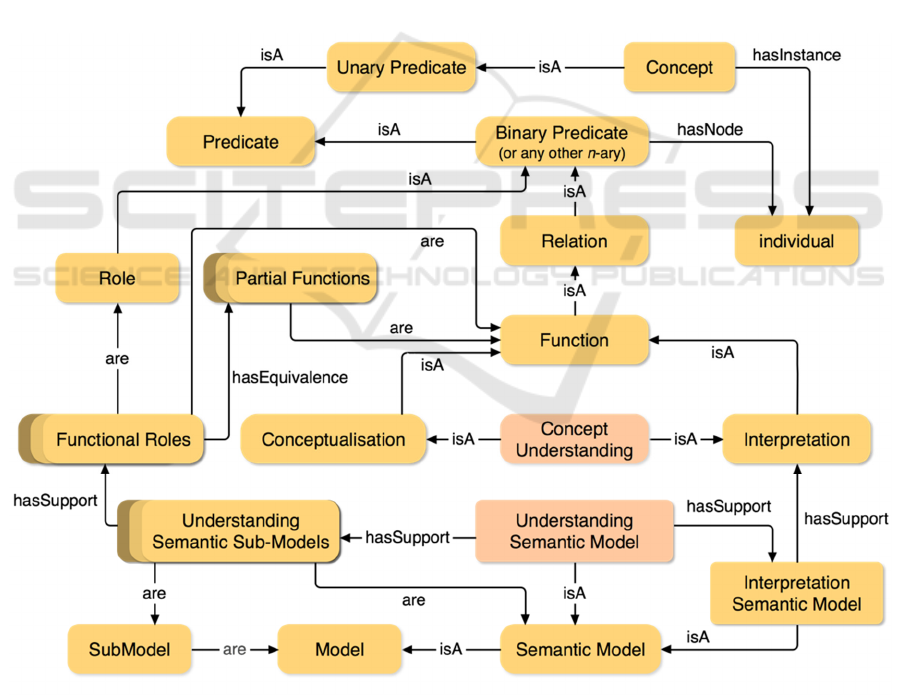
relationships between the most important ingredients
of this research, (2) demonstrates the logical
representation of concept understanding. It shows
how the proposed model attempts to represent
concept understanding. This semantic representation
can be interpreted as a specification of the shared
conceptualisation of concept understanding within
terminological systems. The proposed ontology can
be reformulated and formalised in ALC in the form
of a collection of fundamental terminologies as
following:
A Formal Ontology for Concept Understanding.
{
UnaryPredicate ⊑ Predicate, BinaryPredicate ⊑
Predicate, Concept ⊑ UnaryPredicate, Concept ⊑
∃hasInstance.Individual, BinaryPredicate ⊑
(∃hasNode.Individual ⊓ ∃hasNode.Individual), Role
⊑ BinaryPredicate, Relation ⊑ BinaryPredicate,
Function ⊑ Relation , Interpretation ⊑ Function,
Conceptualisation ⊑ Function, ConceptUnderstanding
⊑ Interpretation, ConceptUnderstanding ⊑
Conceptualisation, PartialFunction ⊑ Function,
FunctionalRole ⊑ Role, FunctionalRole ⊑
hasEquivalence.PartialFunction, FunctionalRole ⊑
Function, SubModel ⊑ Model, SemanticModel ⊑
Model, InterpretationSemanticModel ⊑
SemanticModel, UnderstandingSemanticModel ⊑
SemanticModel, UnderstandingSemanticSubModel ⊑
SubModel, UnderstandingSemanticSubModel ⊑
SemanticModel, InterpretationSemanticModel ⊑
∃hasSupport.Interpretation,
UnderstandingSemanticModel ⊑
∃hasSupport.InterpretationSemanticModel,
UnderstandingSemanticModel ⊑
∃hasSupport.UnderstandingSemanticSubModel,
UnderstandingSemanticSubModel ⊑
∃hasSupport.FunctionalRole
}
Figure 1: An Ontology for Concept Understanding.
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
50

5 CONCLUSIONS
The readers of this article may ask “if the term
‘understanding’ in this research is related to the real
human beings, or if this research’s domain is only
information and computer sciences?” Actually,
that’s why I have employed Description Logics.
Under a plethora of names (among them
terminological systems and Concept Languages),
Description Logics (DLs) attempt to provide
descriptive knowledge representation formalisms
based on formal semantics to establish common
[conceptual and logical] grounds and
interrelationships between human beings and
machines. Description Logics supported me in
revealing some hidden conceptual assumptions that
could support me in having a better understanding of
‘concept understanding’. DLs—by considering
concepts as unary predicates and by applying
terminological interpretations over them—have
proposed a realisable logical description for
explaining the humans’ concept understanding. The
central contribution of the article has been providing
a formal semantics for logical analysis of concept
understanding. According to the logical analysis, a
background for terminological representation of
concept understanding has been expressed.
Consequently, a semantic representation [as an
ontology and a specification of the shared
conceptualisation of ‘concept understanding’] has
been designed and formalised.
REFERENCES
Franz Baader, Diego Calvanese, Deborah McGuinness,
Daniele Nardi, and Peter Patel-Schneider. 2010. The
Description Logic Handbook: Theory, Implementation
and Applications. Cambridge University Press.
Badie, Farshad. 2016a. Concept Representation Analysis
in the Context of Human-Machine Interactions.
Proceedings of the 14th International Conference on
e-Society. International Association for Development
of the Information Society. Portugal.
Badie, Farshad. 2016b. Towards Concept Understanding
relying on Conceptualisation in Constructivist
Learning, Proceedings of the 13th international
conference on Cognition and Exploratory Learning in
Digital Age. International Association for
Development of the Information Society. Germany.
L.W. Barsalou. 1999. Perceptual Symbol Systems. The
Behavioural and BrainSciences. Cambridge University
Press.
John B. Biggs, Kevin F. Collis. 2014. Evaluating the
Quality of Learning: The SOLO Taxonomy (Structure
of the Observed Learning Outcome). Academic Press.
Blackburn, Simon. 2016. The Oxford Dictionary of
Philosophy. Oxford University Press, Web.
G. J. Chaitin. 1987. Algorithmic Information Theory.
Cambridge University Press.
John Davies, Dieter Fensel, Frank van Harmelen. 2003.
Towards the Semantic Web’, Ontology-Driven
Knowledge Management. Wiley Online Publications.
di Pellegrino, G., Fadiga, L., Fogassi, L., Gallese, V. and
Rizzolatti, G. 1992. Understanding Motor Events: A
Neurophysiological Study, Exp Brain Res, 91, 176-
180.
Heinz von Foerster. 2003. Understanding Understanding,
Essays on Cybernetics and Cognition. Springer-
Verlag-New York.
Peter M. D. Gray, Krishna G. Kulkarni, and Norman W.
Paton. 1992. Object-Oriented Databases - A Semantic
Data Model Approach. Prentice Hall International
Series in Computer Science. Prentice Hall.
Stephan Grimm, Pascal Hitzler, and Andreas Abecker.
2007. Knowledge Representation and Ontologies.
Semantic Web Services. Springer. 51—105.
Honderich, T. 2005. The Oxford Companion to
Philosophy. Oxford University Press.
Ray Jackendoff. 1990. Semantic Structures. MIT Press.
Cambridge, MA.
Walter Kintsch, David Welsch, Franz Schmalhofer and
Susan Zimny. 1990. Sentence Memory: A Theoretical
Analysis. Journal of Memory and Language. Elsevier.
D. MacKay. 2003. Information Theory, Inference and
Learning Algorithms. Cambridge University Press.
Markus F. Peschl, Alexander Riegler. 1999. Does
Representation Need Reality? Rethinking
Epistemological Issues in the Light of Recent
Developments and Concepts in Cognitive Science.
Understanding Representation in the Cognitive
Sciences. Springer US. pp 9-17.
P. Resnik. 1999. Semantic Similarity in a Taxonomy: An
information-based measure and its application to
problems of ambiguity in natural language. Journal of
Artificial Intelligence Research, 95–130.
Sebastian Rudolph. 2011. Foundations of Description
Logics. Reasoning Web. Springer. volume 6848 of
LNCS.
Manfred Schmidt-Schauss and Gert Smolka. 1991.
Attributive Concept Descriptions with Complements.
Artificial Intelligence. Elsevier.
J. A. Simpson and E. S. C. Weiner. 1989. The Oxford
English Dictionary. Oxford University Press.
Steffen Staab and Rudi Studer. 2009. Handbook on
Ontologies. Springer Publishing Company.
Incorporated, 2nd edition.
Sebo Uithol, Iris van Rooij, Harold Bekkering and Pim
Haselager. 2011. Understanding Motor Resonance:
Journal of Social Neuroscience. Routledge. 6:4, 388-
397.
A Formal Semantics for Concept Understanding Relying on Description Logics
51

Sebo Uithol, Markus Paulus. 2014. What do infants
understand of others’ action? A theoretical account of
early social cognition. Psychological Research.
Volume 78. Issue 5. pp 609-622
Webb, J.. 2009. Understanding Representation. SAGE
Publications.
Zwaan, R. A. and Taylor, L. J.. 2006. Seeing, Acting,
Understanding: Motor Resonance in Language
Comprehension. Journal of Experimental Psychology:
General 135 (1). 1--11 .
ICAART 2017 - 9th International Conference on Agents and Artificial Intelligence
52
